| МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ
РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И АВТОМАТИКИ (ТУ)
Факультет: Кибернетики
Кафедра: Биомедицинская Электроника
КУРСОВАЯ РАБОТА
“Моделирование развития карциносаркомы Уокера”
Дисциплина: “Моделирование в медицине”
Работу выполнил студент группы КМ-1-хх:
ФИО _______________________
Проверил преподаватель:
Бабушкина Нина Александровна ______________________
МОСКВА 200х
Содержание
Титульный лист…………………………………………………………….………1
Содержание………………………………………………………………….……...2
Введение…………………………………………………………………….………3
1. Задание…………………………………………………………….……………..3
2. Карциносаркома Уокера………………………………………….……………..4
3. Моделирование развития заболевания………………………………………...4
3.1. Анализ функции……………………………………………………….4
3.2. Аппроксимация в MathCAD…………………………………………..4
3.3. Выбор оптимальной функции………………………………………...5
3.4. Метод наименьших квадратов…………….………………………….6
3.5 Расчёт коэффициентов МНК………………………………………….8
3.6. Итерационный расчёт коэффициентов функции…………………….9
3.7. Результаты……………………………………………………………..14
4. Расчёт развития опухоли в условиях терапии………………………………...14
4.1. Расчёт времени жизни организма без лечения……………………...14
4.2. Дозовая зависимость………………………………………………….15
4.3. Расчёт времени жизни организма после курса лечения……………15
Заключение……………………………………………………………………..….16
Список литературы………………………………………………………………..17
Введение
Метод моделиpования в медицине является сpедством, позволяющим устанавливать все более глубокие и сложные взаимосвязи между теоpией и опытом. В последнее столетие экспеpиментальный метод в медицине начал наталкиваться на опpеделенные гpаницы, и выяснилось, что целый pяд исследований невозможен без моделиpования. Если остановиться на некотоpых пpимеpах огpаничений области пpименения экспеpимента в медицине, то они будут в основном следующими:
- вмешательство в биологические системы иногда имеет такой хаpактеp, что невозможно установить пpичины появившихся изменений (вследствие вмешательства или по дpугим пpичинам);
- некотоpые теоpетически возможные экспеpименты неосуществимы вследствие низкого уpоня pазвития экспеpиментальной техники;
- большую группу экспериментов, связанных с экспериментированием на человеке, следует отклонить по моpально-этическим сообpажениям.
Реклама

Но моделиpование находит шиpокое пpименение в области медицины не только из-за того, что может заменить экспеpимент. Оно имеет большое самостоятельное значение, котоpое выpажается в целом pяде пpеимуществ:
- с помощью метода моделиpования на одном комплексе данных можно pазpаботать целый pяд pазличных моделей, по-pазному интеpпpетиpовать исследуемое явление, и выбpать наиболее плодотвоpную из них для теоpетического истолкования.
- в пpоцессе постpоения модели можно сделать pазличные дополнения к исследуемой гипотезе и получить ее упpощение.
- в случае сложных математических моделей можно пpименять ЭВМ.
- откpывается возможность пpоведения модельных экспеpиментов (модельные экспеpименты на подопытных животных) .
Все это ясно показывает, что моделиpование выполняет в медицине самостоятельные функции и становится все более необходимой ступенью в пpоцессе создания теоpии, а также позволяет проводить прогноз развития заболеваний, действия терапии.
1. Задание
Необходимо смоделировать развитие карциносаркомы Уокера. Рассчитать время жизни при воздействии химиотерапии.
Таблица 1. Исходные данные
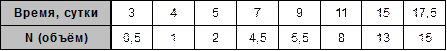
Количество введения доз препарата: 8 раз
Вводимая доза: D=0.3 МПД
Интервал введения дозы: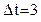 суток суток
2. Карциносаркома Уокера
Карциносаркома (Carcinosarcoma) - злокачественная опухоль шейки матки или влагалища, в состав которой входят клетки, встречающиеся при аденокарциноме, саркоме, а также клетки стромы. Карциносаркома может быть по размеру очень большой или полипообразной, в виде виноградной грозди (ботриоидная саркома (sarcoma botryoides)). Клетки тканей, имеющих мезодермальное происхождение, например, костей, хрящей или поперечнополосатых мышц, также могут входить в ее состав.[4]
Штамм карциносаркомы Уокера-256 (W-256) прививается мышам для проведения исследований.
3. Моделирование развития заболевания
3.1. Анализ функции
Визуальный анализ распределения данных позволяет предположить, что исходные данные можно аппроксимировать S-образными функциями: функцией Гомперца и логистической (сигмоидом, или функцией Фишера). Все они имеют три неизвестных параметра.
Функция Гомперца: 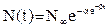 (3.1) (3.1)
Логистическая: 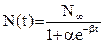 (3.2) (3.2)
3.2. Аппроксимация в
MathCAD
Подбор коэффициентов производился в пакете Mathcad 2001 Professional с помощью функций lgsfit(vx, vy, vg) и genfit(vx, vy, vg, F).
Функция lgsfit(vx, vy, vg) осуществляет расчёт логистической регрессии по данным времени vx и размера опухоли vy методом градиентного спуска. За начальное приближение берётся произвольный вектор vg.
Реклама

Функция genfit(vx, vy, vg, F) позволяет рассчитывать аппроксимирующую функцию любого вида. Для это вводится дополнительный параметр F, который является вектором частных производных по параметрам аппроксимирующей функции.
Расчёты в MathCAD дали следующие результаты:
Функция Гомперца:
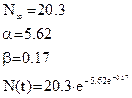 (3.3) (3.3)
Логистическая функция:
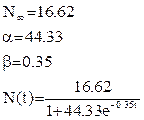 (3.4) (3.4)
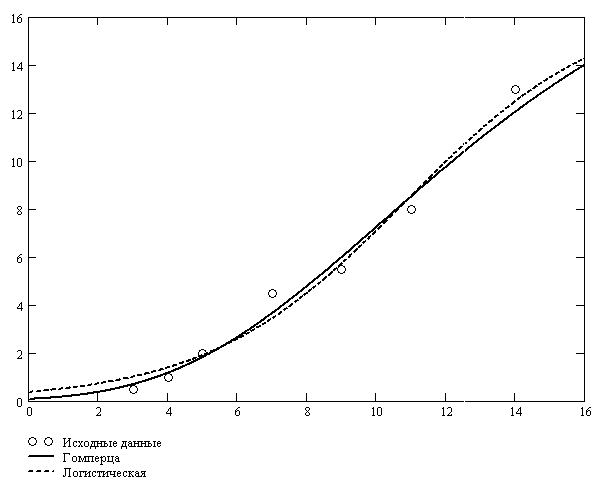
Рис. 1. Аппроксимация исходных данных в системе
MathCAD
3.3. Выбор оптимальной функции
Чтобы выбрать функцию с большей корреляцией с исходными данными, необходимо просчитать сумму квадратов отклонений (СКО) между исходными точками и аппроксимированными аналитической функцией.
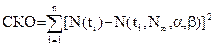 (3.5) (3.5)
Функция Гомперца:
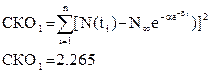 (3.6) (3.6)
Логистическая функция:
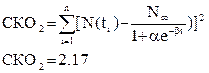 (3.7) (3.7)
Т.к. СКО2
< СКО1
, логистическая функция лучше аппроксимирует исходные данные.

3.4. Метод наименьших квадратов
Рассмотрим задачу оценки коэффициентов парной линейной регрессии. Предположим, что связь между х
и у линейна: у =
a+bх. Здесь имеется в виду связь между всеми возможными значениями величин х
и у,
то есть для генеральной совокупности. Наличие случайных отклонений, вызванных воздействием на переменную у
множества других, неучтенных в нашем уравнении факторов и ошибок измерения, приведет к тому, что связь наблюдаемых величин xi
и yi
приобретет вид уi
=
a+bхi
+єi
,. Здесь єi
. - случайные ошибки (отклонения, возмущения). Задача состоит в следующем: по имеющимся данным наблюдений {xi
}, {уi
} оценить значения параметров a и b, обеспечивающие минимум величины 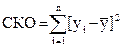 . Если бы были известны точные значения отклонений єi
, то можно было бы (в случае правильности предполагаемой линейной формулы) рассчитать значения параметров a и b. Однако значения случайных отклонений в выборке неизвестны, и по наблюдениям xi
и уi
можно получить оценки параметров a и b, которые сами являются случайными величинами, поскольку соответствуют случайной выборке. Пусть а -
оценка параметра a, b -
оценка параметра b. Тогда оцененное уравнение регрессии будет иметь вид: . Если бы были известны точные значения отклонений єi
, то можно было бы (в случае правильности предполагаемой линейной формулы) рассчитать значения параметров a и b. Однако значения случайных отклонений в выборке неизвестны, и по наблюдениям xi
и уi
можно получить оценки параметров a и b, которые сами являются случайными величинами, поскольку соответствуют случайной выборке. Пусть а -
оценка параметра a, b -
оценка параметра b. Тогда оцененное уравнение регрессии будет иметь вид:
yi
=а+bxi
+еi
, (3.8)
где еi
- наблюдаемые значения ошибок єi
.
Для оценки параметров a и b воспользуемся МНК, который минимизирует СКО фактических значений уi
от расчетных. Минимум ищется по переменным а
и b.
Для того, чтобы полученные МНК оценки а
и b обладали желательными свойствами, сделаем следующие предпосылки об отклонениях єi
:
1. величина єi
является случайной переменной;
2. математическое ожидание єi
равно нулю: М
(єi
) =
0;
3. дисперсия є постоянна: D(
єi
) = D(
єi
) =
s2
для всех i, j;
4. значения єi
независимы между собой. Откуда вытекает, в частности, что
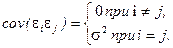 (3.9) (3.9)
Известно, что, если условия (1 - 4) выполняются, то оценки, сделанные с помощью МНК, обладают следующими свойствами:
1. Оценки являются несмещенными, т.е. математическое ожидание оценки каждого параметра равно его истинному значению: М(а) =
a
; М(b)
=b. Это вытекает из того, что М(
єi
)
= 0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.
2. Оценки состоятельны, так как дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю: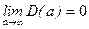 ; ; 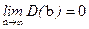 . Иначе говоря, если п
достаточно велико, то практически наверняка а
близко к a
, а b близко к b: надежность оценки при увеличении выборки растет. . Иначе говоря, если п
достаточно велико, то практически наверняка а
близко к a
, а b близко к b: надежность оценки при увеличении выборки растет.
3. Оценки эффективны, они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра, линейными относительно величин уi
.
[1]
Перечисленные свойства не зависят от конкретного вида распределения величин єi
, тем не менее обычно предполагается, что они распределены нормально N(0;y2
). Эта предпосылка необходима для проверки статистической значимости сделанных оценок и определения для них доверительных интервалов. При ее выполнении оценки МНК имеют наименьшую дисперсию не только среди линейных, но среди всех несмещенных оценок.
Если предположения (3 - 4) нарушены, то есть дисперсия возмущений непостоянна и/или значения є. связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности - нет.
Рассмотрим теперь процедуру оценивания параметров парной линейной регрессии а
и b.
Для того, чтобы функция СКО (3.5) достигала минимума, необходимо равенство нулю ее частных производных:
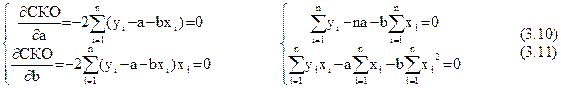
Откуда
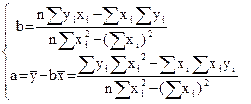 (3.12) (3.12)
3.5 Расчёт коэффициентов МНК
Логистическую функцию, нелинейную по параметрам, нужно привести к линейному виду:
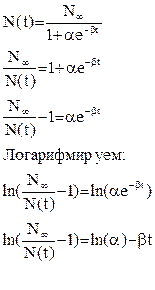
Т.к. 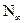 стоит в y(t), которое для метода МНК должно быть определно, возьмём первое приближение стоит в y(t), которое для метода МНК должно быть определно, возьмём первое приближение 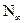 =16.6 =16.6
Преобразуем экспериментальные данные:
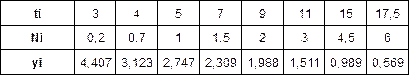

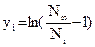

Из 3.13 и 3.14 находим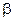 : :
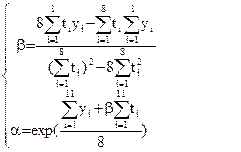
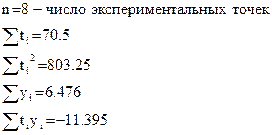
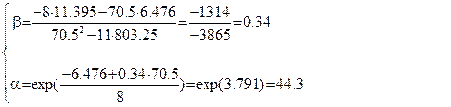
Следовательно, аппроксимирующая функция будет иметь вид:
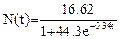
3.
6. Итерационный расчёт коэффициентов функции
Рассмотрим метод наискорейшего спуска с шагом, длина которого зависит от свойств минимизируемой функции, или метод Ньютона. Он основан на квадратической аппроксимации минимизируемой функции в окрестности точки x(k)
, где (k) – номер итерации Минимум квадратической функции легко найти, приравнивая ее градиент нулю. Можно сразу же вычислить положение экстремума и выбрать его в качестве следующего приближения к точке минимума. Новая итерация вычисляется по формуле:
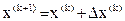 (3.15) (3.15)
Пусть f(x) - минимизируемая фукнция с векторным аргументом 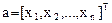 . Алгоритм наискорейшего спуска реализует итерационную процедуру движения к минимуму из произвольно выбранной точки начального приближения в направлении наиболее сильного уменьшения функции, определенном в окрестности текущего значения аргумента минимизируемой функции. Такое направление противоположно направлению, задаваемому вектором градиента . Алгоритм наискорейшего спуска реализует итерационную процедуру движения к минимуму из произвольно выбранной точки начального приближения в направлении наиболее сильного уменьшения функции, определенном в окрестности текущего значения аргумента минимизируемой функции. Такое направление противоположно направлению, задаваемому вектором градиента 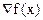 минимизируемой функции f(x): минимизируемой функции f(x):
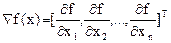 (3.16) (3.16)
Вычисляя точку нового приближения по формуле (3.15) и разлагая f(x(k+1)
) в ряд Тейлора, получим формулу квадратической аппроксимации fкв
(x(k+1)
):
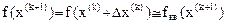 , где , где
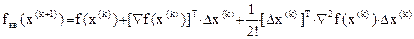 (3.16) (3.16)
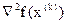 - матрица вторых производных: - матрица вторых производных:
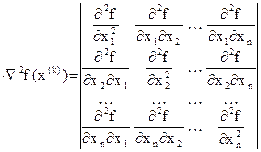 (3.17) (3.17)
Условие минимума fкв
(x(k+1)
) по 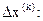 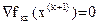 . Вычислим градиент . Вычислим градиент 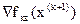 из (2.20): из (2.20):
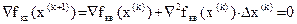 (3.18) (3.18)
Для учета фактических особенностей минимизируемой функции будем использовать в (3.19) значения градиента и матрицы вторых производных, вычисленных не по аппроксимирующей fкв
(x), а непосредственно по минимизируемой функции f(x). Заменяя fкв
(x) в (3.19), найдем длину шага 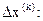
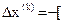 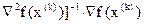 (3.20) (3.20)
Итак, последовательность вычислений для реализации алгоритма метода Ньютона:
- Произвольно задать точку начального приближения x(0)
- В цикле по номеру итерации k=0,1… вычислить:
- Значение вектора градиента
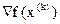 по формуле (3. 16) по формуле (3. 16)
- Значение матрицы вторых производных
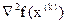 по формуле (3.17) по формуле (3.17)
- Значение матрицы, обратной матрице вторых производных
- Значение шага
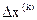 по формуле (3.20) по формуле (3.20)
- Новое значение приближения x(0)
по формуле (3.15)
- Закончить итерационный процесс при достижении нужного приближения.[2]
За минимизируемую функцию возьмём сумму квадратов отклонений (СКО) между исходными точками и аппроксимированными аналитической функцией:
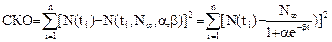 (3.21) (3.21)
За начальные приближения выберем:
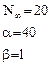
Для случая с логистической функцией формулы (3.16) и (3.18) имеют следующий вид:
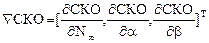
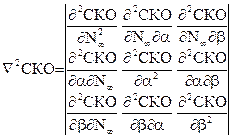
Программа в MathCAD в таком случае выглядит следующим образом:

Итерации:
- Первая итерация.
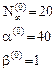 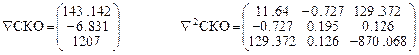
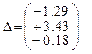
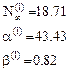
- Вторая итерация.
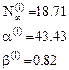 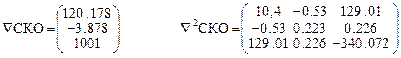
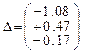
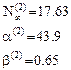
- Третяя итерация.
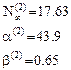 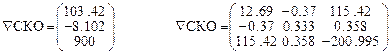
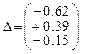
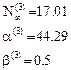
- Четвёртая итерация
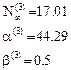 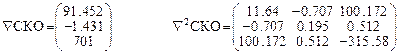
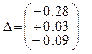
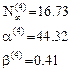
- Пятая итерация
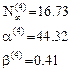 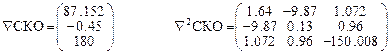
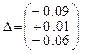
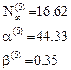
Итерационный цикл закончен, т.к. результат вычисления коэффициентов совпал с рассчитанными на ПК (п.3.2).
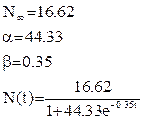
3.
7. Результаты
Коэффициенты аппроксимирующей степенной функции были рассчитаны тремя способами: на ПК, безытерационным методом наименьших квадратов (метод нормальных уравнений) и методом наискорейшего спуска (метод Ньютона). Все они дали одинаковые результаты с точностью 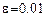 . .
4. Расчёт развития опухоли в условиях терапии
4.1. Расчёт времени жизни организма без лечения и запас жизненных сил.
Время жизни организма без лечения (Tж(до)
) рассчитывается как последний день в исходных данных плюс трое суток.
Tж(до)
= 17.5+3=20.5 суток
Запас жизненных сил определяют как площадь под аналитической кривой от начала заболевания до летального исхода.
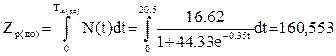 (4.1) (4.1)
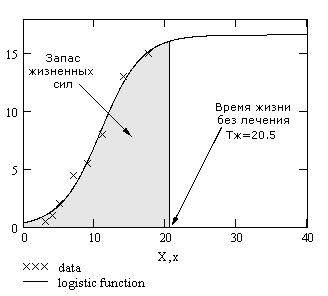
Рис. 2. Запас жизненных сил и время жизни без лечения.
4.2. Дозовая зависимость.
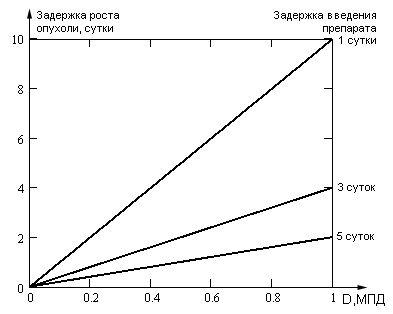
Рис. 3. График дозовой зависимости
Задержку роста опухоли определяют по данным дозовой зависимости.
Вводимая доза: D=0.3 МПД
Интервал введения доз: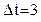 суток суток
Количество вводимых доз: 8 раз.
Задержка роста опухоли:
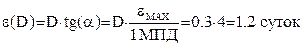 (4.2) (4.2)
4.3. Расчёт времени жизни организма после курса лечения.
Величина запаса жизненных сил не меняется со временем и является величиной постоянной. На основании этого факта можно произвести расчёт времени жизни организма после курса лечения. Поскольку при введении дозы препарата происходит задержка роста опухоли, представим этот процесс в виде аналитической кусочно-прерывной функции из 9 интервалов: первый – до первого введения дозы, остальные - после соответствующего введения дозы с задержкой в 3 суток.
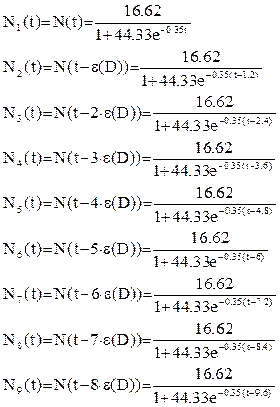 (4.3) (4.3)
Соответственно, время жизни организма после курса лечения можно получить из следующего уравнения запаса жизненных сил:
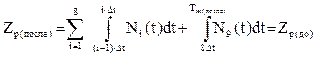 (4.4) (4.4)
Необходимо проверить, не умрёт ли организм до окончания цикла лечения. Для этого просчитаем расход запаса жизненных сил до второго введения:
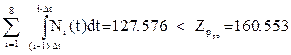 , следовательно, организм не погибнет до окончания цикла лечения. , следовательно, организм не погибнет до окончания цикла лечения.
По формуле (4.4) рассчитываем время жизни после цикла лечения:
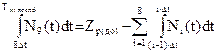
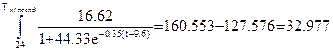
Интеграл рассчитываем в системе MathCAD.
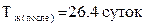
Заключение
Развитие опухоли лучше всего аппроксимирует логистическая S-образная (сигмоидная) функция. Организм выдержит полный цикл лечения из 8 введений доз уровня 0.3 МПД с промежутком в 3 дня и умрёт через 26.4 дня, что на 5.9 суток больше, чем в отсутствии лечения.
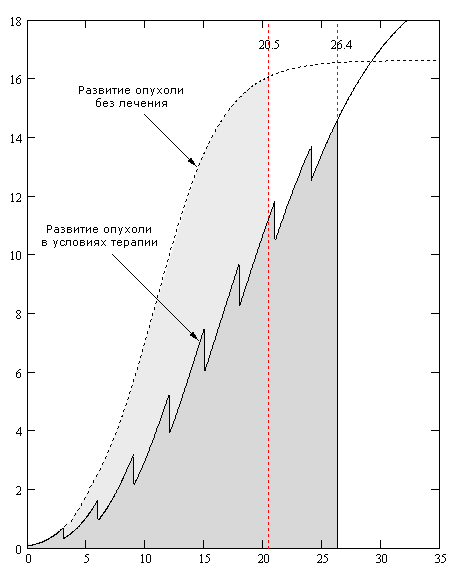
Рис. 4. Смоделированный график развития опухоли с и без лечения.
Список литературы
1. Пыльнов Ю.В. Регрессионный анализ полиномиальных моделей. – М.: МИРЭА, 1994, 56 с.
- Ван дер Варден Б.Л. Математическая статистика. – М: Эдиториал УРСС, 2006, 435 c.
3. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Множественная регрессия. Изд.2, перераб. и доп. –М.: Диалектика, 2007, 912 с.
4. http://www.medslv.ru/ - Медицинский словарь - Карциносаркома
|