| БАЛТИЙСКИЙ ВОЕННО-МОРСКОЙ ИНСТИТУТ
КАФЕДРА МАТЕМАТИКИ
КУРСОВАЯ РАБОТА
Тема: «Элементы математической статистики
и корреляционного анализа»
Руководитель:
кандидат физико-математических наук
доцент Спектор В. Е.
Выполнил:
ст 2 ст Смоколов Т. В.
422я учебная группа
Вариант 18
Содержание
| Введение ……………………………………………………………………….
|
Стр.3
|
| |
|
| Глава I «Обработка данных наблюдений и проверка гипотез» …………….
|
Стр.4
|
| |
|
| §1. Статистическое распределение выборки ………………………………
|
Стр.5
|
| §2. Расчет сводных характеристик выборки……………………………….
|
Стр.6
|
| §3. Расчет интервальных оценок генеральных параметров ………………
|
Стр.7
|
| §4. Проверка гипотезы о нормальном распределении
|
|
| генеральной совокупности по критерию Пирсона ………………………….
|
Стр.8
|
| §5. Построение гистограммы выборки и теоретической
|
|
| нормальной кривой ……………………………………………………………
|
Стр.9
|
| |
|
| Глава II «Элементы корреляционного анализа» …………………………….
|
Стр. 11
|
| |
|
| §1. Корреляционная таблица и корреляционное поле ………………………
|
Стр. 12
|
| §2. Нахождение выборочного коэффициента корреляции …………………
|
Стр. 12
|
| §3. Нахождение доверительного интервала для
|
|
| генерального коэффициента корреляции…………………………………….
|
Стр. 16
|
| §4. Нахождение выборочного уравнения прямой
|
|
| регрессии Y на X и построение ее графика ………………………………….
|
Стр. 16
|
| |
|
| Заключение …………………………………………………………………….
|
Стр. 18
|
| |
|
| Список использованной литературы ………………………………………...
|
Стр. 19
|
ВВЕДЕНИЕ
Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные. Невозможно учесть влияние на результат всех причин, поскольку число их очень велико и законы их действий неизвестны. Поэтому Т.В. не ставит перед собой задачу предсказать, произойдет единичное событие или нет, -она просто не в силах это сделать.
По –иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т.е. если речь идет о массовых однородных случайных событий. Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным закономерностям, а именно вероятностным закономерностям. Установлением этих закономерностей и занимается Т.В. Итак, предметом Т.В. является изучение вероятностных закономерностей однородных массовых случайных событий. Знание закономерностей которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать.
Реклама

Методы Т.В. широко применяются в различных отраслях естествознания и техники. В последние годы методы Т.В. все шире и шире проникают в различные области науки и техники, способствуя их прогрессу.
Краткая историческая справка. Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI–XVII вв.).
Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654–1705). Доказанная им теорема, получившая впоследствии название «Закона больших чисел», была первым теоретическим обоснованием накопленных ранее фактов.
Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др.
Новый, наиболее плодотворный период связан с именами П. Л. Чебышева (1821–1894) и его учеников А.А.Маркова (1856–1922) и А.М.Ляпунова (1857–1918). В этот период теория вероятностей становится стройной математической наукой. Ее последующее развитие обязано в первую очередь русским и советским математикам (С. Н. Бернштейн, В. И. Романовский, А. Н. Колмогоров, А. Я. Хинчин, Б. В. Гнеденко, Н. В. Смирнов и др.) В настоящее время ведущая роль в создании новых ветвей теории вероятностей также принадлежит советским математикам.
ГЛАВА I
Обработка данных наблюдений и проверка гипотез
Задание:
В результате независимых измерений получены n
значений ошибки точности настройки РПУ на заданную частоту: х1
, х2
,…хn
. Произвести полный статистический анализ данных выборки и сделать соответствующие выводы.
Значения выборки
| -0,787
|
1,473
|
0,159
|
0,940
|
-0,842
|
| 0,308
|
-1,266
|
0,889
|
-1,100
|
2,199
|
| 1,159
|
0,702
|
0,533
|
-0,536
|
0,926
|
| -0,660
|
1,071
|
1,306
|
1,121
|
0,571
|
| 0,989
|
-0,383
|
-0,256
|
-0,126
|
2,945
|
| -1,019
|
0,167
|
1,183
|
1,506
|
0,881
|
| 0,090
|
-0,348
|
-0,292
|
0,054
|
0,971
|
| -0,709
|
0,192
|
-0,122
|
-1,671
|
1,033
|
| 0,122
|
-1,447
|
0,525
|
0,349
|
-0,511
|
| 0,476
|
0,495
|
-0,326
|
-0,883
|
0,181
|
| -1,487
|
-1,060
|
0,891
|
-0,056
|
-0,486
|
| 0,062
|
-1,441
|
-1614
|
0,759
|
-0,256
|
| 0,251
|
0,495
|
1,654
|
1,443
|
0,065
|
| -0,381
|
-1,060
|
-0,170
|
0,889
|
1,147
|
| 1,531
|
-1,441
|
0,873
|
0,627
|
-0,199
|
| -0,443
|
-0,598
|
0,845
|
-0,435
|
-0,508
|
| 1,409
|
-0,361
|
0,874
|
-1,220
|
-0,124
|
| 1,730
|
-0,079
|
1,485
|
-1,007
|
-0,992
|
| -0,266
|
0,503
|
0,934
|
0,883
|
0,969
|
| -0,592
|
-1,080
|
0,084
|
1,018
|
0,983
|
§1. Статистическое распределение выборки
1. По данным выборки найдем:
а) Размах варьирования: R = xmax
– xmin
,
Реклама

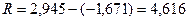
б) Количество интервалов (разрядов):
| k = 5lg n
|
Или
|
k = log2
n+1
|
| k = 5lg 100 = 10
|
k = log2
100+1 = 8
|
k
»
10
.
в) Длину разряда: 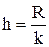
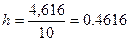
Интервал (-1,671 ; 2,945) расширим до интервала (-1,9 ; 3,1). Сдвиг в каждую стороны при этом не превысит: 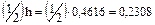 . .
Для нового интервала изменения признака (-1,9;3,1) при k
»
10
длина разряда получается равной 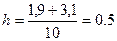
2. Произведем группировку опытных данных и построим интервальный вариационный ряд. Расчет оформим в виде таблицы 1.
Таблица № 1
| Границы
интервалов
|
(-1,9;-1.4]
|
(-1.4;-0.9]
|
(-0.9;-0.4]
|
(-0.4;0.1]
|
(0.1;0.6]
|
(0.6;1.1]
|
(1.1;1.6]
|
(1.6;2.1]
|
(2.1;2.6]
|
(2.6;3.1]
|
| Подсчет
частот
|
|
|
|
|
|
|
|
|
|
|
| Частоты ni
|
6
|
9
|
13
|
19
|
16
|
20
|
13
|
2
|
1
|
1
|
| Относительные
частоты ni
/n
|
6/100
|
9/100
|
13/100
|
19/100
|
16/100
|
20/100
|
13/100
|
2/100
|
1/100
|
1/100
|
| Накопленные
частоты Σni
|
6
|
15
|
28
|
47
|
63
|
83
|
96
|
98
|
99
|
100
|
§2. Расчет сводных характеристик выборки
1. Вычислим моду 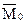 и медиану и медиану 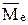 выборочного распределения. выборочного распределения.
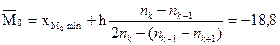
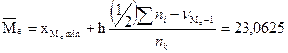
2. По интервальному вариационному ряду, полученному в §1 составить дискретный вариационный ряд в виде таблицы 2, в котором в качестве вариант берём середины разрядов
Таблица № 2
| xi
|
-1.6
|
-1.1
|
-0.6
|
-0.1
|
0.4
|
0.9
|
1.4
|
1.9
|
2.4
|
2.9
|
| n
i
|
6
|
9
|
13
|
19
|
16
|
20
|
13
|
2
|
1
|
1
|
Вычислим выборочную среднюю 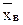 (математическое ожидание) и выборочную дисперсию (математическое ожидание) и выборочную дисперсию 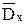 : :
3. Для расчета сводных характеристик выборки по методу произведений составим таблицу 3.
Таблица № 3
| Разряды
|
n
i
|
u
i
|
n
i
u
i
|
n
i
u
i
2
|
n
i
u
i
3
|
n
i
u
i
4
|
(u
i
+
1)
|
(u
i
+
1)4
|
ni
(u
i
+
1)4
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| -1.6
|
6
|
-5
|
-30
|
150
|
-750
|
3750
|
-4
|
256
|
1536
|
| -1.1
|
9
|
-4
|
-36
|
144
|
-576
|
2304
|
-3
|
81
|
729
|
| -0.6
|
13
|
-3
|
-39
|
117
|
-351
|
1053
|
-2
|
16
|
208
|
| -0.1
|
19
|
-2
|
-38
|
76
|
-152
|
304
|
-1
|
1
|
19
|
| 0.4
|
16
|
-1
|
-16
|
16
|
-16
|
16
|
0
|
2
|
0
|
| 0.9
|
20
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
20
|
| 1.4
|
13
|
1
|
13
|
13
|
13
|
13
|
2
|
16
|
208
|
| 1.9
|
2
|
2
|
4
|
8
|
16
|
32
|
3
|
81
|
162
|
| 2.4
|
1
|
3
|
3
|
9
|
27
|
81
|
4
|
256
|
256
|
| 2.9
|
1
|
4
|
4
|
16
|
64
|
256
|
5
|
625
|
625
|
| |
100
|
|
-135
|
549
|
-1725
|
7809
|
|
|
3763
|
Контроль расчетов производим по формуле:
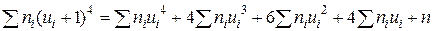
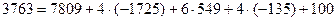
4. Вычислим начальные условные эмпирические моменты:
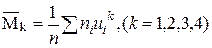
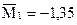 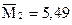 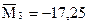 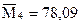
5. Используя начальные моменты 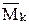 , вычислим центральные моменты: , вычислим центральные моменты:
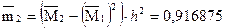
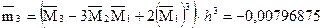
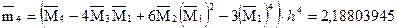
6. Найдем выборочную среднюю (выборочное математическое ожидание):
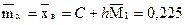 , ,
где С = 0,09
7. Вычислим выборочную дисперсию и исправленную выборочную дисперсию:
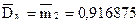 , ,
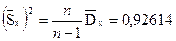
8. Найдем выборочное среднее квадратическое отклонение (с.к.о.) и исправленное выборочное с.к.о.:
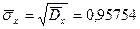
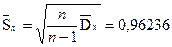 , ,
9. Определим, чему равны выборочная асимметрия и выборочный эксцесс:
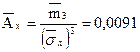
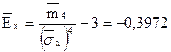
§3. Расчет интервальных оценок генеральных параметров
Построим доверительные интервалы для оценки генерального математического ожидания mx
и генерального с.к.о. σх
. Для этого по заданной доверительной вероятности (надежности) γ из таблицы функции Лапласа найдем значение аргумента tγ
этой функции, для которого Ф(tγ
) = γ.
Используя найденное tγ
, рассчитаем границы доверительного интервала для
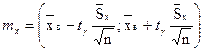
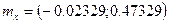
Интервальную оценку генерального с. к. о. определим по одной из формул :
| 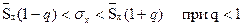
|
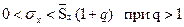
|
| В данном варианте q<1 то 0,77181272<σx
<1,15290728
|
§4. Проверка гипотезы о нормальном распределении
генеральной совокупности по критерию Пирсона
Для того, чтобы при заданном уровне значимости α = 1 – γ проверить гипотезу о нормальном распределении обследуемого признака X генеральной совокупности, заполним таблицу 5.
Таблица №5
| xi
|
ni
|
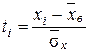
|
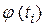
|
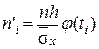
|
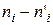
|
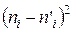
|
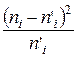
|
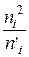
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| -1,6
|
6
|
-1,91
|
0,111
|
5,7961
|
0,20387267
|
0,041564066
|
0,007171
|
6,211043676
|
| -1,1
|
9
|
-1,38
|
0,217
|
11,3312
|
-2,33116784
|
5,434343513
|
0,479593
|
7,148424692
|
| -0,6
|
13
|
-0,86
|
0,332
|
17,3362
|
-4,33616463
|
18,80232367
|
1,084572
|
9,748407658
|
| -0,1
|
19
|
-0,34
|
0,391
|
20,4170
|
-1,41698906
|
2,007858005
|
0,098343
|
17,68135345
|
| 0,4
|
16
|
0,18
|
0,364
|
19,0071
|
-3,00712025
|
9,042772216
|
0,475757
|
13,46863684
|
| 0,9
|
20
|
0,70
|
0,263
|
13,7332
|
6,266833444
|
39,27320141
|
2,859734
|
29,1265673
|
| 1,4
|
73
|
1,23
|
0,144
|
7,5193
|
5,48069968
|
30,03806898
|
3,994796
|
22,47549543
|
| 1,9
|
2
|
1,75
|
0,065
|
3,3941
|
-1,39412862
|
1,9435946
|
0,572634
|
1,178505723
|
| 2,4
|
1
|
2,27
|
0,023
|
1,2010
|
-0,20099936
|
0,040400741
|
0,033639
|
0,832639913
|
| 2,9
|
1
|
2,79
|
0,006
|
0,3133
|
0,68669582
|
0,471551149
|
1,505091
|
3,191786334
|
| |
|
|
|
|
|
|
11,111329
|
111,06286
|
Контроль вычислений производим по формуле:
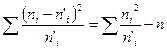
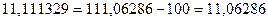
Обозначим сумму элементов восьмого столбца 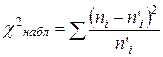 , и для заданного уровня значимости α числа свободы р = k – 3 находим критическую точку , и для заданного уровня значимости α числа свободы р = k – 3 находим критическую точку 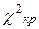 (α; р) (α; р)
ВЫВОД: так как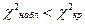 , то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно). , то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).
§5. Построение гистограммы выборки и теоретической
нормальной кривой
1. Для построения гистограммы в выбранной системе координат на оси абсцисс откладываем разряды, а на каждом из разрядов как на основании строим прямоугольник с высотой 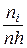 , составляя таблицу 6. , составляя таблицу 6.
Таблица №6
| Разряды
|
-1.6
|
-1.1
|
-0.6
|
-0.1
|
0.4
|
0.9
|
1.4
|
1.9
|
2.4
|
2.9
|
| 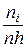
|
0,12
|
0,18
|
0,26
|
0,38
|
0,32
|
0,40
|
0,26
|
0,04
|
0,02
|
0,06
|
В последней строке результаты вычислений округлим до 0,01.
На этом же графике строим гипотетическую (предположительную) теоретическую нормальную кривую. Для этого берем середины разрядов хi
и выравнивающие частоты ni
из таблицы 5. Эти данные заносим в таблицу 7.
3.Таблица №7
| xi
|
-1.6
|
-1.1
|
-0.6
|
-0.1
|
0.4
|
0.9
|
1.4
|
1.9
|
2.4
|
2.9
|
| 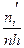
|
0,12
|
0,23
|
0,35
|
0,41
|
0,38
|
0,27
|
0,15
|
0,07
|
0,024
|
0,006
|
наносим точки с координатами 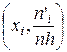 и соединяем их плавной линией, получая искомую кривую. и соединяем их плавной линией, получая искомую кривую.
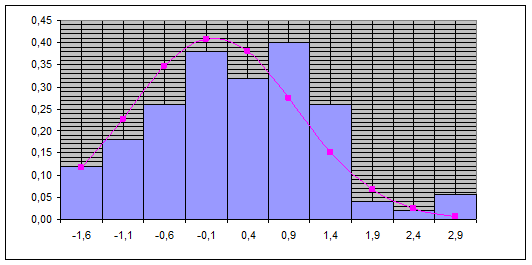
ВЫВОД: В данной части курсовой работы проверена гипотеза Пирсона, ее нет оснований отвергнуть, другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).
ГЛАВА
I
I
Элементы корреляционного анализа
ВАРИАНТ №
18
Дано
: Результаты исследований зависимости между случайными величинами X и Y
представлены в виде таблицы 8:
Таблица №8
| Y
|
X
|
| 30
|
35
|
40
|
45
|
50
|
55
|
ny
|
| 45
|
4
|
2
|
|
|
|
|
6
|
| 55
|
|
5
|
3
|
|
|
|
8
|
| 65
|
|
|
5
|
45
|
5
|
|
55
|
| 75
|
|
|
7
|
8
|
2
|
|
17
|
| 85
|
|
|
|
4
|
3
|
7
|
14
|
| nx
|
4
|
7
|
15
|
57
|
10
|
7
|
|
Произвести корреляционный анализ зависимости Y от X, для чего:
1) построить корреляционное поле;
2) найти выборочный коэффициент корреляции 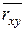 ; ;
3) получить доверительный интервал rxy
для с надежностью γ;
4) найти выборочное уравнение прямой регрессии Y на X;
5) в выбранной системе координат построить точки (xi
,
yi
) и выборочное уравнение регрессии Y на X.
§1. Корреляционная таблица и корреляционное поле
Представим данные корреляционной таблицы в виде корреляционного поля. Для этого в выбранной системе координат изобразим точки (xi
,
yj
) и рядом с каждой точкой укажем, если это позволит масштаб, соответствующую частоту nxy
. По расположению точек можно сделать предположение о наличии (или отсутствии) линейной корреляционной зависимости между обследуемыми признаками X и Y.
Для данных таблицы 8 корреляционное поле имеет вид:
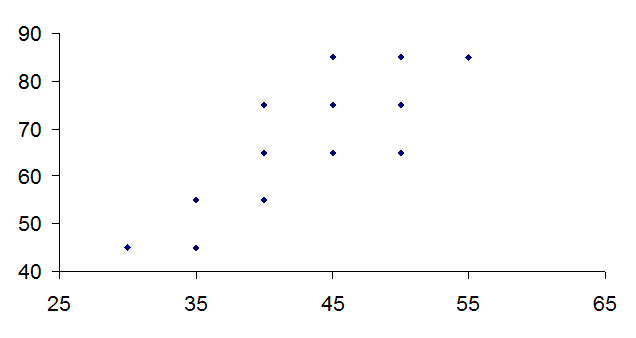
Расположение точек говорит о наличии положительной корреляции между признаками X и Y.
§2. Нахождение выборочного коэффициента корреляции
Вычисления можно значительно упростить, если перейти от истинных вариант xi
, yj
к условным ui
, vj
соответственно, а именно:
| 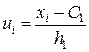
|
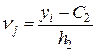
|
| C1
= 45
h1
= 5
u
1
= -3
u
2
= -2
u
3
= -1
u
4
= 0
u
5
= 1
u
6
= 2
|
C2
= 65
h2
= 10
v1
= -1
v2
= 0
v3
= 1
v4
= 2
|
Формула для вычисления эмпирического коэффициента корреляции в условных вариантах имеет вид:
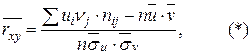
Для нахождения 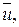 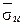 составим расчетную таблицу 9. составим расчетную таблицу 9.
Таблица №9
| xi
|
ui
|
ni
|
ni
ui
|
ni
ui
2
|
(ui
+ 1)
|
(ui
+ 1)2
|
ni
(ui
+ 1)2
|
| 30
|
-3
|
4
|
-12
|
36
|
-2
|
4
|
16
|
| 35
|
-2
|
7
|
-14
|
28
|
-1
|
1
|
7
|
| 40
|
-1
|
15
|
-15
|
15
|
0
|
0
|
0
|
| 45
|
0
|
57
|
0
|
0
|
1
|
1
|
57
|
| 50
|
1
|
10
|
10
|
10
|
2
|
4
|
40
|
| 55
|
2
|
7
|
14
|
28
|
3
|
9
|
63
|
| |
|
100
|
-17
|
117
|
|
|
183
|
Контроль
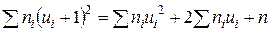 , ,
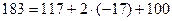
то есть вычисления верны
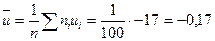
Так как 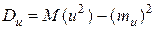 , то , то 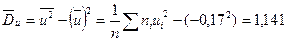
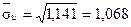
Аналогичные вычисления проводим для v
в таблице 10.
Таблица №10
| yj
|
vj
|
nj
|
nj
vj
|
nj
vj
2
|
(vj
+ 1)
|
(vj
+ 1)2
|
nj
(vj
+ 1)2
|
| 45
|
-2
|
6
|
-12
|
24
|
-1
|
1
|
6
|
| 55
|
-1
|
8
|
-8
|
8
|
0
|
0
|
0
|
| 65
|
0
|
55
|
0
|
0
|
1
|
1
|
55
|
| 75
|
1
|
17
|
17
|
17
|
2
|
4
|
68
|
| 85
|
2
|
4
|
28
|
56
|
3
|
9
|
126
|
| |
|
100
|
25
|
105
|
|
|
255
|
Контроль вычислений производим по формуле:
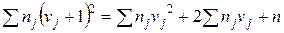
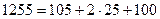
вычисления верны.
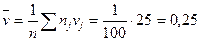
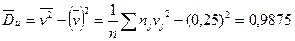
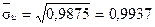
Для вычисления 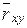 требуется еще найти требуется еще найти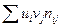 . Для ее нахождения составим корреляционную таблицу 11 в условных вариантах. . Для ее нахождения составим корреляционную таблицу 11 в условных вариантах.
Подставив найденные значения в формулу (*), получим
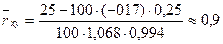
Таблица №11
| ui
vj
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
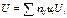
|
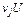
|
| -3
|
|
|
-12
|
|
|
-4
|
|
|
|
|
|
|
|
|
|
|
|
|
-16
|
48
|
| |
4
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -12
|
|
|
-6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -2
|
|
|
|
|
|
-10
|
|
|
-3
|
|
|
|
|
|
|
|
|
|
-13
|
26
|
| |
|
|
|
5
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
-10
|
|
|
-6
|
|
|
|
|
|
|
|
|
|
|
|
| -1
|
|
|
|
|
|
-
|
|
|
-5
|
|
|
0
|
|
|
5
|
|
|
|
0
|
0
|
| |
|
|
|
|
|
|
5
|
|
|
45
|
|
|
5
|
|
|
|
|
| |
|
|
|
|
|
-5
|
|
|
-45
|
|
|
-5
|
|
|
|
|
|
| 0
|
|
|
|
|
|
|
|
|
-7
|
|
|
0
|
|
|
2
|
|
|
0
|
-5
|
0
|
| |
|
|
|
|
|
|
7
|
|
|
8
|
|
|
2
|
|
|
|
|
| |
|
|
|
|
|
0
|
|
|
0
|
|
|
0
|
|
|
|
|
|
| 1
|
|
|
|
|
|
|
|
|
|
|
|
0
|
|
|
3
|
|
|
|
17
|
17
|
| |
|
|
|
|
|
|
|
|
|
4
|
|
|
3
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
4
|
|
|
3
|
|
|
|
|
|
| 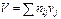
|
-12
|
-16
|
-11
|
-41
|
-2
|
7
|
|
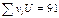
|
| 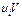
|
36
|
32
|
11
|
0
|
-2
|
14
|
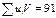
|
контроль
|
§3. Нахождение доверительного интервала
для генерального коэффициента корреляции
Задана надежность γ = 0,99. Доверительный интервал для генерального коэффициента корреляции rxy
имеет вид:
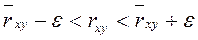
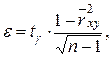 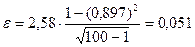
Следовательно с вероятностью 0,99 доверительный интервал имеет вид:
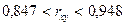
§4. Нахождение выборочного уравнения прямой
регрессии Y на X и построение ее графика
Общий вид уравнения прямой линии регрессии Y на X имеет вид:
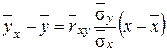
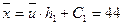
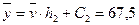
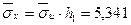
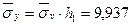
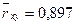
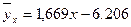
Полученное уравнение регрессии показывает, как в среднем изменяется значение признака Y в зависимости от изменения признака Х.
В выбранной системе координат строим прямую 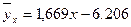 и точки (xi
, yi
) корреляционного поля. и точки (xi
, yi
) корреляционного поля.
Таблица для построения графика
| 30
|
35
|
40
|
45
|
50
|
55
|
| 43,877
|
52,225
|
60,572
|
68,919
|
77,266
|
85,613
|
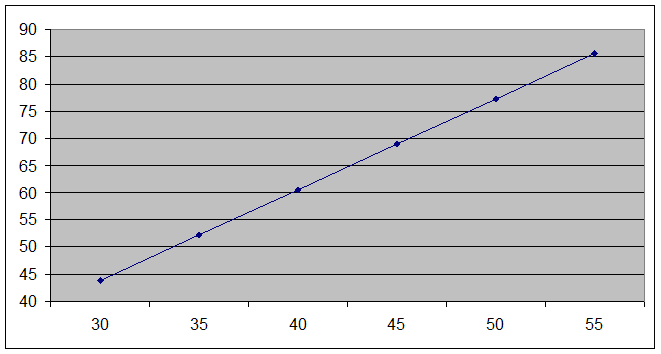
ВЫВОД:. Построив корреляционное поле мы убеждаемся, что расположение точек говорит о наличии положительной корреляции между Х и Y. По расположению точек можно судить о линейной зависимости между Х и Y.
Заключение
В проделанной курсовой работе была предоставлена возможность проверить гипотезу Пирсона, опираясь на полученные результаты я могу утверждать, что эмпирические и теоретические частоты различаются незначительно. Так же был проведен корреляционный анализ, была выявлена сильная линейная зависимость между величинами X и Y
Список использованной литературы
1. Гмурман В.Е. «Теория вероятностей математической статистики» – М.: Высшая школа, 1999 г.
2. «Пособие и методические указания к выполнению курсовой работы» – Калининград: 1998 г.
|