| МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
Кафедра 804 "Теория вероятности и математическая статистика"
КУРСОВАЯ РАБОТА
по курсу
"Математическая статистика"
Выполнил:
студент группы 08-304
Принял:
профессор каф. 804
Кан Ю. С.
2003 г.
Задание 1.
Дан случайный вектор 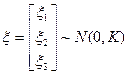 , где , где 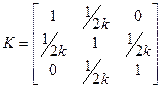 , k
= 15. , k
= 15.
Методом Монте-Карло найти вероятность 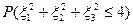 . .
Метод статистических испытаний (метод Монте-Карло) заключается в моделировании требуемой случайной величины с помощью выборки большого объема. При этом вероятность попадания рассматриваемой случайной величины в заданную область Q
определяется, исходя из соотношения:
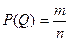 , ,
где n
– объем выборки, m
– количество реализаций случайной величины, попавших в область Q
.
Для того чтобы смоделировать нормальный случайный вектор с ковариационной матрицей K
, задается линейное преобразование, переводящее стандартный нормальный случайный вектор в рассматриваемый случайный вектор с матрицей K
.
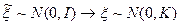
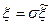
Чтобы найти матрицу преобразования 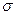 , приводим квадратичную форму , приводим квадратичную форму 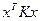 к сумме квадратов: к сумме квадратов:
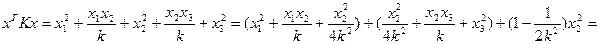
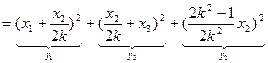
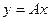 , где , где
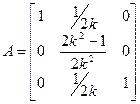 , ,
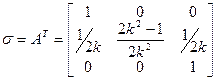 . .
Таким образом, моделируя вектор из трех некоррелированных стандартных нормальных случайных величин, с помощью преобразования 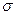 получаем гауссовский вектор с ковариационной матрицей K
. получаем гауссовский вектор с ковариационной матрицей K
.
Вектор моделируется с помощью датчика случайных чисел. Для каждой полученной реализации случайного вектора выполняется проверка на попадание в заданный шар. Итоговая вероятность рассчитывается как отношение количества реализаций, попавших в шар, к объему выборки.
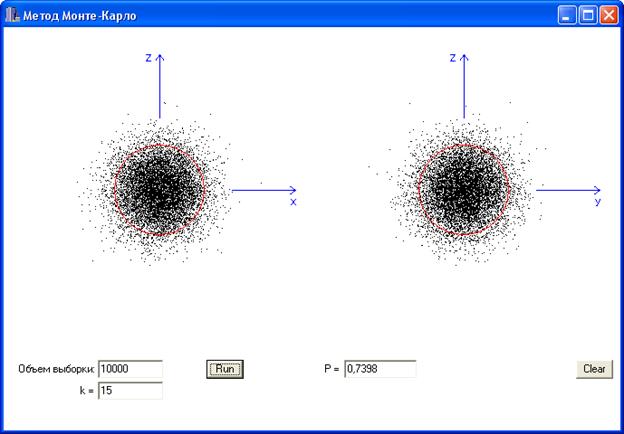
На рис. 1а и 1б показаны результаты статистического испытания при объеме выборки n
= 10000, k = 15 и k = 1.
| 
|
| Рис. 1а (n
= 10000, k
= 15)
|
| 
|
| Рис. 2б (n
= 10000, k
= 1)
|
Задание 2.
Имеются 50 опытов наблюдения X
и Y
:
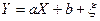 , ,
где 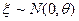 . .
Оценить параметры a
и b
методом наименьших квадратов.
Решение 1:
Для нахождения оценок 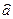 и и 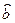 применим метод максимального правдоподобия. применим метод максимального правдоподобия.
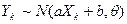 , ,
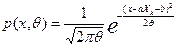
Составляем функцию правдоподобия:
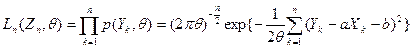 , ,
где n
– объем выборки (n
= 50).
Получаем логарифмическую функцию правдоподобия:
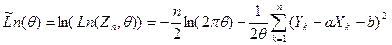 . .
Задача максимизации 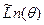 сводится к минимизации суммы квадратов: сводится к минимизации суммы квадратов:
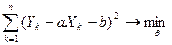
Распишем сумму квадратов:
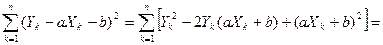
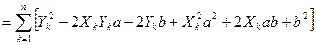 . .
Введем новые обозначения:
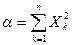
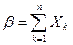
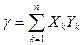
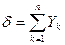
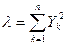
С учетом новых обозначений получаем:
J
(a,b
) = a
a
2
+ nb
2
+ 2b
ab
– 2g
a
– 2d
b
+ l
Реклама

Берем частные производные:
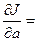 2a
a
+ 2b
b
– 2g
, 2a
a
+ 2b
b
– 2g
,
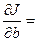 2nb
+ 2b
a
– 2d
. 2nb
+ 2b
a
– 2d
.
Решаем систему:
| 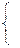
|
a
a
+ b
b
= g
,
|
| nb
+ b
a
= d
.
|
Получаем:
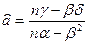 , ,
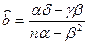 . .
Решение 2:
Оценки параметров можно получить, решая так называемую нормальную систему уравнений:
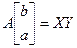 , ,
где 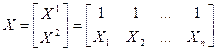 , , 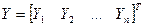 , ,
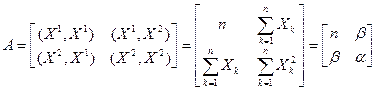
Получаем:
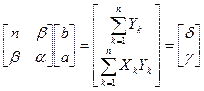
т.е. то же самое в виде системы:
| 
|
nb
+ b
a
= d
.
|
| a
a
+ b
b
= g
,
|
Как видно, это та же система, что и в решении 1.
Таким образом, с учетом данных, полученных в опытах по наблюдению за X
и Y
, получаем значения коэффициентов:
a
= 121.415720807951,
b
= 75.462893127151,
g
= 472.393613346561,
d
= 293.720213200493,
l
= 1838.39078890617.
Получив значения коэффициентов, получаем значения оценки параметров:
a
= 3.86747517626168,
b
= 0.0373869460469762.
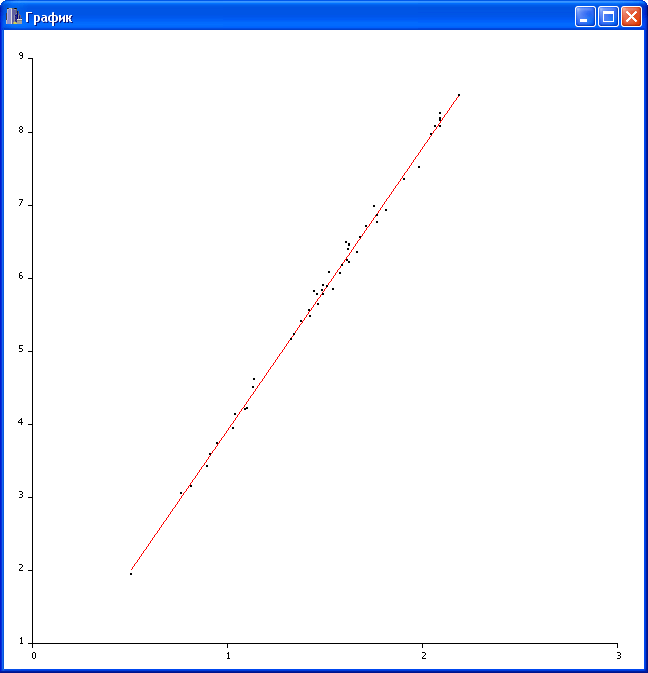
На рис. 2 представлена прямая 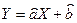 . .
| 
|
| Рис. 2. Результаты оценки параметров.
|
Задание 2а.
Построить доверительные интервалы уровня 0.95 для параметров a
и b
.
Основная МНК-теорема:
Пусть в условия предыдущей задачи
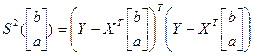 , ,
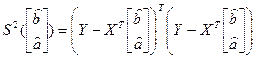 . .
Тогда
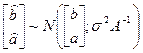 , ,
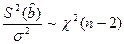 . .
Следствие:
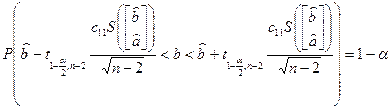 , ,
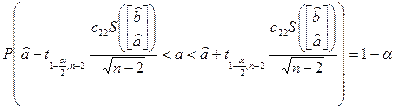 , ,
где 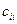 - (i
, i
)-й элемент матрицы - (i
, i
)-й элемент матрицы 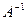 , , 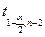 - квантиль уровня - квантиль уровня 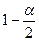 для распределения Стьюдента с для распределения Стьюдента с 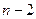 степенями свободы. степенями свободы.
С учетом условия задачи (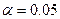 ) и всего вышесказанного, получаем следующее: ) и всего вышесказанного, получаем следующее:
Матрица 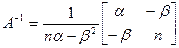 , ,
соответственно,
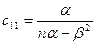 » 0.322795848743494 » 0.322795848743494
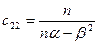 » 0.132930005519663 » 0.132930005519663
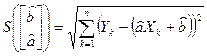 » 0.662505924471855 » 0.662505924471855
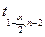 » 2.011 » 2.011
Итого – доверительные интервалы уровня 0.95:
для a
: ( 3.84191262236633 , 3.89303773015703 )
для b
: ( -0,0246869720909494 , 0,0994608641849019 )
Задание 3.
Рассматривая 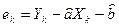 как выборку, построить гистограмму (10 интервалов одинаковой длины). Пользуясь критерием как выборку, построить гистограмму (10 интервалов одинаковой длины). Пользуясь критерием 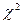 и полученной гистограммой, проверить гипотезу о нормальном законе распределения с уровнем значения 0.01 случайной величины и полученной гистограммой, проверить гипотезу о нормальном законе распределения с уровнем значения 0.01 случайной величины 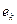 . .
Минимальное и максимальное выборочные значения равны –0.2083122 и 0.2076246, соответственно. Разобьем получившийся промежуток на 10 интервалов одинаковой длины. В таблице 1 представлены характеристики получившегося разбиения.
| №
|
Левый конец
|
Правый конец
|
Кол-во элементов выборки, попавших в интервал
|
| 1
|
-2,2233607326425400
|
-1,7794225005712100
|
2
|
| 2
|
-1,7794225005712100
|
-1,3354842684998800
|
2
|
| 3
|
-1,3354842684998800
|
-0,8915460364285440
|
5
|
| 4
|
-0,8915460364285440
|
-0,4476078043572120
|
9
|
| 5
|
-0,4476078043572120
|
-0,0036695722858795
|
8
|
| 6
|
-0,0036695722858795
|
0,4402686597854530
|
8
|
| 7
|
0,4402686597854530
|
0,8842068918567850
|
7
|
| 8
|
0,8842068918567850
|
1,3281451239281200
|
3
|
| 9
|
1,3281451239281200
|
1,7720833559994500
|
4
|
| 10
|
1,7720833559994500
|
2,2160215880707800
|
2
|
Таблица 1. Данные для гистограммы.
| 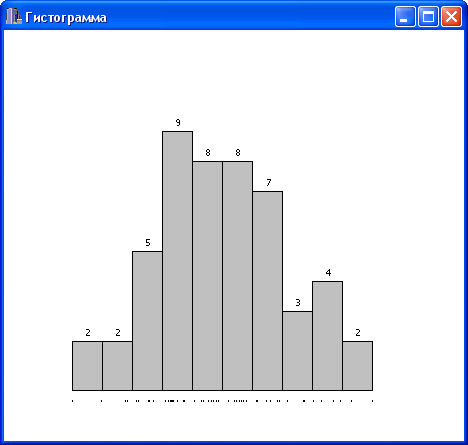
|
| Рис. 3. Гистограмма.
|
Прежде чем проверять гипотезу о нормальном законе распределения случайной величины 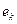 , оценим параметры закона распределения в предположении, что распределение гауссовское. Из условия предыдущей задачи , оценим параметры закона распределения в предположении, что распределение гауссовское. Из условия предыдущей задачи
Реклама

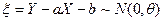
Значит, мат. ожидание равно нулю, а дисперсия оценивается выборочной дисперсией:
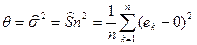
Подставляя выборочные данные, получаем: 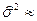 0.00878 0.00878
Таким образом, выдвигаемая гипотеза: 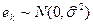
Для каждого интервала вычисляем вероятность, а также частоту попадания выборочных точек. Полученные результаты представлены в таблице 2.
| №
(
k
)
|
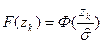
|
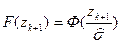
|
Вероятность попадания в
k
-интервал:
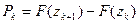
|
Частота попадания выборочных точек в
k
-интервал
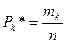 , , 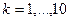
|
| 1
|
0,0131
|
0,0376
|
0,0245
|
0,04
|
| 2
|
0,0376
|
0,0909
|
0,0533
|
0,04
|
| 3
|
0,0909
|
0,1865
|
0,0956
|
0,10
|
| 4
|
0,1865
|
0,3273
|
0,1408
|
0,18
|
| 5
|
0,3273
|
0,4986
|
0,1713
|
0,16
|
| 6
|
0,4986
|
0,6700
|
0,1714
|
0,16
|
| 7
|
0,6700
|
0,8119
|
0,1419
|
0,14
|
| 8
|
0,8119
|
0,9079
|
0,0960
|
0,06
|
| 9
|
0,9079
|
0,9618
|
0,0539
|
0,08
|
| 10
|
0,9618
|
0,9864
|
0,0246
|
0,04
|
Таблица 2. Вероятностные и частотные характеристики.
На основании полученных результатов вычисляем статистику:
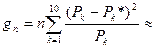 3.077 3.077
Если гипотеза верна, то статистика 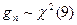
Используя закон распределения 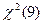 , находим критическое значение для заданного уровня p
= 0.01: , находим критическое значение для заданного уровня p
= 0.01:
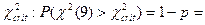 0.99 0.99
Из таблицы распределения 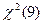 получаем: получаем: 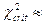 20.8 20.8
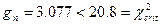 , значит гипотеза принимается. , значит гипотеза принимается.
|