| Российско-Армянский (Славянский) Государственный Университет
Факультет Прикладной математики и информатики
Кафедра Математики и Математического Моделирования
Курсовая работа
на тему:
"Построение конечно-разностных формул на границе дискретной области счёта"
Выполнила: студентка 3-его курса Амирбекян Алиса
Руководитель: к.ф.м.н., доцент В.С. Бондаренко
г. Ереван
2004
Понятие дискретной области при численном решении дифференциальной задачи.
При численном решении уравнений математической физики важным становится вопрос замены непрерывной области изменения аргумента дискретной и замены дифференциального оператора разностным. Сделав указанные замены, мы переходим от дифференциальной задачи к разностной схеме.
Таким образом, задача о численном решении исходного дифференциального уравнения сводится к нахождению решения полученной разностной схемы.
. Так как при численном решении математической задачи не возможно воспроизвести разностное решение для всех значений аргумента, изменяющегося внутри некоторой области, то в этой области нужно выбрать некоторое конечное множество точек и приближенное решение искать только в этих точках. Такое множество точек называется сеткой
, а отдельные точки называют узлами
сетки. Функция, определенная в узлах сетки, называется сеточной
функцией.
Сетка является дискретной областью изменения аргумента, которой заменяется непрерывная область. Всякая сетка характеризуется величиной близости узлов сетки друг к другу. Обозначим эту величину через h
. Ясно, что чем меньше h
, тем лучше описывает сетка реальную непрерывную область, однако уменьшение величины h
увеличивает число узлов сетки, что приводит к увеличению времени счёта и громоздкости программ.
Если непрерывная область квадратная или прямоугольная, то её можно заменить сеткой, раномерной повсюду, а если непрерывная область имеет криволинейную границу, то она заменяется сеткой, которая неравномерна вблизи границы. Узлы, которые отстоят на одинаковом расстоянии от ближайших внутренних узлов, называются регулярными
. Если имеются граничные узлы, отстоящие от границы на меньшем расстоянии, чем от ближайших внутренних узлов, то они называются нерегулярными.
Реклама

Конечно-разностные формулы для производных
Пусть дан линейный диференциальный оператор L
, действующий на функцию u
=
u
(х).
Заменяя входящие в Lu
производные разностными отношениями, мы получим вместо Lu
разностное выражение Lh
uh
, являющееся линейной комбинацией значений сеточной функции uh
на некотором множестве узлов сетки, называемом шаблоном.
Такая приближенная замена Lu
на Lh
uh
называется разностной аппроксимацией оператора
L
.
Прежде чем приступить к разностной аппроксимации оператора L
, необходимо выбрать шаблон, т. е. указать множество соседних с узлом х
узлов, в которых значения сеточной функции u
(х)
могут быть использованы для аппроксимации оператора L
.
Рассмотрим примеры разностной аппроксимации:
Пусть дана гладкая функция u
=u
(
x
).
Фиксируем некоторую точку х
оси Ох
и возьмем точки х
- h
и х
+ h
.
В качестве разностной аппроксимации первой производной u
'(
x
)
можно использовать следующую формулу:
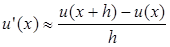 (1) (1)
Ясно, что формулы (1) и (2) приближенные и имеют невязку равную:
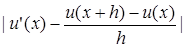
Эта невязка называется погрешностью аппроксимации. Тогда погрешность аппроксимации при замене всех производных, входящих в оператор L, конечно-разностными соотношениями типа (1) будет выглядеть так:
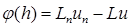 (
2
) (
2
)
В точке x
разложим u
’(
x
+
h
)
в ряд Тейлора:
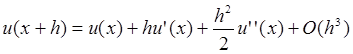 , ,
тогда
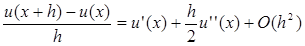 , ,
отбрасывая члены порядка O
(
h
2
)
получим:
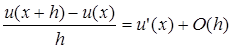 (
3
) (
3
)
Погрешность получаем порядка O
(
h
).
Разностная аппроксимация второй производной:
В качестве разностной аппроксимации второй производной u
''(
x
)
можно использовать следующую формулу:
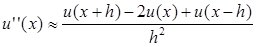 (4) (4)
Вычислим погрешность:
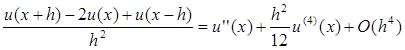
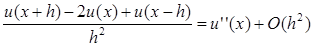
Погрешность получаем порядка O
(
h
2
).
Здесь используются 3 точки х
– h
, х, х
+ h
.
Это трехточечный шаблон.
В качестве примера рассмотрим разностный оператор Лапласа для функции u
(
x
,
y
)
на регулярном шаблоне:
(x,y+h)
 ● ●
 (x-h,y)
● ● (x+h,y) (x-h,y)
● ● (x+h,y)
(x,y-h)
●
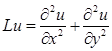
В точке (
x
,
y
)
аппроксимируем 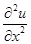 и и 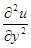 . Здесь используются точки (х
– h
,
y
), ( х,
y
), ( х+
h
,
y
),(
x
,
y
-
h
), (
x
,
y
+
h
).
По формуле (5): . Здесь используются точки (х
– h
,
y
), ( х,
y
), ( х+
h
,
y
),(
x
,
y
-
h
), (
x
,
y
+
h
).
По формуле (5):
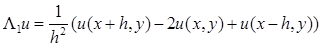
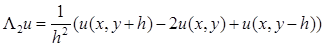
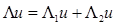
Получим:
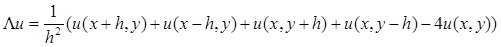
Вычислим погрешность:
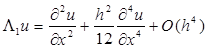
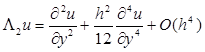
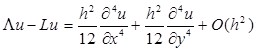
То есть разностный оператор L
u
аппроксимирует оператор Лапласа D
u
со вторым порядком на регулярном шаблоне.
Теперь рассмотрим нерегулярный шаблон. Здесь используются точки (х –
h
,
y
), ( х,
y
), ( х+
d
,
y
),(
x
,
y
-
h
), (
x
,
y
+
h
),
где d
¹
h
.
Реклама

 (x,y+h) (x,y+h)
 (x-h,y) (x+δ,y) (x-h,y) (x+δ,y)
(x,y-h)
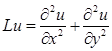
Обозначим:
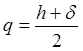
Определим:
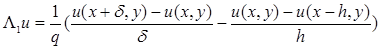
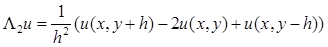
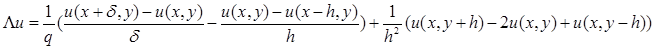
Посчитаем погрешность аппроксимации. В точке (x
,
y
)
разложим в ряд Тейлора:
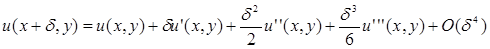
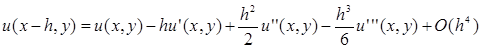
Подставим:
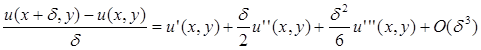
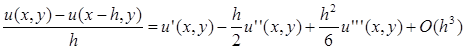
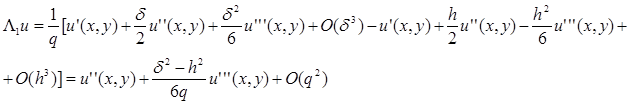 
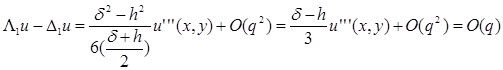
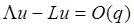
Для точек (х –
h
,
y
), ( х,
y
), ( х+
d
,
y
),(
x
,
y
-
h
), (
x
,
y
+
d
),
где d
¹
h
.
(x,y+δ)
 (x-h,y) (x+δ,y) (x-h,y) (x+δ,y)
(x,y-h)
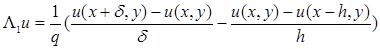
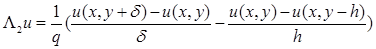
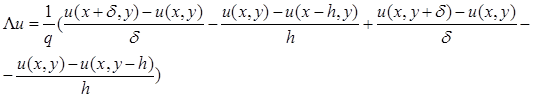
Погрешность, как и в предыдущем случае, равна O
(
q
).
Таким образом, на нерегулярном шаблоне разностный оператор L
u
имеет первый порядок аппроксимации. Для того чтобы ошибка не была столь большой, приближаясь к границу нужно брать шаг h
,
равным h
2
. То есть надо брать шаг равным погрешности аппроксимации на регулярном шаблоне.
Рассмотренный подход показывет, что при приближении к естественной границе области счёта приходится использовать неравномерную сетку. На разных участках естественной границы неравномерность разностной сетки будет иметь разный характер, что порождает использование разных аппроксимаций. Это в свою очередь усложняет общий вид разностной сетки, а также программу, реализующую численный расчёт. Этих трудностей можно избежать передвинув естественную границу так, чтобы разностная сетка была бы регулярной, но при этом уже нарушаются условия задачи.
Литература:
Самарский А.А., Теория разностных схем, М
|