(дистанційне навчання)

Поняття слова “ піраміда ”

“Піраміда” – латинська форма грецького слова “пюраміс”, яким греки називали єгипетські піраміди; це слово походить від давньоєгипетського слова “пурама”, яким ці піраміди називали самі єгиптяни. Сучасні єгиптяни називають піраміди словом “ахрам”, яке також походить від давньоєгипетського слова.

Піраміда як одне із 100 чудес світу

Призначення пірамід у Давньому Єгипті

В релігії давніх єгиптян вирішальне значення мала уява про загробне життя. Ці уявлення вплинули на розвиток і формування стилю пірамід та гробниць, на всю архітектуру Давнього Єгипту в цілому. Люди вважали підготовку до загробного життя одним із головних завдань свого земного життя. Загробне життя єгиптяни уявляли собі як продовження земного існування: людина і після смерті продовжує свій шлях у царстві безсмертя. А тому благоустрій майбутньої гробниці мав важливе значення.

Будівництво пірамід

- Кожна піраміда повинна була слугувати захистом для схованої у ній мумії від будь-якого ворога, від порушення спокою.

- Будівництво навіть середньої піраміди було нелегкою справою. Піраміди були побудовані за допомогою мускульної сили. На правому березі Ніла, в каменоломнях поблизу Мемфіса, тисячі людей були зайняті видобутком тонкозернистого вапняку. У горі спочатку визначали границі майбутнього блоку, потім вибивали глибоку канаву, а в неї забивали дерев ’ яні клини , які обливали водою. Через деякий час дерево збільшувалось в об ’ ємі, тріщина розширялась, і моноліт відділявся від скали. Потім кам ’ яну глибу на місці обробляли інструментами із каменю, міді і дерева. Вона набувала форму куба. Оброблені глиби на човнах перевозили на інший берег Нілу.

Будівництво пірамід

- Щоб підняти блоки, єгиптяни будували із цегли і каменю нахилену насип під кутом 15 ° . Довжину насипу збільшували зі збільшенням розмірів піраміди. По цім насипам кам ’ яні блоки тягнули на дерев ’ яних санях, а щоб зменшити силу тертя, трасу постійно поливали водою. Потім з допомогою дерев ’ яних важелів блоки встановлювали на місце. Коли будівництво в основному закінчувалося, насип вирівнювали, а поверхню піраміди закривали спеціальними блоками.

- Якість праці будівників, які жили ще 47 століть тому, була такою, що незбіг горизонтальних і вертикальних ліній піраміди не більше ширини великого пальця. Камені так тісно приєднувались один до одного, що між ними не можна було всунути навіть голку.

Будівництво пірамід

- У багатьох пірамідах робили лабіринти, сліпі камери і пастки, які повинні були перешкодити грабіжникам добратися до мумій і могильних коштовностей. Та це не допомогло. До того часу, коли вчені серйозно зайнялись вивченням пірамід, вони були вже майже пусті.

- Величезні за розміром, витонченні за формою, бездоганні за точністю математичного розрахунку піраміди і храми слугують доказом високого рівня будівельного мистецтва давніх єгиптян.

Піраміда Хеопса – одне з семи чудес світу

Найвідоміші єгипетські піраміди, збудовані в Гізі між 2600 та 2500 рр. до н. е., - це гробниці фараонів Хеопса (Хуфу), Хефрена (Хафри) та Мікерина (Менкаури). Найбільша серед них – Піраміда Хеопса , збудована ще у 28 ст. до н. е.

Отож, одне із 7 чудес світу, яке відоме людству на протязі кількох століть, переживши в століттях усі останні і дійшовши до наших днів – священна Піраміда Хеопса!

Будівництво враженнями Геродота

“Хеопс змусив працювати на себе весь єгипетський народ, поділивши його на 2 частини. Першим він наказав займатися доставкою до берега Нілу блоків із каменоломень в аравійських горах. Інші займались їх подальшим транспортуванням до підніжжя лівійських гір. Постійно працювали 100000 людей, вони змінювали один одного кожні 3 місяці. За 10 років тяжкої праці була побудована дорога, по якій блоки доставляли до річки. Будівництво цієї дороги було не менш важчою задачею, ніж самої піраміди. Дорога була викладена відшліфованими кам ’ яними плитами, прикрашеними різьбою. Закінчилися будівничі роботи навколо піраміди, завершилось будівництво підземних об ’ єктів, що призначалися для гробниці і погребальної камери фараона. Будівництво ж самої піраміди тривало ще 20 років”.

Велич піраміди

- Велику піраміду Хеопса нерідко називають Біблією в камені. При сході сонця, коли її вершина ще обкутана туманом, піраміда здається рожево-персиковою, у ті рідкісні хвилини, коли горизонт обкутаний хмарами, - сірувато-чорною, а при холодному сяйві місяця вона нагадує засніжену гірську вершину.

- Піраміда Хеопса, можливо, найграндіозніша споруда на землі. Навіть у час найбільшої слави і величі будь-кого з європейських монархів у нього не було такого палацу, котрий зрівнявся б за розміром з гробницею цього фараона. Менше її і Букінгемський палац в Лондоні, і Версаль у Франції, і Зимній палац в Санкт-Петербурзі, і навіть Ескоріал в Іспанії.

Розміри піраміди

– Спочатку піраміда Хеопса підіймалась на 147 м, але через наступ пісків її висота зменшилася до 137 м . Кожна сторона квадратної основи – 233 м, площа – більше 50000 м ²

– Піраміда складається з 2 300 000 кубічних блоків вапняку з гладко відшліфованими сторонами. За підрахунками Наполеона, кам ’ яних блоків від трьох пірамід в Гізі хватило б, щоб обкласти усю Францію стіною висотою у 3 м і товщиною в 30 см

– Середня маса блоку – 2,5 т

– Найважчий блок – 15 т

– Довжина блоку – ≈ 9 м

– Маса піраміди – 5,7 млн. т

Піраміди, як предмет вивчення

Піраміди у фізиці

Історична цінність пірамід – наявність великої кількості енергії, створеної завдяки правильності форми пірамід. Створювані поля у середині пірамід дозволяють нейтралізувати негативну енергію і перетворити її в позитивну. Єдина система пірамід на планеті координує процес перетворення енергії у просторі і у часі.

Піраміди у фізиці

Піраміди виконують також роль стабілізатора параметрів у русі планети. Важною умовою при енергоінформаційному обміні Космос-Земля-Космос є утримання планети на постійній орбіті з постійним кутом нахилу земної осі до Сонця і, звичайно ж, стала швидкість обертання навколо Сонця і своєї осі. Щоб зберегти ці параметри, треба постійно вводити стабілізаційну програму в ядро і плазму Землі.

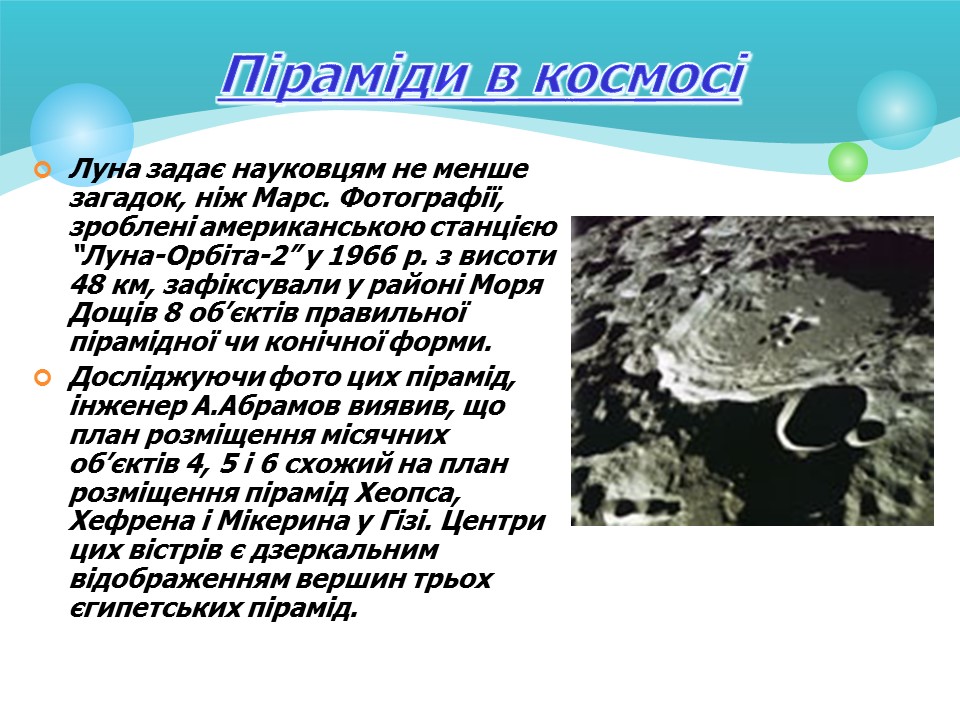
Піраміди в космосі

- Найбільш приголомшеними знахідками минулого століття стали дані НАСА. У 1976 р. американський космічний апарат “Вікінг”, облітаючи Марс, зафіксував і передав на землю дані про споруди на поверхні червоної планети в області Кідонії. Ця сенсація була офіційно підтверджена лише у листопаді 1994 р. Тоді Національне управління з аеронавтики та вивчення космічного простору США заявило: “Сфінкс і піраміди на Марсі існують”.

- У Кідонії було помічено 25 пірамід, з них 5 великих, 20 малих. Сторони основи великих пірамід Марса досягають 1,5 км при висоті в 1 км. Малі піраміди в декілька разів більші великих пірамід Гіз, а весь комплекс розташований на площі 25 км.

Піраміди в космосі

- Луна задає науковцям не менше загадок, ніж Марс. Фотографії, зроблені американською станцією “Луна-Орбіта-2” у 1966 р. з висоти 48 км, зафіксували у районі Моря Дощів 8 об ’ єктів правильної пірамідної чи конічної форми.

- Досліджуючи фото цих пірамід, інженер А.Абрамов виявив, що план розміщення місячних об ’ єктів 4, 5 і 6 схожий на план розміщення пірамід Хеопса, Хефрена і Мікерина у Гізі. Центри цих вістрів є дзеркальним відображенням вершин трьох єгипетських пірамід.

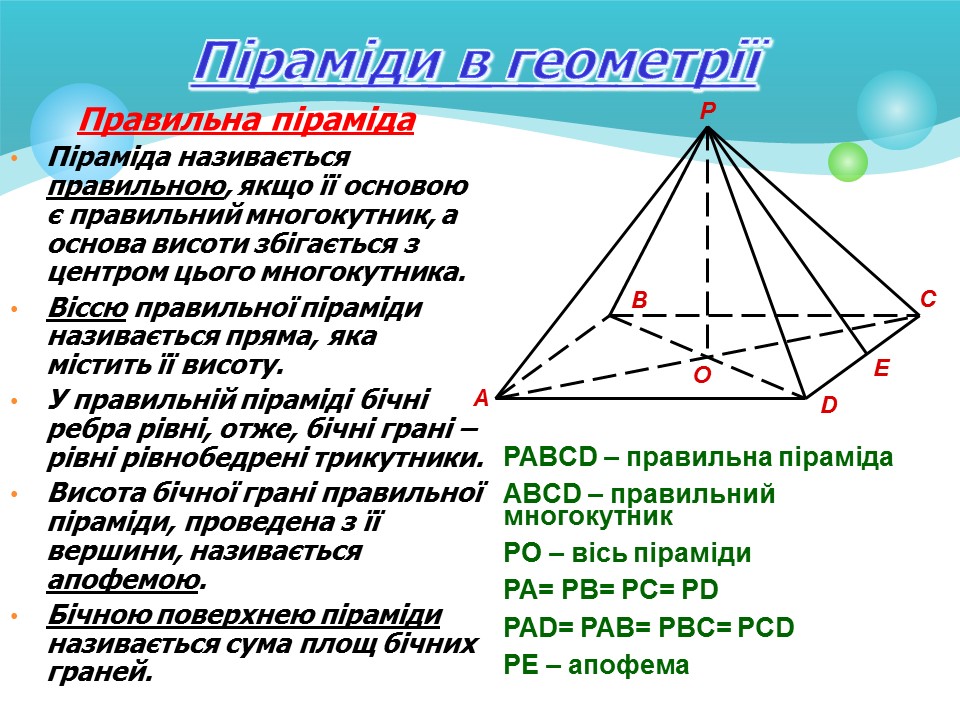
Піраміди в геометрії

Основні поняття

• Піраміда – многогранник, який складається з плоского многокутника – основи піраміди, точки, яка не лежить у площині основи, - вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи.

• Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами .

• Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань – трикутник.

• Висотою піраміди називається перпендикуляр, опущений з вершини піраміди на площину основи.

Піраміди в геометрії

Правильна піраміда

• Піраміда називається правильною , якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника.

• Віссю правильної піраміди називається пряма, яка містить її висоту.

• У правильній піраміді бічні ребра рівні, отже, бічні грані – рівні рівнобедрені трикутники.

• Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою .

• Бічною поверхнею піраміди називається сума площ бічних граней.

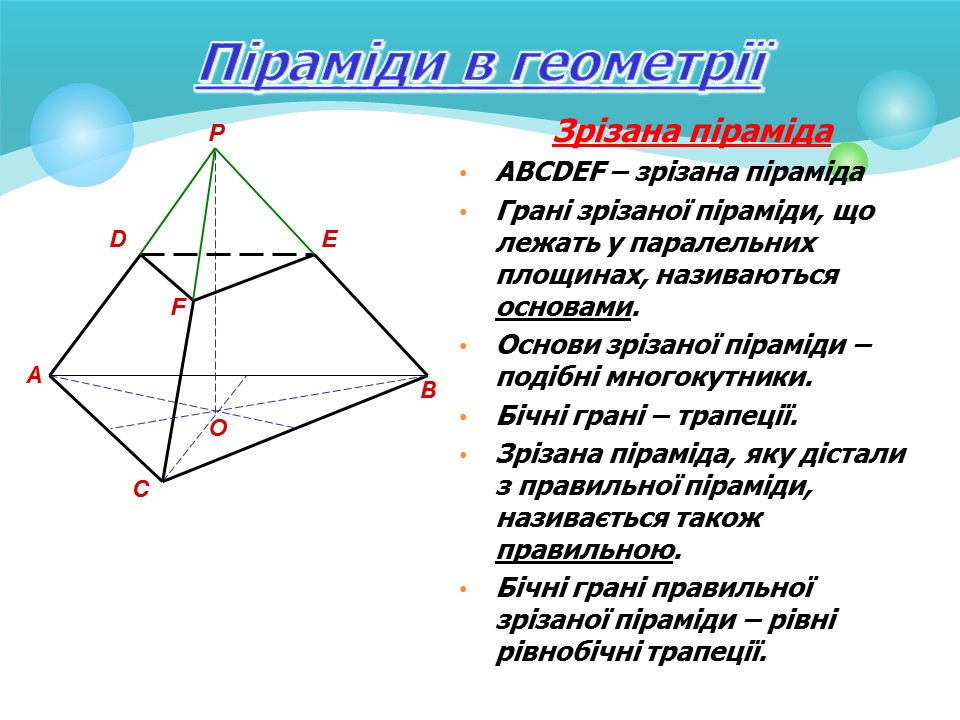
Піраміди в геометрії

Зрізана піраміда

• ABCDEF – зрізана піраміда

• Грані зрізаної піраміди, що лежать у паралельних площинах, називаються основами .

• Основи зрізаної піраміди – подібні многокутники.

• Бічні грані – трапеції.

• Зрізана піраміда, яку дістали з правильної піраміди, називається також правильною .

• Бічні грані правильної зрізаної піраміди – рівні рівнобічні трапеції.

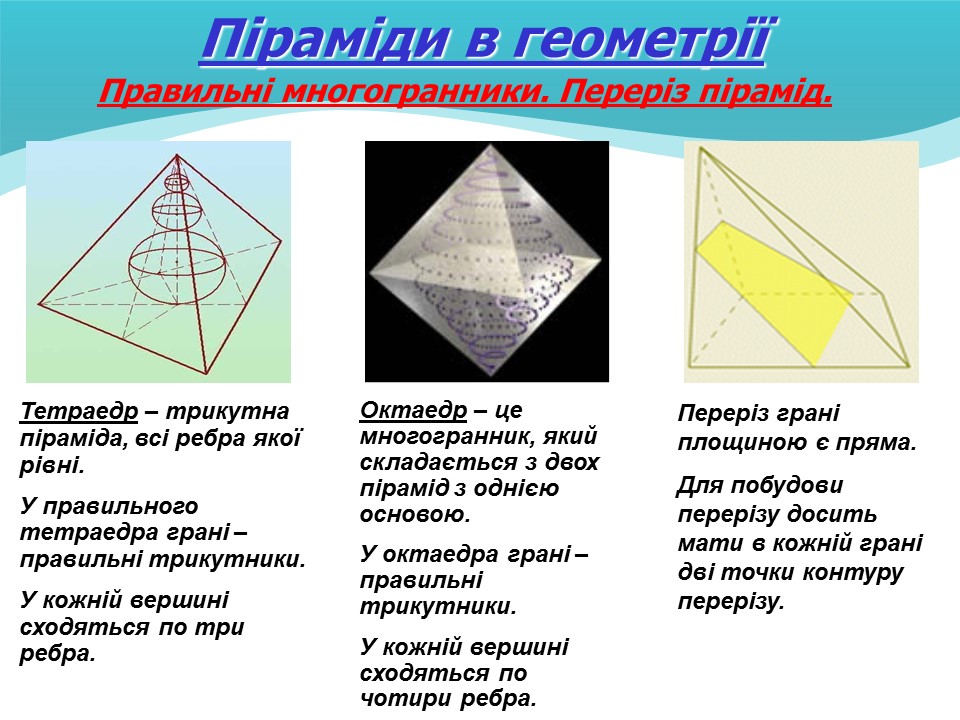
Піраміди в геометрії

Правильні многогранники. Переріз пірамід.

Основні формули стосовно піраміди

Об ’ єм піраміди Хеопса

V = ⅓ S основи · H

Параметри піраміди:

Висота (Н) – 137 м

Основа – квадрат, а тому

S основи = а ²

Сторона піраміди – 233 м

Обчислюємо об ’ єм піраміди:

V = ⅓ · 233² ·1 3 7 = ⅓ · 7437593 ≈

≈ 2500000 м ³ = 2,5 км ³

Отже, об ’ єм піраміди Хеопса

приблизно дорівнює 2,5 км ³

Запитання для самоперевірки

- Дайте означення піраміди (основи піраміди, бічних граней, ребер, висоти).

- Бічні ребра піраміди рівні. У яку точку проектується її вершина?

- Чи може вершина піраміди проектуватися в точку зовні основи, якщо бічні ребра рівні?

- Бічні грані піраміди однаково нахилені до основи. У яку точку основи проектується її вершина?

- Скільки бічних граней, перпендикулярних до основи, може мати піраміда?

Запитання для самоперевірки

Серед наведених нижче тверджень укажіть правильні:

-існує піраміда, яка має 125 ребер;

-існує піраміда, яка має 125 граней;

-піраміда може мати два бічні ребра перпендикулярні до основи;

-сума всіх плоских кутів n-кутної піраміди дорівнює 360°( n -1);

-якщо одна з бічних граней піраміди перпендикулярна до основи,то висота піраміди збігається з висотою однієї грані.

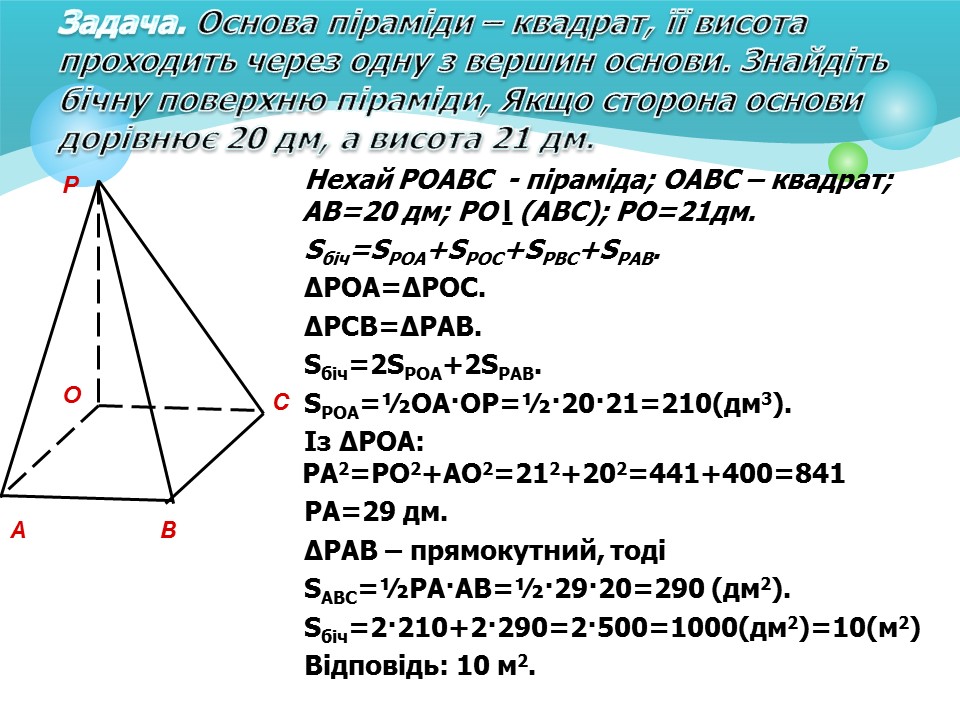
Задача. Основа піраміди – квадрат, її висота проходить через одну з вершин основи. Знайдіть бічну поверхню піраміди, Якщо сторона основи дорівнює 20 дм, а висота 21 дм.

Нехай Р OABC - піраміда; ОАВС – квадрат; АВ=20 дм; РО ḻ (АВС); РО=21дм.

S _біч = S _РОА + S _РОС + S _РВС + S _РАВ .

Δ РОА= Δ РОС.

ΔРСВ= Δ РАВ.

S_біч =2 S _РОА +2 S _РАВ .

S_РОА =½ОА·ОР=½·20·21=210(дм³ ).

Із Δ РОА: РА² =РО² +АО² =21² +20² =441+400=841

РА=29 дм.

ΔРАВ – прямокутний, тоді

S_АВС =½РА·АВ=½·29·20=290 (дм² ).

S_біч =2·210+2·290=2·500=1000(дм² )=10(м² )

Відповідь: 10 м² .

Тестові завдання для самоперевірки (І рівень)

- Якщо сторона основи правильної трикутної піраміди дорівнює 3 см, а апофема 1 см, то бічна поверхня піраміди дорівнює:

а) 1 см² ; б) 3 см² ; в) 1,5 см² ; г) 4,5 см² .

- Основою піраміди є прямокутник зі сторонами 5 см і 8 см. Знайти об'єм піраміди, якщо її висота дорівнює 15 см.

а) 600 см³ ; б) 200 см³ ; в) 130 см³ ; г) 390 см³ .

- Бічне ребро правильної чотирикутної піраміди дорівнює d , а плоский кут при її вершині β . Визначити сторону основи піраміди.

а) d sin β/2 ; б) d cos β/2 ; в)2 d sin β/2 ; г)2 d tg β/2 .

Тестові завдання для самоперевірки (ІІ рівень)

- Якщо периметр основи правильної чотирикутної піраміди дорівнює 4 см, а апофема – 1см, то двогранний кут при основі піраміди дорівнює:

а) 30°; б) 60°; в) arctg 2; г) arctg ½.

- Відстань від центра основи правильної піраміди до бічної грані дорівнює d , бічна грань нахилена до площини основи під кутом φ . Визначити апофему піраміди.

а) 2 d/sin2 φ ; б) d sin2 φ ; в) d/sin ² φ ;

г) d/cos ² φ .

Завдання для самоперевірки
(ІІІ рівень)

- Якщо бічні ребра трикутної піраміди попарно перпендикулярні, а площі бічних граней дорівнюють 3 см, 4 см² , 6 см² , то її об'єм дорівнює:

а) 1 см³ ; б) 2 см³ ; в) 4 см³ ; г) 8 см³ .

- Основа піраміди – прямокутний трикутник з гострим кутом α . Бічна грань, що містить гіпотенузу, перпендикулярна до основи, а дві інші – нахилені до неї під кутом β . Висота піраміди дорівнює Н. Знайдіть об'єм піраміди.

(Відповідь: 1/6 Н³ ctg ² β tg α ( ctg α + 1)² .)