| Корнева М.В., Кулигин В.А., Кулигина Г.А.
Исследовательская группа АНАЛИЗ.
http://kuligin.mylivepage.ru
; http://www.n-t.ru/ac/iga/
Анализ классической электродинамики и теории относительности
Аннотация
. Рассматриваются некоторые математические и физические некорректности, устранение которых радикально меняет наши представления об основах электродинамики и о сущности теории относительности.
Глава 1. Многообразие решений уравнений Максвелла. 3
Глава 2. Причинность и физические взаимодействия. 14
Глава 3. Электромагнитная масса. 27
Глава 4. Лагранжиан взаимодействия двух зарядов. 41
Глава 5. Вариационные основы квазистатических явлений. 53
Глава 6. Объяснение магнитных явлений. 66
Глава 7. Тензор энергии-импульса электромагнитной волны.. 81
Глава 8. Безынерциальные заряды и токи. 96
Глава 9. Новый вид электромагнитного излучения?. 106
Глава 10. Анализ пространственно-временных отношений СТО.. 115
Глава 11. Наблюдаемые и реальные характеристики. 127
Глава 12. «Вариационный» принцип релятивистских теорий. 136
Глава 13. Эфирные теории и баллистическая гипотеза Ритца. 145
Глава 14. Волновой вариант теории Ритца. 159
Глава 15. Волны и функции Бесселя. 168
Заключение
. 186
Введение
Эта книга посвящена анализу проблем классической электродинамики и основ специальной теории относительности. Целью исследований явилось желание дать логически последовательное изложение, избавив эти теории от ошибок и внутренних противоречий. В книге все результаты математически обоснованы и снабжены доказательствами. Изложение не опирается на какие-либо гипотезы. Однако там, где это необходимо, мы указываем возможные направления исследований. Условно содержание книги можно разделить на пять частей.
Первая часть
(Главы 1 и 15) посвящена математическим вопросам электродинамики. Узловой является Глава 1, в которой показано, что решение волнового уравнения не всегда выражается через функции запаздывающих и опережающих потенциалов. Решение волнового уравнения (в зависимости от начальных условий) может содержать члены мгновенно действующего характера.
Вторая часть
(Главы 2, 3, 4, 5, 6) посвящена анализу квазистатических явлений. Дано строгое решение проблемы электромагнитной массы, рассмотрены вариационные основы взаимодействия зарядов и токов, сформулированы законы сохранения для квазистатических полей, дано последовательное объяснение ряда проблем квазистатической электродинамики и объяснение магнитных явлений.
Реклама

Третья часть
(Главы 7, 8, 9) содержит анализ уравнений волновой электродинамики. Дан вывод тензора энергии-импульса электромагнитного поля, приводится доказательство обобщенного закона сохранения энергии-импульса. Показано, что уравнения квазистатической электродинамики не могут быть следствиями предельного перехода от уравнений волновой электродинамики. Рассмотрены вопросы, связанные с безинерциальными зарядами и токами, которые не анализировались в современной литературе, а также вопросы волновой электродинамики, которые в настоящее время не нашли объяснения в рамках уравнений Максвелла.
В четвертой части
(Главы 10, 11, 12) обсуждаются проблемы теории относительности с физических и философских позиций. Показано, что в этой теории имеются три, а не два, постулата, что волновые уравнения инвариантны относительно большого класса преобразований. Доказано, что релятивистский вариационный принцип математически некорректен и принцип наименьшего действия не реализуется в релятивистских теориях. Анализ проблем позволяет сделать заключение, что преобразование Лоренца (как и другие преобразования) применимы только для электромагнитных волн и не применимы для материальных тел.
Пятая часть
(Главы 13, 14) посвящена анализу взаимодействия волновых полей и токов, на основании которого устанавливается, что такое взаимодействие имеет диссипативный характер. Это позволяет отклонить «эфирные» гипотезы и баллистическую теорию Ритца. Однако если рассматривать электромагнитную волну как самостоятельный вид материи, то возникает волновой вариант теории Ритца, который сохраняет неизменной форму волнового уравнения и обеспечивает постоянство скорости света в любых инерциальных системах отсчета.
1.1 Математическая и физическая постановки задачи
Мы начнем с математической постановки задачи для волнового уравнения. Следуя [1], сформулируем задачу. Необходимо найти решение неоднородного волнового уравнения
∂ 2u
2
∂ 2u
 2 = a
2 + f
(x
;t
) 2 = a
2 + f
(x
;t
)
∂t
∂x
при заданных начальных условиях
∂u
 u
(x
,0) = ϕ(x
); = ψ(x
) u
(x
,0) = ϕ(x
); = ψ(x
)
∂t
t
=0
и некоторых граничных условиях. Не ограничивая общности, мы рассмотрим одномерный случай для безграничной струны
Реклама

Такое решение, как известно, существует и оно единственно [1].
ϕ(x
+ at
) + ϕ(x
− at
) 1 x
+at
1 t x
+a
(t
−τ)
 u
(x
;t
) = + ∫
ψ(ξ)d
ξ + u
(x
;t
) = + ∫
ψ(ξ)d
ξ +  2a
∫
0 d
τx
−a
∫
(t
−f
τ)(ξ;τ)d
ξ (1.1.1) 2a
∫
0 d
τx
−a
∫
(t
−f
τ)(ξ;τ)d
ξ (1.1.1)
2 2a
x
−at
Рассматривая структуру решения (1.1.1), можно сделать следующие предположения.
Последнее слагаемое (двойной интеграл) определяет вклад в потенциал u,
создаваемый источником обильностью f
(x
;t
).
Два первых слагаемых дают вклад, не связанный с какими-либо источниками в пространстве («свободный» потенциал). Эта часть потенциала имеет запаздывающие и опережающие составляющие.
Итак, постановка математической задачи.
Имеется неоднородное волновое уравнение. Нам необходимо найти решение, удовлетворяющее заданным начальным и граничным условиям. В рамках такой постановки решение задачи единственно.
В физике встречается ряд задач, когда необходимо найти поля, создаваемые известным источником. По этой причине два первых слагаемых не представляют интереса, поскольку источники их отсутствуют, а потенциал поля источника определяется лишь третьим членом. Можно предположить, что начальные условия не играют существенной роли и ими можно пренебречь. Физическая задача формулируется фактически при этом допущении.
Итак, постановка физической задачи.
Имеется источник (или движущиеся источники) полей. Необходимо найти поля, создаваемые этими источниками и удовлетворяющие заданным граничным условиям при следующих ограничениях.
В решении должны быть поля только этих источников.
«Свободные» поля (поля без источников) и поля, создаваемые другими источниками, не входящими в уравнение, должны отсутствовать, поскольку они не представляют интереса в рамках поставленной задачи.
Как мы видим, различие в постановках задач весьма «небольшое», но весьма существенное. Начальные условия «выпали» из постановки физической задачи. Законна ли такая постановка физической задачи и к чему ведет подобный подход? Это первое
положение, которое нуждается в анализе.
Второе
положение связано со следующим фактом. Запишем уравнение для скалярного потенциала, создаваемого источником заряда с плотностью ρ, локализованным в некотором замкнутом объеме.
1 ∂ 2
φ ρ(x
; y
;z
)
 Δφ − 2 2
= − c
∂t
ε Δφ − 2 2
= − c
∂t
ε
Потенциал φ вне источника является запаздывающим. При c
→ ∞ мы получаем уравнение ρ(x
; y
;z
)
Δφ = −  , потенциал которого мгновенно действующий. Чтобы убедиться, этого ε , потенциал которого мгновенно действующий. Чтобы убедиться, этого ε
достаточно взглянуть на таблицу, приведенную ниже.
Таблица 1
Сравнительные характеристики запаздывающих и мгновенно действующих потенциалов
Запаздывающие потенциалы Мгновенно действующие потенциалы
1. Потенциал в точке наблюдения 1. Потенциал движется синхронно при движении источника со своим источником (безо всякого запаздывает
. Запаздывание зависит запаздывания
).
| от расстояния до источника потенциала.
|
| 2. Потенциал сохраняет информацию
о предшествующем движении источника потенциала.
|
2. Потенциал не сохраняет информации
о предшествующем движении источника поля.
|
| 3. Потенциал описывается
|
3. Потенциал описывается
|
уравнением гиперболического типа
, уравнением эллиптического типа
, например, волновым уравнением. например, уравнением Пуассона.
Существуют ли мгновенно действующие решения при конечной величине c
? Как можно согласовать наличие таких решений с положениями Специальной теории
относительности? Справедлив ли предельный переход при c
→ ∞ от волновых явлений к квазистатическим? На часть этих вопросов мы постараемся ответить сейчас, на другие в следующих главах.
1.2 Потенциал движущегося заряда
Рассмотрим в качестве иллюстрации скалярный потенциал равномерно движущегося заряда, который описывается волновым уравнением
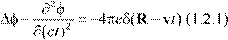
где: φ - скалярный потенциал поля заряда, δ - дельта функция Дирака, v
– скорость заряда q
вдоль оси z
.
Мы ищем решение уравнения (1.1.2) в заданной фиксированной системе отсчета, не прибегая к каким-либо пространственно-временным преобразованиям. С точки зрения математической
постановки задачи нам следовало бы задать начальные условия. С точки зрения физической
постановки задачи, эти начальные условия несущественны, поскольку непосредственно не связаны с источником потенциала (зарядом), как было сказано выше. Решение задачи ищется исходя из физических
соображений, т.е. исходя из физической модели описания процессов.
Покажем, что при физической постановке задачи единственность решения нарушается и не просто нарушается.
Итак, с одной стороны, решение уравнения (1.2.1) определяется формулой (потенциал Лиенара-Виехерта [2], [3]).
e
φ=(1.2.2)
vR
 (R
− ) (R
− )
c
где R
есть расстояние от заряда до точки, где измеряется потенциал. Если точка наблюдения в начале координат, то R
2
= x
2
+ y
2
+ z
2
, где (x
;y
;z
) – координаты заряда.
Потенциалы Лиенара-Виехерта являются запаздывающими. Это видно из самой структуры решения (1.2.2).
С другой стороны, имеется формула Лоренца для потенциала равномерно движущегося заряда
e
φ = 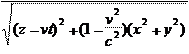 (1.2.3) (1.2.3)
Это выражение получено Лоренцем в результате применения его преобразования к потенциалу покоящегося заряда. Оно тоже удовлетворяет уравнению (1.2.1).
Сравнивая выражения (1.2.2) и (1.2.3), легко убедиться, что они принципиально различны!
Комбинируя их, можно записать ряд новых решений. Например, полусумма выражений (1.2.2) и (1.2.3) тоже является решением поставленной физической задачи. Нарушение единственности решения уравнения (1.2.1) при физической постановке задачи очевидно.
Итак, с математической точки зрения:
Имеем одно исходное волновое уравнение (1.2.1);
Имеем одно и то же пространство и время (систему отсчета);
Имеем одни и те же граничные условия;
Но имеем различные
начальные условия
и, соответственно, получаем различные решения (1.2.2) и (1.2.3).
Покажем, что потенциал (1.2.3) является мгновенно действующим, т.е. он является решением уравнения эллиптического
типа при постоянной скорости движения заряда.
Действительно, в калибровке Лоренца потенциал должен удовлетворять уравнению
1 ∂ 2
φ 4πq
 Δφ − 2 2
= − ⋅δ(x
; y
;z
− vt
) c
∂t
ε Δφ − 2 2
= − ⋅δ(x
; y
;z
− vt
) c
∂t
ε
В то же время, скалярный потенциал φ должен удовлетворять уравнению непрерывности ∂φ
divφv
+  = 0 = 0
∂t
При равномерном движении заряда
∂φ ∂φ
 = −v
gradφ = −v = −v
gradφ = −v
 (1.2.4) (1.2.4)
∂t
∂z
Учитывая условие непрерывности (1.2.4) для потенциала, можно показать, что вторую производную по времени от потенциала в выражении (1.2.1) можно привести к виду
 ∂ ∂φ ∂ ∂φ 2
∂ 2
φ ( ) = − (v
gradφ) = −v
grad ∂ ∂φ ∂ ∂φ 2
∂ 2
φ ( ) = − (v
gradφ) = −v
grad  = v
grad(v
gradφ) = v = v
grad(v
gradφ) = v
 2 2
∂t
∂t
∂t
∂t
∂z
Уравнение (1.2.1) принимает вид
∂ 2
φ ∂ 2
φ v
2
∂ 2
φ 4πq
  2
+ 2
+ (1− 2
) 2
= − δ(x
; y
;z
− vt
) 2
+ 2
+ (1− 2
) 2
= − δ(x
; y
;z
− vt
)
∂x
∂y c
∂z
ε
Левая часть уравнения (1.2.1) теперь представляет собой уравнение эллиптического
(а не гиперболического
) типа, решением которого является выражение (1.2.3), т.е. мгновенно действующий
потенциал. Нарушение единственности решения физической
задачи налицо.
Итак, что бы ни доказывали релятивисты, как бы они ни жонглировали штрихами над переменными и ни манипулировали преобразованиями, выражение (1.2.3) есть мгновенно действующий потенциал
! Сторонники СТО приводят аргументы со ссылками на «пространственно-временные изменения», происходящие при использовании преобразования Лоренца и на теорему о единственности решения. Но это лишь декларации, поскольку начальные условия (как принципиальный элемент) «выпали» из постановки задачи. Без учета этих условий применять теорему о единственности решения задачи Коши математически неграмотно.
1.3 Вырожденные члены в решении волнового уравнения
Вернемся к математической постановке задачи, рассмотренной в начале первого параграфа. Имеем:
– Неоднородное волновое уравнение, описывающее некоторый потенциал u.
∂ 2
u
1 ∂ 2
u
 2
− 2 2
= f
(x
;t
) (1.3.1) 2
− 2 2
= f
(x
;t
) (1.3.1)
∂x c
∂t
– Граничные условия, которым должен удовлетворять этот потенциал.
–  Начальные условия u
(x
;0) =ϕ(x
); ∂
u
=ψ(x
) Начальные условия u
(x
;0) =ϕ(x
); ∂
u
=ψ(x
)
∂t
t
=0
Иногда по условию задачи вводится добавочное условие на производную потенциала во времени, например,
∂u
 = F
(u
; x
;∂x
/ ∂t
) = F
(u
; x
;v
) = F
(u
; x
;∂x
/ ∂t
) = F
(u
; x
;v
)
∂t
(1.3.2)
Например, таким условием может служить уравнение непрерывности для потенциала u
∂u
 +divu
v
= 0 +divu
v
= 0
∂t
.
Покажем, что если решение задачи при дополнительном условии существует, то оно будет содержать вырожденный (мгновенно действующий) член в решении.
Процедура решения.
Пользуясь выражением (1.3.2), найдем вторую производную ∂2
u
/∂t
2
∂ 2
u
∂F
∂u
∂F
∂x
∂F
∂v
 = + + = 2 = + + = 2
∂t
∂u
∂t
∂x
∂t
∂v
∂t
∂F
∂F
∂x
∂F
∂v
 = F
+ + =Ф
(u
;x
;v
;∂v
/∂t
) = F
+ + =Ф
(u
;x
;v
;∂v
/∂t
)
∂u
∂x
∂t
∂v
∂t
Таким образом, дополнительное условие позволяет преобразовать волновое уравнение (1.3.1) (в общем случае) к неоднородному уравнению эллиптического типа, поскольку это уравнение не содержит частных производных от потенциала по времени.
 ∂ 2
u
1 − Ф
= f
(x
;t
) ∂ 2
u
1 − Ф
= f
(x
;t
)
2 2
∂x c
Пусть общим решением этого неоднородного уравнения служит решение u
1 = u
* +C
1x
+C
2
Чтобы это решение было общим решением (1.3.1), в него необходимо добавить два члена.
Итак, общее решение (1.3.1) будет иметь вид u
= u
1
+C
3
(x
+ct
)+C
4
(x
−ct
) = u
*
+C
1
x
+C
2
+C
3
(x
+ct
)+C
4
(x
−ct
) (1.3.3)
Если нам удастся подобрать коэффициенты С
1
, С
2
, С
3
(x
+ ct
), C
4
(x
- ct
) так, чтобы удовлетворялись начальные и граничные условия, то решение задачи при наличии добавочного условия существует. Это решение содержит хотя бы один вырожденный (мгновенно действующий) член u
*.
Добавление.
Вернемся к выражению (1.3.3). В силу теоремы существования и единственности решения решение уравнения (1.3.1) решение (1.3.3) единственно, существует и может содержать (мгновенно действующий) член независимо от добавочного условия
. Добавочное условие мы ввели в математическую постановку задачи только для иллюстрации
появления в решении мгновенно действующих членов. Мы не будем здесь определять класс начальных условий, при которых решение содержит (или не содержит) вырожденных членов. Это задача математики.
Мы обращаем внимание на это потому, что при постановке физических
задач начальные условия «выпадают» (их игнорируют) и возникает «произвол», который частично снимается добавочным
условием. Наличие этого добавочного условия как раз и определяет характер решения при постановке физических
задач.
В качестве примера можно сослаться на уравнения Максвелла в калибровке Лоренца. При решении физических
задач два условия предопределяют появление мгновенно действующих потенциалов в решениях этих уравнений φv
1 ∂φ
A
=  2
; divA
+ 2
; divA
+  2
= 0 c
c ∂t 2
= 0 c
c ∂t
Последнее условие эквивалентно уравнению непрерывности для скалярного потенциала φ
∂φ
divφv
+  = 0. = 0.
∂t
Отсюда следует весьма важные выводы для решений при физической
постановке задачи.
1. Для различных начальных условий решение неоднородного волнового уравнения будет различным. Этот вывод тривиален. Но мы его дополним следующим важным положением: решения неоднородного волнового уравнения в зависимости от начальных условий могут быть функционально
различными. Решения могут иметь либо запаздывающий характер, либо мгновенно действующий характер (вырожденные решения
).
2. Преобразование Лоренца, являясь линейным преобразованием координат и времени, не
меняет функционального
характера полей. Если потенциал неподвижного заряда является мгновенно действующим, то потенциал равномерно движущегося заряда также является мгновенно действующим (но никак не запаздывающим).
3. Функциональная зависимость решений волнового уравнения от выбранных начальных условий это, прежде всего, математическая задача. Именно математики должны дать ее решение. Однако в стандартных учебниках по математической физике внимания этой проблеме практически не уделяется. В результате в электродинамике существует масса проблем, связанных с «вырождением решений» и требующих анализа.
Важно отказаться от иллюзии
(предрассудка), что решение волнового уравнения всегда
является функцией только запаздывающих и опережающих потенциалов, а появление вырожденных членов (мгновенно действующих) в решении волнового уравнения исключено.
Итак, в зависимости от начальных условий решение волнового уравнения может быть как запаздывающим, так и мгновенно действующим (вырожденное
решение).
1.4 Решения и модели
Математика хороша тем, что достаточно одного отрицательного примера, чтобы опровергнуть положение, претендующее на истину. Здесь на примере проблемы существования продольных волн в электродинамике мы покажем, что при физической
постановке задачи решение волнового уравнения (например, уравнений Максвелла) зависит от выбора модели. Под моделью мы понимаем определенные положения, на основе которых дается физическое объяснение явлений.
Рассмотрим электрон, который колеблется относительно начала координат, перемещаясь вдоль оси z
. Выпишем его координаты и скорость
x
= 0; y
= 0; z
= b
cosωt
v
= ∂z
/∂t
= −b
ωsinωt
Вдали от точечного заряда, когда b
<< R
, поле волны должно запаздывать и убывать обратно пропорционально R
. Для простоты рассмотрим поле на больших расстояниях от заряда R
>> b
для нерелятивистского случая v = b
ω << c.
Для вычислений воспользуемся потенциалами Льенара-Виехерта e e e
v
e
v
  φ = ≈ A
= ≈ (1.4.1) vR
R
vR
cR φ = ≈ A
= ≈ (1.4.1) vR
R
vR
cR
(R
− ) c
(R
− ) c c
где R
– радиус-вектор, проведенный из точки нахождения заряда в точку наблюдения.
Значение векторного потенциала в точке наблюдения, отстоящей от начала координат на расстоянии R
, должно быть взято с запаздыванием R
/ c
, определяемым конечной величиной скорости распространения волны.
Поскольку векторный потенциал имеет составляющую только вдоль оси z
, электрическое поле, вычисленное с точностью до членов R
-2
, имеет вид
∂A
z
eb
ω sinω(t
- R/c
)
 E
z
= - ≈ 2
(1.4.2) E
z
= - ≈ 2
(1.4.2)
∂сt с R
Других составляющих электрического поля в этом приближении нет. Строгое решение уравнений Максвелла в калибровке Лоренца для этой задачи дает такую же картину.
Итак, заряд, колеблющийся с малой скоростью относительно положения равновесия, обладает изотропным
излучением. Он равномерно излучает во все стороны, создавая как поперечные, так и продольные
волны. Причем максимальная плотность потока тех и других волн одинакова (о продольных волнах см. Главу 7). Следовательно, продольные волны (если они существуют) можно достаточно просто обнаружить экспериментально! Заметим, что экспериментально таких волн обнаружено не было.
С другой стороны, имеется решение задачи об излучении диполя Герца, где продольные волны отсутствуют. Забегая вперед, скажем, что отсутствие продольных волн связано с условием, приведенным в работе [2] (Градиентная инвариантность):
«Описанная неоднозначность потенциалов дает всегда возможность выбрать их так, чтобы они удовлетворяли одному произвольному, дополнительному условию, - одному, так как мы можем произвольно выбрать одну функцию f в
(8.12). В частности, всегда можно выбрать потенциалы поля так, чтобы скалярный потенциал
φ был равен нулю
».
Как видно из сказанного, даже в рамках одной калибровки можно получить различные по характеру, но функционально одинаковые решения (запаздывающие поля). Это, как уже говорилось, связано с определенными модельными представлениями
в теории электромагнетизма.
Помимо калибровки Лоренца в электродинамике широко используется кулоновская калибровка. Формально последовательный вывод кулоновской калибровки из калибровки Лоренца дан в [4]. Логика доказательства следующая:
1 ∂ψ
Делается замена потенциалов A
→ A
'+gradψ; φ → φ'−  . c ∂t . c ∂t
Показано, что при такой замене поля Е
и Н
сохраняются неизменными.
Заменяя в условии калибровки Лоренца не штрихованные величины штрихованными,
1 ∂φ 1 ∂ 2
ψ 1 ∂φ'
 находят: divA
+ находят: divA
+  = divA
'+Δψ − 2
( 2
− ) = 0 . c
∂t c
∂t c
∂t = divA
'+Δψ − 2
( 2
− ) = 0 . c
∂t c
∂t c
∂t
Для получения кулоновской калибровки необходимо, чтобы выполнялось соотношение
1 ∂ 2
ψ 1 ∂φ'
 Δψ − 2 2 = 2 . c
∂t c
∂t Δψ − 2 2 = 2 . c
∂t c
∂t
При замене потенциалов на штрихованные волновые уравнения для скалярного и векторного потенциалов (в калибровке Лоренца) преобразуются в уравнения
1 ∂ 2
A
' 1 ∂gradφ' ρ
Δ A
'−  2 2
= −μ j
+ 2 2
= −μ j
+  2
; Δ φ'= − 2
; Δ φ'= −  ; divA
'= 0 (1.4.3). c
∂ t c
∂ t
ε ; divA
'= 0 (1.4.3). c
∂ t c
∂ t
ε
Так мы получаем кулоновскую калибровку. Кажется, что с формально-математической точки зрения здесь все корректно, и обе калибровки совершенно равноправны
. Однако:
1. «Корректность» действительно существует, но только формально-символьная.
2. Автор нигде не упоминает о преобразовании начальных
условий.
3. По существу поля Е
и Н
оказываются различными по своей функциональной структуре. Потенциал φ, например, является мгновенно действующим
.
Последнее не совместимо с постулатами СТО. Поэтому не случайно В.Г. Левич, оправдываясь, пишет следующее [4]:
«При кулоновской калибровке скалярный потенциал
φ’ определяется распределением зарядов так, как будто они покоились. Само собой разумеется, напряженности полей Е
и Н,
найденные из решений с кулоновской калибровкой и калибровкой Лоренца,
совпадают».
Выражение: «как будто они покоились
», (хотя заряды движутся (!)
), как раз и отражает мгновенное действие
, поскольку никакого «запаздывания» такие поля не испытывают при движении заряда. Электрическое поле скалярного потенциала движется синхронно
с зарядом, не имеет никакого приписываемого ему «запаздывания
»! Нужно действительно иметь «научное мужество
», чтобы черное назвать белым вопреки фактам. Вернемся к кулоновской калибровке с точки зрения модели электромагнитных явлений.
Во-первых
, классическая связь между скалярным и векторным потенциалами для движущегося заряда A
= φv
/c
2
в общем случае не имеет места. Скалярный потенциал является мгновенно действующим, а векторный (в общем случае) – запаздывающим, поскольку описывается волновым уравнением.
Однако положение можно «исправить». Например, можно записать уравнения (1.4.3) в
другой форме, представив векторный потенциал A
как сумму мгновенно действующего
'
~ "
потенциала и запаздывающего потенциала A
= A
+ A
:
ρ ~ ~ 1 ∂φ'
Δ φ'= −  ; ΔA
= −μj
; divA
+ ; ΔA
= −μj
; divA
+  2
= 0 ε c
∂t 2
= 0 ε c
∂t
2 " ~ 1 ∂ A
1 ∂ ∂A
"
 Δ A
"− 2 2
= 2
(gradφ'+ Δ A
"− 2 2
= 2
(gradφ'+  ); divA
= 0 c
∂ t c
∂t
∂t ); divA
= 0 c
∂ t c
∂t
∂t
Но это уже другая модель описания электромагнитных процессов, которая включает в себя не только запаздывающие потенциалы электромагнитных волн, но и мгновенно действующие потенциалы полей зарядов. Она существенно отличается от калибровки Лоренца. Можно добавить, что здесь поля запаздывающих потенциалов являются вихревыми. Они не создают продольных волн. Источниками электромагнитных волн вихревого характера являются не сами заряды и их движение (как в калибровке Лоренца), а изменение во времени мгновенно действующего поля, создаваемого движущимися
~
~ ∂A
зарядами E
= −(gradφ'+  ) . ) .
∂t
Во вторых
, часто в учебниках по классической электродинамике можно встретить утверждение, что излучение диполя Герца не зависит от выбора калибровки и описывается одинаково в калибровке Лоренца и в кулоновской калибровке. Это утверждение грешит ссылками на теорему о существовании и единственности решений уравнений Максвелла. Однако ни в одном учебнике решения этой задачи в рамках кулоновской калибровки не приводится.
Соответственно, в этих декларативных утверждениях и «доказательствах» ничего не говорится о начальных условиях и их преобразовании при переходе от одной калибровки к другой. Начальные условия игнорируются при постановке физических задач.
Как следствие, физическая
постановка задачи допускает нарушение единственности
решения уравнений. Более того, в рамках уравнений Максвелла может существовать несколько различных физических моделей
описания электромагнитных явлений, связанных с различными калибровками. Это мы уже видели на примере кулоновской калибровки и калибровки Лоренца. Поэтому необходим детальный анализ уравнений Максвелла. Этому вопросу будут посвящены последующие главы книги.
Примечание.
1. Заметим, что мгновенное взаимодействие не противоречит
принципу причинности. Этому сложному философскому вопросу посвящена Глава 2.
2. Мгновенное действие есть и у запаздывающих потенциалов. Например, поперечная электромагнитная волна (однородная плоская волна, ТЕМ волна в однопроводной линии, в двухпроводной линии и т.д.) имеет фазовый множитель ϕ = ωt – kz
. Нетрудно показать, что поперечные компоненты поля должны удовлетворять оператору
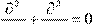 2
. Формально оператор принадлежит эллиптическому типу. Компоненты 2
. Формально оператор принадлежит эллиптическому типу. Компоненты
∂x
∂y
2
электромагнитного поля в поперечной плоскости
x
, y
имеют мгновенно действующий характер. Таким образом, не следует относиться к мгновенному действию как к «монстру» или физической нелепости (см. также [5]).
Можно добавить следующее. Среди различных видов взаимодействий тел в физике имеются контактные
взаимодействия, например, столкновение биллиардных шаров. Ничего предосудительного в таких взаимодействиях физики не видят. Теперь представим себе сферическое материальное тело покрыто слоями резины с различными коэффициентами жесткости. Будем считать, что с ростом радиуса коэффициент жесткости падает.
Можно ли рассматривать столкновение двух тел (покрытых такими слоями) как контактное взаимодействие? Можно. По аналогии кулоновское взаимодействие двух заряженных частиц тоже можно считать «контактным
» взаимодействием. Обратите внимание, как деформируются линии равных потенциалов при столкновении одноименных зарядов. Если при соприкосновении материальных тел (биллиардных шаров, например) осуществляется точечный
контакт, то при взаимодействии зарядов – объемный
, а не точечный контакт. В этом их различие.
Заряд нельзя рассматривать примитивно как, например, биллиардный шар. Заряд окружен своим полем, обладающим абсолютно упругими свойствами. При «столкновении» зарядов они взаимодействуют через свои поля. При этом возникает не точечный
«контакт», а объемный, распределенный по всему пространству. Например, энергию взаимодействия первого заряда со вторым можно записать двумя способами как ρ1
φ2
или как εgradφ1
⋅gradφ2
.
Итак, мгновенное действие относится к контактному типу и не должно вызывать недоумений по поводу бесконечной так называемой «скорости распространения взаимодействий». И, конечно, в «эфирной поддержке» такое взаимодействие не нуждается.
Заключение
Мы покажем далее, что существование в рамках уравнений Максвелла двух типов решений (запаздывающего и вырожденного) проходит «красной нитью» через всю электродинамику. Эти решения не являются взаимоисключающими. Они необходимы для правильного осмысления и описания квазистатических и волновых явлений электромагнетизма.
Причина в том, что поле заряда неразрывно связано со своим зарядом. Какие бы эволюции в пространстве ни совершал заряд, какие бы волны он ни излучал, поле всегда будет определяться только величиной заряда
в системе отсчета, где он покоится.
Соответственно, поля зарядов отвечают за квазистатические явления электродинамики.
Электромагнитные волны после излучения «улетают», в то время как поле заряда остается, сохраняется. Электромагнитные волны и заряды со своими полями это различные
материальные объекты. По этой причине разделение явлений на волновые и квазистатические имеет под собой не только физическую, но одновременно и математическую основу. И с этим мы будем постоянно сталкиваться в дальнейшем.
Источники информации:
1. А.Н. Тихонов, Ф.Ф. Самарский Уравнения математической физики. ГИТТЛ, М. 1953.
2. Л.Д Ландау, Е.М Лифшиц. Теория поля. ГИФФМЛ, М. 1960.
3. В. Пановски, М. Филипс. Классическая электродинамика. ГИФМЛ, М. 1968.
4. В.Г.Левич. Курс теоретической физики, Т.1, ФИЗМАТГИЗ, 1962.
5. М.В. Корнева, В.А. Кулигин, Г.А. Кулигина. Математические ляпы в электродинамике.
http://kuligin.mylivepage.ru/file/index/
Введение
Вопрос о причинности очень важен для обоснования мгновенных взаимодействий.
Философская категория «причинность», как и связанный с ней принцип причинности, восходит к основополагающему принципу диалектического материализма о всеобщей связи и взаимной обусловленности явлений материального мира. Содержание категории «причинность» может быть раскрыто через содержание и конкретизацию взаимной связи исходных философских категорий «причина» и «следствие» (причинно-следственное отношение).
Как известно, раскрытие содержания и конкретизация понятий должны опираться на ту или иную конкретную модель взаимной связи понятий. Модель, объективно отражая определенную сторону связи, имеет границы применимости, за пределами которых ее использование ведет к ложным выводам, но в границах своей применимости она должна обладать не только образностью, наглядностью и конкретностью, но и иметь эвристическую ценность.
Многообразие проявлений причинно-следственных связей в материальном мире обусловило существование нескольких моделей причинно-следственных отношений. Исторически сложилось так, что любая модель этих отношений может быть сведена к одному из двух основных типов моделей или их сочетанию.
a Модели, опирающиеся на временной
подход (эволюционные модели). Здесь главное внимание акцентируется на временной стороне причинно-следственных отношений. Одно событие — «причина» — порождает другое событие — «следствие», которое во времени отстает от причины (запаздывает). Запаздывание — отличительный признак эволюционного
подхода. Причина и следствие взаимно обусловлены. Однако ссылка на порождение следствия причиной (генезис), хотя и законна, но привносится в определение причинно-следственной связи как бы со стороны, извне.
Она фиксирует внешнюю сторону этой связи, не захватывая глубоко сущности. Эволюционный подход развивался Ф. Бэконом, Дж. Миллем и др. Крайней полярной точкой эволюционного подхода явилась позиция Юма. Юм игнорировал генезис, отрицая объективный характер причинности, и сводил причинную связь к простой регулярности событий.
b Модели, опирающиеся на понятие «взаимодействие
» (структурные или диалектические модели). Смысл названий мы выясним позже. Главное внимание здесь уделяется взаимодействию как источнику причинно-следственных отношений. В роли причины выступает само взаимодействие. Большое внимание этому подходу уделял Кант, но наиболее четкую форму диалектический подход к причинности приобрел в работах Гегеля. Из современных советских философов этот подход развивал Г. А. Свечников [1], который стремился дать материалистическую трактовку одной из структурных моделей причинно-следственной связи.
Существующие и использующиеся в настоящее время модели различным образом вскрывают механизм причинно-следственных отношений, что приводит к разногласиям и создает основу для философских дискуссий. Острота обсуждения и полярный характер точек зрения свидетельствуют об их актуальности [2].
Выделим некоторые из дискутируемых проблем.
a Проблема одновременности
причины и следствия. Это основная проблема. Одновременны ли причина и следствие или разделены интервалом времени? Если причина и следствие одновременны, то почему причина порождает следствие, а не наоборот? Если же причина и следствие неодновременны, может ли существовать «чистая» причина, т. е. причина без следствия, которое еще не наступило, и «чистое» следствие, когда действие причины кончилось, а следствие еще продолжается? Что происходит в интервале между причиной и следствием, если они разделены во времени, и т. д.?
b Проблема однозначности
причинно-следственных отношений. Порождает ли одна и та же причина одно и то же следствие или же одна причина может порождать любое следствие из нескольких потенциально возможных? Может ли одно и то же следствие быть порожденным любой из нескольких причин? c Проблема обратного воздействия
следствия на свою причину.
d Проблема связи причины, повода и условий
. Могут ли при определенных обстоятельствах причина и условие меняться ролями: причина стать условием, а условие — причиной? Какова объективная взаимосвязь и отличительные признаки причины, повода и условия?
Решение этих проблем зависит от выбранной модели, т. е. в значительной степени от того, какое содержание будет заложено в исходные категории «причина» и «следствие». Дефиниционный характер многих трудностей проявляется, например, уже в том, что нет единого ответа на вопрос, что следует понимать под «причиной». Одни исследователи под причиной мыслят материальный объект, другие [3]—явление, третьи [4]— изменение состояния, четвертые — взаимодействие и т. д.
К решению проблемы не ведут попытки выйти за рамки модельного представления и дать общее, универсальное определение причинно-следственной связи. В качестве примера можно привести следующее определение:
«Причинность — это такая генетическая связь явлений, в которой одно явление, называемое причиной, при наличии определенных условий неизбежно порождает, вызывает, приводит к жизни другое явление, называемое следствием
» [5].
Это определение формально справедливо для большинства моделей, но, не опираясь на модель, оно не может разрешить поставленных проблем (например, проблему одновременности) и потому имеет ограниченную теоретико-познавательную ценность.
Решая упомянутые выше проблемы, большинство авторов стремятся исходить из современной физической картины мира и, как правило, несколько меньше внимания уделяют гносеологии. Между тем, на наш взгляд, здесь существуют две проблемы, имеющие принципиальное значение: проблема удаления элементов антропоморфизма из понятия причинности и проблема непричинных связей в естествознании. Суть первой проблемы в том, что причинность как объективная философская категория должна иметь объективный характер, не зависящий от познающего субъекта и его активности. Суть второй проблемы: признавать ли причинные связи в естествознании всеобщими и универсальными или считать, что такие связи имеют ограниченный характер и существуют связи непричинного типа, отрицающие причинность и ограничивающие пределы применимости принципа причинности? Мы считаем, что принцип причинности имеет всеобщий и объективный характер и его применение не знает ограничений.
Итак, два типа моделей, объективно отражая некоторые важные стороны и черты причинно-следственных связей, находятся в известной степени в противоречии, поскольку различным образом решают проблемы одновременности, однозначности и др., но вместе с тем, объективно отражая некоторые стороны причинно-следственных отношений, они должны находиться во взаимной связи. Наша первая задача — выявить эту связь и уточнить модели.
2.1 Границы применимости
Попытаемся установить границу применимости моделей эволюционного типа. Причинноследственные цепи, удовлетворяющие эволюционным моделям, как правило, обладают свойством транзитивности [6]. Если событие А есть причина события В (В—следствие А), если, в свою очередь, событие В есть причина события С, то событие А есть причина события С. Если А → В и В → С, то А → С. Таким способом составляются простейшие причинно-следственные цепи. Событие В может выступать в одном случае причиной, в другом — следствием. Эту закономерность отмечал Ф. Энгельс:
«... причина и следствие суть представления, которые имеют значение, как таковые, только в применении к данному отдельному случаю: но как только мы будем рассматривать этот отдельный случай в общей связи со всем мировым целым, эти представления сходятся и переплетаются в представлении универсального взаимодействия, в котором причины и следствия постоянно меняются местами; то, что здесь или теперь является причиной, становится там или тогда следствием и наоборот
» (т. 20, с. 22).
Свойство транзитивности позволяет провести детальный анализ причинной цепи. Он состоит в расчленении конечной цепи на более простые причинно-следственные звенья. Если А → С, то А → В1
, В1
→В2
,..., ВN
→C. Но обладает ли конечная причинноследственная цепь свойством бесконечной делимости? Может ли число звеньев конечной цепи N стремиться к бесконечности?
Опираясь на закон перехода количественных изменений в качественные, можно утверждать, что при расчленении конечной причинно-следственной цепи мы столкнемся с таким содержанием отдельных звеньев цепи, когда дальнейшее деление станет бессмысленным. Заметим, что бесконечную делимость, отрицающую закон перехода количественных изменений в качественные, Гегель именовал «дурной бесконечностью
».
Переход количественных изменений в качественные возникает, например, при делении куска графита. При разъединении молекул вплоть до образования одноатомного газа химический состав не меняется. Дальнейшее деление вещества без изменения его химического состава уже невозможно, поскольку следующий этап — расщепление атомов углерода. Здесь с физико-химической точки зрения количественные изменения приводят к качественным.
В приведенном выше высказывании Ф. Энгельса отчетливо прослеживается мысль о том, что в основе причинно-следственных связей лежит не самопроизвольное волеизъявление, не прихоть случая и не божественный перст, а универсальное взаимодействие. В природе нет самопроизвольного возникновения и уничтожения движения, есть взаимные переходы одних форм движения материи в другие, от одних материальных объектов к другим, и эти переходы не могут происходить иначе, чем через посредство взаимодействия материальных объектов. Такие переходы, обусловленные взаимодействием, порождают новые явления, изменяя состояние взаимодействующих объектов.
Взаимодействие универсально и составляет основу причинности. Как справедливо отмечал Гегель, «взаимодействие есть причинное отношение, положенное в его полном развитии» [7]. Еще более четко сформулировал эту мысль Ф. Энгельс:
«Взаимодействие — вот первое, что выступает перед нами, когда мы рассматриваем движущуюся материю в целом с точки, зрения теперешнего естествознания <...> Так естествознанием подтверждается то ... что взаимодействие является истинной causa finalis
вещей. Мы не можем пойти дальше познания этого взаимодействия именно потому, что позади его нечего больше познавать
» (т. 20, с. 546).
2.2 Диалектическая модель причинности
Поскольку взаимодействие составляет основу причинности, рассмотрим взаимодействие двух материальных объектов, схема которого приведена на рис. 2.1. Данный пример не нарушает общности рассуждений, поскольку взаимодействие нескольких объектов сводится к парным взаимодействиям и может быть рассмотрено аналогичным способом.
Нетрудно видеть, что при взаимодействии оба объекта одновременно воздействуют друг на друга (взаимность действия). При этом происходит изменение состояния каждого из взаимодействующих объектов. Нет взаимодействия — нет изменения состояния [8]. Поэтому изменение состояния какого-либо одного из взаимодействующих объектов можно рассматривать как частное следствие причины — взаимодействия. Изменение состояний всех объектов в их совокупности составит полное следствие.
Очевидно, что такая причинно-следственная модель элементарного звена
эволюционной модели принадлежит классу структурных (диалектических). Следует подчеркнуть, что данная модель не сводится к подходу, развивавшемуся Г. А. Свечниковым, поскольку под следствием Г. А. Свечников, по словам В. Г. Иванова, понимал «...изменение одного или всех взаимодействовавших объектов или изменение характера самого взаимодействия, вплоть до его распада или преобразования
» [9]. Что касается изменения состояний, то это изменение Г. А. Свечников относил к непричинному виду связи.
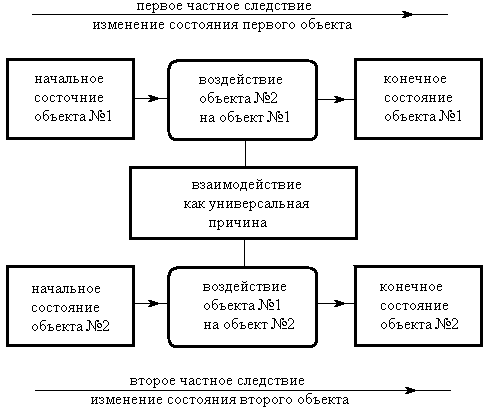
Рис. 2.1 Структурная (диалектическая) модель причинности
Итак, мы установили, что эволюционные модели в качестве элементарного, первичного звена содержат структурную (диалектическую) модель, опирающуюся на взаимодействие и изменение состояний. Несколько позже мы вернемся к анализу взаимной связи, этих моделей и исследованию свойств эволюционной модели. Здесь нам хотелось бы отметить, что в полном соответствии с точкой зрения Ф. Энгельса смена явлений в эволюционных моделях, отражающих объективную реальность, происходит не в силу простой регулярности событий (как у Д. Юма), а в силу обусловленности, порожденной взаимодействием (генезис). Поэтому хотя ссылки на порождение (генезис) и привносятся в определение причинно-следственных отношений в эволюционных моделях, но они отражают объективную природу этих отношений и имеют законное основание.
Вернемся к структурной модели. По своей структуре и смыслу она превосходно согласуется с первым законом диалектики — законом единства и борьбы противоположностей, если интерпретировать:
– единство
— как существование объектов в их взаимной связи (взаимодействии);
– противоположности
— как взаимоисключающие тенденции и характеристики состояний, обусловленные взаимодействием;
– борьбу
— как взаимодействие;
– развитие
— как изменение состояния каждого из взаимодействующих материальных объектов.
Поэтому структурная модель, опирающаяся на взаимодействие как причину, может быть названа также диалектической
моделью причинности. Из аналогии структурной модели и первого закона диалектики следует, что причинность выступает как отражение объективных диалектических противоречий в самой природе, в отличие от субъективных диалектических противоречий, возникающих в сознании человека. Структурная модель причинности есть отражение объективной диалектики природы.
Рассмотрим пример, иллюстрирующий применение структурной модели причинноследственных отношений. Таких примеров, которые объясняются с помощью данной модели, можно найти достаточно много в естественных науках (физике, химии и др.), поскольку понятие «взаимодействие» является основополагающим в естествознании.
Возьмем в качестве примера упругое столкновение двух шаров: движущегося шара А и неподвижного шара В. До столкновения состояние каждого из шаров определялось совокупностью признаков Сa
и Сb
(импульс, кинетическая энергия и т. д.). После столкновения (взаимодействия) состояния этих шаров изменились. Обозначим новые состояния С'a
и С'b
. Причиной изменения состояний (Сa
→ С'a
и Сb
→ С'b
) явилось взаимодействие шаров (столкновение); следствием этого столкновения стало изменение состояния каждого шара.
Как уже говорилось, эволюционная модель в данном случае малопригодна, поскольку мы имеем дело не с причинной цепью, а с элементарным причинно-следственным звеном, структура которого не сводится к эволюционной модели. Чтобы показать это, проиллюстрируем данный пример объяснением с позиции эволюционной модели: «До столкновения шар
А покоился, поэтому причиной его движения является шар
В, который ударил по нему
». Здесь шар В выступает причиной, а движение шара А — следствием. Но с тех же самых позиций можно дать и такое объяснение: «До столкновения шар
В двигался равномерно по прямолинейной траектории. Если бы не шар
А, то характер движения шара
В не изменился бы
». Здесь причиной уже выступает шар А, а следствием — состояние шара В. Приведенный пример показывает:
a определенную субъективность, которая возникает при применении эволюционной модели за пределами границ ее применимости: причиной может выступать либо шар А, либо шар В; такое положение связано с тем, что эволюционная модель выхватывает одну частную ветвь следствия и ограничивается ее интерпретацией;
b типичную гносеологическую ошибку. В приведенных выше объяснениях с позиции эволюционной модели один из однотипных материальных объектов выступает в качестве «активного», а другой — в качестве «страдательного» начала. Получается
так, будто одиниз шаров наделен (по сравнению с другим) «активностью», «волей», «желанием», подобно человеку. Следовательно, только благодаря этой «воле» мы и имеем причинное отношение.
Подобная гносеологическая ошибка определяется не только моделью причинности, но и образностью, которая присуща живой человеческой речи, и типичным психологическим переносом свойств, характерных для сложной причинности (о ней мы будем говорить ниже) на простое причинно-следственное звено. И такие ошибки весьма характерны при использовании эволюционной модели за пределами границ ее применимости. Они встречаются в некоторых определениях причинности. Например: «Итак, причинность определяется как такое воздействие одного объекта на другой, при котором изменение первого объекта (причина) предшествует изменению другого объекта и необходимым, однозначным образом порождает изменение другого объекта (следствие
)» [10]. Трудно согласиться с таким определением, поскольку совершенно не ясно, почему при взаимодействии (взаимном действии!) объекты должны деформироваться не одновременно, а друг за другом? Какой из объектов должен деформироваться первым, а какой вторым (проблема приоритета)?
2.3 Свойства диалектической модели причинности
Рассмотрим теперь, какие качества удерживает в себе структурная модель причинности. Отметим среди них следующие: объективность, универсальность, непротиворечивость, однозначность.
Объективность
причинности проявляется в том, что взаимодействие выступает как объективная причина, по отношению к которой взаимодействующие объекты являются равноправными
.
Здесь не остается возможности для антропоморфного истолкования.
Универсальность
обусловлена тем, что в основе причинности всегда лежит взаимодействие
.
Причинность универсальна, как универсально само взаимодействие.
Непротиворечивость
обусловлена тем, что, хотя причина и следствие (взаимодействие и изменение состояний) совпадают во времени, они отражают различные стороны
причинно-следственных отношений. Взаимодействие предполагает пространственную связь объектов, изменение состояния — связь состояний каждого из взаимодействующих объектов во времени.
Помимо этого структурная модель устанавливает однозначную связь
в причинно-следственных отношениях независимо от способа математического описания взаимодействия. Более того, структурная модель, будучи объективной и универсальной, не предписывает естествознанию ограничений на характер взаимодействий. В рамках данной модели справедливы и мгновенное дально- или близкодействие, и взаимодействие с любыми конечными скоростями
. Появление подобного ограничения в определении причинноследственных отношений явилось бы типичной метафизической догмой, раз и навсегда постулирующей характер взаимодействия любых систем, навязывая физике и другим наукам натурфилософские рамки со стороны философии, либо ограничило пределы применимости модели настолько, что польза от такой модели оказалась бы весьма скромной.
Здесь уместно было бы остановиться на вопросах, связанных с конечностью скорости распространения взаимодействий.
Вопрос о содержании этого термина мы обсудим позже.
Рассмотрим пример. Пусть имеются два неподвижных заряда. Если один из зарядов начал двигаться с ускорением, то электромагнитная волна подойдет ко второму заряду с запаздыванием. Не противоречит ли данный пример структурной модели и, в частности, свойству взаимностидействия, поскольку при таком взаимодействии заряды оказываются в неравноправном положении? Нет, не противоречит. Данный пример описывает не простое взаимодействие, а сложную
причинную цепь, в которой можно выделить три различных звена.
1. Взаимодействие первого заряда с объектом
, который вызывает его ускорение. Результат этого взаимодействия — изменение состояния источника, воздействовавшего на заряд, и, в частности, потеря этим источником части энергии, изменение состояния первого заряда (ускорение) и появление электромагнитной волны, которая излучилась первым зарядом при его ускоренном движении.
2. Процесс распространения
электромагнитной волны, излученной первым зарядом (распространение взаимодействия
?).
3. Процесс взаимодействия второго заряда с электромагнитной волной
. Результат взаимодействия — ускорение второго заряда, рассеяние первичной электромагнитной волны и излучение электромагнитной волны вторым зарядом.
В данном примере мы имеем два различных взаимодействия, каждое из которых укладывается в структурную модель причинности. Таким образом, структурная модель превосходно согласуется как с классическими, так и с релятивистскими теориями, а конечная скорость распространения взаимодействий не является принципиально необходимой для структурной модели причинности.
Касаясь структурной модели причинности, отметим, что ей не противоречат реакции распада и синтеза объектов. В этом случае между объектами либо разрушается относительно устойчивая связь как особый вид взаимодействия, либо такая связь образуется в результате взаимодействия.
Поскольку квантовые теории (равно как и классические) широко используют категории «взаимодействие» и «состояние», то структурная модель принципиально применима и в этой области естествознания. Встречающиеся иногда трудности обусловлены, на наш взгляд, тем, что, обладая хорошо развитым математическим формализмом, квантовые теории еще недостаточно полно развиты и отточены в плане понятийной интерпретации. Марио Бунге [11] пишет, например, об интерпретации ψ -функции:
«Одни относят функцию
ψ к некоторой индивидуальной системе, другие — к некоторому действительному или потенциальному статистическому ансамблю тождественных систем, третьи рассматривают
ψ -функцию как меру нашей информации, или степень уверенности относительно некоторого индивидуального комплекса, состоящего из макросистемы и прибора, или же, наконец, просто как каталог измерений, производимых над множеством идентично приготовленных микросистем
».
Такое многообразие вариантов истолкования ψ-функции затрудняет строгую причинную интерпретацию явлений микромира. Это одно из свидетельств того, что квантовые теории находятся в стадии становления и развития и не достигли уровня внутренней завершенности, свойственной классическим теориям.
Но о проблемах становления квантовых теорий свидетельствует не только интерпретация ψ-функции. Хотя релятивистская механика и электродинамика на первый взгляд представляются законченными теориями, более глубокий анализ показывает, что по ряду причин эти теории также не избежали противоречий и внутренних трудностей. Например, в электродинамике существуют проблема электромагнитной массы, проблема реакции излучения заряда и др. Неудачи в попытках разрешения этих проблем в рамках самих теорий в прошлом и бурное развитие теорий микромира породили надежду, что развитие квантовых теорий поможет ликвидировать трудности. А до тех пор они должны восприниматься какнеизбежное «зло», с которым так или иначе приходится мириться, и ждать успехов от квантовых теорий.
В то же время квантовые теории сами столкнулись со многими проблемами и противоречиями. Любопытно заметить, что часть этих трудностей имеет «классическую
» природу, т. е. досталась «по наследству» от классических теорий и обусловлена их внутренней незавершенностью. Получается «порочный круг
»: разрешение противоречий классических теорий мы возлагаем на квантовые теории, а трудности квантовых определяются противоречиями классических.
Со временем надежда на способность квантовых теорий устранить противоречия и трудности в теориях классических стала угасать, но до сих пор интерес к разрешению противоречий классических теорий в рамках их самих все еще остается на втором плане.
Таким образом, трудности, встречающиеся иногда при объяснении явлений микромира с позиции причинности, имеют объективное происхождение и объясняются особенностями становления квантовых теорий, но они не являются принципиальными, запрещающими или ограничивающими применение принципа причинности в микромире, в частности применение структурной модели причинности.
Причинность и взаимодействие всегда взаимосвязаны. Если взаимодействие обладает свойствами всеобщности, универсальности и объективности, то столь же универсальны, всеобщи и объективны причинно-следственные связи и отношения. Поэтому в принципе нельзя согласиться с утверждениями Бома, что при описании явлений микромира можно в одних случаях опираться на философский индетерминизм, в других — придерживаться принципа причинности [12].
Мы считаем глубоко ошибочной мысль В. Я. Перминова о том, что «понятие дополнительности указывает путь примирения
(!)
детерминизма и индетерминизма
» [13], независимо от того, относится эта мысль к философии естествознания или к конкретной естественнонаучной теории. Путь примирения материалистической точки зрения с позицией современного позитивизма в данном вопросе есть эклектика, есть отрицание объективной диалектики. В. И. Ленин подчеркивал, что «вопрос о причинности имеет особенно важное значение для определения философской линии того или другого новейшего «изма».
..» (т. 18, с. 157). И путь становления квантовых теорий лежит не через отрицание или ограничение, а через утверждение причинности в микромире.
2.4 Описание, объяснение и причинность
Структура научных теорий естествознания и функции научных теорий прямо или косвенно связаны с причинным объяснением явлений материального мира. Если обратиться к структурной модели причинности, то можно выявить два характерных момента, две важные стороны, которые так или иначе связаны с функциями научных теорий.
Первая касается описания причинных связей и отвечает на вопрос: как, в какой последовательности? Ей соответствует любая ветвь частного следствия, связывающая обусловленные состояния. Она дает не только описание
перехода объекта из одного состояния в другое, но описывает и охватывает всю причинную цепь как последовательность связанных и обусловленных состояний, не вдаваясь глубоко в сущность, в источник изменения состояний звеньев цепи.
Вторая сторона отвечает на вопрос: почему, по какой причине? Она, напротив, дробит причинно-следственную цепь на отдельные элементарные звенья и дает объяснение изменений состояний, опираясь на взаимодействие. Это объясняющая
сторона.
Две эти стороны прямо связаны с двумя важными функциями научной теории: объясняющей и описательной. Поскольку принцип причинности лежал, и будет лежать в основе любой естественнонаучной теории, теория всегда будет выполнять эти две функции: описание и объяснение [14].
Однако не только в этом проявляется методологическая функция принципа причинности. Внутреннее структурирование самой теории также связано с этим принципом. Возьмем, к примеру, классическую механику с ее тремя традиционными разделами: кинематикой, динамикой и статикой. В кинематике силовые взаимодействия не рассматриваются, а идет описание
(физическое и математическое) видов движения материальных точек и материальных объектов. Взаимодействие подразумевается, но оно отходит на второй план, оставляя приоритет описанию сложных связанных движений через характеристики их состояний. Разумеется, этот факт не может служить поводом для классификации кинематики как непричинного способа описания, поскольку кинематика отражает эволюционную сторону причинно-следственных отношений, связывающих различные состояния.
Динамика
— теоретический раздел, который включает в себя полное причинноследственное описание и объяснение, опираясь на структурную модель причинноследственных отношений. В этом смысле кинематика может считаться подразделом динамики.
Особый интерес с точки зрения причинности представляет статика, в которой следственные цепи вырождены (отсутствуют), и мы имеем дело только со связями и взаимодействиями статического характера. В отличие от явлений объективной реальности, где не существует абсолютно устойчивых систем, статические задачи — идеализация или предельный случай, допустимый в частнонаучных теориях. Но принцип причинности справедлив и здесь, поскольку не только решать статические задачи, но и понять сущность статики без применения «принципа виртуальных перемещений» или родственных ему принципов невозможно. «Виртуальные перемещения» непосредственно связаны с изменением состояний в окрестности состояния равновесия, т. е., в конечном счете, с причинно-следственными отношениями.
Рассмотрим теперь электродинамику. Иногда ее отождествляют только с уравнениями
Максвелла. Это неверно, поскольку уравнения Максвелла описывают поведение волн (излучение, распространение, дифракцию и т. д.) при заданных граничных и начальных условиях. Они не включают в себя описание взаимодействия как взаимного действия. Принцип причинности привносится вместе с граничными и начальными условиями (запаздывающие потенциалы). Это своеобразная «кинематика» волновых процессов, если подобное сравнение позволительно. «Динамику», а с ней и причинность, вносит уравнение движения Лоренца, описывающее силовые стороны взаимодействия. Именно связь уравнений Максвелла и уравнения движения Лоренца обеспечивает достаточно полное причинно-следственное описание явлений электромагнетизма. Подобные примеры можно было бы продолжить. Но и приведенных достаточно, чтобы убедиться, что причинность и ее структурная модель находят отражение в структуре и функциях научных теорий.
2.5 Эволюционная модель причинности
Если в начале нашей работы мы шли от эволюционной модели причинности к структурной, то теперь предстоит обратный путь от структурной модели к эволюционной. Это необходимо, чтобы правильно оценить взаимную связь и отличительные особенности эволюционной модели.
Уже в неразветвленной линейной причинно-следственной цепи мы вынуждены отказаться от полного описания всех причинно-следственных отношений, т. е. не учитываем некоторые частные следствия. Структурная модель позволяет неразветвленные линейные причинно-следственные цепи свести к двум основным типам.
a Объектная
причинная цепь. Образуется тогда, когда мы выделяем какой-либо материальный объект и следим за изменением его состояния во времени. Примером могут служить наблюдения за состоянием броуновской частицы, или за эволюциями космического корабля, или за распространением электромагнитной волны от антенны передатчика до антенны приемника.
b Информационная
причинная цепь. Появляется, когда мы следим не за состоянием материального объекта, а за некоторым информирующим явлением, которое в процессе взаимодействий различных материальных объектов связано последовательно во времени с различными объектами. Примером может служить передача устной информации с помощью эстафеты и т. п.
Все линейные неразветвленные причинные цепи сводятся к одному из этих двух типов или к их комбинации. Такие цепи описывают с помощью эволюционной модели причинности. При эволюционном описании взаимодействие остается на втором плане, а на первый план выходит материальный объект или индикатор его состояния. В силу этого главное внимание сосредоточивается на описании последовательности событий во времени. Поэтому данная модель получила название эволюционной
.
Линейная неразветвленная причинная цепь сравнительно легко поддается анализу с помощью сведения ее к совокупности элементарных звеньев и анализа их посредством структурной модели. Но такой анализ не всегда возможен.
Существуют сложные причинные сети, в которых простые причинно-следственные цепочки пересекаются, ветвятся и вновь пересекаются. Это приводит к тому, что применение структурной модели делает анализ громоздким, а иногда и технически невозможным.
Помимо этого нас часто интересует не сам внутренний процесс и описание внутренних причинно-следственных отношений, а начальное воздействие и его конечный результат.
Подобное положение часто встречается при анализе поведения сложных систем (биологических, кибернетических и др.). В таких случаях детализация внутренних процессов во всей их совокупности оказывается избыточной, ненужной для практических целей, загромождающей анализ. Все это обусловило ряд особенностей при описании причинно-следственных отношений с помощью эволюционных моделей. Перечислим эти особенности.
1. При эволюционном описании причинно-следственной сети полная причинная сеть огрубляется.
Выделяются главные цепи, а несущественные отсекаются, игнорируются. Это значительно упрощает описание, но подобное упрощение достигается ценой потери части информации, ценой утраты однозначности описания.
2. Чтобы сохранить однозначность и приблизить описание к объективной реальности, отсеченные ветви и причинные цепи заменяются совокупностью условий
. От того, насколько правильно выделена основная причинная цепь и насколько полно учтены условия, компенсирующие огрубление, зависят полнота, однозначность и объективность причинно-следственного описания и анализа.
3. Выбор
той или иной причинно-следственной цепи в качестве главной
определяется во многом целевыми установками исследователя, т. е. тем, между какими явлениями он хочет проанализировать связь. Именно целевая установка заставляет выискивать главные причинно-следственные цепи, а отсеченные заменять условиями. Это приводит к тому, что при одних установках главную роль выполняют одни цепи, а другие заменяются условиями. При других установках эти цепи могут стать
условиями, а роль главных будут играть те, что раньше были второстепенными. Таким образом, причины и условия меняются ролями.
4. Условия
играют важную роль, связывая объективную причину и следствие. При различных условиях, влияющих на главную причинную цепь, следствия будут различными. Условия как бы создают то русло, по которому течет цепь исторических событий или развитие явлений во времени. Поэтому для выявления глубинных, сущностных причинно-следственных отношений необходим тщательный анализ, учет влияния всех внешних и внутренних факторов, всех условий, влияющих на развитие главной причинной цепи, и оценка степени влияния.
5. Эволюционное описание основное внимание уделяет не взаимодействию, а связи событий
или явлений во времени. Поэтому содержание понятий «причина» и «следствие» изменяется, и это весьма важно учитывать. Если в структурной модели взаимодействие
выступает истинной
causa finalis — конечной причиной, то в эволюционной — действующей
причиной (causa activa) становится явление или событие.
6. Следствие
также меняет свое содержание. Вместо связи состояний материального объекта при его взаимодействии с другим в качестве следствия выступает некоторое событие или явление, замыкающее причинно-следственную цепь. В силу этого причина в эволюционной модели всегда предшествует
следствию. В указанном выше смысле причина и следствие в эволюционной модели могут выступать как однокачественные
явления, с двух сторон замыкающие причинно-следственную цепь. Следствие
одной цепи может явиться причиной
и началом другой цепи, следующей за первой во времени. Это обстоятельство обусловливает свойство транзитивности эволюционных моделей причинности.
Мы здесь коснулись только главных особенностей и отличительных признаков эволюционной модели. Структурная модель причинности может успешно использоваться для сравнительно простых причинных цепей и систем. В реальной практике приходится иметь дело и со сложными системами. Вопрос о причинно-следственном описании поведения сложных систем практически всегда опирается на эволюционную модель причинности.
Итак, мы рассмотрели два типа моделей, отражающих причинно-следственные отношения в природе, проанализировали взаимную связь этих моделей, границы их применимости и некоторые особенности. Проявление причинности в природе многообразно и по форме, и по содержанию. Вполне вероятно, что этими моделями не исчерпывается весь арсенал форм причинно-следственных отношений. Но как бы ни были разнообразны эти формы, причинность всегда будет обладать свойствами объективности, всеобщности и универсальности. В силу этого принцип причинности выполнял и всегда будет выполнять важнейшие мировоззренческие и методологические функции в современном естествознании и философии естествознания. Многообразие форм проявления причинноследственных отношений не может служить поводом для отказа от материалистического принципа причинности или утверждений об ограниченной его применимости.
Заканчивая исследование проблемы причинно-следственных отношений, мы можем сказать, что мгновенные взаимодействия не противоречат диалектической (структурной) модели причинности. Мы можем без боязни использовать модели, опирающиеся на мгновенные (контактные) взаимодействия, тем более что вся механика Ньютона уже более 200 лет успешно опирается на них.
2.6 Скорость распространения взаимодействий
В физике широко используется понятие «скорость распространения взаимодействий». Попробуем разобраться в содержании этого понятия. Прежде всего, нам необходимо определиться с понятием «взаимодействие».
Процитируем БСЭ:
«ВЗАИМОДЕЙСТВИЕ
в физике
, воздействие тел или частиц друг на друга, приводящее к изменению состояния их движения. В механике Ньютона взаимное действие тел друг на друга количественно характеризуется силой. Более общей характеристикой В
. является потенциальная энергия. Первоначально в физике утвердилось представление о том, что В.
между телами может осуществляться непосредственно через пустое пространство, к-рое не принимает никакого участия в передаче В
.; при этом В
. перемещается мгновенно…. В этом состояла т.н. концепция дальнодействия
…
».
Такая интерпретация не полна. В механике Ньютона взаимодействие характеризуется двумя сторонами: силовой и энергетической:
«Сила
– это свойство
материального объекта (источника данного свойства), которое проявляется при взаимодействии материальных объектов и приводит к изменению состояния взаимодействующих объектов (импульс, траектория и др.)
».
«Работа
– объективная количественная характеристика качественного
изменения движения материи, характеризующая энергетическую сторону взаимодействия
».
Как было показано в Главе 1, мгновенное взаимодействие относится к контактному типу. Оно, не противоречит принципу причинности. В полевой механике Ньютона такое взаимодействие осуществляется через квазистатические поля, мгновенно действующего характера, окружающие электрические заряды или гравитационные заряды (гравитационные массы). Именно эти поля обеспечивают «контакт».
Тем не менее, концепция мгновенного взаимодействия была незаслуженно отклонена. Причиной послужил предрассудок: для передачи характеристик взаимодействия необходим некий «посредник». Продолжим цитату из БСЭ:
«Было доказано
, что В
. электрически заряженных тел осуществляется не мгновенно
и перемещение одной заряженной частицы приводит к изменению сил, действующих на др.
частицы, не в тот же момент, а лишь спустя конечное время. … Соответственно имеется «посредник
», осуществляющий В
. между заряженными частицами. Этот посредник был назван электромагнитным полем. …. Возникла новая концепция – концепция близкодействия
, к-рая затем была распространена на любые другие В
.»
«Доказательство», о котором говорится, опирается на факт, что уравнения Максвелла в калибровке Лоренца сводятся к волновым уравнениям. Волновое взаимодействие зарядов было нами рассмотрено выше, где показано, что все можно объяснить и без привлечения этого понятия. Несмотря на то, что этими уравнениями пользуются уже более ста лет, надлежащего анализа уравнений не было проведено. Мы в Главе 1 показали, что имеются «вырожденные» решения, отражающие мгновенный характер взаимодействий между зарядами. Далее, в Главе 7 мы покажем, что волновая электродинамика не имеет своим пределом квазистатическую, и не способна дать корректное объяснение квазистатическим явлениям. Более того, мы покажем, что поля зарядов и электромагнитные волны – различные виды материи. По этой причине «доказательство» опирается на укоренившиеся предрассудки. Перенос концепции близкодействия на все без исключения явления материального мира есть неправомерная абсолютизация, превращающая физику в догму.
Итак, взаимодействие есть процесс
, который характеризуется взаимным изменением характеристик состояний материальных объектов (переход видов энергии из одного вида в другой и обратно, от одного материального объекта к другому, изменение параметров самих материальных объектов и т.д.). Взаимодействие локализовано в пространстве и может иметь определенную продолжительность во времени.
Но взаимодействие не материальный объект
. Оно не имеет своих параметров таких, как, например, «масса» и т. п. По этой причине говорить о «скорости распространения взаимодействия», беспредметно. «Скорость распространения взаимодействия» - бессодержательное понятие. Можно говорить об интенсивности взаимодействия, о скорости течения процесса во времени, но не о «скорости его распространения».
Вернемся к третьему параграфу этой главы. Пусть имеются два заряда. Один из зарядов начал двигаться. От него распространяется возмущение (волна). Второй заряд
«почувствует» это возмущение только тогда, когда возмущение достигнет его.
Существует ли взаимодействие второго заряда с этим возмущением, если это возмущение еще только распространяется и не достигло второго заряда? О какой «скорости распространения взаимодействий» можно говорить, если взаимодействие еще не наступило
? Отождествление процесса распространения волны и «распространения взаимодействия» есть следствие философской несостоятельности (философского невежества) человека, придерживающегося такой терминологии.
Источники информации:
1 См., напр.: Свечников Г. А. Причинность и связь состояний в физике. М., 1971; Он же. Диалектикоматериалистическая концепция причинности // Современный детерминизм: Законы природы / Под ред. Г. А. Свечникова и др. М., 1973. С. 125, и др.
2 См., напр.: Тюхтин В. С. Отражение, системы, кибернетика. М., 1972; Уемов А. И., Остапенко С. В.
Причинность и время // Современный детерминизм: Законы природы. С. 214; Оруджев 3. М., Ахундов М. Д. Временная структура причинной связи // Филос. науки. 1969. № 6. С. 63; Жаров А. М. Временное соотношение причины и следствия и неопределенность // Там же. 1984. № 3. С. 89.
3 Кузнецов И. В. Избранные труды по методологии физики. М., 1. 975.
4 Материалистическая диалектика: В 5 т. Т. 1: Объективная диалектика / Под общ. ред. Ф. В. Константинова и В. Г. Марахова; Отв. ред. Ф. Ф. Вяккерев. М., 1981. С. 212.
5 Кузнецов И. В. Указ. соч. С. 237.
6 О парадоксах «нетранзитивности» см.: Налетов Н. 3. Причинность и теория познания. М., 1975.
7 Гегель Г. В. Ф. Энциклопедия философских наук: В 3 т. Т. 1:Наука логики. М., 1974. С. 335.
8 Под термином «состояние» мы понимаем количественную и качественную определенность самодвижения объекта. Другие определения см.: Старжинский В. П. Понятие «состояние» и его методологическая роль в физике. Минск, 1979.
9 Иванов В. Г. Причинность и детерминизм. Л., 1974.
10 Материалистическая диалектика. Т. 1. С. 213.
11 Бунге М. Философия физики. М., 1975. С. 99.
12 Бом Д. Причинность и случайность в современной физике. М., 1959.
13 Перминов В. Я. Проблема причинности в философии и естествознании. М., 1979. С. 209.
14 См., напр.: Никитин Е. П. Объяснение — функция науки. М., 1970.
3.1 Проблема электромагнитной массы (проблема «4/3»)
Анализ уравнений Максвелла мы начнем с проблемы электромагнитной массы. Мы покажем, что в рамках уравнений Максвелла решение этой проблемы существует, т.е. электромагнитная масса заряда обладает стандартными
свойствами инерциальной массы. Это даст нам возможность далее применить хорошо развитый аппарат теоретической механики (механики Ньютона) к описанию и объяснению квазистатических явлений электромагнетизма.
Решение этой проблемы важно для установления четкой связи и преемственности между электродинамикой и механикой. Механика (при решении этой проблемы) найдет поддержку своих основ в электродинамике, а электродинамика получит свою законную основу в механике, используя ее принципы и методы. Сейчас эта взаимная связь может быть охарактеризована как иллюзия. Не случайно Голдсштейн в своей книге
«Классическая электродинамика» [1] называет электромагнитные поля «аномальными», т.е. весьма плохо вписывающимися не только в классическую, но и даже в релятивистскую механику.
Как известно, инерциальная масса частицы m
в механике Ньютона связана со своим импульсом P
соотношением P
=m
v
. Точно такое же соотношение должно иметь место для плотности энергии частицы w
с плотностью потока S:
S
=w
v
.
Теми же свойствами должна обладать и плотность электромагнитной энергии поля заряда S
e
= w
e
v
(3.1.1), где w
e
=  (gradφ) 2
(3.1.2) – плотность энергии электромагнитной массы. (gradφ) 2
(3.1.2) – плотность энергии электромагнитной массы.
В соответствии с формулой Томсона Е
= mc
2
(см. Дополнение в конце Главы 3) электромагнитную массу заряженной частицы можно определить двойственным образом: либо через квадрат электрического поля заряда, либо через плотность пространственного заряда и его потенциал
m
e
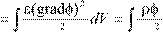 dV dV
2c
2c
где ρ и φ есть, соответственно, плотность пространственного заряда и потенциал этого заряда.
Проблема электромагнитной массы возникла после неудачных попыток связать электромагнитную массу заряженной частицы с ее электромагнитным импульсом и кинетической энергией, подобно тому, как это делается в классической механике. Установление подобной связи могло бы подтвердить электромагнитную природу вещества.
Действительно, электромагнитный импульс поля Р
е
заряда можно вычислить, опираясь на вектор Пойнтинга S
, а кинетическую энергию поля Ке
логически можно связать с энергией магнитного поля, поскольку у неподвижного заряда магнитное поле отсутствует. Магнитное поле заряда возникает тогда, когда заряд движется. Казалось бы, что каждый элемент движущегося заряда, имеющий скорость v
, должен иметь электромагнитный импульс, направленный вдоль вектора скорости.
Однако исследователи на этом пути столкнулись с трудностями, которые в то время решить не удалось. Вычисления для частицы с равномерным распределением плотности пространственного заряда приводили к следующим не характерным для механики соотношениям
{E
×H
] 4 μH
2
4 v
2
 P
e
= ∫ P
e
= ∫
 c
2 dV
= c
2 dV
=  3
m
e
v
; K
e
= ∫ 3
m
e
v
; K
e
= ∫
 2c
2 dV
= 3
m
e
2
(3.1.3) 2c
2 dV
= 3
m
e
2
(3.1.3)
Как мы видим, в формулах появился странный коэффициент «4/3» вместо единицы. По этой причине проблема электромагнитной массы получила название «проблемы 4/3» [2].
Формулы (3.1.3) дают интегральные соотношения. Проанализируем детальную картину плотности потока, вычисленного с помощью вектора Пойнтинга.
Пример
1.
Рассмотрим заряд, движущийся с постоянной скоростью v
вдоль оси z
. Это означает, что любой элемент заряда имеет одну и ту же скорость v
(см. рис. 3.1а
). Для простоты будем считать, что плотность пространственного заряда постоянна. Однако, как показано на этом рисунке (см. рис. 3.1б
), для различных точек заряда векторы Пойнтинга S
имеют различные величины и направления. В точках, наиболее удаленных от оси z
, плотность вектора S
максимальна, а на осевой линии она равна нулю, поскольку здесь нет магнитного поля.
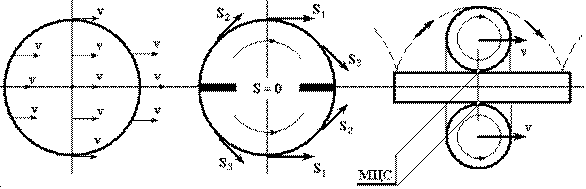 Рис. Рис.
3.1 Движущийся заряд: а) распределение скоростей в движущемся заряде; б) распределение вектора Пойнтинга в этом заряде; в) перемещение резинового тора по деревянной палке; МЦС – мгновенный центр скоростей.
Направление вектора Пойнтинга напоминает перемещение резинового тора, надетого на палку. Внутренние слои тора за счет трения о палку не перемещаются, как показано на рис. 3.1в.
Поэтому для перемещения тора приходится «закручивать» верхние слои тора. При этом слои поперечного сечения тора (имеющие форму окружности, как показано на рис. 3.1в
) движутся по палке подобно колесу по дороге. Их мгновенный центр скоростей расположен на поверхности палки. Мгновенным центром скоростей для движущегося заряда служит отрезок (см. 3.1б
), где вектор Пойнтинга равен нулю (S
= 0).
Вот здесь и возникают вопросы. Почему направление вектора Пойнтинга не совпадает с вектором скорости движения частей заряда? Почему в системе отсчета, где заряд неподвижен
, нет кругового потока вектора Пойнтинга, а в движущейся системе существует круговой поток электромагнитного импульса (в соответствии с вектором Пойнтинга)? Почему различные точки заряда, имеющие один и тот же вектор скорости и одинаковую плотность, дают различный вклад в суммарный электромагнитный импульс заряда?
Абсурдность рассмотренной картины подтверждается и теоремой (Л.Д. Ландау), согласно которой движение тела всегда можно представить как сумму двух независимых движений: поступательного и вращательного
. Следовательно, если есть вращательное движение в одной инерциальной системе отсчета, то оно должно существовать в любой другой инерциальной системе. Если же вращательного движения нет, то его не должно быть и в других инерциальных системах. Здесь явное несоответствие (расхождение) между механикой и электродинамикой.
Пример
2
. Теперь мы рассмотрим бесконечную заряженную плоскость, которая изображена на рис. 3.2. Если плоскость движется вдоль оси y
, то плотность потока вновь в 2 раза больше, чем требуется.
S
y
= [E
×H
] =ε(gradφ)2
v
Если же плоскость перемещается вдоль оси x
, то S
x
равно нулю, поскольку магнитное поле благодаря симметрии будет отсутствовать.
S
x
= [E
×H
] = 0
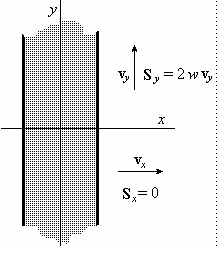
Рис. 3.2
Как известно, в природе масса есть скалярная
величина. Теперь мы, следуя логике, должны признать, что скалярная инерциальная масса должна иметь тензорные
свойства? Это абсурд! Не только в классическом (ньютоновском), но и в релятивистском случае мы сталкиваемся с проблемой «4/3».
3.2 Вектор Умова
Очевидно, что вектор Пойнтинга не приемлем для вычисления плотности потока поля заряда. Запишем уравнения для квазистатического поля заряда в квазистатическом приближении.
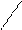 Δφ = −
ρ
(3.2.1) ΔA
= −μj
(3.2.2) divA
+ Δφ = −
ρ
(3.2.1) ΔA
= −μj
(3.2.2) divA
+  1
2
∂φ
= 0 (3.2.3) ε c
∂t 1
2
∂φ
= 0 (3.2.3) ε c
∂t
При этом векторный потенциал А
связан со скалярным φ так же, как плотность тока связана с плотностью заряда. φv
A
=  2
(3.2.4) j
= ρv
(3.2.5) c 2
(3.2.4) j
= ρv
(3.2.5) c
Эти дополнительные уравнения (3.2.4) и (3.2.5) будут необходимы нам для последующего анализа.
Нам необходимо показать, что уравнения (3.2.1), (3.2.2) и (3.2.3) соответствуют классической механике. Для реализации этой цели мы выразим векторный потенциал A
в уравнении (3.2.1) через скалярный потенциал φ , используя уравнения (3.2.4) и (3.2.5).
1 ∂
ΔA
+μj
=  2
{rot[−gradφ×v
]+ 2
{rot[−gradφ×v
]+  (−gradφ) + v
div(−gradφ) = 0 (3.2.6) c
∂t (−gradφ) + v
div(−gradφ) = 0 (3.2.6) c
∂t
В механике сплошных сред
существует уравнение сохраняемости вектора а
и интенсивности его векторных трубок [3],
которое записано ниже:
rot[a
×v
] v
diva
= 0 v
diva
= 0
∂t
Если в нем мы заменим вектор а
вектором Е
= –gradφ/c
2
, тогда мы получим уравнение (3.2.6) для свободного заряда. Подобным образом из уравнения (3.2.3) мы получаем уравнение непрерывности, использующееся в механике сплошных сред
[3].
∂φ
divv
φ+  = 0 (3.2.7) ∂t = 0 (3.2.7) ∂t
Уравнение (3.2.8) определяет потенциал φ , который создается источником с обильностью ρ/ε.
Δφ = − (3.2.8) (3.2.8)
Мы видим, что квазистатическая электродинамика и механика сплошных сред имеют общие уравнения. Это рождает надежду найти решение первого аспекта проблемы электромагнитной массы. Теперь мы можем приступить к доказательству существования электромагнитной массы у заряда.
Доказательство.
Пусть потенциал φ создается источником ρ/ε (3.2.8). Запишем интеграл I.
1 ∂φ ε ∂φ
  I
= ∫ρ ∂t dV
= − 2 ∫Δφ ∂t dV
(3.2.9) 2 где dV
– элемент объема. I
= ∫ρ ∂t dV
= − 2 ∫Δφ ∂t dV
(3.2.9) 2 где dV
– элемент объема.
Используя теорему Гаусса, преобразуем интеграл I
.
ε ∂φ 0
ε ∂ 2
  I
= − ∫
∂t
gradφn
d
σ + 4 ∫
∂t
(gradφ) dV
(3.2.10) 2 I
= − ∫
∂t
gradφn
d
σ + 4 ∫
∂t
(gradφ) dV
(3.2.10) 2
где: d
σ – элемент поверхности; n
о
– единичная нормаль к поверхности.
С другой стороны, используя уравнения (3.2.6) и (3.2.7), мы можем представить уравнение (3.2.9) в следующей форме.
ε 0
ε ∂ 2
  I
= −∫[gradφ×[v
×gradφ]]n
d
σ − 4 ∫
∂t
(gradφ) dV
(3.2.11) 2 I
= −∫[gradφ×[v
×gradφ]]n
d
σ − 4 ∫
∂t
(gradφ) dV
(3.2.11) 2
Сравнивая уравнение (3.2.10) с (3.2.11), получим:
0 ∂w
e
 ∫S
u
n
d
σ + ∫ ∫S
u
n
d
σ + ∫  ∂t dV
= 0 (3.2.12) где: S
u
– плотность потока вектора Умова ∂t dV
= 0 (3.2.12) где: S
u
– плотность потока вектора Умова
ε ∂φ
 S
u
= {− gradφ +[gradφ×[v
×gradφ]} = w
e
v
(3.2.13) S
u
= {− gradφ +[gradφ×[v
×gradφ]} = w
e
v
(3.2.13)
2 ∂t
w
e
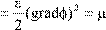 e
с
2
(3.2.14) – плотность энергии поля заряда: μe
- плотность электромагнитной массы. e
с
2
(3.2.14) – плотность энергии поля заряда: μe
- плотность электромагнитной массы.
Уравнение (3.2.12) есть интегральная форма закона сохранения энергии Умова
, который был опубликован им [4] еще в 1874 для механики сплошных сред.
Очевидно уравнения (3.2.13) и (3.2.14) прекрасно соответствуют соотношениям механики Ньютона (3.1.1) и (3.1.2). Используя этот результат, мы можем дать корректное вычисление электромагнитной массы, которое устраняет трудности в рассмотренных ранее примерах. Полученные соотношения справедливы для зарядов произвольной формы.
m
e
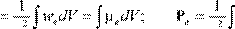 S
e
dV
; P
e
= m
e
v
c c S
e
dV
; P
e
= m
e
v
c c
Что касается вектора Пойнтинга, то его неприменимость для подобных задач очевидна.
3.3 Уравнение баланса кинетической энергии
Теперь мы докажем другой важный результат. Мы получим уравнение баланса кинетической энергии для поля заряда. Вряд ли вызовет сомнение факт, что электромагнитное поле обладает кинетической энергией. Однако мы приведем доказательство, чтобы дать полную картину явлений.
Сначала мы рассмотрим физическую модель кинетической энергии поля заряда. Если на заряд воздействуют внешние силы, заряд ускоряется, и кинетическая энергия поля заряда изменяется. Это изменение связано с изменением плотности тока j
и векторного потенциала А
.
Ускоренное движение заряда мы можем рассматривать как скачок заряда из одной сопутствующей инерциальной системы отсчета в другую. Сопутствующая и ускоренная системы отсчета имеют равные скорости в бесконечно малом интервале времени.
Электрическое поле E
= –gradφ в сопутствующей системе не зависит от времени и векторный потенциал A
равен в ней нулю. Ускоренное движение заряда возбуждает добавочное электрическое поле E'
, которое обусловлено изменением векторного потенциала А
во времени (см. Приложение 1). Это поле мы не можем рассматривать как пренебрежимо малую величину. В сопутствующей системе отсчета оно равно:
1 ∂A
φ ∂v
 E
'= − = − 2
(3.3.1) E
'= − = − 2
(3.3.1)
2 ∂t
2c
∂t
Плотность мощности, которая ускоряет заряд, равна:
∂ jA
∂ v
2
 p
k
= ρvE
= ( ) = μe
(3.3.2) p
k
= ρvE
= ( ) = μe
(3.3.2)
∂t
4 ∂t
2
где μе
– плотность электромагнитной массы.
Эта мощность не зависит от выбора инерциальной системы отсчета в механике Ньютона. Теперь мы должны описать эту модель математически.
Доказательство.
Для доказательства уравнения баланса кинетической энергии воспользуемся формулой Грина для векторного потенциала.
 ∫E
ΔM
dV
=∫(E
divM
+ E
×rotM
)n
0
d
σ − ∫(divE
divM
+ rotE
rotM
)dV ∫E
ΔM
dV
=∫(E
divM
+ E
×rotM
)n
0
d
σ − ∫(divE
divM
+ rotE
rotM
)dV
где: E
и M
–вектора двух некоторых полей.
∂A
Пусть E
= −  будет полем, которое создается ускоренным зарядом, а M
= A
/μ. В этом 2∂t будет полем, которое создается ускоренным зарядом, а M
= A
/μ. В этом 2∂t
случае мы автоматически получаем уравнение баланса кинетической энергии в стандартной форме:
∂w
k
divS
k
+  + p
k
= 0 (3.3.3) + p
k
= 0 (3.3.3)
∂t
где:
1 ∂A
∂ jA
 а) p
k
= − j
= (3.3.4) а) p
k
= − j
= (3.3.4)
2 ∂t
∂t
4
это плотность мощности, которая изменяет кинетическую энергию заряда;
б) 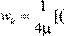  divA
)2
+ (rotA
)2
] (3.3.5) divA
)2
+ (rotA
)2
] (3.3.5)
Выражение (3.3.5) есть плотность кинетической энергии поля заряда: v
2 ε 2 w
e
v
2 v
2
 w
k
= w
k
=  2 (gradφ) = 2 = μe
; 2 (gradφ) = 2 = μe
;
2c
2 2c
2
1 ∂A
∂A
 в) S
k
= − [ divA
+ в) S
k
= − [ divA
+  ×rotA
] (3.3.6) ×rotA
] (3.3.6)
2μ ∂t
∂t
это плотность потока кинетической энергии.
Приложение 1
Запишем интеграл действия частицы, на которую воздействуют потенциальные силы. Все точки заряда движутся с одинаковыми скоростями.
S
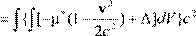 dt
(П.3.1) dt
(П.3.1)
где: μ*
= μe
+ μn
; μe
– плотность электромагнитной массы; μn
– плотность неэлектромагнитной массы.
Из уравнения (П.1) следует уравнение движения.
∂ * * * 2
 (μ v
) + v
×rot(μ v
) − grad(μ c
) + gradΛ = 0 (П.3.2) (μ v
) + v
×rot(μ v
) − grad(μ c
) + gradΛ = 0 (П.3.2)
∂t
a) Пусть внешние силы отсутствуют (Λ = 0). Частица будет устойчива, если выполняется следующее условие:
gradμ*
= gradμe
+ gradμn
= 0 (П.3.3)
б) Если же внешние силы существуют (Λ ≠ 0). Мы можем предположить, что частица тоже устойчива (внешние силы пренебрежимо мало деформируют частицу) и выражение (П.3.3) применимо к ней.
Умножим выражение (П.3.2) на скорость v
. Используя тождество (П.3.3), запишем произведение.
∂ ∂
− v
 (μe
v
) − v (μe
v
) − v
 (μn
v
) + v
gradΛ = 0 (П.3.4) (μn
v
) + v
gradΛ = 0 (П.3.4)
∂t
∂t
Первый член в выражении (П.3.4) есть электромагнитная плотность мощности ускоренной частицы (см. (3.3.4)).
∂ 1 ∂A
∂ jA
 p
k
= −v p
k
= −v
 μe
v
= − j
= − ( ) (П.3.5) μe
v
= − j
= − ( ) (П.3.5)
∂t
2 ∂t
∂t
4
Напомним, что ρ и φ не зависят от времени в собственной системе отсчета. Частица устойчива. Выражение (П.3.5) есть производная по времени от плотности кинетической энергии электромагнитной массы μe
.
3.4 Баланс энергии элемента тока
Теперь предстоит проиллюстрировать выражение для баланса кинетической энергии на примере. В квазистатической электродинамике векторный потенциал элемента тока определяется выражением:
I
(t
)d
l
d
A
= μ  (3.4.1) (3.4.1)
4πr
Подставляя выражение (3.4.1) в уравнения (3.3.6) и (3.3.8), мы можем записать такие результаты.
1. Плотность кинетической энергии равна:
2
μ I
(t
)d
l
2
d  w
k
= ( 2
) (3.4.2) 2 4πr w
k
= ( 2
) (3.4.2) 2 4πr
Распределение энергии обладает радиальной симметрией.
2. Плотность потока кинетической энергии равна:
2
∂ 2
d S
k
= r
 d w
k
(3.4.3) d w
k
(3.4.3)
∂t
Теперь нам следует обсудить характерные особенности плотности потока кинетической энергии d
2
S
k
.
a. Изменение плотности кинетической энергии d
2
wk
, окружающей элемент тока, связано с плотностью потока кинетической энергии d
2
S
k
. Плотность потока d
2
S
k
, в свою очередь, зависит от изменения квадрата силы тока I
во времени. Если величина тока (независимо от его направления) увеличивается, плотность потока кинетической энергии d
2
S
k
положительна и d
2
S
k
направлена вдоль радиуса. Она увеличивает энергию поля векторного потенциала, окружающего элемент тока. Если же ток уменьшается, тогда поток направлен к этому элементу тока. Он стремится поддержать и сохранить величину тока в этом элементе. При любом изменении величины тока потери на излучение отсутствуют. Это по существу напоминает математическую формулировку закона Ленца
.
b. Заметим, что плотность потока d
2
S
k
уменьшается в пространстве по мере удаления от элемента тока как 1/r
3
.
c. Когда изменение тока имеет место, плотность потока кинетической энергии возникает одновременно
во всех точках пространства безо всякого запаздывания, т.е. мгновенно.
d. В противовес вектору Умова
, который описывает конвективный перенос энергии зарядом, движущимся со скоростью v
, плотность потока кинетической энергии существует только при ускоренном движении заряда (при изменении тока).
e. Электрическое поле, равное E
'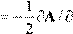 t
, определяет инерцию, т.е. величину t
, определяет инерцию, т.е. величину
силового противодействия ускорению заряда. Мы можем рассматривать его также как напряженность поля, которая создает ЭДС самоиндукции
.
3.5 Поток Умова и поток Пойнтинга
Чтобы уяснить принципиальное различие векторов Умова и Пойнтинга, рассмотрим пример. Пусть вдоль идеального проводника течет ток. В середине провода имеется тонкий разрыв, образующий емкость между торцевыми концами проводов. Будем для простоты считать, что краевые эффекты малы, а поле в зазоре однородно. Каким образом через эту емкость переносится энергия?
Вектор Умова.
Рассмотрим этот процесс в рамках квазистатических
представлений. Пусть ток увеличивается во времени. Это означает, что на левой части проводника нарастает избыток положительных зарядов. На правой части торца, образующего емкость, накапливаются отрицательные заряды. Разность потенциалов между левой и правой частями увеличивается.
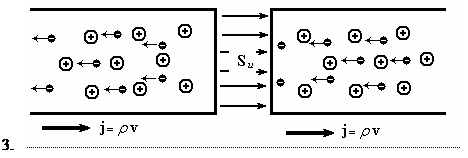
4. Рис. 3.3
В соответствии с этим через емкостный зазор протекает ток смещения, с плотностью тока равной j
=ε∂E
 ∂t
. В левой и правой частях проводника протекает поток основных носителей с плотностью j
= ρv
. Эти плотности токов равны. ∂t
. В левой и правой частях проводника протекает поток основных носителей с плотностью j
= ρv
. Эти плотности токов равны.
С точки зрения теоремы Умова через емкостной зазор проходит поток энергии с плотностью, определяемой формулой (3.2.13). В частности, между пластинами проводника существует плотность потока (вектор Умова), которая направлена вдоль
ε ∂φ ε 2
проводника и равна S
u
= −  gradφ = gradφ =  (gradφ) v
= w
v
. (gradφ) v
= w
v
.
2 ∂t
2
Заметим, что ток в любом сечении цепи (в левом проводнике, в правом проводнике или в зазоре) один и тот же. Благодаря этому свойству «работают» известные законы Кирхгофа для электрических цепей. В любом сечении неразветвленного участка цепи протекает один и тот же ток.
Вектор Пойнтинга.
Рассмотрим ту же задачу с точки зрения волновых
процессов (запаздывающие потенциалы). Она рассмотрена в [5].

Рис. 3.4
Р. Фейнман проводит расчеты и пишет следующее ([5], стр. 295 - 298):
«Рассмотрим поток энергии в медленно заряжающемся конденсаторе.
(Мы не хотим сейчас иметь дело со столь высокими частотами, при которых конденсатор становится похожим на резонансную полость, но нам не нужен и постоянный ток.
) Возьмем конденсатор с круглыми параллельными пластинами.
Между ними создается однородное электрическое поле, которое изменяется с течением времени. …
… Когда конденсатор заряжается, внутренний объем приобретает энергию со скоростью
 ∂U
= ε0πa
2hEE
& ∂U
= ε0πa
2hEE
&
∂t
Так, что должен существовать поток энергии, направленный откуда-то со стороны внутрь объема.
….
… Таким образом, на краях конденсатора, как видно из рисунка, возникает поток энергии, пропорциональный
E
× B
. …
…Удивительная вещь
! Оказывается при зарядке конденсатора энергия идет туда не через провода, а через зазор между краями пластин. Вот что говорит нам эта теория
!
Как это может быть
? Вопрос не из легких…
»
Действительно, почему ток
заряжает конденсатор, а энергия поступает «контрабандным» путем не с зарядами, а «извне» «через зазор между краями пластин
»?
«… Наконец, чтобы убедить вас в том, что это явно ненормальная теория, возьмем еще один пример....
» и т.д.
Дадим объяснение, добавив то, что именно Р. Фейнман упустил из виду. Дело в том, что, используя вектор Пойнтинга, Фейнман заведомо рассматривает волновые
, а не квазистатические процессы.
При анализе волновых процессов конденсатор в линии (проводе) является неоднородностью, от которой происходит отражение части энергии волны.
Рис. 3.5
Электромагнитная волна распространяется над поверхностью идеального проводника, не проникая вглубь. Когда конденсатор заряжается, происходит увеличение энергии между пластинами конденсатора.
Поток, который подсчитывал Фейнман, фактически складывается из потоков трех волн: падающей, отраженной и прошедшей. В такой цепи (в отличие от классической кирхгофовской) ток не будет одинаков в различных сечениях неразветвленной цепи. То, что энергия «втекает» в объем между пластинами конденсатора извне, есть реальный волновой процесс.
Мы вовсе не хотим противопоставлять вектор Умова вектору Пойнтинга. Заметим, что волновой вариант связан с так называемыми безинерциальными зарядами и токами, которые будут рассмотрены позднее. Оба вектора применимы каждый в своей области и описывают свои явления. В последующих главах мы подробно рассмотрим эти вопросы. Здесь мы хотим отметить, что волновые решения уравнений Максвелла и «вырожденные решения» этих уравнений описывают разные явления, присущие классической электродинамике. И те, и другие решения отвечают физической реальности. Нельзя в угоду предрассудкам пытаться описать и объяснять квазистатические процессы, опираясь на волновые представления. Нельзя отождествлять поля электромагнитной волны и поля зарядов. Не случайно Р. Фейнман вынужден был сказать о современной электродинамике: «это явно ненормальная теория
».
3.6 Релятивистский случай
Теперь остается показать, что электромагнитная масса имеет место и в релятивистском случае. Запишем уравнения Максвелла в калибровке Лоренца
∂ 2
A
∂A
∂j
  2
i
= −μj
i
; (3.6.1) i
= 2
i
= −μj
i
; (3.6.1) i
=
∂x
l
∂x
i
 0; i
= 0 (3.6.2) ∂x
i 0; i
= 0 (3.6.2) ∂x
i
где: u
i
= dx
i
/ds
; j
i
= c
ρu
i
; A
i
связанной с зарядом (v
= 0).
= φu
i
/c
, величины ρ и φ берутся в системе отсчета,
Покажем, что для уравнения (3.6.2) существует закон сохранения Умова. Но сначала сделаем важные предварительные замечания.
1. Величины ρ и φ берутся в системе отсчета, связанной с зарядом (v
= 0).
2. Выражение (3.6.1) по форме является уравнением гиперболического
типа. Однако, как было показано в Главе 1, наличие уравнения непрерывности для 4-потенциала (3.6.2) «превращает» уравнение (3.6.1) в уравнение эллиптического
типа.
Для доказательства закона Умова умножим выражение (3.6.2) на − с
 2μ⋅∂A
k 2μ⋅∂A
k
 ∂x
i
и преобразуем полученный результат. ∂x
i
и преобразуем полученный результат.
Правая часть.
с
∂A
k
1 2
∂A
k
c
2
ρ ∂φu
k
c
2
du
k
  j
i
= c
ρu
i
= u
i
= ρφ = 0 j
i
= c
ρu
i
= u
i
= ρφ = 0
2 ∂x
i
2 ∂x
i
2 ∂x
i
2 ds
Итак, правая часть обращается в нуль, поскольку потенциал φ берется в собственной системе отсчета, где он не зависит от времени, а на заряд не действуют внешние силы, и он не испытывает ускорения.
Левая часть
с
∂A
k
∂ 2
A
i
с
∂ ∂ 2
A
i
с
∂ ∂ ρφ
  −
2
= − (A
k
2
) = (A
k
j
i
) = с
( u
k
u
i
) = 0 (3.6.3) −
2
= − (A
k
2
) = (A
k
j
i
) = с
( u
k
u
i
) = 0 (3.6.3)
2μ ∂x
i
∂x
l
2μ ∂x
i
∂x
l
2 ∂x
i
∂x
i
2
Итак, мы получили в левой части выражение для дивергенции тензора плотности энергии-потока
для поля заряда. Если компоненты этого тензора разделить на квадрат скорости света и проинтегрировать по пространственному объему, то получим выражение для тензора энергии-импульса релятивистской частицы с электромагнитной массой me
[1], дивергенция которого определяется выражением:
∂ ∂
 (T
ik
) = (T
ik
) =  (m
e
cu
i
u
k
) = 0 (3.6.4) (m
e
cu
i
u
k
) = 0 (3.6.4)
∂x
i
∂x
i
Из полученного выражения следует, что релятивистский импульс электромагнитной массы постоянен. Это очевидно, поскольку заряд перемещается с постоянной скоростью. Из (3.6.3) вытекает закон сохранения Умова
, который мы запишем ниже
∂ w
v
ρφ
divS
u
+  w
= 0, где S
u
= ; w
= - плотность потока и w
= 0, где S
u
= ; w
= - плотность потока и
  ∂t
1− (v
/c
) 2
1− (v
/c
) 2
плотность энергии поля заряда. ∂t
1− (v
/c
) 2
1− (v
/c
) 2
плотность энергии поля заряда.
Нетрудно видеть, что релятивистское выражение соответствует классическому с точностью до релятивистского множителя.
Обсуждение
1. При решении проблемы электромагнитной массы мы не использовали гипотез
о строении зарядов и показали, что электромагнитная масса имеет стандартные свойства механической инерциальной массы. Это положение справедливо как для малых, так и релятивистских скоростей.
2. При доказательстве мы опирались на мгновенно действующие потенциалы как в классическом, так и в релятивистском варианте (условие (3.5.2)).
3. Как известно, масса покоя заряда m
0
складывается из электромагнитной массы me
и массы неэлектромагнитного происхождения mn
: m
0
= me
+ mn
. Последняя, противодействуя кулоновским силам расталкивания, обеспечивает устойчивость заряженных частиц. Сейчас мы ничего не можем сказать о неэлектромагнитной массе (о ее величине и знаке). Однако если эта масса обладает инерциальными свойствами, то неизбежен следующий вывод: неэлектромагнитная масса также должна обладать стандартными свойствами механической инерциальной массы независимо от ее природы.
4. Мы бы хотели обратить внимание на тензор энергии-импульса поля заряда. Этот тензор отвечает только мгновенно действующим полям движущегося заряда. Действительно, при доказательстве мы использовали уравнение непрерывности и запись векторного потенциала через скалярный потенциал и скорость заряда. А эти выражения, как было показано в Главе 1, превращают волновое уравнение в уравнение эллиптического типа с мгновенно действующими потенциалами. Такие поля имеют свои законы сохранения. Конечно, мгновенное распространение этих полей противоречит постулатам СТО. Позже мы обсудим эту теорию и покажем ее несовместимость
с уравнениями Максвелла.
5. Вернемся к вопросу о двойственном характере выражений для электромагнитной массы и, соответственно, для кинетической энергии и электромагнитного импульса
заряда. m
e
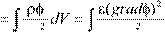 dV
. Возникает вопрос: какое выражение для массы dV
. Возникает вопрос: какое выражение для массы
2c
2c
отвечает физической реальности? Наша точка зрения сводится к следующему. Электромагнитную массу заряда определяет плотность пространственного заряда. Инерция там, где эта плотность отлична от нуля. В свою очередь электромагнитные поля заряда не обладают
инерциальными свойствами (не связаны с массой). Такой подход позволяет «снять» ограничения на скорость перемещения и распространения полей заряда в пространстве.
6. Закон сохранения энергии Умова (в классическом и релятивистском вариантах) отличается от закона сохранения Пойнтинга и не сводится к нему. Этот факт и факт функционального
различия решений для полей зарядов и полей электромагнитных волн свидетельствуют о том, что эти поля принципиально различны.
Например, плотность массы покоя поля заряда отлична от нуля, в то время, как плотность массы покоя электромагнитной волны всегда равна нулю и т.д. Соответственно, использовать вектор Пойнтинга для полей зарядов нельзя.
Итак, использование мгновенного взаимодействия оказалось плодотворным при решении проблемы электромагнитной массы. Ранее эти вопросы были рассмотрены в [6], а также в[7].
Дополнение.
В Интернете на сайте С.Н Артехи: http://www.antidogma.ru/
под заголовком: «ПРОЕКТ "ВСЕХ НАСТОЯЩИХ ПЕРВЫХ ПОМЯНУТЬ
"» представлена следующая справка:
«Так называемая "эквивалентность массы и энергии
" E
= mc
².
Формула впервые появилась за
33 года до А. Эйнштейна в работе
"Die allgemeine Bewegung der Materie als Grundursache aller Naturerscheinungen", Heinrich Schramm, 1872, Wilhelm Braumüller, k.k.Hof- und-Universitäts-Buchhändler.
Обсуждалась в работах Н.А. Умова в
1873 году.
Получена Томсоном в статье "Об электрическом и магнитном эффекте, обусловленном движением наэлектризованных тел", опубликованной в
1881 г.
(см. Кудрявцев П.С. Курс истории физики, М.: Просвещение, 1974).
Получена, исходя из теории Максвелла, в работе О. Хевисайда в
1890 году.
В качестве примера содержится в работе А. Пуанкаре в
1900 году.
Рассмотрена в работе Ф. Газенёрля в
1904 году
: Zur Theorie der Strahlung in bewegten Korpern F. Hasenöhrl, Ann. Phys., Band 15, Seite 344-370, (1904); 16, 589 (1905).» Источники информации:
1 Голдстейн Г. Классическая электродинамика. – М: Наука, 1975.
2 Фейнман Р.Ф. , Лейтон Р.Б. , Сандс М. Фейнмановские лекции по физике. Т. 6, Электродинамика. – М.: Мир. 1975.
3 Кочин Н.Е. . Векторное исчисление и начала тензорного исчисления. – М.: Наука 1965.
4 Umoff (Umov) N.A. Beweg – Gleich. d. Energie in contin. Korpern, Zeitschriff d. Math. and Phys. V. XIX, Schlomilch. 1874.
5 Фейнман Р., Лейтон Р., Сэндс Ь. Фейнмановские лекции по физике. Т. 6. Электродинамика. М.:Мир., 1977.
6 Кулигин В.А., кулигина Г.А. Механика квазинейтральных систем заряженных частиц и законы сохранения нерелятивистской электродинамики. – Деп. в ВИНИТИ 04.09.86 № 6451 – В86. Воронеж. Ун-т. – Воронеж, 1986. http://www.sciteclibrary.ru/rus/catalog/pages/9219.html
7 Кулигин В.А., Кулигина Г.А., Корнева М.В. Кризис релятивистских теорий. Часть 5. Электромагнитная масса. http://kuligin.mylivepage.ru/file/index/
8 Первая десятка "Русского переплета" (Научный форум; Шаляпин А.Л. http://s6767.narod.ru/- СВЯЗЬ ЭНЕРГИИ С МАССОЙ ПО УМОВУ) http://www.pereplet.ru/Discussion/index.html?book=sci
4.1 Классический принцип относительности
Классическая механика построена на принципе относительности Галилея, который гласит:
«Прямолинейное и равномерное движение системы отсчета не влияет на ход механических
процессов в системе
». Этот принцип был обобщен А.Пуанкаре: «Все физические
процессы при одинаковых условиях протекают одинаково во всех инерциальных системах отсчета
». Вторую формулировку можно рассматривать как оправданное философское обобщение принципа относительности Галилея на любые
процессы в природе.
Мы говорим «можно» по той причине, что правильность обобщения зависит не только от правильности формулировки, но и от правильности реализации
этого обобщения. Примером может служить правильное
утверждение о наличии у заряда электромагнитной массы и неправильная реализация
, опиравшаяся на использование вектора Пойнтинга за границами его применимости.
В классической механике реализация принципа относительности очевидна (например, закон Всемирного тяготения, закон Кулона и т.д.). В приведенных выше законах взаимодействие определяется через относительное
расстояние
между двумя взаимодействующими объектами R
12
= R
1
– R
2
. Переход наблюдателя в новую инерциальную систему сохраняет относительное расстояние между первым и вторым взаимодействующими объектами неизменным.
Можно обобщить это положение на случай, когда взаимодействие зависит не только от расстояния, но и от скоростей взаимодействующих объектов. Характер описания взаимодействия не зависит от выбора инерциальной системы отсчета, если взаимодействие двух объектов зависит от их относительной
скорости V
12
= V
1
– V
2
. Для классической механики нет необходимости распространять этот принцип на взаимодействия, зависящие от ускорения, поскольку дифференциал скорости не зависит от выбора инерциальной системы отсчета.
Мы уже выразили сомнение относительно применимости СТО к явлениям квазистатической электродинамики, тем не менее, мы иногда будем использовать математический формализм этой теории. В работе [1] приводится следующий интеграл действия для взаимодействия заряда с полем (например, с полем другого заряда):
S
= ∫(−mcds
+ eA
i
dx
i
) =∫(−mc
+ eA
i
u
i
)ds
Сначала рассмотрим действие для свободного заряда. Действие для электромагнитной массы, выраженное через объемную плотность пространственного заряда, равно
ρA
i
S
= ∫∫
 2
dx
i
dV 2
dx
i
dV
Пользуясь тем, что Ai
= φui
/c
и dxi
= ui
ds
, получим
ρφu
i
ρφ ρφ 2
∫∫
 2c
2 u
i
dsdV
=−∫∫ 2c
2 u
i
dsdV
=−∫∫
 2c
2 dsdV
=−∫mcds
, где: m
= ∫ 2c
2 dsdV
=−∫mcds
, где: m
= ∫
 2c
2 dV
; u
i
= −1 2c
2 dV
; u
i
= −1
Пусть теперь тот же заряд образован двумя заряженными частицами. Плотности их пространственного заряда ρ1
и ρ2
, 4-потенциал этих зарядов соответственно Ai
1
и Ai
2
, а 4дифференциалы координат dxi
1
и dxi
2
Подставляя эти результаты в интеграл действия для одной частицы, получим
S
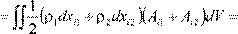
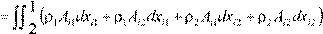  dV dV
Интегрируя по объемам, содержащим заряды, найдем
2 2 1 1 2 2
  S
= ∫(−m
1c
1− v
1 / c dt
+ 2 e
1 A
i
2dx
i
1 + S
= ∫(−m
1c
1− v
1 / c dt
+ 2 e
1 A
i
2dx
i
1 +  2 e
2 A
i
1dx
i
2 − m
2c
1− v
2 / c dt
) 2 e
2 A
i
1dx
i
2 − m
2c
1− v
2 / c dt
)
Для малых
скоростей мы получим следующее «красивое» соотношение для лагранжиана взаимодействия.
2 e
1φ2 ⎡ (v
1 − v
2 ) ⎤
 e
1u
i
1 A
≈ −e
1φ2 ⎢1+ e
1u
i
1 A
≈ −e
1φ2 ⎢1+  2 ⎥ = 2 ⎥ =
⎣ 2c
⎦
e e
⎤ e e
⎡ v
12
2
⎤
= − 1+ 2
⎥ = − ⎢1+ 2
⎥ = e
2
u
i
2
A
i
1
4πεr
12
⎣ 2c
⎦ 4πεr
12
⎣ 2c
⎦
где v
12
относительная скорость, определяемая формулами Эйнштейна для сложения скоростей.
Как следует из формулы, взаимодействие «магнитного» характера определяется относительным
движением зарядов. Следует заметить, что никаких «запаздываний» в полученном результате нет. Относительная скорость не «запаздывает», да и относительное расстояние, являясь истинным скаляром, сохраняется неизменным в любой инерциальной системе отсчета. Но релятивистский математический формализм формально сохраняется.
Теперь мы можем записать интеграл действия зарядов для малых
относительных скоростей движения зарядов.
v
2
e e
⎡ v
2
⎤ v
2
 S
= ∫(m
1 2 S
= ∫(m
1 2 4πεr
12 ⎣ 2c
⎦ m
1
21
)dt
= 4πεr
12 ⎣ 2c
⎦ m
1
21
)dt
=
(4.1.1)
 e e v
2
e e
2
e e v
2 e e v
2
e e
2
e e v
2
=   dt dt
4πε 12 12
Как видно из полученного результата массы заряженных частиц получают «добавки», которые по величине весьма малы
по отношению к массам частиц. Пренебрегая ими, мы получаем известный интеграл действия для нерелятивистского (классического) случая
 v
2 v
2
2 v
2 v
2
2
S
 + ]dt
= + ]dt
=
(4.1.2) 2 2
 v v v v
dt
из которого следуют известные уравнения движения
d
v
1
∂A
2
m
1
 = −e
1
gradφ2
− e
1 = −e
1
gradφ2
− e
1
 + e
1
[v
1
×rotA
2
] dt
∂t + e
1
[v
1
×rotA
2
] dt
∂t
(4.1.3) d
v
2
∂A
1
m
2
 = −e
2
gradφ1
− e
2 = −e
2
gradφ1
− e
2
 + e
2
[v
2
×rotA
1
] dt
∂t + e
2
[v
2
×rotA
1
] dt
∂t
Правая часть в этих выражениях есть сила Лоренца.
В стандартных учебниках выражение (4.1.2) также выводится небрежно. Доказательство приводится как простое и «очевидное». Функцию Лагранжа, отвечающую за взаимодействие, записывают следующим образом [1]
L
int = e
1u
i
(1) A
i
(2) = −e
1φ2 + e
1v
1A
2 (4.1.4)
Конечно, выражения для функции Лагранжа в (4.1.2) и (4.1.4) совпадают. Но в этих выражениях отсутствуют некоторые члены пропорциональные квадратам скоростей, т.е. «добавки» к массам. Можно ли пренебрегать «добавками» к массам, поскольку соответствующие выражения становятся неинвариантными относительно преобразования Галилея? К чему это приводит, мы покажем в следующем параграфе.
4.2 Эксперимент Траутона и Нобла
Рассмотрим два заряда + q
и - q
, находящиеся на концах стержня длиной L
. Кулоновские силы притяжения уравновешены упругими силами стержня. Опираясь на формулы (4.1.3) легко показать, что наблюдатель, движущийся относительно стержня со скоростью v
, обнаружит вращающий момент, действующий на этот стержень. Процитируем работу [2] (параграф 14.2):
«… два заряда
+ q
и – q, находящиеся на концах отрезка, движущегося со скоростью
v,
будут взаимодействовать как два элемента тока величиной Id
l =
q
v
. Силы, действующие на эти элементы тока, будут равны и направлены в противоположные стороны, и в общем случае они не коллинеарны
… Рассчитаем величину этого эффекта
…Сила
1 q
2 v
2
F
=  2 2
sinθ направлена перпендикулярно к
v
в плоскости векторов
L
и
v.
… 2 2
sinθ направлена перпендикулярно к
v
в плоскости векторов
L
и
v.
…
4πε L c

Рис. 4.1
В цитате оговорка. Силы параллельны и равны, но не лежат на одной прямой линии. Этот «вращающий момент» до настоящего времени так и не нашел своего объяснения в рамках классических теорий. А появился он благодаря тому, что были отброшены «добавки»
к массам
частиц в выражении (4.1.2). Читаем далее в параграфе 18.4 из [2]:
«Траутон и Нобл пытались наблюдать этот момент на опыте. Парадокс, вызванный отрицательным результатом опыта, показал трудности в интерпретации скорости движущихся зарядов, существовавшие в дорелятивистской электродинамике
».
«Виновной
» сразу же объявили механику Ньютона и классические представления.
Опишем суть эксперимента Траутона и Нобла. Эти исследователи для наблюдения вращающего эффекта использовали заряженный плоский конденсатор, который был укреплен на упругом подвесе. Экспериментаторы долго и томительно ожидали вращение конденсатора, но так ничего и не обнаружили.
Они и не должны были ничего обнаружить, даже если бы крутящий момент действительно существовал. Вращающий момент должен наблюдаться (согласно (4.2.1)), если конденсатор движется мимо экспериментаторов
с постоянной скоростью. Но обратите внимание, что этот конденсатор покоился
в их системе отсчета.
Чтобы как-то оправдать отрицательный результат эксперимента, было высказано предположение, что вращающий момент создается «эфирным ветром» (!) вследствие движения Земли. Отрицательный результат эксперимента «оправдал» исследователей, поскольку было «доказано», что «эфирного ветра (равно как и эфира) не существует».
Если же исходить из выражения (4.1.1), то никакого вращательного момента на заряды не должно действовать, какую бы инерциальную систему отсчета мы не выбрали. Вращающий момент это результат некорректного устранения «добавок» к массам.
Взаимодействие зарядов зависит от относительных скоростей и относительных расстояний. Если бы даже эфир существовал, его скорость «выпала» бы из интеграла действия. Как следствие, с помощью подобного эксперимента принципиально
невозможно было бы обнаружить движение относительно эфира.
4.3 «Конвективный потенциал»
Выше мы рассмотрели, так называемое, “классическое” объяснение появления вращающего момента для зарядов, движущихся с нерелятивистскими скоростями. Теперь рассмотрим тот же вариант в рамках “релятивистских” представлений. Как мы установили, там источником «парадокса» явилось пренебрежение «добавками» к массам. Теперь мы будем анализировать эту же проблему, опираясь на строгие соотношения (безо всяких приближений). Теория изложена в параграфе 18.4 «Конвективный потенциал» в работе [2], которую мы будем цитировать ниже. Цитаты будем давать курсивом.
Итак,
“Два электрона, движущихся параллельно друг другу с одинаковой скоростью u, взаимодействуют между собой. Сила взаимодействия определяется выражением для силы Лоренца…
F
= e
(E
+ u
×B
)
…после преобразования…
e
2
⎛1−u
2
/c
2
⎞
 F
= − 4πε∇⎜⎜⎝ s
⎟⎟⎠= −∇ψ F
= − 4πε∇⎜⎜⎝ s
⎟⎟⎠= −∇ψ
… Функция e
2
(1−u
2
/c
2
) ψ =  называется конвективным потенциалом»…. называется конвективным потенциалом»….
4πεs
Обращаем ваше внимание на то, что конвективный потенциал является мгновенно действующим, а не запаздывающим в соответствии с Главой 1.

Рис. 4.2
«Сила F
2
, с которой электрон е1
, находящийся в точке (x1
, y1
, z1
), действует на электрон е2
, находящийся в точке (x2
, y2
, z2
), должна быть перпендикулярна поверхности эллипсоида
s
= 
ибо последняя является эквипотенциальной поверхностью…
…Таким образом, за исключением случаев, когда линия, соединяющая электроны, параллельна или перпендикулярна к направлению движения, силы действия и противодействия не коллинеарны”.
Здесь, видимо, также опечатка, поскольку силы коллинеарны, но не лежат на одной прямой. Естественно, что появляется вращающий момент. Заметим, что:
“…для наблюдателя, движущегося с зарядами, заряды не представляют собой элементов тока. Поэтому взаимодействие между ними будет чисто кулоновским
”.
Итак:
«Вращательный момент, предсказываемый теорией, реально существует для наблюдателя, движущегося относительно зарядов со скоростью u.
Он мог бы быть измерен, если бы не нужно было учитывать механические соображения. Мы уже указывали, что представление о «жестком» стержне несовместимо с теорий относительности
…. Положение полностью аналогично тому, которое было при рассмотрении равновесия рычага – вращательный момент компенсируется приростом момента импульса. Во всяком случае, равновесие есть свойство, инвариантное относительно преобразований Лоренца
».
Ясно, что здесь мы имеем дело не с объяснением физического явления, предсказываемого СТО, а с декларацией об «инвариантности» равновесия в любой инерциальной системе отсчета («Во всяком случае, равновесие есть свойство, инвариантное относительно преобразований Лоренца
»).
Обратимся к парадоксу рычага. Может быть там изложена «сермяжная» правда?
4.4 Парадокс рычага
Описание этого парадокса можно встретить в некоторых книгах, посвященных вопросам специальной теории относительности. Обратимся к работе [3], чтобы напомнить суть парадокса.
Пусть в системе К
° имеется рычаг с плечами L
o
x
и L
o
y
, изображенный на рис. 4.3, на которые действуют силы F
o
x
и F
o
y
соответственно. Рычаг уравновешен, т.е. M
= F
y
0 L
0x
− F
x
0 L
0y
= 0
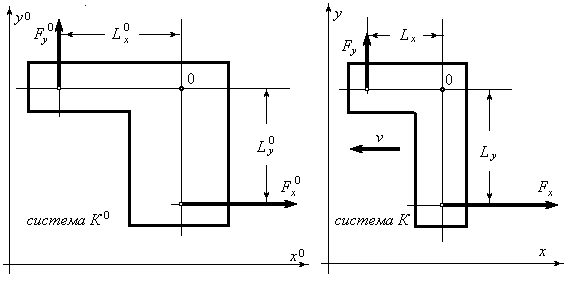
Рис. 4.3 В системе К
будем иметь:
 L
x
= L
0
x
1− (v
/c
) 2
; L
y
= L
0
y
; L
x
= L
0
x
1− (v
/c
) 2
; L
y
= L
0
y
;
F
y
= F
y
0
1− (v
/c
) 2
; F
x
= F
x
0
Таким образом, в системе К
на рычаг будет действовать не скомпенсированный момент сил, равный:
v
2 0 0
M
= F
x L
y
− F
y L
x
=  2 F
x L
y 2 F
x L
y
c
Возникает вопрос: должен ли в согласии с законами механики рычаг повернуться под действием момента сил М
?
Обратимся к [3], сопроводив объяснение комментариями. Цитаты будем приводить как обычно курсивом.
«...На первый взгляд мы приходим к странным выводам. Однако более тщательное рассмотрение показывает, что полученные выводы правильны и имеют непринужденное объяснение. Сначала приведем элементарное объяснение...
...Рассмотрим работу сил Fx
и Fy
в системе К. В системе К рычаг движется и в единицу времени сила Fх
совершает работу – Fх
v. Сила Fy
не совершает работы, т.к. она направлена нормально к скорости рычага. Следовательно, на конце рычага в точке приложения силы Fx
совершается работа и в единицу времени энергия в точке возрастает на величину -Fх
v
»
Комментарий
. Итак, энергия изменяется. Очевидно, речь идет о потенциальной энергии. К сожалению, автор не поясняет: что именно означает “энергия рычага в точке”. Разве энергия передается не всему рычагу, а только одной его точке? Читаем далее:
«..Но это означает, что масса рычага в точке приложения силы в единицу времени возрастает на – Fх
v/c2. Умножив эту величину на скорость рычага v, найдем приращение импульса -Fx
v
2
/c
2
. А момент импульса возрастает на величину -Fx
Ly
v
2
/c
2
»
Комментарий
. "
По мнению автора работы, это возрастание как раз и “компенсирует” вращающий момент М.
Следовательно, масса рычага будет ежесекундно убывать на величину -Fх
v/c
2
. Пройдет время и от массы рычага ничего не останется. Она станет равной нулю. Что же тогда будет поддерживать равновесие? Затем она станет отрицательной. Во-первых, как это следует понимать? Во вторых, для объяснения парадокса жертвуется масса. Она становится зависимой от времени. Однако вновь возникает вопрос: “почему”? Почему в системе К
° масса постоянна, а в системе К
она зависит от времени?
Центр тяжести объяснения парадокса передвинут с “нескомпенсированного момента сил” на “массу, зависящую от времени”. Но объяснений этой зависимости не дано. Что это: софистика или паралогизм? Автор и сам, видимо чувствует порочность “элементарного” объяснения. Далее он пишет:
«... Но в этом элементарном объяснении есть свои слабости. В СТО нет абсолютно жестких тел, и мы обязаны учитывать деформацию рычага, в предыдущем рассуждении полагалось, что рычаг не меняет свою форму...
»
Комментарий.
Вот и вытаскивается гипотеза ad hos
об отсутствии в СТО абсолютно жестких тел. Это и есть современные аналоги средневековых “слонов” и “черепах”. Далее автор утверждает, что в рычаге возникают «натяжения».
«... Изменение этих натяжений должно как раз скомпенсировать момент сил. В принципе эта задача может быть решена, т.к. изгиб балки, закрепленной на одном конце
(кем закрепленный, ведь рычаг может вращаться? – вопрос наш), может быть найден. Однако расчет провести затруднительно
».
Вот и все непринужденное
объяснение, которое посулил нам автор в начале своего объяснения. Что же получается? Теория относительности предсказывает появление не скомпенсированного момента сил М
, который действует на рычаг. Однако автор пытается доказать, что рычаг не должен вращаться. Неизбежен вопрос, что ошибочно: законы механики, утверждающие, что из-за момента сил должно быть вращение, или же СТО, которая предсказывает появление момента сил, не существующего в действительности? Ответ очевиден.
4.5 Определение напряженности поля
Итак, при объяснении парадокса рычага мы сталкиваемся с той же путаницей и несостоятельностью объяснений, как и при объяснении «конвективного потенциала», Но теперь источник противоречия не в математических некорректностях, а в наличии гносеологической
ошибки. Гносеологические ошибки в основном обусловлены неправомерными (ошибочными) интерпретациями явлений.
Для упрощения объяснения «конвективного потенциала» будем полагать, что мы имеем дело с единичными зарядами. В этом случае силы, действующие на заряды, будут численно
равны напряженностям электрических полей и совпадать по направлению с векторами напряженности.
В релятивистской электродинамике, как мы знаем, «конвективный потенциал» учитывает зависимость скалярного потенциала от скорости. Дадим определение напряженности электрического поля Е.
Определение.
Напряженность электрического поля
(в данной точке пространства и в данный момент времени) есть силовая характеристика
этого поля, численно равная силе, действующей на единичный, положительный, точечный заряд (т.е. пробный заряд
), покоящийся
в этой точке, и имеющая направление, совпадающее с направлением вектора силы.
Мы надеемся, что это определение корректно. Отметим его особенности.
a. Во-первых, философская сторона определения - «силовая характеристика
» - позволяет нам не воспринимать напряженность как самостоятельный вид материи.
Она отражает одно из свойств
такого явления
как электромагнитное поле. Заметим, что «энергетической характеристикой
» электрического поля является потенциал (в том числе и конвективный), поскольку он определяется через понятие «работа
». Сила есть одно из свойств
волны или материального тела. Без введения подобных уточнений возможна путаница. Например, некоторые исследователи ошибочно пытаются рассматривать силу, как некий самостоятельный
«материальный объект», существующий как бы независимо от источника, который создает эту силу. Взаимодействуют заряды, а силы, возникающие между ними, это свойства
зарядов (источников этих сил).
b. Во вторых, мы хотим обратить внимание на появление в определении понятия «напряженность» слова «покоящийся
». Дело в том, что в данный момент времени в данной точке пространства мы можем «поместить» в исследуемое поле движущийся
единичный заряд. Конечно, на него со стороны поля будет действовать уже другая
сила (= будет измерена другая
напряженность поля), отличная от той, которая действовала бы на покоящийся
заряд.
Приведем пример
. Пусть мы имеем однородное магнитное поле магнита, покоящегося
в нашей системе отсчета. Если пробный заряд покоится
, то на него магнитное поле не будет воздействовать, т.е. напряженность электрического поля, действующего на пробный единичный заряд, равна нулю. Но если заряд движется со скоростью v
, то в соответствии с формулой Лоренца на него будет действовать сила и существовать, пропорциональная ей напряженность электрического поля
E
=F
/e
=v
×B
Рассмотрим теперь случай, когда этот магнит со своим полем перемещается с постоянной скоростью u
в нашей системе отсчета. Иногда можно встретить утверждения, что и в данном случае на покоящийся заряд магнитное поле не будет воздействовать. При этом сторонники такой точки зрения «кивают» на приведенную выше формулу Лоренца. Действительно, если скорость заряда равна нулю, то и сила (= напряженность электрического поля) должна быть равной нулю. Но это ошибочная точка зрения.
В соответствии с преобразованиями Лоренца движущееся магнитное поле порождает напряженность электрического поля, равную
E
'
= −u
×B
Эта напряженность создает силу, которая будет воздействовать на покоящийся
в нашей инерциальной системе отсчета пробный заряд. Под ее воздействием свободный заряд начнет двигаться ускоренно.
Теперь, опираясь на определение напряженности электрического поля, мы можем дать непротиворечивое объяснение «конвективному потенциалу».
Итак, обратимся к рис. 4.2 и рассмотрим напряженность поля, создаваемую первым зарядом е
1
, которая существует в той точке пространства, где в данный момент находится движущийся заряд е
2
. Для этой цели (в соответствии с определением понятия «напряженность электрического поля») мы поместим в данную точку пространства в момент времени, соответствующий пролету второго заряда, неподвижный
пробный заряд.
Естественно, что на этот неподвижный
заряд будет действовать сила, определяемая формулой Лоренца. Но будет ли действовать та же самая сила на движущийся
заряд? Ответ на этот вопрос должен быть в общем случае отрицательным
. На движущийся заряд будет действовать другая
сила, отличная от той, которую мы измерили с помощью неподвижного пробного заряда.
Но вернемся к рассматриваемому парадоксу. Что же мы имеем? А имеем мы подмену сил, если говорить с точки зрения физики. Мы незаконно
подменяем
силу, которая воздействует на движущийся заряд, другой силой, которая действует на неподвижный
в нашей системе отсчета заряд. Если бы мы вычисленные для неподвижного заряда силы заменили реальными
силами, то никакого парадокса, связанного с появлением вращающего момента, мы бы не обнаружили.
Мы считаем, что взаимодействие в релятивистской механике должно иметь объективный
характер, как это имеет место в механике Ньютона. Оно не может зависеть от выбора наблюдателем инерциальной системы отсчета. Наблюдатели любой
инерциальной системы отсчета должны описывать процесс взаимодействия одинаково (объективно).
4.6 К теории тяготения
Поскольку прослеживается аналогия между квазистатическими явлениями электродинамики и законом Всемирного тяготения, выскажем несколько соображений по этому поводу.
a. Об эквивалентности инерциальной и тяготеющей масс. Наше отношение к этой гипотезе отрицательное. Инерциальная масса отражает способность материального объекта сохранять свое состояние и «противостоять» действию внешней силы. Гравитационная масса (гравитационный заряд) отражает способность материальных тел к взаимодействию между собой (к взаимному притяжению). Отождествление столь разных свойств есть эклектика. С тем же успехом можно было бы «отождествить» красное и сладкое, поскольку красные ягоды и плоды, как правило, являются сладкими.
b. Между квазистатическими явлениями электродинамики и квазистатическими явлениями гравитации имеет место аналогия. По этой причине интеграл действия для двух взаимодействующих гравитационных зарядов (масс) можно записать в следующем виде
 v
1
2 m
g
1m
g
2 ⎡ v
122 ⎤ v
2 v
1
2 m
g
1m
g
2 ⎡ v
122 ⎤ v
2
 S
= ∫(m
1
−γ ⎢1+ 2
⎥+ m
1
dt
, где m
– инерциальная S
= ∫(m
1
−γ ⎢1+ 2
⎥+ m
1
dt
, где m
– инерциальная
2 r
12
⎣ 2c
⎦
масса; mg
– гравитационный заряд; v
12
- относительная скорость тел; γ - постоянная тяготения. Мы не будем приводить расчетов, которые предсказывают смещение перигелия Меркурия такое же, какое следует из эйнштейновских представлений Специальной теории относительности (20” за столетие).
c. Следует отметить, что на смещение перигелия влияют и другие факторы.
Например, солнце испускает большое число нейтральных и заряженных
частиц. Вокруг него на большом расстоянии существует положительный пространственный заряд, сквозь который пролетают Земля и другие планеты. Естественно, что и они в результате столкновений с заряженными частицами приобретают заряд. При этом электрическое поле, где движутся планеты, уже не подчиняется закону R
-2
. Мы также не знаем величину заряда самого солнца. Если, например, этот заряд составляет десятки кулон, то поправка к смещению перигелия может составить величину того же порядка, что и указанная ранее.
d. Обратимся к задаче трех тел. Интересный подход к ее решению предложен в [4]. Мы не собираемся предлагать новое решение, а хотим высказать одно предположение. Дело в том, что при взаимодействии двух гравитационных масс (тел) имеет место закон сохранения энергии. Следовательно, полная масса этой замкнутой консервативной системы (сумма потенциальной и кинетической энергий, деленная на с
2
) в соответствии с формулой Томсона (E = mc
2
) должна сохраняться. Иными словами, энергия взаимодействия также должна обладать массой. Если это предположение справедливо, то при гравитационном взаимодействии этой системы с третьим телом система должна вести себя как инерциальное тело с постоянной инерциальной массой. Это предположение нуждается в экспериментальной проверке. Напомним, что взаимодействие материальных тел обусловлено гравитационными
зарядами, как было сказано выше. Аналогичное допущение можно высказать и по отношению к взаимодействию заряженных частиц.
e. Нетрудно видеть, что тензор напряжений, описывающий взаимодействие
V
2
двух зарядов равен T
ik
= e
1
φ2
[V
i
V
k
+V
k
V
i
]− δik
e
1
φ2
(1+  2
) 2c 2
) 2c
где: V
– относительная скорость движения зарядов; δik
= 1 при i
= k
и δik
= 0 при i
≠ k
; Vi
–проекция относительной скорости на ось i
(i=
1,2,3,4).
Обращаем внимание, что приведенный тензор напряжений симметричен.
4.7 Как проверить закон Кулона?
Рассмотрим движение заряда в поле плоского конденсатора. Будем считать потенциал отрицательной пластины и начальную скорость электрона равным нулю.
 Обозначим величину mc
2
/e
= U
0
. Величина U
0
= 0,512⋅106
вольт. В известном классическом случае, когда взаимодействие не зависит от относительной скорости, мы имеем следующее известное выражение для скорости заряда v
к
/c
= 2eU
/ mc
2
= 2U
/U
0
(4.7.1) Обозначим величину mc
2
/e
= U
0
. Величина U
0
= 0,512⋅106
вольт. В известном классическом случае, когда взаимодействие не зависит от относительной скорости, мы имеем следующее известное выражение для скорости заряда v
к
/c
= 2eU
/ mc
2
= 2U
/U
0
(4.7.1)
Если потенциал зависит от относительной скорости движения (см. (4.1.1)), мы имеем следующий результат
2eU
2U
/U
0
2U
/U
0
(1+ U
/U
0
)
 v
/ c
= 2
= = (4.7.2) mc
+ eU
1+ U
/U
0
1+ U
/U
0 v
/ c
= 2
= = (4.7.2) mc
+ eU
1+ U
/U
0
1+ U
/U
0
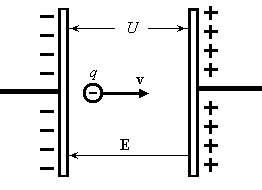
Рис. 4.4
Остается рассмотреть этот вопрос с релятивистских позиций. Скорость в релятивистской теории следующим образом зависит от потенциала
 U
/U
0
(2 +U
/U
0
) U
/U
0
(2 +U
/U
0
)
v
р
/c
= (4.7.3) 1+U
/U
0
Заметим близость результатов (4.7.2) и (4.7.3), которая ставит под сомнение интерпретацию опытов Кауфмана. Именно их, в первую очередь, «приспособили» для подтверждения справедливости СТО.
На рис. 4.5 представлены графики зависимостей скоростей от потенциалов, вычисленные по обозначенным формулам. Следует обратить внимание на тот факт, что при малых значениях U
/ U
0
асимптотические выражения для (4.7.2) и (4.7.3)
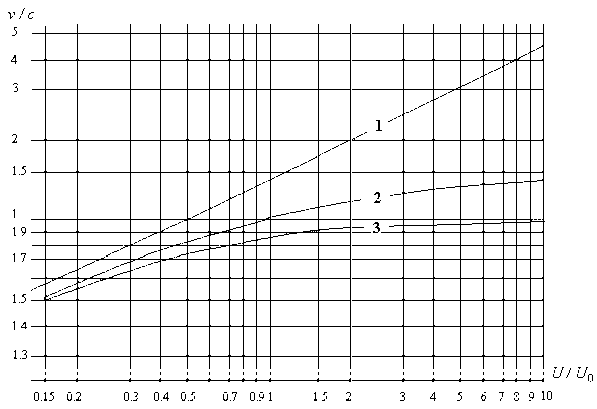
Рис. 4.5 1
– классическая формула Кулона (4.7.1): 2
– формула (4.7.2): 3
– релятивистская формула (4.7.3) совпадают с формулой (4.7.1). Однако при очень больших значениях отношения U
/ U
0
эти формулы имеют различную асимптотику. Результаты приведены в Таблице 1.
Таблица 1
| Формула (4.7.1)
|
Формула (4.7.2)
|
Формула (4.7.3)
|
| Уравнение
|
v
/c
= 
|

2U
/U
0
|
 2U
/U v
/ c
= 0 2U
/U v
/ c
= 0
1+U
/U
0
|
 U
/U
0
(2 +U
/U
0
) U
/U
0
(2 +U
/U
0
)
v
р
/c
=
1+U
/U
0
|
| Асимптотика
|
| U
/ U
0
<< 1
|
v
/c
⇒ 
|
 2U
/U
0 2U
/U
0
|
 v
/c
⇒ 2U
/U
0 v
/c
⇒ 2U
/U
0
|
 v
г
/c
⇒ 2U
/U
0 v
г
/c
⇒ 2U
/U
0
|
| U
/ U
0
→ ∞
|
v
/c
⇒ 
|
 2U
/U
0 2U
/U
0
|
 v
/ c
⇒ 2 v
/ c
⇒ 2
|
v
г
/c
⇒1
|
Современная техника эксперимента позволяет измерять скорости при величинах ускоряющих потенциалов U
/ U
0
порядка 0,7 – 1,5. Возможно, что зависимость скорости от величины ускоряющих потенциалов окажется отличной от записанных закономерностей. Подробно эта проблема изложена в [5], а также в [6].
Заключение
И вновь, как и в предыдущей Главе, мы использовали релятивистский математический формализм для мгновенно действующих потенциалов. Только опираясь на эти потенциалы, удается дать правильное непротиворечивое объяснение квазистатическим явлениям электродинамики.
Важность проверки закона Кулона в том, что его проверка даст ответ на вопросы: как зависит от скорости движения магнитного поля величина, создаваемого им электрического поля, и, соответственно, как зависит от скорости движения заряда (его электрического поля) величина, создаваемого им магнитного поля?
Источники информации:
1 Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: «ФИЗМАТГИЗ», 1963.
2 Пановски В., Филипс М. Классическая электродинамика. М., ГИФФМЛ, 1968.
3 Угаров В.А.. Специальная теория относительности. - М.: Наука, 1969.
4 Ершков С.В. Задача трех тел (новое точное решение) http://www.chronos.msu.ru/RREPORTS/yershkov_zada4a.pdf.
5 Кулигин В.А., кулигина Г.А. Механика квазинейтральных систем заряженных частиц и законы сохранения нерелятивистской электродинамики. – Деп. в ВИНИТИ 04.09.86 № 6451 – В86. Воронеж. Ун-т. – Воронеж, 1986. http://www.sciteclibrary.ru/rus/catalog/pages/9219.html
6 Кулигин В.А., Кулигина Г.А., Корнева М.В. Кризис релятивистских теорий. Часть 6. Магнитные взаимодействия. http://kuligin.mylivepage.ru/file/index/
5.1 Квазинейтральные системы
Итак, в предыдущих главах мы показали, что решение волнового уравнения зависит от начальных условий. Одним из важных результатов является появление решений с мгновенно действующими потенциалами. Это позволяет, опираясь на них, дать не только решение проблемы электромагнитной массы, но и объяснить ряд парадоксов современной электродинамики.
Наличие мгновенно действующих потенциалов в решении волнового уравнения противоречит постулатам теории относительности А. Эйнштейна. Мы обсудим эти постулаты позже.
В Главе 3 мы обсудили нерелятивистскую функцию Лагранжа для взаимодействующих зарядов. Там же мы поставили вопрос об экспериментальной проверке закона Кулона. При малых скоростях зависимость от относительной скорости зарядов известна. Она пропорциональна (v
1
- v
2
)2
. Но какова она при больших относительных скоростях?
  Вариантов много: 1+ v
12
2
/c
2
; 1/ 1− v
12
2
/c
2
; и так далее . Здесь важно экспериментально выявить зависимость лагранжиана взаимодействия от скорости. Вариантов много: 1+ v
12
2
/c
2
; 1/ 1− v
12
2
/c
2
; и так далее . Здесь важно экспериментально выявить зависимость лагранжиана взаимодействия от скорости.
В этой Главе нашей задачей будет анализ магнитных явлений для малых
скоростей. Релятивисты утверждают, что классическая механика оказалась неспособной объяснить магнитные явления, и только теория относительности это сделала. Как она это «сделала», мы уже видели. Подобные декларации
«процветают» на фоне парадоксов, так и не разрешенных релятивистами.
Рассмотрим замкнутую систему, состоящую из большого числа заряженных частиц, взаимодействующих между собой. Пусть эти частицы локализованы в некотором объеме V
0
. Обозначим положительный суммарный заряд всех положительно заряженных частиц через Q
+
, а отрицательно заряженных – через Q
-
. Необходимым условием квазинейтральности системы служит условие:
 Q
+
+ Q
− Q
+
+ Q
−
 << Q
+ << Q
+
Суммарный заряд квазинейтральной системы должен быть значительно меньше по абсолютной величине суммарного заряда всех положительно заряженных частиц.
Мы используем для построения функции Лагранжа квазинейтральной системы выражение
(3.1.1). Однако мы обобщим это выражение, взяв общую форму лагранжиана взаимодействия. Для i
и k
частиц запишем следующую функцию Лагранжа
v
i
2 v
k
2
L
= m
i
 + L
ik
(R
ik
;v
ik
) + m
k
; L
ik
= L
ki
; L
ii
= 0 + L
ik
(R
ik
;v
ik
) + m
k
; L
ik
= L
ki
; L
ii
= 0
2 2
Общий вид функции действия для квазинейтральной замкнутой консервативной системы можно записать в следующем виде [1], [3]:
N m
iv
i
2
S
= ∫∑i
=1 [  2
+∑
k i
> L
ik
(R
ik
;v
ik
)]dt
(5.1.1) 2
+∑
k i
> L
ik
(R
ik
;v
ik
)]dt
(5.1.1)
Изучим свойства системы, описываемойдействием (5.1.1). Прежде всего, найдем уравнение движения для i
-той частицы. Для этого найдем вариацию действия δS
и обратим ее в нуль. Варьировать подынтегральное выражение мы будем при следующих условиях: мы будем менять координату i
-той частицы Ri
, полагая t
и координаты других частиц фиксированными (постоянными). В результате мы получим следующую систему уравнений движения:
  dm
i
v
i
N
⎛⎜ ∂L
ik
− d
∂L
ik
⎟⎞⎟=∑N
F
ki
(5.1.2) dm
i
v
i
N
⎛⎜ ∂L
ik
− d
∂L
ik
⎟⎞⎟=∑N
F
ki
(5.1.2)
=∑⎜∂R
ik dt
∂v
ik
⎠ k
=1 dt
k
=1 ⎝
где: δR
ik
= δR
i
- δR
k
= δR
i
поскольку δR
k
постоянна; δv
ik
= δv
i
- δv
k
= δv
i
, поскольку δR
k
постоянна;
∂L
ik d
∂L
ik
 F
ki
= − =−F
ik F
ki
= − =−F
ik
∂R
ik dt
∂v
ik
Из (5.1.2) видно, что третий принцип Ньютона выполняется, т.е. действие всегда
равно противодействию. Более того, сила F
ki
оказывается инвариантной относительно преобразования Галилея, поскольку зависит от относительных величин v
ik
и R
ik
. Ниже мы обсудим содержание понятий «сила» и «работа», а сейчас найдем работу, совершаемую, i
– частицей.
Умножим (2.2) на скорость i
– частицы.
m
i
v
i
2 N
dK
i
= d
 2 =∑k
=1 F
ki
v
i
dt
i
=1,2,..,N
(5.1.3) 2 =∑k
=1 F
ki
v
i
dt
i
=1,2,..,N
(5.1.3)
Это дифференциал кинетической энергии частицы при ее взаимодействии с другими частицами при условии, что все остальные частицы покоятся. Просуммируем (5.1.3) по индексу i
.
N N N N N N N
dK
= ∑dK
i
=∑∑F
ki
v
i
dt
=∑∑F
ki
(v
i
− v
k
)dt
=∑∑F
ki
d
R
ik
dt
(5.1.4)
i
=1 i
=1 k
=1 i
=1 k
>i i
=1 k
>i
Соотношение (5.1.4) показывает, что изменение кинетической энергии всех взаимодействующих частиц системы равно работе всех сил. Величина dK
инвариантна относительно преобразования Галилея, т.е. не зависит от выбора инерциальной системы отсчета.
Время t
можно рассматривать как четвертую координату частиц. Мы можем варьировать и эту координату. Наложим условие при варьировании t
: положение i
- частицы фиксировано (R
i
– const; v
i
= 0), а все остальные частицы перемещаются, но взаимодействуют только с i
- частицей. Такое взаимодействие описывается следующей частной функцией Лагранжа
m
iv
i
2 N
L
i
=  +∑
L
ik
(R
ik
;v
ik
) L
ii
= 0 (5.1.5) +∑
L
ik
(R
ik
;v
ik
) L
ii
= 0 (5.1.5)
2
k
=1
Найдем вариацию этой функции Лагранжа
dL
i m
iv
i
2 N
d
N
δL
i
=  δt
=δ[ δt
=δ[  +∑L
ik
(R
ik
;v
ik
)] = +∑L
ik
(R
ik
;v
ik
)] =  dt
∑k
=1 L
ik
δt
dt
2 k
=1 dt
∑k
=1 L
ik
δt
dt
2 k
=1
 При выводе последнего выражения мы учли, что i
– частица покоится. Продолжим преобразование, воспользовавшись уравнением движения для k
- частицы (5.1.2) δL
i
=[∑k
N
=1 ⎛⎜⎜⎝ ∂∂R
L
ikki
v
+ ∂∂v
L
ikki d
v
k
⎞⎟
]δt
= k
⎟
dt
⎠ При выводе последнего выражения мы учли, что i
– частица покоится. Продолжим преобразование, воспользовавшись уравнением движения для k
- частицы (5.1.2) δL
i
=[∑k
N
=1 ⎛⎜⎜⎝ ∂∂R
L
ikki
v
+ ∂∂v
L
ikki d
v
k
⎞⎟
]δt
= k
⎟
dt
⎠
⎧ d
N
∂L
ik
⎫ ⎧ N
⎡ ∂L
ik d
∂L
ik
⎤⎫
  ⎨⎩ ∑ ∂v
ki
v
k
⎬⎭δt
+ ⎨⎩∑k
=1 ⎣⎢∂R
ki
− dt
∂v
ki
⎥⎦⎬⎭v
k
δt dt
k
=1 ⎨⎩ ∑ ∂v
ki
v
k
⎬⎭δt
+ ⎨⎩∑k
=1 ⎣⎢∂R
ki
− dt
∂v
ki
⎥⎦⎬⎭v
k
δt dt
k
=1
Перенесем полную производную в левую часть
d
⎧ N
∂L
ik
∂L
ik
⎫ N
 ⎨L
i
−∑ ⎨L
i
−∑ ∂v
ki
∂v
ki
v
k
− L
i
⎬⎭=−∑k
=1 F
ik
v
k dt
(5.1.6) dt
⎩ k
=1 ∂v
ki
∂v
ki
v
k
− L
i
⎬⎭=−∑k
=1 F
ik
v
k dt
(5.1.6) dt
⎩ k
=1
Выражение (5.1.6) – это изменение потенциальной энергии i
– частицы при ее взаимодействии с другими частицами, при условии что i
– частица покоится, а остальные частицы перемещаются и взаимодействуют только с ней. Суммируя (5.1.6) по индексу i
, получим полное изменение потенциальной энергии всех взаимодействующих частиц.
N N N N N N N
dE
= ∑dE
i
= −∑∑F
ik
v
k
dt
= −∑∑F
ik
(v
k
− v
i
)dt
= −∑∑F
ik
d
R
ki
dt
(5.1.7)
i
=1 i
=1 k
=1 i
=1 k
>i i
=1 k
>i
Как и (5.1.4) соотношение (5.1.7) инвариантно относительно преобразования Галилея. Оно выражается через работу всех сил, действующих на заряды замкнутой квазинейтральной системы. Поэтому величину dA
, равную dA
=dK
=−dE
, мы назовем дифференциалом работы, а саму величину A
– работой.
5.2 Работа и сила
Выясним теперь содержание понятий «сила» и «работа». Понятию «сила» можно дать в классической механике следующее определение:
«Сила
– это свойство материального объекта (источника данного свойства), которое проявляется при взаимодействии материальных объектов и приводит к изменению состояния взаимодействующих объектов (импульс, траектория и др.)
».
• Отметим, что сила это свойство
объекта, а не некий материальный объект. «Голой» силы, т.е. силы без источника, как свойства без объекта не бывает. Сила всегда имеет свой источник. Источниками сил могут быть самые разнообразные материальные объекты: заряд со своим полем, электромагнитная волна, которая несет с собой свое свойство – силовую характеристику, т.е. напряженность своего поля и т.д.
• Сила проявляется только во взаимодействии
, т.е. во взаимном действии. Взаимность действия в классической механике отражается третьим принципом Ньютона. Для проявления силы необходимы, по крайней мере, два объекта, которые должны взаимодействовать.
• Очень важно, что сила зависит только от относительных величин: скоростей и расстояний. Положение субъекта-наблюдателя не влияет
на силу взаимодействия. Как нами ранее было установлено, сила инвариантна относительно преобразования Галилея.
Работа является второй стороной (характеристикой) взаимодействия. Дадим следующее определение:
«Работа
– объективная количественная характеристика качественного изменения движения материи, характеризующая энергетическую сторону взаимодействия
».
• Отметим, что работа связана не с движением объекта относительно наблюдателя, т.е. не с самим движением в системе отсчета наблюдателя, а с качественным измерением движения, рассматриваемым в любой
фиксированной инерциальной системе отсчета.
Качественное изменение движенияв широком смысле есть переход одного вида энергии в другой, от одного материального объекта к другому.
• Работа – объективное понятие. Работа определяется в механике относительным
движением материальных объектов, а также движение не зависит от положения наблюдателя. Это определяет инвариантность работы относительно преобразования Галилея, т.е. независимость работы от волевого выбора наблюдателем инерциальной системы отсчета.
Если сопоставить эти понятия с соответствующими понятиями в теории относительности
Эйнштейна, заметно принципиальное концептуальное различие. Интерпретация понятий
«работа» и «сила» в этой теории не соответствует содержанию этих понятий в ньютоновской механике.
Ниже мы рассмотрим примеры, чтобы объяснить характерные гносеологические ошибки, которыми насыщена современная физика.
Первый пример.
Рассмотрим два взаимодействующих тела. Уравнения движения этих тел имеют вид:
  d
v
1
d
v
2 d
v
1
d
v
2
m
1
= F
12
и
m
2
= F
21
(5.2.1) dt dt
Вычислим дифференциал работы.
dA
=F
12
(v
1
−v
2
)dt
=F
12
d
R
12
=F
21
d
R
21
(5.2.2)
Работа, которую совершает каждая частица, равна
  m
2
m
1 m
2
m
1
dA
1
= F
12
d
R
12
и dA
2
= F
12
d
R
12
(5.2.3) m
1 + m
2 m
1 + m
2
Часто в учебниках можно встретить следующее выражение для работы, совершаемой телами:
~ ~
dA
= F v
dt
и dA = F v
dt
(5.2.4)
12 1 21 2
Выражение (5.2.4) может считаться правильным, если источники сил F
12
и F
21
покоятся в системе отсчета наблюдателя одновременно (δR
1
= 0; δR
2
= 0). Однако это невозможно.
Выражение (5.2.4) можно рассматривать как стандартную гносеологическую ошибку. Сила всегда является свойством
взаимодействующего тела. Это свойство ошибочно отрывают от частицы и превращают в некую самостоятельную субстанцию, которая покоится в системе отсчета наблюдателя. В результате такого подхода появляется «работа», которая зависит от субъективного выбора наблюдателем инерциальной системы отсчета (см. Парадокс рычага в Главе 3). Ее нельзя рассматривать как реальную, действительную работу [3].
В научной литературе [4] можно прочитать, что
mv
2
dA
= d
 = e
vE
dt
(5.2.5) = e
vE
dt
(5.2.5)
2
Выражение (5.2.5) справедливо только при условии, что источник поля E
покоится
в системе отсчета наблюдателя. В общем случае это выражение неверно, поскольку движение источника электрического поля не учитывается. К сожалению, до настоящего времени эта кажущаяся работа фигурирует в физике как объективное понятие (см. Приложение 3).
Второй пример.
Здесь мы рассмотрим функцию Гамильтона, используемую в современной физике [4]. В классической механике малых скоростей (v
<< c
) функция Лагранжа для заряда в электромагнитном поле равна:
m
v
2
L
=  + e
vA
− e
φ (5.2.6) + e
vA
− e
φ (5.2.6)
2
В этом приближении импульс частицы равен p
= m
v
= P
− e
A
(5.2.7) и функцию Гамильтона записывают в следующей форме
1 2
H
=  (P
− e
A
) + e
φ (5.2.8) (P
− e
A
) + e
φ (5.2.8)
2m
Такой гамильтониан широко используется в современной физике. Из уравнения (5.2.7) следует, что фактически функция H
равна
m
v
2
H
=  + e
φ (5.2.9) + e
φ (5.2.9)
2
Векторный потенциал A
исчез из выражения (5.2.8). Таким образом, выражение (5.2.8) есть фикция (подлог, если хотите).
Обычно молчаливо предполагается, что в (5.2.8) векторный потенциал A
не зависит от движения заряда. Однако это неверно. Мы вычисляем A
в точке, где движущийся
заряд находится в данный момент. Движущийся заряд проходит поочередно точки с различными значениями A
. Следовательно, потенциал A
в точках нахождения заряда может меняться и зависеть от положения заряда и скорости его движения в поле. Обобщенный импульс должен быть равен
∂L
∂A
P
=  = m
v
+ e
A
+ e
( = m
v
+ e
A
+ e
(  v
) (5.2.10) v
) (5.2.10)
∂v
∂v
Соответственно, и функция Гамильтона должна иметь вид:
m
v
2
∂A
H
=  + e
φ+ e
v
( + e
φ+ e
v
(  v
) (5.2.11) v
) (5.2.11)
2 ∂v
Например, функция Гамильтона для квазинейтральной системы QS
равна
  φ (v
i
− v
k
)2 φ (v
i
− v
k
)2
H
=2
]} (5.2.12)
k
=1 2 i
≠k
2 2c
Она также инвариантна относительно преобразования Галилея. Относительные скорости используется в физике, ошибочно.движения зарядов (и, как следствие, магнитные взаимодействия) сохраняются в выражении (5.2.12). Можно утверждать, что выражение (5.2.8), которое широко
5.3 Законы сохранения
Запишем теперь законы сохранения, вытекающие из (5.1.1). Мы не будем воспроизводить промежуточные результаты, поскольку существуют стандартные способы получения законов сохранения (первых интегралов), изложенные в любом учебнике по теоретической механике.
1 В силутого, что функция Лагранжане зависит явно от времени (инвариантна относительно преобразования t
= t
‘ + t
0
, где t
0
- const) имеет место закон сохранения
N m
iv
i
2 N N
∂L
ik
энергии E
= ∑  +∑∑( +∑∑(  v
ik
− L
ik
) = const
(5.3.1) v
ik
− L
ik
) = const
(5.3.1)
i
=1 2 i
=1 k
>i
∂v
ik
2 Закон сохранения импульса вытекает из инвариантности функции Лагранжа относительно преобразования R
= R’
+ R
0
, где R
0
– const.
N
∂L
N N
∂L
ik N
P
=∑
i
=1  ∂
v
i
=(∑
i
=1 m
i
v
i
+∑
k
=1 ∂
v
i
=(∑
i
=1 m
i
v
i
+∑
k
=1  ∂
v
i
) =∑
i
=1 m
i
v
i
= const
(5.3.2) ∂
v
i
) =∑
i
=1 m
i
v
i
= const
(5.3.2)
3  Из инвариантности функции Лагранжа относительно вращений пространственных координат R
= R
0
+[R
0
×d
ϕ], где R
0
– постоянен, а d
ϕ -
угол поворота, следует закон сохранения момента импульса M
=∑i
N
=1 ⎛⎜⎜
⎝[m
i
R
i
×v
i
]+∑k
N
>i
[R
ik
×∂
∂
v
L
ik
ik
⎟
⎞⎠
= const
(5.3.3) ⎟ Из инвариантности функции Лагранжа относительно вращений пространственных координат R
= R
0
+[R
0
×d
ϕ], где R
0
– постоянен, а d
ϕ -
угол поворота, следует закон сохранения момента импульса M
=∑i
N
=1 ⎛⎜⎜
⎝[m
i
R
i
×v
i
]+∑k
N
>i
[R
ik
×∂
∂
v
L
ik
ik
⎟
⎞⎠
= const
(5.3.3) ⎟
4 Из инвариантности функции Лагранжа относительно преобразования Галилея следует, что центр инерции замкнутой системы, определяемый выражением
N N
R
c
= ∑m
i
R
i
/∑m
i
движется относительно наблюдателя с постоянной скоростью
i
=1 i
=1
d
R
c N N
v
c
=  = ∑m
i
v
i
/∑m
i
. dt
i
=1 i
=1 = ∑m
i
v
i
/∑m
i
. dt
i
=1 i
=1
Таковы следствия, вытекающие из соотношения (2.1) в рамках классической механики для квазинейтральных систем электродинамики. Попутно заметим, что все полученные результаты остаются справедливыми и для случая, когда vik = 0, а Lik зависит только от
Rik
.
5.4 Взаимодействие проводников с током
Инвариантность функции Лагранжа относительно преобразования Галилея позволяет описать магнитные явления с позиции механики Ньютона. Проиллюстрируем это на примерах.
Рассмотрим взаимодействие двух проводников с токами. Проводник мы представим в виде ионной решетки положительных зарядов и электронов проводимости
(квазинейтральная система). Пусть первый проводник, т.е. его кристаллическая решетка, движется со скоростью v
1
, а второй – со скоростью v
3
, как показано на рис. 5.1.
Функция Лагранжа будет определяться суммой парных взаимодействий положительных и отрицательных зарядов двух проводников. Выделим во втором проводнике объем dV,
в котором ρ3
и ρ4
– плотности положительных и отрицательных зарядов соответственно. Пусть в этом объеме положительные заряды первого проводника создают потенциал φ1
, а отрицательные - φ2
.
Будем считать, что оба проводника квазинейтральны: ρ3
+ ρ4
= 0; φ1
+ φ2
= 0. Плотность лагранжиана равна:
φ1
ρ3
(v
1 − v
3 ) 2
φ1
ρ4
(v
1 − v
4 )2
Λ = − 2 (1+  2 ) − 2 (1+ 2 ) − 2 (1+  2 ) − с
2c с
2c 2 ) − с
2c с
2c
φ2
ρ3
(v
2
− v
3
) 2
φ2
ρ4
(v
2
− v
4
) 2
 − 2
(1+ 2
) − 2
(1+ 2
) = (5.4.1) с
2c с
2c − 2
(1+ 2
) − 2
(1+ 2
) = (5.4.1) с
2c с
2c
φ1
v
12
= 2
ρ3
v
34
= jA
c
где: j
= ρ3
v
34
=
ρ4
v
43
–
плотность тока в проводнике 2; A
= φ1
v
12
/ c
2
=φ2
v
21
/ c
2
– векторный потенциал, создаваемый проводником 1 в объеме dV
проводника 2.
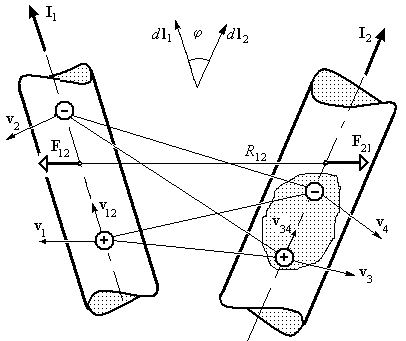
Рис. 5.1 Обозначения: v
1
– скорость положительных зарядов проводника 1; v
2
–
средняя скорость отрицательных зарядов проводника 1; v
3
-
скорость положительных зарядов проводника 2; v
4
- средняя скорость отрицательных зарядов проводника 2; v
21
= v
2
– v
1
-
средняя скорость движения отрицательных зарядов в проводнике 1 относительно положительных; v
43
= v
4
– v
3
-
средняя скорость движения отрицательных зарядов в проводнике 2 относительно положительных.
Легко видеть, что плотность функции Лагранжа совпадает с общепризнанной. Однако заметим также, что это является следствием полной компенсации кулоновских потенциалов в квазинейтральных системах, а не релятивистским эффектом. Помимо этого, следует подчеркнуть, что (5.4.1) инвариантно относительно преобразования Галилея. Для получения функции Лагранжа необходимо (5.4.1) проинтегрировать по всему объему, содержащему проводники.
L
= ∫ jA
dV
(5.4.2)
Теперь мы можем, опираясь на (5.4.2), рассмотреть взаимодействие двух бесконечно малых проводников с токами, т.е. взаимодействие двух элементарных токов. Пусть длины проводников dl
1
и dl
2
, а также размеры их поперечных сечений s
1
и s
2
малы по сравнению с расстоянием R
12
между этими проводниками. В этом случае векторный потенциал первого проводника можно записать в известной форме:
μ I
1
d
l
1
A
= 
4π R
12
где: I
1
– ток, протекающий через поперечное сечение первого проводника, I
1
=∫ρ2
v
d
s
21
Подставим это выражение в (5.4.2)
μ I
1
d
l
1
L
= ∫  j
dV j
dV
4π R
12
и, учитываямалость объема dV,
в котором векторный потенциал А,
можно считать постоянным, получим:
 L
j
dV L
j
dV
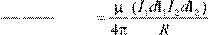 (5.4.3) (5.4.3)
12
где I
2
= ∫ρ4
v
43
d
s
2
Отметим, что (5.4.3) инвариантно относительно преобразования Галилея.
Существующая в современной литературе [5] асимметрия закона Ампера (или формулы Био-Саварра) в ряде случаев приводит к нарушению Третьего закона Ньютона. Это видно из современной записи выражений для сил:
μ I
1
d
l
1
×[R
12
× I
2
d
l
2
] μ I
1
d
l
1
×[R
12
× I
2
d
l
2
]
F
21 =  3 ; F
21 = 3 ; F
21 =  3 3
4π R
12 4π R
12
В общем случае F
12
≠ F
21
. Пример подобного нарушения приведен в [5], а рисунок из этой работы воспроизведен ниже.
На рис. 5.2 показано, что второй элемент тока воздействует на первый с силой F
21
, отличной от нуля, а сам не испытывает никакого воздействия со стороны первого элемента тока.
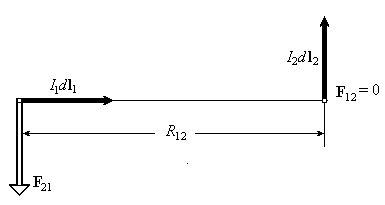
Рис. 5.2
Полученное нами соотношение (5.4.3) позволяет устранить асимметрию закона Ампера, которая до сих пор не получила бесспорного объяснения. Чтобы выяснить особенности взаимодействия элементарных токов, запишем интеграл действия, опираясь на (5.4.3):
S
= ∫ Ldt
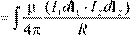 dt dt
12
 Варьировать мы можем только две величины R
12
– расстояние между двумя проводниками и ϕ12
– угол взаимной ориентации элементов тока. a. Будем варьировать R
12
при угле ϕ12
постоянном. μ (I
1d
l
1 ⋅ I
2d
l
2 ) μ 1 Варьировать мы можем только две величины R
12
– расстояние между двумя проводниками и ϕ12
– угол взаимной ориентации элементов тока. a. Будем варьировать R
12
при угле ϕ12
постоянном. μ (I
1d
l
1 ⋅ I
2d
l
2 ) μ 1
δS
= δ∫ 4π R
12 dt
= 4π ∫(I
1d
l
1 ⋅ I
2d
l
2 )δ( R
12 )dt
= R
12 )dt
=
Отсюда следует, что
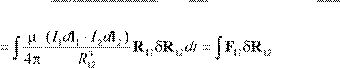 dt
= 0 dt
= 0
μ (I
1
d
l
1
⋅I
2
d
l
2
)
F
12
=  R
12
= −F
21
(5.4.4) R
12
= −F
21
(5.4.4)

Как мы видим, Третий принцип Ньютона выполняется.
b. Будем варьировать угол взаимной ориентации элементов тока ϕ12
при неизменном R
12
.
δS
=   )dt
= )dt
=
 12 4π 12 12 4π 12
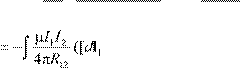 × d
l
2
]δϕ12
)dt
= ∫M
21
δϕ12
dt
= −∫M
12
δϕ12
dt
= 0 × d
l
2
]δϕ12
)dt
= ∫M
21
δϕ12
dt
= −∫M
12
δϕ12
dt
= 0
μ [I
1
d
l
1
× I
2
d
l
2
]
Отсюда следует, что M
21
=  = −M
12
(5.4.5) = −M
12
(5.4.5)
4π R
12
Результаты (5.4.4) и (5.4.5) полностью описывают явления, связанные с взаимодействием двух элементарных токов. Третий принцип Ньютона не нарушается.
Правильность полученного вывода можно подтвердить, используя выражение для силы Лоренца при отсутствии кулоновских сил.
∂A
1
F
12
= −q
2
 + q
2
v
2
×rotA
1
(5.4.6) + q
2
v
2
×rotA
1
(5.4.6)
∂t
Вычислим значения
φ1
v
1
q
1v
1 ∂A
1 v
1 ∂φ1 μ
 A
1 = 2 = μ A
1 = 2 = μ  q
2 = q
2 = − 3 q
1v
1 (q
2 v
2R
21 ) c
4πR
12
∂t c
2
∂t
4πR
12 q
2 = q
2 = − 3 q
1v
1 (q
2 v
2R
21 ) c
4πR
12
∂t c
2
∂t
4πR
12
μ
q
2 v
2 ×rotA
1 = −  3 q
2 v
2 ×[R
21 ×q
1v
1 ] 3 q
2 v
2 ×[R
21 ×q
1v
1 ]
4πR
12
Подставляя эти выражения в (5.4.6), получим
μ
F
12 = −  3 R
21 (q
1v
1q
2 v
2 ) = −F
21 3 R
21 (q
1v
1q
2 v
2 ) = −F
21
4πR
12
По своей форме полученное выражение соответствует выражению (5.4.4). Действительно, если q
1
v
1
соответствует I
1
d
l
1
, а q
2
v
2
соответствует I
2
d
l
2
, то придем к выражению (5.4.4), что и требовалось показать.
5.5 Взаимодействие проводника с током и заряда
Рассмотрим, как взаимодействуют заряд и проводник с током. Как и прежде, проводник мы будем рассматривать как ионную решетку, в которой со средней скоростью движутся электроны проводимости. Пусть заряд и проводник движутся со своими скоростями.
Будем считать, что количество положительных и отрицательных зарядов проводника велико и заряд q
не влияет на ток в проводнике.
Пусть в точке, где находится заряд q, положительные заряды создают потенциал φ1
, а отрицательные - φ2
. Проводник квазинейтрален, т.е. φ1
+ φ2
= 0.
Запишем функцию Лагранжа
mv
2
(v
1
− v
) 2
(v
2
− v
) 2
L
=  − q
φ1
[1+ − q
φ1
[1+  2
]− q
φ2
[1+ 2
]− q
φ2
[1+  2
] (5.5.1) 2
] (5.5.1)
2 2c
2c
Учитывая условие квазинейтральности, придадим (5.5.1) форму, удобную для дальнейшего исследования
(v
1
+ v
2
)
 L
= + q
φ1 2 L
= + q
φ1 2
2 c
Обозначим v
0
= (v
1
+v
2
) / 2 . Это скорость базовой
системы отсчета. Базовой системой отсчета для проводника мы будем считать систему отсчета, в которой положительные и отрицательные заряды движутся относительно наблюдателя с одной скоростью, но в противоположные стороны.
mv
2
(v
1
− v
2
)(v
− v
0
)
L
=  + q
φ1 + q
φ1
 2
(5.5.2) 2
(5.5.2)
2 c
Соотношению (5.5.2) можно придать стандартную форму, если ввести следующие обозначения φ1
(v
1
− v
2
)
A
= 2
- векторный потенциал в точке, где находится заряд q
; c
v
r
= v
− v
0
- скорость заряда относительно базовой системы отсчета.
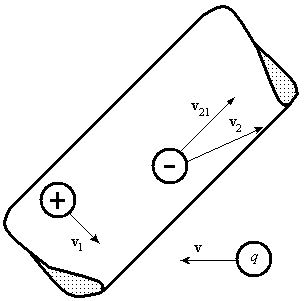
Рис. 5.3 Обозначения: v
1
– скорость движения положительных зарядов проводника; v
2
– скорость движения электронов проводника; v –
скорость свободного заряда; v
21
= v
2
- v
1
– средняя скорость электронов проводимости относительно проводника.
mv
2
Итак, L
=  + q
v
r
A
2 + q
v
r
A
2
Заметим, что (v
1
– v
2
) весьма мало, поэтому потенциал φ1
является функцией (R –v
0
t
), а производная d
R /
dt
есть скорость v
движения заряда q
.
Учитывая эти замечания, нетрудно записать уравнение движения для заряда, в правой части которого стоит сила Лоренца d
v
∂A
 m
= −q
+ q
(v
− v
0
)×rotA
(5.5.3) dt
∂t m
= −q
+ q
(v
− v
0
)×rotA
(5.5.3) dt
∂t
Выражение (5.5.3) можно записать и в другой форме d
v
∂A
m
 = q
E
'−q = q
E
'−q
 + q
v
×rot
A
dt
∂t + q
v
×rot
A
dt
∂t
где E
'= −v
0
×rotA
= −v
0
×B
представляет известный результат [4] преобразования магнитного поля с помощью формулы Лоренца при переходе наблюдателя из базовой системы отсчета в другую инерциальную систему, движущуюся относительно базовой со скоростью v
0
.
Обратимся вновь к (5.5.3) и преобразуем это выражение, выразив векторный потенциал через скалярный.
d
v
(v
1
− v
2
)(v
− v
0
)
m
 = q
gradφ1 = q
gradφ1
 2
(5.5.4) dt c 2
(5.5.4) dt c
Из (5.5.4) следует, что заряд и проводник с током не будут взаимодействовать, если; 1 v
1
– v
2
=
0 – тривиальный случай отсутствия тока в проводнике:
2 v - v
0
= 0 – заряд покоится в базовой системе отсчета;
3 (v
1
– v
2
)( v - v
0
)
= 0 , но v
1
– v
2
≠ 0 и v - v
0
≠ 0; заряд в базовой системе движется перпендикулярно проводнику с током.
Обычно средняя скорость движения электронов проводимости в проводнике мала, поэтому приближенно можно считать, что базовая система отсчета связана с проводником. Аналогичные базовые системы отсчета имеют магниты, электромагниты и т.д.
Если заряд движется относительно базовой системы отсчета, пересекая магнитные силовые линии поля (неподвижные в базовой системе), то на заряд со стороны магнитного поля будут действовать силы. Если же покоится, то силы равны нулю.
Все изложенное хорошо согласуется со здравым смыслом. Отсюда можно сделать вывод, что магнитным явлениям и взаимодействиям зарядов с магнитным полем для нерелятивистских случаев можно дать непротиворечивое объяснение с позиции механики Ньютона, т.е. при использовании мгновенно действующих потенциалов.
Источники информации:
1 Кулигин В.А., Кулигина Г.А. Механика квазинейтральных систем заряженных частиц и законы сохранения нерелятивистской электродинамики. – Деп. в ВИНИТИ 04.09.86 № 6451 – В86. Воронеж. Ун-т. – Воронеж, 1986. http://www.sciteclibrary.ru/rus/catalog/pages/9219.html
2 Кулигин В.А., Кулигина Г.А., Корнева М.В. Кризис релятивистских теорий. Часть 6. Магнитные взаимодействия. http://kuligin.mylivepage.ru/file/index/
3 Kuligin V.A. , Kuligina G.A. , Korneva M.V. "Epistemology and Special Relativity", Apeiron, no 20, 1994.
4 Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: «ФИЗМАТГИЗ», 1963.
5 Тамм И.Е. Основы теории электричества. – М.: ГИТТЛ, 1954.
Введение
В этой главе мы рассмотрим некоторые парадоксы, связанные с магнитным взаимодействием для иллюстрации результатов предыдущей главы. Здесь мы рассмотрим некоторые парадоксы, часть которых собрана в статье Г.В. Николаева [1], и подтвердим эффективность использования мгновенно действующих потенциалов.
6.1 Униполярная индукция
Специальная теория относительности никогда не могла дать корректного объяснения этому явлению (см., например, [1]). Здесь мы дадим новое объяснение в рамках классической механики Ньютона. Качественное объяснение не представляет принципиальных трудностей. Однако количественный пример, как правило, связан с громоздкими вычислениями, за которыми утрачивается его наглядность. Это первая причина, заставившая нас отыскивать наиболее простые модели для анализа. Вторая причина заключалась в том, чтобы подобрать наиболее универсальную модель, на которой мы могли бы исследовать разные модели униполярных генераторов.
Модель униполярного генератора представлена на рис. 6.1. Устройство содержит токовое кольцо, эквивалентное магниту, и проводящий диск со скользящим контактом. Кольцо и диск могут вращаться независимо друг от друга с разными угловыми скоростями. Такое устройство является универсальным и позволяет моделировать униполярные генераторы разных типов. Например, если диск и кольцо с током вращаются с одинаковой угловой скоростью, мы имеем униполярный генератор с вращающимся магнитом. Если же токовое кольцо неподвижно, но вращается диск, тогда мы имеем дело с другим типом униполярного генератора.
Рассмотрим работу униполярного генератора в общем случае. Будем считать, что h
<< a
(см. рис. 6.1). Иными словами, вращающийся диск, кольцо с током и цепь AVC
лежат в одной плоскости z
= 0.
Сделаем несколько предварительных замечаний. ЭДС индукции генерируется кольцом с током в двух частях замкнутой цепи AVCOA
.В первой неподвижной части цепи AVC
возбуждается ЭДС индукции U
1
. Если кольцо с током неподвижно, ЭДС U
1
= 0. Второй участок, где возникает ЭДС индукции, есть отрезок OC
на диске. Здесь индуцируется ЭДС U
2
. Суммарная ЭДС в цепи AVCOA
равна
U
= U
1
– U
2
(6.1.1)
Когда ω1
= 0, вся цепь AVCOA
покоится и суммарная ЭДС равна нулю, U
= 0.
Порядок вычисления ЭДС U
простой. Мы будем вычислять суммарную напряженность поля в некоторой точке D
на оси x.
Величина U
получается в результате интегрирования суммарной напряженности поля. Выделим элемент dl
на кольце с током. Его можно рассматривать как элемент тока, который движется со скоростью v
0
.
1.
Пусть точка D
неподвижной цепи AVC
расположена на расстоянии R
от оси z.
Легко видеть, что напряженность поля в точке D
равна
∗
(v
12
v
0
) dq
1
R
d
E
1
= −grad
(d
φ ) = −  2 3
d
ϕ (6.1.2) где: q
1
– суммарный c d
ϕ 4πεR 2 3
d
ϕ (6.1.2) где: q
1
– суммарный c d
ϕ 4πεR
положительный заряд вращающегося кольца с током; R
есть расстояние между dl
и точкой D
; v
0
-скорость базовой системы отсчета элемента с током dl
(v
0
, v
12
<< c
);

Рис. 6.1.
1
– проводящий диск; 2
– кольцо с током; 3
– скользящий контакт.
2.
Рассмотрим теперь точку D
на вращающемся диске. Скорость перемещения точки D
равна:
v
=ω2
r
(6.1.4)
Напряженность поля в этой точке D
равна
(v
12
(v
0
− v
)) dq
1
R
d
E
2
= −  2 3
d
ϕ (6.1.5) c d
ϕ 4πεR 2 3
d
ϕ (6.1.5) c d
ϕ 4πεR
Рассмотрим физический смысл уравнения (6.1.5). Очевидно, что напряженность поля можно представить как сумму напряженностей.
d
E
2
= d
E
'
2
+ d
E
"
2
(6.1.6)
где:
a. d
E
'
2
= −  (v
12
2
v
0
) dq
1
R
3
d
ϕ – напряженность поля, которое возбуждается при (v
12
2
v
0
) dq
1
R
3
d
ϕ – напряженность поля, которое возбуждается при
c d
ϕ 4πεR
условии, что кольцо с током вращается, а проводящий диск неподвижен.
"
(v
12
v
) dq
1
R
b. d
E
2
=  2 3
d
ϕ – напряженность поля, которое возбуждается при 2 3
d
ϕ – напряженность поля, которое возбуждается при
c d
ϕ 4πεR
условии, что проводящий диск вращается, а неподвижно теперь кольцо с током.
3.
Общая напряженность поля равна разности напряженностей полей.
d
E
= d
E
1
− d
E
2
(6.1.7)
Легко видеть, что компоненты dE
1
и dE
`2
взаимно уничтожаются, и мы получаем следующие компоненты напряженности общего поля d
E.
(v
12
v
) dq
1
(a
− r
cosϕ)
 dE
r
= −μ 2
cosϕ 3
d
ϕ (6.1.8) c d
ϕ R dE
r
= −μ 2
cosϕ 3
d
ϕ (6.1.8) c d
ϕ R
(v
12
v
) dq
1
a
sinϕ
 dE
ϕ
= −μ 2
cosϕ 3
d
ϕ (6.1.9) c d
ϕ R dE
ϕ
= −μ 2
cosϕ 3
d
ϕ (6.1.9) c d
ϕ R
Полная напряженность поля, создаваемого всем кольцом с током, вычисляется путем интегрирования этих выражений в пределах от 0 до 2π. Очевидно, что в суммарной напряженности поля E
сохраняется только радиальный компонент в силу четности dEr
и нечетности dE
φ
.
Iar
ω2
2
π
cosϕ(a
− r
cosϕ)
 E
r
= −μ ∫
R
3 d
ϕ ; E
ϕ
= 0. (6.1.10) 4
π
0 E
r
= −μ ∫
R
3 d
ϕ ; E
ϕ
= 0. (6.1.10) 4
π
0
dq
1
где: I
= v
12
 ; dl=ad
ϕ. dl ; dl=ad
ϕ. dl
Теперь, интегрируя Er
по r
, вычислим ЭДС индукции U
C C
2π
Iar
ω2
cosϕ(a
− r
cosϕ)
 U
= ∫0 E
r
dr
=−∫0 μ 4
π
[∫
0 R
3 d
ϕ]dr
(6.1.11) U
= ∫0 E
r
dr
=−∫0 μ 4
π
[∫
0 R
3 d
ϕ]dr
(6.1.11)
Из формулы видно, что эта ЭДС не зависит от угловой скорости ω1
.
4
. Теперь покажем, что ЭДС (6.1.11) можно вычислить другим способом, например, d
Φ
используя закон Фарадея U
= −  . .
dt
Рассмотрим точки C
и C
∗
,
которые расположены, как показано на рис. 6.2. Точка C
расположена на неподвижном скользящем контакте, а C
∗
на вращающемся диске.
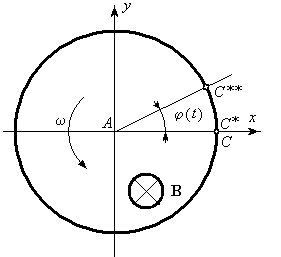
Рис. 6.2
В начальный момент времени t
координаты этих точек равны. В следующий момент времени t
+ Δt
точка C
∗
переместится и займет положение C
∗∗
. Полный поток Φ, который протекает через сектор ACC
∗∗
, равен
ϕ(t
) C
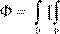 rB
(r
)dr
]d
ϕ (6.1.13) rB
(r
)dr
]d
ϕ (6.1.13)
Этот поток Φ не зависит от угловой скорости ω1
. Используя выражение (9.12) найдем ЭДС U.
d
Φ C
U
= −  dt
= −ω2
∫0
rB
(r
)dr
(6.1.14), dt
= −ω2
∫0
rB
(r
)dr
(6.1.14),
d
ϕ(t
) где ω2
=  . .
dt
Теперь, используя закон Био-Саварра, вычислим индукцию магнитного поля B
(r
).
2
π
Ia
cosϕ (a
− r
cosϕ)
 B
(r
) = ∫ μ d
ϕ (6.1.15) B
(r
) = ∫ μ d
ϕ (6.1.15)
0 4π R
3
Если мы сравним уравнения (6.1.14) и (6.1.15) с выражением (6.1.11), то окажется, что они эквивалентны.
Таким образом, мы провели детальный анализ униполярной индукции.
6.2 Униполярная индукция и мотор Фарадея
В статье Г.В. Николаева [1] приводится эксперимент № 37 (Опыт А.Родина) [1].
Теория униполярного генератора детально разобрана и изложена выше. В силу обратимости можно тем же способом объяснить принцип действия униполярного мотора. Но есть несколько важных моментов, которые следовало бы здесь рассмотреть. А.Родин экспериментально установил, что реакция на цилиндрическом магните-статоре при вращающемся диске-роторе в униполярном двигателе полностью отсутствует. Здесь мы ответим на два вопроса.
Первый вопрос
: еще раз рассмотрим вопрос о том, вращается ли магнитное поле вместе с магнитом в униполярном генераторе или же оно покоится, хотя магнит вращается? Причина появления этого вопроса в том, что ЭДС не зависит от скорости вращения магнита, т.е. магнит остается как бы «безучастным» к взаимодействию. Л.Д. Ландау считал, что поле движется вместе с магнитом
[2]. И.Е. Тамм имел другую точку зрения. Он настаивал, что магнитное поле неподвижно
, даже если магнит вращается [3]. Именно книга Тамма сформировала у многих ошибочную точку зрения.
Попробуем решить простенькую задачку. Пусть имеется бесконечный стержневой магнит прямоугольного сечения (рис. 6.3), ориентированный вдоль оси х.
Рис. 6.3
Допустим, этот магнит закрыт от Вас непрозрачной диэлектрической пластиной. Можно ли определить
: движется ли магнит вдоль оси х
или же он неподвижен?
Чтобы дать ответ на этот вопрос экспериментатор может поставить такой эксперимент. Он может наполнить пластмассовый тазик трансформаторным маслом и взять пенопластовые кружки с закрепленными на них сверху металлическими шариками. Затем он может зарядить эти шарики разными зарядами и поместить их в тазик, расположив тазик над телом магнита. Если магнитное поле неподвижно, кружки будут плавать, располагаясь случайным образом. Но если магнитное поле движется, то произойдет разделение зарядов. Кружки с положительными зарядами соберутся в одной стороне, а с отрицательными - на противоположной от них стороне!
Если при движении магнита его магнитное поле неподвижно, какая сила их смогла разделить? Магнитное поле есть свойство
магнита. Мы не сможем магнитное поле и «железку» магнита разнести в разные стороны, сделать их независимыми друг от друга.
Второй вопрос мы сформулируем, после рассмотрения эксперимента Родина.
Эксперимент № 37.
Описание. «Обнаружено, что реакция на цилиндрическом магнитестаторе при вращающемся диске-роторе в униполярном двигателе полностью отсутствует. В рамках известных представлений явление не имеет корректного объяснения, так как находится в противоречии с законами механики.
В действительности к магниту приложены скомпенсированные продольные силы F║
от вращающегося диска и неподвижного проводника токоподвода, в результате чего суммарный момент на магните равен нулю и он остается в состоянии покоя. Роль статора выполняет неподвижный проводник токоподвода, на который передается реакция от магнита - поперечная сила F┴
, однако непосредственного действия на вращающийся диск-ротор магнитное поле токоподводящего проводника-статора не оказывает. Таким образом, от токоподводящего проводника-статора вращающийся момент передается на магнит, а от магнита, в свою очередь, вращающийся момент передается на диск-ротор, при этом магнит выполняет роль активного передаточного тела, оставаясь все время неподвижным. Суммарный вращающий момент на магните всегда остается равным нулю
».
Рис. 6.4
Второй вопрос:
Всегда ли суммарный вращающий момент на магните остается равным нулю?
Вопрос этот достаточно важный, поскольку он связан с соблюдением 3 принципа Ньютона (равенство действия противодействию). Мы рассмотрим случай прямолинейного движения, поскольку никаких принципиальных
отличий в работе униполярных моторов и генераторов от линейных моторов и генераторов нет.

Рис. 6.5
Как видно из рисунка в контуре abcd
протекает ток. На ток, протекающий по движущейся пластине от b
к a
, со стороны магнита действует сила F
1
,
направленная вдоль скорости пластины. Точно такая же сила, но направленная в противоположную сторону, действует на движущийся магнит. На неподвижную перемычку cd
со стороны магнита тоже действует сила, поскольку от d
к c
протекает тот же ток. Точно такая же сила, но направленная в противоположную сторону, действует на движущийся магнит. В результате на магнит воздействует разностная величина Δ F
, направленная вдоль скорости магнита (рис. 6.5).
Она равна: Δ F = F
1
- F
2
.
Поскольку F
1
= F
2
, силовое воздействие на магнит будет действительно отсутствовать.
6.3 Мотор Маринова
Принцип действия мотора Маринова изложен в [4], а эксперименты, подтверждающие эксперимент Маринова в [5], [6]. Одна из реализаций этого мотора показана на рис. 6.6.

Рис. 6.6
Два подковообразных магнита соединены противоположными полюсами. В плоскости, которая проходит через соединение полюсов магнитов, расположен круговой проводящий виток. В качестве витка Маринов использовал ртуть. Через два скользящих контакта к ртутному кольцу подключается источник тока, который создает ток i
в каждой из половин кольца.
Согласно формуле Лоренца сила, действующая на любой элемент d
l
этого кольца, равна:
d
F
= [id
l
×B
] где: i
– ток; B –
индукция магнитного поля;
d
l –
элемент проводящего
кольца.
Она должна действовать перпендикулярно элементу d
l.
Такая сила не может создавать вращающий момент, действующий на кольцо. Однако это вращение не только наблюдалось экспериментально, но была измерена величина вращающего момента [5], [6]. Было предложено объяснение этого явления.

Рис. 6.7
Мы приведем свое объяснение, опирающееся на ньютоновскую теорию. Упрощенная схема мотора Маринова приведена на рис. 6.7. Постоянный кольцевой магнит, магнитные силовые линии которого перпендикулярны плоскости рисунка, представлен двумя замкнутыми кольцевыми токами i
1
. Внешнее проводящее кольцо снабжено двумя скользящими контактами, подключенными к источнику постоянного тока. Все упомянутые элементы лежат в одной плоскости.
Рассмотрим элемент тока d
l,
расположенный в позиции 1 на рис. 6.7. Сила d
F
(a
<< r
), которая воздействует на этот элемент тока со стороны кольцевого тока, направлена вдоль линии, связывающей d
l
с кольцевым током в соответствии с принципом равенства действия и противодействия (см. (6.3)). Эта сила имеет две проекции. Первая проекция d
F
N
направлена вдоль радиуса R
. Вторая проекция d
F
T
направлена по касательной к окружности с током i
. Эта сила создает угловой момент d
M
.
dM
= RdF
T
= RdF
sinθ (6.3.1)
Другие три элемента тока, расположенные симметрично, как показано на рис. 6.7, создают точно такие же вращающие моменты. Суммарный момент, действующий на кольцо с током i
, равен:
π
dF
M
= 4R
∫
0  d
ϕ
sinθd
ϕ (6.3.2) d
ϕ
sinθd
ϕ (6.3.2)
В то же время, согласно теории Лоренца сила, действующая на проводник с током, всегда перпендикулярна проводнику с этим током и вращающий момент, действующий на кольцо с током i
, должен быть равен нулю. Объяснение магнитных явлений с позиции ньютоновской механики не имеет затруднений и позволяет получить правильные объяснения этих явлений.
6.4 Эксперименты Р. Сигалова
Приведем описание первого эксперимента [1]. Другие эксперименты (Сигалова и др. № 5, 6, 7, 8, 14, 15, 17, 19 и Николаева № 2, 4, 20, 21, 23) являются вариациями на ту же тему.
Эксперимент № 1.
Цитируем:
«При подключении тока к П-образному проводнику последний приходит в поступательное движение. В рамках известных представлений подобное движение возможно только при взаимодействии П-образного проводника с собственным магнитным полем.
Рис. 6.8
Объяснение основывается на предположении, что магнитное поле Н боковых участков тока 1, 2 оказывает давление на жестко связанный с ними участок тока 3 проводника, под действием которого последний приходит в поступательное движение, увлекая за собой и участки тока 1, 2 П-образного проводника. При длине контура в 2-3 раза больше ширины, на 3 порядка меньшей силой действия магнитного поля Н неподвижного проводника 4 на участок тока 3 подвижного П-образного проводника можно пренебречь. Для разрешения противоречий с законами механики Ампером было допущено существование продольной силы F║
, действующей вдоль проводников 1, 2, однако существование данной силы противоречит основам классической электродинамики
».
Можно объяснить это явление через взаимодействие проводников или же с энергетической точки зрения. Мы рассмотрим оба подхода, которые приводят к одинаковым качественным и количественным результатам.
1 Энергетический подход
. Рассмотрим плоский замкнутый кольцевой контур радиусом R
, образованный проводом радиусом r.
Пусть вдоль этого контура течет ток I.
Подсчитаем энергию поля векторного потенциала, создаваемую током. Она равна
W
= LI
2
/2
Индуктивность этого контура с точностью до членов порядка (r
/ R
)4
равна [7]
8R
7
 L
= μ0
[R
(ln − ) r
4 L
= μ0
[R
(ln − ) r
4
Рис. 6.9
На части контура будут действовать растягивающие сил с погонной величиной f .
Они будут создавать натяжение Т
, стремящееся «растянуть» контур, разорвать его.
Допустим, что в результате этого контур увеличил свой радиус на величину ΔR.
Ток при этом не изменится. Изменится индуктивность контура и, соответственно его энергия. Изменение энергии есть работа, совершенная силами f
.
Итак
ΔA
= [L
(R
+ ΔR
) − L
(R
)]I
2
/2 = ΔLI
2
/ 2 = 2πRf
⋅ΔR
= 2πΔRT
Отсюда можно найти величину погонной силы
ΔA I
2
ΔL I
2
dL I
2
8R
3
 f
= = ≈ = μ0
[ln − ] f
= = ≈ = μ0
[ln − ]
ΔR
4πR
ΔR
4πRdR
4πR r
4
Соответственно
I
2
8R
3
 T
= μ0
[ln − ] T
= μ0
[ln − ]
2 r
4
Таким образом, ничего «странного» в этих экспериментах не обнаруживается. Все плоские замкнутые контура должны растягиваться при прохождении по ним тока.
В этом смысле эксперименты № 5 и 6
«не вписываются» в это объяснение (противоречат ему). Либо авторы дали не полного описания эксперимента, либо он проведен некорректно, либо дано неверное объяснение.
2 Силовой подход.
Проводники контура 1-2-3 (рис. 6.10) образуют жесткую систему, которая взаимодействует с проводником 4. В соответствии с формулой (4.4.4) мы можем рассматривать парные взаимодействия частей контура 1-2-3 с проводником 4. Равнодействующая этих сил стремиться «отодвинуть» проводник 4 от остальной части этого контура. Здесь третий закон Ньютона не нарушается. Что касается моментов сил, то эти моменты взаимно уничтожаются.
Рис. 6.10
Точно так же можно рассмотреть и объяснить другие эксперименты этой группы.
6.5 Эксперимент Г. Николаева
Эксперименты, рассмотренные выше, относились к такому классу, когда движение проводника происходило в направлении, перпендикулярном самому проводнику. Здесь мы рассмотрим эксперименты, когда движение проводника коллинеарно его ориентации.
Эксперимент №3
[1]. Описание. «Для демонстрации выполнимости законов механики при взаимодействии перпендикулярных элементов тока подвижный прямолинейный проводник 1 на подвесе размещается на расстоянии 2—4 мм от остальных проводников прямоугольного контура. Емкость С заряжается до 10-20 кВ. При пробое промежутков между подвижным проводником 1 и проводниками контура подвижный проводник приходит в поступательное движение вдоль направления тока в нем в направлении действующей на него продольной силы F
║
. Поперечные силы F
┴
реакции от подвижного проводника 1 приложены к боковому проводнику 3 контура
».
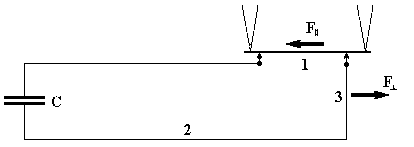
Рис. 6.11
В этом объяснении нет объяснения причин появления сил. При большом напряжении на емкости возникает большой импульсный разрядный ток. Основным переносчиком заряда являются электроны проводимости. При разряде электроны движутся против направления тока, создавая мощный механический импульс. Соответственно, в силу закона сохранения импульса положительные ионы проводника должны двигаться в обратном направлении.
По этой причине их движение (т.е. движение проводника) совпадает с направлением тока.
6.6 Эксперимент Черникова
Эксперимент № 40
[1]. Описание. «На проводник стоком в магнитном поле постоянного магнита действует сила Лоренца. Однако если проводник закрыть цилиндрическим экраном из магнитомягкого материала, то действие на проводник магнитного поля практически исчезает, но зато сила оказывается приложенной теперь к обесточенному экрану. Явление объяснимо только при учете взаимодействия токов проводника и индуцированных эквивалентных токов экрана с полями векторного потенциала во внутренней полости экрана
».
Однако имеется и другое объяснение. Цилиндрический экран «забирает на себя» силовые внешнего линии магнитного поля. Проводник с током оказывается под меньшим воздействием внешнего магнитного поля (эффект экранирования). В силу этого «действие на проводник магнитного поля практически исчезает
». Это одна часть объяснения.
Рассмотрим другую часть. Вокруг проводника с током существует напряженность магнитного поля Н
. Она убывает как R
-1
по мере удаления от проводника. В магнитном экране индукция магнитного поля В
будет приблизительно в μ раз больше, чем в воздухе вблизи экрана.
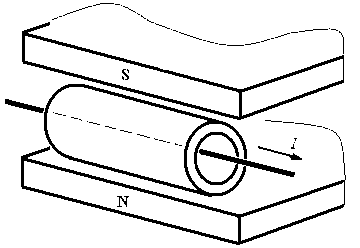
Рис. 6.12
Внешнее магнитное поле тоже создает свою индукцию в этом экране. В результате в одной половине экрана индукция оказывается больше, чем в другой (в одной половине внешнее и токовое поля складываются, а в другой - вычитаются). Это создает градиент энергии поля, который воздействует на экран, заставляя его перемещаться. Причем сила воздействия оказывается во много раз больше, чем сила воздействия на проводник без экрана.
Если бы не было этого явления, т.е. если бы сила действовала не на экран, а непосредственно на проводник с током, то электромоторы и генераторы оказались бы недолговечными. Из-за переменного давления на проводник его изоляция не могла бы долго служить (истирание изоляции).
6.7 Эксперимент Солунина и Костина
Эксперимент № 33
[1]. «Для демонстрации явления взаимодействия движущегося заряда с полем векторного потенциала А на электронно-лучевую трубку 1 в месте расположения отклоняющих пластин 2 одета тороидальная обмотка 3. Тороидальная обмотка выполнена из наружного и внутреннего слоев, намотанных медным проводом 0.62 мм с общим количеством витков 500. Необходимость двухслойной намотки вызвана тем, чтобы исключить магнитные поля кольцевого тока (одна обмотка лево-винтовая, другая - правовинтовая): Обмотки включены так, чтобы их магнитные потоки суммировались. Электроны в трубке ускорялись разностью потенциалов 400 В. На вертикальные пластины подавалось постоянное; отклоняющее напряжение для задания базисного смещения электронного луча на экране (5-20 мм). Ток в обмотке менялся в пределах 0-5 А.
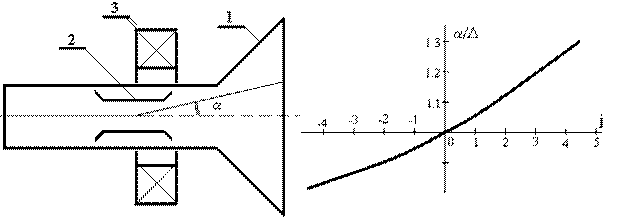
Рис. 6.13 Обозначения: 1 – электроннолучевая трубка; 2 – отклоняющие пластины: 3 – Катушка с током.
Результаты эксперимента представлены на графике. При увеличении тока одного направления угол отклонения электронного луча увеличивает свою величину по отношению к базисному отклонению. Увеличение угла отклонения электронного луча при неизменном напряжении на отклоняющих пластинах обусловлено уменьшением скорости движения электронов пучка за счет взаимодействия их с полем векторного потенциала А тороидальной обмотки. При изменении тока в обмотке на обратный угол отклонения электронного луча уменьшает свою величину по отношению к его базисному отклонению, регистрируя эффект увеличения скорости электронов пучка при их взаимодействии с полем векторного потенциала А тороидальной обмотки.
Таким образом, положительными результатами описываемого опыта однозначно доказывается существование обычного классического аналога известного опыта Аронова-Бома
и существование эффекта изменения скорости движения электронов при их взаимодействии с полем векторного потенциала А. Положительными результатами опыта однозначно подтверждается также существование неизвестного ранее в науке явления продольного магнитного взаимодействия
».
Это весьма интересный эксперимент. К сожалению, источники, на которые ссылается автор работы [1] найти не удалось, а из описания трудно судить о корректности эксперимента и его интерпретации. Ниже мы предложим другой вариант эксперимента, родственного эксперименту Солунина и Костина, и предлагаем его поставить. Предлагаемый эксперимент.
Схема эксперимента представлена на рис. 6.14.
На подвесе установлен диск, соединенный скользящими контактами с источником питания. По диску протекает ток I
2
, который взаимодействует с магнитным полем тонкой катушки (кольцо с N
витками) и может поворачиваться вокруг своей оси. Многовитковая катушка запитывается током I
1
. В результате взаимодействия диска с катушкой на диск должен действовать вращающий момент, поворачивающий диск на определенный угол.
2
μ 2
d
M
1
2
=  [I
1
d
l
1
× I
2
d
l
2
] = −d
M
21
(4.4.5) [I
1
d
l
1
× I
2
d
l
2
] = −d
M
21
(4.4.5)
4πR
12
Величина момента сил М
(или угла отклонения) зависит от расстояния а
, см. рис. 6.14. Предполагаемая зависимость дана на рис. 6.15.

Рис. 6.14 Вариант с кольцевой катушкой Рис. 6.15 Предполагаемый график зависимости
Заключение
Мы рассмотрели не все эксперименты, изложенные в работе [1]. Для анализа оставшихся экспериментов у нас нет необходимой информации. Тем не менее, можно сделать оптимистический вывод. Если при описании квазистатических явлений электродинамики опираться на механику Ньютона
(а не на релятивистские «фантазии»), можно с успехом дать корректное объяснение существующим «парадоксальным» экспериментальным результатам.
Источник информации:
1. Николаев Г.В. Современная электродинамика и причины ее парадоксальности.
http://www.trinitas.ru/rus/doc/0231/004a/02310011.htm
2. Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: ФИЗМАТГИЗ, 1963.
3. Тамм. И.Е. Основы теории электричества. – М.: ГИТТЛ, 1954.
4. Marinov S. . Forces between current elements. Galilean Electrodynamics, vol. 9, no 2, 1998.
5. Wesley J.P.. "The Marinov Motor, Notional Induction without a Magnetic B Field", Apeiron, July- October, V. 5, no. 3...4, 1998.
6. Thomas E. Phipps. "Observations of the Marinov Motor", Apeiron, July – October, V. 5, no. 3...4, 1998
7. .Калантаров П.Л., Цейтлин Л.А.. Рвсчет индуктивностей. (Справочная книга), - Л.: Энергия, 1970.
Введение
Теперь нам необходимо рассмотреть вопросы, связанные с волновыми явлениями электродинамики. Но прежде подведем некоторые итоги.
1. В первой главе было показано, что у волнового уравнения имеются вырожденные (мгновенно действующие) решения. Этот факт находится в противоречии с постулатами СТО, которые позже будут исследованы. По этой причине, используя математический формализм СТО, мы будем решать вопросы не «согласуя» их с теорией относительности.
2. Опираясь на вырожденные решения, нами были исследованы явления квазистатической электродинамики и дано решение ряда проблем. Различие в свойствах мгновенно действующих полей зарядов и волн позволяет сделать вывод, что поля зарядов и электромагнитные волны суть различные поля. Их отождествление – предрассудок, который укоренился в физике.
В качестве источника анализа основ электродинамики мы выбрали книгу Л.Д. Ландау и Е.М. Лифшица «Теория поля» [1]. Это обусловлено тем, что книга [1] рекомендована в качестве учебного пособия для университетов.
На первый взгляд кажется, что теоретические основы теории электромагнитного поля изложены изящно и логично. Но это только на первый взгляд. Изложение имеет недостатки, достойные пересмотра. Например (см. параграфы 23 – 33 в [1]):
– исходный тензор энергии-импульса электромагнитного поля несимметричен
, поэтому к нему добавляется еще «нулевой» тензор ∂Ai
Fkl
/∂(4πxl
);
– из тензора энергии-импульса
электромагнитного поля вытекают не законы
сохранения
, а только одно из четырех уравнений Максвелла;
– закон сохранения энергии Пойнтинга выводится «дедовским» методом, т.е. путем «комбинации» двух из четырех уравнений Максвелла и т.д.
При изложении мы будем опираться на работы [2], [3].
7.1 Плотность функции Лагранжа электромагнитного поля волны
В учебнике [1] построение теоретических основ электродинамики идет от функции Лагранжа для заряда. Затем получают тензор электромагнитного поля Fkl
. От него идут к тензору энергии-импульса электромагнитного поля, к уравнениям Максвелла и теореме Пойнтинга.
Мы будем проводить анализ в обратной последовательности и начнем с плотности функции Лагранжа для электромагнитного поля волны, продвигаясь к полям заряда. В современной теории плотность функции Лагранжа определяется через тензор электромагнитного поля волны [1]
Fik
= [∂Ak
/∂xi
- ∂Ai
/∂xk
]
Запишем это выражение для плотности функции Лагранжа
Λ = [− (Fik
)2
/4 + μji
Ai
]/ μ =
= − [(∂Ak
/∂xi
)2
- 2∂Ai
/∂xk
⋅∂Ak
/∂xi
+ (∂Ai
/∂xk
)2
]/4μ+ ji
Ai
/μ (7.1.1)
 Поскольку функция Лагранжа определена неоднозначно, преобразуем выражение (7.1.1) и придадим ему иную форму, используя интеграл действия Поскольку функция Лагранжа определена неоднозначно, преобразуем выражение (7.1.1) и придадим ему иную форму, используя интеграл действия
S
(7.1.2)
где: d
Ω = dx
1
dx
2
dx
3
dx
4
; jk
= с
ρuk
– 4-вектор плотности тока; uk
= dxk
/ds
– 4-вектор скорости; ρ - плотность пространственного заряда. Напомним уравнения непрерывности
∂Ak
/∂xk
= 0 и ∂jk
/∂xk
= 0, которые являются самостоятельными условиями, которые наложены на поля.
Раскроем подынтегральное выражение, преобразуем и проинтегрируем по частям
 1 1 ∂A
i
2 1 ∂ ∂A
k 1 1 ∂A
i
2 1 ∂ ∂A
k
S
= ∫ μ [− 2 (∂x
k
) + 2 ∂x
k
(A
i
∂x
i
) + μj
i A
i
]d
Ω =
(7.1.3)
  1 1 ∂A
i
2 1 ∂A
k 1 1 ∂A
i
2 1 ∂A
k
= ∫ μ [− 2 (∂x
k
) + μj
i A
i
]d
Ω + ∫ 2μ A
i
∂x
i dS
k
Во втором интеграле конечного выражения (7.1.3) пределами интегрирования является бесконечность, где при интегрировании по координатам поле исчезает. При интегрировании по времени начальные и конечные точки варьирования фиксированы и там вариация интеграла равна нулю. Следовательно, последний интеграл в выражении (7.1.3) обращается в нуль. Таким образом, получаем новое выражение для плотности функции Лагранжа
Λ = - (∂Ai
/∂xk
)2
/2μ + ji
Ai
(7.1.4)
Выражение (7.1.4) полностью эквивалентно
выражению (7.1.1).
7.2 Уравнения движения
Теперь мы можем получить «уравнения движения», т.е. уравнения для нахождения потенциалов электромагнитного поля, порожденных 4-вектором тока jk
. Для этого запишем выражение для интеграла действия, которое будем варьировать.
1 ∂A
i
∂δA
i
 δS
== ∫[− + j
i
δA
i
]d
Ω (7.2.1) δS
== ∫[− + j
i
δA
i
]d
Ω (7.2.1)
μ ∂x
k
∂x
k
Интегрируя по частям, получим
1   ∂A
i
1 ∂2
A
i
δS
= − ∫( δA
i
)dS
k
+ ∫ [ 2
μ ∂x
k
μ ∂x
k ∂A
i
1 ∂2
A
i
δS
= − ∫( δA
i
)dS
k
+ ∫ [ 2
μ ∂x
k
μ ∂x
k
+ μj
i
]δA
i
d
Ω = 0 (7.2.2)
Первый интеграл по гиперповерхности Sk
обращается в нуль по тем же причинам, что и последний интеграл в выражении (7.1.3). Таким образом, мы получаем окончательное выражение для уравнений движения
∂2 A
i
 = −μj
(7.2.3) = −μj
(7.2.3)
2 i
∂x
k
к которым следует добавить, как уже говорилось, уравнения непрерывности для 4потенциала поля и 4-плотности тока: ∂Ai
/∂xi
= 0; ∂ji
/∂xi
= 0
Система уравнений представляет собой уравнения Максвелла в калибровке Лоренца.
  ∂2
A
∂2
A
∂2
A
∂2
A
∂2
φ ∂2
φ ∂2
φ ∂2
φ ρ + + − = −μj
; + + − = − ; 2 2 2 2 2 2 2 2 ∂2
A
∂2
A
∂2
A
∂2
A
∂2
φ ∂2
φ ∂2
φ ∂2
φ ρ + + − = −μj
; + + − = − ; 2 2 2 2 2 2 2 2
∂x
∂y
∂z
∂(ct
) ∂x
∂y
∂z
∂(ct
) ε
(7.2.4)
1 ∂φ ∂ρ
divA
+  2
= 0; divj
+ 2
= 0; divj
+  = 0 c
∂t
∂t = 0 c
∂t
∂t
Таким образом, новое выражение для плотности лагранжиана приводит к правильным
уравнениям электродинамики (уравнения Максвелла в калибровке Лоренца).
7.3 Тензор энергии-импульса и законы сохранения
Теперь нам необходимо записать тензор энергии-импульса электромагнитного поля волны Tik
. Общий вывод формулы для вычисления тензора энергии-импульса, получаемой из плотности лагранжиана, приведен в [1]. Эта формула имеет вид
∂A
l
∂Λ
 T
ik
= δik
Λ − ∑
l
∂
x
i
∂
A
l
(7.3.1) T
ik
= δik
Λ − ∑
l
∂
x
i
∂
A
l
(7.3.1)
∂x
k
где Λ = - (∂Al
/∂xk
)2
/2μ
Вычисления дают следующий результат
 1 ∂A
l
∂A
l
1 ∂A
l
2 1 ∂A
l
∂A
l
1 ∂A
l
2
T
ik
= − δik
( ) (7.3.2) μ ∂x
i
∂x
k
2μ ∂x
i
Он совпадает с тензором энергии-импульса, приведенном в [4]. Нетрудно заметить, что тензор энергии-импульса симметричен Tik
= Tki
. Для полноты описания к этому тензору можно было бы добавить тензор взаимодействия 4-вектора тока с 4-потенциалом ji
Ak
.
Здесь мы ограничимся рассмотрением полей в свободном пространстве и не будем этого делать.
Известно, что 4-дивергенция этого тензора для свободного пространства (когда поля рассматриваются за пределами источников) равна нулю ∂Tik
/∂xk
= 0. Из этого выражения должны вытекать законы сохранения энергии и импульса (в нашем случае мы должны получить выражения для закона сохранения плотности электромагнитной энергии и закона сохранения плотности импульса) электромагнитной волны в свободном пространстве.
Эти законы, вытекающие из дивергенции тензора энергии-импульса Tik
, в общей форме имеют следующий вид:
1. Закон сохранения плотности потока S
электромагнитного поля волны
∂S
1
 + 2
gradw
= 0 (7.3.3) + 2
gradw
= 0 (7.3.3)
∂t c
2. Закон сохранения плотности энергии w
электромагнитного поля волны
∂w
divS
+  = 0 (7.3.4) ∂t = 0 (7.3.4) ∂t
где:
1 ∂A
1 ∂A
∂φ
S
= −  divA
− divA
−  ×rotA
+ ε(gradφ ×rotA
+ ε(gradφ  ) (7.3.5) μ ∂t
μ ∂t
∂t ) (7.3.5) μ ∂t
μ ∂t
∂t
1 2 2
∂A
2
ε 2
∂φ 2
 w
= w
=  [(divA
) + (rotA
) + ( ) ]− [(gradφ) + ( [(divA
) + (rotA
) + ( ) ]− [(gradφ) + (  ) ] (7.3.6) ) ] (7.3.6)
2μ ∂ct
2 ∂ct
Из полученных соотношений следуют весьма интересные выводы.
1. Во-первых
, в общем случае уравнения Максвелла в калибровке Лоренца описывают три различных вида потоков. Первый поток энергии есть известный поток
поперечных
электромагнитных волн, описываемый вектором Пойнтинга. Его
1 ∂A
плотность равна S
1
= −  × rotA
. Второй поток – поток продольных
электрических μ ∂t × rotA
. Второй поток – поток продольных
электрических μ ∂t
1 ∂A
волн векторного потенциала А
. Его плотность равна S
2
= −  divA
. Третий поток – μ ∂t divA
. Третий поток – μ ∂t
поток продольных
волн, образованный скалярным потенциалом φ с плотностью
∂φ
потока S
3
= ε  gradφ. gradφ.
∂t
2. Во вторых
, плотность энергии и плотность потоков S
1
и S
2
, образованных векторным потенциалом А, положительны
, а плотность энергии и плотность потока S
3
, созданного скалярным потенциалом φ, отрицательны
. Это отнюдь не новый факт. Об этом знают специалисты по квантовой теории поля, но этот факт, как обычно, мало известен физикам
, которые специализируются в других направлениях.
3. В третьих
, из выражений (7.3.3) и (7.3.4) вытекает новое интересное следствие. В свободном пространстве плотности потоков и плотности энергий должны удовлетворять волновому
уравнению, т.е. плотность потока и плотность энергии тоже являются запаздывающими, подобно потенциалам полей электромагнитной волны.
∂2S
∂2S
∂2S
∂2S
∂2w
∂2w
∂2w
∂2w
  + + − = 0; + + − = 0 (7.3.7) Это означает, 2 2 2 2 2 2 2 2 + + − = 0; + + − = 0 (7.3.7) Это означает, 2 2 2 2 2 2 2 2
∂x
∂y
∂z
∂(ct
) ∂x
∂y
∂z
∂(ct
)
что решение некоторых задач, например, по дифракции волн, связанных с решением векторных волновых уравнений, можно свести к тем же задачам, но описываемых волновым уравнением для скалярной плотности энергии w
. Иными словами, в принципе возможно уменьшение громоздкости вычислений при решении подобных задач.
4. В четвертых,
полученные результаты нетрудно распространить на любые волновые процессы, описываемые волновым уравнением.
7.4 Условие отсутствия продольных волн
Классической общепринятой формой уравнений электродинамики являются уравнения Максвелла в калибровке Лоренца. Как было показано в параграфе 3 Главы 1, решение в виде продольных волн может существовать в рамках уравнения Максвелла. Как известно, продольные электромагнитные волны не существуют в природе. По крайней мере, они до сих пор не были обнаружены, хотя порядок величины их мощности излучения должен быть соизмерим с мощностью излучения поперечных волн. Возникает следующая проблема: выяснить условия, при которых два потока продольных волн компенсируют (взаимно уничтожают) друг друга.
Чтобы удобнее и нагляднее было решить проблему взаимной компенсации продольных волн, этим уравнениям можно придать несколько иную форму. Разделим векторный потенциал и плотность тока на две составляющих вихревую (соленоидальную) составляющую и безвихревую (полярную) и запишем уравнения.
A = A
1
+ A
2
j
= j
1
+j
2
2
 1 ∂ A
1 1 ∂ A
1
ΔA
1
−
2 2
= −μj
1
; divA
1
= 0; divj
1
= 0;
c
∂t
 1 ∂2
A
2 1 ∂2
A
2
ΔA
2
−
2 2
= −μj
2
; rotA
2
= 0; rotj
2
= 0;
c
∂t
1 ∂2
φ ρ 1 ∂φ
 Δφ− 2 2
= − ; divA
2
+ Δφ− 2 2
= − ; divA
2
+  2
= 0 (7.4.1) c
∂t
ε c
∂t 2
= 0 (7.4.1) c
∂t
ε c
∂t
где: A
1
и j
1
– вихревая составляющая векторного потенциала и вихревая составляющая плотности тока; A
2
и j
2
– соответственно безвихревые составляющие.
Любой волновой процесс описывается волновым уравнением. Он связан с переносом энергии волной. Из результатов, полученных в [1] и в Части 1, следует, что уравнениям Максвелла в калибровке Лоренца должны отвечать три потока энергии.
Первый поток – поперечные
электромагнитные волны, описываемые вихревым векторным потенциалом A
1
; второй – поток продольных
волн безвихревого векторного потенциала A
2
; третий – поток продольных
волн скалярного потенциала φ.
Как было показано, закон сохранения имеет стандартный вид.
∂w
divS
+  + p
= 0 (7.4.2) ∂t + p
= 0 (7.4.2) ∂t
где: S
– плотность потока энергии; w
– плотность энергии волны; p
– плотность мощности сторонних сил. Значения этих величин приведены в Табл. 1.
Таблица 1. Энергетические компоненты волновых полей
| Поперечные волны векторного потенциала
1 ∂ A
1 ∂
  S
1 = − 1 ×rotA
1 w
1 = S
1 = − 1 ×rotA
1 w
1 =  [(rotA
1)2 + ( A
1 )2] p
1 = −j
1 [(rotA
1)2 + ( A
1 )2] p
1 = −j
1  ∂ A
1 μ ∂ t
2μ ∂ ct
∂ t ∂ A
1 μ ∂ t
2μ ∂ ct
∂ t
Продольные волны векторного потенциала
1 ∂ A
1 ∂ A
∂ A
S
2
= −  2
divA
2
w
2
= 2
divA
2
w
2
=  [(divA
2
)2
+ ( [(divA
2
)2
+ (  2
)2
] p
2
=−j
2 2
)2
] p
2
=−j
2
 2
μ ∂ t
2 μ ∂ ct
∂ t 2
μ ∂ t
2 μ ∂ ct
∂ t
Продольные волны скалярного потенциала
∂ φ ε ∂ φ ∂ φ S
3
= ε  gradφ w
3
= − gradφ w
3
= −  [(gradφ)2
+ ( [(gradφ)2
+ (  )2
] p
3
= ρ )2
] p
3
= ρ 
∂ t
2 ∂ ct
∂ t
|
Хорошо известно из экспериментов, что продольные электромагнитные волны в природе отсутствуют. По этой причине логически правильно заключить, что продольные волновые потоки S
2
и S
3
«гасят» друг друга.
В [5] было показано, что необходимым и достаточным условием взаимной компенсации этих потоков на бесконечности является
∂A
2
limE
L
= lim(−  − gradφ) = 0 (7.4.3) − gradφ) = 0 (7.4.3)
r
→∞ r
→∞ ∂t
Иными словами, суммарное продольное
электрическое поле Е
L
должно убывать быстрее, чем 1/r
при r
→ ∞. При выполнении условия (7.4.3) энергия не уносится в бесконечность. Кажется, что это происходит благодаря интерференции продольного безвихревого поля векторного потенциала A
2
и продольного безвихревого поля, образованного потенциалом φ. Но это внешняя сторона.
На самом деле имеют место более сложные отношения. Оказывается, что такая компенсация потоков возможна в том, и только в том
случае, если энергия поля скалярного потенциала отрицательна
. Соответственно, отрицательной должна быть и плотность потока, образованного скалярным потенциалом,
что имеет место.
Заметим, что известное решение задачи об излучении диполя Герца опирается на эти безынерциальные токи. Именно по этой причине диполь Герца не излучает продольных волн.
7.5 Источники продольных волн
Теперь мы поговорим об источниках этих волн – токах и зарядах. Продольных волн не будет, если не будет источников, возбуждающих эти волны. Нам необходимо рассмотреть правую часть уравнений Максвелла в калибровке Лоренца. Запишем для анализа необходимые уравнения.
2
 1 ∂ A
2 1 ∂ A
2
ΔA
2
− 2 2
= −μj
2
; (7.5.1) rotA
2
= 0; rotj
2
= 0;
c
∂t
1 ∂2
φ ρ 1 ∂φ
 Δφ−
2 2
= − ; (7.5.2) divA
2
+ Δφ−
2 2
= − ; (7.5.2) divA
2
+  2
= 0 (7.5.3) c
∂t
ε c
∂t 2
= 0 (7.5.3) c
∂t
ε c
∂t
Используя идею Ландау Л.Д. [1] о возможности исключения одного из четырех уравнений (см. гл. 3, параграф 18, стр. 66), о чем говорилось в Главе 1 (векторное содержит три уравнения), можно исключить одно уравнение. Например, можно исключить уравнение для скалярного потенциала, чтобы привести два волновых уравнения (векторное и скалярное) к одному векторному.
Для этой цели продифференцируем выражение для A
2
в (7.4.1) по времени, возьмем градиент от выражения для скалярного потенциала φ в (7.4.2), а затем сложим результаты. Получим
 1 ∂2E
L 1 ∂2E
L
ΔE
L
− 2 2 = c
∂t
(7.5.4)
2
   ∂A
2
1 ∂ ∂A
2
∂j
2
1 ∂A
2
1 ∂ ∂A
2
∂j
2
1
= Δ(− − gradφ) − 2 2
(− − gradφ) = μ + gradρ
∂t c
∂t
∂t
∂t
ε
Итак, электрическое поле, обуславливающее продольные волны вектора Е
L
, описывается выражением (7.5.4). В правой части имеются источники продольного электрического поля.
Чтобы поле E
L
= 0, необходимо отсутствие источников этого поля, т.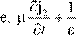 gradρ= 0 . gradρ= 0 .
Помимо этого, мы должны использовать уравнение непрерывности для безвихревого
∂ρ
компонента тока divj
2
+  = 0. = 0.
∂t
Совместно оба условия приводят к следующим конечным уравнениям
2 2
1 ∂ j
2
1 ∂ ρ
Δj
2
−  2 2
= 0 Δρ − 2 2
= 0 Δρ −  2 2
= 0 (7.5.5) c
∂t c
∂t 2 2
= 0 (7.5.5) c
∂t c
∂t
Это означает, что продольные волны будут отсутствовать, если
1. полный ток j
= j
1
+j
2
имеет вихревой характер divj
= div(j
1
+ j
2
) = 0 ;
2. безвихревой компонент тока j
2
является запаздывающим, т.е. удовлетворяет однородному волновому уравнению (7.5.5); заряды, образующие этот ток должны перемещаться со скоростью света (безынерциальные заряды).
7.6 Безынерциальные заряды
Безынерциальные заряды и токи не плод досужего измышления или некорректных теоретических выкладок. Они явно появляются при наличии металлических стенок (граничные условия на поверхности металлов) в виде поверхностных токов и зарядов. Специалисты по антенно-фидерным устройствам используют эти токи и заряды в своих расчетах, даже не подозревая, что имеют дело с новым видом носителей
электричества, отличным от инерциальных электронов. Теперь придется принять это и считаться с тем, что помимо либо электронно-дырочной проводимости, либо электронно-ионной имеет место проводимость, обусловленная безынерциальными зарядами.

Рис. 7.1
. Заряды и токи в коаксиальной линии
Приведем пример
. Рассмотрим бесконечную коаксиальную линию (см. рис. 7.1), к началу которой подключается идеальный источник постоянного напряжения. При подключении источника в линии будет распространяться поперечная электромагнитная волна (ТЕМ).
Выделим в коаксиальной линии цилиндрический объем V
и определим скорость движения зарядов.
Пусть радиус центрального проводника равен а
. Подсчитаем величину тока, протекающего по этому проводнику. Ток пропорционален напряженности магнитного поля у поверхности проводника и равен
I =
2πaH
(7.6.1)
Теперь подсчитаем заряд, находящийся внутри объема V
, когда фронт волны находится внутри нашего объема. Пусть при t
= 0 фронт волны находится у передней стенки объема. Применим теорему Гаусса. Заряд внутри нашего объема пропорционален напряженности поля у поверхности проводника и зависит от положения фронта волны, т.е. от времени
Q =
2πa
εEvt
(7.6.2)
Остается найти скорость движения зарядов. С одной стороны мы имеем соотношение (7.7.1), с другой
I = dQ
/dt =
2πa
εEv
(7.6.3)
Сравнивая их, легко найти, что
V = H
/εE = c
(7.6.4)
Здесь мы учли, что отношение Н
/Е
равно (ε/μ)1/2
.
Таким образом, из самой электродинамики следует, что скорость распространения поверхностных зарядов в проводнике равна скорости света
.
Возникает вопрос о природе безынерциальных зарядов и токов. Одно из предположений содержало мысль, что это электроны, по какой-то причине «потерявшие» свои инерциальные свойства. Однако такая гипотеза имеет трудности. Рассмотрим длинный проводник, вдоль которого распространяется электромагнитная волна (ТЕМ тип). Проводник это квазинейтральная система. В ней при отсутствии источников напряжения и тока средняя сумма плотности положительных и отрицательных зарядов равна нулю (значки говорят о соответствующих одноименных зарядах) ρ+
+ ρ-
= 0 .
Пусть безынерциальные электроны создают синусоидальный ток вдоль проводника, ориентированного вдоль оси z
. Положительные ионы неподвижны. Как показано на рис. 7.2 возникают области, где поле направлено от проводника (избыток положительных зарядов) и к проводнику (избыток отрицательных зарядов). Выделим тонкий поверхностный слой, в котором движутся заряды. Результирующая поверхностная плотность зарядов σ в этом случае равна σ = σ+
+ σ-
[1+sin(ωt – kz
)] = σ-
sin(ωt - kz
)
Это как раз соответствует знакопеременному электрическому полю, перпендикулярному поверхности проводника, поскольку вектор напряженности пропорционален поверхностной плотности заряда и направлен перпендикулярно поверхности.
Рис. 7.2
Движение электронов в проводнике Теперь запишем выражение для поверхностной плотности тока τ
τ = τ+
+ τ-
[1+ sin(ωt – kz
)] = σ+
v
+
+ σ-
v
-
[1 + sin(ωt - kz
)] = σ-
v-
[1 + sin (ωt - kz
)] где: v
+
и v
-
скорости соответствующих зарядов.
Поскольку положительные ионы неподвижны (v
+
= 0), ток будет определяться только движением отрицательных зарядов. Как нетрудно заметить, этот переменный ток должен иметь как переменную,
так и постоянную
составляющие. Соответственно, магнитное поле, окружающее проводник, тоже должно иметь постоянную
и переменную
составляющие при прохождении переменного тока. А это противоречит опыту, поскольку постоянное магнитное поле вокруг проводника не может возникать при переменном токе. Экспериментально постоянное поле при переменном токе не обнаруживается.
Таким образом, гипотеза о безынерциальных «электронах» отпадает. В создании поверхностного тока должны участвовать как положительные
, так и отрицательные
безынерциальные (виртуальные) заряды. Они создают, как уже говорилось, особый вид проводимости, отличный от электронной и дырочной проводимости. Заметим, что поскольку исходные уравнения не изменились, не предвидится никаких изменений в теории дифракции, теории антенно-фидерных систем и др. Эти теории полностью сохраняют свою силу. В следующей главе мы подробно обсудим проблему безынерциальных зарядов.
7.7 Предельный переход
Переход от волновых явлений электродинамики к квазистатическим явлениям это узловая
проблема не только самой электродинамики. От ее правильного решения зависит судьба квантовой механики, квантовой теории поля, СТО и ОТО. Существует ли действительно возможность предельного перехода, как считается в настоящее время, или же это иллюзия, навеянная ошибками современной физики? Сейчас это мы увидим.
Запишем уравнения Максвелла в калибровке Лоренца
1 ∂2
A
1 ∂2
φ ρ
 ΔA
− ΔA
−  2 2
= −μj
; (7.7.1) Δφ− 2 2
= − (7.7.2) c
∂t c
∂t
ε 2 2
= −μj
; (7.7.1) Δφ− 2 2
= − (7.7.2) c
∂t c
∂t
ε
1 ∂φ
divA
+  2
= 0 (7.7.3) j
= ρv
(7.7.4) c
∂t 2
= 0 (7.7.3) j
= ρv
(7.7.4) c
∂t
Считается, что уравнения, описывающие квазистатические явления, можно легко получить путем предельного перехода при с
→ ∞. Действительно, при этом предельном переходе мы получаем следующую систему уравнений
ΔA = -
μj
(7.7.5); Δφ = - ρ/ε (7.7.6); j
= ρv
(7.7.7)
Казалось бы, система уравнений (7.6.5) - (7.6.7), как мы знаем, достаточно хорошо согласуется с известными квазистатическими явлениями. Однако предельный переход не является законным
по ряду причин. Рассмотрим некоторые особенности предельного перехода с точки зрения полученных результатов.
1. Во-первых
, рассмотрим этот переход с энергетических
позиций. Энергетический подход не менее важен, чем силовой или векторный. Ранее мы уже обратили внимание, что энергия поля скалярного потенциала, вытекающая из тензора энергии-импульса электромагнитного поля, отрицательна
. В то же время при описании квазистатических явлений она рассматривается всегда как сугубо положительная
величина, которая может быть записана в двух формах
mc
 grad grad 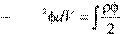 dV
. Отсюда возникает вопрос: может ли отрицательная dV
. Отсюда возникает вопрос: может ли отрицательная
энергия поля скалярного потенциала изменить свой знак
при предельном переходе с
→ ∞? Очевидно, не может. Если мы будем логически строго и последовательно
проводить этот предельный переход и рассматривать квазистатические явления с точки зрения вариационного принципа, то с неизбежностью придем к парадоксальному теоретическому выводу: современный закон Кулона не верен
! Логика вариационного принципа должна привести нас к заключению, что при отрицательной
энергии поля скалярного потенциала заряда одноименные
заряды должны притягиваться
, а разноименные
–
отталкиваться
! Но это уже абсурд!
Вот к каким нелепым выводам ведет признание отрицательности
энергии поля скалярного потенциала для инерциального заряда. Так и сохраняется это противоречие: в релятивистской электродинамике эта энергия отрицательна
(хотя этот факт в учебниках по электродинамике предельно «завуалирован»), но при рассмотрении квазистатических явлений она незаконно (вопреки всякой логике) «превращается» в положительную
.
2. Во вторых,
зададим вопрос: а какой физический смысл такого перехода? Как известно, квадрат скорости света выражается через постоянные ε и μ для свободного пространства с
2
= 1/με. Для получения бесконечной скорости света мы должны устремить к нулю какую-либо из этих постоянных. В результате мы лишимся либо вектора D
, либо вектора B.
Тем самым нарушатся законы электростатики или магнитостатики (закон Ампера, закон Фарадея, закон Кулона и т.д.). А это уже бессмыслица.
Вообще говоря, правильным можно было бы считать только предельный переход при скоростях V
→ 0 и рассматривать явления, например, при V
<< c
. Однако и этот подход не решает проблему отрицательной энергии
поля скалярного потенциала.
Итак, предельный переход не приводит и не может привести к правильному последовательному описанию квазистатических явлений. По этой причине он не является законным
. Поля зарядов и поля электромагнитных волн, хотя и могут иметь общую природу, но по своим свойствам существенно отличаются
друг от друга. Следовательно, квазистатические поля зарядов должны описываться самостоятельной
группой независимых уравнений.
Это, в конечном счете, означает, что электромагнитная волна является самостоятельным видом материи
, который обладает своими специфическими свойствами и который отличается от другого вида материи – материальных тел.
В этой связи возникает вопрос: одинаковы ли величины ε и μ для уравнений, описывающих поля зарядов, и уравнений, описывающих электромагнитные волны? Иными словами: являются ли ε и μ универсальными
константами?
7.8 Ускоренный электрон не излучает
Рассмотрим вопрос об излучении ускоренного заряда. Мы будем опираться на следующие положения, установленные ранее.
1. Ранее нами было строго установлено, что поле заряда имеет мгновенно действующий характер. Этот вывод является непосредственным следствием отсутствия продольных волн в электродинамике.
2. Было также установлено, что поперечные электромагнитные волны излучаются «безынерциальными» зарядами и токами. Электроны самостоятельно излучать электромагнитную энергию не могут, даже если движутся с ускорением и по круговым орбитам.
3. Преобразование Лоренца в силу мгновенно действующего характера полей не применимо к полям зарядов. Заряженные частицы могут иметь действительные скорости, во много раз превышающие скорость света в вакууме
Обратимся к независимым исследованиям. Вот что пишет Ю.К. Сахаров [5]:
Таблица
[5]
| Место установки
|
W
Гэв
|
R
м
|
an
= v
2
/R
при v
→
c
, м/сек2
|
a
n
_________ a
n
(Дубна)
|
Наблюдаемое излучение
|
| Циклическ
ие
ускорители
|
Дубна
|
10
|
36
|
2,5 1015
|
1
|
Мягкий рентген
υ ≥ 1018 с-1
|
| Серпухов
|
76
|
236
|
3,8 1014
|
0,15
|
| Женева
|
400
|
1100
|
8,1 1013
|
0,03
|
«Ускорение, которое испытывают электроны у катода электронной пушки кинескопа современного телевизора, на два порядка превышают максимальные нормальные ускорения в циклических ускорителях, но излучение в рентгеновском диапазоне вблизи телевизоров не наблюдается…. В циклических ускорителях, по мнению автора, источником синхротронного излучения являются не сами заряженные частицы, но возбуждаемые ими атомы газа (азот, аргон), часть которых неизбежно остается в камере прибора после его промывки и вакуумирования. (При разряжении
10-13
мм. рт. ст. в
1 см3
содержится
4000 атомов газа)….
….. Однако элементарный расчет показывает, что СИ (синхротронное излучение) не может являться следствием нормального ускорения частиц, так как последнее на ускорителях различного диаметра варьируется на два порядка и более, что показано в приведенной ниже таблице, тогда как параметры СИ на всех ускорителях достаточно близки
».
К сожалению, мы не нашли в литературе данных по измерению спектров синхротронных излучений.
7.9 Скорость переноса энергии волной
Результаты, полученные в третьем параграфе, позволяют найти скорость переноса энергии волной. Вопрос это связан с парадоксами, возникающими при распространении волны в среде с аномальной дисперсией. Например, в такой среде вектор групповой скорости направлен против вектора Пойнтинга.
Для примера рассмотрим две волны, распространяющиеся в среде с дисперсией в одну сторону вдоль оси z
. Для простоты будем считать их амплитуды равными, а частоты разными. Сумма их полей равна
E
x
= E
cos(ω1
t
− γ1
z
) + E
cos(ω2
t
− γ2
z
) =
= 2E
cos[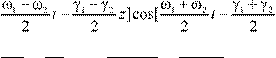 z
] = z
] =
= 2E
cos[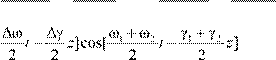
где ω и γ- частота и постоянная распространения сигнала в среде.
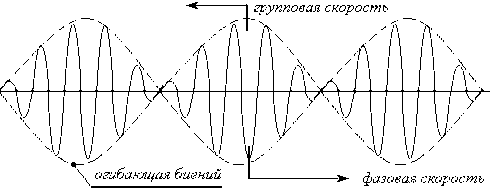
Рис. 7.3 Сложение двух колебаний.
Первый косинус произведения при Ех
определяет амплитуду биений (огибающую суммарного сигнала). Огибающая суммарного сигнала, как следует из формулы, перемещается в пространстве с групповой скоростью v
гр
= Δω/Δγ, где: Δω = ω1
- ω2
; Δγ = γ1
- γ2
.
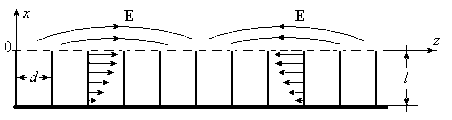
Рис. 7.4 Гребенчатая структура
Для гребенчатой структуры, изображенной на рис. 7.4, γ = ω/vф
= ω/(с
cos kl
) и, следовательно, групповая скорость равна
∂ω cos2
kl
 v
гр
= = c v
гр
= = c
∂γ coskl
+ kl
sinkl
Из формулы вытекает, что групповая скорость может принимать любые значения от - ∞ до + ∞, т.е. она может быть не только отрицательной, но и превышать скорость света в вакууме. А для переноса энергии это уже абсурд.
Групповая скорость есть скорость перемещения огибающей интерференционной картины, образованной группой волн, распространяющихся в одном направлении. Такая интерференция к переносу энергии не имеет отношения, поскольку каждая волна из группы интерферирующих волн переносит свою энергию самостоятельно.
Опираясь на результаты третьего параграфа, найдем действительную скорость переноса энергии волной.
В качестве примера рассмотрим произвольную ТМ волну, которая распространяется вдоль оси z
с фазовым множителем ϕ =i
(ωt -
γz
). Распространение волны мы будем рассматривать в обобщенных цилиндрических координатах ξ, η и z
. Пусть η0
,
ξ0
и z0
орты.
Электромагнитные поля могут быть выражены через потенциал Герца U
[6].
1 ∂2
U i
γ ∂U i
ωε ∂U
 E
ξ
= = − ; H
ξ
= E
ξ
= = − ; H
ξ
= 
h
ξ
∂ξ∂z h
ξ
∂ξ h
η
∂η 2
1 ∂ U i
γ ∂U i
ωε ∂U
 E
η
= = − ; H
ξ
= − E
η
= = − ; H
ξ
= − h
η
∂η∂z h
η
∂η h
ξ
∂ξ h
η
∂η∂z h
η
∂η h
ξ
∂ξ
2 ∂2U
2 2
E
z
= k U
+  2
= (k
+ γ )U
; H
z
= 0 2
= (k
+ γ )U
; H
z
= 0
∂z
где: h
ξ
(ξ;η) и h
η
(ξ;η) коэффициенты Ламе;
U
– потенциал Герца, который удовлетворяет уравнению Гельмгольца:
 ΔU
+ k
2U
= 1 ⎢⎡ ∂ ⎜⎜⎛ hh
ηξ ∂∂U
ξ ⎞⎟⎟⎠+ ∂∂η⎜⎜⎝⎛ hh
ηξ ∂∂U
η ⎟⎟⎠⎞⎤⎥⎥⎦+ h
ξh
η ⎢⎣∂ξ⎝ ΔU
+ k
2U
= 1 ⎢⎡ ∂ ⎜⎜⎛ hh
ηξ ∂∂U
ξ ⎞⎟⎟⎠+ ∂∂η⎜⎜⎝⎛ hh
ηξ ∂∂U
η ⎟⎟⎠⎞⎤⎥⎥⎦+ h
ξh
η ⎢⎣∂ξ⎝
 + +  ∂2U
+ k
2U
= 1 ⎡⎢ ∂ ⎛⎜ h
η ∂U
⎞⎟+ ∂ ⎛⎜ h
ξ ∂U
⎞⎟⎥⎤+ ∂2U
+ k
2U
= 1 ⎡⎢ ∂ ⎛⎜ h
η ∂U
⎞⎟+ ∂ ⎛⎜ h
ξ ∂U
⎞⎟⎥⎤+
∂z
2 h
ξh
η ⎢⎣∂ξ⎜⎝ h
ξ ∂ξ ⎠⎟ ∂η⎜⎝ h
η ∂η ⎠⎟⎥⎦
+ (k
2
−γ 2
)U
= 0
Потенциал бегущей волны есть U
=U
0
(ξ;η)e
−
i
γ
z
; где γ = ω/vф
есть постоянная распространения волны.
Волны типа ТЕ и ТМ можно представить в виде своеобразной интерференции волн, имеющих одну частоту, но направленных под разными действительными (например, в волноводах) или мнимыми (например, в замедляющих системах) углами. В результате интерференции появляется продольный компонент либо электрического, либо магнитного поля. Формально мы можем искать скорость распространения энергии волны отдельно для поперечных полей и отдельно для продольной составляющей поля. Результат будет одинаков.
Рассмотрим поперечные компоненты полей и запишем выражения для плотности энергии и плотности потока
 1 2
ε 2
1 2
∂ A
⊥
2 1 2
ε 2
1 2
∂ A
⊥
2
 w
= w
=  (H
) + (H
) +  (E
) = (E
) =  [(rotA
⊥
) + ( ) ] [(rotA
⊥
) + ( ) ]
∂ ct
 1 &
⋅rotA
∗
⊥
)2
+ k
2
A
&
⊥
A
∗
⊥
] = комплексная плотность энергии w
&
⊥
= [(rotA
⊥
4μ 1 &
⋅rotA
∗
⊥
)2
+ k
2
A
&
⊥
A
∗
⊥
] = комплексная плотность энергии w
&
⊥
= [(rotA
⊥
4μ
 ε 2 2
1 2 2
ε 2 2
1 ∂U
2
1 ∂U
2
= ε 2 2
1 2 2
ε 2 2
1 ∂U
2
1 ∂U
2
=  [(E
ξ
) + (E
η
) ]+ [(E
ξ
) + (E
η
) ]+  [(H
ξ
) + (H
η
) ] = [(H
ξ
) + (H
η
) ] =  (γ + k
)[( ) + ( ) ] (γ + k
)[( ) + ( ) ]
4 2μ 4 h
ξ
∂ξ h
η
∂η
 1 ∂ A
⊥ 1 ∂ A
⊥
S
⊥
= −E
⊥
×H
⊥
= − ×rotA
⊥
μ ∂ t
комплексная плотность потока S
&
⊥
= −  i
ω
A
&
⊥
×rotA
∗
⊥
= i
ω
A
&
⊥
×rotA
∗
⊥
=
2μ
1 0 0 0 0
γωε 1 ∂U
2
1 ∂U
2 0
 = =  [(E
ξ
ξ + E
η
η )×(H
ξ
ξ + H
η
η )] = [( ) + ( ) ]z [(E
ξ
ξ + E
η
η )×(H
ξ
ξ + H
η
η )] = [( ) + ( ) ]z
2μ 2 h
ξ
∂ξ h
η
∂η
Легко видеть, что
 S
&
⊥
2γω 0
2v
ф
z
0 S
&
⊥
2γω 0
2v
ф
z
0
v
e
= &
⊥
= γ 2
+ k
2
z
= 1+ (v
ф
/c
)2 (7.9.1)
w
Теперь рассмотрим плотность потока и плотность энергии, создаваемые продольным компонентом Еz
.
Это условно можно рассматривать как «продольную» волну.
Пусть формально Ez
выражается через некоторый векторный потенциал A//
E
z
= Re[−∂A
//e
i
(ωt
−γz
) /∂t
Re[−∂A
//e
i
(ωt
−γz
) /∂t
] =−Re i
ωA
∗//e
i
(ωt
−γz
)
Для упрощения мы будем писать соотношения для комплексных амплитуд. Запишем основные соотношения
~ & e
i
(ωt
−γz
) ;
A
= Re A
//
~
 ∂A
комплесная амплитуда i
ωA
& ; ∂A
комплесная амплитуда i
ωA
& ;
//
∂t
~ &
divA
комплесная амплитуда -i
γA
//
Вычислим плотность энергии и плотность потока
~
1 ∂A
2
~ 2
 w
//
= [( ) +(divA
) ] w
//
= [( ) +(divA
) ]
2μ ∂ct
1 ω2
 комплесная плотность энергии w
& //
= [ 2
(A
& // A
∗// )+ γ 2 (A
& // A
∗// )] комплесная плотность энергии w
& //
= [ 2
(A
& // A
∗// )+ γ 2 (A
& // A
∗// )]
4μ c
~
1 ∂A
~
S
//
= −  divA
μ ∂t divA
μ ∂t
комплесная плотность потока S
&
//
=  ωγ(A
&
//
A
∗
//
)z
0 ωγ(A
&
//
A
∗
//
)z
0
Таким образом, окончательно получаем выражение для скорости переноса энергии
 S
& // 2ωγz
0 2v
ф
z
0 S
& // 2ωγz
0 2v
ф
z
0
v
e
= &
//
= k
2
+γ2
= 1+ v
ф
2
/c
2
(7.9.2)
w
Итак, выражения (7.9.1) и (7.9.2) совпадают. Совершенно аналогично можно показать, что для ТЕ волны имеет место то же самое выражение для скорости переноса энергии электромагнитной волны.
Возвращаясь к предыдущему примеру, получим для него следующее выражение для скорости переноса энергии. Учитывая, что фазовая скорость в гребенчатой структуре равна v
ф
= c
⋅coskl
, получим
2c
⋅coskl
v
e
=  2 2
1+ cos kl
Скорость переноса энергии волной в волноводах равна (без вывода)
2c
v
e
= 2 2
 1− (λ/λkp
) +1/ 1− (λ/λkp
) 1− (λ/λkp
) +1/ 1− (λ/λkp
)
Очевидно, что:
– скорость переноса энергии всегда совпадает по направлению с фазовой скоростью;
– скорость переноса энергии не превышает скорости света в вакууме;
– выражения (7.8.1) или (7.8.2) являются универсальными и не зависят от дисперсии фидерной системы или среды;
– эти выражения не зависят также от типа волны (ТЕ, ТМ или ТЕМ);
– групповая скорость не имеет отношения к переносу энергии; она определяет скорость переноса интерференционной картины, образующейся вдоль направления распространения интерферирующих волн.
Источники информации:
1. Ландау Л.Д , Лифшиц Е.М. Теория поля. ГИФФМЛ, М. 1960.
2. Корнева М.В., Кулигин В.А., Кулигина Г.А.. Ревизия теоретических основ релятивистской электродинамики n-t.ru/tp/ns/rt.htm
3. Кулигин В.А. Электродинамика отвергает теорию относительности. http://www.sciteclibrary.ru/rus/catalog/pages/8037.html
4. Ахиезер А.И., Берестецкий В.Б. Квантовая электродинамика. - М.:, «Наука», 1969.
5. Сахаров Ю.К.. Противоречия в современной концепции излучения заряженных частиц и строения атома. //Проблемы пространства, времени, тяготения. (IV Международная конференция 16-21.09.1996). ПОЛИТЕХНИКА, С.-П., 1997.
6. Вайнштейн Л.А. Электромагнитные волны. - М.: Сов. радио, 1957.- 483 с.
Введение
Любая теория, к какой бы области естествознания она ни относилась, всегда имеет границы, за которыми ее предсказания будут неточными или ошибочными. Это касается СТО с ее постулатом о том, что все уравнения должны иметь «ковариантную» форму и подчиняться преобразованиям Лоренца. Это касается и уравнений Максвелла.
Неполнота описания явлений уравнениями Максвелла обусловлена двумя причинами. Первая причина – некорректная (ошибочная) интерпретация уравнений, в результате которой мы имеем не только логические противоречия, но и ошибочные предсказания. Причиной тому, например, является игнорирование существования вырожденных решений волнового уравнения (Глава 1). Это кажущаяся неполнота, так как при правильной интерпретации предсказания укладываются без противоречий в рамки экспериментов, и расширяется область применимости уравнений. Вторая причина – естественная физическая ограниченность теории, когда выясняется, что существуют эксперименты, которые теория принципиально не вписываются в теории.
Ниже будут рассмотрены вопросы, связанные с «появлением» в классических уравнениях Максвелла безынерциальных зарядов и токов, а также вопросы, обусловленные открытием «нового вида» излучения, которое эти уравнения пока не описывают.
Последний вопрос весьма интересен и мы включили оригинальную статью В.И. Коробейникова «Новый вид электромагнитного излучения?» без изменения как самостоятельную Главу 9.
8.1 Граничные условия и безынерциальные токи.
В предыдущей главе мы получили следующие выражения для безвихревого компонента плотности безынерциального тока и плотности заряда:
1 ∂ 2
j
2
1 ∂ 2
ρ
Δj
2
−  2 2
= 0 Δρ − 2 2
= 0 Δρ −  2 2
= 0 (7.5.5) c
∂t c
∂t 2 2
= 0 (7.5.5) c
∂t c
∂t
Это означает, что продольные волны будут отсутствовать, если безвихревой компонент тока j
2
является запаздывающим, т.е. удовлетворяет однородному волновому уравнению
(7.5.5). Заряды, образующие этот ток должны перемещаться со скоростью света (безынерциальные заряды).
Что касается вихревой составляющей, то мы вправе сделать следующее допущение. Вихревая плотность j
1
(если она существует) также должна удовлетворять волновому уравнению, поскольку она также создается благодаря движению безынерциальных зарядов.
Уравнения (7.2.4) описывают потенциалы полей, создаваемых безынерциальными зарядами и процесс излучения электромагнитной волны. Эти уравнения должны быть дополнены двумя группами уравнений:
– Уравнения, описывающие взаимодействие инерциальных зарядов с полями безынерциальных зарядов и электромагнитными волнами.
– Уравнения, описывающие рождение и уничтожение безынерциальных зарядов полями электромагнитной волны и полями других безынерциальных и инерциальных зарядов.
Рассмотрим граничные условия на поверхности металлов.
ρпов
= (n
0
E
); j
пов
=[H
×n
0
],
где: ρпов
– поверхностная плотность пространственного заряда; j
пов
– поверхностная плотность тока; n
0
– единичная нормаль к поверхности; Е
и Н
– поля у поверхности металла.
Нетрудно заметить, что коль скоро электрические и магнитные поля у поверхности металла имеют волновой характер (запаздывающие), то и поверхностные токи в силу граничных условий тоже будут запаздывающими. Эти поверхностные токи носят безвихревой характер divj
пов
= div[H
×n
0
] = (n
0
rotH
) и являются запаздывающими.
Говоря о поверхностных токах и зарядах, мы должны понимать, что такое представление есть идеализация. Эта идеализация связана с макроскопическим описанием явлений на границе раздела сред. Реально заряды и токи занимают некоторый слой и имеют объемную плотность.
Физическая причина существования безынерциальных зарядов и токов пока не ясна. Мы скептически относимся к эфиру и «физическому вакууму». На наш взгляд возможно следующее макроскопическое объяснение появления безынерциальных токов. Мы предполагаем, что любая инерциальная частица (протон, нейтрон, атом и т.д.) окружена некоторой субстанцией (“шубой”), подобно Земле, окруженной атмосферой. Именно эта “шуба” ответственна за проявление (рождение и уничтожение) безынерциальных зарядов и их движение со скоростью света.
В проводниках субстанции отдельных ионов кристаллической решетки металла смыкаются, образуя между собой мостики и, в конечном счете, образуя пространственную решетку. Она является не только источником безынерциальных зарядов, но и создает пути для их распространения. Здесь возможны две модели этой субстанции.
Полевая модель.
Субстанция есть образование, обладающее свойствами поля. Любое электромагнитное воздействие на субстанцию вызывает в ней возмущения. Эти возмущения проявляются как токи безынерциальных зарядов, распространяющиеся со скоростью света.
Дискретная модель
. Субстанция есть сумма нейтральных безынерциальных заряженных частиц, удерживаемых некими силами вблизи ионов. При воздействии электромагнитной волны эти частицы «разделяются» на положительные и отрицательные. Двигаясь по мостикам объемной решетки, они создают токи безынерциальных зарядов. Мы предполагаем, что имеет место дискретная модель.
Такова предварительная картина природы безынерциальных зарядов и токов.
Безынерциальные заряды и токи встречаются не только в диапазоне СВЧ, но и на низких частотах. Здесь мы воспроизведем эксперимент, проведенный С.В. Авраменко [1].
8.2 Эксперимент Авраменко С.В. [1].
Итак, 5.08.90 в одной из лабораторий МЭИ был продемонстрирован эксперимент, схема которого изображена на рис. 8.1. Были приглашены профессора.
В экспериментальную установку входил машинный генератор 1
мощностью до 100 кВт, генерирующий напряжение с частотой 8 кГц. Этот машинный генератор питал первичную обмотку трансформатора Тесла 2
.
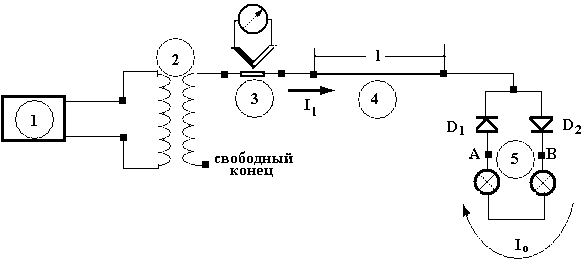
Рис. 8.1
Один конец вторичной обмотки был свободен (ни к чему не подключен, как показано на рис. 8.1). Ко второму концу были подсоединены последовательно следующие элементы: термоэлектрический миллиамперметр 3
, тонкий вольфрамовый провод 4
(длина провода 2,75 м, диаметр 15 мкм) и “вилка Авраменко” 5
.
Вилка Авраменко представляет собой замкнутый контур, содержащий нагрузку и два последовательно соединенных диода, у которых общая точка подсоединена к описанной ранее цепи. Нагрузкой служили несколько подсоединенных лампочек накаливания.
По этой разомкнутой цепи Авраменко смог передать от генератора к нагрузке (лампам накаливания) электрическую мощность порядка 1300 Вт. Электрические лампочки ярко светились.
Профессора с интересом наблюдали эксперимент и … пожелали автору дальнейших успехов.
Казалось бы, это явление легко объяснимо. Схема содержит уединенную емкость, образованную диодами, лампами накаливания и соединяющими их проводами. При положительном полу периоде напряжения через диод D
1
в эту цепь течет зарядный ток. И потенциал уединенной емкости возрастает. При отрицательном полу периоде напряжения эта емкость разряжается через диод D
2
, приобретая новую величину потенциала. Зарядноразрядный ток I
0
имеет всегда одно направление и его величины достаточно, чтобы поддерживать на лампах накаливания в вилке Авраменко среднюю мощность 1300 Вт.
Ток I
1
в цепи, соединяющей конец обмотки трансформатора Тесла с вилкой Авраменко, должен быть близок или приблизительно равен по величине току I
0
. Если, например, нагрузка вилки Авраменко представляет собой параллельное соединение 6-ти двухсотваттных ламп накаливания, то разрядно зарядный ток I
0
будет приблизительно равен 6 А. Соответственно, такой же примерно величины должен был бы быть и ток I
1
.
Однако такое объяснение противоречит следующему факту. Термоэлектрический миллиамперметр 3
зафиксировал очень малую величину тока I
1
(I
1
≈ 2 мА !), а тонкий вольфрамовый провод 4
даже не нагрелся! Именно это обстоятельство послужило главной причиной трудности объяснения результатов эксперимента Авраменко.
Приведем некоторые выводы, сделанные Авраменко и его коллегами на основании этих исследований.
a. Ток I
0
в вилке Авраменко линейно увеличивается
с ростом частоты (диапазон измерений 5 – 100 кГц) и практически линейно возрастает с ростом напряжения генератора при постоянной частоте. Это свидетельствует о емкостном
характере электрической цепи. Магнитное поле в проводнике, соединяющем вилку Авраменко с генератором, не было практически обнаружено (весьма мало!).
b. Ток I
1
был очень мал
по сравнению с током I
0
и практически не обнаруживался ни тепловым, ни магнитоэлектрическим измерителем тока.
По этой причине наличие в соединительной цепи (трансформатор Тесла – вилка Авраменко) последовательно соединенных резисторов (до нескольких десятков МОм), конденсаторов и индуктивностей оказывало чрезвычайно малое ослабляющее действие на ток I
0
в вилке Авраменко.
Здесь мы не будем обсуждать гипотезу авторов, изложенную в [2], о предполагаемом механизме передачи энергии. Отметим лишь ее основные моменты.
– Согласно их точке зрения в цепи течет продольный ток смещения, не создающий магнитного поля. Величина ε металла изменяется с удвоенной частотой от 1 до ∞ и это изменение связано с фазой подаваемого в цепь напряжения. Продольный переменный ток смещения I1 обладает “сверхпроводящими” свойствами, т.е. не выделяет тепла в резисторах и практически не создает на них падения напряжения.
– В вилке Авраменко этот ток преобразуется в обычный пульсирующий ток I0. Однако и здесь не все ясно. Если измерять напряжение U в точках АВ электростатическим вольтметром, а ток обычным амперметром, то при вычислении мощности в нагрузке наблюдается несоответствие с классическими законами. Вычисленные мощности
P
2'
=
I
02
R
, P
2"
=
I
0
U
и закон Ома U
=
I
0
R
(где R –сопротивление цепи, содержащей лампочки) не соответствовали друг другу. Авторы пишут, что резисторы “как бы теряют свои номиналы” [3]. Отметим забавный факт. «Борцами с лженаукой» эти эксперименты были отнесены к «лженаучным».
Ниже мы дадим свою трактовку эксперимента С.В. Авраменко.
8.3 Уединенная емкость.
В стандартных учебниках физики рассматриваются два вида емкостей: уединенная или собственная емкость и взаимная емкость двух тел, т.е. конденсатор, которые изображены на рис. 8.2. Уединенная емкость есть металлическое тело, изолированное от других проводников.
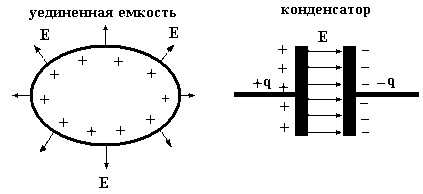
Рис. 8.2
В учебниках этой емкости обычно не уделяется много внимания, и описание емкости ограничивается формулой
q
= C
φ (φ∞
= 0) (8.2.1)
где: С
– величина уединенной емкости; φ - потенциал проводящего тела по отношению к бесконечности; q
-–заряд на уединенной емкости.
Составим теперь цепь из генератора, двух соединительных проводов и двух металлических тел (уединенные емкости), изображенную на рис. 8.3а. При наличии переменного напряжения U
в ветвях разомкнутой цепи будет течь ток. Эту цепь можно заменить эквивалентной схемой замещения, изображенной на рис. 8.3б. На этой схеме C
1∞
и C
2∞
- уединенные емкости первого и второго тела, C
21
– взаимная емкость между этими телами (конденсатор).
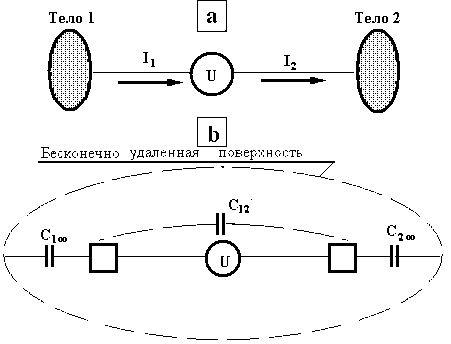
Рис. 8.3
Если считать бесконечно удаленную поверхность S
проводником, то разомкнутую цепь мы как бы свели к замкнутой кирхгофовской цепи. Но такой вывод ошибочен. Замкнутой кирхгофовской цепью служит последовательное соединение элементов: тело 1 – проводник – генератор U
– проводник – тело 2 – емкость С
12
– тело 1. Если емкость С
12
мала и ею можно пренебречь, то оставшаяся часть схемы представляет собой некирхгофовскую
цепь, подчиняющуюся своим волновым законам.
В такой цепи ток в различных сечениях проводов между каждым телом и генератором будет различен. Это принципиально отличает такие цепи от кирхгофовских цепей. В цепи установится стоячая волна тока и напряжения. Подобная цепь обладает любопытными свойствами.
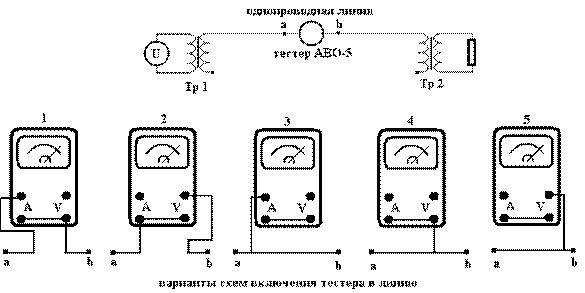
Рис. 8.4
Например, при экспериментальных исследованиях мы пытались измерить ток в соединительном проводе (повторение эксперимента Авраменко) с помощью прибора АВО-5 (тестер на полупроводниковых диодах), как показано на рис. 8.4. Напряжение в линии 900 В, частота 18 кГц. На этом же рисунке показаны 5 способов включения этого прибора. Оказалось, что при любом способе включения стрелка прибора отклонялась практически на один и тот же угол. Этот угол не зависел от положения ручек переключателей диапазонов измерения токов и напряжений.
8.4 Физические явления в эксперименте Авраменко С.В.
Опираясь на изложенные ранее теоретические результаты и результаты экспериментальных исследований, мы можем предложить свое объяснение эффектов, обнаруженных С.В. Авраменко.
Для простоты объяснения будем считать, что паразитная емкость между свободным выводом вторичной обмотки трансформатора Тесла и вилкой Авраменко пренебрежимо мала. Такая цепь не является кирхгофовской, и в ней протекают токи, образованные безынерциальными зарядами.
Из теории длинных линий известно, что в проводе длиной L
, подсоединенном одним концом к выходу генератора, устанавливается стоячая волна. Узел тока и пучность потенциала приходятся на свободный конец линии L. Распределение тока в проводе имеет вид:
U
2πx
 I
1
(x
) = sin (8.4.1) w
λ I
1
(x
) = sin (8.4.1) w
λ
где: U
– потенциал свободного конца провода; w
– волновое сопротивление провода (120π Ом); х
– расстояние от свободного конца провода; λ - длина волны.
Проведем теперь численную оценку для эксперимента Авраменко. Поскольку все данные нам не известны, мы проведем прикидочные расчеты. Предположим, что потенциал на конце соединительного провода и вилке Авраменко составляет величину порядка 2 кВ. В этом случае при отсутствии паразитной емкости свободный
вывод вторичной обмотки трансформатора Тесла будет иметь потенциал, по крайней мере, раз в 10 – 50 выше (явление перекоса
потенциала, обнаруженное нами), чем “нагруженный
” вывод вторичной обмотки трансформатора. Примем длину L
= 5 м. Длина волны, соответствующая частоте 8 кГц, равна 37500 м. Учитывая, что волновое сопротивление провода составляет 377 Ом, запишем выражение для I
1
.
I
1
(x
) ≈ 5,3sin8,3⋅10−
5
x
≈ 4,4⋅10−
4
x
В приведенной формуле ток в амперах, если х
в метрах. При х
= 5 м ток равен I
1
(5) = 2,2 мА. Эта величина соответствует току, измеренному в экспериментах Авраменко. Величина тока I
0
должна быть порядка 5,3 А. Для шести ламп по 200 Вт, соединенных параллельно ток должен быть равен I
0
= 6А.
Обсудим теперь вопрос о прохождении безынерциальных токов через p-n
переход диода. Поскольку такая проблема еще никем не обсуждалась, мы выскажем некоторые гипотетические
соображения.
Пусть поток безынерциальных зарядов проходит через p-n
переход. Поток этих зарядов частично отражается от перехода, а частично проходит через диод. Если положительные безынерциальные заряды движутся от p
-слоя к n
-слою (отрицательные, соответственно, в обратном направлении), то они вызывают появление тока дырочно-электронной проводимости из основных носителей. Если же безынерциальный ток имеет обратное направление, то ток из инерциальных носителей образоваться уже не может. Здесь будет существовать ток, благодаря туннельному переходу (или же барьерной емкости), а также слабый ток, обусловленный малой обратной проводимостью диода.
Если эта гипотеза верна, мы можем предложить следующее объяснение эксперимента Авраменко. Заметим, что мы будем рассматривать процессы, протекающие в очень короткий интервал времени τ = 2L
/c
≈ 3,5·10-7
секунды, который значительно короче периода переменного напряжения Т
= 1,25·10-4
секунды.
Падающая волна тока из безынерциальных зарядов подходит к точке B
вилки Авраменко и разветвляется. Волна I
1 прош
, проходящая через диод D
1
(как показано на рис. 8.5), вызывает появление тока I
0
из электронов проводимости. Эти электроны будут двигаться, в конечном счете, к диоду D
2
и проходить через него. Волна же будет заряжать уединенную емкость С
∞
. Другая часть волны, подходя к точке В
и диоду D
2
, будет отражаться, и лишь малая ее часть I
2прош
дойдет до уединенной емкости С
∞
.
Отраженная от уединенной емкости волна разветвится. Одна ее часть I
2отр
пройдет через диод D
2
, вызывая движение электронов проводимости и поддерживая ток I
0
. Другая, отразившись от диода D
1,
вновь вернется обратно к уединенной емкости и от нее к диоду D
2
.
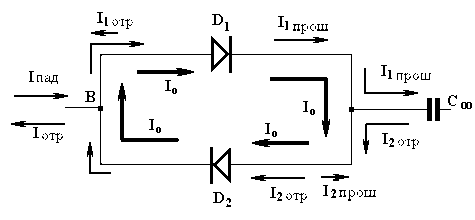
Рис. 8.5
Кольцевое движение электронов проводимости в вилке Авраменко, образующее ток I
0
, будет сохраняться независимо
от того, заряжается ли уединенная емкость или же идет процесс ее разряда.
Ток в соединительном проводе I
1
равен разности прямого тока (идущего к вилке Авраменко) и обратного (идущего от вилки) I
1
= Iпад
- Iотр
. Отсюда следует, что ток I
0
может быть во много раз больше тока I
1
.
Безынерциальные же токи образуют стоячую волну с узлами тока на концах цепи. По этой причине в разомкнутой цепи существует хотя бы маленький ток, который
2πz
пропорционален sin  , где z
– расстояние от точки обрыва цепи. λ , где z
– расстояние от точки обрыва цепи. λ
8.5 Диполь Герца
Теперь мы можем обсудить вопросы, связанные с излучением диполя Герца.
Как мы выяснили, поля зарядов являются мгновенно действующими. Описывающие их уравнения не связаны с полями запаздывающих потенциалов электромагнитных волн. Поля зарядов и электромагнитные волны описываются самостоятельными уравнениями. По этой причине движущийся ускоренно заряд не способен излучать электромагнитных волн. Однако, как будет показано ниже, заряженные частицы взаимодействуют с волновыми электромагнитными полями.
Рассмотрим теперь диполь Герца, который изображен на рис.8.6. Ток через диполь обусловлен движением электронов проводимости и безынерциальных зарядов.
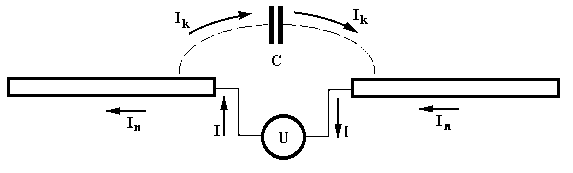
Рис. 8.6
Суммарный ток I
,
создаваемый источником напряжения U
, складывается из двух токов: I
= Ik
+ In
, где: In
– ток, создаваемый безынерциальными зарядами (некирхгофовский ток); Ik
– ток, созданный электронами проводимости (кирхгофовский ток).
Электрическая кирхгофовская цепь замыкается взаимной емкостью C
, существующей между “усами” диполя Герца. Некирхгофовская цепь заканчивается на уединенных емкостях, образованных “кончиками усов” диполя Герца.
Рассмотрим теперь поля в дальней зоне. Поскольку поля зарядов убывают не медленнее, чем R
-2
, в дальней зоне будут превалировать поля запаздывающих потенциалов, которые убывают как R
-1
.
В ближней зоне будут существовать как мгновенно действующие поля, образованные движением электронов проводимости, так и поля, создаваемые безынерциальными зарядами и токами.
В силу этого, структура полей в ближней зоне диполя Герца должна быть гораздо более сложной, чем предсказывается современной теорией. К сожалению, экспериментальных исследований полей в ближней зоне не проводилось или же результаты исследований не публиковались. В Интернете появляются сообщения (например, [3]) о том, что в ближней зоне наблюдаются серьезные отклонения распределения поля от предсказываемого теорией линейного вибратора.
Источники информации:
1. Заев Н.Е. Сверхпроводники инженера Авраменко. Техника Молодежи, №1, М., 1991. См. также http://vksn.narod.ru/myst/tm191.html
2. Заев Н.Е., Авраменко С.В., Лисин В.Н. Измерения тока проводимости, возбуждаемого поляризационным током. Русская физическая мысль, №2, Реутово, Московской обл., 1990. См. также
Н.Е. Заев, Однопроводная ЛЭП. Почему спят законы? ИР № 10/94 ; http://www.skif.vrn.ru/
3. Иванько Ю. В.К физической сущности электромагнитных явлений. Механические аналоги или эфирная механика? http://www.nodevice.ru/article/545.html
Глава 9.
Новый вид электромагнитного излучения?
Владимир Коробейников
Введение
Радиосвязь на, так называемых, ЕН антеннах новое неизведанное направление. Родилась эта радиосвязь усилиями радиолюбителей
сравнительно недавно (несколько лет тому назад), но представляется перспективной. К примеру, эта радиосвязь может работать под землей и под водой. Исследовательских (как теоретических, так и экспериментальных) работ на этом пути хватит на всех желающих и еще останется, поскольку принцип работы и теоретические основы связи на ЕН антеннах еще в стадии становления. Причина в том, что ЕН антенны работают на новом, практически
неизвестном электромагнитном принципе.
Они используют ранее неизвестный вид электромагнитного излучения. В этой статье будут в популярной форме изложены результаты исследований в данной области.
9.1 Принципы радиосвязи
Чтобы пояснить суть эксперимента людям, далеким от радиосвязи приведем некоторые пояснения. Антенна передатчика излучает электромагнитную волну по-разному в разных направлениях. Чтобы иметь наглядное представление о свойствах излучения электромагнитной волны вводят диаграмму направленности
антенны. Эта диаграмма показывает, как меняется излучаемая энергия неподвижной антенны от направления излучения. Простейшей антенной является комнатная телевизионная антенна, которая представляет собой видоизмененный диполь Герца. У диполя Герца «усы» антенны направлены в противоположные стороны (на 180о
).
Диаграмма направленности диполя Герца изображена на рис. 9.1 [1]. Она представляет собой тор («бублик без дырки»), поперечный разрез которого есть две соприкасающиеся окружности. Примерно такую форму (форму «искаженного бублика») имеют диаграммы антенн направленности многих приемо-передатчиков и радиотелефонов. Антенны приемников имеют аналогичные диаграммы направленности. Они показывают, с какого направления по отношению к ориентации антенны наиболее хорошо принимается волна.
Нетрудно сообразить, при каком расположении и ориентации антенн приемника и передатчика будет наилучший прием, а когда прием невозможен (см. рис. 9.1). Наилучшая связь будет тогда, когда радиотелефоны имеют общую экваториальную плоскость и их антенны параллельны друг другу. Если же антенны расположены под углом 90о
или ориентированы вдоль одной линии, то связи не будет. В этом случае либо приемная антенна не принимает сигнал с данного направления, либо передающая антенна не излучает в этом направлении.

Рис. 9.1 Диаграмма направленности диполя Герца и связь при различных ориентациях антенн
9.2 Эксперимент, который «ломает» теорию
Ниже описывается эксперимент, который в буквальном смысле «ломает» сложившиеся в электродинамике положения. В эксперименте в качестве передатчика использовалась типовая портативная радиостанция "Беркут-603". Диаграмма направленного действия ее штыря (антенны) хорошо известна и напоминает диаграмму направленности диполя Герца. Как и в диполе Герца антенна радиостанции не может излучать или принимать электромагнитный сигнал, идущий вдоль антенны. Это явление описывается в учебниках, а на радиоэлектронных факультетах университетов такие диаграммы направленности снимают в лабораторных работах.
Однажды мне пришлось продемонстрировать своему другу (классному специалисту в области радиосвязи) следующий «фокус». Я подключил в качестве приемной антенны для снятия диаграммы направленности медную «таблетку». На фотографии, приведенной ниже (см. рис. 9.2), показаны радиостанция «Беркут-603» и приемная антенна - медная «таблетка», соединенная с приемником, которые использовались в эксперименте.

Рис. 9.2 Приборы, использовавшиеся при эксперименте. Слева антенна «таблетка», справа «Беркут-603»
Произошло «чудо». С помощью медной «таблетки» диаграмма направленности радиостанции изменилась! Новая
диаграмма направленности радиостанции, которая была экспериментально снята с использованием «таблетки», принципиально отличалась от известного «бублика», приводимого в учебниках! Она напоминала две соединенные «капли», ориентированные перпендикулярно экваториальной плоскости антенны (т.е. вдоль штыря) как представлено на рис. 9.3.

Рис. 9.3. Диаграмма направленности, снятая «таблеткой», и обычная диаграмма, снятая с помощью штыревой антенны
Этот результат поверг моего друга буквально в шок. Конечно, «таблетка» не могла изменить диаграмму направленности радиостанции. Значит, помимо привычного электромагнитного поля антенна радиостанции излучает в пространство еще какое-то поле, которое уловила медная «таблетка»! В любом случае, электроны в антенне «Беркут603» имеют две динамические компоненты: мощную поступательную и очень слабую вращательную. Конструкция «таблетки» максимально реагирует лишь на вращательную (магнетон Бора) компоненту.
Это поле излучается вдоль
антенны передатчика «БЕРКУТ603 », обладает иными свойствами, и на него не реагируют обычные
приемные антенны типа диполя Герца.
9.3 «Секрет» медной «таблетки»
Теперь необходимо раскрыть «тайну» антенны, которая была названа медной «таблеткой». Устройство ее достаточно просто (см. рис. 9.4). Она состоит из двух катушек, расположенных соосно на некотором расстоянии друг от друга. Катушки включены так, что их магнитные поля H
Z
направлены друг против друга, т.е. имеет место противофазное включение этих индуктивностей. Для увеличения чувствительности включается емкость, которая вместе с катушками индуктивности образует контур. Этот контур настраивается на частоту принимаемого сигнала. Катушки помещены в медный цилиндр или же в медный экран. Такого типа антенны получили название Hz антенн, принадлежащих классу ЕН антенн.
Я хотел бы обратить особое внимание на следующий факт. Помещать антенну в экран, означает экранирование антенны от окружающего ее пространства. Для обычных антенн такой экран не дает возможности антенне принимать сигнал из окружающего пространства или излучать его в пространство. Однако, как показали исследования, экран не только не подавляет, но усиливает
эффект, улучшает
работу антенны (на это следует обратить внимание!). И еще одно обстоятельство должно быть принято во внимание. Излучение в экваториальной плоскости имеет малый угловой размер (узкую диаграмму) по углу θ. Видимо, по этой причине такое излучение не регистрировалось ранее, т.к. его «проскакивали».
Между одинаковыми катушками, включенными противофазно, возникает плоскость симметрии аб
, показанная на рис. 9.4, в которой электрическое и магнитное поля равны нулю. В литературе [2] эта плоскость получила название кулоновской плоскости
. Подводящие провода помещены в экран и излучение от них отсутствует. На рис. 9.4 изображена электрическая схема, когда «таблетка» служит антенной передатчика (работает на излучение).
Между коллектором и эмиттером транзистора включен последовательный резонансный контур (низкоомная «нагрузка»). Почему желательно выбирать последовательный резонансный колебательный контур? Общее напряжение на последовательном LC контуре не выше напряжения источника питания. А вот по отдельности на L и C напряжения за счет резонанса очень высокие при высокой добротности контура Q. Эти переменные напряжения в Q раз выше, чем переменное напряжение на коллекторе. Значение Q может колебаться от десятков до сотен единиц и зависит от частоты и качества выполнения контура.

Рис. 9.4 Включение ЕН антенны («таблетка») в выходной каскад передатчика и катушки ЕН антенны
«Таблетку» (Hz антенну) не надо ставить на железную опору. От этого полоса пропускания будет очень узкой. Желательно применять пластик или алюминий. В этом случае полоса пропускания превосходит полосу пропускания типовой штыревой антенны.
Радиолюбители, используя ЕН антенны, практически заметили множество необычных свойств поля антенны [3]. В нескольких случаях, когда не было никакой возможности изза плохих условий распространения радиоволн установить радиосвязь при использовании обычных антенн, станции, использующие ЕН антенны, были способны устанавливать связь между собой.
Проводились эксперименты, когда большой лист алюминия помещали близко перед ЕН антенной и позади нее. Но это не отразилось на уровне сигнала. Тогда это было очень большой неожиданностью, поскольку все эти эксперименты выполнялись до появления теории, представленной позже [3]. Тогда не обратили внимания и не предали значения, что в цилиндрах ЕН антенн изменилась динамика зарядов. Усилилась вращательная
(магнетон Бора) компонента и уменьшилась обычная поступательная у электрических зарядов в цилиндрах.
Другая особенность ЕН антенны, которая была предсказана теорией и доказана практически, высокая проникающая способность вектора Hz [3]. ЕН антенна может излучать через воду и другие среды, которые представляют серьезную преграду другим полям. Это было экспериментально установлено, когда маленький передатчик и ЕН антенну, заключенную в пластмассовый, герметичный корпус, помещали под воду. В качестве приемных антенн использовались как обычная антенна, так и ЕН антенна. Только ЕН антенна оказалась способной принимать сигнал от передатчика, расположенного под водной.
ЕН антенна также может работать в шахте под землей. Ее сигнал способен проникать сквозь большие толстые стены здания из железобетона. Эксперименты с обычными антеннами доказывают слабую способность приема проникающего поля, в то время как ЕН антенны, помещенные в чрезвычайные условия, доказывают высокую проникающую способность полей ЕН антенн.
9.4 Немного математики
Теперь нам предстоит рассмотреть, что предсказывает классическая электродинамика. Помимо электрического диполя Герца существует магнитный диполь Герца, который называется иногда «рамочной антенной» [1]. Он представляет собой рамку с током. Диаграмма направленности этого диполя ничем не отличается от диаграммы электрического диполя Герца. Это тот же «бублик» (см. рис. 9.5).

Рис. 9.5. Рамочная антенна и ее диаграмма направленности
«Таблетка» - это две рамочных антенны, расположенных соосно и параллельно друг другу на расстоянии а.
Но магнитные поля рамок направлены в противоположных направлениях (запитываются в противофазе). Поле в дальней зоне излучения, когда расстояние от антенны значительно превышает диаметр рамочных антенн и расстояние между ними, можно определить как сумму полей от каждой из рамочных полей.
Запишем выражение для электрического поля в дальней зоне. Оно будет равно сумме полей.
e
−ikr
1
e
−ikr
2
 Е
ϕ
= −iE
0
( − )cosθ kr
1
kr
2 Е
ϕ
= −iE
0
( − )cosθ kr
1
kr
2
где: r
1
= [x
2
+ y
2
+ (z +a
/2)2
]1/2
, r
2
= [x
2
+ y
2
+ (z - a
/2)2
]1/2
; Е
0
– амплитуда электрического поля.
Приближенное выражение для электрического поля дальней зоне при ka<<
1 имеет вид:
e
−ikr a
−ikr
Е
ϕ
= 2E
0
 sin(ka
cosθ)sin θ ≈ 2E
0 sin(ka
cosθ)sin θ ≈ 2E
0
 e
sin 2θ kr r e
sin 2θ kr r

Рис. 9.6. Диаграмма направленности двух рамочных антенн, запитываемых противофазными токами
Диаграмма направленности «таблетки» теперь напоминает две воронки с совмещенными горлышками как показано на рис. 9.6. Экваториальная плоскость является плоскостью антисимметрии. Вдоль нее не будет распространения
электромагнитной энергии, и будут отсутствовать реактивные поля ближней зоны.
Мы видим, что современная
интерпретация электродинамики отрицает возможность излучения сигнала (или приема сигнала) в экваториальной (кулоновской) плоскости с помощью поперечной электромагнитной волны. Следовательно, мы имеем дело с новым
видом излучения [4], [5], [6]. Здесь мы не будем излагать теоретических основ новых антенн [3].
9.5 Ответ критикам
Мне уже приходилось давать ответ критикам [7], которые пытались отнести исследования в области нового излучения (магнетон Бора)
к «лженауке». Сделаю это и сейчас. Авторы работы [8] пишут:
«…Следующими "на ринг" вызываются ЕН-антенны. Т.н. ЕН-антенны, вероятно, появились в результате практической модификации CFA-антенн. … Естественно, данные изобретатели не имели тех знаний, которыми обладали авторы (т.е. F.M. Kabbary, M.C.
Hately and B.G. Stewart. Maxwell's equations and Crossed-field Antenna. — EWAWW, 1989, March, p.216,.,218. – прим. мое, В.К.
), чтобы замаскировать теоретическую
несостоятельность своих детищ, посему сколько-нибудь внятного описания теоретических принципов работы ЕН-антенн в различных публикациях не обнаружено. ... Возможно, жажда славы подтолкнула некоторых экспериментаторов к "маленькой афере," и с их легкой руки появился "новый" вид антенн, который назвали ЕН-антеннами. ... Это следует из теоремы Пойнтинга, поскольку для выполнения условия (3) поля Е
и Н
должны быть синфазны. Следовательно, в основе работы ЕН-антенн лежат классические законы электродинамики, и ничего нового в теорию антенн авторы данного типа антенн не внесли…» Как видим никакого внимания и акцента к динамике
зарядов в элементах (цилиндрах) антенны не делается. Это, как говорят, «за пределами понимания или существования».
Выше мы уже рассмотрели принципиальные отличия двух видов излучения и их несовместимость. Поэтому, можно ли, не разобравшись в сути
проблемы, утверждать, что новое излучение описывается законами классической электродинамики и навешивать «ярлычки» на бескорыстных радиолюбителей? Это научная недобросовестность и непорядочность авторов. Плохо, когда люди, считающие себя учеными
, полны высокомерного самомнения и лишены элементарной любознательности. Перед любым новым, ранее неизвестным явлением все равны: и профессор, и новичок-радиолюбитель. Новые экспериментальные результаты нельзя запретить ни административными указами, ни «теоретическими заклинаниями». Как любил говаривать «отец народов»: «Факты – упрямая вещь». Эти факты посылают цитированных авторов в нокдаун.
Можно для иллюстрации привести еще пример. Для проведения эксперимента был изготовлен передатчик и приемник с ЕН-антеннами. Одновременно в эксперименте использовался приемник с обычной антенной. Высокочастотный сигнал передатчика модулировался зуммером с частотой 1000 Гц.
Все три прибора были настроены на одну и ту же частоту (радиовещательный диапазон
100 мгц). На этой частоте находилась маленькая «щель» между соседними радиовещательными станциями. Передатчик находился в дальней зоне
от приемников (не менее 10 метров
). Приемник с «лженаучной» антенной воспроизводил сигнал зуммера, а приемник с обычной антенной не реагировал на сигнал передатчика. Но он оказался настроенным на частоту вещательной радиостанции, и из него полилась песня Высоцкого «Товарищи ученые, доценты с кандидатами…». Это было удивительно. Две системы, работая на одной и той же частоте, не мешали друг другу.
Заключение
В одной популярной статье трудно изложить весь экспериментальный материал, накопленный за небольшое время существования и использования ЕН антенн. Однако о некоторых результатах наблюдений и измерений следует сказать.
– Во-первых, новое излучение хорошо проходит через диамагнетики и парамагнетики. Как показали предварительные эксперименты, новое излучение, в отличие от электромагнитных волн, может распространяться в воде и в земле.
– Во вторых, по опыту сравнения радиосвязи на обычных и на ЕН антеннах можно предположить, что это излучение имеет либо очень высокую скорость распространения (намного превосходящую скорость света), либо бесконечную скорость распространения.
Все это дает надежду на создание систем подводной и подземной (в шахтах) связи. Если же подтвердится высокая скорость передачи информации, то открываются перспективы использования ее в космической области.
Что касается радиолюбительской радиосвязи, то здесь много трудностей, обусловленных отсутствием количественной
теории. Приходится строить ЕН антенны, опираясь на опыт и интуицию. Однако, чем больше будет экспериментальных и теоретических исследований в этой области, тем быстрее мы приблизимся к цели. Мы только в начале пути. ЕН антенна и «таблетка» образно лишь «зацепились» за новое, неисследованное. Усилив вращательную (магнетон Бора) динамику зарядов и уменьшив привычную поступательную в конструкции антенн, мы уходим в новую радиосвязь с непривычными и необычными свойствами [9].
Здесь, как и в других статьях, я еще раз хочу повторить:
«Давайте общими усилиями «закрасим» это «белое пятно» в науке!».
Источники информации:
1. Гольдштейн Л.Д., Зернов Н.В. Электромагнитные поля и волны. – М.: «Советское радио», 1971.
2. Коробейников В.И. Радиосвязь на спиновом электромагнитном поле. 2005. http://tech.freelook.msk.ru/?gl=science&dir=sv&fl=sv01
3. Vladimir Korobejnikov, Ted Hart. Теория ЕH и Hz антенн (англ.). 2004. http://ehant.narod.ru/theory.pdf
4. Коробейников В.И. Никола Тесла и мгновенная электрическая связь!!! 2005. http://vladomire.h1.ru/science.php?dir=tesla&link=teor_sv
5. Коробейников В.И. Магнитные антенны для сверхдальней связи. 2005. http://www.qrz.ru/schemes/contribute/antenns/eh/index.shtml
6. Кисель Н.А. Что можно сказать об антеннах ЕН? 2005.
http://www.qrz.ru/schemes/contribute/antenns/eh/ua3aic.shtml
7. Коробейников В.И. Истоки «лженауки», или чего не понимают в мгновенной электрической связи. 2003. http://anomalia.narod.ru/text6/467.htm
8. Кудинов В., Федоров В. Старая теория в новых тенденциях практики антенн. 2005. http://qrx.narod.ru/anten/st_na.htm
9. Коробейников В.И. Мифы и реальность ЕН антенн 2005 http://www.qrz.ru/articles/detail.phtml?id=282
Дополнение к статье В.И. Коробейникова «Новый вид электромагнитного излучения?»
Виктор Кулигин
Поскольку по согласованию с автором и редакцией мне пришлось редактировать статью В.И. Коробейникова, я хотел бы добавить некоторые соображения.
В настоящее время нет достоверной количественной
теории, но есть модель, предлагаемая В.И. Коробейниковым. С целью проверки и развития теории, необходимо проведение дальнейших теоретических и экспериментальных исследований.
–
Необходимо убедиться, что мы имеем дело не с мгновенно действующим, а с волновым процессом.
–
Необходимо определить скорость распространения излученной волны. Эта скорость может существенно отличаться от скорости света в вакууме и зависеть не от μ и ε, а от других параметров среды. Об этом качественно свидетельствуют эксперименты по хорошему прохождению нового вида волн через воду и железобетонные здания по сравнению с электромагнитными волнами.
–
Необходимо исследовать поляризацию этих волн. Есть в статье моменты, которые свидетельствуют о продольном характере этих волн (особенности диаграмм направленности).
–
Необходимо исследовать также явления отражения от различных сред, интерференции этих волн и дифракции.
–
Наибольший интерес представляет выяснение механизма излучения и, ответ на вопрос: что является источником волн и как они формируются?
Можно предположить, что явления, обнаруженные Авраменко [1], и явления, исследовавшиеся
Шпильманом [2], имеют общую природу
с экспериментальными наблюдениями, изложенными в статье. По этой причине необходимо их совместное исследование.
Отсутствие в настоящее время количественной теории не есть причина ставить на экспериментальные результаты клеймо «лженауки». Как было показано в [3], электродинамике вовсе не противоречат, ни мгновенное взаимодействие, ни существование продольных волн, ни волн со скоростями, превышающими скорость света. Приходится сожалеть, что теоретическая физика
, приняв за первичное
постулаты и оторвавшись
от своей экспериментальной основы, уже давно представляет собой самостоятельный «нарост» в науке. Что касается теории относительности, то она стала анахронизмом.
Использование нового вида излучения в промышленности и технике (например, подземная и подводная связь, возможное применение приборов в медицине и т.д.) представляется перспективным. Остается надеяться, что здравомыслящие ученые РАН и РАЕН смогут преодолеть существующие в физике предрассудки и совместно
с практиками-экспериментаторами не только дадут достоверное теоретикоэкспериментальное обоснование новых явлений, но и пробьют брешь в догматизме, парализующем научную творческую мысль.
Источники информации:
1. Стребков Д.С., Авраменко С.В., Некрасов А.И., Рощин О.А. О возможности однопроводной передачи энергии. // Техника в сельском хозяйстве. - 2004. - N 4. - С. 35-36.
2. Шпильман А.А. Генератор аксионного поля. 2005. http://prometheus.al.ru/english/medic/s4_1.htm
3. Кулигин В.А., Кулигина Г.А., Корнева М.В.. Ревизия теоретических основ релятивистской электродинамики. НиТ
, 2004. www.n-t.ru/tp/ns/rt
.
Из личного сообщения В.И. Коробейникова
(публикуется с разрешения автора)
«Эксперимент 17 июля 2005 года
На озере глубиной 5-6 метров был проведен эксперимент по подводной радиосвязи на HZ антеннах. Эксперимент проводился с участием Владимира Васильевича Кононова (UA1ACO). Впечатляющие результаты.
Самодельный "дохленький" передатчик (КТ315 - ЗГ, КТ315 - буфер-усилитель, нагруженный на НZ-антенну и зуммер-мультивибратор, как модулятор на двух КТ315, питание от батареи "Крона"). Передатчик настроен на частоту 100 мгц. Самодельный УКВ приемник из радио набора "Мастер Кит" NK116 с НZ-антенной. Для дополнительного контроля был и второй портативный высокопрофессиональный, высокочувствительный приемник "Kenwood TH-F6", которым вооружены спецслужбы для поисков "жучков" в офисах и для других целей. Утапливали с лодки в герметичной стеклянной банке этот передатчик. Сигнал принимали приемниками в лодке.
"Чудо" обнаружили сразу. Когда передатчик находился на глубине 1,5 метров, то приемник "Kenwood TH-F6" перестал принимать сигнал, а до дна передатчику еще далеко. УКВ приемник-самоделка устойчиво принимает сигнал-зуммер (пищит). Достигли дна. УКВ самоделка-приемник принимает сигнал, а приемник "Kenwood TH-F6" молчит (шипит). Через несколько минут самоделку-приемник пришлось подстроить. На дне озера холодно, а передатчик с параметрической стабилизацией. Был малый уход частоты.
6 метров воды для "дохляка" - передатчика на УКВ это очень серьезно. Вот то самое, что никак не увидят оппоненты на сайте. Что принимает самоделка с НZ-антенной и не видит профессионал "Kenwood"? Куда "приткнуть-пристроить" Теорию АФУ для этого случая? Это совершенно другая дорога в радиосвязи».
Введение
До появления уравнений Максвелла (1864 г.) законы механики и электродинамики (законы Ньютона, Кулона, Ампера и др.) удовлетворяли принципу относительности Галилея:
«Механический эксперимент дает одинаковые результаты в неподвижной лаборатории
(системе отсчета) и в любой лаборатории, которая движется равномерно и прямолинейно относительно первой».
Иными словами, законы природы и уравнения, описывающие их, не должны меняться при преобразованиях Галилея:
x
' = x - Vt
; y
' = y
; z
' = z
; t
' = t
где V
- относительная скорость движения двух инерциальных систем отсчета (лабораторий), направленная вдоль оси x
, т.е. галилеевская
скорость относительного движения.
Уравнения Максвелла " нарушили" этот фундаментальный принцип. Форма уравнений Максвелла уже не сохранялась при преобразованиях Галилея.
Ранние попытки сохранить преобразование Галилея для электродинамики путем ссылки на возможное существование эфира в то время были неубедительны. Лоренц и Пуанкаре длительное время в переписке обсуждали эту проблему между собой. В результате
Пуанкаре приходит к выводу о необходимости обобщения принципа относительности Галилея и распространения его на электродинамику. Он следующим образом формулирует принцип, который позже стал одним из важных принципов теории познания
[1]:
«Законы физических явлений должны быть одинаковыми как для неподвижного наблюдателя, так и для наблюдателя, движущегося прямолинейно и равномерно, поскольку у нас нет возможности убедиться в том, участвуем ли мы в таком движении или нет».
Несмотря на то, что этот принцип опирался, главным образом, на негативные результаты по обнаружению эфира, существовавшие тогда, он и по сей день играет большую эвристическую и критериальную ценность. Он ограничивает или отсекает от физики те фундаментальные теории, которые ему не удовлетворяют. Этот принцип мы назовем принципом Галилея-Пуанкаре
.
Обратим внимание, что принцип Галилея-Пуанкаре не содержит "привязки" к какому-либо конкретному преобразованию пространственновременной системы отсчета, т.е. является философским
принципом.
Хотя этот принцип имеет под собой достаточно прочное основание, его реализация оказалась трудным делом, породив позитивистскую (субъективно-идеалистическую) концепцию под названием «Специальная теория относительности». Чтобы правильно реализовать принцип Галилея-Пуанкаре, мы должны правильно определять физическое и философское содержание понятия «взаимодействие
» в физических теориях.
Как было показано Лоренцем и др., уравнения Максвелла сохраняют свою форму при преобразовании, получившем название «преобразования Лоренца». x
− vt ct
− xv
/c
x
'=; y
'= y
; z
'= z
; ct
'=
  1− (v
/c
) 2
1− (v
/c
) 2 1− (v
/c
) 2
1− (v
/c
) 2
Эйнштейн после многочисленных «мысленных экспериментов» вводит два постулата:
1. Опираясь на корень, стоящий в знаменателе преобразования Лоренца, он утверждает, что никаких скоростей, превышающих скорость света в вакууме, в природе существовать не может (постулат о конечной скорости распространения взаимодействий).
2. Опираясь на принцип Галилея-Пуанкаре, он утверждает, что скорость света постоянна в любой инерциальной системе отсчета (α), а преобразование Лоренца должно быть справедливым для всех без исключения явлений материального мира
(β), т.е. все уравнения должны быть ковариантными относительно этого преобразования. Если положение (α) не вызывает сомнений, то обобщение (β) является, мягко говоря, мало обоснованным. Причина в том, что любая физическая концепция, теория и т.д. имеет границы применимости, за которыми она становится ошибочной. Обобщение (β) «отвергает» такие границы. Оно, вслед за принципом Галилея-Пуанкаре, претендует на статус философского
принципа.
К сожалению, исследователи не добавляют к этим двум положениям третье, которое является принципиально важным.
3. Эйнштейн предложил свою уникальную интерпретацию пространственновременных отношений
, которая поставила все с ног на голову. Эта интерпретация является наиболее слабым звеном
теории Эйнштейна. Именно ей СТО обязана появлением большинства своих парадоксов.
Постулаты Эйнштейна разрушили материалистические представления не только о пространственно-временных отношениях в физике. Они разрушили философские основания механики, заменив материалистическую интерпретацию субъективизмом (позитивизмом).
10.1 Логика парадоксов
Изучим логику наиболее распространенных парадоксов.
ПАРАДОКС ВРЕМЕНИ
Рассмотрим парадокс времени. Пусть имеются две инерциальные системы отсчета K
и K'
, движущиеся друг относительно друга со скоростью v
. В системе К
находятся два наблюдателя. Наблюдатели сравнивают темп хода своих часов. Затем один из наблюдателей переходит из системы К
в систему K'.
Сравнивая темп хода часов, наблюдатель системы K
обнаружит, что его часы идут быстрее
, чем часы у наблюдателя в K'
. Но инерциальные системы равноправны
. Поэтому наблюдатель системы K'
, сравнив показания часов, станет утверждать обратное: его часы идут быстрее
, чем часы наблюдателя системы K
.
И тот, и другой излагают объективные факты. Следовательно, между суждениями двух наблюдателей имеется логическое
противоречие, которое легло в основу парадокса времени. Как разрешить парадокс? В какой системе отсчета время течет быстрее
?
ПАРАДОКС ЛИНЕЙКИ
Рассмотрим теперь парадокс линейки. Пусть имеются две инерциальные системы отсчета K
и K'
, движущиеся друг относительно друга со скоростью v
. В системе К
покоятся два наблюдателя снабженные одинаковыми линейками. Один из наблюдателей переходит в систему K'.
Сравнивая длины движущейся и неподвижной линеек первый наблюдатель системы K
обнаружит, что его линейка длиннее
, чем линейка у наблюдателя в K'
. Но инерциальные системы равноправны. Поэтому наблюдатель системы K'
, сравнив длины линеек, станет утверждать обратное: его линейка длиннее
, чем линейка наблюдателя системы K
.
В какой системе отсчета линейка длиннее
?
Известный ученый Бриджмен так писал о «равноправии» интервалов времени и длин масштабов, измеренных в различных инерциальных системах отсчета (цит. по [2]): «было бы жестоко снабжать физиков резиновыми линейкам и исключительно неправильно идущими часами
». Можно не принимать операционализм Бриджмена, но с данным остроумным замечанием нельзя не согласиться.
КОНВЕКТИВНЫЙ ПОТЕНЦИАЛ
Вновь рассмотрим две инерциальные системы отсчета K
и K'
, движущиеся друг относительно друга со скоростью v
. В одной системе отсчета у наблюдателя имеется заряженный конденсатор (Траутон), который покоится относительно наблюдателя. В другой также имеется наблюдатель (Нобл) со своим заряженным конденсатором [3].
Траутон, опираясь на СТО, говорит Ноблу: «Сэр! Мой конденсатор уравновешен, а Ваш не уравновешен. Я вижу, что на него действует момент сил, и Ваш конденсатор должен повернуться согласно законам механики».
Нобл возражает ему: «Увы, сэр! Это «барахлит» ваш конденсатор. Он должен повернуться. Мой конденсатор в порядке. На него не действует никакой момент сил».
Кто из них прав? В чьей системе отсчета конденсатор должен повернуться
?
ПАРАДОКС РЫЧАГА
Опять рассмотрим двух наблюдателей, расположенных в разных инерциальных системах отсчета K
и K'
. У каждого из наблюдателей имеется уравновешенный рычаг [4].
Наблюдатель системы K
будет утверждать, что рычаг в системе K'
не уравновешен, и он наблюдает момент М
, который обязан повернуть рычаг в системе K'.
Но его собственный рычаг уравновешен и не вращается.
Наблюдатель системы K'
будет утверждать прямо противоположное: его рычаг уравновешен, а на рычаг системы K
действует не скомпенсированный момент сил.
Кто из них прав? В какой системе отсчета рычаг должен действительно повернуться
?
ОБСУЖДЕНИЕ
Как видно из изложенных парадоксов, их логическая
структура идентична
и, как следствие, должно быть единообразное объяснение. Общая логическая структура парадоксов свидетельствует о наличии в них общей логической (гносеологической) ошибки. Эта ошибка, как правило, связана с некорректной интерпретацией явлений. Что касается объяснений, то они и различны (выдвигаются свои объяснения для каждого из парадоксов), и неудовлетворительны. Нам остается найти эту логическую ошибку в СТО.
Чтобы это сделать, можно изложить обычный «парадокс», который по своей логической структуре идентичен
этим трем парадоксам.

Рис. 10.1
Пусть два джентльмена одинакового роста входят в комнату, разделенную прозрачной невидимой перегородкой. Они не знают, что эта перегородка представляет собой большую двояковогнутую линзу. Первый джентльмен видит, что его коллега ниже ростом. Второй джентльмен, сравнивая свой рост с ростом своего коллеги, убеждается, что выше он. Кто из них прав? Кто из них «выше» на самом деле
?
Ответ на последний парадокс очевиден. Нельзя принимать мнимое изображение (явление) за действительный рост. Отождествление кажущегося роста джентльмена с его действительным есть истолкование явления как сущности
. Мы не будем останавливаться на этой типичной ошибке. Она существует, например, в известной теории Птолемея. Более подробно об этом можно прочесть, например, в [5], [6], [7].
Итак, мы убедились ранее, что существует только видимость объяснения парадоксов. А ведь мы рассмотрели далеко не все из них. Однако уже сейчас можно сделать однозначный вывод. Теория относительности это теория одного наблюдателя. Как только появляется второй наблюдатель, между наблюдателями возникает конфликт. СТО внутренне противоречивая теория и не может считаться научной.
10.2 Закон "преломления" светового луча
Критики СТО ограничиваются, как правило, анализом эффектов "сокращения" масштабов движущихся тел и "замедлением" времени. К сожалению, они не принимают во внимание, что движущийся объект пролетает
мимо них со скоростью v,
и наблюдатель вынужден будет рассматривать этот объект под различными углами наблюдения θ, как показано на рис 10.2.
Рис. 10.2 Рис. 10.3
Угол θ образован двумя векторами: вектором скорости движущегося тела и вектором, направленным вдоль светового луча от движущегося источника к наблюдателю.
Теоретически он может меняться от 0 до 180 градусов в системе отсчета K, связанной с наблюдателем. В системе отсчета, связанной с движущимся объектом, этот луч будет иметь другое направление, т.е. идти под другим углом. Обозначим этот угол как θ'.
Причина отличия θ от θ' видна из рис 10.2. В системе K
' наблюдатель и световой луч будут двигаться к общей точке встречи А. Только в этой точке наблюдатель увидит этот световой луч.
Из преобразования Лоренца известны следующие соотношения:
cosθ − v
/c
1− (v
/c
) 2
sinθ 1− (v
/c
) 2
   cosθ'=; sinθ'=; ω'= ω v v v cosθ'=; sinθ'=; ω'= ω v v v
1− cosθ 1− cosθ 1− cosθ c c c
где: ω и ω' частоты принимаемого и излучаемого сигналов соответственно.
Запишем теперь угол расхождения между лучами (угол аберрации), который нам понадобится в дальнейшем:
cosθ− v
/c
 δ=θ'−θ= arccos−θ (10.2.1) v δ=θ'−θ= arccos−θ (10.2.1) v
1− cosθ c
Допустим, что движущийся объект это линейка длиной Δx
', ориентированная вдоль вектора скорости v.
Нетрудно видеть, что наблюдаемая длина линейки будет зависеть от v
и θ. Кажущаяся длина линейки есть:
1−(v
/c
) 2
 Δx
= Δx
'. Δx
= Δx
'.
v
1− cosθ c
 Из этого выражения следует, что известное "сокращение" масштаба Δx
= Δx
' 1− (v
/c
) 2
мы получаем, когда θ = 900
. При всех других углах мы будем измерять другие значения Из этого выражения следует, что известное "сокращение" масштаба Δx
= Δx
' 1− (v
/c
) 2
мы получаем, когда θ = 900
. При всех других углах мы будем измерять другие значения
1− v
/c
1+ v
/c
1+ v
/c
1− v
/c
  "длин" линейки, лежащие в пределах Δx
'≤ Δx
≤ Δx
'. "длин" линейки, лежащие в пределах Δx
'≤ Δx
≤ Δx
'.
Другими словами, в общем случае измеряемая длина может быть как больше, так и меньше истинной длины линейки.
Формула, связывающая Δx
и Δx
', позволяет получить очень важное соотношение. Для этой цели умножим Δx
на sinθ и преобразуем это произведение.
1− (v
/c
) 2
 d
= Δx
sinθ = Δx
'sinθ = Δx
'sinθ' (10.2.2) v d
= Δx
sinθ = Δx
'sinθ = Δx
'sinθ' (10.2.2) v
1− cosθ c
Это и есть «закон преломления
» светового луча при переходе наблюдателя из одной системы отсчета в другую. Физический смысл полученного выражения можно проиллюстрировать с помощью рис. 10.4.
Рис 10.4.
Величина d
это толщина светового луча. Она сохраняется постоянной в любой инерциальной системе отсчета. Если учесть, что ширина этого луча не зависит от выбора инерциальной системы отсчета, можно сформулировать закон "преломления" света при переходе наблюдателя из одной инерциальной системы отсчета в другую. Световой луч
"поворачивается" на угол δ = θ - θ' (изменяется направление фронта световой волны) и изменяется частота его колебаний.
10.3 Наблюдаемая и измеряемая форма движущегося объекта
Полученное соотношение можно с успехом использовать для описания видимой формы движущегося объекта. Пусть мимо нас со скоростью v
, параллельной оси x
, пролетает куб, ориентированный по осям x
, y
, z
или x
', y
', z
'.
Конечно, если куб находится очень далеко от нас, то человеческий глаз увидит плоское изображение. Однако если человек знает, что форма предмета куб, его мозг быстро восстановит "изображение". Наблюдателю будет казаться, что летящий куб "развернут" на угол δ по отношению к своей истинной ориентации.
Рис 10.5.
Оставим в стороне иллюзии, связанные с субъективным человеческим восприятием (оптической иллюзией). Реальная форма объекта может быть получена методами радиолокации или иными объективными методами измерений расстояния с помощью световых лучей (лазер, например) или электромагнитных волн. Однако
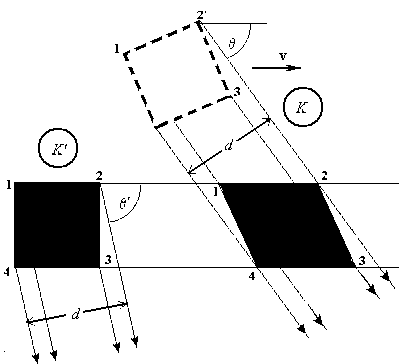
Рис 10.6.
нам нет необходимости использовать столь сложные средства, поскольку мы знаем следующие результаты, вытекающие из преобразования Лоренца:
а) закон "преломления" светового луча в СТО;
б) независимость поперечных координат (y
= y
' и z
= z
') от выбора инерциальной системы отсчета в СТО. На рис. 10.6 показан принцип построения формы движущегося куба, а на рис. 10.7 приведены визуально наблюдаемые и измеряемые формы движущегося куба для нескольких углов наблюдения θ.
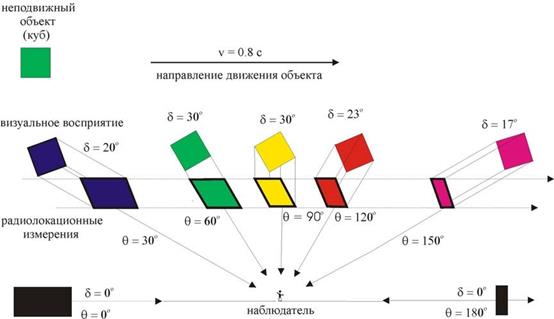
Рис 10.7.
Из рис. 10.7 видно, что объективно движущийся куб имеет отнюдь не кубическую форму.
Он будет иметь форму параллелепипеда со скошенными торцами. При этом наблюдаемая форма куба будет меняться при его движении. Меняется и цвет куба. Поэтому необходимо ответить на следующие вопросы:
1. Форма движущегося куба меняется
на самом деле (сущность) или же наблюдаемая форма куба есть явление
, обусловленное искажением фронта световой волны, а с кубом на самом деле не происходит никаких изменений
?
2. Связано ли изменение формы куба с изменением свойств пространства
или же с изменением направления фронта светового луча
?
3. 3.Связано ли изменение цвета куба с эффектом Доплера или же с различным темпом времени
в двух инерциальных системах отсчета K
и K
'?
Ответ очевиден, но чтобы правильно разобраться в этих вопросах, не ссылаясь на интуицию и "очевидность", необходимо знать признаки, отличающие сущность от явления, т.е. необходимо понимать и уметь применять теорию познания объективной истины.
10.4 Явление и сущность
Хотя физики не очень почитают философию, нам к ней придется обратиться. Вопрос о взаимосвязи и признаках, отличающих явление от сущности, рассмотрен в [5], [6], [7]. Здесь мы опишем кратко эти признаки. Предположим, что, наблюдая явления, мы можем менять некоторые параметры, влияющие на явление. В рамках СТО есть два таких параметра: относительная скорость движения двух инерциальных систем отсчета v
и угол наблюдения движущегося объекта θ. Каждой совокупности этих параметров соответствует свое объективное явление,
которое чем-то отличается от других явлений данной совокупности. Сущность есть инвариантное
(т.е. не зависящее от θ и v
) представление о протекающих процессах и наблюдаемых явлениях. Есть такое правило:
ЯВЛЕНИЕ
ЗАВИСИТ
ОТ УСЛОВИЙ ЕГО НАБЛЮДЕНИЯ СУЩНОСТЬ
ОТ ЭТИХ УСЛОВИЙ НЕ ЗАВИСИТ
.
Таким образом, изменяющаяся длина линейки, замедление времени, искажение формы объекта суть объективные явления.
Эйнштейн фактически предложил считать, что при угле наблюдения θ = 90о
все явления отображаются из системы K
’ в систему K
без каких-либо искажений.
 При θ = 90о
мы видим, что в системе K
’ время течет «медленнее»
, чем в K
, а продольные размеры объектов «сокращаются»
в 1− (v
/c
)2
раз. При θ = 90о
мы видим, что в системе K
’ время течет «медленнее»
, чем в K
, а продольные размеры объектов «сокращаются»
в 1− (v
/c
)2
раз.
Интересно, что бы он сказал об искажениях формы объекта?
10.5 Пространство и время в преобразовании Лоренца
Чтобы проанализировать проблему связи времен различных инерциальных систем отсчета
(ИСО), обратимся к рис.10.8, на котором представлено взаимное расположение наблюдателей в сопоставляемых системах отсчета А
и В
. В каждой из систем имеется генератор, задающий световые сигналы через равные промежутки времени Т
, и наблюдатель, регистрирующий временные интервалы между импульсами (вспышками).
Будем считать, что при относительной скорости инерциальных систем А
и В
, равной нулю, выполняется условие ТА
= TВ
= Т'A
= Т'B
. Рассмотрим теперь случай, когда относительная скорость движения инерциальных систем А
и В
отлична от нуля. Очевидно, что значения интервалов ТA
и ТB
не изменятся
, т.к. это характеристики сущности
. Преобразование Лоренца это линейное алгебраическое
преобразование.
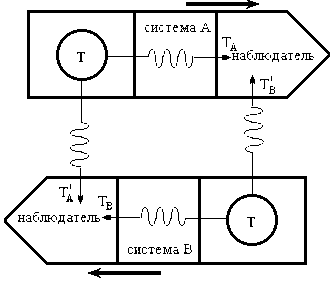
Рис. 10.8 Обозначения: ТА
и TВ
- интервалы времени, измеренные в собственных ИСО, являющиеся характеристиками сущности; Т'A
и Т'B
- интервалы времени, наблюдаемые их "чужих" систем (явления).
Оно устанавливает взаимно-однозначную связь между точками xi
системы К
и точками x'i
системы К
'. Эта связь не зависит от способа
перехода наблюдателя из К
в К
' и обратно.
Иными словами, наблюдатели не увидят изменения частоты собственного генератора, даже испытывая ускорения. Здесь мы имеем в виду «идеальные» часы, точно регистрирующие время в собственной системе отсчета.
Оно устанавливает взаимно-однозначную связь между точками xi
системы К
и точками x'i
системы К
'. Эта связь не зависит от способа
перехода наблюдателя из К
в К
' и обратно.
Иными словами, наблюдатели не увидят изменения частоты собственного генератора, даже испытывая ускорения. Здесь мы имеем в виду «идеальные» часы, точно регистрирующие время в собственной системе отсчета.
Изменятся
наблюдаемые "чужие" интервалы времени Т'A
и Т'B
(явления
). В соответствии с преобразованием Лоренца будем иметь:
I) ТA
< Т'B
(система А), 2) TB
< T'A
(система В).
Для полного определения логической связи между 4-мя величинами (ТА
; TВ
; Т'A
;
Т'B
) двух записанных нами неравенств недостаточно. Необходимы еще два условия.
А.Эйнштейн предложил считать, что Т'A
есть собственное время системы А
, т.е. ТА
, а Т'B
есть собственное время системы В
, т.е. ТВ
. Эта связь не зависит от инерциальной системы отсчета.
3) Т'A
= ТA
4) T'B
=TB
Так Эйнштейн подошел к своему пониманию и объяснению физического смысла преобразования Лоренца. Очевидно, что система из четырех соотношений оказалась логически противоречивой
. Выражения 1) и 2) примут вид:
I) ТA
< ТB
, 2) TB
< TA
.
Эйнштейн подобно Птолемею допустил типичную гносеологическую сшибку. Наблюдаемое явление (Т'A
и Т'В
) он истолковал как сущность (ТA
и ТВ
).
Птолемей утверждал, что, поскольку мы видим движение солнца по небосводу, это и есть на "самом деле" движение его вокруг Земли. Точно так и Эйнштейн истолковывал явления
"сокращения" масштабов и "замедления" времени. Коль скоро мы "видим" эти изменения
(т.е. они следуют из преобразования Лоренца), это так есть "на самом деле" (такова сущность
пространства и времени). Эта гносеологическая ошибка называется: подмена сущности явлением или истолкование явления как сущности.
Ошибочное истолкование породило ряд логических противоречий, например, парадокс близнецов, "сжатие" масштаба и другие.
Единственно
возможным
вариантом, который не противоречит равноправию инерциальных систем отсчета и логике, является вариант, опирающийся на соотношения:
1) ТА
< Т'A
; 2)TВ
< Т'B
; 3) Т'A
= Т'B
; 4) ТА
= TВ
Смысл его очевиден.
Собственное время во всех инерциальных системах отсчета едино
, т.е. течет в одном ритме, темпе (ТА
= TВ
).
Явления
обладают симметрией
(Т'A
= Т'B
; ТА
< Т'A
; TВ
< T'B
). Это и есть реализация принципа равноправия
инерциальных систем отсчета.
Именно здесь выявляется различие между эйнштейновской и новой интерпретациями сущности преобразования Лоренца.
1. Эйнштейновский (= птолемеевский) подход. Замедление времени, которое мы наблюдаем (явление), есть "действительное" замедление времени. Время в движущейся системе отсчета действительно течет медленнее, чем в неподвижной (сущность).
2. Материалистический (= коперниканский) подход. Замедление времени есть объективное явление, которое мы наблюдаем и регистрируем в нашей инерциальной системе. Однако в самой движущейся системе время течет в том же темпе (сущность), что и в неподвижной.
Кажущееся замедление времени обусловлено свойствами преобразования Лоренца (эффект Доплера).
Итак, все параметры и характеристики, полученные с помощью преобразования Лоренца, относятся к разряду явлений и не всегда совпадают с действительными параметрами и характеристиками, измеренными в системе отсчета, связанной с исследуемым объектом. Однако при преобразовании Лоренца некоторые величины остаются неизменными (инвариантными). Среди них:
1. Сохраняется действительное равноправие
всех инерциальных систем отсчета.
2. Физическое время
остается общим и единым
для всех ИСО. Это единое мировое время.
3. Общим
для всех ИСО остается трехмерное пространство
.
4. Скорость света и сечение светового луча
остаются неизменными
(инвариантными) для всех ИСО.
Преобразование Лоренца теперь следует писать в такой форме
Δx
− v
Δt c
Δt
− Δxv
/c
Δx
'=; Δy
'= Δy
; Δz
'= Δz
; c
Δt
'=
  1− (v
/c
) 2
1− (v
/c
) 2 1− (v
/c
) 2
1− (v
/c
) 2
Преобразование дает отображение
пространственных отрезков и интервалов времени, измеренных в системе К’
, в систему К
с помощью световых лучей
.
Наблюдаемые "замедление" времени и "сжатие" масштаба - суть объективные явления, т.е. искаженные отображения интервалов времени (единого для всех ИСО) и пространственных отрезков (общего для всех ИСО пространства) из одной системы отсчета в другую. Такой подход «ликвидирует» парадоксы, подобные изложенным в первом параграфе.
Уже сам принцип равноправия инерциальных систем предполагает, например, единство времени во всех ИСО. В противном случае различие в темпах изменения времени могло бы служить критерием для дифференциации различных ИСО.
10.6 Поворот осей
Преобразование Лоренца или родственное ему обобщенное преобразование, о котором мы будем писать в Главе 11, осуществляют поворот осей на мнимый угол. Если обозначить ict
через τ, то поворот на мнимый угол можно свести к повороту осей на действительный угол и дать соответствующую интерпретацию.
Рассмотрим объекты в системе К
’ двух координат (x
’; τ’), поскольку при движении системы отсчета вдоль оси x
координаты y
и z
остаются теми же. Сначала рассмотрим отрезок (х
’1
; х
’2
), покоящийся в системе К
’.
Поскольку он существует сколь угодно долго, его отображение в указанных координатах представляет полосу, протянувшуюся вдоль оси τ’.
Для измерения его длины достаточно зафиксировать время и измерить проекцию на ось х
’. Длина проекции совпадает с действительной длиной отрезка. Проекция на ось τ’ равна нулю.

Рис. 10.9
Переход в движущуюся систему отсчета K
равнозначен повороту осей на некоторый угол, как показано на рис. 10.9. Соответственно, теперь мы будем иметь две не равные нулю проекции на разные оси. Изменилась ли длина стержня? Конечно, не изменилась. Она является истинным скаляром и равна
 Δx
'= x
'2
−x
'1
= (x
2
− x
1
)2
+ (τ2
− τ1
)2 Δx
'= x
'2
−x
'1
= (x
2
− x
1
)2
+ (τ2
− τ1
)2
Изменились проекции на оси координат. Так почему же мы считаем, что после поворота и измерения координат x
1
и x
2
длина отрезка изменилась? На каком основании о длине отрезка мы судим только по одной
его проекции? Почему мы не учитываем, что существует отличная от нуля проекция на ось τ? Это пренебрежение законами математики или же незнание их?
В мысленных экспериментах Эйнштейна при измерении длины движущегося отрезка засекают в пространстве точки «вспышек» и измеряют расстояние между ними. Но ведь эти «вспышки» происходят не одновременно; и это известно. Почему их это не учитывается? Гипноз авторитета?
Аналогичная ситуация при измерении интервалов времени. Здесь также временной интервал образует «полосу», поскольку время для всех точек системы K
’ одно.
Пусть в системе K
’ в некоторой точке происходят одна за другой две вспышки в моменты времени τ’1
и τ’2
(рис. 10.10). Поскольку проекция Δx
’= 0, интервал времени между вспышками равен Δτ = ( τ’2
- τ’1
).
В системе отсчета К
мы обнаружим, что интервал времени между вспышками изменился и стал другим: τ2
- τ1
. Действительно ли изменился интервал времени или же это просто явление, т.е. искаженное движением отображение реального интервала времени?

Рис. 10.10
Так как вспышки мы наблюдали в разных точках пространства х
1
и х
2
, действительный интервал времени Δτ равен
 Δτ = (τ2 − τ1 )2 + (x
2 − x
1 )2 = τ'2 − τ1' Δτ = (τ2 − τ1 )2 + (x
2 − x
1 )2 = τ'2 − τ1'
Очевидно, что в мысленных экспериментах у Эйнштейна с математикой не все в порядке. Подменять реальные величины (истинные скаляры
) их проекциями и, пользуясь этим, говорить о каких-то пространственно-временных искажениях не корректно. Эйнштейн, конечно, гений хотя бы потому, что его точка зрения продержалась более ста лет. Но куда смотрели современники Эйнштейна и смотрят наши современники?
Источники информации:
1. Кристиан Маршаль. Решающий вклад Анри Пуанкаре в специальную теорию относительности (Перевод с английского Ю. В. Куянова). Препринт ИВФЭ, - Протвино, 1999.
2. Бриллюен Л. Новый взгляд на теорию относительности. – М.: Мир, 1973.
3. Пановски В., Филипс М.. Классическая электродинамика. –М.: ГИФМЛ, 1963.
4. Угаров В.А. Специальная теория относительности. – М.: Наука, 1969.
5. Кулигин В.А., Кулигина Г.А., Корнева М.В. К столетнему юбилею СТО. http://www.nt.students.ru/tp/ns/sto.htm
6. В.А.Кулигин, Г.А.Кулигина, М.В.Корнева. Преобразование Лоренца и теория познания. / Воронеж. ун-т. - Воронеж, 1989. Деп. в ВИНИТИ 24.01.89, № 546.
7. V.A.Kuligin, G.A.Kuligina, M.V.Korneva. Epistemology and Special Relativity. Apeiron, (20:21). 1994.
11.1 Наблюдаемая и истинная скорость объекта
Сейчас нам необходимо дать пояснения, поскольку за 100 лет выводы из СТО уже столь основательно «вбиты» в сознание обывателя, что осмысление нового превращается в трудную работу.
1.
Классическое отображение
. Со школьной скамьи, решая физические задачи механики, мы привыкли к тому, что положение тела в пространстве в данный момент времени отображается объективно (без каких либо искажений). Такое отображение опирается по своей сути на «мгновенное взаимодействие» (мгновенную передачу информации). Оно никогда и ни у кого не вызывало подозрений в некорректности, хотя никто и никогда не предлагал физической модели реализации
этого способа. В любой фиксированной инерциальной системе отсчета наблюдатель мгновенно получает информацию обо всех точках пространства без какого либо «запаздывания».
2.
Отображение с помощью световых лучей
. Иное дело – световые лучи. Ни один «мысленный эксперимент» А. Эйнштейна не обходится без световых лучей. Это не случайно. Сейчас наша задача будет состоять в том, чтобы проанализировать этот способ и сравнить его с классическим.
Заметим, что оба способа отображения существуют одновременно. Они не исключают друг друга. Рассматривая «закон преломления» во втором параграфе Главы 9, мы выяснили, что отображение частот, интервалов времени и длин отрезков из одной инерциальной системы отсчета в другую в специальной теории относительности существенно зависит от угла наблюдения θ. В частности, v v
1− cosθ 1− cosθ
  ΔT
= ΔT
' c
; Δx
= Δx
' c ΔT
= ΔT
' c
; Δx
= Δx
' c
1− (v
/ c
)2
1− (v
/ c
)2
Интересно отметить, что существует «критический» угол наблюдения, при котором
ΔТ =
ΔT’
и Δх =
Δх’ .
Этот угол равен
 1− 1− (v
/c
) 2 1− 1− (v
/c
) 2
θкрит
= arccos
v
/c
Величины, зависящие
от условия их регистрации (от v
или θ), относятся к явлениям
, т.е.
 искаженным отображениям действительных величин [1], [2]. Это проекции
действительных отрезков (неподвижная система) на оси 4-координат движущейся системы отсчета. Сами действительные отрезки являются истинными скалярами
(т.е. характеристиками сущности
). Например, интервал Δ ct’
, измеренный в системе K
’, будет иметь в системе К
две проекции: Δx
и Δ ct
. Зная их, всегда можно найти длину действительного интервала Δ ct’
: Δсt
'= (Δct
) 2
− (Δx
) 2
и т.д. искаженным отображениям действительных величин [1], [2]. Это проекции
действительных отрезков (неподвижная система) на оси 4-координат движущейся системы отсчета. Сами действительные отрезки являются истинными скалярами
(т.е. характеристиками сущности
). Например, интервал Δ ct’
, измеренный в системе K
’, будет иметь в системе К
две проекции: Δx
и Δ ct
. Зная их, всегда можно найти длину действительного интервала Δ ct’
: Δсt
'= (Δct
) 2
− (Δx
) 2
и т.д.
Более, того, подавая световые импульсы под углом θкрит
в движущуюся систему отсчета, мы можем без помех осуществить, так называемую, «синхронизацию часов» двух инерциальных систем.
Относительную скорость движения инерциальных систем можно измерить разными способами.
Первый способ.
В системе К'
имеется неподвижный источник. Он излучает через равные интервалы времени ΔT'
короткие световые импульсы.
В системе К
мы будем видеть траекторию, "разделенную" этими вспышками на равные интервалы времени Δx
, которые покоятся в системе К.
Измеряя интервал времени между вспышками ΔT'
, в системе К
можно определить наблюдаемую
(или кажущуюся) скорость движения инерциальных систем. "Кажущейся" мы называем эту скорость потому, что мы наблюдаем в системе К
искаженный
движением интервал времени ΔT
. Эта скорость будет зависеть от угла наблюдения θ.
Второй способ
.
Мы можем в системе К'
разместить линейку длиной Δx'
, которая сориентирована вдоль скорости относительного движения инерциальных систем. В системе К
траекторией движения будет прямая линия, на которой мы зафиксируем неподвижную
точку. Измеряя время ΔT
, за которое линейка проходит эту точку, можно вычислить кажущуюся
скорость движения. Кажущейся мы называем эту скорость потому, что мы наблюдаем в системе К
искаженную
движением длину отрезка Δx
. Эта скорость будет также зависеть от угла наблюдения θ.
Независимо от способа измерения, мы имеем следующее выражение для этой скорости:
v
 v
наб
= (11.1.1) v v
наб
= (11.1.1) v
1− cosθ c

Рис. 11.1 Зависимость кажущейся скорости от угла наблюдения.
Поскольку наблюдаемая скорость vнаб
изменяется во времени (зависит от угла наблюдения θ, который постоянно меняется), наблюдаемое "ускорение
" равно
dv
наб
(v
sinθ)3
 a
= где у
- координата движущейся точки. a
= где у
- координата движущейся точки.
v
cy
(1− cosθ)
c
В частности, при θ = 900
ускорение равно a
= v
3
/cy
.
Существует ли "на самом деле
" это ускорение или же нам это "кажется
" (объективная "кажимость")? Означает ли это, что на движущуюся частицу действуют какие-то силы? "Реальны
" ли эти силы или же они тоже "кажущиеся
"?
Ответ очевиден. Световые лучи, передавая информацию, искажают ее. Из выражения (11.1.1) трудно определить действительную скорость относительного движения.
Но как, все-таки, найти действительную скорость относительного движения инерциальных систем отсчета? Заметим, что она не может зависеть от угла наблюдения. Она одна и та же для всех углов наблюдений.
Действительная скорость будет равна отношению двух истинных скаляров. В первом способе длина отрезка есть истинный скаляр, поэтому необходимо найти действительную «длину» интервала времени (величину истинного скаляра). Во втором способе интервал времени в К
будет по величине совпадать с величиной истинного скаляра. Необходимо определить истинную длину линейки (величину истинного скаляра). Но есть еще более простой способ, который приводит к тем же результатам, что и два первые.
Если мы измерим наблюдаемый интервал времени и длину отрезка, которую материальная точка проходит за этот интервал, мы получим величину скорости. Но для этого необходимо измерения проводить, когда движение объекта наблюдается под критическим углом θкрит
. При этом угле наблюдения ΔТ =
ΔT’
и Δх =
Δх’ .
Действительная относительная скорость движения двух инерциальных систем отсчета связана со скоростью, входящей в преобразование Лоренца. При θ =
θкрит
имеем
v
/c
V
=
 1− (v
/c
) 2 1− (v
/c
) 2
Эту истинную
скорость относительного движения инерциальных систем отсчета V
, которая не зависит от угла наблюдения θ, мы назовем галилеевской
скоростью. Именно она соответствует мгновенному (классическому
) отображению действительной скорости. Скорость v
, входящая в преобразование Лоренца, это кажущаяся
скорость (явление), которая будет наблюдаться, когда свет от объекта идет к наблюдателю под углом 900
к траектории перемещения объекта. Если мы выразим скорость v
через V,
то получим модифицированное преобразование.
  Δx
= Δx
' 1+ (V
/ c
)2
−Vt
';Δy
= Δy
';Δz
= Δz
';Δct
= Δct
' 1+ (V
/ c
)2
−Vx
'/ c Δx
= Δx
' 1+ (V
/ c
)2
−Vt
';Δy
= Δy
';Δz
= Δz
';Δct
= Δct
' 1+ (V
/ c
)2
−Vx
'/ c
Это преобразование показывает, что никаких ограничений
на действительную относительную скорость движения инерциальных систем отсчета не существует
!
11.2 Эксперимент, «подтверждающий» СТО
Приведенные выше результаты имеют интересное применение для объяснения появления у поверхности Земли μ-мезонов, рождающихся в верхних слоях атмосферы. Существующее объяснение использует следующую формулу.
Δτ
Δx
= v
ΔT
= v
(11.2.1)
 1− (v
/ c
) 2 1− (v
/ c
) 2
Расстояние, проходимое μ-мезоном, равно произведению наблюдаемой скорости v
на наблюдаемое "время жизни" μ-мезонов ΔΤ
. Это время жизни "удлиняется" для наблюдателя на Земле благодаря релятивистскому "замедлению времени".
Мы дадим другое объяснение, опирающееся на ту же формулу.
v
Δx
= Δτ= ΔτV
(11.2.2)
 1− (v
/c
) 2 1− (v
/c
) 2
Расстояние, проходимое μ-мезоном, равно произведению истинной скорости V
на действительное "время жизни" μ-мезонов Δτ. При этом скорость μ-мезонов превышает скорость света в вакууме.
Здесь мы не сталкиваемся с теми трудностями, которые существуют в СТО. С Земли, глядя вверх, мы будем видеть, что скорость движения мезонов зависит от угла наблюдения (11.1.1) и «время жизни» уже не будет постоянным. Оно также будет зависеть от угла наблюдения.
В классической теории Ньютона взаимодействие протекает объективно и его описание не зависит от выбора наблюдателем системы отсчета. В отличие от ньютоновской теории теорию относительности можно назвать теорией одного наблюдателя. Действительно, как только при описании процессов мы вводим других наблюдателей, покоящихся в разных инерциальных системах, между их показаниями возникают противоречия.
Рассмотрим пример: наблюдение движущегося объекта несколькими наблюдателями.
Пусть светящийся объект движется вдоль оси х
с лоренцевской скоростью v
(галилеевская, соответственно, V
). Расположим вдоль оси х
наблюдателей на равном расстоянии L
. Каждый наблюдатель будет видеть картину, изображенную на рис. 11.2, но с запаздыванием на некоторое время Т
относительно картины предыдущего наблюдателя.
Наблюдатели имеют часы (синхронизированные
! – показывающие одно время). В момент прохождения объектом зенита каждый наблюдатель засекает время, а затем они определяют время Т
прохождения участка L
.
Как связано время пролета Т
с указанными на рис. 11.2 скоростями? Здесь могут быть только два ответа: либо L
= v T
, либо L
= V T.

Рис. 11.2
Рассмотрим первый вариант. Пусть объект проходит расстояние от первого наблюдателя до второго. У всех четырех наблюдателей показания окажутся разными, не укладывающимися в формулу L
= v T
. Тот же эффект будет, если объект перемещается от второго наблюдателя к третьему и т.д. Аналогичную ситуацию мы рассматривали выше при объяснении ситуации с μ-мезонами. Там релятивисты настаивали на «увеличении» времени жизни μ-мезона. Но эти ссылки неуместны, поскольку время для всех инерциальных систем едино
.
Остается второй вариант: отрезок между соседними наблюдателями объект проходит с галилеевской скоростью V
.
11.3 Проблемы вращательного движения
Обычно, критикуя СТО А.Эйнштейна, рассматривают парадокс близнецов. Но есть весьма широкая область, где СТО вообще не может дать серьезных объяснений. Это область вращательных движений. Здесь парадоксов не меньше.
Рассмотрим вращающийся диск (рис. 11.3а
). Пусть ось вращения диска совпадает с осью z
. При малых угловых скоростях линейная скорость пропорциональна радиусу.

Рис. 11.3
По мере увеличения угловой скорости возрастает линейная скорость периферийных слоев, которая в соответствии со СТО не может превышать скорость света. По этой причине угловая скорость внешних слоев будет меньше, чем внутренних. Это должно привести к возникновению внутренних напряжений и, в конечном счете, к разрушению диска. Такова суть парадокса Эренфеста.
Прежде, чем переходить к другому парадоксу, процитируем [3]:
«Здесь же полезно провести простое рассуждение, наглядно иллюстрирующее неизбежность возникновения неевклидовости пространства при переходе к неинерциальным системам отсчета. Рассмотрим две системы отсчета, из которых одна (К) инерциальна, а другая (К') равномерно вращается относительно К вокруг общей оси z. Окружность в плоскости x, y системы К (с центром в начале координат) может рассматриваться и как окружность в плоскости x', y' системы К'. Измеряя длину окружности и ее диаметр масштабной линейкой в системе К, мы получаем значения, отношение которых равно
π, в соответствии с евклидовостью геометрии в инерциальной системе отсчета. Пусть теперь измерение проводится неподвижным относительно K' масштабом. Наблюдая за этим процессом из К, мы найдем, что масштаб, приложенный вдоль окружности, претерпевает Лоренцево сокращение, а радиально приложенный масштаб не меняется. Ясно поэтому, что отношение длины окружности к ее диаметру, полученное в результате такого измерения, оказывается больше
π»
Проиллюстрируем этот вывод. Итак, пусть по краю диска на равном расстоянии размещены 10 лампочек (рис. 11.3b
). При релятивистских скоростях расстояние между ними должно уменьшаться. Если v
/ c
≈ 0,6, то, сфотографировав диск, мы должны увидеть на снимке 12 лампочек. Какие из них сумели «сфотографироваться» дважды?
Обратимся теперь к рис. 11.2. Если условно «развернуть» круговое движение тела в прямолинейное, то наблюдатель (покоящийся на оси вращения) как бы мгновенно «перескакивает» из положения «наблюдатель № 1» к положению «наблюдатель № 2» и так далее (см. рис. 11.2). Он будет видеть движение объекта с галилеевской скоростью, причем угол аберрации сохраняется для него постоянным
. Объект наблюдения будет всегда находиться в зените, т.е. на линии, перпендикулярной траектории. Никакой лоренцевской скорости он не обнаружит и не измерит.
Этот парадокс имеет непосредственное отношение к работе ускорителей элементарных частиц. Пусть заряженная частица влетает в область однородного магнитного поля и далее движется по окружности. Здесь возможны 3 варианта интерпретации движения (рис. 11.4). Рассмотрим их.

Рис. 11.4
Вариант первый.
Рассмотрим сначала классический способ отображения. Частица, летящая с галилеевской скоростью V,
подлетает к точке А
и затем с той же скоростью движется по окружности в магнитном поле.
Вариант второй
. Отображение с помощью световых лучей
имеет особенность. К точке А
частица подлетает с лоренцевской скоростью v
(наблюдаемая, кажущаяся скорость). После ее прохождения частица мгновенно принимает галилеевскую скорость V
и с этой скоростью движется по окружности. Здесь мы будем наблюдать галилеевскую скорость даже с помощью световых лучей.
Вариант третий
- современный подход. Частица (как до точки А
, так и после нее) имеет лоренцевскую скорость движения v
. Кажется, что непрерывность скорости здесь существует. Но, как мы показали выше, это самообман: лоренцевская скорость есть кажущаяся скорость (наблюдаемая с помощью световых лучей). При такой интерпретации скорость должна испытывать скачок в точке А
. Это необходимо учитывать при анализе циклических ускорителей.
Мы процитируем критические замечания А.В. Мамаева [4], касающиеся работы циклических ускорителей. Хотя мы по разному относимся к решению релятивистских проблем, но его критические замечания считаем квалифицированными. Мамаев следующим образом оценивает характеристики армянского ускорителя (синхротрон АРУС) и объяснение его работы. Цитируем:
«Интересующие нас технические характеристики электронного синхротрона АРУС имеют следующие значения. (Быстров Ю. А., Иванов С. А. Ускорительная техника и рентгеновские приборы. - М.: Высшая школа,
1983. - с.
159 - - 162):
• - длина орбиты
2πR = 216,7 м;
• - энергия инжекции электронов W =
50 МэВ;
• - частота ускоряющего поля f =
132,8 МГц;
• - кратность ускорения g =
96;
• - энергия покоя электрона E0
=
0,511 МэВ.
Согласно формуле
(10.4), вытекающей из специальной теории относительности, частота обращения электронных сгустков по орбите ускорителя АРУС в момент инжекции электронов при кинетической энергии электронов W
= 48,55 МэВ будет равна
 f
SRT
==1,3843МГц
(11.9) W f
SRT
==1,3843МГц
(11.9) W
2πR
( +1) E
А согласно формуле
(10.3), вытекающей из новой теории пространства-времени, частота обращения электронных сгустков по орбите ускорителя АРУС в момент инжекции электронов с кинетической энергией W =
48,55 МэВ будет равна
 c
0
(1+W
/ E
0
) 2
−1 c
0
(1+W
/ E
0
) 2
−1
f
==132,8МГц
(11.10)
2πR
т. е. по новой теории пространства-времени частота обращения электронных сгустков в ускорителе АРУС в момент инжекции электронов точно равна частоте ускоряющего поля.
Но в настоящее время специальная теория относительности считается абсолютно истинной теорией и поэтому частота обращения электронных сгустков в момент инжекции электронов в ускоритель АРУС считается равной значению
1,3843МГц, рассчитанному по формуле
(11.9), вытекающей из специальной теории относительности.
Однако если на траектории движения электронных сгустков в ускорителе АРУС установить мишень, то период облучения этой мишени электронными сгустками при W =
48,55 МэВ окажется равным не величине
TСТО
= 1/fСТО
=
1/(1,3843 MГц
) =
722,39 нс
(11.11) соответствующей частоте обращения
1,3843 МГц, а величине
T = 1/f =
1/(132,8 MГц
) =
7,53 нс,
(11.12)
т. е. величине, соответствующей частоте обращения сгустков по новой теории пространства-времени.
Но период
7,53 нс обращения электронных сгустков по орбите длиной
216,7 м означал бы, что электроны движутся со скоростью, в
96 раз большей скорости света c
0
. Согласно же специальной теории относительности сверхсветовые скорости электронов невозможны.
Поэтому для того, чтобы объяснить экспериментальное значение периода облучения мишени
7,53 нс в рамках специальной теории относительности, потребовалось ввести понятие "кратность ускорения
" и объявить, что "под действием ускоряющего поля частицы инжектированного пучка распадаются на сгустки, группирующиеся вокруг устойчивых равновесных фаз. Число таких сгустков, располагающихся по окружности ускорителя, равно кратности ускорения g
". (Бурштейн Э. Л. Ускорители заряженных частиц // Большая советская энциклопедия,
3-е изд., т.
27. - М.: Советская энциклопедия,
1977. - с. 108).
И действительно, разделив величину из выражения
(11.11) на величину из выражения
(11.12), получим g =
96 - кратность ускорения электронного синхротрона АРУС. А, разделив величину из выражения
(11.6) на величину из выражения
(11.7), получим, что кратность ускорения протонного синхротрона ЦЕРН в эксперименте равна
19.
(Test of the second postulate of special relativity in the GeV region / Alvager T., Farley F., Kjellman J., Wallin J. // Physical Letters. -
1964. - v.
12. –No.
3. - p.
260 -262)
Таким образом, экспериментальные значения частоты обращения сгустков элементарных частиц в рассмотренных двух ускорителях подтверждают не формулу
(11.4) из специальной теории относительности, а формулу
(11.3) из новой теории пространства-времени. Для объяснения же экспериментальных значений частоты обращения сгустков элементарных частиц в рамках специальной теории относительности и согласования этих значений с формулой
(11.4) используется специальная гипотеза, основанная на введении ad hoc понятия "кратность ускорения"».
Мы уже говорили, что современное объяснение работы циклических ускорителей опирается на третий вариант. В результате физики сталкиваются с проблемой «скачка реальной скорости
» в точке А
(рис. 11.4 а
, с
), которая появляется в третьем варианте. Вот и приходится теоретикам вводить гипотезу ad hoc
о существовании кратности ускорения – g.
На самом деле никакого «распада
на сгустки
, группирующиеся вокруг устойчивых равновесных фаз
» в синхротроне не существует. Это домысел.
Действительные (галилеевские) скорости частиц превышают скорость света в вакууме.
11.4 Класс преобразований
Мы поставим следующую задачу. Будем искать класс преобразований 4-координат, при которых уравнения Максвелла сохраняют свою форму в соответствии с принципом Галилея-Пуанкаре [5]. Задача существования преобразования уже решена, т.к. существует преобразование Лоренца.
Фактически задача сводится к сохранению неизменной формы оператора волнового
1 ∂ 2
уравнения Δ −  2 2
= 0 при переходе из одной инерциальной системы отсчета в другую. с
∂t 2 2
= 0 при переходе из одной инерциальной системы отсчета в другую. с
∂t
Это согласуется с принципом Галилея-Пуанкаре.
Рассмотрим две инерциальные системы отсчета К
и К'
, которые движутся друг относительно друга с галилеевской скоростью V
. Пространственно-временные координаты системы К
(x
;y
;z
;ct
) должны быть связаны с соответствующими координатами К'
(x'
;y'
;z'
;ct'
) с помощью матрицы преобразования T
(V
/c
).
X' = T(V
/c
)⋅ X (11.4.1)
где: X
и X'
- вектор-столбцы 4-координат систем K
и K'
; Т
(V
/c
) - матрица преобразования, зависящая только от скорости относительного движения сравниваемых инерциальных систем.
К матрице Т
предъявляются следующие требования:
c. Определитель матрицы должен быть равным единице; det T
= 1.
d. Должна существовать матрица обратного преобразования для перехода из K'
в K,
т.е. матрица Т-
1
(V
/c
).
e. Матрица обратного преобразования должна получаться заменой V
на -V
в матрице
T
(V
/c
). Это следует из равноправия инерциальных систем отсчета T
(V
/c
)-1
= T
(-V
/c
).
Из этих условий можно определить общий вид матрицы преобразований координат и времени, сохраняющей инвариантную форму уравнений Максвелла. Уравнения (4.1), удовлетворяющие сформулированным условиям, можно записать в следующей форме:
x
= x
' 1+ f
2
(V
/ c
) − ct
' f
(V
/ c
); y
= y
';
 (11.4.2) z
= z
'; ct
= ct
' 1+ f
2
(V
/ c
) − x
' f
(V
/ c
) (11.4.2) z
= z
'; ct
= ct
' 1+ f
2
(V
/ c
) − x
' f
(V
/ c
)
где f
(V
/c
) есть некоторая нечетная функция относительно V
/c.
Выражение (11.4.2) есть обобщенное
преобразование. При малых V
/c
функция f
≈ V
/c.
Перечисленных выше условий не достаточно, чтобы определить явный вид функции f
(V
/c
). Она может быть V
/c,
или sin(V
/c
), или sh(V
/c
) и т.д. В частном случае, когда
 f
= v
/ c
2
− v
2
, мы получаем преобразование Лоренца.
Если же f = V
/c ,
то получим f
= v
/ c
2
− v
2
, мы получаем преобразование Лоренца.
Если же f = V
/c ,
то получим
модифицированное преобразование. При малых значениях V
/c
эти функции стремятся к
V
/c.
К сожалению, сейчас не ясно: какой вид имеет функция f
(V
/c
)? Экспериментальных исследований никем не проводилось.
Заметим, что помимо рассмотренных выше существуют преобразования, связанные с вращательным движением, при которых оператор волнового уравнения сохраняет свою форму. Пусть ось вращения неинерциальной системы отсчета совпадает с осью z
. Преобразование для вращения вокруг оси z
имеет вид:
 2
ct
' ϕ = ϕ' 1+ f
(ω0
R
/ c
) − f
(ω0
R
/ c
); R
R
= R
'; z
= z
'; 2
ct
' ϕ = ϕ' 1+ f
(ω0
R
/ c
) − f
(ω0
R
/ c
); R
R
= R
'; z
= z
';
 ct
= ct
' 1+ f
2
(ω0
R
/ c
) − R
ϕ' f
(ω0
R
/ c
) ct
= ct
' 1+ f
2
(ω0
R
/ c
) − R
ϕ' f
(ω0
R
/ c
)
где: ϕ’ - угол поворота; ω0
- угловая скорость вращения неинерциальной системы отсчета.
Имеет ли физический смысл это преобразование, и какой? - предстоит выяснить в будущем.
Источники информации:
1. Кулигин В.А., Кулигина Г.А.,.Корнева М.В. Преобразование Лоренца и теория познания. / Воронеж. ун-
т. - Воронеж, 1989. Деп. в ВИНИТИ 24.01.89, № 546.
2. Кулигин В.А., Кулигина Г.А.,.Корнева М.В. От явления к сущности теории относительности http://nt.ru/tp/ns/ys.htm
3. Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: Физматгиз, 1961.
4. Мамаев А.В..
Высшая физика. (Эксперимент на электронном синхротроне АРУС) http://www.acmephysics.narod.ru/b_r/r10.htm
5. Кристиан Маршаль. Решающий вклад Анри Пуанкаре в специальную теорию относительности (Перевод с английского Ю. В. Куянова). Препринт ИВФЭ, - Протвино, 1999.
Введение
В современной физической литературе очень часто говорится о «блестящем математическом формализме», положенном в основу релятивистских теорий и, в частности, в основу Специальной теории относительности (СТО). Механика СТО разрабатывалась как обобщение принципа Гамильтона для 4-пространства. Главная цель Главы 12 – провести математический анализ этого обобщения.
12.1 Классический интеграл действия
Мы начнем с краткого описания классического интеграла действия, чтобы затем использовать его для сравнения с релятивистским интегралом действия. Классический интеграл действия имеет следующий вид:
t
2
S
= ∫ L
(r
,v
)dt
(12.1.1)
t
1
где L
= K
– U
– функция Лагранжа для частицы, на которую действует внешнее поле; K
– кинетическая энергия частицы и U
– потенциальная энергия взаимодействия.
Заметим, что точки t
1
и t
2
жестко фиксированы. Интеграл действия имеет минимум δS
= 0, если интегрирование ведется вдоль траектории частицы. Чтобы определить траекторию частицы мы должны получить из интеграла действия уравнение ее движения (уравнение Эйлера). Это уравнение ищется путем варьирования координаты частицы r
так, чтобы выполнялось условие минимума интеграла действия (12.1.1): δS
= 0. При этом время t
рассматривается как постоянный параметр: δt
= 0. Окончательная форма вариации интеграла действия имеет вид:
 t
2
⎛ ∂L d
∂L
⎞ δS
= ∫
t
1 ⎜⎝ ∂
r
− dt
∂
v
⎟⎠
δr
dt
(12.1.2) t
2
⎛ ∂L d
∂L
⎞ δS
= ∫
t
1 ⎜⎝ ∂
r
− dt
∂
v
⎟⎠
δr
dt
(12.1.2)
Поскольку δr
это произвольная переменная, условие δS
= 0 выполняется, если равно нулю подынтегральное выражение. При этом выражение в скобках в (12.1.2) и вариация независимой переменной δr
не являются ортогональными
по отношению друг к другу за исключением, быть может, конечного числа точек траектории. Окончательно имеем уравнение движения, определяющее траекторию частицы (12.1.3) d
∂L
∂L
 = (12.1.3) dt
∂v
∂r = (12.1.3) dt
∂v
∂r
Интеграл действия имеет минимум, когда траектория частицы описана этим уравнением.
12.2 Интеграл действия в Специальной теории относительности
Исторически математический формализм релятивистской механики строился по образу и подобию формализма классической, опираясь на принцип соответствия между релятивистской и классической механиками при v
<< с
и принцип наименьшего действия.
При этом по утверждению апологетов теории относительности, форма математических операторов и уравнений в релятивистской механике сохраняется, а при v
<< с
релятивистская механика должна переходить в классическую. Поэтому форма релятивистского интеграла действия должна быть подобна (12.1.1). Как уже было установлено, такого перехода в действительности не существует.
s
1 2
S
=  ∫
L
(x
i
,u
i
)ds
(12.2.1) ∫
L
(x
i
,u
i
)ds
(12.2.1)
c
s
1
где: L
– функция Лагранжа для частицы, на которую действует внешнее поле; с
– скорость света; xi
– 4-координата частицы (ict
, x
, y
, z
); ui
– 4-вектор скорости частицы.
 ds
= − (dx
i
)2
= c
2
dt
2
− dx
2
− dy
2
− dz
2
(12.2.2) ds
= − (dx
i
)2
= c
2
dt
2
− dx
2
− dy
2
− dz
2
(12.2.2)
Известно, что 4-координата xi
зависит от s
, и при дифференцировании ее по s
мы имеем 4скорость частицы.
 dx
i dx
i
x
i
= x
i
(s
), u
i
= = u
i
(s) (12.2.3) ds
Таким образом, параметр s
должен играть ту же роль, что и параметр t
в классической теории.
Изучая литературу, мы столкнулись с двумя вариантами построения интеграла действия релятивистской механики, которые будут рассмотрены ниже.
Первый вариант.
Он изложен в [1], [2]. Здесь параметр s
подобен параметру t
в классической механике. При варьировании интеграла действия он остается неизменным (δds
= 0). В результате мы имеем уравнение движения частицы по форме полностью соответствующее классическому уравнению (12.1.3) (Приложение 1). d
∂L
∂L
 = (12.2.4) ds
∂u
i
∂x
i = (12.2.4) ds
∂u
i
∂x
i
Итак, внешняя форма соблюдена, и мы можем рассмотреть ее содержание на конкретном примере. Авторы [2] для заряда в магнитном поле предлагают следующее выражение функции Лагранжа:
 m
0c
2u
i
2 m
0c
2u
i
2
L
= + eu
i
A
i
(12.2.5) 2
где: е
и m
заряд и масса заряда соответственно; Ai
– 4-потенциал электромагнитного поля.
Используя уравнение (12.2.4), нетрудно найти следующее уравнение движения для заряда:
  dsd
( 2 ) ⎛ ∂A
i
∂A
k
⎞⎟⎟u
k
(12.2.6) dsd
( 2 ) ⎛ ∂A
i
∂A
k
⎞⎟⎟u
k
(12.2.6)
m
0c u
i
= e
⎜⎜∂x
k
− ∂x
i
⎠
⎝
Это и есть релятивистское уравнение движения, которое при v
<< с
переходит в известное классическое уравнение: d
v
d
A
m
 = −e
gradφ− e = −e
gradφ− e
 + e
v
×rotA
, dt dt
где А
и φ – потенциалы электромагнитного поля; v
– скорость заряда. + e
v
×rotA
, dt dt
где А
и φ – потенциалы электромагнитного поля; v
– скорость заряда.
Казалось бы, все прекрасно, но существует обстоятельство, свидетельствующее не в пользу этого варианта. В СТО есть одно важное тождество
(u
i
)2
+1= u
t
2
− u
x
2
− u
2
y
− u
z
2
+1= 0 (12.2.7)
Учитывая это соотношение, можно показать, что выражение (12.2.5) фактически не соответствует
своему классическому аналогу.
 m
0
c
2 m
0
c
2
L
1
= − + eu
i
A
i
= L
(12.2.8)
2
Очевидно, что из него мы не можем получить уравнение движения (12.2.6).
Более того, мы можем записать много других новых функций Лагранжа, которые равны предшествующей функции Лагранжа (12.2.5), и из них мы можем получить много других различных уравнений движения. Например, пусть функция Лагранжа равна:
1 2 2K K
+1 2N
+1 N
( 2 ) m
0c
2u
i
2
L
2
=  m
0
c u
i
(−1) + eu
i
(−1) A
i
+ u
i
+1Φ(x
i
,u
i
) = L
= m
0
c u
i
(−1) + eu
i
(−1) A
i
+ u
i
+1Φ(x
i
,u
i
) = L
=  + eu
i
A
i
(12.2.9) + eu
i
A
i
(12.2.9)
2 2
где: N
и K
– некоторые положительные целые числа (N
, K
= 0; 1; 2;...); Ф (xi
; ui
) – произвольная скалярная функция, зависящая от ; xi
и ui
.
Теперь уравнение движения будет отлично от (12.2.6).
  dsd
[ 2
] ⎛⎝ ∂A
i
∂A
m
⎞⎟⎟
u
m
(12.2.10) m
0
c Ku
+ 2NeA
i
+ 2Φ(x
i
,u
i
)u
i
= e⎜⎜∂
x
m
− ∂
x
i
⎠ dsd
[ 2
] ⎛⎝ ∂A
i
∂A
m
⎞⎟⎟
u
m
(12.2.10) m
0
c Ku
+ 2NeA
i
+ 2Φ(x
i
,u
i
)u
i
= e⎜⎜∂
x
m
− ∂
x
i
⎠
Итак, мы можем получить много различных
уравнений движения, изменяя K
, N
и Φ. Почему – это имеет место?
Возможно, что переменная s
в СТО не может рассматриваться как независимая переменная подобно t
в механике Ньютона. С одной стороны, s
зависит от xi
(2.2), с другой, xi
должен зависеть от s
(12.2.3). Благодаря этому, требование для вариационного исчисления нарушено. Как результат, рассмотренный вариант не может служить основой для математического формализма СТО.
В отличие от классической механики релятивистский интеграл действия дает множество различных уравнений движения, и неизвестно: какое из них отвечает объективной реальности?
Второй вариант.
Другая версия интеграла действия приводится в учебнике [3]. Авторы [3] учитывают, что s
зависит от xi
. Они дают новый интеграл действия:
s
2 s
2 s
1 2
1 2
1 2
S
=  ∫
1 (−m
0
c ds
+ eA
i
dx
i
) = ∫
1 (−m
0
c ds
+ eA
i
dx
i
) =  c
∫
s
1 (−m
0
c
+ eA
i
u
i
)ds
= c
∫
s
1 (−m
0
c
+ eA
i
u
i
)ds
=  c
∫
s
1 Lds
(12.2.12) c
s c
∫
s
1 Lds
(12.2.12) c
s
Теперь правильный классический предел имеет место:
t
2
2
 ⎛ m
0
v
⎞⎟⎟dt
(12.2.13) S
= ∫
1 ⎜⎜⎝ 2 − e
ϕ + e
v
⋅A
⎠ ⎛ m
0
v
⎞⎟⎟dt
(12.2.13) S
= ∫
1 ⎜⎜⎝ 2 − e
ϕ + e
v
⋅A
⎠
t
Однако здесь мы сталкиваемся с другой проблемой. Новая общая форма уравнения движения отличается от классической (см. Приложение 1). Более того, нарушение единственности решения также имеет место
d
⎛ ∂L
∂L
⎞ ∂L
 ⎜⎜∂u
i
− Lu
i
+ ⎜⎜∂u
i
− Lu
i
+  ∂u
k u
ku
i
⎟⎠⎟ = ∂u
k u
ku
i
⎟⎠⎟ =  ∂x
i
(12.2.14) ∂x
i
(12.2.14)
ds
⎝
Итак, второй вариант также имеет трудности:
1. Основная форма уравнения движения отличается от классической.
2. Мы имеем бесконечный ряд уравнений движения.
12.3 Ортогональность, но не произвольность
Чтобы понять причины неудач релятивистского обобщения интеграла действия, рассмотрим общий вид вариации интеграла действия для двух вариантов.
Первый вариант
[1], [2].
Он определяется условием δds
= 0.
s
2 s
2 s
2 dL
δS
= δ∫1
Lds
=∫s
1 δLds
= ∫s
1  ds
δsds
(12.3.1) ds
δsds
(12.3.1)
s
 dL
∂L du
i
∂L
∂L dL
∂L du
i
∂L
∂L
где = + u
i
+ ds
∂u
i
ds
∂x
i
∂s
Проинтегрируем выражение (12.3.1) по частям.
s
2
s
2
δS
= L
δs
 s
1 − ∫ Ld
δs
= 0 (12.3.2) s
1 − ∫ Ld
δs
= 0 (12.3.2)
s
1
Первый член правой части равен нулю, поскольку концы траектории s
1
и s
2
жестко фиксированы и вариация в этих точках равна нулю по условиям вариации. Интеграл также равен нулю в силу соотношения δds
= 0.
Отсюда следует, что интеграл действия не имеет экстремумов. Его значение зависит только от пределов интегрирования и не зависит от формы траектории частицы. Принцип наименьшего действия не имеет места
.
Второй вариант
[3].
В этом варианте вариация δds
≠ 0. Запишем вариацию интеграла действия для этого варианта.
s
2 s
2 s
2
δS
= δ∫s
1 Lds
=∫s
1 (δLds
+ L
δds
)= ∫
s
1 ⎜⎛
⎝  dL
ds
δsds
+ L
δds
⎞
⎟⎠ (12.3.3) dL
ds
δsds
+ L
δds
⎞
⎟⎠ (12.3.3)
Как и в предыдущем случае, мы проинтегрируем первый член в интеграле действия по частям.
s
2
s
2
δS
= L
δs
 s
1 + ∫(−Ld
δs
+Ld
δs
) = 0 (12.3.4) s
1 + ∫(−Ld
δs
+Ld
δs
) = 0 (12.3.4)
s
1
Очевидно, что первый член правой части равен нулю по указанным ранее причинам, а второй должен быть тождественно равен нулю по результату интегрирования.
Следовательно, для второго варианта справедливы те же выводы. Интеграл действия для второго варианта не имеет экстремумов. Его значение зависит только от пределов интегрирования и не зависит от формы кривой.
Принцип наименьшего действия не имеет места.
 Теперь нам необходимо понять причину постоянства интеграла действия. Рассмотрим изменение длины отрезка xi
при бесконечно малой вариации δxi
и δs
(i
)
= − (δx
i
)2
≠ 0. Теперь нам необходимо понять причину постоянства интеграла действия. Рассмотрим изменение длины отрезка xi
при бесконечно малой вариации δxi
и δs
(i
)
= − (δx
i
)2
≠ 0.
x
k
= x
i
+ δx
i
(12.3.5) Вычислим длину отрезков.
s
(k
)
= s
(i
)
− x
i
δx
i
(12.3.6)
С другой стороны, изменение 4-отрезка в рамках преобразования Лоренца не может быть произвольным. Существует жесткое условие:
x
k
= αki
x
i
(12.3.7) где αki
– матрица преобразования Лоренца или обобщенного преобразования.
Из (12.3.7) следует, что длины сравниваемых отрезков (как истинные скаляры) должны быть равны друг другу, т.е. s
(k
) = s
(i
).
Сравнивая это соотношение с выражением (12.3.6), получим xi
δxi
= 0. Иными словами, вариация δxi
всегда должна быть ортогональна 4-вектору xi
. Это соответствует обычному повороту 4-вектора в 4-пространстве или переводу 4-вектора из одной инерциальной системы отсчета в другую.

Рис. 12.1
Пределы интегрирования s
1
и s
2
представляют собой две концентрических 4-поверхности, в которые «упираются» концы траектории частицы. При варьировании траектории эти концы свободно скользят по указанным поверхностям. Сама же траектория не претерпевает никаких изменений. Она вращается в 4-пространстве. В классическом интеграле действия концы траектории жестко «зафиксированы» в точках t
1
и t
2
, а траектория изменяется.
Математический формализм Специальной теории относительности часто именуют «теорией инвариантов»
. В классической теории интеграл действия инвариантен относительно преобразования Галилея. Именно релятивистские инварианты (относительно преобразования Лоренца) являются слагаемыми современной формы релятивистской функции Лагранжа. Как известно, любой релятивистский инвариант сохраняет неизменным свое значение при повороте в 4-пространстве (при переходе из одной инерциальной системы в другую). Следовательно, вариация любого инварианта, образованного 4-вектором, всегда ортогональна
этому 4-вектору. Например, вариация квадрата 4-вектора скорости (инвариант) равна нулю.
δu
i
2
= 2u
i
δu
i
= 2δ(−1) = 0
Таким образом, изменение релятивистского интеграла действия всегда равно нулю не в силу произвольности вариации, а в силу ортогональности
4-вариации уравнению движения. Это справедливо для каждого
релятивистского инварианта.
Чтобы подтвердить этот вывод, запишем из [3] конечное выражение, из которого получают формулу Лоренца.
s
2 s
2
  δS
= ∫s
1 ⎡⎢⎣− mc
du
i
+ e
⎛
⎜ dA
k
− dA
i
⎟⎟⎞⎥
⎤δx
i
ds
=∫
1 ⎡⎢
− mc
du
ds
i
+ e
⎜⎝⎛
⎜ dA
dx
k
i
− dx
dA
k
i
⎞
⎟⎟⎠⎦⎥
⎤u
i
δsds
(12.3.8) δS
= ∫s
1 ⎡⎢⎣− mc
du
i
+ e
⎛
⎜ dA
k
− dA
i
⎟⎟⎞⎥
⎤δx
i
ds
=∫
1 ⎡⎢
− mc
du
ds
i
+ e
⎜⎝⎛
⎜ dA
dx
k
i
− dx
dA
k
i
⎞
⎟⎟⎠⎦⎥
⎤u
i
δsds
(12.3.8)
ds
⎝⎜ dx
i dx
k
⎠⎦ s
⎣
Убедимся, что вариация интеграла равна нулю не в силу произвольности δxi
.= ui
δs
, а в силу ортогональности уравнения движения (выражение в квадратных скобках) и δxi
.
2
 du
i
d
(u
i
) d
⎛
1
⎞ du
i
d
(u
i
) d
⎛
1
⎞
a)
− mc
 u
i
= −mc
= mc
⎜ ⎟ = 0 ds
2ds ds
⎝ 2⎠ u
i
= −mc
= mc
⎜ ⎟ = 0 ds
2ds ds
⎝ 2⎠
(12.3.9)
b)
 e
⎛⎜ dA
k dA
i
⎞⎟⎟u
iu
k
= e
⎜⎜⎛ e
⎛⎜ dA
k dA
i
⎞⎟⎟u
iu
k
= e
⎜⎜⎛  dAdx
ki u
iu
k
− dAdx
ki u
iu
k
−  dxdA
ki u
iu
k
⎟⎠⎞⎟ = ⎜⎜⎝⎛ dxdA
ki u
iu
k
⎟⎠⎞⎟ = ⎜⎜⎝⎛  dxdA
ki u
ku
i
− dxdA
ki u
ku
i
−  dxdA
ki u
iu
k
⎠⎟⎟⎞ = 0 dxdA
ki u
iu
k
⎠⎟⎟⎞ = 0
⎜ dx
i
− dx
k
⎠ ⎝
⎝
В выражение (12.3.9) входят скалярные слагаемые, и мы имеем право заменить одновременно индексы i
на k
, а k
на i
в первом слагаемом. Именно благодаря ортогональности
мы получаем счетное множество уравнений движения, поскольку к любому уравнению движения мы можем добавить произвольное слагаемое, ортогональное к δxi
. Вариация интеграла действия от этой процедуры не изменится и будет всегда равна нулю.
Обобщение.
Рассмотренные выше выводы оказываются справедливыми и для интегралов действия, использующих плотность функции Лагранжа для получения уравнений полей.
 1
⎛ ∂
A
i
⎞
⎟ 1
⎛ ∂
A
i
⎞
⎟
S
= ic
∫Λ⎜⎜⎝∂x
k
; A
i
; ...⎟⎠d
Ω (12.3.10)
где: Λ – плотность функции Лагранжа; d
Ω – элементарный 4-объем (dx·dy·dz·icdt
).
Как мы писали выше, вариация любого инварианта, входящего в функцию Лагранжа, всегда ортогональна
к вектору, образующему инвариант. Приведем примеры. Инвариант мы будем обозначать символом I.
2 2
   ⎛⎝ ∂A
i
⎞⎟⎟ ; δ⎛⎜⎜ ∂∂xA
ki
⎟⎟⎠⎞ = 2 ∂∂xA
ki
δ ∂∂xA
ki
= δI
1 = 0 и т.д. ⎛⎝ ∂A
i
⎞⎟⎟ ; δ⎛⎜⎜ ∂∂xA
ki
⎟⎟⎠⎞ = 2 ∂∂xA
ki
δ ∂∂xA
ki
= δI
1 = 0 и т.д.
I
1 = ⎜⎜ ∂x
k
⎠ ⎝
I
2
= F
ik
[1]
; δF
ik
2
= 2F
ik
δF
ik
= δI
2
= 0 где Fik
– тензор электромагнитного поля.
Неоднозначность уравнений движения можно проиллюстрировать, сравнивая вариацию одного и того же инварианта в разных формах его записи.
I
= j
k
A
k
; δI
= j
k
δA
k
= 0
I
= 5 j
k
A
k
-4I
; δI
= 5j
k
δA
k
-4δI
= 5 j
k
δA
k
= 0 где jk
не зависит от Ak
.
Мы видим различные коэффициенты при произведении jk
δAk
.
Следовательно, уравнения для электромагнитных и гравитационных полей, которые были получены с помощью «релятивистского принципа наименьшего действия», неоднозначны,
а потому весьма сомнительны. Неоднозначными являются и законы сохранения. «Блестящий математический формализм», которым всегда так гордились апологеты релятивистских теорий, на деле оказывается некорректным. Мефистофель, видимо, решил посмеяться над незадачливыми физиками-позитивистами.
Приложение 1.
Доказательство нового уравнения движения Рассмотрим первый
вариант. [1], [2].
s
δu
i
= δ(dx
i
/ds
) = (ds
δdx
i
− dx
i
δds
)/ds
2
= δdx
i
/ds
(П.11.2) Теперь, после интегрирования выражения (П. 11.1) по частям, получим
s
2 s
2
∂L
⎡∂L d
∂L
⎤
  dS
= δx
i
−
∫ ⎢ −
⎥
δx
i
ds
= 0 (П. 11.3) ∂u
i
s
1 s
1 ⎣∂x
i
ds
∂u
i
⎦ dS
= δx
i
−
∫ ⎢ −
⎥
δx
i
ds
= 0 (П. 11.3) ∂u
i
s
1 s
1 ⎣∂x
i
ds
∂u
i
⎦
Первый член в правой части равен нулю, поскольку концы траектории закреплены и вариация в конечных точках должна быть равна нулю. В силу произвольности δxi
выражение в квадратных скобках под интегралом должно быть равно нулю. d
∂L
∂L
 = (П.11.4) ds
∂u
i
∂x
i = (П.11.4) ds
∂u
i
∂x
i
Это есть уравнение движения для первого варианта.
Теперь рассмотрим второй
вариант [3].
Запишем вариацию интеграла действия для этого случая.
s
2
s
2
⎡ ∂L
∂L
⎤
δS
= ∫(ds
δL
+ L
δds
) =∫ ⎢ds
 δx
i
+ ds δx
i
+ ds
 δu
i
+ L
δds
⎥
=0 (П.11.5) s
1 s
1 ⎣ ∂x
i
∂u
i
⎦ δu
i
+ L
δds
⎥
=0 (П.11.5) s
1 s
1 ⎣ ∂x
i
∂u
i
⎦
Сначала мы сделаем следующие промежуточные вычисления
a) δds
= −dx
i
δdx
i
/ds
= −u
i
δdx
i
(П.11.6)
δu
i
= δ(dx
i
/ds
) = (ds
δdx
i
− dx
i
δds
)/ds
2
=
б) (П.11.7)
= (ds
δdx
i
+ dx
i
dx
k
δdx
k
)/ds
2
Учитывая (П.11.6) и (П.11.7), получим:
s
2
⎡∂L
⎛ ∂L
∂L
⎞ ⎤
 δS
= ∫
s
1 ⎢⎣ δS
= ∫
s
1 ⎢⎣  δx
i
ds
+ ⎜⎜ ∂u
i
+ ∂u
k u
k
u
i
− Lu
i
⎠⎟⎟δdx
i
⎥⎦ = 0 (П.11.8) δx
i
ds
+ ⎜⎜ ∂u
i
+ ∂u
k u
k
u
i
− Lu
i
⎠⎟⎟δdx
i
⎥⎦ = 0 (П.11.8)
∂x
i
⎝
После интегрирования выражения в круглых скобках в (П.11.8) по частям находим уравнение движения:
d
⎛ ∂L
∂L
⎞ ∂L
 ds
⎜⎜
∂
u
i
+ ∂
u
k u
k
u
i
− Lu
i
⎟
⎠
⎟ = ds
⎜⎜
∂
u
i
+ ∂
u
k u
k
u
i
− Lu
i
⎟
⎠
⎟ =  ∂
x
i
(П.11.9) ⎝ ∂
x
i
(П.11.9) ⎝
Источники информации:
1. Г. Голдштейн. Классическая механика. – М.: Наука, 1975.
2. В.К. Пановски, М. Филлипс. Классическая электродинамика. – М: Мир, 1975.
3. Л.Д. Ландау, Е.М. Лифшиц. Теория поля. – М: Физматгиз, 1961.
4. В.А. Кулигин. Интеграл действия релятивистской механики./ Проблемы пространства, времени, тяготения. С.-Петербург.: Политехника, 1997.
Введение
Наиболее распространенным вариантом, альтернативным СТО, являются многочисленные теории на основе эфира, как особой материальной среды. К использованию этой «среды» физиков подталкивает непонимание сути и, как следствие, отрицание мгновенных взаимодействий. Однако такие взаимодействия объективно существуют в механике Ньютона, они являются решениями уравнений Максвелла и превосходно описывают квазистатические явления электродинамики. Так неужели ради модели, кажущейся «приемлемой», неужели ради моды
следует отвергать математически корректное описание физических процессов?
Эфир всегда связан с абсолютной системой отсчета. Любые взаимодействия распространяются с характеристической скоростью относительно абсолютной системы отсчета. Эта характеристическая скорость относительно эфира может быть постоянной для всего пространства или же различной для разных точек этого пространства.
Именно эта среда, по мнению сторонников эфира, является тем посредником, который передает взаимодействия от одного объекта к другому. Моделей эфира достаточно много (газоподобные, жидкостные, твердотельные и т.д.). Разнообразны и представления о свойствах эфира (неподвижный, увлекаемый и др.). Но все они принципиально отвергают мгновенное взаимодействие, характерное для механики Ньютона. Ниже мы рассмотрим некоторые математические аспекты, общие для волновых процессов при наличии эфира.
13.1 Диссипативный характер излучения
Рассмотрим математическую сторону передачи взаимодействия, не привязываясь к конкретной модели. Пусть маленький шарик массой m
(материальная точка) закреплен на бесконечной натянутой струне. Этому шарику с помощью молоточка сообщается импульс p
. Начальная скорость шарика равна V
0
. От удара шарик начнет движение, и вместе с ним будут распространяться две поперечные волны, бегущие по оси x
в разные стороны от шарика, как показано на рис. 13.1.
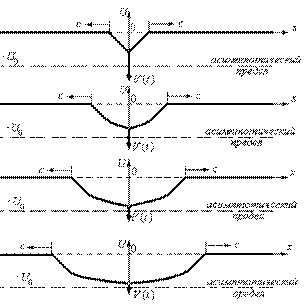
Рис 13.1. Распространение волн и движение шарика.
Для смещения струны от положения равновесия необходима энергия. Кинетическая энергия шарика постепенно расходуется на изменение положения элементов струны, скорость шарика уменьшается, и он постепенно останавливается. При этом струна стремится к своему асимптотическому пределу.
Запишем процесс математически.
∂V
∂V
 Уравнение движения шарика: m
= m
− F
, где U
– смещение шарика; V
= ∂U
/∂t
– Уравнение движения шарика: m
= m
− F
, где U
– смещение шарика; V
= ∂U
/∂t
–
∂t
∂t
скорость шарика; F
– сила, действующая на шарик со стороны струны. Здесь нет необходимости использовать полную производную, которая совпадает с частной производной (см. Приложение 1).
∂ 2U
∂ 2U
 Уравнение движения струны [1]: T
0
2 = ρ 2 − F
δ(x
), где: Т
0
– натяжение струны; ρ – Уравнение движения струны [1]: T
0
2 = ρ 2 − F
δ(x
), где: Т
0
– натяжение струны; ρ –
∂x
∂t
линейная плотность массы струны.
Уравнение движения струны можно привести к виду
∂ 2U
∂ 2U
 c
2 2
= 2
− f
δ(x
), c
2 2
= 2
− f
δ(x
),
∂x
∂t
где: c
2
= T
0
/ ρ - квадрат скорости распространения волны; f
= F
/ ρ – плотность силы, отнесенная к плотности массы струны.
По аналогии с теорией длинных линий параметр (T
0
ρ) - ½
можно назвать «волновым сопротивлением» струны.
Можно решить эти уравнения «в лоб» (см. [1], Задача № 9, стр. 80). Мы будем исходить из закона сохранения энергии, поскольку это нагляднее.
1.
Шарик.
Изменение скорости шарика происходит по экспоненциальному закону, поэтому можно предположить, что сила F
пропорциональна скорости движения заряда.
∂V
∂ 2
U
∂U
 m
= m
2
= −F
= −λ m
= m
2
= −F
= −λ  , ,
∂t
∂t
∂t
где λ – некоторая постоянная.
Решение для вертикальной координаты шарика имеет вид
U
= −U
0 (1− e
−λ
t
/ m
) (13.1.1)
Начальная скорость, импульс и кинетическая энергия шарика соответственно равны
2 2 2
  −λt
/ m
−λt
/ m
W
k
= U
0 λ e
−2λt
/ m
= V
0 m e
−2λt
/ m −λt
/ m
−λt
/ m
W
k
= U
0 λ e
−2λt
/ m
= V
0 m e
−2λt
/ m
V
0
= −λU
0
/ m
P
= λU
0
e
= mV
0
e
2m
2
2. Струна.
Рассмотрим теперь энергетические соотношения для струны и определим параметр λ. Мы будем исходить из того, что точка соприкосновения шарика со струной изменяет свое положение U
в соответствии с выражением (1.1). Соответственно, соседние точки (х
≠ 0) будут определяться следующими выражениями
U
= −U
0
[1− e
−λ
(t
−
x
/ c
) / m
](1−η(t
− x
/c
)) x
> 0
U
= −U
0
[1− e
−λ
(t
+
x
/ c
) / m
]η(t
+ x
/c
) x
< 0
⎧1 ξ > 0
η(ξ) = ⎨
⎩0 ξ < 0
Подсчитаем энергию струны, учитывая симметричность ее распределения
ct
 ∂U
−2λt
/ m
2 −2λt
/ m
W
c
=
∫0 [T
(
∂
x
) +ρ( ∂U
−2λt
/ m
2 −2λt
/ m
W
c
=
∫0 [T
(
∂
x
) +ρ(
 ∂
t ∂
t
 λ
m λ
m
 λ λ
Сложим энергии струны и шарика. Учитывая закон сохранения энергии, найдем величину параметра λ.
 λ = 2c
ρ = 2 T
0
ρ λ = 2c
ρ = 2 T
0
ρ
Здесь мы подобрали λ так, чтобы энергия не зависела от времени. Проверим теперь закон сохранения импульса. Суммарный импульс шарика и возбужденных элементов струны не должен зависеть от времени. Действительно
ct
−λt
/ m
∂U
(x
;t
) −λt
/ m
−λt
/ m
−U
0λe
− 2∫ρ  ∂t dx
=−2c
ρU
0e
− 2c
ρU
0 (1− e
) = ∂t dx
=−2c
ρU
0e
− 2c
ρU
0 (1− e
) =
0
= 2c
ρU
0
= mV
0
= const
Величина силы зависит только от параметров струны и скорость шарика
∂U
−λt
/ m
 F
= λ = −2 ρT
0V
0e F
= λ = −2 ρT
0V
0e
∂t
Итак, кинетическая энергия механического движения шарика преобразуется в волновую энергию струны, распространяющуюся от шарика.
Как нетрудно заметить, процесс передачи энергии от материального тела к волне носит диссипативный
характер. Кинетическая энергия шарика преобразуется в энергию колебания струны и уже больше не возвращается шарику. Такой процесс характерен не только для механических волн, но и для любого волнового процесса, в том числе и для электромагнитных волн. Например, излучение диполя Герца также диссипативный процесс. Энергия, подводимая к диполю от генератора, уносится в бесконечность со скоростью света и уже не возвращается обратно в генератор.
Приложение 1
Некоторые читатели наших статей просили объяснить, в каких случаях полную производную по времени можно заменить частной производной. Покажем это на примерах. Обратимся к рис. 13.2. Рассмотрим удар клюшкой по шайбе.

Рис. 13.2
1. Если шайба несжимаемая, а удар центральный, то из-за сил трения шайба будет двигаться замедленно. Все точки шайбы имеют одинаковые скорости и ускорения, а шайбу можно рассматривать как материальную точку. В этом случае полную производную можно заменить частной 13.2 (1). Шайбу можно рассматривать как материальную точку.
2. Если мы по несжимаемой шайбе наносим удар не по центру, шайба будет перемещаться по дуге, вращаясь, как показано на рис. 13.2 (2). Здесь каждая точка шайбы будет иметь свою скорость, и мы уже не сможем описать движение шайбы как материальной точки. Мы должны учитывать энергию вращательного движения. А это можно сделать только с помощью полной производной.
3. То же положение имеет место при центральном ударе по упругой
шайбе. Она будет двигаться с замедлением, обусловленным трением, одновременно совершая упругие колебания (периодически сжимаясь в одном направлении и растягиваясь в другом), как показано на рис. 13.2 (3).
Итак, в тех случаях, когда материальный объект можно заменить материальной точкой
, мы можем использовать частную производную. Это касается также потока материальных частиц, между которыми отсутствует взаимодействие или по условиям задачи таким взаимодействием можно пренебречь. Когда же мы рассматриваем непрерывную среду, точки которой связаны между собой взаимодействием, мы обязаны использовать полную производную по времени.
13.2 Краткие сведения из теории длинных линий
Теперь мы рассмотрим пример из электродинамики. Мы будем исследовать разряд конденсатора на длинную линию, которая будет иметь свойства «эфира». Простейшими длинными линиями, в которых может распространяться волна со скоростью света, являются линии, в которых распространяется волна типа ТЕМ (поперечная электромагнитная волна). К ним относятся двухпроводные линии и коаксиальные линии. В этих линиях поля Е
и Н
имеют специфическую форму. Пусть волны распространяются коллинеарно проводникам, ориентированным вдоль оси z
. Поля будут перпендикулярны этой оси, т.е. направлению распространения волны.
E
= E
(x
; y
)[ f
1
(t
− z
/c
) + f
2
(t
− z
/c
)]
H
= H
(x
; y
)[ f
1
(t
− z
/c
) + f
2
(t
− z
/c
)]
Такую волну можно однозначно описать «квазистатическими методами», т.е. с помощью токов и напряжений в этой линии. Это упрощает выкладки и делает процесс анализа более наглядным.
Итак, рассмотрим двухпроводную линии, в которой существует емкость между проводниками и индуктивность проводников. Эти реактивности характеризуются
~
параметрами: погонной емкостью на единицу длины C
[Ф/м] и погонной индуктивностью
~
L
[Гн/м]. Однако более удобно использовать производные от этих параметров
1.  Скорость распространения волны в линии c
=1/ L
~
C
~
. Скорость распространения волны в линии c
=1/ L
~
C
~
.
2.  Волновое сопротивление линии w
= L
~
/C
~
. Волновое сопротивление линии w
= L
~
/C
~
.
Соответственно, погонные параметры легко выразить через эти величины
~ ~
L
= w
/c
; C
=1/ wc
Запишем теперь уравнения и основные соотношения для длинной линии для токов и напряжений.
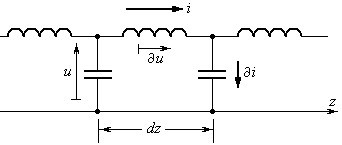
Рис. 13.3
∂u
~ ∂i w
∂i
∂i
~ ∂u
1 ∂u
  = L
= ; = C
= = L
= ; = C
=
∂z
∂t c
∂t
∂z
∂t cw
∂t
Исключая ток или напряжение, получим
∂2
u
1 ∂2
u
∂2
i
1 ∂2
i
  2 − 2 2 = 0; 2 − 2 2 = 0 2 − 2 2 = 0; 2 − 2 2 = 0
∂z c
∂t
∂z c
∂t
Энергия поля на единицу длины равна
∂W
~ i
2 ~ u
2 1 2 2
 = L
+ C
= [u
+ (wi
) ] = L
+ C
= [u
+ (wi
) ]
∂z
2 2 2cw
13.3 Разряд конденсатора на неподвижную линию
Рассмотрим бесконечную двухпроводную линию, к которой будет подключаться заряженный конденсатор, как показано на рис. 13.4.
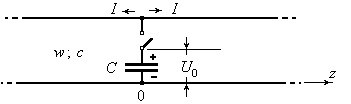
Рис. 13.4
При замыкании контакта по линии потечет ток, и потенциал будет распространяться со скоростью света в обе стороны от точек подключения конденсатора.
По мере разряда конденсатора напряжение на нем будет убывать U
=U
0e
−λ0t
, где λ0
параметр.
Энергия конденсатора будет также убывать по экспоненциальному закону
2 −2λ0
t
CU
0
e
W
C
= 
2
Запишем закон изменения потенциала в линии
U
=U
0
e
−
(t
−
z
/c
)
λ
0
(1−η(z
− ct
)) ct
> z
> 0
U
=U
0
e
−λ
(t
+
z
/c
)
λ
0
η(z
+ ct
) − ct
< z
< 0
⎧1 ξ> 0
η(ξ) = ⎨
⎩0 ξ< 0
Распространение потенциала в линии показано на рис. 13.5.

Рис. 13.5
Подсчитаем теперь энергию, которую уносит с собой распространяющийся потенциал, учитывая симметричный характер потенциала.
1 0 2 2 1 ct
2 2 СU
02 −2λ0t
W
=  ∫
[u
+ (wi
) ]dz
+ ∫
[u
+ (wi
) ]dz
+  2cw
∫
0 [u
+ (wi
) ]dz
= 2cw
∫
0 [u
+ (wi
) ]dz
=  w
λ
[1− e
] w
λ
[1− e
]
2cw
−ct
где: i
= u
/ w –
для волны, бегущей вдоль оси z
; i
= - u
/ w
для волны, бегущей против оси z
.
Очевидно, что суммарная энергия (энергия конденсатора и энергия в линии) должна оставаться постоянной. Учитывая это, найдем значение параметра затухания λ0
λ0
= 2 / Cw.
Итак, напряжение на конденсаторе будет равно U
=U
0
e
−
2t
/ wC
. Ниже мы рассмотрим процессы для случаев, когда конденсатор движется вдоль оси z
с постоянной скоростью.
13.4 Конденсатор, движущийся относительно линии
В «эфирной» модели скорость распространения волны постоянна относительно неподвижного «эфира», с которым в нашем случае связана длинная двухпроводная линия (абсолютная система отсчета).
Обозначим скорость движения конденсатора относительно линии как V
. Поскольку конденсатор движется относительно неподвижной линии («эфира»), а скорость волны относительно эфира неизменна, мы получим следующие выражения в системе отсчета связанной с «эфиром» (линией).
t
−z
/ c
−
u
=U
0
e
(1
−
V
/ c
)
λ
[1−η(z
− ct
)] ct
> z
>Vt
t
+z
/ c
−
u
=U
0
e
(1
+
V
/ c
)
λ
η(z
+ ct
) -ct
< z
<Vt
где λ – диссипативный параметр.
Введение этого параметра обусловлено тем, что мы пока не знаем насколько быстро будет разряжаться движущийся конденсатор по сравнению с неподвижным.
При движении конденсатора вдоль оси z
потенциал с правой от конденсатора стороны оказывается как бы «спрессован» в 1 – V
/c
раз и «растянут» в 1 + V
/c
с левой стороны, как показано на рис. 13.4. Это связано с тем, что скорость волны относительно конденсатора справа равна с
– V,
а слева с
+ V.
Однако скорость самой волны относительно линии сохраняется постоянной, равной с
.
Проведем баланс энергий, чтобы определить диссипативный параметр. Подсчитаем энергию «до» и «после» движущегося конденсатора.
А)
Запишем выражение для энергии в линии, считая, что V
< с.
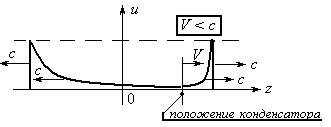
Рис. 13.6
Энергия, распространяющаяся от конденсатора вдоль оси z
равна
сt
2
 U
0 U
0 (c
−V
) −2λt U
0 U
0 (c
−V
) −2λt
W
+ = Vt
∫ сw e dz
= 2wс
λ [1− e
]
Энергия, распространяющаяся от конденсатора против оси z
равна
Vt
2
 U
0 U
0 (c
+V
) −2λt U
0 U
0 (c
+V
) −2λt
W
− = −∫ct сw e dz
= 2wс
λ [1− e
]
Суммарная энергия в линии равна
2
U
0 −2λt
W
+ +W
− =  [1− e
] [1− e
]
w
λ
Складывая это значение с энергией конденсатора, найдем, что λ = 2 / Cw
= λ0
.
Таким образом, имеет место закон сохранения энергии, а диссипативный параметр не изменился.
Б)
Случай, когда V
= c.
Здесь распространяется от конденсатора только волна, бегущая назад. Легко тем же способом показать, что конденсатор будет разряжаться вдвое медленнее λ = 1/Cw
= λ0
/2 Конденсатор разряжается как бы на полубесконечную длинную линию
В)
Теперь рассмотрим случай, когда V
> c.
Эпюры потенциала (V
> c
) показаны на рис. 13.7.
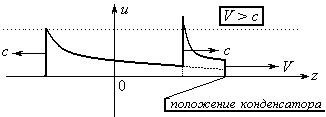
Рис. 13.7
Потенциалы имеют вид
u
= u
+
+ u
−
t
−z
/ c
 λ λ
u
+
=U
0
e
(V
/ c
−
1)
[η(z
− ct
) −η(z
−Vt
)] ct
< z
<Vt
 t
+z
/ c
−λ t
+z
/ c
−λ
u
−
=U
0
e
(1
+
V
/ c
)
η(z
+ ct
) -ct
< z
<Vt
Суммарная энергия в линии равна
U
02 −2t
/ λ
W
+ +W
− =  [1− e
] [1− e
]
4w
λ
Следовательно, здесь диссипативный параметр λ = 1/2Cw
= λ0
/4.
Процесс протекает так, как будто к конденсатору подсоединена линия с волновым сопротивлением в 2 раза больше.
Выводы.
С точки зрения законов сохранения энергии теории на основе эфира законны. Однако имеется ряд явлений, вызывающих сомнение в возможности физического приложения этих теорий. Прежде всего, эти теории противоречат фундаментальному принципу Галилея-Пуанкаре. Это выражается в существовании абсолютной системы отсчета и зависимости физических законов от такого выбора. Но есть также физические явления, не укладывающиеся в рамки здравого смысла:
1. Прежде всего, отметим, что взаимодействие материального тела с волнами эфира носит диссипативный
характер. В общем случае это означает, что консервативных
систем, присущих механике Ньютона, в теориях эфира быть не может принципиально.
2. При движении взаимодействующих между собой материальных тел принцип равенства действия противодействию не выполняется
. Одно тело может воздействовать через эфир с силой большей, чем второе тело воздействует через эфир на первое. Приведем цитату из работы [2]: «Ритцу не нравилось, что фундаментальные электрические и магнитные поля не были обнаружены непосредственно, и он показал, подобно Анри Пуанкаре до него, что их физическая интерпретация, привлекающая гипотезу неподвижного эфира, нарушает закон действия и противодействия
. Он пренебрежительно называл эфир
“математическим фантомом”, не обнаруживаемым и не заслуживающим широкого приёма, который он получил …Он стремился избавиться от всех выражений и принципов, имеющих отношение к абсолютному движению и эфиру
». Здесь мы придерживаемся точки зрения Ритца.
3. Если скорость движения одного из взаимодействующих тел превышает скорость распространения волн эфира, то возможен такой случай. Неподвижное относительно эфира тело не будет «замечать» движение второго тела, если оно приближается со скоростью, превышающей скорость волн эфира.
Итак, физические теории на основе представлений об эфире как переносчике взаимодействий не могут претендовать на роль альтернативных. Более того, они не способны привести даже при малых скоростях тел к законам Ньютона. Конечно, если использовать «вырожденные решения» (см. Главу 1), тогда эту преграду можно преодолеть. Но тогда придется смириться с эклектикой: на словах взаимодействие распространяется со скоростью волн в эфире, а на деле «тайком» протаскивается математический формализм, содержащий мгновенные взаимодействия.
13.5 Разряд движущегося конденсатора (модель Ритца)
Согласно гипотезе Ритца скорость волны равна с
относительно источника излучения волны. Следовательно, результаты, полученные в параграфе 3, будут соответствовать случаю, когда скорость конденсатора равна нулю.
U
=U
0
e
−
(t
−
z
'/ c
)
λ
(1−η(z
'−ct
)) ct
> z
'> 0
U
=U
0
e
−
λ
(t
+
z
'/ c
)
λ
η(z
'+ct
) − ct
< z
'< 0
Чтобы получить решение в произвольной инерциальной системе отсчета, нам достаточно использовать преобразование Галилея. Пусть теперь конденсатор движется относительно наблюдателя вдоль оси z
со скоростью v
, т.е. его координата z’
= z
- vt
. В системе отсчета этого наблюдателя потенциал будет следующим
u
=U
0
e
−
[t
(1
+
v
/ c
)
−
z
/ c
]
λ
[η(z
− vt
) −η[z
− (c
+ v
)t
]] (c
+ v
)t
> z
> vt
u
=U
0
e
−
λ
[t
(1
−
v
/ c
)
+
z
/ c
]
λ
[η[z
+ (c
− v
)t
] - η(z
− vt
)] (−c
+ v
)t
< z
< vt
В системе отсчета неподвижного наблюдателя левый фронт волны будет двигаться относительно него со скоростью c - v
, а правый будет двигаться со скоростью c + v,
как показано на рис. 13.8.
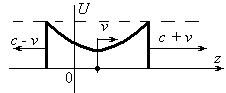
Рис. 13.8 Подсчитаем энергию в линии.
(c
+v
)t
1 2 2
W
= ∫  [u
+ (wi
) ]dz [u
+ (wi
) ]dz
−(c
−v
)t
2cw
Энергия, распространяющаяся от конденсатора вдоль оси z
равна
 (с
+v
)t
2 UU
0
λ −
2
λ
t (с
+v
)t
2 UU
0
λ −
2
λ
t
W
+
= ∫  e dz
= e dz
=  [1− e
] vt сw
2w [1− e
] vt сw
2w
Энергия, распространяющаяся от конденсатора против оси z
равна
vt
2 2
U
0 −2λ[t
(1−v
/ c
)+z
/ c
] U
0 λ −2λt
W
−
=
∫  e dz
= e dz
=  [1− e
] [1− e
]
(с
−v
)t
сw
2w
Суммарная энергия в линии равна
2
U
0 c
λ −2λt
W
+ +W
− =  [1− e
] [1− e
]
w
И здесь λ = 2 / Cw
= λ0
. С точки зрения закона сохранения энергии процесс описывается корректно.
13.6 Баллистическая гипотеза Ритца
Вальтер Ритц был одним из тех, кто не принял Специальную теорию относительности А. Эйнштейна и искал пути альтернативного объяснения волновых явлений. Он, опираясь на принцип причинности, установил, что источник не может создавать «опережающие» потенциалы. Видимо, идея запаздывания взаимодействия была определяющей при создании им своей «баллистической гипотезы».
«Ритц утверждал, что электромагнитные, а, следовательно, и оптические явления согласуются с принципом относительности, подобно механическим явлениям. Следовательно, испускание света должно быть механически идентично другим материальным испусканьям: скорость света относительно данной системы отсчёта должна зависеть от движения источника света в момент испускания, подобно тому, как скорость снаряда зависит от движения испустившего его орудия. В таком случае свет должен распространяться в виде концентрических сфер, окружающих источник, если тот не станет ускоряться. Чтобы сделать световые процессы наглядными, Ритц использовал для описания движения света термин “метание” (“projection” - англ. бросание, метание, выстреливание – С.С.) вместо слова “распространение” (“propagation”), поскольку последнее рождало представление о волнах, движущихся в среде. Он стремился избавиться от всех выражений и принципов, имеющих отношение к абсолютному движению и эфиру. Он показал, что свет или излучаемую энергию проще представлять как состоящую из бесконечно малых частиц, находящихся в движении, о которых он говорил как о “фиктивных” частицах
» [2].
Ритц пересмотрел уравнения Максвелла, поскольку в решении этих уравнений возникали опережающие потенциалы. Два уравнения он сохранил:
∂B
∂A
divB
= 0; rotE
= −  ; где : B
= rotA
; E
= −gradφ − ; где : B
= rotA
; E
= −gradφ − 
∂t
∂t
Волновые уравнения для скалярного и векторного потенциала он заменил следующими:
  1 ρ(r
;(t
− r
/(c
+ v
r
)) μ j
(r
;(t
− r
/(c
+ v
r
)) 1 ρ(r
;(t
− r
/(c
+ v
r
)) μ j
(r
;(t
− r
/(c
+ v
r
))
φ = ∫
r dV
; A
= 4π ∫
r dV
; (13.6.1)
4πε где vr
–компонента скорости источника в направлении излучения. Это обычные запаздывающие потенциалы, определяющие поля движущихся зарядов.
К сожалению, такой подход не мог дать положительных результатов по ряду причин.
1. Ритц опирался на неполноценный закон сохранения энергии Пойнтинга, который не учитывал потоки продольных
волн скалярного и векторного потенциала. В теории Ритца скалярный потенциал имеет положительную энергию. В силу этого формально возможен предельный переход от волновых явлений к квазистатическим. Однако в его теории неизбежно должны появиться продольные
волны, которые до сих пор не обнаружены экспериментально.
2. Выражения (13.6.1) удовлетворяют волновому уравнению. По этой причине словесный отказ от волновых уравнений не спасает теорию Ритца от проблем. Такой проблемой является проблема диссипативного
характера
взаимодействий при запаздывающих потенциалах. По этой причине критика теорий, опирающихся на эфир, во многом относится и к теории Ритца (исключая существование абсолютной системы отсчета). Нарушение
принципа равенства действия противодействию между взаимодействующими телами неизбежно имеет место и в теории Ритца.
Таким образом, рассмотренные теории не могут претендовать на то, чтобы заменить Специальную теорию относительности.
13.7 Волна как самостоятельный вид материи
Рассмотрим теперь случай, когда электромагнитная волна рассматривается как самостоятельный вид материи
, который существует параллельно другому виду материи – материальным телам, но имеет свои особые свойства. Уравнения, описывающие электромагнитную волну, в соответствии с принципом Галилея - Пуанкаре сохраняют свою форму инвариантной в любой инерциальной системе отсчета. Иными словами, скорость света в любой инерциальной системе отсчета неизменна. Рассмотрим для иллюстрации пример.
Выше мы анализировали разряд конденсатора на неподвижную и движущуюся линию для случая «эфирного» подхода и баллистической гипотезы Ритца. Рассмотрим теперь ту же задачу для волны как самостоятельного вида материи. В системе отсчета, где координата z’
конденсатора постоянна, решение нам известно. u
+
=U
0
e
−λ
(t
'
−
z
'/ c
)
[1−η(t
'−z
'/c
)] z
'> 0
(13.7.1) u
−
=U
0
e
−λ
(t
'
+
z
'/ c
)
η(t
'+z
'/c
) z
'< 0
Теперь нам необходимо записать решение в произвольной инерциальной системе отсчета, движущейся вдоль оси z
.
   Волновое уравнение сохраняет свой вид при обобщенных преобразованиях z
'= 1+ f
(V
/ c
)2
z
− f
(V
/ c
)ct
; ct
'= 1+ f
(V
/ c
)2
ct
− f
(V
/ c
)z
(13.7.2) где f
(V/c
) – нечетная функция V/c
; для преобразования Лоренца f
(V
/ c
) = v
/ c
2
− v
2
для модифицированного преобразования f
(V
/ c
) =V
/ c Волновое уравнение сохраняет свой вид при обобщенных преобразованиях z
'= 1+ f
(V
/ c
)2
z
− f
(V
/ c
)ct
; ct
'= 1+ f
(V
/ c
)2
ct
− f
(V
/ c
)z
(13.7.2) где f
(V/c
) – нечетная функция V/c
; для преобразования Лоренца f
(V
/ c
) = v
/ c
2
− v
2
для модифицированного преобразования f
(V
/ c
) =V
/ c
Используя (13.7.2) , преобразуем выражение (14.5.1)
 ~ −λ
a
(t
−
z
/ c
)
f
(V
/ c
)ct ~ −λ
a
(t
−
z
/ c
)
f
(V
/ c
)ct
u
+
=Ue
ct
> z
> a
=+ f
(V
/ c
);
1+ f
(V
/ c
)2
(13.7.3)
~ −λ
b
(t
+
z
/ c
)
f
(V
/ c
)ct
 u
−
=Ue
- ct
> z
< b
=− f
(V
/ c
); u
−
=Ue
- ct
> z
< b
=− f
(V
/ c
);
1+ f
(V
/ c
)2
Мы выбрали другую амплитуду напряжения, поскольку волна может исказить ее. Заметим, что скорость распространения волны не зависит от выбора инерциальной системы отсчета и скорости источника. Она равна с
.
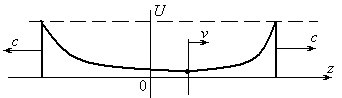
Рис. 13.2
Подсчитаем энергию в конденсаторе в новой системе отсчета. Координата конденсатора
f
(V
/ c
)ct
z
== vt
,
 1+ f
(V
/ c
) 2 1+ f
(V
/ c
) 2
где v
– есть «кажущаяся» скорость конденсатора, т.е. отображение
действительной (галилеевской) скорости конденсатора волной
в систему отсчета наблюдателя.
Энергия в конденсаторе равна
~ 2
 W
С
= CU e
−2λt
/ 1+ f
2 (13.7.4) W
С
= CU e
−2λt
/ 1+ f
2 (13.7.4)
2
Мы будем исходить из закона сохранения энергии по следующим причинам. Во-первых, выражение E
d
l
есть истинный скаляр и, как следствие, потенциал U
должен сохранять свое значение в любой инерциальной системе отсчета. Во вторых, имеет место закон сохранения заряда. Следовательно, энергия конденсатора, пропорциональная произведению заряда на разность потенциалов конденсатора, будет инвариантной величиной.
Помимо этого, условия задачи не оговаривают ни ориентацию конденсатора, ни его форму. Пластины конденсатора могут быть ориентированы как параллельно вектору скорости, так и перпендикулярно ему. Что касается формы, то конденсатор может иметь любую форму, например, состоять из коаксиальных цилиндров. Неужели в рамках СТО решение каждой из таких задач зависит от конструкции конденсатора?
~
Итак, энергия конденсатора сохраняется при условии U
=U
0
. Теперь вычислим энергию в длинной линии
1 ct
2 2
W
=  2cw
−∫ct
[u
+ (wi
) ]dz
= 2cw
−∫ct
[u
+ (wi
) ]dz
=
  ct ct
1 2 −2λb
(t
−z
/ c
)2 −2λa
(t
+z
/ c
) (13.7.5)
= ∫U e
dz
+ cw
−∫ctU
0 e
dz
=
2
 −2λt
/ 1+ f
2 U
0 2 −2λt
/ 1+ f
2 −2λt
/ 1+ f
2 U
0 2 −2λt
/ 1+ f
2
 =(1− e
) = 1+ f
(1− e
) λw
λw =(1− e
) = 1+ f
(1− e
) λw
λw
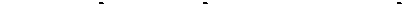  Сумма выражений (13.7.4) и (13.7.5) должна оставаться постоянной, т.е. быть равной энергии заряженного конденсатора до момента разряда (закон сохранения энергии) Сумма выражений (13.7.4) и (13.7.5) должна оставаться постоянной, т.е. быть равной энергии заряженного конденсатора до момента разряда (закон сохранения энергии)
Cw
0
Теперь мы можем записать выражение для изменения потенциала движущегося конденсатора и изменения энергии этого конденсатора
2 2
  −λt
/ 1+ f
2 −λ0t CU
0 −2λt
/ 1+ f
2 CU
0 −2λ0t −λt
/ 1+ f
2 −λ0t CU
0 −2λt
/ 1+ f
2 CU
0 −2λ0t
U
=U
0e
=U
0e
; W
C
= e
= e
2 2
Итак, энергия движущегося конденсатора уменьшается во времени точно так же (в том же темпе), что и энергия неподвижного конденсатора. Более того, напряжение на движущемся конденсаторе будет точно таким же, как и на неподвижном, для любого момента времени.
1. Никакого реального «замедления времени»
разряда движущегося конденсатора по отношению ко времени разряда неподвижного не существует.
2. Энергия не зависит от выбора инерциальной системы отсчета
и остается в движущейся системе той же самой, что и в неподвижной.
Этот вариант в своих статьях мы назвали «Волновой вариант теории Ритца». Он, на наш взгляд, заслуживает внимания.
Источники информации:
1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. ГИТТЛ, М., 1953.
2. Альберто А. Мартинез. РИТЦ, ЭЙНШТЕЙН И ЭМИССИОННАЯ ГИПОТЕЗА (Ritz, Einstein, and the Emission Hypothesis, Alberto A. Martínez) перевод на русский – С.Семиков, 2006 г.
14.1 Эта «неуловимая» электромагнитная волна.
В Главе 7 мы пришли к выводу, что электромагнитная волна есть самостоятельный вид материи. В соответствии с принципом Галилея-Пуанкаре волновое уравнение должно сохранять свою форму (= сохранять неизменность скорости света) в любой инерциальной системе отсчета (см. Главу 11). Теперь остановимся на вопросе о постоянстве скорости света в любой инерциальной системе отсчета. Когда мы переходим в новую систему отсчета, скорость волны сохраняется той же самой. Как понять этот факт?
Как нами было установлено: евклидово пространство является общим
для всех инерциальных систем отсчета; время во всех инерциальных системах отсчета едино;
электромагнитная волна это особый, самостоятельный вид
материи; ее свойства
отличаются от свойств обычных тел.
Последнее обстоятельство позволяет волне сохранять свою скорость в любой инерциальной системе отсчета. Волна это особый вид
материи и к ней нельзя применять «шаблонно» те методы, которые используются для обычных материальных тел.
Представьте себе, что мимо вас со скоростью света распространяется электромагнитная волна. Предположим также, что в одном направлении с волной движется материальный объект с такой же галилеевской скоростью V
= c
.
Вам будет казаться, что и волна и этот объект двигаются вместе синхронно и объект находится в точке постоянной фазы волны. Перейдем теперь в систему отсчета, связанную с движущимся объектом. Старая система будет теперь двигаться в обратную сторону относительно неподвижного объекта. Оказывается, что и здесь в новой системе отсчета волна вновь распространяется со скоростью света! Однако параметры волны изменились, например, частота ее колебаний стала ниже. Такова особенность этих волн.
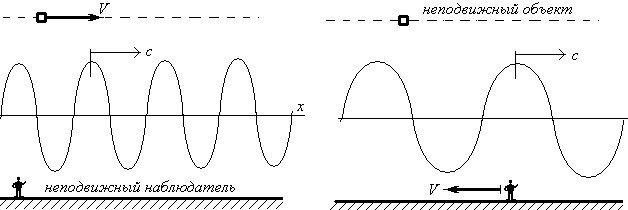
Рис. 14.1
Если бы мы попытались отобразить движение этого объекта с помощью световых лучей
, находясь в системе отсчета неподвижного наблюдателя, то в отличие от классического способа
отображения (см. Глава 11):
мы видели бы объект не в том месте, где он в данный момент находится (аберрация); наблюдаемая (лоренцевская) скорость движения v
была отличной от ее истинной (галилеевской) скорости V
.
Наблюдаемая
с помощью световых лучей скорость («кажущаяся скорость») никогда не может превысить скорость света, хотя действительная
скорость тела может значительно ее превышать. Таковы специфические свойства электромагнитной волны и ее способность отображать собственное движение и движение материальных тел.
14.2 Принцип относительности при взаимодействиях
Рассматривая в Главах 3, 4 и 5 вопросы, связанные с взаимодействием зарядов, мы определили, что ньютоновская механика и квазистатические явления электродинамики подчиняются преобразованию Галилея именно по той причине, что взаимодействие зависит от относительного расстояния R
12
и относительной скорости v
12
двух взаимодействующих объектов. При таком подходе описание взаимодействия материальных объектов не зависит от выбора наблюдателем инерциальной системы отсчета. Сколько бы наблюдателей не регистрировали процесс взаимодействия, находясь в различных инерциальных системах отсчета, они будут фиксировать одно и то же.
Перейдем от квазистатических явлений к волновым. Пусть имеется источник, создающий электромагнитные волны. Эти волны воздействуют на некий движущийся относительно этого источника материальный объект. Здесь нет произвола.
Рассматривая воздействие волны от источника на движущийся объект, мы видим, что такое воздействие (как и в ньютоновской механике) тоже будет зависеть от относительного расстояния
между источником электромагнитных волн и зарядом R
12
и относительной скорости
между источником излучения электромагнитных волн и объектом v
12
. Тем самым описание волнового взаимодействия остается инвариантным относительно преобразования Галилея.
С другой стороны, величины R
12
и v
12
являются истинными скалярами, заведомо инвариантны
не только относительно преобразования Галилея, но и обобщенного преобразования (равно преобразования Лоренца). Они не зависят от субъективного выбора наблюдателем инерциальной системы отсчета. Следует заметить, что в силу сказанного выше, необходимость в последовательном применении нескольких преобразований Лоренца (или обобщенных преобразований) при переходе из одной инерциальной системы в другую отпадает. Остаются «за бортом» и парадоксы типа «прецессии Томаса». Величины R
12
и v
12
определяют взаимодействие (с пространственновременной стороны) полностью.
Взаимодействие сопровождается обменом энергией между частицей и волной (изменение кинетической энергии частицы) и рассеянием электромагнитной волны в свободное пространство (изменение энергии волны). Привилегированной
для волны является система отсчета, связанная с источником излучения
(распространения) волны, поскольку в ней эта волна не имеет характерных релятивистских эффектов (эффект Доплера, искажение направления фронта волны и т.д.). Привилегированной для вторичной
волны является сопутствующая система отсчета, связанная с источником вторичного излучения
(с зарядом и т.д.). Привилегированной для материальных сред, волноводов и замедляющих систем является система отсчета, связанная со средой
, где волна распространяется.
14.3 Время распространения волны
Трудность нового объяснения кинематических эффектов, связанных с волнами, не в их сложности, а в том, что люди часто «сбиваются» из-за «привычной» интерпретации, навязанной учебниками. Они принимают «кажущиеся» (искаженные относительным движением) пространственные и временные отрезки за «действительные» времени и пространственные интервалы.
В качестве примера рассмотрим вопрос о локации Венеры с поверхности Земли. Электромагнитный импульс излучается с Земли в сторону Венеры и, отразившись, возвращается обратно к Земле. Мы рассчитываем расстояние, пройденное лучом и, зная относительную скорость планет, можем вычислить расстояние между ними. Сравнивая это расстояние с эфемероидным (как результатом астрономических наблюдений), мы можем оценить корректность той или иной модели (например, ньютоновской или эйнштейновской). Мы сопоставим три варианта:
1. Ньютоновская теория.
2. Эйнштейновская теория.
3. Теория, в которой волна является самостоятельным видом материи (волновой вариант теории Ритца).
Мы рассмотрим простой случай, когда планеты сближаются, и относительная скорость направлена вдоль радиус-вектора, который соединяет планеты.

Рис.14.2 Обозначения: 1 – Земля; 2 – Венера; ΔТ
1
и Δ Т
2
– интервалы времени прохождения радиоимпульса от Земли до Венеры и от Венеры до Земли; R
12
– расстояние в момент излучения с Земли радиоимпульса; v
12
– скорость относительного движения планет.
Ньютоновская теория.
Время прохождения от Земли до Венеры ΔТ
1
определяется отношением относительного расстояния R
12
к сумме скорости света и относительной скорости сближения планет v
12
.
ΔT
1
= R
12
/(c
+ v
12
)
Время, затраченное на обратный путь ΔТ
2
равно
ΔT
2
= (R
12
− v
12
ΔT
1
)/(c
+ v
12
)
Таким образом, расстояние между планетами в момент излучения равно
 (ΔT
1 + ΔT
2 ) (c
+ v
12 )2
(ΔT
1 + ΔT
2 ) 3 (ΔT
1 + ΔT
2 ) (c
+ v
12 )2
(ΔT
1 + ΔT
2 ) 3
R
12
= ≈ (c
+ v
12
) 2 c
+ v
12
/ 2 2 2
Эйнштейновская теория.
Время прохождения от Земли до Венеры ΔТ
1
определяется, как и в предыдущем случае, отношением относительного расстояния R
12
к сумме скорости света и относительной скорости сближения планет v
12
.
ΔT
1
= R
12
/(c
+ v
12
)
Время, затраченное на обратный путь ΔТ’
2
равно отношению расстояния (R
12
– v
12
ΔT
1
) к скорости света c
.
ΔT
'2
= (R
12
− v
12
ΔT
1
)/c
(14.3.1)
Таким образом, расстояние между планетами в момент излучения будет равно
R
12
= 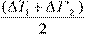 (c
+ v
12
) (c
+ v
12
)
Волновой вариант теории Ритца.
Время прохождения от Земли до Венеры ΔТ
1
определяется, как и в предыдущих случаях, отношением относительного расстояния R
12
к сумме скорости света и относительной скорости сближения планет v
12
.
ΔT
1
= R
12
/(c
+ v
12
)
Отражение от поверхности Венеры происходит в момент, когда расстояние между планетами равно
c
R
21 = R
12 − v
12ΔT
1 = R
12 
c
+v
12
Источник излучения (Венера) движется. Поэтому время ΔТ
2
, рассчитываемое по формуле Эйнштейна и равное R
21
/ c
, является «кажущимся», т.е. не является действительным временем, пройденным светом. Это проекция
действительного времени прохождения в систему отсчета, связанную с Землей. Действительное время, как говорилось, должно отсчитываться в системе отсчета, связанной с источником излучения.
С учетом этого замечания действительное время ΔТ’
2
будет равно
c
− v
12 ΔT
2
 ΔT
'2 = ΔT
2 ≈ ΔT
'2 = ΔT
2 ≈
c
+ v
12
(1+ v
12
/c
)
Тогда полное время, пройденное светом на пути Земля-Венера-Земля, равно
 R
12 cR
12 2R
12 (c
+ v
12 / 2) 2R
12 R
12 cR
12 2R
12 (c
+ v
12 / 2) 2R
12
ΔT
= ΔT
1
+ ΔT
'
2
= + 2
= 2
≈
c
+ v
12
(c
+ v
12
) (c
+ v
12
) c
+ 3v
12
/ 2
Учитывая это, получим классический результат (с точностью до членов (c
/ v
12
)2
)
R
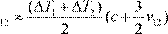
Таким образом, волновой вариант теории Ритца и ньютоновская теория в первом приближении дают одинаковые результаты.
14.4 Экспериментальное подтверждение
Этот факт имеет экспериментальное подтверждение. Процитируем отрывок из статьи Б. Дж. Уоллеса «Проблема пространства и времени в современной физике» (в сб. Проблема пространства и времени в современном естествознании. Ленинградское отделение АН РСФСР. С.-Петербург. 1991):
«
… Радиолокация Венеры в
1961 г. Впервые дала возможность преодолеть технический барьер и выполнить решающий эксперимент по проверке относительной скорости света в пространстве. Предполагалось, что радар даст погрешность
± 1,5 км
, и при этом из-за вращения Земли в вычисленных расстояниях могла возникнуть разность до
260 км
в зависимости от того, какую принять из двух моделей для распространения волн. Венера наблюдалась в нижнем соединении.
В
[3] на рис.
4 значения большой полуоси орбиты Земли – астрономические единицы
(а.е.
), полученные по ньюкомбовским орбитам Земли и Венеры и вычисленные по лазерным наблюдениям в Мильстоуне с использованием эйнштейновской модели
(с - модели
) для распространения света; при этом были обнаружены чрезмерно большие вариации в значении а.е.,
превосходящие иногда
2000 км
….
»
Действительно если экспериментально обнаруженные вариации иногда превосходят 2000 км
при максимально возможном ожидаемом отклонении в 260 км, это уже не «погрешность вычислений», а непригодность теории. Для сравнения заметим, что
«ньютоновский вариант» укладывается в пределы ошибок измерений ± 1,5 км
. Продолжим цитирование:
«…Естественно, астрономическая единица имеет единственное значение, вариации же наблюдаемой величины превышали максимальное значение всех возможных ошибок. Вариации а.е.
содержали суточную компоненту, пропорциональную скорости вращения Земли, тридцатидневную компоненту , пропорциональную скорости движения системы Земля – Луна и синодическую компоненту, пропорциональную относительным скоростям.
Я провел анализ восьми радарных наблюдений Венеры, опубликованных в
1961 г
. [4], используя две модели: с
и с + v
. Результаты были опубликованы в
1969 г. В статье
«Радарная проверка относительной скорости света в пространстве»
[5]. На рис.
1 в
[5] представлен график разностей между средними гелиоцентрическими радиус-векторами Венеры
(вычисления велись по таблицам Ньюкомба
) и
1) Ньюкомбовскими возмущенными радиусами – эта разность обозначена через N
, и
2) радиусами, найденными по радарным измерениям расстояний для эйнштейновской с
- модели
(Е
) и
3) ими же для галилеево-ньютоновской c + v
- модели
(G
). Все разности выражены в миллионных долях а.е.
Так полный анализ с
– модели по всем данным радиолокации дал значение планетных масс почти такие же, как у Ньюкомба, и при этом в Мильстоуне использовалась эйнштейновская с – модель
[3], то кривая Е
должна совпадать с N
с точностью до максимально возможных ошибок в наблюдениях. Однако проанализированные мною наблюдения свидетельствуют против с
– модели Эйнштейна, поскольку разности N – E
значительно превосходят ошибку.
Точки на кривой G
представляют значения, полученные по эфемеридам, которые я вычислил по методу Коуэлла для численного интегрирования уравнений движения. Хорошее согласие между эфемероидными точками и кривой G
неопровержимо свидетельствует в пользу с + v
- модели, т.е. подтверждает ньютоновскую модель движения света в пространстве
! …»
Когда-то некий экспериментатор обратился к Эйнштейну, утверждая, что теория относительности противоречит его экспериментам. На это Эйнштейн ответил: «Тем хуже для эксперимента». Но это хуже и для научной истины, на которую опирается наука. Без экспериментального подтверждения наука превращается в схоластику, примеров которой предостаточно (например, схоластическая теория суперструн, теория Большого взрыва и т. п.).
Для иллюстрации приведенной цитаты Б. Уоллеса мы приложили ниже часть другой его статьи «РАДАРНЫЕ ИЗМЕРЕНИЯ ОТНОСИТЕЛЬНОЙ СКОРОСТИ СВЕТА В
КОСМОСЕ
», размещенную на сайте http://www. btr.nnov.ru. В ней содержится график, на который автор ссылается в приведенной выше цитате.
(Брайан Г. Уоллес (перевод на русский – С. Семиков, 2006 г.). 7210 12-е Авеню, Санкт-Петербург, США.)
SPECTROSCOPY LETTERS, 2(12), рр. 36l-367 (1969). RADAR TESTING OF THE RELATIVE
VELOCITY OF LIGHT IN SPACE ; Bryan G. Wallace ; 7210 12th Av No ; St Petersburg, Fla. 33710 U.S.A.)
Цитируем:
«… Рис.
1 представляет собой график расхождений между средними гелиоцентрическими радиус- векторами Венеры как рассчитанных по таблицам Ньюкомба возмущённых радиус- векторов Ньюкомба N и расчётных радарных расстояний E(c) и G(c + v) как преобразованных в гелиоцентрические радиус- векторы. возможной оценки ошибок радарных данных. Средние величины формируют математически чистый эллипс, так что вариации в величинах расхождений не могут им соответствовать. Поскольку полный анализ всех радиолокационных данных дал величины планетарных масс предельно близкие к тем, что использовал Ньюкомб, и поправки времени Ньюкомба для оптических данных были основаны на c- теории, кривая E должна соответствовать N в пределах максимально. Радарные данные представляют свидетельство против c- теории, поскольку N – E расхождения много больше любой возможной ошибки, и они пропорциональны изменениям в относительной лучевой скорости радарной станции и Венеры.
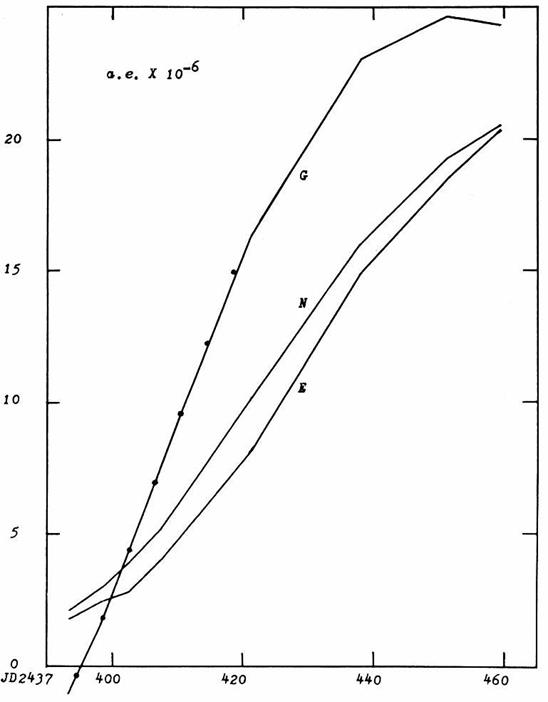
Рис. 1
Точки на кривой G рис. 1 изображают величины по эфемеридам, которые я рассчитал, используя метод Коуэлла численного интегрирования орбит и величины планетарных масс по Ньюкомбу. Обратите внимание на близкое согласие между законом Ньютона и его c + v корпускулярной теорией. И это несмотря на то, что величины планетарных масс по Ньюкомбу были основаны на c поправках времени, и не было сделано никакой попытки, исправить расстояния для ощутимого эффекта проходимой лучом плазмы, поскольку данные для разных частот на тот момент времени и для той станции были недоступны. Сравнительно близкое совпадение между данными и законами Ньютона – это свидетельство в пользу c + v корпускулярной теории Ньютона.
ЗАКЛЮЧЕНИЕ
В недавнем письме Шапиро выказал интерес к сотрудничеству в исчерпывающем исследовании относительной скорости света в космосе. Он пишет, что лаборатория Линкольна прошла через серьёзное "затягивание поясов". И я надеюсь, что базы данных станут в итоге доступными, и что лаборатория Линкольна произведёт полное исследование c + v теории. Хотя анализ данных предоставляет сильное свидетельство против c и в пользу c + v теории, я не считаю, что это можно рассматривать как убедительный вывод, пока не будет проведено исчерпывающее c + v исследование.
»
Специальная теория относительности уже пережила свой «старческий возраст» и должна быть заменена другой. Она основана на некорректном математическом формализме, не отвечает логике и не вписывается в существующие эксперименты.
14.5 Структурная схема описания взаимодействия
Обсудим качественную картину взаимодействия волны и заряда. Для этого рассмотрим электромагнитную волну, в поле которой оказалась заряженная частица. Скорость волны в любой инерциальной системе отсчета равна скорости света. Схема энергетического баланса представлена на рис. 14.3.

Рис. 14.3
Электромагнитное поле падающей волны взаимодействует с заряженной частицей, т.е. воздействует на заряд с некоторой силой. Частица начинает двигаться, т.е. забирает у волны энергию (или же отдает ей часть кинетической энергии). При этом кинетическая энергия частицы изменяется.
В свою очередь, двигаясь в поле электромагнитной волны, частица совершает в этом поле работу, т.е. создает новое поле, которое распространяется в обе стороны от частицы (диссипативный процесс). Это вторичные
волны: отраженная назад и отраженная вперед. Последняя, складываясь с полем невозмущенной волны, создает прошедшую волну. В общем случае частоты всех трех волн могут отличаться друг от друга в различных инерциальных системах отсчета. Заметим, что энергетический баланс (баланс энергий или мощностей) не должен зависеть от выбора наблюдателем системы отсчета.
Этот подход аналогичен процессу распространения волны в длинной линии, в которую включен четырехполюсник. Этот четырехполюсник может не только потреблять энергию волны, но и отдавать волне свою, запасенную в нем энергию.

Рис. 14.4
В предыдущей главе мы приводили пример для одномерного случая. Он наиболее характерен для СВЧ приборов с длительным взаимодействием электронного потока с электромагнитной волной и некоторых ускорителей элементарных частиц. Мы полагаем, что в общем случае процесс взаимодействия сохранит эти черты.
Задача описания складывается из следующих частей:
1. Описание воздействия падающей электромагнитной волны на заряд.
2. Введение диссипативного члена в это взаимодействие.
3. Определение по диссипативному члену параметров отраженной и прошедшей волн.
Эта задача достаточно сложная. Причина в том, что поля заряда являются мгновенно действующими и необходимо задать модель взаимодействия волны и заряда. Есть много вариантов: взаимодействие с продольной составляющей электромагнитного поля, с поперечной составляющей; длительное взаимодействие с замедленными волнами; кратковременное взаимодействие с волнами в резонаторах и т.д. На этом мы сейчас не будем останавливаться по двум причинам.
Во-первых, модели требуют анализа и экспериментальной проверки.
Во вторых, Эти вопросы достаточно обширны и требуют специального изложения.
В третьих, для нас сейчас более важной задачей является обсуждение полученных результатов. Мы не хотим, чтобы обсуждение свелось к анализу предлагаемых вариантов и гипотез.
14.6 Атом Бора
Результаты, полученные выше, позволяют по-новому взглянуть на гипотезу Бора о строении атома. Как известно, Бор выдвинул следующие положения:
1. Электрон, двигаясь по стационарной орбите вокруг атомного ядра, не излучает электромагнитных волн. Добавление.
Проведенный анализ подтверждает это положение. Поля заряда являются мгновенно действующими и не рождают волн. Добавим, что положение электрона на стационарной орбите является относительно устойчивым
.
2. При воздействии электромагнитной волны (квантов) электрон может перейти с низкого на более высокий энергетический уровень, т.е. на соответствующую этому уровню стационарную орбиту. Добавление.
При этом переходе электрон не только поглощает энергию электромагнитной волны, но и должен рассеивать
падающую на него волну.
3. При переходе с более высокого энергетического уровня на более низкий электрон излучает квант энергии. Добавление.
Поскольку положение электрона на орбите относительно устойчиво, он должен переходить на более низкий энергетический уровень только при наличии некоторого внешнего
воздействия, например, при воздействии электромагнитной волны, но не «спонтанно».
С позиции классической электродинамики можно добавить следующее. Поскольку излученная энергия (квант) представляет собой электромагнитный импульс, имеющий узкополосный спектр, «связку» электрон – ядро можно рассматривать как резонансную
систему с высокой добротностью. Существование дискретных энергетических уровней свидетельствует о том, что «связка» должна описываться нелинейными уравнениями или же нелинейными параметрическими уравнениями.
Есть еще точки, о которых следует помнить. Между макромиром и микромиром нет «непроходимых» границ. Природа не имеет «разрывов». Можно предположить следующее:
1. Вокруг атомного ядра существует короткодействующее
поле неэлектромагнитного происхождения, которое не дает электрону приблизиться к ядру. Это поле должно определять устойчивые орбиты движения электрона.
2. Заряд это протяженная
структура. Точечный заряд это идеализация, которая справедлива, когда внешние поля внутри заряда однородны (см. Главу 3, Приложение 1 к параграфу 3). Если заряд находится вблизи атомного ядра, то справедливость предположения об однородности электрического поля ядра внутри заряда зависит от соотношения размера электрона (радиуса электрона) и расстояния до ядра. По этой причине истинный размер электрона становится важным параметром.
3. Если внешнее поле внутри электрона неоднородно, то неизбежна «перестройка
» структуры электрона. При этом должно быть изменение массы электрона (и заряда?). Более того, возможно, что такие изменения имеют «дискретный» характер (существует набор устойчивых состояний).
4. Описание устойчивой частицы вероятностными методами квантовых теорий есть паллиатив, полумера
. Что касается «корпускулярно-волнового дуализма», то противоречивость этой гипотезы очевидна.
Таковы возможные подходы к микромиру с классических позиций.
15.1 Постановка задачи
Эта задача появилась благодаря желанию разобраться в процессах, происходящих при прохождении волной фокуса. В геометрической оптике пучки параллельных лучей, проходя тонкую круглую линзу, сходятся в точку, именуемую фокусом, как показано на рис. 15.1.

Геометрическая оптика это предел волновой оптики. А что же происходит «на самом деле» в этой точке, т.е. в окрестности фокуса? Анализ показывает, что при конечной длине волны такой точки не существует. Волновая оптика свидетельствует, что волна, имеющая после прохождения линзы сферический фронт, по мере приближения к фокусу преобразуется. В окрестности фокуса она превращается в «трубку», где форма фронта становится плоской, как показано на рис. 15.2 [1].
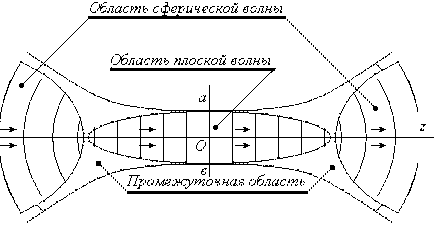
Рис. 15.2. Характер фронтов волны в окрестности фокуса
Между областями плоской и сферической волн появляется промежуточная (дифракционная) область, где происходят амплитудные и фазовые преобразования сферической волны в плоскую и обратно. Пример распределения интенсивности светового потока в фокальной плоскости приведен на рис. 15.3.
Рис. 15.3. Распределение интенсивности по сечению луча в фокальной плоскости
Все это согласуется с представлениями, сложившимися в волновой теории света и в теории электромагнитных колебаний. Например, в теории синфазных антенн (рупорные или зеркальные антенны) плоскость а
-О-в
(фокальная плоскость) рассматривается как излучающая поверхность синфазной антенны. А область, простирающаяся от фокальной плоскости до перехода плоской волны в сферическую, является зоной формирования главного луча антенны.
Однако при детальном рассмотрении есть аспект в существующих представлениях, который вызывает сомнения с физической точки зрения. Речь идет о «скачке фазы» волны при прохождении волной фокальной плоскости. Как утверждается в современной теории (см., например, [2]), волна, проходя фокальную плоскость (фокус) изменяет свою фазу на угол 180о
, как показано на рис. 15.4.
Рис. 15.4. Скачок фазы при прохождении волной фокуса
Хотя эти «скачки фазы» следуют как из приближенных, так и из точных математических решений уравнений волновой электродинамики, они вызывают сомнение в своей «физичности». В природе таких резких скачков не существует.
15.2 Переопределение областей изменения аргумента
Уравнение Гельмгольца для потенциала u
,
Δu
+ k
2
u
= 0 (15.2.1)
распространяющегося вдоль оси z
и сходящегося в фокус в начале координат сферической системы, приводит к следующему решению
u
(15.2.2)
 n
m
kr n
m
kr
где amn
и bmn
постоянные, которые определяются из условий задачи; Pm
n
– шаровые функции; Jn+1/2
(kr
) – функция Бесселя; m
, n
= 0, 1, 2, … .
По условию задачи угол раствора конуса сходящейся в фокус волны должен быть ограничен величиной 0 < θ < π / 2.
Расположим ось z
вертикально, как показано на рис. 15.
5.
Рис. 15.5
В современной теории область определения независимых переменных в сферических координатах определяется следующим образом: r
(0 ÷ ∞); θ (0 ÷ π); ϕ (0 ÷ 2π). Однако мы можем изменить ее, приняв, например, следующие:
r
(- ∞ ÷ ∞); θ (0 ÷ π); ϕ (0 ÷ π), или r
(- ∞ ÷ ∞); θ (0 ÷ π/2); ϕ (0 ÷ 2π) и др.
Конечно, здесь могут возникнуть возражения, касающиеся цилиндрической системы координат. Этот вопрос будет рассмотрен и обоснован позже.
Итак, сделаем очевидную замену переменных r
→ - r
; θ → (π - θ) и ϕ → (ϕ + π) в выражении (15.2.2). При такой замене точка А сохраняет неизменным свое положение в пространстве. u
 n
m
kr n
m
kr
 n
m
kr n
m
kr
Как мы видим, выражение сохранило прежний вид, что подтверждает наше допущение о возможности использовать функцию r
в области ее отрицательных
значений. А это, в свою очередь позволяет анализировать различные представления функций Бесселя и записывать математические результаты в удобно интерпретируемой форме.
В последующем мы будем использовать следующие известные соотношения [3], которые мы позже обоснуем с других позиций.
1 i
π
e
i
πn
(−1)n
   J
n
+
1/ 2
(kre
) = n
+
1/ 2
(kr
)] = (kr
) (15.2.3) J
n
+
1/ 2
(kre
) = n
+
1/ 2
(kr
)] = (kr
) (15.2.3)
N
n
+
1/ 2
(kre
i
π
) =N
n
+
1/ 2
N
n
+
1/ 2
(kr
) (15.2.4)
H
n
(1+)1/ 2 (kre
i
π) =n
(2+1) / 2 (kr
) (15.2.5)
H
n
(2+1) / 2 (kre
i
π) =n
(1+)1/ 2 (kr
) (15.2.6)
Вернемся к выражению (15.2.2) и представим функцию Бесселя в виде суммы функций Ганкеля первого и второго рода
1 m
 u
= ∑∑ J
n
+
1/ 2
(kr
)P
n
(cosθ)[a
mn
cosm
ϕ+ b
mn
sinm
ϕ] = u
= ∑∑ J
n
+
1/ 2
(kr
)P
n
(cosθ)[a
mn
cosm
ϕ+ b
mn
sinm
ϕ] =
n m
b
mn
sinm
ϕ]
n
m
2 kr
В силу обозначенных ранее условий для сходящейся в фокус волны, решение может выражаться через функцию Ганкеля второго рода. По этой причине мы преобразуем первый член суммы функций Ганкеля в скобках, используя область отрицательных значений r
(см. рис. 15.5).
Сделаем очевидную замену переменных в функции Ганкеля первого рода r
→ - r
; θ → π - θ и ϕ → ϕ + π и воспользуемся выражением (15.2.5). При такой замене, как уже говорилось, точка А сохраняет свое положение в пространстве неизменным.
 b
mn
sinm
(ϕ + π)] = (15.2.7) b
mn
sinm
(ϕ + π)] = (15.2.7)
b
mn
sin m
ϕ]
Выражения (15.2.2) или (15.2.7) для той же задачи мы можем преобразовать и к другой форме
 1 1
Хотя мы провели все выкладки формально корректно, результат получился неожиданным (можно сказать: фантастическим
). Его необходимо каким-то образом объяснить, поскольку выражения (15.2.2), (15.2.7), (15.2.8) несопоставимы с физической точки зрения. Заключение о том, что нельзя использовать область отрицательных значений радиуса, мы отбросим, как некорректное.
15.3 «Скрытые» источники потенциала
Итак, попытаемся выяснить причины получения противоречивых результатов. Обратимся к закону сохранения энергии [4] и запишем интегралы для потоков.
1 ∂u
* 0 *
П
= ∫
S
2i
ωu
 ∂r
r
ds
, где u
- комплексно сопряженное значение потенциала. ∂r
r
ds
, где u
- комплексно сопряженное значение потенциала.
Интегрирование будем вести по поверхности сферы постоянного радиуса R
с областью определения переменных: r
(- ∞÷ ∞); θ (0 ÷ π/2); ϕ (0 ÷ 2π)
Рассмотрим для сравнения один и тот же член суммы в выражениях (15.2.2), (15.2.7), (15.2.8), например, с индексами m
и n.
Выражение (15.2.2)
i
ωr
2 ∂ (J
n
+1/ 2 ) 2 π / 2 2πi
ω m
2
  П
= ∫ ∫
4 [P
n
(cosθ)[a
mn
cosm
ϕ+ b
mn
sin m
ϕ] sinθd
ϕd
θ − П
= ∫ ∫
4 [P
n
(cosθ)[a
mn
cosm
ϕ+ b
mn
sin m
ϕ] sinθd
ϕd
θ −
4 ∂r kr
0 0R
  [P
n
m
(cosθ)[a
mn
cosm
ϕ+ b
mn
sin m
ϕ]2
sinθd
ϕd
θ = 0 [P
n
m
(cosθ)[a
mn
cosm
ϕ+ b
mn
sin m
ϕ]2
sinθd
ϕd
θ = 0
Мы получили нуль, поскольку меняется направление
вектора плотности потока по отношению к внешней нормали поверхности сферы n
0
.
Выражения (15.2.7) и (15.2.8). Здесь для оценки выберем достаточно большой радиус R
, чтобы воспользоваться асимптотическими формулами для функций Ганкеля.
 H
n
(1+)1/ 2 (kr
) ≈e
i
(kr
−n
π / 2−π / 2) (1+ O
(1/ kr
)); H
n
(1+)1/ 2 (kr
) ≈e
i
(kr
−n
π / 2−π / 2) (1+ O
(1/ kr
));
H
n
(2+1) / 2 (kr
) ≈e
−i
(kr
−n
π / 2−π / 2) (1+ O
(1/ kr
))
Нетрудно видеть, что при больших R
имеем для (15.2.8)
π / 2 2π
 2k
ω m
2 2 2k
ω m
2 2
 П
≈ −2[P
n
(cosθ)] [a
mn
cosm
ϕ + b
mn
sin m
ϕ] sinθd
ϕd
θ = П
≈ −2[P
n
(cosθ)] [a
mn
cosm
ϕ + b
mn
sin m
ϕ] sinθd
ϕd
θ =
(15.3.1)
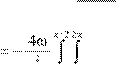 [P
n
m
(cosθ)]2
[a
mn
cosm
ϕ + b
mn
sinm
ϕ]2
sinθd
ϕd
θ π k
0 0 [P
n
m
(cosθ)]2
[a
mn
cosm
ϕ + b
mn
sinm
ϕ]2
sinθd
ϕd
θ π k
0 0
и для (15.2.7)
 4ω m
2 2 4ω m
2 2
П
∫ ∫
(15.3.2) π
k
0 0
Здесь мы учли, что интегралы для R
и для -R
одинаковы.
Поскольку в свободном пространстве нет источников, поток направлен от центра системы координат (15.2.7) или к центру (15.2.8). Исходя из физических соображений, можно сказать, что это может быть только в том случае, если в начале координат существует излучающий источник (15.2.7) или источник, поглощающий энергию (152.8). Сингулярность при r
= 0 в уравнении Бесселя приводит к появлению «скрытых» источников, что фактически равнозначно неоднородному уравнению Бесселя с мультипольными источниками типа δ - функций в начале координат (см. рис. (15.6)).
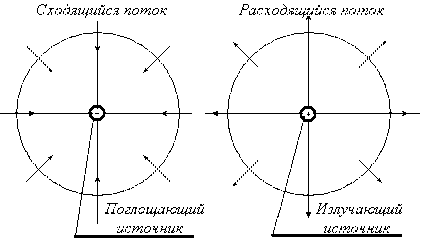
Рис. 15.6 Иллюстрация к функциям Ганкеля
С этой физической точки зрения использовать функции N
ν
и H
ν
следует осмотрительно.
Все волновые решения в свободном
пространстве всегда могут быть выражены формулой
u
 n
m
kr n
m
kr
Эту формулу можно рассматривать как суперпозицию полей, создаваемых излучающими и поглощающими мультипольными источниками, когда эти источники одной природы как бы взаимно уничтожают («гасят») друг друга, но их поля, распространяющиеся в противоположных направлениях, сохраняются.
15.4 Поведение волны в окрестности фокуса
Теперь мы можем вернуться к первому параграфу «Постановка задачи».
Пусть мы имеем волновой поток, сходящийся в фокус в начале координат (15.2.2). Не ограничивая общности рассуждений, будем считать его симметричным, независимым от угла ϕ. Окружим начало координат сферической поверхностью радикса R
. Будем также считать, что внутренняя поверхность тонкой линзы также сферическая, и выбранная нами сфера касается этой поверхности. Дифракционные явления на краях линзы мы рассматривать не будем. Нас будет интересовать потенциал внутри сферы.
Общее поле внутри сферы можно представить в виде суммы полей, бегущих к центру (к «скрытым» поглощающим
мультипольным источникам) и суммы полей, убегающих от центра (от «скрытых» излучающих
мультипольных источников). Опираясь на принцип суперпозиции, рассмотрим волну, идущую к центру (к поглощающим источникам).
 a
n a
n
 u
1 = ∑H
nn
+1/ 2 (kr
)P
n
(cosθ) n kr u
1 = ∑H
nn
+1/ 2 (kr
)P
n
(cosθ) n kr
Распределение амплитуды синфазного потенциала на поверхности линзы определяется выражением
a
n
   u
1
= ∑H
nn
+
1/ 2
(kr
)P
n
(cosθ)=U
0
(θ) u
1
= ∑H
nn
+
1/ 2
(kr
)P
n
(cosθ)=U
0
(θ)
n kr
r
=R
где U
0
(θ) – комплексная амплитуда потенциала. Она отлична от нуля на внутренней поверхности линзы и равна нулю на остальной поверхности.
Найдем коэффициенты an
в этом выражении. Опираясь на ортогональность полиномов
Лежандра, можно записать
 (2n
+1) kR
1
a
n
=
(2
) ∫
U
0
(arccosx
)P
n
(x
)dx (2n
+1) kR
1
a
n
=
(2
) ∫
U
0
(arccosx
)P
n
(x
)dx
H
n
+1/ 2 (kR
)
−1
Итак, для волны, идущей к началу координат мы имеем
R H
(2) (kr
) 1
 u
1
= ∑
n
r H
n
+1/ 2 (kR
)
−1 (arccosx
)P
n
(x
)dx
(15.4.1) u
1
= ∑
n
r H
n
+1/ 2 (kR
)
−1 (arccosx
)P
n
(x
)dx
(15.4.1)
Теперь запишем волну, уходящую из начала координат. Ее можно получить, заменив r
на –r
, а θ → π - θ и преобразуя полученное выражение.

Теперь осталось записать суммарное решение
u
1
+ u
2
R J
n
+
1/ 2
(kr
) 1
 u
= = ∑
(2n
+1) r H
n
(2
+1) / 2 (kR
)
P
n
(cosθ)−∫
1U
0
(arccosx
)P
n
(x
)dx
(15.4.2) u
= = ∑
(2n
+1) r H
n
(2
+1) / 2 (kR
)
P
n
(cosθ)−∫
1U
0
(arccosx
)P
n
(x
)dx
(15.4.2)
2
n
Как можно заметить, потенциал u
непрерывен вместе со своей первой производной, а каких-то скачков фазы нет и быть не может. Характер изменения потенциала иллюстрируется рис. 15.1.
В частности, если мы рассмотрим плоскую волну в сферической системе, то при сколь угодно большом радиусе сферы (R
→ ∞) потенциал можно записать как u
= U
0
exp(ikz
) = = U
0
exp(ikr
cosθ). Следуя приведенной выше методике, можно получить хорошо известное выражение для плоской волны, бегущей против оси z
.
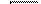 ∞ ∞
u
=U
0e
ikz
=U
0e
ikr
cos θ =U
0∑i
n
(2n
+1)J
n
+1/ 2 (kr
)P
n
(cosθ)
n
=0
15.5 Вронскиан функции Бесселя
Как мы обещали, перейдем теперь к цилиндрической системе. Однако прежде сделаем небольшое замечание. Как известно, фундаментальное решение уравнения Бесселя индекса ν
d
2
R
(z
) dR
(z
) 2
 2
+ +[1− (ν / z
) ]R
(z
) = 0 (15.5.1) dz zdz 2
+ +[1− (ν / z
) ]R
(z
) = 0 (15.5.1) dz zdz
есть
R
(z
) = C
1
J
ν
(z
) + C
2
N
ν
(z
)
где J
ν
(z
) и N
ν
(z
) – функция Бесселя и функция Неймана.
Запишем определитель Вронского [5] для уравнения (15.5.1)
1
 W
(z
) = Ce
−
∫ z
dz
= Ce
−ln W
(z
) = Ce
−
∫ z
dz
= Ce
−ln  z z
где С
некоторая константа, которая выбирается из определенных соображений.
 Итак, мы показали, что W
(z
) есть четная
функция независимой переменной. В то же время, в современной математической литературе [3] вронскиан уравнения Бесселя также не зависит от индекса ν, но оказывается пропорциональным не 1/ z
, а 1/z
, т.е. является нечетной
функцией z.
Для положительных значений аргумента z
вещественной оси такое представление не имеет значения. Однако для отрицательных значений вещественной оси (равно как и для комплексных) это весьма принципиально. Итак, мы показали, что W
(z
) есть четная
функция независимой переменной. В то же время, в современной математической литературе [3] вронскиан уравнения Бесселя также не зависит от индекса ν, но оказывается пропорциональным не 1/ z
, а 1/z
, т.е. является нечетной
функцией z.
Для положительных значений аргумента z
вещественной оси такое представление не имеет значения. Однако для отрицательных значений вещественной оси (равно как и для комплексных) это весьма принципиально.
15.6 В каких случаях вронскиан является четной (нечетной) функцией?
Рассмотрим общий случай, т.е. линейное дифференциальное уравнение второго порядка, сохраняющее свой симметричный вид относительно замены положительного аргумента на отрицательный аргумент. Такое уравнение имеет вид y
''+p
(z
)y
'+q
(z
)y
= 0 (15.6.1)
В силу выбранного нами типа уравнений, коэффициент p
есть нечетная
функция, а q
четная
функция переменной z
.
Рассмотрим теперь случаи, в каких случаях вронскиан уравнения (15.6.1) является четной, а в каких - нечетной функцией.
Для этого запишем определитель Вронского в следующей форме
' ' 2
d y
2
W
(z
) = y
1
y
2
− y
2
y
1
= y
1
 (15.6.2) dz y
1 (15.6.2) dz y
1
где функции y
1
(z
) и y
2
(z
) образуют фундаментальную систему решений уравнения
(15.6.1).
Выберем в качестве y
1
(z
) и y
2
(z
) такие функции, которые были бы четными (нечетными) относительно знака z.
Это следует из четности уравнения (15.6.1).
Здесь возможны два варианта:
f. Функции y
1
(z
) и y
2
(z
) являются одновременно четными
или же нечетными.
g. Одна из функций (y
1
(z
) или y
2
(z
)) является четной
, а вторая – нечетной
.
Нетрудно видеть, что в первом случае отношение y
2
(z
) / y
1
(z
) является четной
функцией. Следовательно, определитель Вронского будет нечетной
функцией z.
Во втором случае это отношение будет нечетной
функцией z.
По этой причине вронскиан останется четной
функцией.
Итак, чтобы определитель Вронского был бы четной
функцией z,
необходимо и достаточно, чтобы фундаментальная система решений могла быть представлена в виде четной и нечетной функций. Общее решение уравнения (15.6.1), составленное из такой фундаментальной системы, мы назовем физическим
решением.
15.7 Физическое решение
Запишем уравнение Бесселя для цилиндрической системы отсчета d
2
R
(r
) dR
(r
) 2
 2
+ +[1− (n
/ r
) ]R
(r
) = 0 dr rdr 2
+ +[1− (n
/ r
) ]R
(r
) = 0 dr rdr
Из уравнения следует, что в начале координат имеет место особенность (сингулярность).
Для положительных значений r
общее решение уравнения Бесселя имеет вид
R
(r
) = C
1
J
n
(r
) + C
2
N
n
(r
)
Функция Бесселя Jn
(r
) является четной
функцией для четных
значений n
(n =
0, 2, 4, …) и нечетной
для нечетных
значений n.
Теперь нам необходимо «построить» второе фундаментальное решение так, чтобы оно было нечетным
для четных
значений n
и четным
для нечетных
значений. Иными словами, нам необходимо заново определить Nn
(r
) для отрицательных
значений аргумента.
Мы поступим следующим образом. Поскольку функция Nn
(r
) имеет сингулярность в нуле, мы пока исключим из рассмотрения точку 0 и доопределим эту функцию для отрицательных значений r
следующим образом.
Пусть Nn
(- r
) = Nn
(r
) для нечетных
значений n
(четная
функция) и Nn
(- r
) = - Nn
(r
) для четных
значений (нечетная
функция). Вблизи нуля нечетная функция Nn
(r
) обращается в ± ∞. Несмотря на это, в точке 0 нечетная
функция Nn
(r
) должна принимать значение 0.
Заметим, что при таком определении Nn
(r
) будет соблюдаться правильное чередование нулей функций Jn
(r
) и Nn
(r
) на всей действительной оси в полном соответствии с теоремой Штурма [4]. Мы не будем вводить специальные обозначения для нового определения функции Nn
(r
).
Мы изложили схему построения физического решения. Обоснование ее должно опираться на теорию обобщенных функций, что выходит за рамки нашей статьи.
Соотношения для бесселевых функций целого индекса (физические решения
) при изменении знака аргумента приведены ниже.
Jn
(- r
) = (- 1)n
Jn
(r
); Nn
(- r
) = (- 1)n+
1
Nn
(r
);
H
(1)
n
(- r
) = H
(2)
n
(r
); H
(2)
n
(- r
) = H
(1)
n
(r
)
В этой связи мы можем использовать не только традиционные области определения переменных в цилиндрической системе координат: z
(- ∞ ÷ ∞); r
(0 ÷ ∞); ϕ (0 ÷ 2π), но и, например, такие: z
(- ∞ ÷ ∞); r
(- ∞ ÷ ∞); ϕ (0 ÷ π).
Рассмотрим цилиндрическую волну, сходящуюся в начале координат плоскости (r
; ϕ) и расходящуюся после прохождения начала. Как и в случае сферических волн никаких скачков фазы при прохождении волной начала координат не образуется. Это можно показать тем же способом, что и для сферической волны.
Замечание
. Аналогичным образом можно построить фундаментальную систему из четной и нечетной функций и для мнимых значений r.
Здесь имеется возможность продолжить в некотором смысле аналогию с тригонометрическими и гиперболическими функциями.
15.8 Скачки фазы в каустиках и фокусе
Из дифференциальной геометрии известно, что всякая поверхность имеет для каждого своего бесконечно малого элемента два, в общем случае, различных радиуса кривизны. Как показано на рис. 15.7, линии aОc
и bОd
есть главные круги кривизны с радиусами кривизны R
1
и R
2
, центры кривизны которых расположены в точках О
1
и О
2
.
С точки зрения геометрической оптики интенсивность волнового потока будет обращаться в бесконечность в центрах кривизны О
1
и О
2
. Отталкиваясь от элемента поверхности и переходя ко всей волновой поверхности, можно утверждать, что интенсивность волнового потока будет бесконечно возрастать, вообще говоря, на двух поверхностях, которые являются геометрическим местом кривизны волновой поверхности. Эти поверхности носят название каустик
. В частном случае, когда поверхность имеет сферический фронт, обе каустики сливаются в точку, которая именуется фокусом
. В случае цилиндрического волнового фронта каустики вырождается в линию.
Рис. 15.7
Конечно, бесконечное возрастание интенсивности при прохождении каустики или при прохождении фокуса есть «огрех» геометрической оптики как предела волновой. На самом деле плотность потока в этих случаях действительно сильно возрастает, но, как мы убедились, не до бесконечности.
Рассмотрим более важный для нас вопрос о скачках фазы. Обратимся к доказательству, приведенному в монографии [6]. Цитируем:
«Если плоскости XY и XZ выбраны совпадающими с главными плоскостями кривизны волновой поверхности в точке
0, то вблизи этой точки уравнение поверхности есть
y
2 z
2
 X
= + X
= +
2R
1
2R
2
где R1
и R2
- главные радиусы кривизны. Расстояние же R от точки волновой поверхности с координатами X, y, z до точки Р с координатами
x
, 0, 0 есть
2 2
2 2 2
y
1 1 z
1 1
  R
= (X
− x
) + y
+ z
≈ x
+ ( − )+ ( − ) R
= (X
− x
) + y
+ z
≈ x
+ ( − )+ ( − )
2 x R
1
2 x R
2
Вдоль волновой поверхности поле u можно считать постоянным; то же касается множителя
1 / R. Поскольку мы интересуемся только изменением фазы волны, то коэффициент опускаем и пишем просто
 1 ikR e
ikx
∞ ik y
22 ( 1x
−R
11 ) e
ikx
∞ ik z
22 ( 1x
−R
12 ) 1 ikR e
ikx
∞ ik y
22 ( 1x
−R
11 ) e
ikx
∞ ik z
22 ( 1x
−R
12 )
u
P
∝  ∫e df
n
≈ i
−∫
∞e dy
i
−∫
∞e dz
(59,3) ∫e df
n
≈ i
−∫
∞e dy
i
−∫
∞e dz
(59,3)
i
Центры кривизны волновой поверхности лежат на рассматриваемом луче в точках
x
= R
1
и x
= R
2
; это и есть точки касания лучом каустик. Пусть
R
2
< R
1
. При
x
< R
2
коэффициенты при i в показателях подынтегральных выражений в обоих интегралах
(по dy и dz
) положительны, и каждый из этих интегралов пропорционален
(1+ i
). Поэтому на каждом участке луча до касания первой каустики имеем
uP
∝ eikx
. При
R
2
< x
< R
1
, т.е. на отрезке луча между двумя точками касания, интеграл по dy пропорционален
(1+ i), а интеграл по dz пропорционален
(1- i
), так что их произведение не содержит
i
. Таким образом имеем здесь uP
∝ - i eikx
, т.е. при прохождении луча вблизи первой каустики фаза дополнительно меняется на
- π / 2. Наконец, при
x
> R
1
имеем
uP
∝ - eikx
= eikx
+ i
π
, т.е. при прохождении луча вблизи второй каустики фаза еще раз меняется на
- π / 2.».
Покажем теперь ошибку.
 Величина R
= (X
− x
) 2
+ y
2
+ z
2
всегда положительна
. Поэтому приближенное выражение в отличие от цитированного выше должно иметь следующий вид Величина R
= (X
− x
) 2
+ y
2
+ z
2
всегда положительна
. Поэтому приближенное выражение в отличие от цитированного выше должно иметь следующий вид
R
=  ) ≥ 0 ) ≥ 0
По этой причине интеграл (59,3) не может изменять фазу скачком на - π / 2 при касании каустики. По той же причине волна не может испытывать скачок фазы на - π при прохождении фокуса даже в рамках геометрической
оптики.
Краткие выводы
a. Решения, выражаемые через функции Ганкеля, содержат «скрытые» источники поля. Последние возникают благодаря наличию сингулярностей в однородных уравнениях
Бесселя или в уравнениях сводимым к ним. По этой причине требуется корректное (физически интерпретируемое, а не формальное) использование этих функций.
b. Учет «скрытых» источников однородных уравнений (возникающих из-за
сингулярностей в коэффициентах уравнений) позволяет дать физически ясное объяснение волновым процессам и упростить в некоторых случаях постановку задачи и ее решение.
c. Помимо этого, показана возможность построения решений для области отрицательных
значений радиуса как в цилиндрической, так и в сферической системах координат.
d. Дан анализ причины, по которой определитель Вронского для уравнения Бесселя
считается нечетной функцией аргумента. Рассматривается возможность построения такой фундаментальной системы, в которой этот определитель становится четным, что важно для построения решений в цилиндрической системе координат.
e. Полученные результаты позволяют изучать особенности потенциала волны в
окрестности фокуса (каустики). Анализ поведения волны в окрестности фокуса (каустик) показал, что при прохождении фокуса (или касания лучом каустики) волна не испытывает скачка фаз. Решение в этой области непрерывно вместе со своей первой производной. Утверждения типа: «волна при прохождении фокуса изменяет фазу на - π» - некорректны как с физической точки зрения, так и с математической (т.е.
ошибочны).
f. Рассмотрен физический смысл задачи по определению потенциала внутри замкнутого объема по заданному потенциалу и его нормальной производной на поверхности, ограничивающей объем. Рассмотрена подробно задача для сферической поверхности. Показано, что формула Кирхгофа имеет несколько вариантов, физический смысл которых рассматривается.
15.9 Определение потенциала поля внутри сферы
Плоский случай.
Рассмотрим бесконечно малый элемент поверхности. Его можно считать плоским. Пусть на поверхности задан потенциал и задана нормальная производная этого потенциала. Поскольку поверхность элемента мала, потенциал и его производную можно считать постоянными, а поле вблизи этой поверхности можно представить как сумму двух плоских волн, распространяющихся в противоположных направлениях коллинеарно нормали. Потенциал удовлетворяет уравнению Δu
= 0.

Рис. 15.8
Потенциал падающей волны uп
eikx
, а выходящей волны uв
e-ikx
. При малых расстояниях и размерах амплитуды этих постоянны, но имеют комплексную форму. На поверхности S
(при х = Х
) будем иметь следующие выражения для потенциала на поверхности и его производной:
U
( X
) = u
п
( X
)e
ikX
+ u
в
( X
)e
−
ikX
(15.9.1)
 ∂u
ikX
−
ikX ∂u
ikX
−
ikX
 = ikV
(X
) == ik
[u
п
e
−u
в
e
] (15.9.2) = ikV
(X
) == ik
[u
п
e
−u
в
e
] (15.9.2)
∂n
x
=Xx
=X
Комбинируя (15.9.1) и (15.9.2) можно найти амплитуды падающей и выходящей волн.
U(X)
+V(X)
-ikX
U
(X
) −V
(X
) ikX
u
п
=  e u
в
= e u
в
=  e (15.9.3) e (15.9.3)
2 2
Таким образом, задача решена, т.е. найдены комплексные амплитуды падающей и выходящей волн.
Косое падение волны.
Тот же подход возможен при подходе волны под углом π - ϕ к поверхности y
= 0.
Пусть волна описывается потенциалом
u
(x
; y
) =Ue
ik
(x
cos ϕ+y
sin ϕ)
На поверхности y
= 0 потенциал будет равен u
(x
;0) =Ue
ikx
cos
ϕ
=Ue
i
ψ
, (15.9.4) где ψ(х
) можно рассматривать как фазу волны в точке х.
Нормальная производная при y
= 0 равна (нормаль совпадает по направлению с осью у
)
∂u
∂u
i
ψ
 = = ikU
sinϕe
(15.9.5) = = ikU
sinϕe
(15.9.5)
∂n
∂y
Нам необходимо, пользуясь этими значениями, записать волны, переносящие энергию. Но необходимо записать их так, чтобы эти волны удовлетворяли специфическому волновому уравнению в окрестности бесконечно малой площадки поверхности.
∂ 2u
2
 2 + k u
= 0 2 + k u
= 0
∂n
Иными словами, это волны, идущие колинеарно нормали. С этой точки зрения выражения (15.9.4) и (15.9.5) мы формально можем представить в виде суммы двух волн с волновым вектором k
, идущих нормально к поверхности, но в противоположных направлениях.
i
ψ
(x
)
∂u
i
ψ
( x
)
 u
(x
;0) =Ue
= u
п
+ u
в
= ikU
sinϕe
= ik
(u
п
−u
в
) u
(x
;0) =Ue
= u
п
+ u
в
= ikU
sinϕe
= ik
(u
п
−u
в
)
∂n
н
=0
Отсюда можно найти u
п
=  U
(1+ sinϕ)e
i
ψ
(x
)
u
в
= U
(1+ sinϕ)e
i
ψ
(x
)
u
в
= 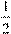 U
(1−sinϕ)e
i
ψ
( x
) U
(1−sinϕ)e
i
ψ
( x
)
Такова, на наш взгляд, интерпретация этой задачи.
Сферическая поверхность.
Задача определения потенциала внутри сферы
, ограничивающей некоторый объем, по заданной величине потенциала и его нормальной производной на поверхности решается аналогично.
Пусть имеется сферическая поверхность, на которой задан потенциал и его нормальная производная. Пусть потенциал внутри сферы, включая ее границы (поверхность) описывается уравнением Гельмгольца Δu
= 0. Источники, создающие потенциал, находятся вне этой сферы. Необходимо определить потенциал внутри сферы.
Это обычная (классическая) задача, с которой сталкиваются в теории дифракции, теории антенн и т.д. Ее решение сводится к решению предыдущей задачи.
Потенциал на поверхности сферы радиуса R
определяется суммой волн, которые распространяются как внутрь сферы, так и из этой сферы. Можно сказать, что потенциал на поверхности и вблизи нее в каждом бесконечно малом элементе поверхности складывается из потенциала уходящей из сферы волны и потенциала входящей в сферу волны
U
(R,
θ;ϕ) = uп
(θ;ϕ) eikR
+ uв
(θ;ϕ) e-ikR
, (15.9.4)
где θ;ϕ – координаты поверхности сферы радиуса R.
Амплитуды uп
(θ;ϕ) и uв
(θ;ϕ) являются, вообще говоря, комплексными.
Будем считать, что потенциал и его нормальная производная непрерывны вблизи поверхности сферы и имеют следующий вид на сколь угодно малом расстоянии от нее
U
(r,
θ;ϕ) = uп
(θ;ϕ) eikr
+ uв
(θ;ϕ) e-ikr
, R
+ ε > r
> R -
ε; где ε - сколь угодно малая величина.
Нормальная производная на поверхности R
= const также будет складываться из производных по нормали от потенциалов этих волн, как и в предыдущем случае
 ∂u ∂u
 = ikV
(θ;ϕ) = = = ikV
(θ;ϕ) = =
∂n
r
=
R
(15.9.5)
= ik
[u
п
(θ;ϕ)e
ikR
+ u
в
(θ;ϕ)e
−
ikR
]
Комбинируя выражения (15.9.4) и (15.9.5), можно определить амплитуды uп
(s
) и uв
(s
) на поверхности сферы.
U
(θ;ϕ) +V
(θ;ϕ) =
ikR
u
п
(θ;ϕ) =  e (15.9.6) e (15.9.6)
2
U
(θ;ϕ) −V
(θ;ϕ) ikR
u
в
(θ;ϕ) =  e (15.9.7) 2 e (15.9.7) 2
 Теперь, зная амплитуды падающей и выходящей волн, можно определить потенциалы внутри сферы. Для этого запишем выражения для каждой из этих волн в виде ряда. u
п
= ∑∑a
mn
H
n
(1
+
)
1/ 2
(kr
)Y
mn
(θ;ϕ) (15.9.8) Теперь, зная амплитуды падающей и выходящей волн, можно определить потенциалы внутри сферы. Для этого запишем выражения для каждой из этих волн в виде ряда. u
п
= ∑∑a
mn
H
n
(1
+
)
1/ 2
(kr
)Y
mn
(θ;ϕ) (15.9.8)
n m
u
в
= ∑∑b
mn
H
n
(2
+
1
)
/ 2
(kr
)Y
mn
(θ;ϕ) (15.9.9)
n m
где amn
и bmn
–
неизвестные коэффициенты, H
(kr
) – функции Ганкеля первого и второго рода, Ynm
– шаровые (сферические) функции.
Приравняем выражения (15.9.6) и (15.9.8), а также (15.9.7) и (15.9.9) попарно при r
= R
. Теперь, раскладывая выражения (15.9.6) и (15.9.7) в ряд по шаровым функциям, можно определить неизвестные коэффициенты amn
и bmn
.
Здесь следует обратить внимание на тот факт, что выражения (15.9.8) и (15.9.9) имеют особенность в начале координат («скрытые» источники). Об этом мы писали. В решении, которое определяется суммой выражений (15.9.8) и (15.9.9), таких источников не будет. Покажем это.
Пусть потенциал внутри сферы определяется суммой выражений (15.9.8) и (15.9.9).
 1 (2) u
(r
;θ;ϕ) = ∑∑n m a
mn kr H
n
+1/ 2 (kr
)Y
mn
(θ;ϕ) + 1 (2) u
(r
;θ;ϕ) = ∑∑n m a
mn kr H
n
+1/ 2 (kr
)Y
mn
(θ;ϕ) +
(15.9.10)
1 (1)
+ ∑∑n m b
mn kr H
n
+1/ 2 (kr
)Y
mn
(θ;ϕ)
Сделаем замену переменных в этом выражении: r
→ - r
; θ → π - θ; ϕ → π + ϕ . Как следует из [1], мы используем тождественное преобразование, когда каждая точка возвращается на свое место (не меняет своего положения). Выражение (15.9.10) примет вид
  u
(r
;θ;ϕ) = H
n
(2+1) / 2 (−kr
)Y
mn
(π−θ;ϕ+ π) + u
(r
;θ;ϕ) = H
n
(2+1) / 2 (−kr
)Y
mn
(π−θ;ϕ+ π) +
+ ∑∑b
mn
(−kr
)Y
mn
(π−θ;ϕ+ π) = (15.9.11)
n m
= ∑∑a
mn
mn
(θ;ϕ) + ∑∑b
mnH
n
(2+1) / 2 (kr
)Y
mn
(θ;ϕ)
n mn m
 Сравнивая (15.9.10) и (15.9.11), можно заметить, что оба выражения совпадут, если коэффициенты amn
и bmn
будут тождественно равны друг другу. В этом случае мы получаем окончательное выражение для потенциала внутри сферы и на ее поверхности u
(r
;θ;ϕ) = 2∑∑a
mn
J
n
+
1/ 2
(kr
)Y
mn
(θ;ϕ) Сравнивая (15.9.10) и (15.9.11), можно заметить, что оба выражения совпадут, если коэффициенты amn
и bmn
будут тождественно равны друг другу. В этом случае мы получаем окончательное выражение для потенциала внутри сферы и на ее поверхности u
(r
;θ;ϕ) = 2∑∑a
mn
J
n
+
1/ 2
(kr
)Y
mn
(θ;ϕ)
n m
Это есть решение поставленной задачи.
15.10 Разные варианты формулы Кирхгофа
Как известно, потенциал u
волнового поля внутри объема Т
, ограниченного замкнутой поверхностью Σ, можно найти с помощью формулы Кирхгофа. Для вычисления потенциала в любой точке М
внутри объема Т
достаточно знать потенциал u
(Р
) и нормальную производную потенциала на этой поверхности ∂u
(Р
) / ∂n
[8], где Р
– точка, принадлежащая поверхности Σ (см. [2]).
1 ∂ e
−ikr e
−ikr
∂u
(Р
)
 u
(M
) = − u
(M
) = −  ∫∫
[u
(P
) ∂n
( k
) − k
∂n
]d
σP
(15.10.1), 4π Σ ∫∫
[u
(P
) ∂n
( k
) − k
∂n
]d
σP
(15.10.1), 4π Σ
где r
– расстояние между точками М
и Р.
Результаты позволяют записать несколько эквивалентных формулировок уравнения Кирхгофа, которые приводят к одному и тому же решению.
1 ∂ sin kr
sin kr
∂u
(Р
)
 u
(M
) = − u
(M
) = −  ∫∫
[u
(P
) ∂n
( k
) − k
∂n
]d
σP
(15.10.2) ∫∫
[u
(P
) ∂n
( k
) − k
∂n
]d
σP
(15.10.2)
4π Σ
1 ∂ e
ikr e
ikr
∂u
(Р
)
 u
(M
) = − u
(M
) = −  ∫∫
[u
(P
) ∂n
( k
) − k
∂n
]d
σP
(15.10.3) 4π Σ ∫∫
[u
(P
) ∂n
( k
) − k
∂n
]d
σP
(15.10.3) 4π Σ
Однако есть и отличие. Поясним причину такого утверждения. Сама логика доказательства формулы Кирхгофа корректна. Однако есть один момент, который допускает определенный произвол.
В качестве функции v
в формуле Грина [8] мы могли бы выбрать любую другую функцию, удовлетворяющую однородному уравнению Гельмгольца Δu
+k
2
u =
0, а не только функцию e-ikr
/ r.
Любое решение этого уравнения, которое мы выберем в качестве функции v,
позволяет однозначно дать решение задачи по нахождению потенциала внутри объема.
Действительно, потенциал на замкнутой поверхности Σ (равно его производная по нормали на поверхности) определяет не только волны, проникающие внутрь объема, но и волны, которые движутся изнутри объема к его поверхности и выходят из него.
По этой причине в объеме Т
в окрестности точки М
обязательно будут существовать не только поля, сходящиеся к этой точке (типа e-ikr
/ r
), но также поля, уходящие от нее (типа eikr
/ r
). Потенциал и нормальная производная на поверхности Σ полностью определяют искомый потенциал u
. В первом параграфе мы уже об этом говорили.
Хотя все три формулы дают одинаковый результат, между ними имеется одно отличие. Попробуем ответить на вопрос: получим ли мы равенство u
(M
) = u
(Р
), если мы точку М
совместим с точкой Р
, лежащей на поверхности Σ? Логика подсказывает, опираясь на непрерывность потенциала и его нормальной производной, что в пределе мы должны иметь это равенство при М
= Р.
u
(M
) = u
(Р
) (15.10.4)
Оказывается, что такое равенство не всегда возможно. Оно возможно лишь в том случае, если только в качестве функции v
выбрана функция sin (kr
) / r.
Если же мы выберем функцию eikr
/ r
или же е-ikr
/ r
, то в пределе мы получим бесконечное значение величины u
(M
) , т.е. u
(M
) ≠ u
(Р
), если M
→ Р
. Это обусловлено появлением на поверхности Σ
«скрытых» источников потенциала, обусловленных выбором функции v
, а также «скрытых» источников потенциала при r
→0.
Источники информации:
1. Кулигин В.А. Поведение волны в окрестности фокуса. // Вопросы рассеяния и оптимального приема радиоволн.ВГУ, Воронеж. 1975.
2. Каценеленбаум Б.З. Высокочастотная электродинамика. Наука. М. 1966.
3. Ватсон Г.Н. Теория бесселевых функций. Перев. с англ., М., ИЛ. 1949.
4. Кулигин В.А., Кулигина Г.А., Корнева М.В. Ревизия теоретических основ релятивистской электродинамики. http://www.n-t.org/tp/ns/rt.htm 25.06.2006.
5. Степанов В.В. Курс дифференциальных уравнений. ГИФФМЛ. М. 1958.
6. Ландау Л.Д., Лифшиц Е.М. Теория поля. ГИФФМЛ. М. 1960.
7. Кулигин В.А., Кулигина Г.А., Корнева М.В. «Конвективный потенциал» и философия. http://www.inauka.ru/blogs/article66754.html , 01.09.2006.
8. Тихонов А.Н., Самарский А.А. Уравнения математической физики. ГИТТЛ, М. 1953.
Итак, нами были проанализированы основы классической электродинамики и, как следствие, оценена совместимость ее со специальной теорией относительности. Результаты оказались отличными от тех предрассудков, которые сопровождают эти теории в настоящее время.
Перечислим их:
Поля электромагнитной волны и поля зарядов обладают разными свойствами и соответствуют различным видам материи. Они должны описываться самостоятельными группами уравнений.
Взаимодействие зарядов между собой описывается мгновенно действующими потенциалами. Такое взаимодействие отвечает контактному типу объемного характера и не противоречит принципу причинности.
Теоретически были получены свои законы сохранения для электромагнитных волн и свои законы для квазистатических полей зарядов. Эти законы не сводимы друг к другу.
Выяснено, что предельный переход от волновых явлений к квазистатическим не существует.
Попытки описать все явления электродинамики, опираясь на эфир и волны в нем, заведомо не могут привести к положительному результату в силу диссипативного характера взаимодействия волны с материальными объектами. Такое взаимодействие должно приводить к неизбежному рассеянию электромагнитных волн и к нарушению принципа равенства действия противодействию.
Теория относительности не «вписывается» в современную электродинамику и противоречит ей. Основные причины в том, что (во-первых) эйнштейновская интерпретация пространственно-временных отношений ошибочна и ведет к логическим противоречиям, и (во вторых) в том, что преобразование Лоренца было произвольно (бездоказательно) распространено на все явления материального мира. Отметим математическую некорректность релятивистского вариационного принципа.
Такое положение сложилось благодаря господству в физике позитивистского мировоззрения и сложившемуся, благодаря этому, догматизму. Мы специально говорим о философии (как научном мировоззрении), поскольку любая теория, любая интерпретация опирается именно на мировоззренческие позиции ученого.
Здесь следует иметь в виду, что не существует «чистого» эксперимента. Эксперимент должен иметь объяснение, которое неизбежно опирается на какую-либо теорию или физическую модель. Без теории невозможно дать объяснение эксперименту.
Точно также не существует «чистой» физической теории (гипотезы, модели) вне мировоззрения. Мировоззрение (= миропонимание) есть неотъемлемая часть интерпретации физической теории. Она невозможна вне рамок мировоззренческих установок.
Физическая теория не сводится к «чистому» математическому формализму. Она содержит концептуальную составляющую, т.е. описательную и объяснительную сторону. По этой причине материалистическая философия (мировоззрение) должна быть таким же мощным инструментом познания, как и математика. Именно эта сторона весьма бледно представлена в современной квантовой механике, СТО, ОТО и КЭД. Здесь не место обсуждать проблемы этих теорий. Но в них «голое мастерство математического формализма» доминирует над физическим смыслом (= мировоззренческим содержанием).
В работах [1], [2], [3] и др. мы постарались показать важную роль, которую играет материалистическая теория познания (материалистическая философия) в фундаментальных исследованиях. Но эти работы выглядят «белыми воронами» на фоне преобладающих в философской литературе позитивистских «исследований», лояльных мнениям авторитетов.
Роль материалистической философии не только в этом. Поскольку ее теория познания нацелена на поиск научной истины и обладает для этого необходимыми качествами (выполняет определенные критериальные функции), она формирует правильные нравственные
установки у исследователей: честность, ответственность, добросовестность, взаимное уважение и т.д. Для позитивизма это непосильная задача, поскольку он опирается на поклонение авторитетам, на достижение успеха «любой ценой» и т.п. Мы убеждены, что материалистическое мировоззрение, в конце концов, пробьет себе путь в физике, и физика освободится от существующих догм и предрассудков, сообразно здравому смыслу и логике.
Источники информации:
1. Кулигин В.А., Кулигина Г.А., Корнева М.В. Физика и философия физики. n-t.ru/tp/ns/fff.htm
2. Кулигин В.А. Вавилонская башня вульгарного позитивизма. n-t.ru/tp/ns/vb.htm
3. Кулигин В.А., Кулигина Г.А., Корнева М.В. «Конвективный потенциал» и философия. btr.nnov.ru/kuligin-1
[1]
⎡∂L
∂L
⎤
δS
= ∫
s
1 ⎢
⎣ ∂
x
i
δx
i
+ ∂
u
i
δu
i
⎥
⎦
ds
= 0 (П.11.1) ∂
x
i
δx
i
+ ∂
u
i
δu
i
⎥
⎦
ds
= 0 (П.11.1)
Учитывая, что δds
= 0, найдем
|




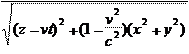 (1.2.3)
(1.2.3) 
 Рис.
Рис. 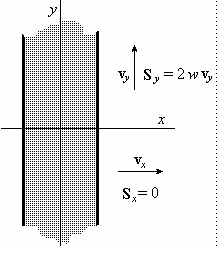






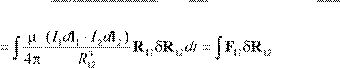 dt
= 0
dt
= 0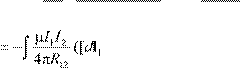 × d
l
2
]δϕ12
)dt
= ∫M
21
δϕ12
dt
= −∫M
12
δϕ12
dt
= 0
× d
l
2
]δϕ12
)dt
= ∫M
21
δϕ12
dt
= −∫M
12
δϕ12
dt
= 0












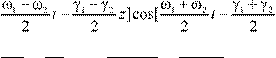 z
] =
z
] = 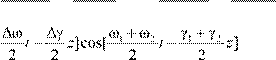


 ωγ(A
&
//
A
∗
//
)z
0
ωγ(A
&
//
A
∗
//
)z
0




























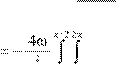 [P
n
m
(cosθ)]2
[a
mn
cosm
ϕ + b
mn
sinm
ϕ]2
sinθd
ϕd
θ π k
0 0
[P
n
m
(cosθ)]2
[a
mn
cosm
ϕ + b
mn
sinm
ϕ]2
sinθd
ϕd
θ π k
0 0
