| 1 ˝ ºŁ Ø ß Ł
| — ææ
|
Ł
|
æ
|
ı
|
Ł
|
ŁØ
|
Ø x
= x
∗
,
|
º
|
| Œ
|
ßı æ
|
ºŁ
|
æ
|
|
|
|
|
| |
|
|
|
f
(x
) = 0.
|
|
|
(1)
|
´ ŁŁŁ f
(x
) - Œ ºŁ Ø Œ Ł x
.
¯æºŁ ŒŁ Ł æ ø æ , Ł ß æ Œ Ł -
Ł (1). ˚ ß æ æ ß , æºŁ f
0
(x
∗
) 6= 0 Ł Œ ß , æºŁ f
(k
)
(x
∗
) = 0 º k
= 1,...,n
− 1, f
(n
)
(x
∗
) 6= 0. º n
ß æ Œ æ Œ .
1.1 ˛ º Ł Œ Ø
ˇ º Ł Œ Ø Ł (1) Ł º Ł æ -
Œ ª Ł º (a,b
), Œ º Ł Œ Ł . ˛æ Ø º Ł Œ Ø æº Ł
[1]
. ˇ æ Œ Ł º Ł ß Œ -
Π[a,b
], Œ ı Œ ª Ł Ł Ł ßı Œ .
ª a
Ł b
Ø æ ı Æß Œ c
, Œ Ø Œ Ł Æ ø æ º :
f
(c
) = 0, a < c < b.
¯æºŁ Œ Ł f
(x
) Ł º , Ł ª º Ł
º Œ Ł Œ Ł f
(x
) = 0 .
ºª Ł º Ł ºŁ æº øŁ Æ
YesDo:=True; While YesDo do
Input a,b, M
; h
= (b
− a
)/M
; fmin
:= 1.
0e
20; xi
:= a
; fi
:= f
(a
); for i:=1 to M do begin {i
}
x
i
−1 := x
i
; f
i
−1 := f
i
; xi
:= a
+ h
∗ i
; fi
:= f
(xi
); If fi
< fmin
Then begin {min
}
f
min
:= f
i
; x
min
:= x
i
; end; {min
} If fi
−1
∗ fi
≤ 0 Then
Output x
i
−1,f
i
−1, x
i
,f
i
; end; {i
}
Output f
min
,x
min
; Input YesDo; end; {While
}
1.2 ÆŁæ Œ ŁØ ÆŁæ Œ ŁØ( º Ł º ) æ æº ø Ł -
Ł ææ : Ł º a,b
, Π(fa
= f
(a
)) · (fb
= f
(b
)) <
0,
Реклама

ºŁ æ º - xs
= (a
+b
)/
2 Ł ß Łæº æ fs
= f
(xs
). ¯æºŁ fs
·f
(a
) ≥ 0, a
:= xs
, fa
:= fs
, Ł b
:= xs
, fb
:= fs
; ˜ º ß º æ æº øŁØ ł ª, Ł . .
˝ i- ł ª ŁÆºŁ ß Ł Œ æº Ł º æ (a
+b
)/
2,
Œ Ø ª ł æ Ł - º æ (b
− a
)/
2.
ÆŁæ Œ ŁØ Łæ æº øŁ ºª Ł [2]
1: Input a,b, δ,N
;
2: i
:= 0;
3: fa
:= f
(a
); fb
:= f
(b
);
4: Repeat
5: xs
:= (a
+ b
)/
2; fs
:= f
(xs
);;
6: If fs
∗ fa
≥ 0
7: Then begin fa
:= fs
; a
:= xs
end;
8: Else begin fb
:= fs
; b
:= xs
end;
9: i
:= i
+ 1;
10: xi
:= (a
+ b
)/
2;
11: dx
:= (b
− a
)/
2;
12: Until ((|dx
| ≤ δ
|xi
|) OR (i
≥ N
));
13: Output i,xi
,dx
;
1.3 ı
´ ı æ º Ł Œ (a,b
) º Łæ º æ ºŁØ Ł º Ł ª Ł ßı ŁØ Œ ŁŁ f
(x
)
f
ˆ(t
) = f
(a
)(1 − t
) + f
(b
)t,
0 ≤ t
= (x
− a
)/
(b
− a
) ≤ 1.
º ø Œ º Œ ı Ł æ Ł Ł f
ˆ
(t
) = 0:
t
∗
= f
(a
)/
(f
(a
) − f
(b
)), xs
= a
+ t
∗
(b
− a
);
˜ º Łæı Ł æ Łª ª Ł Ł º Œ , Œ Œ ÆŁæ Œ ŁØ. ı Łæ æº øŁ ºª Ł
1: Input a,b, δ,N
;
2: fa
:= f
(a
); fb
:= f
(b
);
3: i
:= 0;
4: fa
:= f
(a
); fb
:= f
(b
);
5: Repeat
6: y
:= x
2 − x
1;
7: t
:= fa/
(fa
− fb
); xs
:= a
+ y
∗ t
8: fs
:= f
(xs
);;
9: If fs
∗ fa
≥ 0
10: Then begin fa
:= fs
; a
:= xs
end;
11: Else begin fb
:= fs
; b
:= xs
end;
12: i
:= i
+ 1;
13: xi
:= (a
+ b
)/
2;
14: dx
:= (b
− a
)/
2;
15: Until ((|dx
| ≤ δ
|xi
|) OR (i
≥ N
));
Реклама

16: Output i,xi
,dx
;
| ÆŁæ Œ ŁØ Ł
|
ı
|
º
|
Łæ
|
º
|
|
|
ª
|
|
æº
|
!
|
1.4 æ º Ł
¨ ª æ æ Ł ı ºŁ Ø ª Ł (1) Œ
Æߌ Ł Ł º Ł
dx/dt
= f
(x
), x
(0) = x
0
.
(2)
Ł º ƺ æ Ø Ł ß º ß æ Ł ß æ æ Ł , Æß Ł t
→ ∞ x
(t
) → x
∗
. ª ŁÆºŁ ł Ł
ŁŁ (2) æ ø æ Ø Ł ª Łæº ª ( º -
| æ
|
Æ º łŁı t
) ı ł ŁÆºŁ Ł Œ ł Ł
|
(1).
|
|
| ˇ
|
æ ØłŁ ºª Ł Æ Øº , º
|
øŁØæ
|
Ł
|
| |
æ
|
Ø Ł ŁŁ
|
|
|
| |
|
xi
+1
= xi
+ τf
(xi
).
|
|
(3)
|
| |
æ
|
º Ł Łæ æº øŁ ºª
|
Ł
|
|
| 1:
|
Input
|
x
0
, τ
, δ, N
;
|
|
|
| 2:
|
|
i
:= 0;
|
|
|
| 3:
|
|
Repeat
|
|
|
| 4:
|
|
dx
= τ
∗ f
(xi
);
|
|
|
| 5:
|
|
i
:= i
+ 1;
|
|
|
| 6:
|
|
xi
:= xi
+ dx
;
|
|
|
| 7:
|
|
Until ((|dx
| ≤ δ
|xi
|) OR (i
≥ N
));
|
|
|
| 8:
|
Output
|
i,xi
,dx
;
|
|
|
| ˜º
|
ª ł
|
æ Ł ²k
= xk
− x
∗
Ł (3) º æ æº
²k
+1
= ²k
+ τ
(f
(xk
) − f
(x
∗
)).
|
ø
|
Ł
|
| ˇ
|
æ Ł
|
f
(xk
) − f
(x
∗
) = f
0
(x
˜)²k
, º Ł æ ł
²k
+1
= (1 + τf
0
(x
˜))²k
,
|
Ł
|
|
| Ł Œ ª æº , º æı Ł æ Ł æ
|
º Ł º ß
|
ß º æ æº øŁ æº Ł : æº º æ {xk
,k
= 0,
1,...
}º ı Ł æ ƺ æ Ł |xk
−x
∗
| < R
, Œ Ø Ł ª Ł-
Ł æ ı æ Ø Œ. ª ßÆ τ
, º ø ª
æº Ł ,
sign
(τ
) = −sign
(f
0
),
|τ
| <
2/
max|f
0
|,
Æ æ Ł æı Ł æ æ º Ł .
1.5 ˝
˝ º Ł (1) Łæß æ Ł
xi
+1
= xi
− [df/dx
]−1
f
(xi
).
(4)
˛ º Ł :
ª , Œ Ł g
(x
) ∈ Lipc
(X
) , æºŁ |g
(x
) − g
(y
)| ≤ c
|x
− y
| º æ ı (x,y
) ∈ X
.
( æı Ł æ Ł ˝ ). ˇ æ f
: D
→ R
ª D
- Œ ß ßØ Ł º , R
- ø æ æ ,
Ł æ f
0
∈ Lipc
(D
). ˇ º Ł , º Œ ª ρ >
0 |f
0
| ≥ ρ
Ł æ ı x
∈ D
. ¯æºŁ Ł f
(x
) = 0 Ł ł Ł , æ ø æ
Œ η >
0, Œ , æºŁ |x
0
− x
∗
| < η
, æº º æ , º Ø
xk
+1
= xk
− f
(xk
)/f
0
(xk
), k
= 0,
1,
2,...,
æ ø æ Ł æı Ł æ Œ x
∗
. ` º ª , º k
= 0,
1,
2,...
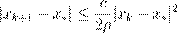 . .
˙ Ł 1. ˚ Œ æº Ł ß, Ł f
0
(x
∗
) = 06 æı Ł æ Œ Ł . ¯æºŁ f
0
(x
∗
) = 0 , º Œ ºŁ Ø .
˙ Ł 2. ˜º æı Ł æ Ł ˝ º ŁÆºŁ Ł x
0
º Æß æ ƺŁ Œ Œ Œ . ¯æºŁ ææ Ł |x
0
−x
∗
|
ºŁŒ , ˝ Æø æı Ł æ . ˝ ºŁ æº øŁ ºª Ł
1: Input x
0
, δ, N
;
2: i
:= 0; 3: Repeat
4: df
:= [df/dx
](xi
);
5: dx
= f
(xi
)/df
;
6: i
:= i
+ 1;
7: xi
:= xi
− dx
;
8: Until ((|dx
| ≤ δ
|xi
|) OR (i
≥ N
)); 9: Output 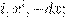

| —Łæ. 1: — ÆŁ
|
Ł º æŒ æ Ł Ł
|
ex
− a
− bx
3
= 0
|
| 1.6 æ
|
Ł
|
|
| 1. ´ Œ æ 1-ª
|
æ ª Łæ º æ Ł
|
|
| |
f
(x
) = exp(x
) − a
− bx
3
= 0.
|
(5)
|
| ´ ŁæŁ æ Ł
|
ŁØ a,b
|
Ł Ł
|
| m
= 0,
1,
2,
4 Œ
|
. ˜º Łææº Ł Œ 1-Ø
|
Ł Ø Œ ŁŁ
|
| f
(x
) º ı
|
Ł Œ Ł Ł
|
|
g
(x
) = f
0
(x
) = exp(x
) − 3bx
2
= 0.
(6)
˝ Łæ Œ 1 Œ ÆŁ Ł º æŒ æ Ł a,b
ƺ æ Ł æ ºŁ ß Łæº Œ Ø Ł (5).
2. ´ Œ æ 2-ª æ ª Łæ º æ Ł
f
(x
) = exp(−1/
(x
− 1)2
) = 0.
(7)
Ł Ł Ł æ ßØ Œ x
∗
= 1 Æ æŒ Ø Œ æ Ł( f
(k
)
(1) = 0, k
= 0,
1,...
). ˇ Ł f
0
(x
) <
0 º x <
1 Ł f
0
(x
) >
0 º x >
1 .
1.7 ˚ ß Œæ Ł ß
1. ˜º Œ ŁŁ Ł (5) æ Ł a
= 1.
15,b
= 1.
25 Ø Ł
ª Ł ß Œ Ø. ˜º Œ ŁŁ Ł (6) æ b
= 1.
25 ØŁ ª Ł ß Œ Ø Ł ŒŁ æ Ø ø æ Ø æŁ.
˚ º Ł Ł :
Œ Ł f
(x
): Œ Ł( ŁÆºŁ )
x
1
= −0.
83, x
2
= 0.
14, x
3
= 1.
20, x
4
= 5.
14
Œ Ł g
(x
) = f
0
(x
): ŒŁ Ł Œ Ł
(−...
−) − 0.
41 (+...
+) 0.
75 (−...
−) 4.
18 (+...
+)
2. ˛ Łæ ß Ł ßł Ł(ÆŁæ Œ ŁØ, ı , æ º Ł , ˝ -
) º ŁØ δ
= 1.
0e
− 2,
1.
0e
− 3,
1.
0e
− 4,
1.
0e
− 5 Ø Ł Œ Ł Œ ŁŁ (5)æ Ł Ł a
= 1.
15,b
= 1.
25. ˜º Łı Œ Ø æ æ Ł ƺŁ ß ŁæŁ æ Ł Łæº Ł ŁØ δ
.
3. æ º Ł ß æ Ø Ł Œ Œ ŁŁ (5), Æ Ł τ
, º Œ ßı æı Ł æ Ł. ˚ ŒŁ Æ º æ æı Ł æ Ł Ł ª ææ ?
4. ˝ :
æº Œ Œ æ Ł 2 ˝ æı Ł æ ºŁ Ø , . .æ ø æ
º , æº æ ª Œ . ˇ Ł , Æ ºŁ Ł ŁŁ ßØ ˝
xi
+1
= xi
− 2[df/dx
]−1
f
(xi
)
Ł º Œ Œ æ Ł 2 æŒ æ æı Ł æ Ł, Ł æ ßØ º æ ª Œ . ˜º ŒŁ Łæ º Ł
h
(x
) = sin((x
− 1)2
) = 0.
˜º Ł δ
= 1.
0e
− 7 Ø Ł Œ ª Ł æ ß Ł Ł Ł Ł ß ˝ . Ł Łæº Ł ŁØ.
[1]
1ˇ ` º -˚ łŁ
[2]
2´ Ł Ł ßı Ł ºª Ł ı Łæ º æ º Œ æ Ł Ł ŁØ. ˝ -
Łı Ł Ł Ł , Łæ º æ Œ ß Ł غ it_gen.pdf
|