| .
Ł
1 ˇ ƺ ß Ł Ł Ø ŁŁ Łæ º. 3
1.1 ˇ ƺ ´ Ł ª . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2 ˇ ƺ ˆ º Æ ı . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.2.1 ( Œ Łª Ł æŒŁı æ . ( ¨. . ´Ł ª -
) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3 ˇ ƺ Ł - ¸Ł º . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3.1 ´Ł ª - ` Æ Ł. . . . . . . . . . . . . . . . . . . . 7
1.4 Ł Ł ƺ ºŁ º Ø. . . . . . . . . . . . . . . . . . . . . . . . 8
1.5 ˇ ƺ ºŁ º Ø Ł ł . . . . . . . . . . . . . . . . . . . . . . . . 8
1.5.1 ˆŁ —Ł . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2 ß ł Ł ƺ Ł Ł Ø ŁŁ Łæ º. 10
2.1 Œ ŁŁ Œ Ł øŁ Œ Ł . . . . . . . . . . . . . . . . . 10
2.2 ß ł . ¨ææº Ł æ Œ ß æ . . . . . . . . . . . . . 11
2.2.1 º Æ ª . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.2.2 — ł æ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.3 ˜Łæ æŁ ßØ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3 ˛æ ß ß ß. 15
Ł Ł ß Æº ß ŁŁ Łæ º XVII - XX .
´ Ł .
Ł Ł Ł Łæ º - º ŁŁ Łæ º, Œ Ł æ Ł
º ŁŁ ºßı Łæ º æº ª ß ª Ł , Œ ºª Æ Ł æŒŁ Ł ª Ł æŒŁ º ªŁ ŒŁı , æ øŁ æ Œ º ºª Æ Ł æŒŁı Łæ º Ł Œ æ Œ ł ŒŁ. Ł Ł ß æ Ł Ł ß Ł Ł. ˛Æß æ-
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
æ Ł æ Ł Ł ß Ł º ŁŁ Æ º łŁı Łæ º.
1 ˇ ƺ ß Ł Ł Ø ŁŁ Łæ º.
| ˚ Œº ææŁ æŒŁ
|
ƺ Ł Ł Ø ŁŁ Łæ º æ æ :
|
| 1. ˇ ƺ
|
´ Ł ª (1770) æ º ŁŁ æ Œ ª º ª Łæº Ł
|
| æ ß s
= s
(k
)
|
Ł º ßı k
− ı æ Ø æ ŁŒæŁ ß k
> l
;
|
| 2. ˇ ƺ
|
ˆ º Æ ı æ º ŁŁ ßı º ßı Łæ º, Æ º łŁı 5,
|
| æ Ø ı
|
æ ßı Ł ƺ غ - ˆ º Æ ı æ º ŁŁ ßı Łæ º,
|
| Æ º łŁı 2, æ
|
Ø ı æ ßı ( æ º ß 1742);
|
| ˛æº ƺ
|
ƺ ˆ º Æ ı . ˇ ƺ æ º Ł º ßı Łæ º æ -
|
| Ø ª Ł
|
ª Łæº æ ßı;
|
| 3. ˇ ƺ
|
Ł - ¸Ł º æ º ŁŁ æ Œ ª º ª Łæº , Æ º ł ª 1,
|
| Ł æ ß
|
æ ª Ł ı Œ (æ ºŁ 20-ı ªª. 20 .);
|
| 4. Ł Ł
|
ƺ ºŁ º Ø;
|
| 5. ˇ ƺ
|
ºŁ º Ø Ł ł ;
|
| 6. ˙ Ł
|
æ º ŁŁ æ ı æ Æ º łŁı ßı Łæ º æ Ł ı
|
| Łæ º æ ª Ł
|
ß Łæº æ ßı æ Ł º Ø;
|
| 7. ˙ Ł
|
æ º ŁŁ ºßı Łæ º Œ Ł ß Ł Ł æ Ł ß -
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
|
| ß Ł Ł º ªŁ ß Ł; Œ ªŁ Ł.
˜º ł Ł Ł Ł Ø ŁŁ Łæ º Ł æ ºŁ Ł æŒŁ , ºª Æ-
Ł æŒŁ , º ß Ł æ ł ß ß, Œ ß, æ ß -
|
æ ßı æ Æ Ł ı. ´ ŁæŁ æ Ł ł Ł , Ł Ł ß Ł ı
æ æ Ø æ ªŁ ºß ŁŁ Łæ º - ºŁ Ł æŒ Ł Łæ º, ºª Æ Ł æŒ Ł Łæ º, æ Ł Łæ º. ææ Ł æ ß ß Ł Ł Ł Ø ŁŁ Łæ º º æ Ł.
1.1 ˇ ƺ ´ Ł ª .
| ˇ ƺ ŁŁ Łæ º, æ ºŁ . ´
|
Ł ª (¯. Waring) 1770 ª. æº -
|
| ø Ł : æ Œ º Łæº æ æ
|
ß ı Œ , Ł Œ Æ ,
|
| Ł ßı æ Ø. ˜ ªŁ Ł æº
|
Ł:
|
º º Æ ª n
> 2 æ ø æ -
|
| Πk
= k
(n
) , Łæ ø º Œ n
, º Æ
|
º Łæº æ æ A
: n
−
|
| æ Ø Ł º ßı ºßı Łæ º. ˇ
|
Æø
|
ł Ł ƺ ß ´ Ł ª æ
|
| ª Æ Ø Œ Ø ºŁ Ł ß k
ŁæŁ æ Ł
|
n
|
1909 ª. ˜. ˆŁº Æ (D.
|
| Hilbert), æ Ł æ ƺ ´ Ł ª Ł ª
|
ß
|
æ ƺ Ø ˆŁº Æ - ´ -
|
| Ł ª . ¯æºŁ Jk,n
(N
) Æ Ł Łæº ł
Ł
|
ŁØ
|
ºßı Ł º ßı Łæº ı
|
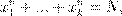
| ˆŁº Æ
Ł º Æ N
> 1.
|
, æ ø æ K
= k
(n
), º Œ ª Jk,n
(N
) > 1
|
| ´ 1928 ª. ˆ. X.
|
Ł Ł ˜
|
. ¨. ¸Ł º (G. ˝. Hardy, J . ¯. Littlewood), Ł Ł
|
Œ ƺ ´ Ł ª Œ ª Ø , Œ ºŁ, Ł k
> (n
− 2)2n
−1
+ 5 º Jk,n
(N
)
Ł æ æŁ Ł æŒ º Ł
Jk,n
(N
) = AN
k/n
−1 + O
(N
k/n
−1−γ
)
ª A
= A
(N
) > c
0
>
0, c
0
Ł γ >
0 - Œ ß æ ß . º º , Ł
N
> N
0
(n
) Łæı Ł Ł ł Ł . ´ æ Ł æ Ł º ŁŒºŁ
Ł ƺ ß: æ Ł Œ ı ºŁ Ł G
(n
),g
(n
),k
0
− Ł łŁı ºßı
Łæ º, º Œ ßı:
) Łæı Ł łŁ Ł k
> G
(n
) Ł N
> N
0
(n
);
Æ) Łæı Ł łŁ Ł k
> g
(n
) Ł N
> 1;
) º ºŁ Ł ß Jk,n
(N
) Ł k
> k
0
(n
) Ł æ Ł … ßł æŁ ŁæŒ º .
) ¨ æ , G
(n
) > n
+ 1
´ 1934 ª. ¨. . ´Ł ª Ł øŁ æ ª Ł Œ º, G
(n
) 6
3n
(lnn
+ 9)
˚ ª , Ł æ ª º æŁ º G
(n
) º Æ º łŁı ŁØ n
: G
(4) = 16 (X. ˜ , ˝. Davenport, 1939), G
(3) = 7 ( . ´. ¸Ł Œ, 1942).
Æ) ´ 1936 ª. ¸. ˜ŁŒæ . ˇŁºº (L. Dickson, S. Pillai), Ł Ł ´Ł ª -
, Œ ºŁ,
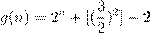
º æ ı n >
6, º Œ ßı
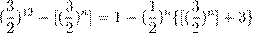
ˇ æº æº Ł Œ ˚. º (˚. Mahler) 1957 ª. º æ ı æ
Æ º łŁı n
.
) ˝ Łº łŁØ º Ł º Ł ¨. . ´Ł ª , Œ ßØ Œ º,
k
0
6 4n
2
lnn.
º Œ º æ ƺ ß ´ Ł ª . ´. ¸Ł ŁŒ 1942 ª. ø æ ª ºŁ ßı Æ Æø ŁØ ƺ ß ´ Ł ª ( ß Æ ª
Œ æ æ º ßı Łæ º; æ º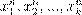 
æ º ŁŁ Łæº n
ææ Ł æ ª º ß f
1
(x
1
),f
2
(x
2
),...,fk
(xk
); æ
Łæı ª Ł 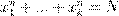 ææ Ł æ æ Ł Ł . .). ˛æ Æ Ł ƺ ß ´ Ł ª æ æ Ł , Ł ł ŁŁ æ ß ø ß ß ºŁ Ł æŒ Ø ŁŁ Łæ º.
1.2 ˇ ƺ ˆ º Æ ı .
˛ Ł Ł æ ßı ƺ ŁŁ Łæ º. ˙ Œº æ Œ º æ ª , æ Œ º Łæº , Æ º ł ŁºŁ ł æ Ł, Æß æ º Ł æ ß ı æ ßı Łæ º. ƺ ß Ł º 1742 ª. X. ˆ º Æ ı (Ch. Goldbach)
Łæ Œ ¸. غ (L. Euler). ´ ¸. غ Łº, º ł Ł ƺ ß æ Œ , Œ Łæº æ æ ı æ ßı. ´ Ł
ºª ª Ł º æ Ø Ł ŁŒ ŒŁı Ø Łææº Ł ƺ ß ˆ º Æ ı .
´ 1923 ª. ˆ. Ł Ł ˜ . ¸Ł º (G. Hardy, J. Littlewood) º æ Œ , æºŁ ß Œ ß ß ( Œ ß Ł ß ) æŁ º L˜Ł Łıº , æ Œ æ Æ º ł Łæº æ æ ı æ ßı Łæ º.
´ 1937 ª. ¨. . ´Ł ª æ º ßØ º æŒ Ø ŁŁ Łæ º Œ Łª Ł æŒŁı æ æ æ ß Ł Łæº Ł, æ ø Œ ª -
| Œ º æŁ Ł æŒ º º Œ ºŁ æ æ º ŁØ ª Łæº æ Ø ı æ ßı Łæ º. ¨ Ø ºß æº , Œ æ Æ º ł
Łæº æ æ ı æ ßı Łæ º. - Ł Œ ØłŁı æ Ł ŁØ æ Ø ŁŒŁ.
¨. . ´Ł ª ºŁº łŁ Ł æ ø æ Æ º ÆøŁı . ˙ ÆŁ ŁŁ ª Łæº æ ı æ ßı ø ł .
1.2.1 ( Œ Łª Ł æŒŁı æ . ( ¨. . ´Ł ª )
˛ Ł Ł æ ßı æŁº ßı Ł ÆøŁı ºŁ Ł æŒ Ø ŁŁ Łæ º Łª Ł æŒŁı æ Æߺ æ ¨. . ´Ł ª ß . ªŁ ƺ ß ºŁ Ł æŒ Ø
ŁŁ Łæ º º æ ºŁ æ ߌ Œ ßı æ æº ª ßı Ł
|
| cosF
(x
1
,...,xn
) + i
sinF
(x
1
,...xn
),
|
| ª F
(x
1
,...,xn
) Øæ
|
Ł º º Łæº Œ Ł . ŒŁ Æ ,
|
| æ Ł Łı ƺ
|
æŁ æ Ł Ł ŒŁı æ Ł, æ æ Ł, -
|
| º Ł
|
Æ º Ø ŒŁ º ŒŁı æ . ¨. . ´Ł ª ,
|
| Łæ º ªº Æ ŒŁ Ł
|
Ł æŒŁ æ Øæ ææ Ł ßı æ , º Łº ŁæŒº -
|
| Ł º æŁº ß ŒŁ
|
º łŁ Œ ª Œº ææ ŒŁı æ . ºŁº
|
| ´Ł ª º Ł
|
º ß , ƺŁ ŒŁ Œ º ß º -
|
| ß º æ
|
ŁŁ Łæ º ŒŁı Œº ææŁ æŒŁı ı, Œ Œ ƺ
|
| ´ Ł ª , ƺ ˆŁº Æ
|
˚ Œ , ƺ Œ æ ´ غ . ˜ ªŁ æº æ Ł-
|
| Œ Łª
|
Ł æŒŁı æ Æߺ ł Ł Ł Ł ßı ƺ
|
| æ æ ß Ł Łæº Ł Ł,
|
æ æ Ł, ł Ł ƺ ß ˆ º Æ ı .
|
| 1.3 ˇ ƺ
|
Ł - ¸Ł º .
|
| ˙ ı Ł æŁ
|
Ł æŒ Ø ºß º Łæº Q
(n
) ł ŁØ Ł
|
p
+ x
2
+ y
2
= n,
ª p
- æ , x
Ł - ºß , n
- º Łæº . º ª Ø Ł º æ ƺ ı Ł æŁ ŁŒŁ º Łæº ł ŁØ Ł
p
− x
2
− y
2
= l,
| ª l
- ŁŒæŁ
|
º
|
Łæº , p
6 n
(n
→ ∞).
X. -¸.
|
. Æߺ
|
æ º ˆ.
|
-
|
| Ł (G. Hardy) Ł ˜
|
. ¸Ł º
|
(J. Littlewood) 1923 Ł
|
ææ
|
Ł Ł æ
|
| Łæ Ł æŒŁı Ł ªŁ
|
Ł
|
æŒŁı æ Æ ŁØ.
|
| ˜Łæ æŁ ßØ
|
,
|
Æ ßØ . ´. ¸Ł ŁŒ ,
|
ºŁº
|
Ø Ł æŁ
|
-
|
| ŁŒ º ª
|
Ł :
|
 ,
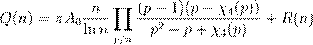ª
| ¨
|
º ªŁ Ø ºß º ª Ł æº Æ æŒ
|
æ æ
|
| æ ßı
|
Łæ º Ł = x
2
+ y
2
+ l
. ø Łæ æŁ ª
|
Ø æŁ
|
-
|
| ŁŒ
|
º Łæº ł ŁØ Æ Æø ª Ł Ł - ¸Ł º
|
p
+ ϕ
(x,y
) ª
|
p
|
| - æ
.
|
, ϕ
(x,y
) - Ł Ł Ł º Ł º º
|
Œ Ł
|
| — ææ
|
Ł º ªŁ ª Ł p
− ϕ
(x,y
) = l
Ł Ł
|
Œ Œ º æ
|
| Æ æŒ
|
æ Ł æ æ ßı Łæ º Ł p
= ϕ
(x,y
) + l
|
| ´Ł ª - ` Æ Ł æ º ŁŁ æ ßı Łæ º Ł Ł æŒŁı
|
  .
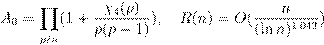ª ææŁ ı æ Œ æ º ł Ł ƺ Ł - ¸Ł º , Œ Ł æŒŁ æłŁ ªŁ —Ł Ł Ł Æ º ł ª ł .
1.3.1 ´Ł ª - ` Æ Ł.
ˇ æ Ł Łæ º æ Œ Ł :
 ,
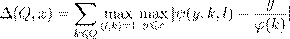ª
ψ
(y,k,l
) = X
= X
λ
(n
).
n
6yn
≡lmodk
, æ ø æ æ ß c
1
>
0 Ł c
2
>
0 ŒŁ ,
 ,
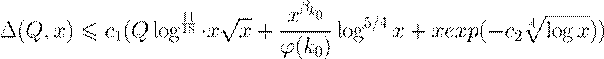 √4
logx
ª k
0
< e
= z
1
− º , º Œ ª æ ø æ Ł æ ßØ Ł Ł Ł ßØ
Øæ Ł º ßØ Ł Ł Ł ßØ ı Œ χk
0
Œ Ø, L
(s,χk
0
) Ł º Ł s
=
| √ 11/
18 −A
∆(Q,x
) 6 c
(A
)( xQ
logx
+ x
logx
)
|
| Ł º Æ A
.
1.4 Ł Ł ƺ ºŁ º Ø.
|
| Ł Ł ƺ ºŁ ª Ł æ Ł :
,
|
º Ø - ƺ , Œº ø æ
X
τ
k
1τ
k
2(m
+ a
) m
6n
X
τk
1
τk
2
(n
− m
),
m<n
|
ŁæŒ
|
æŁ Ł
|
æŒ -
|
| ª τk
(m
)− Œ ºŁ æ
|
ºŁ ßı º ŁØ º ª Łæº
|
k
|
Ł
|
º Ø, æ Ł
|
Ł
|
| Πk
1
,
Ł k
2
> 2− -
|
º ß Łæº , a
- ŁŒæŁ
|
º
|
Łæº ,
|
ºŁ -
|
| º , n
- æ
|
Æ º ł º Łæº . ´
|
æ
|
æ Ł, τ
2
(m
) = τ
(m
) -
|
| Łæº ºŁ º Ø º Łæº
ŁØ
|
m
. ß ß , æ æ
x
1
x
2
...xk
2
− y
1
y
2
...yk
1
= a, x
1
x
2
...xk
1
− y
1
y
2
...yk
2
= n.
|
, Œ ºŁ æ
|
ł ŁØ
|
| Ł Ł ƺ
|
ºŁ º Ø Ł k
1
= 2 Ł º Æ
|
º
|
k
2
Æߺ
|
ł æ
|
| ø Łæ æŁ ª
|
. ´. ¸Ł ŁŒ .
|
Æ
|
ææ
|
º .
|
| 1.5 ˇ ƺ ºŁ
|
º Ø Ł ł .
|
| ˇ ƺ ºŁ º Ø Ł
|
ł : ?= - æ , ? = xy, x, y
|
º ß ;
|
| ˇ ƺ ßæŒ Ł æŁ Ł æŒ Ø ºß º Łæº ßı ŁØ Ł :
p
− xy
= a,p < N, p
+ xy
= N,p < N,x,y
∈ N
ª p
− æ Łæº a
− ŁŒæŁ º .
Æø - ŁæŒ æŁ ŁŒŁ º æ Ł :
|
ł ŁØ
|
º… -
|
  .
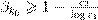˛ æ Ł Ł ß ˙Łª º ß Œ ,
X
τ
(p
− 1),
p<N
ª τ
(p
)− Łæº ºŁ º Ø n
.
ˇ ƺ ºŁ º Ø Ł ł Æߺ æ º . Ł ł (¯. Titchmarsh, 1930) Ł ł Ł æº º ŁŁ æ ºŁ æ Ł æłŁ Ø ªŁ ß —Ł ( … ææ Ł Ł ) . ˜Łæ æŁ ßØ , Æ ßØ . ´. ¸Ł ŁŒ , º Ø Ł æŁ ŁŒ Łæº ł ŁØ º º… ª Ł :
| p
−xy
= a,p < N,
Ł a
= 1, `. . ` ŁıŁ
|
łŁº
|
º º Æ ª ŁŒæŁ -
|
| ª a
6= 0. ` ª ε >
0.
|
ŁıŁ Œ º æŁ
|
Ł
|
æŒ
|
º æ æ Œ O
(N/
(ln1+ε
N
)),
|
| ´Ł
|
ª - ` Æ Ł
|
æ
|
º ŁŁ
|
æ ßı Łæ º Ł Ł æŒŁı
|
| ª ææŁ ı
|
æ Œ Ł Ł
|
Œ
|
ł Ł
|
ƺ ß ºŁ º Ø Ł ł .
|
| ˇ Ł
|
º Ł æ ºŁ
|
æ Ł
|
æłŁ
|
Ø ªŁ ß —Ł æ
|
| Œ Ł æŒŁ
).
|
Ł Ł Æ º ł ª
|
ł
|
( Ł
|
ß Æ ææ ß Ł
|
| 1.5.1 ˆŁ
|
—Ł .
|
| ˜º º
|
æ Ł º Ł
|
- Œ ŁŁ. ˜ - Œ Ł ζ
(s
)− -
|
| ºŁ Ł æŒ
|
Œ Ł Œ º Œæ ª
|
ª s
= σ
+ it,
Ł σ >
1 º æ
|
| Ææ º Ł
|
æı øŁ æ
|
˜Ł Łıº :
|
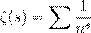
| ˙ Ł
|
- Œ ŁŁ
|
,
|
º
|
Łæº
|
ºŁ ßı ª ª
|
| æ
Łæº .
|
: μ
|
æ
|
æ ß
|
Łæº ,
|
ª Œº
|
Ł ª æ ª
|
| —Ł
|
1859 ª. ßæŒ
|
º
|
º
|
Ł
|
æ
|
Ł æ ßı
|
Łæ º æ Re
= 1/
2 -
|
| Œ ŁŁ,
|
Œ º
|
Łº,
|
æ
|
Øæ
|
Ł
|
º ß ºŁ
|
- Œ ŁŁ æ º -
|
| ß
|
Ø Re
= 1/
2.
|
| ¨ Œ,
|
Œ Ł ζ
(s
)
|
º
|
º æ ı Œ
|
º Œæ ßı s
6= 1, Ł Ł ºŁ º Ł-
|
º ßı ºßı s
= −2,
−4,
−6...
¨ Œ Ł º ª Ł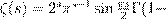 
s
)ζ
(1 − s
), Ł ª ß Ł 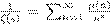 Ł s >
1 æº , æ æ º ß
ºŁ, ß ß Ł Ł º ß Ł¿, æ º ß º æ 0 6 s
6 1 æŁ Ł æŁ º Œ ß Ø "Œ Ł Ł æŒ Ø ºŁ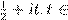 ŁŁ" R. ˆŁ —Ł , :
´æ Ł Ł º ß ºŁ - Œ ŁŁ Ł Øæ Ł º æ , .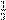
| ˛Æ Æø…
|
ªŁ —Ł
|
æ æ
|
Ł Ł ª æ ª
|
Ł
|
º Æ Æø -
|
| ŁØ -
|
Œ ŁØ, ß
|
ßı L-
|
Œ Ł Ł ˜Ł Łıº .
|
| 2 æ º.
|
ß ł
|
Ł
|
ƺ Ł Ł
|
Ø
|
ŁŁ Ł-
|
| ˇ ß æŁæ
|
Ł æŒŁ
|
º ß
|
Ł Ł Ø ŁŁ
|
Łæ º ÆߺŁ
|
º ß ¸ -
|
| غ
|
(1748), Œ
|
ßØ Łææº
|
º æ ø æ
|
ßı
|
º Ł
|
| ºßı Łæ º
|
º Ł º
|
ß æº ª
|
ß , æ æ Ł, Ł Æߺ ææ
|
| º ŁŁ
|
Łæº
|
Œ ºŁ
|
æ æº ª ßı.
|
2.1 Œ ŁŁ Œ Ł øŁ Œ Ł .
ªŁ Œº ææŁ æŒŁ Ł Ł Ł Ø ŁŁ Łæ º ł æ Œ ŁŁ Œ Ł øŁ Œ Ł . æı Ł Œ ¸. غ Ł º Ł æ -
ºŁ Ł æŒŁı , Ł ßı ˆ. X. Ł (G. H. Hardy), ˜ . ¨. ¸Ł º (J. ¯.
Littlewood) Ł ¨. . ´Ł ª ß . ¨æı Ø º æ Ł æ æ º Ł ß æº º æ :
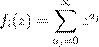 Ai
= {ai
},ai
> 0,a
∈ Z,i
= 1,
2,
3,...
æ ßı : æ Ł ø Ø Œ Ł Ø
 ,
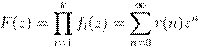ª r
(n
) = rk
,A
(n
)
− Œ ºŁ æ æ º ŁØ Łæº Ł :
n
= a
1
+ a
2
+ ...
+ ak
,ai
∈ Ai
,A
= {A
1
A
2
,...
}.
ˇ Ł r
(n
) ß Łæº æ Ł øŁ Ł ª º ˚ łŁ. ´ ´Ł ª æ ß ß æ Łª Ł æŒŁ Ł æ Ł:
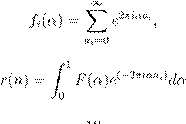
| ¨ r
(n
) ß º æ ªº
|
æ , æ æ ø
|
Ł Ł º , æ æ ßı
|
| Œ æ æ Ł Œ ßı Ł
|
º ßı Œ. ´
|
æ ºŁ Ł æŒŁı æ Øæ F
(z
), -
|
| Æ øŁı Ł Ł
|
Ø ŁŁ Łæ º
|
Ł º Ł ªŁ , º ªŁ ßı ªŁ-
|
| —Ł , º
|
º Ł ß Łæº
|
ŁŁ r(n) Łª Łæ Ł Ł æŒŁ
|
| ŒŁ Łª Ł . æ
|
´Ł ª
|
Ł Œ ß æ º Ł æ ßı
|
| Łæ º Ł Ł æŒŁı ª
|
ææŁ ı, º
|
ß æ ß Ł Ł -
|
| ŁŁ L- Œ ŁØ ˜Ł Łıº . æ
|
ºŁ æ ,
|
ŁæŁ æ Ł k ºŁÆ r
(n
) 6= 0 º
|
| æ ı n
> 1, ºŁÆ r
(n
) 6= 0 º
|
æ Æ º łŁı n n
> n
0
(A
), ºŁÆ Ł º æ ı
|
ß º æ æ ł Ł r
(n
) 6= 0, . .
 ,
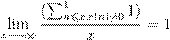| ŁºŁ, Œ , º r
(n
) Ł æ æŁ Ł
|
æŒ
|
º . ˝ Ł
|
ł Łæº k, º -
|
| ø Ł Łæº ßı æº
|
ŁØ, Æ
|
æ æ
|
æ g
(A
), G
(A
),
|
| G
0
(A
), k
0
(A
).
´ æº {ai
} = {p
},
ª {p
}−
|
æº
|
º æ
|
æ ßı Łæ º, Ł k =
|
| 3 º æ ´Ł ª : æ Œ
|
æ
|
Æ º ł
|
Łæº
|
Æß æ º Ł æ ß ı æ ßı Łæ º; Ł k = 2 - Œ : Ł æ ß Łæº ª Æß æ º ß Ł æ ß ı æ ßı Łæ º.
2.2 ß ł . ¨ææº Ł æ Œ ß æ .
˝ Œ ß Ł Ł Ł Ø ŁŁ Łæ º ł æ Ł øŁ Łææº Ł æ Œß æ , º øŁıæ º æ Ł Ł æº º æ Ø Ai
ai
,
ßı ºŁł Łı º æ Ł ,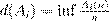
ª Ai
(n
) = P
16
ai
6
n
1.
¨ º Ł º æ Ł dn
(Ai
) Ł A
1
= A
2
= ...
= Ak
= A
æº , g
(A
) <
∞. ˇ Ł Ł ª
Œ Œ Ł Ł Ø ŁŁ Łæ º, Œ ßı æ Ł æ æº º æ Ł º Ø º æ Ł, æ ø æ º æ Œ æ Ł Ł Ł ßı æº -
º æ Ø ßı æº º æ Ø æ º Ł º Ø º æ . ´ ø º
Ł Łª ß ł , æ ø Œ ßı Œ ß æ º Ł º æ
d
(Ai
).
ŒŁ æ æ Æ ¸. ˆ. Ł º Œ æ Ł æ Ł -
º ßı Łæ º Ł æ ß ª Ł ª Łæº æ ßı æº ª ßı, . ´. ¸Ł ŁŒ
Ø º ł Ł ƺ ß ´ Ł ª .
º ß ß ł , Ł º øŁ ´. ´ Ł . º Æ ª , Ł
Ł Ł Ø ŁŁ Łæ º Œ º , æ ß Œ æ ß
ºŁ Ł æŒŁ æ æ . ˛ Œ ŁÆ º Œ ß ł Ł Œ ßı Ł Ł Ø ŁŁ Łæ º º æ Œ ÆŁ Ł Ł ºŁ Ł æŒŁı Ł º ßı . ´ ı ł Ł Ł ßæ Ł Ł æ ßı Łæ º Ł º ª
( ł æ ) æ æ æ æ Œ æ Ł æº º æ Ø. Œ, ßæ Ł Ł æ º Ø æ Ł æº º æ Ø {m} Ł
{2n - m} æ ßı Łæ º, 6 nθ
1
Ł, æ æ 6 nθ
2
ª (θ
1
<
1 Ł θ
2
<
1 º øŁ
Æ ßÆ ß º Ł º ß Œ æ ß), Ł Ł Œ ł Ł Œ ß Ø
Œ Ł ƺ ß ˆ º Æ ı - غ æ º ŁŁ ª Łæº æ Ø ı Łæ º, Ł Œ ßı Ł Æ º k
1
,
ª - Æ º k
2
æ ßı Ł º Ø.
2.2.1 º Æ ª .
º Æ ª - æ Ł º ßØ Ł æ Ł æ º ßØ ł -
, æ ßØ º º Æ ª . — ł º Æ ª º ı ł Ł æ ı æ Ł ø Œ Ł S
(;,z
), Æ ø Œ ºŁ æ º Œ ª -
æ A
ºßı Łæ º, Œ ß º æ æ ß Łæº p < z
Ł Ł º Œ æ P
æ ßı Łæ º.
ˇ æ P
(z
) = Qp<z,p
∈P
p.
º Æ ª æ Ł æ
 ,
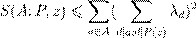Œ Ł l
1
= 1 º Ł º ßı Øæ Ł º ßı Łæ º. ¨ º Æ -
ª æ æ Ł , Æß, º Ł ld
= 0 º d
> z
, Ł Ł Ł Ł æ æ º ø ª ßÆ æ łŁıæ Łæ º λd
(2 6 d < z
).
´ Œ ÆŁ ŁŁ æ ªŁ Ł Ł ł ł º Æ ª º º
ŒŁ æ Ł , æ Æ æŁº ß Ł Łæ º ŁŁ æ ßı Œ ŁØ.
2.2.2 — ł æ .
— ł æ - , Æ ßØ æ (3 . . .) Ł º øŁØ æ Ł æ æ ß Łæº Ł º ª . ø æ æ
Œº æ æº ø . ˙ ŒŁ æ Ł Ł . Łæº 2 - æ . ˙ ŒŁ æ æ º ß Łæº , º øŁ æ 2. Łæº 3 - Œ Łæº - Æ æ ß . ˜ º ŒŁ æ æ º ß Łæº , Œ- ß º æ Ł
2 Ł 3. Łæº 5 - Œ Łæº - Æ æ ß . ˇ º º -
ªŁ ß ß Łæº Ł , Ø Ł æŒ º ª Æ º ł Ø Œ æº º æ Ł æ ßı Łæ º. — ł æ łº Ł Ł ªŁı Æ º æŁº ßı ı ł ( Ł ł ´ ).
2.3 ˜Łæ æŁ ßØ .
´ 1959 . ´. ¸Ł ŁŒ Æߺ Æ ˜Łæ æŁ ßØ . ˛ Ł Ł ŁŁ Łæ º º ł Ł Œ ßı ÆŁ ßı ŁØ (ÆŁ ßı Ł Ł ßı ƺ
) Ł
α
+ β
= n,
ª α
Ł β
Ł º Œ æ ª æ ß Ł ı ł æ º ß Ł Ł æŒŁı ª ææŁ ı æº º æ º ßı Łæ º. ˜Łæ æŁ ßØ , æ Ł æ Æ º ß ŁŒ - æ ß Ł ( æ æ Ł, -
Ł Łæ æŁŁ Ł æ Ł Æßł ) æ ºŁ Ł æŒŁ Ł Ł ºª Æ Ł æŒŁ Ł
Ł Ł ¨. . ´Ł ª Ł . ´ غ (A. Weil). ø æ æ æ Ł æº -
ø . ¨æı ÆŁ Ł æ Ł æ Œ Ł Ł :
υD
0
+ β
= n
;
æ υ,D
ŁæŁ Æ ª Œ ß Ł Ł ª º Ø Æº æ Ł ª υ
Ł D
- Œ ß Ł ºß; Ł Łæº υ
- æ ß , D
ª Æß º ß ºŁ ß º Ł º ß æº Ł . ˇ æ F
Æ Łæº ł ŁØ ª Ł . ª º Ł Ł :
υD
+ β
= n
Ł Ł º D
∈ (D
),
Ł (n,D
) Æ Łæº ª ł ŁØ, Ø ßı
Ł Œ ŒŁı-ºŁÆ Łæ Ł æŒŁı æ Æ ŁØ. ª ªŁ Ł æŒŁ Łæº Ł ßı ł ŁØ Ł Łæß æ Ł :
 .
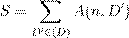˛ Œ æ Ł F
− S
= V
Ł Ł :
V
= X
( X
1 − A
(n,D
0
)).
D
0
∈(D
) υD
0
+β
=n
ˇ Ł Ł æ ˚ łŁ Ł Ł Œ æ :
V
2 6 D
0V
0,
ª D
0
- ºŁ Ł º (D
),
V
0
= X
( X
1 − A
(n,D
0
))2
−
D
0
∈(D
) υD
0
+β
=n
æ Łæ æŁ Łæº ł ŁØ Ł υD
0
+ β
= n
| ¯æºŁ
|
æ æ
|
Ł
|
æ
|
Ł
|
Ł
|
æº
|
ŁŁ
|
æ ı D
∈ (D
),
|
| Æ æ
|
ß æ
|
º Ł
|
º
|
ß
|
æº Ł ,
|
º
|
ß
|
D
0
. ´
|
ºŁ Ł
|
Łæ æŁŁ º Œ æ Ł. ˇ
ß Σ1
,
Σ2
Ł Σ3
Œ ßı æº ı æ ß ŁæºŁ æŁ Ł æŒŁ. ˆº -
| æ æ º ß Łæº Ł Σ1
- æ Ø æ ß ˜Łæ æŁ ª .
æŁ Ł æŒŁØ æ æ ß Σ1
æ ø æ º æ Ł øŁ ´Ł ª æ º Œ ßı Œ ŁØ Œ ºŁ æ Łı Æ ßı æ Ø, øŁı ßØ æ ª , Œ æ Łæ º Ł ØłŁı Œ Łª Ł æŒŁı æ , º ßı æ æ Ł ºª Æ Ł æŒ Ø ª ŁŁ. æŁ ŁŒ º æ Σ2
Ł
Σ3
ı Ł æ º ª æ Ł Ł . ¯æºŁ, º , Łæ æŁ Œ ßæ æºŁłŒ Æ º ł Ø, º æ æŁ ŁŒ º Łæº ł ŁØ Ł
|
| υD
0
+β
= n
. ˛Æœ Ł Ł Łæº ł ŁØ æ ı
|
ŁØ Ł υD
0
+β
= n
Ł Ł Œ
|
| æŁ Ł æŒ Ø º º Łæº ł ŁØ
|
Ł α
+ β
= n
.
|
| — ææ ßØ Ł Ł Ł º ł Ł
º Łæº , ºŁ º .
|
ŁØ Ł α
− β
= l,
ª l
-
|
| ˇ Ł øŁ Łæ æŁ ª Æߺ ł
|
Œº ææŁ æŒŁı ÆŁ ßı Ł-
|
| Ł ßı ƺ , Œ ß æ Ł Łæ æŁ ª
|
ªºŁ Æß ł ß º -
|
| Œ æ Łæ Ł æŒŁı ŁºŁ ªŁ Ł æŒŁı æ Æ
|
ŁØ. ˚ Łæº ƺ , ł… -
|
| ßı æ ø ª , æ æ : Ł Ł
ºŁ º Ø Ł ł , ƺ Ł-¸Ł º .
|
ƺ ºŁ º Ø, ƺ
|
| ˛Æº æ Ł Ł Łæ æŁ ª
Æ º ł ª ł . ´. ¸Ł ŁŒ .
|
æ Œ æ æ ƺ æ Ł Ł
|
| 3 ˛æ ß ß ß.
|
| ˜º ł Ł Ł Ł ßı ƺ Ł æ ºŁ Ł æŒŁ ,
|
ºª Æ Ł
|
æŒŁ , º -
|
| ß Ł æ ł ß ß. ˙ Ł º æ Ł Ł ßı
æ Œ Œº ææ :
) ß Ł Ł ß Æº ß Ł
n
= α
+ β
+ γ
|
ƺ
|
Æß
|
| Ł º Œ æ ª æ ß Ł ı ł æ º ß
|
Ł Ł
|
æŒŁı
|
-
|
| ª ææŁ ı æº º æ ºßı Łæ º, γ
Ł º Ł æº
|
º
|
æ Ł,
|
| Æß Ł Œ Ø, æ ı łŁ Ł Œ ßı, æ æ
Ł æŒŁı æ .
Æ) `Ł ß Ł Ł ß Æº ß Ł
n
= α
+ β
æ Ł æº Ł Ł º α
Ł β
Ł Œ ).
|
øŁı Ø,
|
Łª
|
-
|
| Ł æ º ß æ æ ł Ł ßı Ł Ł ßı
|
ƺ º
|
æ
|
-
|
| Æ º łŁı n
º æ ÆøŁØ ºŁ Ł æŒŁØ Ł - ¸Ł º
|
- ´Ł
|
ª
|
| Łª Ł æŒŁı æ ( Œ 1.2.1 æŒŁı æ ).
|
Œ Łª
|
Ł
|
-
|
| `Ł ß Ł Ł ß Æº ß Æß ª Æß ł
|
ß Ł Ł Ł.
|
| ˜º ł Ł ŒŁı Ł Ł ßı ƺ Ł æ ºŁ ß Ł ß º -
ª ł ( Œ 2.2 ß ł . ¨ææº Ł æ Œ ß æ ). ˛æ -
Æ æŁº ß º ß º æ Ł øŁ Æ º ł ª ł Ł Łæ æŁ ª
|
. ´. ¸Ł ŁŒ .
Ł Ł ß Æº ß Ł æ º Ł ºßı Łæ º Œ Ł ß Ł Ł æ Ł ß ß Ł Œ º æ ÆŁ ß Ł. ˛ Ł Łææº æ æ Æ ß Ł Ł ŁŒ - ª Ł æŒŁ Ł Ł ŁŁ Œ Ł ßı .
¸Ł
1. http://dic.academic.ru - Ł æŒ ŁŒº Ł .
2. www.mathnet.ru/rus - æ Ø " Ł æŒŁ ŒŁ".
3. ˝. . Ł , "˛ ´Ł ª ` Æ Ł", Ł æŒŁ ŒŁ, .38,
6 (1985).
4. . . ˙ ŒŁ , "ˇ ƺ ´ Ł ª º æ Œ º Ł º ßı Łæ º", -
Ł æŒŁ ŒŁ, .54, 5 (1993).
| 5. . ˚. ˚ łŁ , . ´. Œ º æŒŁØ "˛Æ Æø… Ł æŒŁ ŒŁ, .3, 2 (1968).
6. http://mirslovarei.com - æ Ø " Ł æº Ø".
|
ƺ
|
ºŁ º Ø Ł
|
ł ",
|
| 7. ˝. . Ł , . `. Ł "ˇ ƺ
|
Ł ł
|
æ Łæº Ł, Ł
|
øŁ Ł
|
| Łæº ºŁ º Ø", Ł æŒŁ
|
ŒŁ, .59,
|
4 (1996).
|
|
