|
Это принцип Ферма: среди виртуальных траекторий, соединяющих точки x 1 и x 2 , так что x (t 1 ) = x 1 , x (t 2 ) = x 2 , истинная траектория выделяется требованием, чтобы время достижения конечной точки было минимально. Пьер Ферма (1601–1665) сформулировал его в оптике в более общем случае неоднородной среды. • П. Ферма — юрист и по совместительству великий математик, знал интегрирование и дифференцирование до Ньютона и Лейбница, а декартовы координаты и уравнения прямых, плоскостей и поверхностей второго порядка — до Декарта. Он научился находить максимумы и минимумы функций (помните теорему Ферма?). Весьма значительный вклад внес Ферма в физику, а также в теорию чисел. Многие открытые и доказанные им теоремы являются классическими. Знаменитая великая теорема Ферма (до сих пор неизвестно, доказал ли ее он сам) была предметом упорной и безрезультатной работы многих математиков в течение трех столетий, пока ее, наконец, завершая усилия многих ученых, не доказал английский математик Эндрью Уайлс (1995). Преломление света. Закон СнеллиусаХотя еще Птолемей в II в. н. э. сделал довольно точные измерения углов падения и преломления луча света, проходящего через поверхность раздела между водой и воздухом, закон преломления света был открыт лишь в XVII веке Снеллиусом (1615) и носит его имя. Голландский профессор Виллеброрд Снелл (1580–1626) не публиковал своих работ. Их разыскал Рене Декарт и опубликовал в 1637 году. Декарт предложил качественное и довольно туманное объяснение закона. Сейчас мы увидим, что закон Снеллиуса следует из принципа Ферма, который его впервые обосновал. Предположим, что луч света выходит из точки A , преломляется в поверхности раздела двух сред и попадает в точку B , см. Рис. 5. Предположим, что в среде I скорость света есть v 1 , а v 2 — скорость света в среде II. Задача состоит в том, чтобы найти угол преломления β, если задан угол падения α. Применим принцип наименьшего времени Ферма. Если путь, пройденный лучом от A до точки преломления O есть ` 1 , а его путь от точки O до B есть ` 2 , то время t , за которое луч проходит весь путь от A до B , определяется равенством Примем границу раздела за ось x , а точку преломления за начало декартовых координат. Пусть координаты точки A суть (−a, −h ), а точки B — (b,k ). Тогда справедливы соотношения:
I
A Точки A и B фиксированы, так что величины h и k заданы. Имеем равенства: С другой стороны, точка O не определена, как и величины a и b , лишь сумма a + b известна заранее. Справедливо равенство ` 1 sinα + ` 2 sinβ = a + b. (14.26)Подстановка выражений (14.25) в это равенство дает соотношение h tgα + k tgβ = a + b. (14.27) Подстановка (14.25) в (14.23) дает выражение времени прохождения луча через углы α и β: Теперь нам нужно решить задачу об условном минимуме функции t = t (α, β) с условием связи (14.27). Варьирование дает соотношение: Варьирование уравнения связи (14.27) приводит к равенству Согласно принципу Ферма, δt = 0. С учетом формул (14.29), (14.30) отсюда выводим Это и есть закон Снеллиуса с конкретизацией правой части; сам Снеллиус нашел это соотношение экспериментально. 15. Применение принципа Гамильтона в механике сплошной средыПринцип Гамильтона применим и к системам с бесконечным числом степеней свободы, каковыми являются сплошные среды — жидкости, газы, деформируемые твердые тела. Он также применим к различным физическим полям, например, к электромагнитному полю, в некотором формальном смысле это превращает электродинамику , а точнее — некоторую ее существенную часть, в раздел механики. Замечу, что уже при рассмотрении уравнения обобщенного второго закона Ньютона (11.18) размерность конфигурационного пространства не играла сколько-нибудь серьезной роли, наш вывод был по сути «безразмерным». Для физических теорий, однако, характерно, что лагранжианы, потенциальная энергия, кинетическая энергия, работа внешних сил и т.д. выражаются в виде интегралов по области, занятой сплошной средой. Введенные ранее понятия производной функционала и градиента функционала приобретают новые специфические черты, возникает интересное и важное понятие функциональной производной , которое ввел впервые Вито Вольтерра. В этом разделе мы сначала в качестве примера выведем волновое уравнение из принципа Гамильтона. Уже в этом случае мы увидим дополнительную выгоду использования принципа Гамильтона в механике и физике сплошных сред: он не только приводит к уравнениям движения, но дает также вывод некоторых краевых условий. Такие краевые условия называются естественными. Обычно они возникают на разного рода свободных границах — свободных от внешних воздействий. Затем мы рассмотрим некоторые обобщения вместе с понятием функциональной производной. Завершается этот раздел рассмотрением конечномерных аппроксимаций бесконечномерных систем и важной роли принципа Гамильтона в построении таких аппроксимаций. Волновое уравнениеВолновое уравнение является, пожалуй, наиболее непосредственным обобщением уравнения второго закона Ньютона на сплошную среду. С формальной стороны оно даже является частным случаем этого уравнения в гильбертовом пространстве. Самый существенный новый момент состоит в появлении неограниченных операторов. Именно по этой причине в теории нелинейных волновых уравнений остается немало белых пятен. Здесь я ограничу изложение формальным выводом. Рассмотрим нелинейное дифференциальное уравнение в частных производных которое должно выполняться при x ∈ D , t ∈ R. Область D ⊂ Rm будем считать ограниченной, а ее границу ∂D — гладкой. Здесь c — положительная постоянная, а γ — неотрицательная, при γ = 0 уравнение становится линейным. Функция f (x,t ) считается заданной и достаточно регулярной. Предположим, что граница ∂D состоит из двух поверхностей S 1 и S 2 , причем на S 1 поставлено краевое условие первого рода, а на S 2 — условие второго рода: Здесь выбран довольно частный случай уравнения и краевых условий, чтобы на нем объяснить основные идеи. На самом деле, можно рассматривать гораздо более общие волновые уравнения и граничные условия, в частности, условия третьего рода, притом неоднородные. Как известно, чтобы определить эволюцию, для уравнения второго порядка по времени нужно поставить пару начальных условий: Назовем u
(x,t
) перемещением, а ∂t u (x,t ) может иметь совсем другой физический смысл, в частности, электродинамический: например, напряженности электрического и магнитного полей удовлетворяют волновому уравнению, обычно линейному, но, возможно, и нелинейному. Руководствуясь аналогией с уравнением второго закона Ньютона, введем следующие функционалы, которые будем называть соответственно кинетической и потенциальной энергиями: Первое слагаемое в (15.5) есть внутренняя потенциальная энергия среды. Второе слагаемое описывает своего рода нелинейно-упругое взаимодействие данной сплошной среды с внешней средой, такого рода слагаемые возникают, например, когда рассматривается упругое тело на упругом основании, γ — соответствующий коэффициент жесткости. Наконец, последнее слагаемое в (15.5) есть потенциальная энергия, связанная с заданной внешней силой f . Лагранжиан L определим равенством L = T − V , а действие по Гамильтону S — равенством (t 2 > t 1 , а в остальном t 1 и t 2 произвольны) t 2 Z S = Ldt. (15.6) t 1 В более подробной записи Давно пора уточнить определения конфигурационного и фазового пространств данной системы. Вопрос этот не очень прост. Ясно, конечно, что конфигурационное пространство должно состоять из функций, заданных в области D с некоторыми условиями регулярности внутри области, а также и при подходе к границе ∂D . Однако выяснение правильных ограничений на дифференциальные свойства функций u (x,t ) и в данном случае, и вообще всякий раз, когда мы имеем дело с уравнениями в частных производных, — достаточно деликатное дело, и, во всяком случае, здесь нет однозначного ответа. Для одного и того же уравнения в частных производных можно поразному выбирать конфигурационное и фазовое пространства. Первую ориентировку в этом вопросе дают нам выражения (15.4) и (15.5) для кинетической и потенциальной энергий, а также выражение (15.7) для действия S. Разумеется, нужно потребовать, чтобы все интегралы в этих выражениях сходились. Кроме того, нужно подчинить функцию u , принадлежащую конфигурационному пространству, по крайней мере, некоторым из краевых условий. На первый взгляд кажется естественным потребовать, чтобы функция u (x,t ) имела все производные, входящие в дифференциальное уравнение, то есть была C 2 -гладкой по x , t , а кроме того, удовлетворяла краевым условиям (15.2) в классическом смысле. Оказывается, однако, что такие классические решения начально-краевой задачи (15.1) – (15.3) далеко не всегда существуют, и далеко не всегда для них можно доказать единственность. Будем пока считать, что конфигурационное пространство есть пространство Говоря точнее, пространство Z (u 1 ,u 2 ) = ∇u 1 (x ) · ∇u 2 (x )dx. (15.9)D ◦ Если функция
Функцию u
(x,t
) мы теперь представляем себе как вектор-функцию u
(t
)(x
) времени t
со значениями в пространстве um dx (15.10) D следует из существования интеграла R (∇u )2 dx , согласно теореме вложе- D ния С.Л.Соболева. Фазовым пространством будем считать декартово произведение L
2
(D
). Элементом этого пространства является пара функций (u
(x
),v
(x
)), причем Приходится сразу признать, что дальнейший вывод волнового уравнения из принципа Гамильтона невозможно провести, строго придерживаясь сформулированных минимальных предположений о регулярности функции u . В ходе этого вывода мы будем считать ее, скажем, C ∞ -гладкой, хотя достаточно C 2 -гладкости по x и t . Возникающий здесь логический разлад носит принципиальный характер. Дальше я постараюсь объяснить, каким образом здесь наводится порядок. Оказывается, нужно уточнить и изменить само понятие решения уравнений в частных производных. Внимательный читатель заметил, по-видимому, что мы «забыли» о втором краевом условии (15.2). Далее будет показано, что это условие не надо вводить заранее — оно является следствием принципа Гамильтона. Итак, принцип Гамильтона требует, чтобы действие, определенное равенством (15.7), на истинном движении было экстремально: δS = 0. (15.11) Как обычно, вариация δu определяется как производная от деформации при этом деформация u ˜(x,t, ε) зависит от параметра деформации ε гладко, ε изменяется в некоторой окрестности нуля. Для всех малых ε и для любого t деформация есть достаточно гладкая функция от x, t , удовлетворяющая краевому условию первого рода Кроме того, должно выполняться равенство u ˜(x,t, 0) = u (x,t ) и, как обычно в принципе Гамильтона, должно быть выполнено «условие неподвижности концов»: u ˜(x,t 1 , ε) = u (x,t 1 ), u ˜(x,t 2 , ε) = u (x,t 2 ) (15.14) при любом малом ε. Соответственно для вариации получаем δu (x,t 1 ) = 0, δu (x,t 2 ) = 0. (15.15)Замечу, что именно требование гладкости деформации как раз и вносит тот логический разлад, о котором я упоминал. Дальше — формальные выкладки. Вычисляя вариацию, находим t 2 Z Z δS = (ut δut − c 2 ∇u · ∇δu − γu 3 δu + f δu )dxdt. (15.16) t 1 D Посредством интегрирования по частям перебросим производные по t
и по xi
с δu
на соответствующие множители. Учитывая равенства (15.15) и краевое условие
Вариация δu исчезает при t = t 1 и t = t 2 . Можно, однако, считать, что она исчезает и в полуокрестностях этих точек на [t 1 ,t 2 ]. Тогда она теряет зависимость от t 2 , и дифференцирование по t 2 дает равенство которое должно выполняться в любой момент t (непосредственно получается в момент t 2 , но он произволен). На поверхности S 2 вариация δu не обязана удовлетворять каким-либо краевым условиям. Если, однако, рассмотреть такие вариации, которые исчезают в окрестности границы ∂D , то мы избавимся от поверхностного интеграла в (15.18): Z
Согласно лемме на стр. 71, из этого равенства следует, что для всех x ∈ D и t ∈ R выполняется уравнение utt = c2 ∆u − γu3 + f(x,t). (15.20)Теперь вернемся к равенству (15.18) для произвольных допустимых вариаций δu . В силу (15.20) объемный интеграл исчезает, и получается равенство Еще раз повторю: δu
на S
2
можно выбирать произвольно, лишь бы существовала гладкая функция η(x
) такая, что Если положить в (15.21) а значит, Обобщенные решенияПри выводе волнового уравнения из принципа Гамильтона мы были вынуждены наложить на (неизвестное!) решение дополнительные и ниоткуда не вытекающие ограничения гладкости. Когда речь идет о динамических системах с конечным числом степеней свободы, тоже приходится налагать подобные условия. Однако там это не носит принципиального характера, поскольку, получив решение, удается доказать, что оно и в самом деле обладает нужной гладкостью (это делается с помощью известной леммы Дюбуа–Реймона в вариационном исчислении). Когда же речь идет об уравнениях в частных производных, вопрос о гладкости решения всегда принципиален. Классическое решение — такое, для которого и уравнение, и краевые и начальные условия выполняются в обычном смысле, — далеко не всегда существует. Для уравнений гиперболического типа, каковым является волновое уравнение, проблема существования классического решения сложна в принципе, поскольку возможно, что в условиях очень гладких данных (коэффициентов уравнения, границы области, граничных и начальных функций) решение оказывается нерегулярным — его производные, а то и оно само, претерпевают разного рода разрывы. В современной математической физике само понятие решения начальнокраевой задачи существенно изменено по сравнению с классическим. Рассматриваются различного рода обобщенные решения . Один из наиболее оправданных физических подходов к определению обобщенного решения основывается на принципе Гамильтона. Принцип Гамильтона не менее, а даже более фундаментален, чем уравнения Лагранжа второго рода. Вместе с тем, формулировка принципа Гамильтона не требует дополнительных предположений о гладкости решения, нужны лишь такие предположения о регулярности, которые обеспечивают существование интегралов, входящих в определение действия. В рассматриваемом случае начально-краевой задачи (15.1)–(15.3) определение обобщенного решения основывается фактически на равенстве (15.11): δS = 0, причем δS выражается формулой (15.16) посредством интегрирования по частям. По своему существу принцип Гамильтона не связан с конкретными начальными условиями и в регулярном случае является эквивалентом уравнения движения. Примем и здесь такую точку зрения, сделаем лишь некоторые непринципиальные упрощения. Во-первых, договоримся всегда выбирать t 1 = 0. Далее будем полагать t 2 = τ > 0 и интересоваться решением на отрезке времени [0, τ]. При этом мы ничего не теряем, так как τ — произвольно фиксировано, а если отрезок [t 1 ,t 2 ] содержится в [0, τ], мы получим прежнее определение, попросту выбирая δu так, чтобы δu (x,t ) = 0 для всех t вне [t 1 ,t 2 ]. Наконец, вместо δu (x,t ) будем для краткости писать η(x,t ). Теперь перейдем к строгому определению обобщенного решения. Определение. Обобщенным решением начально-краевой задачи (15.1)– (15.3) на отрезке времени [0, τ] при любом положительном τ называется функция u (x,t ) такая, что выполнены следующие условия: 1) Для любого t ∈ [0, τ] существуют и равномерно ограничены интегралы
, (∇u (x,t ))2 dx ≤ C 2 , D (15.23) где C 1 , C 2 , C 3 — положительные константы. 2)
Для любого
t
∈ [0,
τ] функция
u
(x,t
) удовлетворяет в обобщенном смысле краевому условию
для любой гладкой функции
η(x,t
) такой, что
η(x,
0) = 0,
η(x,
τ) = 0, и выполнено краевое условие
4) Функция u (x,t ) удовлетворяет начальным условиям в обобщенном смысле (в среднем) при t → +0
(15.25) Несколько комментариев к этому определению. При выводе волнового уравнения из принципа Гамильтона мы фактически установили, что если обобщенное решение имеет непрерывные вторые производные по x и по t , то оно удовлетворяет волновому уравнению в обычном смысле. Если к тому же сама функция и ее нормальная производная допускают определение на границе ∂D посредством предельного перехода («по непрерыввности»), то и краевые условия выполняются в обычном смысле. Выходит, что функция, удовлетворяющая условиям данного определения, оказывается классическим решением начально-краевой задачи при одном лишь дополнительном условии достаточной гладкости. Именно это и дает нам право называть ее обобщенным решением . Мы рассматривали решение u (x,t ) для положительных времен. В случае t < 0 все аналогично. Более того, замена t → −t приводит этот случай к предыдущему. Нетрудно проверить, что из предположения о конечности интегралов (15.23) следует, что все интегралы в интегральном тождестве (15.24) сходятся. Относительно заданной функции f достаточно предположить, что она «не чересчур разрывна», например, интегрируема с квадратом по x, t . В определении мы предположили, что функция η гладкая. При помощи предельного перехода можно убедиться, что это тождество остается в силе и для широкого класса разрывных функций η. Например достаточно, чтобы ∂ η ∂ η
∂t ∂xi Важность применения обобщенных решений уравнений в частных производных была осознана лишь в середине прошлого века. Даже когда классическое решение существует, естественным этапом исследования оказывается доказательство существования обобщенного решения. Долгая и упорная работа математиков в этой области привела к наиболее глубоким результата в теории функций и функциональном анализе. К сожалению, здесь нет места остановиться на этом более подробно. Замечу, что одна из первых работ по обобщенным решениям волновых уравнений была выполнена И.И. Воровичем [8], который рассматривал сложные задачи о колебаниях упругих оболочек. Функциональные производныеВ том случае, когда функционалы заданы на гильбертовом пространстве функций, скажем, на пространстве L 2 (D ), понятие градиента grad ϕ может быть существенным образом конкретизировано. Соответствующее определение строится по аналогии с понятиями дифференциала и частных производных гладкой функции f (x ), x ∈ Rn . Как Вам хорошо известно, главная линейная часть приращения функции, когда ее аргумент x = (x 1 ,...,xn ) получает приращение (dx 1 ,...,dxn ), есть Это равенство может служить определением частной производной Пусть теперь Φ : L 2 (D ) → R — функционал на гильбертовом пространстве L 2 (D ), где D — область в Rn . Допустимо рассматривать функционалы, заданные не на всем пространстве L 2 , а лишь на некотором всюду плотном линейном многообразии, дальше будем считать, что вводимые нами функции принадлежат области определения D(Φ) функционала Φ. Пусть теперь u ∈ D(Φ), и εδu — приращение функции u . Рассмотрим приращение Φ(u +εδu )−Φ(u ) функционала Φ. Мы рассматриваем частный случай деформации — линейной по параметру ε. Тогда производная по ε при ε = 0 дает нам вариацию функционала Φ в точке u Предположим, что эта вариация может быть представлена в виде Z δΦ(u ) = A (x )δu (x )dx. (15.28)D Разумеется, функция A (x ) вполне может довольно сложным образом зависеть от функции u — от всех ее значений, а не только от значения в точке x . В этом случае скажем, что A (x ) есть функциональная производная функционала Φ по аргументу u (x ), и введем обозначение: Обычно это обозначение сокращают и пишут Чтобы лучше пояснить аналогию между формулой (15.26) для df (x ) и формулой (15.28) для δΦ(u ), замечу, что вектор x = (x 1 ,...,xn ) можно рассматривать как функцию x (k ), определенную для k ∈ {1,...,n }, при этом попросту x (k ) = xk . С другой стороны, функцию u , заданную на D , можно трактовать как вектор, с бесконечным числом компонент, каждая из которых есть ux = u (x ), точка x ∈ D играет роль индекса. Формула (15.28) получается из формулы (15.26) в результате замен: f → Φ, x → u , n f
(x
) → Φ(u
), и далее: нечно, нужно сделать замены: df (x ) → δΦ(u ), dxk → δu (x ). Проделайте все эти замены в формуле (15.26). Получится формула (15.28). Приведу примеры вычисления функциональной производной. Пример 1. Пусть Z Φ(u ) = F (u (x ),x )dx (15.31)D с гладкой функцией F . Тогда очевидно, Если, например F (u,x ) = ρ(x )u 2m +1 , m — натуральное число, то Пример 2. На плотном в L 2 (D ) множестве гладких функций, исчезающих на границе, определим функционал (интеграл Дирихле) Z Φ(u ) = (∇u )2 dx. (15.34) D Имеем Z δΦ(u ) = 2 (∇u ) · ∇δudx. (15.35)D Интегрируя по частям, с учетом краевого условия Z δΦ(u ) = −2 ∆u · δudx. (15.36) D Следовательно, Обобщенное волновое уравнениеНе стремясь довести обобщение до крайности, рассмотрим континуальную механическую систему, определенную лагранжианом где ρ и F — известные функции своих аргументов. Будем считать, что область D ограничена, а на ее границе поставлено условие Применяя принцип Гамильтона, в предположении существования и гладкости функции u (x,t ), реализующей экстремум действия, придем к равенству Интегрируя по частям, с учетом краевого условия Отсюда следует уравнение движения Это уравнение, применяя понятие функциональной производной, можно записать в форме, вполне аналогичной конечномерному случаю, а именно: Замечу, что подобным формальным путем можно получить уравнения типа utt + ∆u = 0, для которых задача с начальными данными некорректна. Чтобы уравнение (15.43) было действительно волновым, нужно наложить определенное условие эллиптичности на функцию F . 16 Принцип Гамильтона и конечномерные аппроксимации бесконечномерных систем 129
Упражнения1. Выведите из принципа Гамильтона уравнение поперечных колебанийупругой оболочки utt = −c 2 ∆2 u + f (x,t ), где u = u (x 1 ,x 2 ,t ), а точка (x 1 ,x 2 ) ∈ S (ограниченной области R2 ). На границе ∂S = Γ должны выполняться краевые условия Эти краевые условия не являются естественными. А какие являются? 2. Докажите, что полная энергия T + V , где T и V определены формулами (15.4), (15.5), есть интеграл волнового уравнения (15.1). 16. Принцип Гамильтона и конечномерные аппроксимации бесконечномерных системЧтобы решить эволюционную задачу для бесконечномерной системы при помощи численных методов, ее приходится аппроксимировать конечномерными системами. Применяемые для этого методы дискретизации в основном сводятся к замене производных разностными отношениями значений функции в узлах, либо к аппроксимации решения конечными отрезками рядов Фурье по тому или иному базису. Первый подход приводит к различным сеточным методам, а второй — к методу Галеркина. Бывают полезны и различные комбинации этих двух методов. Мы рассмотрим здесь такие аппроксимации, которые сохраняют производные по времени, так что задача приводится к решению систем обыкновенных дифференциальных уравнений, иногда очень высокого порядка. Конечно, решая численно задачу для уравнения в частных производных, нужно заботиться о хорошей аппроксимации неизвестной функции и ее производных. Однако зачастую даже более важно, чтобы аппроксимирующие системы сохраняли фундаментальные свойства исходной системы. Когда заданная система получается из принципа Гамильтона, очень важно, чтобы это свойство сохранялось и для приближенных систем. В итоге возникает очень полезная в построении численных, а также асимптотических методов идея: аппроксимировать не заданные уравнения, а лагранжиан . После этого аппроксимирующее уравнение получается из принципа Гамильтона. Я приведу здесь два простеньких примера применения этой идеи. Разностный метод решения волновых уравненийРассмотрим одномерное линейное волновое уравнение ρ(x )utt = uxx (16.1) с краевыми условиями При этом функция ρ(x ) предполагается непрерывной и положительной: ρ(x ) > 0 для всех x . Поставим также начальные условия: Мы уже знаем, что эта задача получается из принципа Гамильтона с лагранжианом Будем решать начально-краевую задачу (16.1)–(16.3) методом прямых. Разделим отрезок [0,`
] на n
равных частей, и пусть h
Краевым условиям мы удовлетворим, полагая u 0 = 0 и un = 0. Выберем некоторую квадратурную формулу для аппроксимации интеграла (16.4), например, формулу прямоугольников (или трапеций). Тогда приближенный лагранжиан будет иметь вид
Соответствующие этому лагранжиану уравнения Лагранжа второго рода имеют вид В подробной записи имеем систему Здесь не нужно суммировать по k , хотя индексы повторяются, и нужно помнить, что u 0 = 0, un = 0. Как видим, в правой части само собой возникло стандартное разностное отношение, аппроксимирующее вторую производную uxx . Выходит, что эта наиболее популярная разностная схема получается из принципа Гамильтона. Принцип Гамильтона и метод ГалеркинаМетод Галеркина в его нестационарном варианте (иногда называемый также методом Галеркина – Фаэдо) особенно хорошо связан с принципом Гамильтона. На самом деле, стандартные галеркинские уравнения сохраняют свойство консервативности исходной системы и подчиняются принципу Гамильтона. Вместе с тем, применение принципа Гамильтона позволяет ускорить вывод галеркинских уравнений. Это я теперь и собираюсь продемонстрировать на примере начально-краевой задачи (15.1) – (15.3). Для упрощения разговоров давайте считать, что на всей границе ∂D области D выполнено краевое условие первого рода (S 1 = ∂D ) Решение уравнения (15.1) разыскивается в виде обобщенного ряда Фурье: ∞ u (x,t ) = X uk (t )ϕk (x ), (16.10) k =1 где ϕk
— гладкие функции, которые удовлетворяют краевому условию Известно, что все собственные значения λk положительны, собственные ◦ функции ϕk образуют ортогональную систему как в L 2 (D ), так и в W
Z 2 ϕk dx = 1, k = 1, 2,... (16.12)D Конечно, вместе с функцией ϕk , также и −ϕk удовлетворяет этому условию. Считаем, что из этих двух функций произвольно выбрана одна. Подставив выражение (16.10) в уравнение (15.1) и приравняв коэффициенты Фурье в левой и правой частях, можно получить бесконечную систему обыкновенных дифференциальных уравнений для неизвестных функций uk (t ). Идея метода Галеркина состоит в том, что эта бесконечная система урезается: оставляются лишь уравнения для u 1 (t ),...,um (t ), причем в этих уравнениях все высшие коэффициенты um +1 ,um +2 ,... полагаются равными нулю. Выходит, что приближенное решение имеет вид m um (x,t ) = X uk (t )ϕk (x ). (16.13)k =1 Следуя высказанной выше идее, мы должны вычислить приближенные кинетическую энергию Tm и потенциальную энергию Vm , подставляя um (x,t ) вместо u (x,t ) в (15.4) и (15.5). Затем определяется приближенный лагранжиан Lm как функция от обобщенных координат u 1 ,...,um — и пишется уравнение Лагранжа второго рода, вытекающее из принципа Гамильтона в случае лагранжиана Lm . Дальше мы применяем свойства ортогональности системы {ϕk } в L 2 и ◦ (1) W 2 : Z Z ϕk ϕl dx = δkl , ∇ϕk · ∇ϕl dx = λk δkl , (16.14) D D где δkl — символ Кронекера. Имеем Далее получаем
. Здесь известные коэффициенты ck 1 k 2 k 3 k 4 и fk определяются равенствами Z
D ∞ При этом очевидно, что f (x,t ) = P fk (t )ϕk (x ), так что fk — коэффи- k =1 циент Фурье функции f . Поясню вычисление слагаемого четвертой степени в (16.16). Здесь применяется простой технический прием — представление четвертой степени суммы в виде четырехкратной суммы:
(16.19) Интегрируя это равенство по x , приходим к выражению для коэффициента, данному в (16.17). Уравнения Лагранжа, отвечающие лагранжиану Lm = Tm −Vm , имеют вид Учитывая выражения (16.15) и (16.16) для Tm и Vm , получаем систему обыкновенных дифференциальных уравнений:
Если здесь взять m = ∞, то получится бесконечная система, эквивалентная исходной краевой задаче. Я предоставляю вам самостоятельно проверить, что метод Галеркина в стандартной форме приводит к той же системе (16.21). В принципе, метод Галеркина является весьма общим, он применим и в случае неконсервативных систем — когда сила не может быть определена посредством ее потенциальной энергии (потенциальную энергию вообще невозможно определить). Впрочем, известны и соответствующие неголономные обобщения принципа Гамильтона, в которых уже нет функционала действия, но постулируются соотношения для вариаций, из которых вытекают уравнения движения. По-видимому, использование приближенных методов типа метода Галеркина и метода сеток является самым мощным средством доказательства теорем существования и единственности решения для начально-краевых задач механики и физики сплошных сред. В частности, галеркинские уравнения типа уравнений (16.21) содержат лишь полиномиальные нелинейности, так что их правые части оказываются гладкими. Теорема единственности решения и теорема о локальной разрешимости задачи Коши для таких уравнений непосредственно следуют из классических результатов. Вместе с тем, сохраняя консервативную природу исходной задачи, эти уравнения обладают интегралом энергии, а иногда и другими интегралами. Это дает возможность во многих случаях, и в частности для системы (16.21) (см. упражнение 5), получить априорную оценку решения, а вместе с тем, и глобальную теорему существования решения задачи Коши. Обоснование приближенного метода, скажем, метода Галеркина состоит в доказательстве сходимости последовательности приближенных решений при m → ∞. Это действительно удается сделать с использованием современных средств функционального анализа и теории функций вещественных переменных. Замечу, что во многих случаях, особенно в стационарных задачах, удается установить лишь компактность множества приближенных решений. Случается, что различные последовательности приближенных решений сходятся к различным решениям краевой задачи для уравнений в частных производных. Здесь нет ничего удивительного — многие нелинейные стационарные краевые задачи действительно допускают несколько решений. К сожалению, здесь нет места остановиться на этих увлекательных вопросах подробнее (см. [22]). Упражнения1. Доказать, что уравнение движения, отвечающее кинетической энергии T и потенциальной энергии V вида
имеет вид
где Убедитесь в том, что в случае
это уравнение превращается в уравнение (15.1). 2. Рассмотрим волновое уравнение u tt = c 2∆u в ограниченной области D ⊂ Rn с краевым условием третьего рода
Докажите, что это уравнение имеет интеграл
3. Докажите, что уравнение малых поперечных колебаний упругой пластины utt = −k ∆2 u, например, с краевыми условиями может быть получено из принципа Гамильтона, если определить потенциальную энергию равенством
4. Докажите, что в случае Φ(u ) = R ρ(x )|u (x )|α dx при α > 1 и регуD лярной функции ρ(x ) функциональная производная имеет вид
5. Докажите, что галеркинская система (16.21) обладает интеграломэнергии Em = Tm + Vm . Пользуясь этим, докажите, что задача Коши для данной системы глобально разрешима для положительных t . 17. Динамика гибкой нерастяжимой нитиСпецифические, очень интересные, широко применяемые на практике и во многом таинственные в теории динамические системы со связями возникают в механике сплошной среды. Среди них наиболее важные — несжимаемая жидкость и гибкая нерастяжимая нить . Сейчас мы применим принцип Гамильтона для систем со связями, обобщив его на системы с бесконечным числом степеней свободы, каковой является нить, и выведем уравнение движения нити. Сразу скажу, что наш вывод будет во многом формальным (хотя и гораздо более строгим, чем в обычных книгах по механике). Мы увидим, какие нужно ставить краевые условия. В частности, будет найдено естественное краевое условие, которое «возникает само собой» из принципа Гамильтона. Начинать следует с определения положения системы, а затем определить конфигурационное и фазовое пространства. Физики говорят, что
нить — это деформируемое твердое тело, у которого один из размеров много больше двух других. Конечно, это скорее относится к области применимости той математической модели, которую мы собираемся построить. Ясно, что необходимо иметь хотя бы интуитивное представление о том объекте, который мы стремимся описать при помощи математики. Нить есть одномерная сплошная среда , другие одномерные сплошные среды — стержни, балки (в простейшем варианте, когда не учитывается их толщина), струйки пыли (одномерные пылевые среды ). Представим себе, что фиксировано стандартное состояние нити — отрезок [0,` ] на вещественной оси, ` — длина нити. С точки зрения механики, мы рассматриваем недеформированное состояние нити. Но лучше понимать его абстрактно — не интересоваться поначалу, как эта недеформированная нить вложена в пространство, в котором происходит движение реальной нити. Положение нити в данный момент t есть отображение x : [0,` ] → R 3 (см. Рис. 6). Технически удобно считать, что точка на отрезке [0,` ] задается своей декартовой координатой s . Мы сейчас имеем дело с нитью в пространстве R 3 , иногда интересно рассматривать нить в Rn или на некотором подмногообразии в Rn , а то и на произвольном многообразии. Условие нерастяжимости нити означает, что не только ее полная длина ` не меняется в ходе движения, но и длина каждой ее дуги между s 1 и s 2 также не может меняться. Это можно записать в дифференциальной форме, для квадратов элементов длины: dx 2 = ds 2 . Замечая, что dx 2 = x 02 ds 2 , запишем условие нерастяжимости нити в виде x 02 = 1. (17.1) Здесь x 0 = x 0 (s,t ) — производная по s от x . Заметим, что x = (x 1 ,x 2 ,x 3 ) ∈ R 3 . Соотношение (17.1) далее трактуется как уравнение идеальной стационарной связи. Итак, положение нерастяжимой нити есть отображение x : [0,` ] → R 3 , удовлетворяющее уравнению ( 17.1). Если ничего больше не добавлять, получится, что мы рассматриваем нить со свободными концами. В случае, когда конец нити (скажем, левый s = 0) закреплен или совершает движение по заданному закону, нужно еще поставить дополнительное условие где x 0 (t ) — заданный закон движения этого конца. В случае, когда x 0 (t ) = a , т.е. положение не зависит от времени, выходит, что конец нити зафиксирован в точке a . Условие (17.2) также можно трактовать как идеальную связь. Это, конечно, означает, что мы пренебрегаем трением в точке закрепления нити. Для определенности дальше будем рассматривать нить, у которой левый конец двигается по заданному закону, а правый — свободен. В этом случае условие (17.2) следует включить в определение конфигурационного пространства. Нить — натуральная механическая система, её лагранжиан есть разность между кинетической энергией T и потенциальной энергией V : L = T − V. (17.3) Чтобы определить кинетическую энергию, нужно задать линейную плотность ρ(s ). Тогда В более общей ситуации имеется функция распределения µ = µ(s ) массы вдоль нити. Функция µ(s ) есть масса отрезка нити [0,s ). Тогда кинетическая энергия задается интегралом Стилтьеса В том случае, когда функция µ(s ) непрерывно дифференцируема (или хотя бы абсолютно непрерывна), выражение (17.5) переходит в (17.4), причем ρ(s ) = µ 0 (s ). Дальше будем считать что кинетическая энергия выражается формулой (17.4). Потенциальную энергию одномерной сплошной среды, которая двигается в R 3 , вообще говоря, можно подразделить на внутреннюю и внешнюю. Модель абсолютно гибкой нити строится на предположении, что внутренняя потенциальная энергия Vi = 0. В общей ситуации приходится учитывать как потенциальную энергию сжатия (её сейчас нет, потому что нить несжимаема), так и потенциальную энергию изгиба — тогда получаются различные модели упругого стержня или балки . Внешняя потенциальная энергия создается внешними силами, действующими на нить. Если, например, нить находится в поле силы тяжести, то гравитационная потенциальная энергия задается формулой где g — вектор ускорения силы тяжести. Предполагая, что кроме силы тяжести, нет иных внешних сил, мы можем записать лагранжиан абсолютно гибкой нити в виде (17.3), где T дается формулой (17.4), а V = Ve — формулой (17.6). Действие тогда записывается в форме Теперь перейдем к применению принципа Гамильтона (δS = 0), с учетом связи (17.1) (точнее, бесконечного множества связей (17.1)). Итак, пусть x = x (s,t ) — истинное движение. Рассмотрим его деформацию x ˜ = x ˜(s,t, ε), определенную для ε ∈ (−ε0 , ε0 ), ε0 > 0; величина ε0 далее нигде не фигурирует, так что достаточно сказать, что ε изменяется в некоторой окрестности нуля. При этом мы предполагаем, что отображение x ˜ : (s,t, ε) →7 x ˜(s,t, ε) обладает некоторой гладкостью, достаточной для следующих преобразований. Если угодно, можно считать сначала, что x ˜ ∈ C ∞ , а затем уточнить, сколько производных на самом деле нужно. По определению деформации для всех s и t имеет место равенство x ˜(s,t, 0) = x (s,t ). Кроме того, деформация x ˜(s,t, ε) для всех малых ε должна удовлетворять уравнениям связей. В нашем случае это условие нерастяжимости нити (17.1), а также и условие закрепления (17.2): x ˜02 (s,t, ε) = 1, (17.8) x ˜(0,t, ε) = x 0 (t ). (17.9) В принципе Гамильтона требуется, чтобы при заданных начальном и конечном моментах времени t 1 и t 2 деформация удовлетворяла условиям «закрепления концов» x ˜(s,t 1 , ε) = x (s,t 1 ), x ˜(s,t 2 , ε) = x (s,t 2 ). (17.10)Варьируя эти равенства, получаем условия для вариации Напомню еще, что операция варьирования δ есть дифференцирование по параметру деформации ε при ε = 0, так что Применение варьирования дает вариацию. Например, вариация δx определяется равенством Варьирование связей (17.8) и (17.9) дает равенства
(17.15) Ради краткости, в формуле (17.14) опущены аргументы s и t , а в (17.15) — t . Варьируя действие (17.7), получаем t 2 ` Z Z δS = (ρx ˙ · δx ˙ + ρg · δx )dsdt. (17.16)t 1 0 Преобразуя первое слагаемое посредством интегрирования по частям по t с учетом (17.11) и применяя принцип Гамильтона, приходим к соотношению t 2 ` Z Z (−ρx ¨ + ρg ) · δxdsdt = 0, (17.17)t 1 0 которое должно выполняться для всех вектор-функций δx (s,t ), удовлетворяющих условиям (17.11), (17.14), (17.15) и, конечно, достаточно гладких. Чтобы избавиться от мешающих двигаться дальше ограничений на вариацию δx , применим метод Лагранжа. Умножая уравнение (17.14) на новую неизвестную (пока произвольную) функцию λ = λ(s,t ) (множитель Лагранжа) и интегрируя по s , t , получим t 2 ` Z Z
Условие связи (17.15) пока оставляем без внимания, дальше оно будет использовано. Мы можем теперь считать, как обычно в вариационных задачах со связями, что функция λ выбрана таким образом, что равенство (17.19) выполняется для вариаций δx , которые уже не обязаны удовлетворять условию (17.14). Учитывая, что равенство (17.19) имеет место для любых t 1 и t 2 , можно убрать интеграл по t (формально дифференцируем по t 2 и учитываем, что t 2 произвольно). Таким образом, имеем Это соотношение выполняется в каждый момент времени t . Перебросим производную по s с δx 0 на второй множитель λx 0 в последнем слагаемом посредством интегрирования по частям. Учитывая краевое условие на левом конце (17.15), получаем Теперь мы еще раз применим идею вывода естественного краевого условия, которая была уже использована раньше в случае волнового уравнения. Сначала мы рассматриваем равенство (17.21) в том частном случае, когда δx = 0 при s = ` , и показываем, что из полученного интегрального равенства уже следует уравнение движения ρx ¨ = (λx 0 )0 + ρg, (17.22) которое должно выполняться для всех t и s ∈ (0,` ). Но после того, как уравнение (17.22) выведено, мы видим, что интеграл в (17.21) исчезает для любых δx . В результате имеем равенство Поскольку
вие на свободном конце нити s = ` : Еще раз мы убеждаемся в двойной пользе принципа Гамильтона в механике сплошной среды — он дает не только уравнения движения, но и естественные краевые условия. Последние получаются на тех частях границы области, занятой сплошной средой, где первоначально не ставятся никакие краевые условия или задан неполный набор краевых условий. Примерами могут служить свободные границы (никаких краевых условий для деформаций) или подвижные твердые границы. Таким образом, для описания динамики нити при поставленных выше условиях мы получили уравнение (17.22) с краевыми условиями (17.24) и (17.2)). В начальный момент времени должны быть заданы положение нити и соответствующее поле скоростей:
(17.26) Заметим, что вектор-функции x 0 и v не вполне произвольны. Они должны удовлетворять условиям, вытекающим из уравнения связи Второе равенство получается дифференцированием по t при t = 0 уравнения (17.1). Физический смысл множителя Лагранжа λ. Когда мы применяем принцип Гамильтона, физический смысл множителя Лагранжа остается в тени.
( ((((((XX(
Рис. 7 Рассмотрим элемент нити между точками s и s + ds (см. Рис. 7). Так как нить не сопротивляется изгибу, силы, действующие на выбранный элемент со стороны остальных частей в точках s и s + ds , касательны к нити (поперечных сил нет). Поэтому такую силу можно записать в виде λx 0 , где λ = λ(s,t ) — некоторая функция. Внутренняя сила λx 0 (s + ds,t ) действует на элемент нити «справа» — со стороны больших значений s . Она возникает в результате взаимодействия выбранного элемента нити с остальной частью нити. По третьему закону Ньютона слева действует сила −λx 0 , отличающаяся лишь знаком. Мы видим, что равнодействующая двух сил, растягивающих элемент нити (s,s + ds ), есть (λx 0 )0 ds — с точностью до малых высшего порядка относительно ds . Сравнивая это выражение с правой частью уравнения (17.22), заключаем, что λ есть величина растягивающего усилия в точке нити. При этом положительным λ соответствует растяжение, а отрицательным — сжатие нити. Дальше мы покажем, что λ(s,t ) > 0 для всех s , t , так что нить всегда находится в растянутом состоянии в каждой своей точке. Нить всегда растянута. Интуиция говорит нам, что нить, не сопротивляющаяся изгибу, не может выдержать сжатия. Если её всё-таки сжать, то при малейшем отклонении от строго прямолинейной формы она начнёт сильно морщиться, по ней пойдут очень короткие волны. Так как нет никаких ограничений на длину таких волн и их амплитуды, окажется, что возникнут волны сколь угодно малой длины с большими амплитудами. Это означает, что гладкость решения сильно портится — настолько, что решение вообще может быть разрушено. Все это типично для некорректных задач типа задачи теплопроводности для отрицательных времен или задачи Коши для уравнения Лапласа. Дальше мы увидим, что именно эта последняя задача, действительно, возникнет, если мы вздумаем рассматривать задачу о сжатой нити. Понятно, что описанные патологии связаны с чрезмерной идеализацией модели. Они исчезают, если учесть изгибную жесткость и/или внутреннее вязкое трение. Замечу, что в подобных ситуациях большой интерес представляет исследование асимптотического поведения решений соответствующих краевых задач (для равновесий одномерной сплошной среды), а также и начально-краевых задач для движений нити при стремлении к нулю изгибной жесткости и коэффициента трения. Те же вопросы возникают, конечно, и для многомерных сплошных сред. В настоящее время проблемы такого рода почти не изучены. Сейчас мы в простейшем случае докажем, что нить всюду растянута. Результат, который будет получен, допускает довольно сильное расширение. Но всё-таки в самой общей ситуации, когда на нить действуют внешние силы, а концы её совершают произвольное движение, может оказаться, что она кое-где и сжата. В таких случаях приходится заключить, что модель абсолютно гибкой нити недостаточна для описания реального движения реальной нити. Следует всегда помнить, что в науке мы умеем работать лишь с моделями реальных объектов, а не с самими объектами. Предположим, что нить двигается в невесомости (g = 0), а её левый конец фиксирован. При этих условиях уравнение движения (17.22) принимает вид
По-прежнему должно выполняться условие нерастяжимости нити (17.1) x 02 = 1. Мы докажем теперь, что λ(s,t ) > 0 при всех t и s ∈ [0,` ), правый конец исключен ввиду краевого условия (17.30). Разделим уравнение (17.28) на ρ и продифференцируем его по s . В результате получится уравнение Мы намереваемся умножить это уравнение скалярно на x 0 . При этом будут полезны соотношения, получаемые из уравнения связи (17.1) двумя последовательными дифференцированиями по s : x 0 · x 00 = 0, x 0 · x 000 = −x 002 . (17.32) Нужна ещё и формула, получаемая из уравнения связи (17.1) двумя дифференцированиями по t : x 0 · x ¨0 = −x ˙02 . (17.33) Теперь всё готово. Умножим (17.31) скалярно на x 0 , с использованием уравнения связи (17.1) и выведенных из него соотношений (17.32) и (17.33) получаем уравнение Это уравнение Штурма–Лиувилля относительно λ с коэффициентами, которые выражаются через производные по s от x (s,t ). Заметим, что в каждый момент времени, зная x (s,t ), можно определить λ(s,t ) — не нужно решать задачу с начальными данными. Это общая ситуация для задач со связями. Однако я немножко поторопился сказать, что можно определить растягивающее усилие для λ — нужны еще краевые условия. На правом конце (s = ` ) имеется условие (17.30). Условие на левом конце (s = 0) мы выведем из уравнения движения (17.28). Если предположить, что решение является достаточно гладким, можно использовать это уравнение и на конце s = 0. Тогда получается, что при s = 0 0 = λx 00 + λ 0 x 0 , (17.35) так как Итак, уравнение Штурма–Лиувилля (17.34) следует решать при краевых условиях Из теории краевых задач Штурма–Лиувилля следует, что решение λ(s,t ) краевой задачи (17.34), (17.36) положительно при 0 ≤ s < ` . Здесь существенно, что в (17.34) коэффициент при λ неположителен, равно как и свободный член. Доказательство Вы можете провести самостоятельно, усвоив идеи доказательства принципов максимума-минимума, например, по книгам [56, 57]. Жесткость систем со связями. Сейчас я собираюсь, отправляясь от примера нерастяжимой нити, обсудить явление жесткости , которое специфично для систем со связями. Я поколебался в выборе эпитета, но так и не решил, «приятное» или «неприятное» это явление, и ни на одном из них не остановился. С явлением жесткости или частичной жесткости связаны интересные следствия — как позитивные, так и негативные. Рассмотрим нерастяжимую нить с закреплёнными концами. Соответствующие краевые условия имеют вид где a и b — известные точки пространства R 3 . Очевидно, что при этом должно быть выполнено условие |a − b | ≤ `, (17.38) где ` — длина нити. Если |a − b | > ` , то не существует ни одной векторфункции x (s,t ), удовлетворяющей условию связи x 02 = 1 и краевым условиям (17.37). Если же расстояние между точками a и b в точности равно ` , то, очевидно, существует лишь одна такая вектор-функция, соответствующая прямолинейному положению нити между точками a и b . Нить не сможет двигаться! Это и есть явление жесткости. Более общее условие |a − b | ≤ ` назовем условием совместности связей (17.37) и x 02 = 1 (нерастяжимость). Понятно, что всякий раз, когда назначаются условия связей, нужно позаботиться об их совместности (непротиворечивости), не то получится, что движение невозможно, и мы ставим задачу с пустым содержанием. Если связи совместны, то всё равно может случиться, что им удовлетворяет лишь одно положение системы или некоторый дискретный набор положений, а движение все-таки невозможно. Более интересно явление частичной жесткости . Если система имеет конечное число степеней свободы, скажем, объемлющее пространство есть Rn , и наложено конечное число r связей, то в условиях невырожденности размерность k конфигурационного пространства системы есть n −r . Если же оказалось, что k < n − r , то скажем, что система частично жесткая, а величина n − r − k есть мера этой жесткости.
Особенно интересен тот случай, когда и размерность объемлющего пространства, и количество связей бесконечны. В результате может получиться, что система имеет конечное число степеней свободы. Именно эта ситуация возникает в задаче о движении абсолютно твёрдого тела (например, в R 3 ). Связи в этом случае требуют, чтобы расстояния между любыми двумя точками тела оставались неизменными в ходе движения. В результате оказывается, что конфигурационное пространство конечномерно, именно шестимерно, число степеней свободы твердого тела равно 6. Если же одна точка тела закреплена, то получается система с тремя степенями свободы. А когда закреплены две точки, то остается одна степень свободы — тело может лишь вращаться вокруг оси, проходящей через эти две (ну, конечно, различные) точки. Кстати, именно по этой, довольно формальной причине, динамика абсолютно твердого тела попадает в курсы классической механики, а не в курсы механики сплошной среды. Дальше я собираюсь рассмотреть задачу о движении твердого тела подробнее. Динамика нити с одним закрепленным концом. Рассмотрим абсолютно гибкую нерастяжимую нить с закрепленным левым концом, и пусть к её правому концу приложено растягивающее усилие T = T i , см. Рис. 8. Правый конец подвижен, но ему разрешается перемещаться лишь вдоль оси x 1 . Нетрудно представить себе, каким образом можно практически обеспечить изображенный на Рис. 8 способ приложения нагрузки: достаточно прикрепить к жесткому шарниру на правом конце нити еще одну нить, перебросить её через ворот и к её свободному концу подвесить груз, см. Рис. 9. Мы предположим, что все виды трения пренебрежимо малы (честнее говорить: отсутствуют, равны нулю), и что эта дополнительная нить (а может, стержень или трубка, через которую пропущена нить) остается всё время параллельной оси x 1 .
Рис. 9 гией Ek и потенциальной энергией V : L = Ek − V. (17.39) В определении лагранжиана пришлось изменить обозначение, так как буква T занята — общепринято через T обозначать растягивающее усилие. В предположении, что нить однородна, и погонная масса нити ρ (она же — линейная плотность) равна единице, кинетическая энергия задается равенством При этом x = x (s,t ), s ∈ [0,` ], t ∈ R — параметрическое уравнение положения нити в момент t , ` — её длина. Потенциальная энергия V , связанная с заданным растягивающим усилием T , имеет вид
к числу связей относятся также краевые условия на левом конце и два условия на правом конце нити: Еще одно условие на правом конце получится далее из самого принципа Гамильтона как естественное. Согласно принципу Гамильтона для систем со связями δS = 0. Для деформаций уравнения связей (17.43), (17.44) должны быть выполнены, а вариация δx должна удовлетворять условиям, получающимся при варьировании равенств (17.43), (17.44) Равенство δS = 0, согласно (17.42), имеет вид t 2 ` t 2 Z Z Z x ˙ · δxdsdt ˙ + T δx 1 (`,t )dt = 0. (17.47)t 1 0 t 1 Как и ранее, проводим в первом слагаемом (17.47) интегрирование по частям, а затем дифференцированием по t 2 избавляемся от интеграла по времени. В результате получим соотношение ` Z −x ¨ · δxds + T δx 1 (`,t ) = 0, (17.48)0 которое должно выполняться в каждый момент t (мы заменили t 2 на t ). Из уравнения (17.45), умножая его на множитель Лагранжа λ = λ(s,t ), после интегрирования по частям получаем С учетом условий (17.46) имеем Вычитая это равенство из (17.48), получаем Применяя стандартное рассуждение, связанное с переходом к вариациям δx , исчезающим на границе, снова получаем уравнение движения нити x ¨ = (λx 0 )0 , (17.52) а затем, возвращаясь к произвольным вариациям, удовлетворяющим условиям (17.45) и (17.46), и учитывая, что Таким образом, уравнение движения (17.52) остается прежним. Вообще, уравнения движения, как легко понять, не меняются при переходе к новым краевым условиям. Также должно выполняться условие нерастяжимости нити (17.43), а краевые условия задаются равенствами (17.44) и (17.53). Конечно, краевое условие (17.53) можно вывести и непосредственно, заодно лучше поняв его механический смысл. Для этого нужно разложить заданное растягивающее усилие T
, см. Рис. 8, на сумму двух компонент, одна из которых ортогональна линии действия усилия — оси x
1
, а другая — касательна к нити и равна λx 0 = (T · x 0 )x 0 , (17.54) что совпадает с (17.53). Присмотримся к краевому условию (17.53). Из него следует не слишком приятный вывод: продольное усилие λ при s
= `
оказывается бесконечно большим, если Здесь m — масса «держалки», а уравнение (17.55) получается применением II-го закона Ньютона; массой нити мы по-прежнему пренебрегаем, считая, что она «много меньше» (так обычно говорят, хотя точнее было бы сказать «во много раз меньше»). Подробнее о задачах с краевыми условиями типа (17.55) рассказано в работе [54]. Было бы «математической глупостью», применяя нашу модель на практике, совсем забыть о той компоненте усилия T , которая уравновешивается реакцией связи. Если она оказывается слишком большой, то связь может разорваться, и условия применимости нашей модели будут наруше- ны. А потому докажите, что эта реакция равна вектору
бесконечности при Подведем итог. В условиях, соответствующих Рис. 8, уравнение движения нити и условие её нерастяжимости имеют вид
Соответствующие краевые условия суть
(17.59) Напомню, что третье краевое условие (17.59) выполняется лишь в предположении, что Начальные условия состоят в задании положения нити и поля скоростей составляющих её точек при t = 0: Как всегда при наличии связей, начальные данные должны быть с ними согласованы. Начальное положение x 0 должно удовлетворять условию нерастяжимости нити (17.57) и краевым условиям (17.58) вместе с первыми двумя условиями (17.59):
. (17.62) Начальное поле скоростей должно быть подчинено условиям, получаемым дифференцированием уравнений связи по t при t = 0:
. (17.64) 18. Уравнение колебаний струныУдивительное дело — едва ли не во всех распространенных учебниках по математической физике уравнение поперечных колебаний струны выводится некорректно — и с физической, и с математической точки зрения. Некоторым исключением является лишь классическая книга Р. Куранта и Д. Гильберта [18]. Линейное уравнение струны описывает малые, а точнее говоря, бесконечно малые колебания около её прямолинейной формы равновесия. Обычно вне обсуждения остается вопрос о законности перехода от более точных нелинейных уравнений к линеаризованным. Для уравнений гиперболического типа, описывающих волновые процессы, эта проблема все ещё составляет немалую трудность. К тому же, в механике и в математической физике нередко случается, что истинные нелинейные уравнения вообще выпадают из поля зрения, не выписываются явно, и остается неясным, какую, собственно говоря, задачу мы решаем приближенно, переходя к линейным уравнениям. Сама проблема исследования взаимосвязи между решениями нелинейных и соответствующих им линеаризованных уравнений «заметается под ковер». Случается, что к линейному уравнению струны дописываются довольно произвольно нелинейные слагаемые, и такие уравнения называются уравнениями нелинейной струны (пример: utt − uxx + u 3 = 0). Разумеется, подобные уравнения бывают очень интересными, описывают разнообразные волновые процессы, служат хорошими моделями, помогающими понять роль нелинейности в проблеме распространения волн. И всё-таки можно довольно уверенно предположить, что не искусственно составляемые уравнения, а фундаментальные модели, выводимые из «первых принципов» (таких, как закон сохранения энергии, закон возрастания энтропии в замкнутой системе, принцип Гамильтона), лучше описывают явления реального мира и оказываются проще для исследования. В истории науки не раз бывало, что модели, составленные по принципу их (кажущейся на первый взгляд!) простоты, на деле оказываются как раз наиболее сложными, вырожденными и трудно поддающимися анализу. Я говорю это как некоторое оправдание рассмотренной дальше, внешне довольно сложной системы уравнений абсолютно гибкой нити, которая при линеаризации и порождает уравнение струны. Проблема обоснования законности линеаризации здесь отнюдь не проста и на сегодняшний день остается открытой. Дальше мы увидим, что уравнение струны получается как уравнение малых колебаний нити, растягиваемой продольной силой, около её прямолинейного положения равновесия. Определенная тонкость постановки этой задачи связана с необходимостью как-то обойти эффект жесткости связи. Имеются разные способы снятия жесткости. Можно было бы рассмотреть растяжимую нить, отказавшись вовсе от условия связи (довольно интересно проделать это подробно). Оставаясь в рамках механики систем со связями, интересно (и идейно) рассмотреть минимальное ослабление связей, допустив подвижность одного из концов нити и сохранив условие её нерастяжимости. По этому пути мы теперь и пойдем. Еще один вариант вывода уравнения струны возникает, когда рассматривается нить переменной длины — скажем, длинная нитка, у которой один конец закреплен, пропущена через игольное ушко и растягивается заданной силой, а мы следим за событиями лишь по одну сторону от игольного ушка. К этой задаче я надеюсь вернуться позднее. Прямолинейное равновесие нити и его возмущения. Довольно очевидно, что система уравнений и краевых условий (17.56)–(17.59) допускает решение, не зависящее от времени и отвечающее прямолинейной форме равновесия нити: x ¯1 = s, x ¯2 = 0, x ¯3 = 0, λ ¯ = T. (18.1)Первые три соотношения говорят, что нить располагается вдоль оси x 1 — линии действия силы T . Величина λ ¯ после этого определяется из уравнения (17.56). Для произвольного решения (x, λ) положим x = ¯x + u, λ = λ ¯ + µ, (18.2) где x ¯ = (s, 0, 0) = s i (i — координатный орт оси x 1 ), λ ¯ = T . Векторфункция u (s,t ) называется возмущением формы равновесия x ¯, а функция µ(s,t ) — возмущением продольного усилия λ ¯ = T . Подставляя выражения (18.2) в уравнения и краевые условия (17.56)– (17.59), получим нелинейную систему для возмущений u , µ u ¨ = (Tu 0 + µi + µu 0 )0 , (18.3)
Характерной чертой уравнений возмущений является наличие тривиального решения, в данном случае это u = 0, µ = 0. Действительно, когда возмущения исчезают, мы возвращаемся к известному решению — равновесию (18.1). Вывод уравнения колебаний струны. Линеаризуем систему (18.3)– (18.6). Это значит — в каждом из этих уравнений оставим лишь линейные 0 , u 0 2 и т.п. члены, а чисто нелинейные относительно µ и u , например, µu отбросим. В результате придём к линеаризованной системе
(18.8) (18.9) ,
µ Разумеется, уравнения, которые были линейными и однородными, остались без изменения. Как видим, переход от нелинейнных уравнений к линеаризованным — довольно грубая операция. При использовании линеаризованных уравнений можно надеяться лишь на описание движений, достаточно близких к основному режиму. Когда речь идет об уравнениях в частных производных, неизбежно встает вопрос и о том, в каком смысле понимается близость решений полной системы и линеаризованной. Например, отбрасывая в (18.4) слагаемое u 02 и переходя к (18.8), приходится предполагать, что не просто возмущение u , но и его производная достаточно малы. Нелегко определить, что значит «достаточно». Когда математики произносят такие слова, то это означает лишь, что существует или должна существовать такая положительная константа η > 0, что при условии |u 0 | < η известна некоторая хорошая оценка разности между решениями двух систем. Даже когда теория установила, что такая константа η существует, обычно бывает непросто получить для неё хорошие оценки. В конце концов, как правило, приходится прибегать к численному или натурному эксперименту. Замечу еще, что во многих случаях никак нельзя ожидать, что решения полной нелинейной задачи остаются близкими неограниченно долго. Мы можем потребовать, чтобы возмущения были малы в начальный момент. Если окажется, что соответствующее решение линеаризованной системы неограниченно возрастает со временем, то очевидно, что исходное предположение о малости отброшенных слагаемых нарушается. При этом, во многих случаях удается строго доказать — для обыкновенных дифференциальных уравнений это сделал А.М. Ляпунов, — что подобное поведение решений линеаризованной системы означает неустойчивость основного решения полной системы. Результаты Ляпунова о законности линеаризации в проблеме устойчивости перенесены и на некоторые классы бесконечномерных задач, см. [11], [58]. Однако в рассматриваемой нами сейчас проблеме, как и во многих других аналогичных проблемах о нелинейных колебаниях, вопрос о законности линеаризации до сих пор не рассмотрен. Тем более замечательно, что многие выводы, вытекающие из анализа уравнения колебаний струны, прекрасно подтверждаются опытом. Тут даже хочется чуть-чуть пофилософствовать и спросить, не относится ли это вообще ко всем математическим проблемам естествознания. Ведь каждый раз при построении математической модели приходится пренебрегать столь многими факторами, что совпадение теоретических выводов с экспериментом выглядит просто как чудо. Быть может, самое сильное переживание исследователя — видеть, как экспериментальные точки ложатся на теоретический график (или точки, рассчитанные по теории, ложатся на экспериментальный график). Вернемся, однако, к системе (18.7)–(18.10). Из (18.8) следует, что u 1 не зависит от s , а тогда, согласно краевому условию (18.9), u 1 ≡ 0. С учетом этого факта векторное уравнение движения (18.7) в координатной форме примет вид
Из (18.11) и краевого условия (18.10) следует, что µ = 0, так что в принятом приближении сила натяжения нити остается равной T . Уравнения (18.12) и (18.13) имеют одну и ту же форму — это уравнение поперечных колебаний струны . Мы его запишем в виде u ¨ = c 2 u 00 , (18.14) где c 2 — квадрат скорости распространения поперечных волн Раньше мы принимали погонную массу нити ρ (она еще называется линейной плотностью) равной единице. Вообще, она появляется как множитель в левой части уравнений (18.12), (18.13), откуда и получается выражение (18.15). Глядя на эту формулу, особенно ясно, что упругость нити тут не при чем, странно, что этого не заметили авторы многих учебников. Предыдущий вывод дал также краевые условия для уравнения струны (18.14), см. (18.9), (18.10): u 2 и u 3 должны исчезать на концах. Опуская индексы, запишем эти условия первого рода для уравнения (18.14): Другие краевые условия. Помимо условий первого рода (18.16), для уравнений струны часто используются также краевые условия второго и третьего рода. Они соответствуют иным способам закрепления подвижного правого конца нити. Пусть на правый конец нити действует внешняя сила с известной потенциальной энергией ϕ(x (` )). Например, можно себе представить, что нить прикреплена к подвижному шарниру на твердой подставке, а последняя приделана к подвижной платформе, но не жестко, а при помощи упругих пружин, см. Рис. 10.
Рис. 10 В этом случае краевое условие при s = ` примет вид Предположим, что потенциальная энергия ϕ такова, что нелинейная система уравнений движения нити допускает равновесие (18.1): x ¯1 = s , x ¯2 = 0, x ¯3 = 0, λ ¯ = T . Это налагает на функцию ϕ ограничения ϕx 1 (`, 0, 0) = −T, ϕx 2 (`, 0, 0) = 0, ϕx 3 (`, 0, 0) = 0. (18.18) Поворотом осей x 2 , x 3 можно добиться исчезновения слагаемого с x 2 x 3 в выражении потенциальной энергии (привести квадратичную форму от x 2 , x 3 к главным осям). При таком выборе осей x 2 , x 3 разложение Тейлора функции ϕ в точке (`, 0, 0) принимает вид Здесь опущены члены степени 3 и выше. Переходя к возмущениям равновесия (18.1), т.е. полагая x (s,t ) = ¯x + u (s,t ), λ(s,t ) = T +µ(s,t ), запишем краевое условие (18.17) при s = ` в виде (T + µ)(i + u 0 ) = −grad ϕ(` + u 1 ,u 2 ,u 3 ). (18.20)Здесь через uk обозначено uk (`,t ), k = 1, 2, 3. В координатах имеем соотношения (T + µ)(1 + u 0 1 ) = −ϕx 1 (` + u 1 ,u 2 ,u 3 ), (T + µ)u 0 2 = −ϕx 2 (` + u 1 ,u 2 ,u 3 ), (18.21) (T + µ)u 0 3 = −ϕx 3 (` + u 1 ,u 2 ,u 3 ). Правые части вычисляем при помощи равенства (18.19). Имеем ϕx 1 (` + u 1 ,u 2 ,u 3 ) = −T + k 1 u 1 − q 2 u 2 − q 3 u 3 , ϕx 2 (` + u 1 ,u 2 ,u 3 ) = k 2 u 2 − q 2 u 1 , (18.22) ϕx 3(` + u 1,u 2,u 3) = k 3u 3 − q 3u 1. Линеаризация соотношений (18.21) дает краевые условия для струны Tu 01 + µ = −k 1u 1 + q 2u 2 + q 3u 3, Tu 0 2 = −k 2 u 2 + q 2 u 1 , (18.23) Tu 03 = −k 3u 3 + q 3u 1. Линеаризация условия нерастяжимости на равновесии (18.1) дает по-прежнему равенство µ = q 2 u 2 + q 3 u 3 , Tu 0 2 = −k 2 u 2 , (18.24) Tu 03 = −k 3u 3. Как и раньше, первое условие служит для определения величины µ, а остальные два дают краевые условия при s = ` для уравнений струны. При k 2 6= 0 и k 3 6= 0 — это условия 3-го рода, которые, опуская индексы, можно записать в виде u0
(`,t) = −βu(`,t),
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| и уравнение движения есть |
|
| ρ(s )x ¨ = (λx 0 )0 . |
(18.27) |
Некорректность задачи о сжатой нити. Выше мы предполагали, что нить растягивается внешней нагрузкой и T > 0. Однако ничто не мешает, как-будто, проделать все предыдущие выводы и при T < 0 — когда внешняя сила сжимает нить. В результате, однако, вместо гиперболического уравнения струны получается (пусть линейная плотность ρ = const ) уравнение эллиптического типа
![]() ,
(18.28)
,
(18.28)
которое несущественно отличается от уравнения Лапласа (а при k = 1) совпадает. Хорошо известно (см., например, [28]), что задача Коши для уравнения (18.28) некорректна . Решение при начальных условиях
![]() (18.29)
(18.29)
даже для C ∞ -гладких функций u 0 (s ), v 0 (s ), как правило, не существует, а если и существует, то малейшее начальное возмущение чрезвычайно быстро возрастает по времени и за конечное время уходит на бесконечность. Это показывает, что сжатая нить ужасающе неустойчива.
Снова модель заявляет нам о своей неадекватности. На сей раз к корректной задаче можно прийти, если учесть сопротивление реальной нити изгибу. Это соответствует добавлению потенциальной энергии, зависящей от кривизны κ = x 00 , точнее, от ее квадрата:
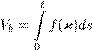 (18.30)
(18.30)
с заданной функцией f
. В простейшем варианте полагают![]() , D >
0. В итоге получается модель несжимаемого стержня (балки)
.
, D >
0. В итоге получается модель несжимаемого стержня (балки)
.
Было бы очень интересно рассмотреть динамику балки при очень малой изгибной жесткости D и понять, возможно ли, и в каком смысле, осуществить предельный переход при D → 0. Я ожидаю, что лишь привлечение методов теории вероятности поможет описать эту весьма сложную динамику, не поддающуюся детерминированному анализу.
О необходимом числе краевых условий и практическом значении теоремединственности. Постановка краевых условий на подвижном конце нити — непростое дело, в особенности, если мы хотим не только получить корректную математическую модель, а намереваемся описать реальную ситуацию — скажем, колебания струн гитары и скрипки или электрического провода между двумя столбами. Разумеется, те схемы закрепления подвижного конца нити, которые изображены на Рис. 8–10, не следует понимать слишком буквально, они приведены лишь для иллюстрации. Например, пружинки просто означают, что в точке опоры действует упругая сила, которая стремится возвратить конец нити в его равновесное положение. Эта сила зависит только от величины отклонения — линейно (по Гуку) или нелинейно.
Дальше я еще собираюсь обсудить иной вариант закрепления и рассмотреть «нить, продетую сквозь игольное ушко» или тонкую трубку. Принципиальное отличие этого способа закрепления от всех предыдущих состоит в том, что на сей раз длину нити нельзя считать фиксированной, потому что мы держим под наблюдением лишь её часть. В итоге задача попадает в тот разряд моделей, которые описывают системы с переменным составом частиц . Аналогичные проблемы возникают в гидродинамике, когда изучается движение жидкости в некоторой известной области, граница которой или, по крайней мере, её часть проницаема для жидкости. В результате частицы жидкости могут входить в область извне и уходить из неё. Принцип Гамильтона неприменим к системам с переменным составом материальных частиц.
Обсудим парадоксальное различие между краевым условием (17.24) на свободном конце нити (![]() ) и краевым условием (17.59) в случае, когда нить растягивается (
) и краевым условием (17.59) в случае, когда нить растягивается (![]() при s
= `
).
при s
= `
).
Почему в случае растяжения (T > 0) необходимо три краевых условия, а если его нет (T = 0), то достаточно одного? А может быть, и на свободном конце нужны дополнительные условия?
Такого рода сомнения разрешает лишь теорема единственности решения начально-краевой задачи. Если при поставленных условиях её удается доказать, то это, безусловно, означает, что никаких иных условий ставить не нужно. Замечу, что теорема существования, напротив показывает, что поставленные условия непротиворечивы, нет лишних условий, которые следовало бы отбросить.
Доказательства теорем единственности и теорем существования решения различных начально-краевых задач для нити технически довольно сложны, а глобальные теоремы существования вообще неизвестны.
Здесь я ограничусь простейшим случаем, когда в начальный момент нить неподвижна, а её форма может быть произвольной. Итак, рассмотрим случай начальных условий
![]() ,
,
![]() (18.31)
(18.31)
для всех s ∈ [0,` ]. Краевые условия соответствуют закреплённому левому концу и свободному правому
![]() ,
,
![]() .
(18.32)
.
(18.32)
Докажем, что уравнениедвижениянити x ¨ = (λx 0 )0 ,подчинённойтребованию нерастяжимости x 02 = 1 и условиям (18.31), (18.32), имеет единственное решение x (s,t ) = x 0 (s ), λ(s,t ) = 0.
Доказательство. Умножив уравнение движения (17.52) на x ˙ и интегрируя по s , выводим
![]() (18.33)
(18.33)
Внеинтегральные члены обращаются в ноль в силу краевых условий (18.32);
так как![]() , также и
, также и![]() . Дифференцируя по t
уравнение связи x
02
= 1, получаем равенство
. Дифференцируя по t
уравнение связи x
02
= 1, получаем равенство
x 0 · x ˙0 = 0, (18.34)
из которого следует, что интеграл в правой части (18.33) также равен нулю. Таким образом,
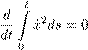 .
(18.35)
.
(18.35)
Из этого равенства и начального условия (18.32), следует, что x ˙ ≡ 0. Выходит, что x (s,t ) = x (s ), а от t не зависит. Поэтому x (s,t ) = x (s, 0) = x 0 (s ) для всех t и s , ввиду начального условия (18.31). Наше утверждение, таким образом, доказано.
Разумеется, «физически очевидно», что нить, на которую не действуют никакие силы, вечно остается в покое при любой её начальной форме (начальное поле скоростей — нулевое). Математик, однако, обязан подобные утверждения проверять, исходя из построенной модели, что хотя бы в какой-то мере подтверждает ее правильность. Физики, часто выступая против «теорем существования» (я поставил кавычки, потому что они обычно имеют в виду вообще чрезмерно педантичные обоснования, и нередко в этом бывают правы), обычно признают полезность теорем единственности. Когда некоторое решение удается получить, приятно знать, что нет других решений. Тут все согласны. Впрочем, фон Карман утверждал, что физики обычно пишут правильные дифференциальные уравнения движения, но никогда не пишут правильно краевые условия.
19. Специальная теория относительности Эйнштейна
Теория относительности хорошо изложена во многих книгах — см. «Теория поля» Л.Д. Ландау и Е.М. Лифшица [21], «Теория относительности» Вольфганга Паули [34]. Последний труд был написан 20-летним студентом, был очень высоко оценен, попал в физическую энциклопедию и до сих пор является одним из лучших обзоров раннего периода развития этой теории. А всё-таки я рекомендую начать с чтения работы самого А. Эйнштейна «К электродинамике движущихся сред», она сейчас легко доступна [52].
В основе теории Эйнштейна лежат два постулата.
1. Постулат относительности. Постулируется существование трехпараметрического семейства систем отчета, называемых инерциальными , в которых все законы природы «выглядят одинаково». Все эти системы движутся друг относительно друга поступательно с постоянной скоростью (3 параметра — три компоненты этой скорости).
Этот постулат далее конкретизируется посредством указания преобразований перехода от одной системы отсчета к другой. Таковыми оказываются преобразования Лоренца. Эйнштейн понял, что электромагнитное поле столь тесно связано с пространством и временем, что его свойства инвариантности суть не что иное, как свойства инвариантности пространства и времени.
2. Постулат постоянства скорости света. Во всех инерциальных системах отсчета скорость света c в вакууме одна и та же и равна (с хорошей
точностью) 3 · 1010 см/сек. Более точное значение: c = 2. 99792 · 1010 см/сек.
Этот постулат кажется особенно поразительным, поскольку мы уж очень привыкли к галилееву правилу сложения скоростей. Его «экспериментальное обоснование» парадоксально и состоит, по Эйнштейну, в том, что никто не наблюдал стоячих электромагнитных волн. А если бы выполнялись обычные правила Галилея, то, как кажется, электромагнитные волны в надлежащей движущейся системе координат остановились бы.
Сейчас уже почти забыт замечательный популяризатор науки, особенно астрономии, Камилл Фламмарион. Возможно, он вообще был первым популяризатором, автором–изобретателем жанра. Иногда он немного отклонялся от популяризации в сторону фантастики. В одной его книге космический путешественник летит в космическом корабле со скоростью, большей скорости света и наблюдает события на Земле в обратном порядке. Убитый Цезарь поднимается, Брут и Кассий разбегаются от него, прячут ножи, и т. д. Скоро мы увидим, что движение со сверхсветовой скоростью невозможно. Интересно заметить, что и другое экспериментальное обоснование специальной теории относительности столь же парадоксально и состоит в том, что попытки обнаружить так называемый эфирный ветер, «обдувающий» Землю, привели к отрицательному результату. Эфир — гипотетическая среда, заполняющая все пространство, колебания которой и представляют собой электромагнитные волны. Примечательно, что целью Майкельсона, который в течение десятилетий проводил все более точные эксперименты, было как раз обнаружение эфира. Эксперименты, однако, привели к выводу, что эфир не существует. Казалось бы, логика развития науки такова, что, основываясь на результатах опытов Майкельсона (а также Майкельсона-Морли и ряда других, аналогичных), Эйнштейн и вывел свой постулат. Нередко так логично и излагают эту историю в книгах. Однако сам Эйнштейн утверждал, что до публикации его знаменитой статьи он ничего не слышал об опытах Майкельсона. Мне лично кажется, что соображение об отсутствии стоячих электромагнитных волн — посильнее любых конкретных экспериментальных результатов. Поражает также положенное в основу работы Эйнштейна убеждение физика, что электромагнитное поле столь интимно связано с пространством и временем, что его свойства, собственно говоря, и есть свойства пространства и времени.
Возвращаясь от общей философии к делу, посмотрим, какие следствия вытекают из 2-го постулата. Представим себе, что зафиксирована некоторая инерциальная система отсчета (декартова система координат x 1 , x 2 , x 3 и время t ). Замечу, что возможность пользоваться единой для всего пространства декартовой системой координат характерна (постулируется) для специальной теории относительности . В общей теории относительности, называемой также теорией гравитации , приходится рассматривать неевклидово пространство, обладающее кривизной.
Теперь введем подвижную систему координат![]() и соответствующее ей время t
0
. Предположим, что в начальный момент времени t
= 0 обе системы координат совпадают. Будем предполагать, что "штрихованная" система координат движется с постоянной скоростью v
в направлении оси x
3
. (Поостережемся, однако, использовать формулу
и соответствующее ей время t
0
. Предположим, что в начальный момент времени t
= 0 обе системы координат совпадают. Будем предполагать, что "штрихованная" система координат движется с постоянной скоростью v
в направлении оси x
3
. (Поостережемся, однако, использовать формулу![]() — в теории относительности она неверна!).
— в теории относительности она неверна!).
Теперь представим себе, что в начальный момент времени t = 0 (при этом и t 0 = 0) в общем начале координат двух систем вспыхнула лампочка, возник источник электромагнитной волны. В исходной системе координат её фронт (множество точек, до которых в момент времени t дошла волна) задаётся уравнением
![]() .
(19.1)
.
(19.1)
Это сфера радиуса ct , где c — скорость света.
Но в подвижной системе координат уравнение этой поверхности, согласно двум постулатам, можно записать в аналогичной форме
![]() .
(19.2)
.
(19.2)
Замечу, что с точки зрения подвижной системы координат свет достигает границы сферы (19.1) неодновременно. Изменяется наш взгляд на природу времени. События, которые происходят одновременно в некоторой системе отсчета оказываются не одновременными в другой, движущейся относительно первой системе отсчета. одновременность событий относительна.
Эйнштейн предположил, что между старыми и новыми координатами имеется линейная зависимость (это можно доказать при помощи теоремы Мазура-Улама, см. Приложение 2). После линейной замены квадратичная форма (19.2) перейдет в квадратичную форму от x 1 , x 2 , x 3 , t . Чтобы при этом сфера (19.2) перешла в сферу (19.1), необходимо и достаточно выполнение соотношения
![]() .
(19.3)
.
(19.3)
Фронт волны есть физическая реальность, а системы координат мы вводим сами. В (19.3) κ = κ(v
) может зависеть лишь от v
. Но "неподвижная" система координат x
1
, x
2
, x
3
двигается относительно подвижной системы координат![]() со скоростью −v
, поэтому должно выполняться также
со скоростью −v
, поэтому должно выполняться также
равенство
![]() .
(19.4)
.
(19.4)
Сравнение этих двух равенств дает соотношение
κ(v )κ(−v ) = 1. (19.5)
В специальной теории относительности сохраняются постулаты об однородности и изотропности пространства. Изотропность, независимость свойств пространства от направления движения, влечет равенство κ(v ) = κ(−v ). Тогда из (19.5) следует, что κ2 (v ) = 1. Отсюда κ(v ) = ±1. Знак минус следует отбросить, потому что при v = 0 мы должны, очевидно, иметь κ(0) = 1. Если еще предположить, что κ(v ) непрерывно зависит от v (физики обычно считают ниже своего достоинства упоминать о таких математических «мелочах» — до тех пор, пока не произойдут большие неприятности из-за разрывов), получается, что κ(v ) = 1 для всех v . Выходит, что координаты и время в двух рассматриваемых системах отсчета должны быть связаны соотношением
![]() .
(19.6)
.
(19.6)
Связь между координатами и временем в двух системах отсчета разыскиваем теперь в виде x 01 = x 1 x 02 = x 2
x 03 = α x 3 + β t (19.7) t 0 = γx 3 + δt.
Константы α, β, γ, δ (зависящие от v ) находятся из условия (19.6). Искомое преобразование представляет собой известное преобразование Лоренца :
![]() (19.8)
(19.8)
,
где ε = v/c . К этим же формулам можно придти, разыскивая преобразования, относительно которых инвариантно волновое уравнение. Когда скорость движения v мала по отношению к скорости света, то есть в пределе ε → 0, преобразования Лоренца переходят в преобразования Галилея
![]() (19.9)
(19.9)
Как видим, с математической точки зрения вывод соотношений (19.8) весьма прост. Однако физические выводы поразительны. Оказывается, время не абсолютно, в чем был уверен Ньютон, а зависит от движения выбранной системы отсчета.
Раньше мы уже установили, что замена преобразований Галилея на преобразования Лоренца приводит к изменению закона сложения скоростей. Например, рассмотрим еще одну систему координат, которая движется также в направлении оси x 3 с постоянной скоростью u по отношению к подвижной системе координат. Тогда её скорость w по отношению к неподвижной системе координат оказывается равной не v + u (как получилось бы согласно преобразованиям Галилея), а определяется равенством
![]() .
(19.10)
.
(19.10)
Сокращение длин и отрезков времени. Еще до развития теории относительности Х. Лоренц и Дж. Фицджеральд для объяснения результатов некоторых экспериментов ввели предположение о сокращении длины тел в направлении их движения. Сначала казалось, что эффект Лоренца– Фицджеральда является динамическим , и сокращение длин происходит под действием некоторых неизвестных нам сил, скажем, сопротивления эфира движению тел. Возникала несколько смутная аналогия с движением тел в воздухе или воде. Быть может, главное достижение А. Эйнштейна (так считают многие физики) состоит в том, что он понял кинематический характер всех основных релятивистских эффектов — просто (просто!) так устроены пространство и время.
Теперь посмотрим, как непринужденно теория относительности объясняет эффект Лоренца–Фицджеральда, а заодно предсказывает еще более поразительный эффект сокращения отрезков времени. Ход времени зависит от движения тел! Время течет по-разному в движущемся поступательно с постоянной скоростью корабле и на «неподвижном» берегу. Это нелегко было усвоить современникам.
![]() Итак, представим себе, что в фиксированной («неподвижной») системе координат имеется стержень, длины `
, расположенный вдоль оси x
3
между r r r PP
Итак, представим себе, что в фиксированной («неподвижной») системе координат имеется стержень, длины `
, расположенный вдоль оси x
3
между r r r PP
z 1 z 2 z 3
Рис. 11
точками z 1 и z 2 , так что z 2 − z 1 = ` . Если теперь измерить длину этого стержня в подвижной (штрихованной) системе координат в момент t 0 , то получим
![]() ,
,
![]() .
(19.11)
.
(19.11)
Обозначим через![]() длину стержня в подвижной системе координат. Вычитая формулы (19.11) одну из другой, придем к равенству
длину стержня в подвижной системе координат. Вычитая формулы (19.11) одну из другой, придем к равенству
![]() .
(19.12)
.
(19.12)
Получается, что длина `
в неподвижной системе координат больше, чем длина стержня в движущейся системе. Аналогично воспользуемся связью между моментами времени![]() . Имеем
. Имеем
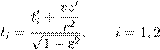 .
(19.13)
.
(19.13)
Далее получаем соотношения между отрезком времени t
2
− t
1
и соответствующим отрезком времени![]() в движущейся системе координат
в движущейся системе координат
![]() .
(19.14)
.
(19.14)
Эта простая формула влечет следствия, которые с большим трудом укладываются в сознание. Вы, наверное, слышали о так называемом парадоксе близнецов.
Представим себе, что один из двух близнецов садится в космический корабль и путешествует на нем со скоростью, достаточно близкой к скорости света. Потом он возвращается на Землю. Формула (19.14) говорит, что на Земле, к моменту его возвращения, прошло времени в ![]() больше, чем то время
больше, чем то время![]() , которое близнец-путешественник провел в своем космическом корабле. Таким образом, если ε достаточно близко к 1, то есть v
близко к c
, на Земле могло пройти сколь угодно большое время. Писателифантасты не раз эксплуатировали эту идею.
, которое близнец-путешественник провел в своем космическом корабле. Таким образом, если ε достаточно близко к 1, то есть v
близко к c
, на Земле могло пройти сколь угодно большое время. Писателифантасты не раз эксплуатировали эту идею.
Высказывались и различные возражения против парадокса близнецов. Главное из них состоит в том, что космический корабль, чтобы набрать скорость v , должен двигаться ускоренно, а специальная теория относительности не может описать, что происходит в движущейся ускоренно системе. Ответ другой спорящей стороны состоит в том, что корабль может набрать скорость с очень малым ускорением, а затем находиться в свободном полете со скоростью v значительно более долгое время. Разумеется, и тормозить при посадке на Землю он должен с малым ускорением. Тогда условия будут близки к тем, которые хорошо описываются теорией относительности. Другое возражение основывается на том, что при разгоне тела до скорости, близкой к скорости света, нужно затратить невообразимо огромную энергию. Ну, это уж не кажется таким принципиальным. Кстати, движение в ускоренных системах координат прекрасно описывается общей теорией относительности, и парадокс близнецов при этом сохраняется. Так что дело лишь за экспериментальной проверкой на людях. На элементарных частицах «парадокс» полностью подтвержден.
Механика теории относительности. Я уже говорил раньше, что Эйнштейн развил кинематику теории относительности, обнаружив при этом новые удивительные свойства пространства и времени. Но он пошел и дальше, создав релятивистскую динамику . Ее специфика связана с относительностью времени, отсутствием абсолютного ньютоновского времени, зависимостью времени от движения системы отсчета, естественно связанной с движущимся телом или материальной частицей.
Нетрудно убедиться, что в теории относительности инвариантна следующая величина
(¯x 1 − x 1 )2 + (¯x 2 − x 2 )2 + (¯x 3 − x 3 )2 − c 2 (t ¯− t )2 , (19.15)
которой присвоено несколько странное название «интервал». Здесь (x 1 ,x 2 ,x 3 ,t ), (¯x 1 ,x ¯2 ,x ¯3 ,t ¯) — две точки в одной и той же системе отсчета. Каждая такая точка четырехмерного пространства называется (может, чересчур пышно) событием . Разумеется, инвариантность в теории относительности, или релятивистская инвариантность , означает инвариантность относительно преобразования Лоренца. Лишь величины, не зависящие от нашего субъективного выбора системы отсчета, могут иметь физический смысл.
В случае, когда все приращения в (19.15) бесконечно малы, это выражение принимает вид
![]() .
(19.16)
.
(19.16)
Оказывается естественным ввести собственное время τ движущейся по произвольному закону xj = xj (t ) точки, полагая
![]() .
(19.17)
.
(19.17)
Отсюда для определения функции τ = τ(t ) получаем дифференциальное уравнение
![]() .
(19.18)
.
(19.18)
![]() Здесь ε = v/c
, причем скорость
Здесь ε = v/c
, причем скорость![]() определяется по заданному закону движения точки. Добавив начальное условие τ(0) = 0, мы определим собственное время частицы однозначно.
определяется по заданному закону движения точки. Добавив начальное условие τ(0) = 0, мы определим собственное время частицы однозначно.
Георг Минковский существенно упростил теорию, заметив, что после введения комплексной (чисто мнимой) переменной x 4 = ict , интервал (19.15) преобразуется к сумме квадратов. После этого становится ясно, что преобразование Лоренца получается попросту из преобразования вращения четырехмерного пространства переменных x 1 , x 2 , x 3 , x 4 . При этом, проводя многие аналитические выкладки, можно надолго забыть, что переменная x 4 играет особую роль (алгебра — сильная наука!), и вспомнить об этом лишь тогда, когда нужно осмыслить окончательный ответ. Такое четырехмерное пространство, с выделенной особо переменной x 4 , носит название четырехмерный мир Минковского . (К слову сказать, когда идут дискуссии о том, является ли наше пространство трехмерным или четырехмерным, а может, имеет большую размерность, то речь идет именно о пространстве. Существование еще одной переменной t подразумевается. В современной квантовой теории поля рассматриваются и варианты очень больших размерностей: быть может, наше пространство 9-мерно или даже 20-мерно. Главным аппаратом в этой науке служит теория групп Ли.)
В механике (точнее, в динамике) теории относительности, как и в классической механике, работает принцип Гамильтона. Изменение, однако, состоит в том, что вместо абсолютного времени, которого не существует, нужно использовать собственное время движущейся материальной частицы. Я ограничусь здесь случаем материальной частицы. Случай твердого тела вызвал известные трудности в связи с невозможностью передачи «сигнала» с произвольно большой скоростью. Ведь твердое тело целиком и мгновенно реагирует на движение любой его части. Трудности здесь разрешил
П. Эренфест. Впрочем, Ландау считал, что твердые тела просто невозможны в теории относительности.
В четырехмерном пространстве Минковского определяется релятивистский лагранжиан L = L (x,u, τ), где x = (x 1 ,x 2 ,x 3 ,x 4 ), u = (u 1 ,u 2 ,u 3 ,u 4 ), τ — собственное время движения частицы, а величины uj (j = 1,..., 4) суть компоненты релятивистской 4-скорости, определяемой дифференцированием по τ (а не по t ):
![]() .
(19.19)
.
(19.19)
Здесь t — время в некоторой фиксированной системе отсчета, которую мы можем считать неподвижной. Четвертая координата — особая:
![]() .
(19.20)
.
(19.20)
Целесообразно ввести еще компоненты скорости ![]() в неподвижной системе координат.
в неподвижной системе координат.
Далее, для любых двух моментов τ1 и τ2 (пусть τ1 < τ2 ) собственного времени τ мы определяем релятивистское (инвариантное относительно преобразования Лоренца) действие
![]() .
(19.21)
.
(19.21)
| Теперь постулируется вариационный принцип Гамильтона |
|
| δI = 0. |
(19.22) |
По-прежнему предполагается, что деформации не меняют начального и конечного положений частицы. Замечу, что вариационный принцип (19.22) имеет двойственную природу — он похож и на классический принцип Гамильтона, и на принцип Мопертюи–Якоби, описывающий движение на изоэнергетических поверхностях.
Чтобы найти лагранжиан свободной материальной частицы, можно действовать по аналогии с классической механикой. Пространство по-прежнему предполагается изотропным и однородным, но вместо принципа относительности Галилея, принимается принцип относительности Эйнштейна — инвариантность относительно преобразований Лоренца. Если воспользоваться представлением Минковского для четырехмерного пространства– времени, то нетрудно прийти к лагранжиану
![]() .
(19.23)
.
(19.23)
Сравните это выражение с классическим:
![]() .
(19.24)
.
(19.24)
Величина m 0 в (19.23) называется массой покоя частицы. Дальше мы увидим, что в отличие от классической механики, масса частицы зависит от её скорости (!).
Зная лагранжиан (19.23), мы можем определить релятивистские импульсы :
![]() .
(19.25)
.
(19.25)
Уравнения движения, вытекающие из вариационного принципа (19.22), имеют вид
![]() .
(19.26)
.
(19.26)
Для свободной материальной частицы (лагранжиан (19.23)) эти уравнения принимают вид
![]() .
(19.27)
.
(19.27)
Когда на частицу действуют внешние силы с компонентами Kj , в уравнениях появляется правая часть
![]() .
(19.28)
.
(19.28)
Величины Kj суть компоненты вектора, называемого силой Минковского.
Если перейти в уравнениях (19.27) и (19.28) к дифференцированию по t , получим
![]() .
(19.29)
.
(19.29)
Мы использовали формулы (19.19), (19.20) и тот факт, что![]() .
.
Если теперь ввести обозначение
![]() ,
(19.30)
,
(19.30)
то можно увидеть, что релятивистское уравнение движения (19.29) есть попросту уравнение движения частицы с переменной массой m :
![]() .
(19.31)
.
(19.31)
Итак, выяснилось, что масса — понятие относительное, она зависит от скорости движения. При этом масса m движущейся частицы всегда больше массы покоя m 0 .
В развитии физики играет существенную роль принципсоответствия . Мы уверены, что классическая механика, подтвержденная невообразимо огромным экспериментальным материалом, не будет опровергнута никакими новыми открытиями — в своей области применимости . Всякая новая теория должна содержать новый параметр, в теории относительности это — скорость света c или ε = v/c , такой, что в пределе, в данном случае при c = ∞ или ε = 0, новая механика переходит в классическую. То же самое относится и к другим обобщениям фундаментальных теорий классической физики, и в первую очередь, к квантовой механике. Конечно, принцип соответствия работает и при дальнейших обобщениях новых физических теорий.
Итак, мы ожидаем, что при ε → 0 релятивистские уравнения движения должны переходить в классические. Подсчитаем лагранжиан (19.23). Имеем
![]() .
(19.32)
.
(19.32)
Теперь перепишем выражение для релятивистского действия (19.21) в случае лагранжиана (19.23), переходя к интегрированию по времени t . Имеем
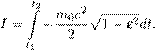 (19.33)
(19.33)
При малых ε подынтегральное выражение в (19.33) можно представить в виде
![]()
Итак, в классическом пределе, при ε → 0 лагранжиан в (19.33) принимает вид
![]() .
(19.35)
.
(19.35)
Постоянный множитель ![]() , конечно, несущественен. Дополнительное слагаемое −m
0
c
2
заставляет нас насторожиться. Если представить себе, что лагранжиан есть разность между кинетической и потенциальной энергиями, то выходит, что появилась дополнительная потенциальная энергия
, конечно, несущественен. Дополнительное слагаемое −m
0
c
2
заставляет нас насторожиться. Если представить себе, что лагранжиан есть разность между кинетической и потенциальной энергиями, то выходит, что появилась дополнительная потенциальная энергия
E = m 0 c 2 , (19.36)
которой обладает неподвижная материальная частица. Пока что трудно утверждать, что эта формула имеет серьезный физический смысл, потому что постоянный лагранжиан тривиален. Такое слагаемое в (19.35) можно просто отбросить, это не повлияет на уравнение движения. Итак, мы установили, что при ε → 0 релятивистские уравнения движения частицы переходят в классические.
Энергия в теории относительности. Мы будем пользоваться общим определением энергии в механике Гамильтона-Лагранжа:
E = vLv − L. (19.37)
Подправим выражение (19.33), внося в него такой постоянный множитель, чтобы в пределе ε → 0 получались в точности классическое действие и классический лагранжиан. Согласно (19.35), для этого нужно умножить (19.33) на 2. В результате получаем релятивистское действие в виде
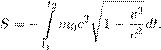 (19.38)
(19.38)
Лагранжиан дается формулой
![]() .
(19.39)
.
(19.39)
Теперь вычислим энергию E . Из (19.39) имеем
![]() .
(19.40)
.
(19.40)
По формуле (19.37) получаем
![]() .
(19.41)
.
(19.41)
Вот теперь нет сомнений, что при v = 0 частица действительно обладает энергией покоя , определяемой по формуле (19.36). Вообще, формула (19.41) описывает глубокую связь между массой и энергией и, в некотором смысле, их эквивалентность. Множитель c 2 выглядит как коэффициент перехода от одних единиц измерения к другим, вроде механического эквивалента теплоты. При желании энергию можно было бы измерять в граммах или других единицах массы.
Когда элементарные частицы — протоны, нейтроны и электроны — объединяются в один атом, масса атома оказывается меньше суммарной массы этих частиц. Теряется свойство аддитивности массы. Причина состоит в том, что при таком соединении испускается свет, электромагнитная волна. Частицы света имеют нулевую массу покоя (для них m 0 = 0). Двигаются они, понятно, со скоростью c . Если при этом излучается энергия ∆E , то возникает дефект массы
![]() .
(19.42)
.
(19.42)
Так теория относительности непринужденно объяснила, почему атомные массы (чаще говорят о весах) элементов меньше, чем суммарные массы составляющих атомы частиц.
20. Каноническая гамильтонова форма уравнений механики
При определенных условиях общего положения (невырожденности системы) уравнения Лагранжа могут быть приведены к канонической форме
Гамильтона. В случае n степеней свободы уравнения Лагранжа представляют собой систему n уравнений второго порядка, а соответствующая гамильтонова система содержит 2n уравнений первого порядка. Канонические (ныне чаще называемые гамильтоновыми ) уравнения не только отличаются особым изяществом, но обладают рядом специфических алгебраических и геометрических свойств, делающих их наиболее удобным инструментом исследования в механике и ее приложениях. В дальнейшем я продемонстрирую применение гамильтоновых уравнений в статистической механике .
ПреобразованиеЛежандра. Рассмотрим функцию двух скалярных переменных f (x,y ). Ее дифференциал запишем в виде
![]() .
(20.1)
.
(20.1)
Замечая, что udx = d (ux ) − xdu , можно переписать равенство (20.1) в виде
d (xu − f ) = xdu − vdy. (20.2)
Теперь сделаем одновременную замену функции и ее аргументов, полагая
g (u,y ) = xu − f. (20.3)
Здесь, вместо x , y , введены аргументы u и y .
Это и есть преобразование Лежандра по переменной x . Заметим, что такое преобразование можно провести не всегда, а лишь в том случае, когда замена переменных (x,y ) → (u (x,y ),y ) взаимно однозначна в области определения функции f . Для того, чтобы эта взаимная однозначность имела место, хотя бы локально, достаточно (согласно теореме о неявной функции), чтобы был отличен от нуля якобиан:
![]() .
(20.4)
.
(20.4)
Гамильтоновы уравнения. Канонические уравнения Гамильтона получаются из уравнений Лагранжа второго рода посредством преобразования Лежандра по всем обобщенным скоростям q ˙i . Можно применить формулу (20.3), но, как и во многих других случаях, целесообразно воспользоваться лишь идеей, а выкладки провести непосредственно.
Запишем дифференциал функции Лагранжа L (q,q,t ˙ ) при фиксированном t в виде
![]() .
(20.5)
.
(20.5)
Введем обозначения
![]() (20.6)
(20.6)
и назовем p вектором импульса , pi — его i -ая компонента; i = 1,...,n , если n — число степеней свободы.
Далее используем равенства
![]() .
(20.7)
.
(20.7)
| В компактной форме они записываются как |
|
| Lq ˙ · dq ˙ = d (p · q ˙) − q ˙ · dp. Введем функцию Гамильтона H = H (p,q,t ), полагая |
(20.8) |
| H = p · q ˙ − L = pi q ˙i − L. |
(20.9) |
Теперь, подставляя выражение (20.8) в (20.5), приходим к формуле
dH = q ˙ · dp − Lq · dq. (20.10)
Отсюда следуют равенства
Hp = q, ˙ Hq = −Lq . (20.11)
До этого момента мы не вспоминали об уравнении Лагранжа
![]() ,
(20.12)
,
(20.12)
которое теперь запишем в виде p ˙ = Lq .
В результате из соотношений (20.11) и (20.12) выводим канонические уравнения Гамильтона
p ˙ = −Hq , q ˙ = Hp , (20.13)
или, в координатах,
![]() ,
,
![]() (20.14)
(20.14)
Гамильтониан H = H (p,q,t ), как видно из его определения (20.9), есть не что иное как полная механическая энергия системы, выраженная через координаты и импульсы . В случае, когда он не зависит от времени, выполняется закон сохранения энергии: H (p,q ) есть интеграл гамильтоновой системы (20.14) (проверьте!).
Подчеркну, что преобразование Лежандра, которое привело нас к гамильтоновым уравнениям (20.14), применимо не всегда. Может оказаться, что в фазовом пространстве имеются поверхности, линии или отдельные точки, в которых отсутствует взаимно однозначная связь между обобщенными скоростями q ˙i и импульсами pj . Это происходит, когда нарушаются условия теоремы о неявной функции для уравнения p = Lq ˙ (q,q ˙):
![]() .
(20.15)
.
(20.15)
Гамильтонова система (20.14) допускает красивую и полезную трактовку как одно векторное уравнение в R2n
. Определим вектор x
∈
R2n
, полагая x
= (q,p
) = (q
1
,...,qn
,p
1
,...,pn
). Вместо H
(p,q
) будем теперь писать H
= H
(x
). Тогда grad H
можно записать в виде grad![]()
Введем оператор J : R2n → R2n , задав его операторной матрицей
![]() ,
(20.17)
,
(20.17)
где In : Rn → Rn — тождественный оператор в Rn . Заметим, что J 2 = −I 2n (I 2n — тождественный оператор в R2n ). Система (20.14) записывается теперь в виде
x ˙ = J grad H (x ). (20.18)
Гамильтонова форма уравнения второго закона Ньютона. Обобщенное уравнение второго закона Ньютона определяется лагранжианом
![]() ,
(20.19)
,
(20.19)
где x — точка евклидова пространства H. В случае конечномерного евклидового пространства H, dimH = n , его можно отождествить с Rn . Замечу, однако, что развиваемый формализм не зависит от размерности и применим, например, к волновому уравнению. Иное дело, что в случае бесконечномерного гильбертова пространства H нужны, конечно, дополнительные обоснования производимых нами операций. Аналогично (20.7) вводим импульс p , полагая
p = Lx ˙ = Mx ˙ . (20.20)
Гамильтониан, соответствующий лагранжиану (20.19), получаем с использованием формулы (20.9), выражая скорость через импульс посредством равенства x ˙ = M −1 p . Он имеет вид
![]()
Соответственно, гамильтонова форма обобщенного уравнения второго закона Ньютона имеет вид
| p ˙ = −grad V (x ), x ˙ = M −1 p. Мы воспользовались здесь простой общей формулой |
(20.22) |
grad ![]() (20.23)
(20.23)
справедливой для любого линейного самосопряженного
оператора A
(для произвольного линейного оператора справа следует написать ![]()
Хотя здесь нет места для строгого изложения, не могу удержаться от того, чтобы не привести следующий пример из математической физики. Волновое уравнение. Рассмотрим волновое уравнение в области D ⊂
Rn
ρ(x )utt = c 2 ∆u (20.24)
с краевым условием
![]() .
(20.25)
.
(20.25)
Здесь ρ(x ) — непрерывная неотрицательная функция, удовлетворяющая условию ρ(x ) ≥ ρ0 > 0, c > 0 — положительная константа, как и ρ0 . Мы уже видели, см. формулы (5.20) – (5.27), что это уравнение допускает интеграл энергии. Кинетическая энергия T и потенциальная энергия V задаются формулами
![]() (20.26)
(20.26)
(20.27)
Вы помните, что градиент функционала V , заданного на гильбертовом пространстве H , в точке u ∈ H определяется равенством
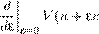 ) = (grad V
(u
),v
),
(20.28)
) = (grad V
(u
),v
),
(20.28)
которое должно выполняться для любого v ∈ H . Левая часть этого равенства есть дифференциал Гато в точке u , и предполагается, что он является также и дифференциалом Фреше.
В нашем случае H = L
2
(D), и grad V
(u
) определен не для всех u
, а лишь для достаточно гладких функций, скажем, для u
∈ C
2
(D) (а более того, для![]() ). Для такой функции u
имеем
). Для такой функции u
имеем
![]()
В промежуточном равенстве использована C
1
-гладкость функции v
, но последнее равенство имеет смысл уже для любой функции![]() . Его можно обосновать непосредственно, приближая
. Его можно обосновать непосредственно, приближая![]() гладкими функциями. Таким образом, для достаточно гладких функций u
получаем
гладкими функциями. Таким образом, для достаточно гладких функций u
получаем
grad ![]() (20.30)
(20.30)
Подчеркну, что градиент в (20.30) берется в пространстве H = L 2 (D ). Вы, конечно, помните, что градиент зависит от выбора скалярного произведения.
Поскольку рассматриваемая система натуральна, так что L = T − V , имеем
![]()
Lu = −grad V = c 2 ∆u
Таким образом, гамильтонова форма волнового уравнения имеет вид
![]() (20.31)
(20.31)
(20.32)
Вырожденныелагранжианы. Для вырожденных лагранжианов — линейных по скорости и имеющих вид L (q,q ˙) = A (q,t )q ˙ + B (q,t ), см. (10.23), очевидно, Lq ˙q ˙ = 0 тождественно. Поэтому преобразование Лежандра неприменимо ни в какой точке. В этом случае гамильтониан H не зависит от q ˙ и даже тождественно равен нулю при B ≡ 0. Действительно, согласно общему определению, p = Lq ˙ = A (q,t ), и
H = p · q ˙ − L = A (q,t ) · q ˙ − A (q,t ) · q ˙ − B (q,t ) = −B (q,t ). (20.33)
Действуя формально, мы можем написать соответствующие гамильтоновы уравнения в виде p ˙ = Bq , q ˙ = 0. Однако эти уравнения не имеют никакого отношения к исходной системе уравнений Лагранжа (объясните, почему?). Это лишний раз напоминает нам о необходимости контролировать законность проводимых формальных выкладок.
Интересно заметить, что в математической физике встречаются такие системы, которые имеют гамильтонову форму по своей исходной постановке. Замечательный пример тому — уравнения Кирхгофа , описывающие динамику системы вихревых нитей (или точечных вихрей на плоскости, либо на иной поверхности) в жидкости. По всей видимости, их нельзя получить ни из каких лагранжевых уравнений. Эта система последние десятилетия вызывает повышенный интерес исследователей и как своеобразный пример, на котором испытываются и развиваются новые методы качественной теории дифференциальных уравнений, и как подходящая модель для описания вихрей в атмосфере, а также электронных колонн при электрическом газовом разряде. О системе уравнений Кирхгофа можно прочитать практически в любом учебнике по гидродинамике. С новейшим развитием теории можно познакомиться по книге [45].
Интересный вопрос о возможности построения системы уравнений Лагранжа, которой бы отвечала заданная гамильтонова система, по-моему, совсем не разобран. Дело сводится к решению нелинейного дифференциального уравнения в частных производных первого порядка, которое получает-
∂L
ся подстановкой выражения импульса p
= ![]() через обобщенные коорди-
через обобщенные коорди-
∂q ˙
наты q и обобщенные скорости q ˙ в равенство (20.9), выражающее гамильтониан через лагранжиан. Это дифференциальное уравнение относительно неизвестной функции L = L (q,q,t ˙ ) записывается в виде
![]() (20.34)
(20.34)
Далеко не всегда у него есть решение, определенное на всем расширенном фазовом пространстве переменных (q,q,t ˙ ). Подобные результаты можно получить, лишь налагая на гамильтониан специальные ограничения. Вместе с тем, механика не содержит никаких ограничений такого рода. Выходит, что нужно искать дополнительные свойства гамильтонианов, которые вытекают из законов термодинамики.
Замечу, что подобные проблемы постоянно возникают в механике и в математической физике. И уравнения механики, и уравнение диффузии, и волновые уравнения зачастую содержат функции от переменных состояния и параметры, которые предлагается определять из экспериментов. Любые знания об этих функциях, скажем, о зависимости коэффициента теплопроводности от температуры или о зависимости скорости распространения волны в данной среде от параметров ее состояния, могут существенно сократить необходимую экспериментальную работу. В идеале, дело должно сводиться к экспериментальному определению небольшого числа констант. Иногда к такому приятному результату нас приводят те или иные асимптотические методы.
Скобка Пуассона. Для любой гладкой функции F (p,q ), заданной на фазовом пространстве гамильтоновой системы (20.13), можно найти ее производную F ˙ (p,q ) в силу уравнения движения (20.13) в векторной форме
| F ˙ = F q H p − F p H q , или в координатах |
(20.35) |
![]() .
(20.36)
.
(20.36)
Правая часть этого уравнения называется скобкой Пуассона функций F и H и обозначается как {F,H }. Очевидно, функция F является интегралом гамильтоновой системы с гамильтонианом H в том и только в том случае, когда
{F,H } = 0. (20.37)
Оказывается полезным определить скобку Пуассона {F,G } для произвольных гладких функций F (p,q ) и G (p,q ), полагая
{F,G} = Fq Gp − Fp Gq . (20.38)
Введенная таким образом билинейная операция над функциями кососимметрична:
{F,G } = −{G,F }. (20.39)
Скобка Пуассона определяет своего рода умножение пары функций. Эта операция, согласно (20.39), кососимметрична и неассоциативна. Некоторой заменой ассоциативности служит тождество Якоби для тройки произвольных гладких функций f , g , h :
{f,{g,h}} + {g,{h,f}} + {h,{f,g}} = 0. (20.40)
Билинейная операция, обладающая свойствами (20.39) и (20.40) для произвольных пар и, соответственно, троек из некоторого линейного пространства, определяет важную алгебраическую структуру — алгебру Ли.
Тождество Якоби допускает красивую алгебраическую трактовку. Оператор A , действующий в алгебре Ли, называется дифференцированием этой алгебры, если для него справедливо равенство, которое можно назвать равенством Лейбница
A{g,h} = {Ag,h} + {g,Ah}. (20.41)
Каждый элемент f определяет линейный оператор Af по формуле
Af g = {f,g }. (20.42)
Тождество Якоби говорит, что оператор Af есть дифференцирование алгебры Ли . Действительно, учитывая кососимметричность скобки Пуассона, равенство (20.40) можно переписать в виде
{f,{g,h}} = {{f,g},h} + {g,{f,h}}, (20.43)
что совпадает с (20.41) при A = Af .
Как доказал Пуассон, если F и G — два интеграла гамильтоновой системы (20.13), их скобка Пуассона {F,G } также есть интеграл. Это означает, что множество всевозможных C ∞ -гладких интегралов гамильтонова уравнения образует алгебру Ли.
Результат Пуассона может вызвать неоправданный оптимизм по поводу проблемы интегрируемости уравнений Гамильтона. Может показаться, что последовательно вычисляя скобки Пуассона известных нам интегралов, можно найти достаточное их число для полного решения гамильтоновой системы. Увы, скобка двух интегралов может оказаться тривиальным интегралом (константой) или функцией от уже известных интегралов. Так оно обычно и получается. Например, знание интегралов энергии, импульса и момента импульса не позволяет найти новые интегралы гамильтоновой системы.
21 Силы трения. Диссипация энергии
Интересная и очень важная для механики, геометрии и вариационного исчисления теория канонических гамильтоновых систем рассмотрена во многих книгах, см. классическое изложение в [14, 46]. Современное изложение в рамках геометрии многообразий дано в книге В.И.Арнольда [3].
Упражнения
1. Докажите, что гамильтонову систему (20.14) можно записать в виде
p ˙i = {pi ,H }, q ˙i = {qi ,H },
или, вводя очевидные векторные обозначения,
p ˙ = {p,H }, q ˙ = {q,H }.
2. Докажите, что если бы скобка Пуассона обладала свойством ассоциативности, то отсюда следовало бы тождество Якоби.
3. Докажите (а если не получится, найдите доказательство в рекомендованных книгах [14, 46, 3]) тождество Якоби (20.40).
4. Из тождества Якоби (20.40) выведите утверждение Пуассона: вместес двумя интегралами F и G , также их скобка Пуассона {F,G } есть интеграл.
5. Докажите, что для любых трех гладких функций F , G , K от p и p в случае, когда K обращается в ноль вне некоторого шара, справедливо равенство
Z Z
{G,F }K dpdq = F {K,G }dpdq.
R2n R2n
Отсюда следует, что в случае недифференцируемой функции F скобке Пуассона {F,G } можно придать смысл обобщенной функции — распределения.
6. Докажите, что преобразование Лежандра переводит выпуклые функции в выпуклые. Более того, справедливо равенство guu (u,y ) = fxx (x,y ) в обозначениях (20.2), (20.3).
7. Запишите интегралы импульса и момента импульса для гамильтоновой формы второго закона Ньютона (20.22) в условиях, когда все они существуют. Найдите их скобки Пуассона. Докажите, что эти 6 интегралов порождают алгебру Ли, так что новых интегралов этим способом получить не удается.
21. Силы трения. Диссипация энергии
В природе все реальные механические системы находятся под действием тех или иных сил трения. Брошенный на Земле камень не сохраняет постоянную поступательную скорость движения, как то предписывается законом Галилея (он же — первый закон Ньютона), а довольно скоро останавливается из-за сопротивления воздуха и сухого трения о поверхность, когда он катится по земле. Силы трения — немеханического происхождения. Поэтому, как правило, в курсах механики, написанных физиками (Ландау и Лифшиц, Голдстейн, Синг), силы трения не рассматриваются. Вместе с тем, механики, рассчитывающие на инженерные приложения своей науки, уделяют значительное внимание силам трения (Лойцянский и Лурье, Аппель, Леви – Чивита и др.). Пожалуй, наиболее полное представление о большой сложности законов трения и о современном состоянии их изучения можно получить по книге И.И. Воровича [8]. Вообще, надо признать, что силы трения, возникающие из-за взаимодействия системы с окружающей средой, пожалуй, наиболее сложные из известных нам сил природы.
Простейшее, и не вполне точное, определение сил трения состоит в том, что они ведут к уменьшению, к рассеянию энергии . Часто употребляемый синоним слова рассеяние — диссипация . Неточность этого определения связана с тем обстоятельством, что зачастую силы трения имеют двойственную природу и могут иногда приводить и к увеличению энергии. Вообще, силы трения очень разнообразны, и трудно, если не сказать невозможно, сформулировать единообразно общие законы трения. Здесь мы рассмотрим лишь простейшие виды трения.
Само понятие о диссипации энергии возникает, когда рассматриваются незамкнутые системы и не все виды энергии принимаются во внимание. Скажем, диссипация механической энергии означает, что часть энергии превращается в другие виды, обычно — в тепловую энергию.
Начнем с обобщенного уравнения второго закона Ньютона в евклидовом пространстве H :
Mx ¨ = −grad V (x ). (21.1)
Как мы знаем, для этого уравнения справедлив закон сохранения механической энергии: полная механическая энергия
![]() (21.2)
(21.2)
является интегралом уравнения (21.1). Когда система двигается во внешней среде, действует дополнительная сила, возникающая из-за взаимодействия со средой (сила сопротивления внешней среды), которая в обычных условиях (скажем, в спокойной и безветренной атмосфере) приводит к затуханию движения. Когда тело находится в покое, сила сопротивления равна нулю. Если допустить, что она гладко зависит от скорости x ˙, то можно утверждать, что хорошим приближением при малых скоростях будет закон трения
F = −B (x )x, ˙ (21.3)
где B (x ) для каждого x ∈ H есть линейный оператор. Тогда уравнение (21.1) придется заменить уравнением
Mx ¨ = −grad V (x ) − B (x )x. ˙ (21.4)
Вычисляя производную по времени от энергии E , получаем уравнение изменения энергии :
![]() .
(21.5)
.
(21.5)
Поскольку согласно определению, действие силы трения приводит к уменьшению энергии, нужно считать, что B (x ) для каждого x является положительно определенным, или хотя бы положительным оператором, так что для любого ξ ∈ H и любого x выполняется неравенство
(B (x )ξ, ξ) ≥ 0. (21.6)
Если это неравенство может превратиться в равенство лишь для ξ = 0, так что оператор B (x ) является строго положительным , то говорят, что сила трения −B (x )x ˙ обладает свойством полной диссипации . В этом случае, согласно уравнению (21.5), энергия E уменьшается, диссипирует при любых движениях. Замечу, что в конечномерном случае из строгой положительности следует положительная определенность оператора, в бесконечномерных задачах это уже не так.
Естественно ввести диссипативную функцию Рэлея W , полагая
![]() .
(21.7)
.
(21.7)
Тогда сила трения F = −B (x )x ˙ выражается в виде
F = −grad x ˙ W. (21.8)
Силу трения, определяемую диссипативной функцией, называют рэлеевской . Чаще всего встречается рэлеевская сила трения F = −Bx ˙ с оператором B , не зависящим от x .
В определении Рэлея весьма существенно требование симметричности оператора B . Именно это свойство однозначно определяет оператор B при заданной диссипативной функции W , которая является квадратичной формой от x ˙. Произвольный линейный оператор A : H → H можно представить в виде суммы
A = Ar + Ac , (21.9)
где Ar — симметричный оператор, а Ac — кососимметричный. Они выражаются формулами
![]() .
(21.10)
.
(21.10)
Ясно, что кососимметрическое слагаемое не дает вклада в квадратичную форму (A ξ, ξ), поскольку (Ac ξ, ξ) = 0 для всех ξ ∈ H . Силы вида Ac x ˙ тоже, конечно, встречаются в механике, но имеют совсем иную физическую природу: это гироскопическиесилы . Такая сила не совершает работы при реальных движениях, не вносит вклада в уравнение изменения энергии (21.5). Рэлей, вводя требование симметричности для оператора B , со вкусом разделил эти два вида сил. Интересно, что еще Ньютон, выводя закон сохранения живой силы (так тогда называли кинетическую энергию), заметил, что сила, в каждый момент времени ортогональная к скорости, не препятствует сохранению живой силы. Курьезно, что это замечание Ньютона несколько сот лет оставалось почти неизвестным из-за того, что при переводе главного труда Ньютона с латыни на английский как раз в этом месте допустили ошибку.
Приведу здесь общее определение. Оператор Γ : H → H , действующий в евклидовом (в частности, гильбертовом) пространстве H , называется гироскопическим , если для всех ξ ∈ H выполняется равенство
(Γξ, ξ) = 0. (21.11)
В частности, кососимметрический оператор есть линейный гироскопический. Можно еще сказать, что гироскопическим называется оператор, который является косимметрией тождественного оператора Ix = x .
Одним из классических примеров гироскопической силы служит сила Кориолиса Fc = 2ω ∧ v , возникающая в уравнениях относительного движения, записываемых в подвижной системе координат, вращающейся с угловой скоростью ω. Гироскопическую силу, например, приходится учитывать при расчете движения тел относительно Земли.
Диссипация энергии при движении вязкой жидкости, функционал Рэлея
Уравнения Навье–Стокса в случае несжимаемой жидкости имеют вид
![]() (21.12)
(21.12)
div v = 0, (21.13)
где v = v (x,t ) — поле скорости, p = p (x,t ) — давление, x — точка
пространства R
3
(или R
2
), t
— время, а материальная производная
![]() дается равенством:
дается равенством:![]() . Будем считать, что жидкость заключена в области D
⊂ R
3
, граница которой ∂D
неподвижна и непроницаема для жидкости, так что выполняется краевое условие
. Будем считать, что жидкость заключена в области D
⊂ R
3
, граница которой ∂D
неподвижна и непроницаема для жидкости, так что выполняется краевое условие
![]() .
(21.14)
.
(21.14)
Предполагается, что на жидкость не действуют никакие внешние силы, впрочем, если сила потенциальна, какова, например, сила тяжести, то её удельную потенциальную энергию можно просто добавить к давлению, а на скорость она не влияет.
Наша цель сейчас — во-первых, показать, что сила ньютоновского трения ν∆v (ν > 0 — кинематический коэффициент вязкости) является рэлеевской — при естественном обобщении данного понятия. Для этого мы введем соответствующий функционал Рэлея. Затем мы покажем, что при сформулированных условиях кинетическая энергия жидкости экспоненциально затухает при t → +∞. Замечу, что в следующих рассмотрениях существование и единственность решения задачи (21.12)–(21.14) с начальным условием
![]() (21.15)
(21.15)
предполагается. В (21.15) начальное поле скорости v 0 — достаточно гладкое и соленоидальное (div v 0 = 0). На самом деле, существование и единственность доказаны лишь в двумерном случае, а в трехмерном — это одна из самых трудных проблем математической гидродинамики, решенная лишь для малых начальных скоростей v 0 . Недавно частный институт Клэя в США объявил премию в 1 млн долларов за её решение. О современном состоянии проблемы Вы можете прочитать в моей статье [53].
На пространстве гладких соленоидальных полей, удовлетворяющих краевому условию (21.14), определим квадратичный функционал W , полагая
![]() (21.16)
(21.16)
Интегрируя по частям, можно и полезно привести функционал W к виду, содержащему лишь первые производные. Учитывая, что граничные интегралы пропадают ввиду краевого условия (21.14), получаем
![]() (21.17)
(21.17)
Варьируя W , находим
![]() (21.18)
(21.18)
Таким образом, градиент функционала W в пространстве L 2 (D ) имеет вид
grad W = −ν∆v. (21.19)
Итак, W, действительно, есть диссипативный функционал Рэлея, ньютоновское трение является рэлеевским. Вспоминая определение функциональной производной и функционального градиента, можно также написать
− ν∆v = Grad W [v ], (21.20)
или в координатах
![]() .
(21.21)
.
(21.21)
Теперь докажем, что нелинейный член в уравнении Навье – Стокса обладает гироскопическим свойством. Мы установим более общее равенство
Z
(u,∇)v · v dx = 0, (21.22)
D
если векторное поле u
соленоидально и касательно к границе ![]() 0. Имеем
0. Имеем
![]() (21.23) Интегрируя по частям, получаем
(21.23) Интегрируя по частям, получаем
![]() div
div ![]() (21.24)
(21.24)
Оба слагаемых справа исчезают, ввиду предположенных свойств поля u , что и приводит к равенству (21.22).
Заметим, что от поля v
не пришлось ничего требовать, кроме достаточной регулярности. Кроме того, краевое условие (21.14) использовано здесь не в полной мере — требуется лишь, чтобы на границе исчезла нормальная компонента скорости. Поэтому равенство (21.22) справедливо и в том случае, когда u
— поле скоростей идеальной жидкости при условии непроницаемости границы (![]()
Теперь умножим уравнение движения вязкой жидкости (21.12) скалярно на v и проинтегрируем по области D . Примем в расчет равенство (21.22) при u = v , а также равенство
Z
| v · ∇pdx = 0. D В результате получим уравнение диссипации энергии |
(21.25) |
![]() (21.26)
(21.26)
которое в терминах кинетической энергии T и функционала Рэлея W записывается в виде
![]() (21.27)
(21.27)
Замечу, что равенство (21.27) весьма желательно, по существу даже необходимо, сохранять при любых способах аппроксимации уравнения Навье – Стокса. Можно даже рекомендовать при построении сеточной или спектральной аппроксимации начинать с аппроксимации функций T и W . Опыт говорит, что нарушение фундаментального уравнения (21.27) приводит к непригодности приближенной схемы решения, которая в таком случае может давать даже качественные неправильные результаты. Например, кинетическая энергия T может оказаться бесконечно большой, хотя, согласно точному уравнению (21.26), она монотонно убывает со временем.
Экспоненциальное затухание энергии
В случае сил трения с полной диссипацией, в предположении, что система конечномерна, можно доказать, что возмущения устойчивого равновесия затухают экспоненциально. Решения линейной задачи суть линейные комбинации элементарных решений вида e λ t ϕ, причем все собственные значения λ лежат в левой полуплоскости: Reλ < 0; в отсутствие гироскопических сил все они вещественны. В достаточно общих условиях теорема Ляпунова о законности линеаризации устанавливает, что экспоненциальное затухание сохраняется и для нелинейной задачи. В бесконечномерных задачах, скажем, в механике сплошной среды, ситуация осложняется. Линеаризованная задача может обладать непрерывным спектром, так что для ее решений уже нет такого простого представления. Даже когда подобное представление решений линеаризованной задачи, на сей раз в виде бесконечного ряда, имеет место, может статься, что вообще невозможно дать никакой квалифицированной оценки скорости затухания — возмущения могут затухать сколь угодно медленно, см. упражнения 1,2.
Сейчас мы покажем, что в случае ограниченной области D , при условии неподвижности границы, возмущения все-таки затухают экспоненциально. Решающую роль далее играет неравенство Фридрихса
Z Z
u 2 dx ≤ γ −1 (∇u )2 dx, (21.28)
D D
которое справедливо для любых функций u , исчезающих на границе области D , константа γ = γD зависит лишь от области D , которая сейчас предполагается ограниченной.
Если векторное поле v исчезает на границе ∂D , то записываем неравенство (21.28) для каждой его декартовой компоненты vi , i = 1, 2, 3 и, суммируя полученные неравенства, приходим к неравенству Фридрихса для векторного поля
Z Z
v 2 dx ≤ γ −1 (∇v )2 dx, (21.29)
D D
Замечу, что неравенство Фридрихса заведомо несправедливо для неограниченных областей D , содержащих окрестность бесконечно удаленной точки, например, для областей, внешних по отношению к шару или другой ограниченной области. Вместе с тем, оно остается справедливым например для слоя между двумя плоскостями, если предполагать, что функция u исчезает на бесконечности. На самом деле, неравенство (21.28) остается верным, если расстояние ρ(x,∂D ) точки x ∈ D от границы ∂D ограничено сверху. Слой этим свойством обладает, а угол на плоскости или клин в R3 — не обладает, и для них неравенство (21.28) уже неверно; (см., однако, упражнение 3).
Понятно, что неравенство (21.28) остается верным, если константу γ уменьшить. Наилучшее, то есть наибольшее, значение константы γ в этом неравенстве есть наименьшее собственное значение оператора Лапласа при краевом условии первого рода. Известен вариационный принцип (см. [28]): наименьшее собственное значение λ1 спектральной краевой задачи
![]() (21.30)
(21.30)
можно определить как минимум функционала
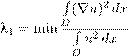 ,
(21.31)
,
(21.31)
Минимум здесь берется по всевозможным функциям, исчезающим на границе области D .
Вообще для оператора Лапласа с краевым условием первого рода существует бесконечная последовательность собственных значений λ1 ≤ λ2 ≤ ... ≤ λn ≤ ... , причем λn → ∞, когда n → ∞. Все они положительны и полупросты. В случае скалярных функций можно доказать, что λ1 — простое собственное значение, которому отвечает единственная (с точностью до ненулевого скалярного множителя) собственная функция ϕ1 ; известно, что она не меняет знака в области D . Можно считать, что ϕ1 (x ) > 0 для всех x ∈ D , см.[28]; [18].
Обратимся к уравнению изменения энергии (21.26) ((21.27)). Оценивая правую часть при помощи неравенства Фридрихса (21.29)
![]() (21.32)
(21.32)
| Из (21.32) стандартно выводим оценку |
|
| T (t ) ≤ T (0)e −2 γν t . |
(21.33) |
Таким образом, кинетическая энергия жидкости экспоненциально убывает. В качестве γ можно взять определенное выше собственное значение λ1 .
Однако наилучшее (то есть наибольшее) значение этой постоянной находится посредством решения спектральной задачи Стокса
| −∆v = µ v − ∇q, |
(21.34) |
| div v = 0, |
(21.35) |
![]() .
(21.36)
.
(21.36)
Можно доказать, что и эта спектральная задача имеет последовательность положительных собственных значений µ1 ≤ µ2 ≤ ... ≤ µn ≤ ... , µn → +∞ при n → ∞, см.[58]. В качестве γ в (21.33) можно взять µ1 , и этот результат уже не улучшаем: существуют решения линеаризованной на равновесии v 0 = 0 системы Навье – Стокса, которые затухают в точности по закону e −2 νµ 1 t . Более того, решения с таким же поведением имеются и у нелинейной системы Навье – Стокса.
Остается повторить, что наш вывод основывается на предположении, что существует гладкое решение, определенное для всех t > 0. В настоящее время это предположение доказано для произвольных гладких начальных полей лишь в двумерном случае, а для трехмерного случая представляет собой одну из самых жгучих нерешенных проблем современной математики.
Нужно еще подчеркнуть, что проблема поведения решения при t → +∞ резко усложняется, когда на границе области D задана ненулевая скорость, и когда имеются непотенциальные массовые силы. Один из классиков математической гидродинамики Э.Хопф меланхолически заметил, что в такой общей ситуации течение жидкости при t → +∞ по-прежнему стремится к чему-то, “но это что-то далеко от того, чтобы быть единственным стационарным течением” (“...but this something is far from to be a single stationary point”). Здесь мы встречаемся с новым, до сих пор таинственным явлением — турбулентностью. Возникают сложные режимы течения жидкости, в которых скорость и давление претерпевают сложные хаотические колебания в пространстве и во времени.
Упражнения
1. Рассмотрим дифференциальное уравнение x ˙ = −Ax в гильбертовом пространстве H . Предположим, что A самосопряженный оператор, и его спектр состоит из положительных собственных значений λ1 ,..., λk ,... , причем λk → 0 при k → ∞, а также предельной точки 0. Докажите, что все решения этого уравнения стремятся к нулю при t → ∞, но могут стремиться к нулю сколь угодно медленно: какова бы ни была положительная функция ρ(t ), определенная при t > 0, найдется такое решение данного уравнения, для которого выполнено предельное равенство
![]() .
.
Указание. Докажите, что эволюционный оператор U (t ) этого уравнения при t → +∞ стремится к нулю поточечно, но неравномерно. Примените теорему Банаха–Штейнгауза.
2. Докажите, что всякое решение уравнения теплопроводности ![]()
∆u
во всем пространстве Rn
с условием![]() и с начальным условием u
(x,
0) = ϕ(x
), причем ϕ
∈ L
2
(Rn
), стремится к нулю при t
→ +∞ по норме L
2
: R
u
2
(x,t
)dx
→ 0, причем эта сходимость может быть сколь
и с начальным условием u
(x,
0) = ϕ(x
), причем ϕ
∈ L
2
(Rn
), стремится к нулю при t
→ +∞ по норме L
2
: R
u
2
(x,t
)dx
→ 0, причем эта сходимость может быть сколь
R n угодно медленной (см. упражнение 1).
3. Пусть D есть угол на плоскости, определяемый в полярных координатах (r, θ) неравенством 0 < θ < α, где 0 < α < 2π. Докажите, что неравенство Фридрихса в этом случае уже несправедливо, но для любой функции u , исчезающей на границе, справедливо неравенство
![]()
причем µ — положительная постоянная, зависящая только от α, но не от функции u . Сформулируйте и докажите аналогичный результат для случая, когда D — конус в Rn .
4. Докажите, что всякая функция, определенная на пространстве R 3 , непрерывно дифференцируемая и затухающая на бесконечности, удовлетворяет неравенству Лерэ
![]()
если интеграл в правой части сходится; x ∈ R 3 — произвольная точка.
Указание. Рассмотрите интеграл
![]()
Примените интегрирование по частям и неравенство Коши–Буняковского.
ЭЛЕМЕНТЫСТАТИСТИЧЕСКОЙМЕХАНИКИ
В статистической механике наиболее удобной формой уравнений оказалась гамильтонова. Механическая система определяется заданием ее гамильтониана H (q,p ). Предполагается, что он не зависит от времени, так что выполняется закон сохранения энергии и H есть интеграл системы
q ˙ = Hp , p ˙ = −Hq .
Число степеней свободы n в приложениях статистической механики очень велико. Вы помните число Авогадро 6. 023 · 1023 — число молекул в одной грамм-молекуле вещества. Нет надежды не только на то, чтобы решить столь большие системы уравнений, но даже их записать. Другая трудность состоит в том, что нет никакой возможности найти или измерить начальные данные для такой системы.
С другой стороны, нам и не нужны столь детальные знания, скажем, о движении молекул воздуха. Что бы мы с ними стали делать? Здесь возникает довольно обычная для физики проблема сокращения информации . Цель, конечно, состоит в том, чтобы уменьшить объем информации о процессе до уровня, допускающего ее хранение и обработку, а вместе с тем, достаточного для предсказания и управления. Выходом оказывается применение идей и подходов теории вероятностией.
Главный постулат статистической механики гласит, что измеряемые в опытах макроскопические величины — температура, плотность, концентрации компонент (например, соли в рассоле), напряженности электрического и магнитного полей и т.д. суть средние (математические ожидания), вычисленные в соответствии с надлежащей инвариантной плотностью. В принципе, здесь могла бы фигурировать инвариантная мера общего вида, не обязательно абсолютно непрерывная относительно меры Лебега. Однако в известных мне работах по статистической физике применяются исключительно инвариантные меры, определяемые инвариантными плотностями. Могу предположить, что использование более общих инвариантных мер — дело будущего.
Из приведенного выше постулата следует вывод, что все макроскопические уравнения физики суть уравнения для средних, для математических ожиданий соответствующих величин. Это относится и к уравнению тепло-
22 О законах термодинамики
проводности (диффузии), и к уравнениям механики сплошной среды. Такая трактовка, например, уравнения теплопроводности позволяет объяснить его парадоксальное свойство — тот факт, что изменение температуры (или концентрации) в некоторый момент времени мгновенно влияет на поле температуры (концентрации) во всей области, занятой проводником тепла. Выходит, как будто, что тепло распространяется с бесконечно большой скоростью. На самом деле, с бесконечной скоростью распространяется плотность вероятности.
Другое важное следствие основного постулата состоит в том, что макроскопические уравнения, в принципе, должны быть дополнены уравнениями для случайных отклонений от средних. Эти отклонения называются флуктуациями соответствующих величин, и обычно они бывают малыми. Несмотря на это, именно флуктуации вызывают некоторые макроскопически наблюдаемые явления. Например, голубой цвет неба объясняется рассеиванием солнечного света на флуктуациях плотности воздуха в высоких слоях атмосферы. О другом замечательном явлении того же рода — о броуновском движении — дальше мы поговорим подробнее.
Как и многие другие общие положения естествознания, приведенный выше принцип не содержит ясных условий его применимости. Вам, наверное, бросилось в глаза, что он ничего не говорит о том, какая именно инвариантная плотность (если их много) является «надлежащей». Мы теперь рассмотрим то распределение вероятности в фазовом пространстве системы, которое, если не всегда, то, во всяком случае, для весьма широкого круга явлений оказывается адекватным и блестяще подтверждается экспериментом.
22. О законах термодинамики
В настоящее время термодинамика, по крайней мере, некоторое ее ядро, вполне формализовано и может считаться с формальной точки зрения одним из разделов математической физики. Она основывается на небольшом числе аксиом, обычно называемых законами или началами. Перед тем как напомнить Вам начала термодинамики, замечу, что название «термодинамика» неточно. На самом деле, эта наука изучает равновесные, статические состояния, а не эволюцию. Более правильным было бы название «термостатика», хотя в термодинамике рассматриваются также квазистатические процессы — столь медленные, что в каждый момент времени к ним применимы начала термодинамики. Поскольку термин термодинамика был уже занят, истинную термодинамику стали называть неравновесной термодинамикой.
Нулевоеначалотермодинамики. Оно состоит в том, что в число параметров, описывающих состояние изучаемой системы, входит температура T . Другими параметрами могут быть объем, плотность, концентрации различных компонент вещества, а также и параметры, характеризующие электромагнитное поле, скажем, напряженности электрического и магнитного полей. Возможно и появление иных параметров, характеризующих различные поля и виды вещества.
Термодинамика, особенно неравновесная термодинамика — наука с большой претензией, полагающая, что она должна описывать любую физическую систему. Если даже температура не входит в число параметров состояния некоторой системы, то физик скажет, что в ней процессы изотермичны (происходят при постоянной температуре).
Первое начало термодинамики. Первым началом термодинамики называют закон сохранения и превращения энергии применительно к термодинамическим системам. Этот закон в дифференциальной форме может быть выражен равенством
dE = δQ + δA. (22.1)
Здесь E — внутренняя энергия системы. Постулируется , что E — функция состояния системы. Далее δQ — элементарное количество тепла, переданное системе в результате данного процесса. Подчеркннем, что, вообще говоря, не существует функции состояния Q , так что обозначение δQ следует понимать как единый символ, δQ — функция процесса, а не состояния. Наконец, δA — элементарная работа, произведенная над системой внешними силами, это также функция процесса, и не существует такой функции состояния A . Однако во многих важных случаях внешние силы оказываются потенциальными, и тогда можно записать, что δA = dW , где W — потенциальная энергия внешних сил, которая уже является функцией состояния.
С математической точки зрения, dE , δQ и δA суть дифференциальные 1–формы, называемые также пфаффовыми формами. Если x 1 ,...,xn — параметры состояния, то каждую из 1–форм, например δA , можно представить в виде
![]() .
(22.2)
.
(22.2)
Не всякая такая форма может быть представлена как дифференциал некоторой функции, если это возможно, то форму называют точной . Напри-
О законах термодинамики
мер, для энергии E = E (x 1 ,...,xn ) имеем
![]() .
(22.3)
.
(22.3)
Второе начало (второй закон) термодинамики. Этот закон по существу состоит из двух частей. Первая из них (мало известная широкой публике) состоит в том, что существует функция состояния S, называемая энтропией, такая, что дифференциальная форма δQ может быть представлена в виде
δQ = TdS. (22.4)
Таким образом, форма δQ , не будучи точной, является голономной — превращается в точную пфаффову форму после умножения на интегрирующий множитель 1/T . При обратимых процессах энтропия остается постоянной.
Вторая часть закона состоит в том, что при необратимых процессах в замкнутой термодинамической системе энтропия всегда возрастает. Система называется замкнутой , если она не взаимодействует с другими системами, в частности, на нее не действуют извне механические или, скажем, электрические силы, а также исключена теплопередача — поступление теплоты от других систем или отвод тепла.
Второе начало термодинамики широко известно и зачастую поминается в различных вульгаризованных формах. Стоит подчеркнуть, что энтропия возрастает лишь в замкнутых системах, а в столь сложных системах как живые организмы, росту энтропии противостоит взаимодействие с внешним миром (питание, дыхание), дающее постоянный приток энергии. В форме замкнутой системы живые организмы не могут существовать. В конечном счете, условием жизни на Земле является приток энергии от солнца. Гораздо меньше приток энергии от радиоактивного распада веществ, входящих в состав вещества Земли.
Замечу еще, что у второго начала термодинамики имеются и другие, более приземленные формулировки. Например, можно его выразить так: теплота не может передаваться от холодного тела к горячему (с более высокой температурой) . Теплота не может передаваться от холодного тела к горячему ни в каком процессе, если в нем не участвуют другие тела.
Второе начало термодинамики занимает особое место среди всех физических законов. Это единственный закон, который, как говорят, определяет «стрелу времени», направление эволюции.
Основные законы термодинамики были установлены в середине XIX века в трудах Джоуля, Майера, Карно (первое начало термодинамики) и Карно, Клаузиуса, Кельвина (второе начало). Имеется еще третье начало термодинамики (постулат Нернста), которое гласит, что абсолютный нуль температуры недостижим. Первой задачей статистической механики, которую стал развивать Людвиг Больцман, было объяснение законов термодинамики на основе представления о веществе как о совокупности атомов и молекул.
23. Теоремы Пуанкаре о возвращении
Прелесть математической физики для исследователя состоит и в том, что никогда не знаешь, чем нужно будет заниматься завтра. Математическая физика изумительно разнообразна и по постановке проблем, и по привлекаемому математическому аппарату. Признаюсь, мне иногда трудно понять, как это у многих чистых математиков хватает терпения десятки лет заниматься одним и тем же, оставаясь в узких рамках одного предмета.
Мы сейчас начинаем постепенно переходить от классической механики к статистической физике (механике). Первой основной целью этой науки является объяснение и углубленное понимание основных законов термодинамики. Например, мы с вами увидим, как из классической механики с применением идей теории вероятностей можно вывести закон Клапейрона– Менделеева для газов. В основе этого исследования лежит представление о веществе, скажем, о газе, как о совокупности взаимодействующих материальных частиц. Из всех мыслимых форм уравнений движения в механике наиболее подходящими для развития статистической механики оказались гамильтоновы уравнения. Мы уже сделали первый шаг к развитию статистической механики, когда вывели уравнение Лиувилля и нашли инвариантную меру на изоэнергетической поверхности. И вот оказывается, что для второго шага нужно теперь заняться работой на значительно более высоком уровне абстракции.
Вообще, математические идеи и теории становятся наиболее понятными и обозримыми, когда они излагаются в надлежащей степени общности. Тут, конечно, нужно чувство меры, бывает и так, что чрезмерная общность рассмотрения затемняет главные идеи.
Анри Пуанкаре в конце XIX-го века первым понял, сколь безнадежно пытаться найти полный набор интегралов для достаточно сложных и общих механических систем. Он построил примеры таких систем, у которых нет
иных интегралов, кроме интеграла энергии. Более того, именно такая ситуация является типичной. Пуанкаре рассматривал системы, получаемые малым возмущением некоторой вполне интегрируемой системы. Оказалось, что таким путем в условиях общего положения получаются неинтегрируемые системы.
Как вообще доказать, что некоторая система не имеет интеграла? Это может случиться, если движения системы весьма сложны, например, имеется движение — решение x (t ) соответствующей системы дифференциальных уравнений в Rn , траектория T которого всюду плотна в некоторой области D в Rn . Если теперь предположить, что имеется интеграл ϕ(x ), так что ϕ(x (t )) = c (c — постоянная) для всех t , то в итоге получится, что функция ϕ(x ) постоянна всюду на плотном множестве в D — на траектории T . Но если ϕ — непрерывная функция, постоянная на плотном множестве, то она постоянна и на его замыкании, так что ϕ(x ) = c всюду в области D. Выходит, ϕ — тривиальный интеграл, по крайней мере, в области D.
Если допустить, что ϕ — аналитическая функция, то по теореме единственности для аналитических функций выйдет, что ϕ(x ) = c всюду в Rn .
Для аналитических функций ϕ при определенных дополнительных условиях бывает даже достаточно предположить, что траектория T плотна не во всей области D, а лишь, на некоторой гиперповерхности. И отсюда уже удается вывести, что эта функция есть константа.
Оказывается, траектории со столь сложным поведением действительно существуют в механических системах, что и препятствует существованию нетривиальных интегралов.
Пространство с мерой. Пусть X — множество, его элементы могут иметь любую природу. Предположим, что выделен некоторый класс Σ его подмножеств, который является σ-алгеброй. Это означает, что теоретикомножественные операции — взятие объединения, пересечения, разности, дополнения, примененные даже счетное число раз, не выводят за пределы класса Σ. Например, если множества E 1 , E 2 ,... принадлежат классу Σ (в символах En ∈ Σ, n = 1, 2,... ), то их объединение и пересечение также принадлежат классу Σ, или в символах,
![]() ,
,
(23.1)
Если E ∈ Σ, и E 0 = X \ E — его дополнение, то и E 0 ∈ Σ.
Мера. Согласно определению, мера µ есть неотрицательная σ-аддитивная функция множеств, заданная на некоторой σ-алгебре Σ. Это означает, что класс Σ содержит пустое множество ∅ и все множество X , и для любого счетного набора непересекающихся множеств E 1 ,E 2 ,... ∈ Σ справедливо равенство
µ![]() .
(23.2)
.
(23.2)
Подчеркну, что это равенство постулируется лишь для случая, когда Ek ∩ En = ∅ при k 6= n . На самом деле, оно справедливо и при несколько более широких условиях (см. ниже).
Множества, принадлежащие классу Σ, называются измеримыми, а точнее, µ-измеримыми. Это уточнение нужно, конечно, лишь в случае, когда мы имеем дело с несколькими мерами.
Замечу, что в современной математике в ходу и различные обобщения понятия меры — рассматриваются конечно-аддитивные меры, знакопеременные меры (почему-то не привился выразительный термин заряд ), векторнозначные меры. Знакомясь с литературой, посмотрите, что означает в каждом случае термин мера .
Зачастую разрешается, чтобы мера µ принимала и бесконечное значение. Если µ(X ) < ∞, то и мера любого измеримого множества конечна. В этом случае мера µ называется конечной.
Согласно принятой идеологии, множествами меры ноль мы пренебрегаем — не считаем, что два измеримых множества E и F различны, если они отличаются на множество меры ноль. В символах это означает, что µ(E ∆F ) = 0; напомню, что симметрическая разность E ∆F определяется как E ∆F = (E \ F ) ∩ (F \ E ).
Точно также не различаются отображения пространств с мерой, если их значения различны лишь для множества значений аргумента, которое имеет нулевую меру.
Очень часто то или иное свойство устанавливается не для всех точек пространства с мерой, а лишь для всех точек за исключением множества точек, имеющих меру ноль. В этом случае говорят, что данное свойство имеет место для почти всех точек или почти всюду , или для почти любой точки. Заметим, что понятие «почти всюду» зависит от выбора меры, поэтому, когда нужно быть более точными, говорят «µ-почти всюду» и т. д.
Говоря более строго, в теории пространств с мерой и их отображений, мы имеем дело не с множествами и не с отображениями, а с классами эквивалентных множеств и классами эквивалентных отображений. При этом всякое множество меры ноль рассматривается по сути, как пустое множество, потому что оно эквивалентно пустому. Соответственно, если µ(E 1 ∩ E 2 ) = 0, то измеримые множества E 1 и E 2 трактуются, как непересекающиеся. В частности, равенство (23.2) верно и в том случае, когда µ(Ek ∩ E` ) = 0 при всех k и ` , лишь бы k 6= ` . (Проверьте это).
Отображения, сохраняющие меру. Отображение T : X → X называется измеримым, если (полный) прообраз T −1 (E ) всякого измеримого множества E есть измеримое множество. Если отображение T взаимно однозначно, то можно сформулировать это определение в эквивалентной и чуть более наглядной форме. Именно, потребуем, чтобы отображение T переводило всякое измеримое множество в измеримое: E ∈ Σ → TE ≡ T (E ) ∈ Σ.
Скажем, что измеримое и взаимно однозначное отображение T : X → X сохраняет меру µ, если для всякого E ∈ Σ
µ(TE ) = µ(E ). (23.3)
Для взаимно однозначных отображений равенство (23.3) можно записать в эквивалентной форме
µ(T −1 E ) = µ(E ) (23.4)
для всех E ∈ Σ. На самом деле, определение (23.4) имеет преимущества по сравнению с (23.3). Первое преимущество носит технический характер и состоит в том, что в дальнейших рассмотрениях гораздо чаще придется пользоваться именно равенством (23.4). Второе преимущество — более принципиально: определение (23.4) распространяется и на не взаимно однозначные отображения. При этом T −1 E означает полный прообраз — множество всех тех x ∈ X , которые под действием отображения T переходят в E , то есть, по определению,
T −1 E = {x : Tx ∈ E }.
Теорема 1 (теорема Пуанкаре о возвращении множеств). Пусть E — измеримое множество в пространстве с конечной мерой (X, Σ, µ), причем µ(E ) > 0. Пусть T : X → X — отображение, сохраняющее меру µ. Тогда найдется такое натуральное n, что (см. рис. 12)
µ(Tn E ∩ E ) > 0. (23.5)
Доказательство. Рассуждая от противного, предположим, что для всех n = 1, 2,...
µ(Tn E ∩ E ) = 0. (23.6)
Рис. 12
Тогда из (23.6) последует, что множества Tk E и Tn E тоже имеют пересечение меры ноль: µ(Tk E ∩ Tn E ) = 0 для всех натуральных k и n при k 6= n . Для определенности будем считать, что k < n . Тогда
µ(Tk E ∩ Tn E ) = µ(Tk (E ∩ Tn −k E )) = µ(E ∩ Tn −k E ) = 0. (23.7)
Мы учли, что Tk сохраняет меру µ, как и отображение T , а затем воспользовались равенством (23.6).
Таким образом, мы построили последовательность измеримых, попарно непересекающихся множеств E , TE , T 2 E,... . Все они имеют одну и ту же меру: µ(Tk E ) = µ(E ) = m > 0. Но отсюда следует равенство
µ![]() (23.8)
(23.8)
для любого n = 1, 2,... (мы считаем, что T 0 = id ). Так как мера любого подмножества в X не превосходит µ(X ), получаем
nm < µ(X ). (23.9)
Ввиду конечности меры µ, это неравенство не может выполняться для всех натуральных n . Полученное противоречие показывает, что равенство (23.6) при некотором n нарушается. Теорема доказана.
• Замечу, что на последнем шаге доказательства мы воспользовались аксиомой Архимеда. Это он в своей работе «Псаммит, или исчисление песчинок» установил, что выбрав любую единицу измерения, скажем, веса или длины (у нас это m ), можно для любого сколь угодно большого числа (у нас это µ(X )) найти столь большое n , что неравенство (23.9) будет нарушено. В этой работе Архимед очень близко подошел к открытию позиционной системы счисления (многие, самые крупные математики, считают, что это было величайшим открытием за всю историю науки). Конечно, сейчас все это очевидно, но кто-то должен был первым это понять. Это сделал Архимед.
Английский историк Арнольд Тойнби написал работу, в которой попытался предугадать, как развивалось бы человечество, если бы Архимед действительно сделал это открытие. Получилось, что развитие техники пошло бы несравненно быстрее, возможно, она развилась бы в других странах, и мир сейчас был бы совсем иным.
Из теоремы Пуанкаре вытекает важное следствие, которое применяется, пожалуй, чаще, чем сама теорема.
Следствие 1. В условиях теоремы 1 существует последовательность натуральных чисел n 1 , n 2 ,..., стремящаяся к бесконечности ( nk → +∞), такая что
µ(Tn k E ∩ E ) > 0. (23.10)
Доказательство. Пусть N — натуральное число. Применим теорему 1 к отображению TN : X → X , которое, конечно, тоже сохраняет меру µ. Получится, что для некоторой его степени TNk
µ(TNk E ∩ E ) > 0. (23.11)
Положим n 1 = Nk . Повторим это рассуждение с заменой N на n 1 . Тогда получится, что пересечение множества Tn 1 k 1 E = TNkk 1 E с E имеет положительную меру. Положим n 2 = Nkk 1 . Продолжая аналогично, мы построим последовательность n 1 < n 2 < ... < nk < ... такую, что выполняется (23.10).
Согласно этому следствию, «возвращение» (частичное) множества E будет происходить бесконечно много раз, при сколь угодно больших значениях дискретного времени n .
Теорема 2 (теорема Пуанкаре о возвращении точек). Пусть E — измеримое множество в пространстве с мерой (X, Σ, µ), и преобразование T : X → X сохраняет меру µ. Предположим, что мера µ конечна: µ(X ) < +∞. Тогда для почти любой точки x ∈ E найдется натуральное число n = n (x ) такое, что Tn x ∈ E .
Доказательство. Напомню, что выражение «почти любая» означает, что множество исключительных точек имеет меру ноль. Более точное выражение: µ-почти любая. Хотя формально мы не обязаны вводить в условия теоремы требование, чтобы мера множества E была положительна, ясно, что случай µ(E ) = 0 бессодержателен — все множество E может тогда быть исключительным. Таким образом, дальше можно считать, что µ(E ) > 0.
Построим подмножество F ⊂ E , состоящее из исключительных точек. Обозначим дополнение X \E через E 0 . Тогда T −1 E 0 есть множество точек, которые не попадают в E после однократного применения преобразования T (после одного шага итераций), T −2 E 0 — множество точек, не попадающих в E после двух шагов, ..., T −n E 0 — после n шагов, и т. д. Ясно, что множество
F = E ∩ T −1 E 0 ∩ ... ∩ T −n E 0 ∩ ...
есть множество точек множества E , не возвращающихся в E никогда.
Множества F и T −n F не пересекаются при любом натуральном n . Действительно, если x ∈ F ∩ T −n F , то Tn x ∈ F ⊂ E , то есть точка x возвращалась бы, в противоречии с определением множества F .
Теперь мы можем установить, что множества F , T −1 F , ..., T −n F,... попарно не пересекаются. Действительно, T −k F ∩ T −n F = T −k (F ∩ T −(n −k ) F ), когда, например, n > k . Понятно, что образ пустого множества (при отображении T −k ) пуст.
Построена последовательность непересекающихся множеств F , T −1 F ... , T −n F,... , имеющих одну и ту же меру: µ(T −n F ) = µ(F ). Как мы уже видели, ввиду конечности меры µ, это возможно лишь в случае µ(F ) = 0. Теорема доказана.
Следствие 2. Для почти любого x ∈ E существует бесконечная последовательность натуральных чисел n 1 , n 2 ,... такая, что nk → ∞ и Tn k x ∈ E .
Доказательство. Доказательство проводится, по сути, так же, как и в случае теоремы о возвращении множеств. Проведите его сами. Заметьте лишь, что когда мы говорим «почти для всех точек», то каждый раз приходится иметь в виду различные множества меры ноль. Но счетное объединение множеств меры ноль (вот она — σ-аддитивность!) есть множество меры ноль.
24 Гидродинамическая интерпретация систем дифференциальных
уравнений и теорема Лиувилля 205
![]()
В приложениях к механике мы можем выбрать в качестве множества E сколь угодно малую окрестность (любого!) заданного состояния в фазовом пространстве. Получится, что в будущем система много раз будет возвращаться в эту — сколь угодно малую окрестность. Представим себе, например, что рассматриваемая механическая система есть совокупность молекул воздуха в этой аудитории. Выберем состояние, в котором весь воздух сосредоточился вблизи одного угла, а остальная часть аудитории — вакуум. Выходит, время от времени весь воздух в этой комнате будет собираться вблизи угла (если бы однажды было создано такое состояние). Всем, кто находится далеко от этого угла, придется плохо.
Сейчас это уже трудно себе представить, но в конце XIX века многие выдающиеся ученые сильно сомневались в существовании атомов. Примеры вроде нашего примера с воздухом считались сильными возражениями против статистической теории газов. Конечно, никто еще не видел, чтобы весь воздух собрался в одной части комнаты. Людвиг Больцман, внесший огромный вклад в развитие этой теории, на подобные возражения ответил очень коротко: «Долго же вам придется ждать!» И в самом деле, современные оценки показывают, что подобное явление очень мало вероятно, вероятное время его ожидания составляет много миллиардов лет, что превосходит время существования Вселенной. Философы спорят, считать ли такие явления возможными, но мало вероятными, или попросту объявить их невозможными. На практике мы конечно, считаем их невозможными, во всяком случае, действуем, не принимая такие «возможности» во внимание.
24. Гидродинамическая интерпретация систем дифференциальных уравнений и теорема Лиувилля
Рассмотрим дифференциальное уравнение в Rn
x ˙ = v (x,t ). (24.1)
Предположим, чтобы не отвлекаться от главного, что задача Коши для уравнения (24.1) с начальным условием
x (0) = a (24.2)
глобально однозначно разрешима: для любого a ∈ Rn задача Коши (24.1)– (24.2) имеет, и притом единственное, решение x = x (a,t ), определенное для всех t ∈ R. Кроме того, будем предполагать, что поле v гладко зависит от x и от t .
В этих условиях эволюционный оператор Nt : Rn → Rn определен для всех t ∈ R, a ∈ Rn , так что
x (a,t ) = Nt a. (24.3)
Для неавтономного уравнения (24.1) оператор Nt зависит, конечно, от выбора начального момента, но здесь мы не собираемся его менять.
Представим себе, что пространство Rn заполнено некоторой жидкостью. Решение x (a,t ) будем трактовать как движение жидкой частицы, которая в момент времени t = 0 находилась в точке a . Векторное поле v (x,t ) приобретает смысл скорости той жидкой частицы, которая в момент t находится в точке x ∈ Rn .
В гидродинамике применяются два подхода к описанию движений жидкости. В первом из них, который называется эйлеровым , изучается эволюция поля скорости v (x,t ) течения жидкости. Второй подход называется лагранжевым и состоит в описании движения жидкой частицы x (a,t ). Названия эти условны — Эйлер знал оба подхода. Эйлерово и лагранжево описания течения жидкости связаны между собой посредством задачи Коши (24.1)–(24.2). Если известно поле скорости v (x,t ), то чтобы найти движение частиц x (a,t ), нужно решить задачу Коши (24.1)–(24.2) для всех a . Если известно движение x (a,t ) любой частицы, то поле скорости v (x,t ) определяется как x ˙(a,t ), где a выражено через x , так что
v (X,t ) = x ˙(a (X,t ),t ), (24.4)
где a = a (X,t ) находится из уравнения x (a,t ) = X для любого X ∈ Rn .
Уравнение неразрывности — уравнение Лиувилля
Изложенная гидродинамическая интерпретация задачи Коши (24.1)– (24.2) вызывает к жизни новые вопросы. Теперь начальное значение a не будет фиксированным, мы будем заниматься всей совокупностью задач Коши, рассматривая a как новую векторную переменную. Как Вам известно из курса обыкновенных дифференциальных уравнений, в случае гладкого поля v (x,t ) вектор-функция x (a,t ) гладко зависит от a ∈ Rn и от t ∈ R.
Зная, как двигаются жидкие частицы, мы можем проследить и за эволюцией областей, состоящих из одних и тех же частиц. Если D — некоторая область в Rn , то составляющие ее при t = 0 жидкие частицы в момент t занимают объем Dt = Nt (D ). Представим себе, что при t = 0 задана плотность ρ0 (a ) рассматриваемой жидкости. Поставим вопрос о том, как найти плотность жидкости ρ(x,t ) в момент t в предположении, что выполняется
Рис. 13
закон сохранения массы. К решению этого вопроса можно применить как эйлеров подход, так и лагранжев.
Лагранжев подход. В лагранжевой форме закон сохранения масс записывается в виде
ρ(x,t )dx = ρ0 (a )da. (24.5)
Это дифференциальная форма закона. Если вспомнить формулу преобразования объемных интегралов при замене переменных, придем к формуле
![]() (24.6)
(24.6)
в которой появляются матрица Якоби
![]()
и абсолютная величина ее определителя — якобиана. В результате приходим к уравнению неразрывности в лагранжевой форме
![]() ,
(24.7)
,
(24.7)
где a
= (Nt
)−1
x
; в автономном случае, когда v
= v
(x
) и не зависит от t
, можно записать![]() .
.
Якобиан![]() , на самом деле, положителен, поэтому и опущен знак модуля в (24.7). Действительно, J
≡ 1 при t
= 0 и не может обращаться в ноль (см. упражнение 2).
, на самом деле, положителен, поэтому и опущен знак модуля в (24.7). Действительно, J
≡ 1 при t
= 0 и не может обращаться в ноль (см. упражнение 2).
Заметим, что положительность функции ρ никак не использована, так что предыдущий вывод годится и для знакопеременной функции ρ. Например, он применим, когда ρ — плотность электрических зарядов, да и вообще, к произвольной функции ρ.
Эйлеров подход. Закон сохранения массы дает соотношение
Z Z
ρ(x,t )dx = ρ0 (a )da (24.8)
Dt D
для любой области D ⊂ Rn и ее образа Dt = Nt (D ) под действием эволюционного оператора Nt . Действительно, справа стоит масса жидкости, заключенной в области D , а слева — масса той же жидкости, занимающей в момент t область Dt .
Воспользуемся известной формулой дифференцирования по параметру интеграла по области, зависящей от этого параметра,
![]() (24.9)
(24.9)
Предполагается, что функция ρ достаточно регулярна, скажем, непрерывно дифференцируема по параметру t , а граница ∂Dt — гладкая и гладко зависит от t . Через vn = vn (x,t ), x ∈ ∂Dt , обозначена нормальная компонента скорости точки границы (иногда говорят «кажущаяся» скорость). Знак плюс у второго слагаемого соответствует выбору внешней нормали. Если граница области Dt (или ее часть) задана уравнением Φ(x,t ) = 0, причем
Φ(x,t ) < 0 при x ∈ Dt , то орт внешней нормали n можно представить в
![]() ∇
∇
виде n— в предположении, что нигде на границе знаменатель не
обращается в ноль. При этом vn дается формулой
![]() .
(24.10)
.
(24.10)
В случае области Dt можем написать: vn = v · n. Вообще же, формула (24.9) не требует знания движения частиц внутри области и поля их скоростей v . По-видимому, формула (24.9) Вам известна из курса механики сплошной среды, см. также книгу С.Л.Соболева [40].
Формула (24.9) имеет весьма наглядный смысл, она говорит, что масса жидкости изменяется лишь вследствие двух причин: изменения плотности внутри области со временем и наличия потока плотности внутрь области через границу.
Поскольку поле скорости v (x,t ) известно, поверхностный интеграл в
(24.9) можно преобразовать в объемный интеграл при помощи формулы Гаусса–Остроградского, в результате получим
![]() + div(
+ div(![]() .
(24.11)
.
(24.11)
Последнее равенство выполняется в силу (24.8). Напомню, что в декартовых координатах дивергенция поля v
= (v
1
,...,vn
) выражается в виде div![]() .
.
Очевидно, в качестве Dt можно выбрать произвольную область в Rn . Ее прообраз есть D = (Nt )−1 (Dt ). Но если интеграл от некоторой непрерывной функции по произвольной области равен нулю, то сама эта функция тождественно равна нулю. Если о функции известно лишь, что она интегрируема по Лебегу, то она при таком условии равна нулю почти всюду. Таким образом, из (24.11) следует уравнение неразрывности в эйлеровой форме , называемое также уравнением Лиувилля
![]() + div ρv
= 0.
(24.12)
+ div ρv
= 0.
(24.12)
Наш вывод представляет собой вполне очевидное обобщение вывода уравнения неразрывности в механике сплошной среды. Разумеется, для этого вывода физический смысл функции ρ, а также ее положительность, не имеют значения.
Можно также получить уравнение неразрывности (24.12) из лагранжева уравнения неразрывности (24.7). Для этого достаточно продифференцировать уравнение (24.7) по t (при фиксированном a ) и применить результат упражнения 2. Уравнение неразрывности получится в виде
![]() div v
= 0.
(24.13)
div v
= 0.
(24.13)
Здесь через![]() обозначена производная по t
при фиксированном a
, то есть при фиксированной жидкой частице. Она называется материальной производной
(а также субстанциональной
или индивидуальной
). В эйлеровых переменных материальная производная выражается формулой
обозначена производная по t
при фиксированном a
, то есть при фиксированной жидкой частице. Она называется материальной производной
(а также субстанциональной
или индивидуальной
). В эйлеровых переменных материальная производная выражается формулой
![]() .
(24.14)
.
(24.14)
Разумеется, уравнения (24.12) и (24.13) совпадают.
В общей теории дифференциальных уравнений в частных производных первого порядка (см., например, несколько старомодное, но весьма наглядное изложение в книге В.В. Степанова [41]) переход к лагранжеву описанию называется методом характеристик . Характеристики уравнения неразрывности (24.12) суть движение жидких частиц. Полученное выше лагранжево уравнение неразрывности (24.7) дает возможность свести решение задачи Коши для уравнения (24.12) с начальным условием ρ(x, 0) = ρ0 (x ) к решению задачи Коши (24.1), (24.2) для уравнения характеристик.
Ответ записывается в виде
![]() ,
(24.15)
,
(24.15)
где
Инвариантная мера и инвариантная плотность
В случае, когда v = v (x ), т.е. не зависит от t , особый интерес представляют решения уравнений Лиувилля, не зависящие от времени. Если такое решение ρ(x ) всюду неотрицательно: ρ(x ) ≥ 0 для всех x ∈ Rn , то его называют инвариантной плотностью . Если еще выполняется равенство
Z
ρ(x )dx = 1, (24.16)
Rn
то такую плотность называют нормированной или вероятностной , а также плотностью вероятности . Знание плотности вероятности ρ позволяет для любой наблюдаемой ϕ, то есть функции ϕ : Rn → R на фазовом пространстве системы, определить ее среднее значение равенством
![]() (24.17)
(24.17)
В теории вероятностей наблюдаемое ϕ носит название случайной величины
, а ее среднее ϕ![]() называется математическим ожиданием
данной случайной величины.
называется математическим ожиданием
данной случайной величины.
Инвариантная плотность определяет инвариантную меру µ(Ω) всякого измеримого по Лебегу множества Ω. Достаточно положить
µ![]() (24.18)
(24.18)
Свойства инвариантности выражается равенством
µ(Nt Ω) = µ(Ω). (24.19)
Замечу, что, во-первых, не всякая мера обладает плотностью, а лишь меры, абсолютно непрерывные по отношению к мере Лебега. Во-вторых, определение инвариантной меры естественно распространяется и на необратимое отображение N произвольного пространства с мерой (X, µ). В таком случае, однако, определение следует видоизменить: вместо (24.19), потребовать, чтобы выполнялось равенство
µ(N −1 Ω) = µ(Ω). (24.20)
При этом N −1 Ω означает полный праобраз измеримого относительно µ отображения N . Для обратимых отображений оба определения, конечно, эквивалентны.
Проблемам, связанным с инвариантными мерами динамических систем — потоков и каскадов, посвящена эргодическая теория динамических систем — одна из самых красивых и увлекательных областей математики; читайте книги [48, 31]. Подробнее об инвариантных мерах мы поговорим дальше.
Наиболее простой и весьма важный случай инвариантной плотности представится, если уравнение Лиувилля (24.12) допускает постоянное решение ρ = 1. Для этого, очевидно, нужно, чтобы выполнялось условие
div v = 0. (24.21)
Лагранжево уравнение неразрывности (24.7) в этом случае принимает вид
![]() .
(24.22)
.
(24.22)
В частности, это означает, что имеет место сохранение объемов
Vol Dt = Vol D (24.23)
для любой области D ⊂ Rn , причем Dt = Nt D . Жидкость, таким образом, в этом случае несжимаема (конечно, и нерастяжима). Сформулируем полученные результаты подробнее.
Предложение. Для того чтобы фазовая жидкость уравнения (24.1) была несжимаемой, и жидкие объемы не менялись со временем, необходимо и достаточно, чтобы поле скоростей v (x,t ) было соленоидально, то есть удовлетворяло уравнению (24.21). При этом уравнение Лиувилля принимает вид
![]() .
(24.24)
.
(24.24)
Функция ρ,такимобразом,являетсявэтомслучаеинтеграломуравнения (24.1).
Отсюда вытекает важное для статистической механики следствие: если векторное поле v = v (x ) соленоидально, а ρ(x ) — некоторый интеграл уравнения (24.1), то Φ(ρ) является решением уравнения Лиувилля (а также, конечно, и интегралом) при любой гладкой функции одного переменного Φ.
Стоит подчеркнуть, что, существование инвариантной плотности, как и существование нетривиального интеграла, есть весьма специальное свойство дифференциального уравнения — вообще говоря, дифференциальное уравнение в Rn инвариантных плотностей не имеет (см. упражнения 4 и 5).
Несжимаемость фазовой жидкости для гамильтоновой системы
В случае гамильтоновой системы (см. (20.14))
![]() (24.25)
(24.25)
уравнение Лиувилля (24.12) принимает вид
![]() .
(24.26)
.
(24.26)
Надеюсь, Вас не затруднит, что первые n переменных 2n -мерной системы (24.25) обозначаются через q 1 ,...,qn , а остальные — через p 1 ,...,pn .
Припомнив определение скобки Пуассона (20.38), можем записать уравнение (24.26) в компактной форме
![]() .
(24.27)
.
(24.27)
Физики обычно называют уравнением Лиувилля именно формулу (24.27) или (24.26). Это уравнение даже в общем случае гамильтониана H (q,p,t ) всегда имеет постоянное стационарное решение. Таким образом, плотность ρ = 1 инвариантна. Фазоваяжидкостьгамильтоновойсистемынесжимаема . Этот вывод полагается в основу статистической механики , которой мы скоро станем заниматься.
Вероятностная трактовка уравнения Лиувилля и инвариантной плотности
Рассмотрим снова задачу Коши (24.1)–(24.2). Предположим теперь, что a — случайная точка в Rn , и ее случайное распределение задается
25 Распределение Гиббса
плотностью вероятности ρ0 (a ). При этом считаем, что дальнейшее движение точки уже не является случайным, а происходит в соответствии с дифференциальным уравнением (24.1). Это означает, что плотность вероятности ρ(x,t ) в момент времени t удовлетворяет уравнению (24.7). Но из уравнения (24.7) следует, как мы уже установили, уравнение Лиувилля (24.12). Таким образом, мы приходим к важному выводу.
Если случайное распределение начальных точек a определяется плотностью вероятности ρ0 (a ), причем дальнейшее движение, когда точка a уже зафиксирована, определяется дифференциальным уравнением (24.1), то в момент времени t соответствующая плотность вероятности ρ(x,t ) есть решение уравнения Лиувилля (24.12) с начальным условием ρ(x, 0) = ρ0 (x ).
Упражнения
1. Пусть D — ограниченная область с гладкой границей S . Предполо-
![]()
жим, что гладкое в замкнутой области D поле v (x,t ) для любого t касается поверхности S (имеет на S нулевую нормальную компоненту). Докажите, что в этом случае задача Коши (24.1)–(24.2) глобально однозначно разрешима. Докажите также, что в случае неограниченной области D это утверждение становится уже неверным, но будет все-таки верным, если на бесконечности поле v растет не быстрее, чем линейно.
2. Применяя формулу дифференцирования определителя по параметру, докажите, что якобиан![]() , где x
= x
(a,t
) — решение задачи
, где x
= x
(a,t
) — решение задачи
Коши (24.1)–(24.2), удовлетворяет уравнению
![]()
3. Докажите формулу
div ρv = ρdiv v + v · ∇ρ
и установите совпадение уравнений (24.12) и (24.13). 4. Докажите, что скалярное уравнение
x ˙ = −x
не имеет инвариантной плотности.
5. Какими свойствами должен обладать спектр n × n матрицы A , чтобы линейное дифференциальное уравнение x ˙ = Ax в Rn допускало инвариантную плотность. (Ответ покажет Вам, сколь редким свойством является наличие инвариантной плотности.)
25. Распределение Гиббса
Поскольку гамильтониан H есть интеграл гамильтоновой системы (?? ), а фазовая жидкость гамильтоновой системы несжимаема, то H = H (q,p ) является решением уравнений Лиувилля. Тогда и функция ρ = ρ(H ) = ρ(H (q,p )) также удовлетворяет уравнению Лиувилля. Потребуем, чтобы инвариантная плотность ρ была вероятностной, то есть, чтобы выполнялось равенство Z
ρdx = 1. (25.1)
R2n
Здесь dx = dq dp — элемент объема фазового пространства. Возможно, что конфигурационным пространством системы оказывается не все Rn , а область D ⊂ Rn . Тогда фазовое пространство есть D ×Rn , и вместо (25.1) должно быть выполнено
Z
ρdx = 1. (25.2)
D ×Rn
При столь слабом ограничении существует обычно бесконечно много инвариантных плотностей вида ρ = ρ(H ). Сейчас мы опишем принцип выбора единственной инвариантной плотности посредством предположения о максимальном хаосе в системе. Следующий ниже вывод появился лишь в середине XX-го века, сам Гиббс рассуждал иначе [9].
Дальше для определенности считаем, что фазовое пространств есть R2n .
Энтропия вероятностной системы. Рассмотрим систему, которая может принимать n состояний, причем вероятность j -го состояния есть pj . Энтропия S этой системы по определению дается равенством
![]() .
(25.3)
.
(25.3)
Если pj = 0 для некоторого j , то будем считать, что pj lnpj = 0, и это слагаемое в (25.3) можно пропустить.
Энтропия является мерой беспорядка (хаоса, неопределенности в системе), лишь постоянным множителем log 2 e она отличается от информации по Клоду Шеннону , поскольку в теории информации приняты двоичные логарифмы.
Естественным обобщением (25.3) на случай непрерывного распределения с плотностью ρ служит равенство
![]() (25.4)
(25.4)
В случае условия (25.2) следует интегрировать по D × Rn .
Выберем среди всех инвариантных плотностей ρ(H ) ту, которая доставляет максимум энтропии S при дополнительном условии постоянства средней энергии системы
![]() (25.5)
(25.5)
![]()
Здесь E — заданная средняя энергия.
Мы пришли к задаче на условный экстремум. Решаем ее хорошо известным Вам методом Лагранжа. Вводим гладкую деформацию ρ ˜(x, ε) искомой функции ρ и определяем соответствующую этой деформации вариацию
![]() .
.
Варьируя функционал S и полагая δS = 0, получаем равенство
Z
(lnρ + 1)δρdx = 0. (25.6)
R2n
Это равенство выполняется, однако, не для произвольных вариаций δρ, а лишь для таких, которые удовлетворяют дополнительным условиям, выводимым посредством варьирования условий связи (25.1) и (25.5)
Z
δρdx = 0, (25.7)
R2n
Z
H δρdx = 0. (25.8)
R2n
Умножая (25.7) на постоянную λ, а равенство (25.8) — на µ, и складывая с
(25.6), придем к равенству
Z
(lnρ + 1 + λ + µH )δρdx = 0. (25.9)
R2n
При этом множители Лагранжа λ и µ можно считать выбранными таким образом, что условия связи (25.1) и (25.5) выполнены, так что равенство (25.9) выполняется уже для произвольной функции δρ. Отсюда следует равенство
lnρ + 1 + λ + µH = 0. (25.10)
В итоге приходим к распределению Гиббса
![]() .
(25.11)
.
(25.11)
Мы всего лишь изменили обозначения констант, положив A = e −1− λ ,
1
B
= ![]() . Постоянные A
и B
должны быть найдены из условий связи (25.1)
. Постоянные A
и B
должны быть найдены из условий связи (25.1)
µ и (25.5). В частности, из условия нормировки (25.1) выводим
![]() (25.12)
(25.12)
Равенство (25.5) перепишется теперь в виде
![]() (25.13)
(25.13)
Сделаем теперь обычные для статистической механики предположения о гамильтониане H . Разумеется, в каждом конкретном случае их следует проверять перед тем, как применять дальнейшие выводы статистической механики.
1◦ . Функция H ограничена снизу. Поскольку гамильтониан определен с точностью до произвольной аддитивной постоянной, мы можем и будем считать, что H (p,q ) ≥ 0 всюду.
2◦ . Интеграл (25.12) сходится при любом B > 0.
3◦ . Функция E (B ) на луче B > 0 строго монотонно возрастает, изменяясь от нуля (при B → 0) до +∞ (Рис. 14)
![]()
Из предположения 3◦ следует, что при любом заданном E > 0 из уравнения (25.13) однозначно находятся значения B . Тогда P (B ) определяется однозначно равенством (25.12). Замечу, что в проблемах, связанных с фазовыми переходами , встречаются гамильтонианы, для которых такой однозначности нет.
Энтропия S , определенная равенством (25.4), также может быть выражена как функция от B . Подставляя в это равенство выражение (25.11) для
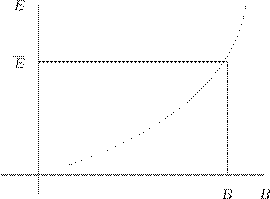
Рис. 14
ρ, получаем
![]() .
(25.14)
.
(25.14)
Теперь заметим, что E (B ) можно выразить через P (B ). Действительно, дифференцируя по B интеграл P (B ) в (25.12), получаем
![]() .
(25.15)
.
(25.15)
Отсюда находим искомое выражение E (B )
![]() .
(25.16)
.
(25.16)
Мы пришли к важному выводу: основные в данной теории функции энергия E (B ) и энтропия S (B ) выражаются через единственную функцию P (B ):
![]() (25.17)
(25.17)
Это выражение называется статистическим интегралом .
В приложениях статистической механики к конкретным системам главная часть работы как раз и состоит в вычислении и исследовании статистического интеграла. Это может даже показаться курьезным, так как P (B ) в теории играет чисто служебную роль, определяя нормирующий множитель. В порядке нравоучения прикладным математикам замечу, что теоретики вообще очень легко в своих рассуждениях переходят, например, к нормированному базису. Это «всего лишь» операция умножения заданных функций на константы. Реализуя соответствующие алгоритмы в программах для ЭВМ, не следует обычно воспроизводить такие операции буквально — вычисление этих нормирующих множителей может оказаться весьма трудоемким и во многих случаях существенно увеличить время вычислений.
Физический смысл параметра B . Его невозможно понять, рассматривая лишь одну систему. Пусть заданы две системы с гамильтонианами H 1 = H 1 (q 1 ,p 1 ) и H 2 = H 2 (q 2 ,p 2 ). Предположим, что они независимы и составляют вместе одну систему с гамильтонианом H = H 1 + H 2 . При этом H = H (q 1 ,p 1 ,q 2 ,p 2 ) — функция, определенная на декартовом произведении фазовых пространств двух подсистем. Первой системе соответствует параметр B 1 , а второй — параметр B 2 . Ввиду предположенной независимости двух подсистем, распределение Гиббса для объединенной системы должно иметь вид
(25.18)
![]() .
.
С другой стороны, поскольку постулируется универсальность распределения Гиббса, должно иметь место равенство
![]() .
(25.19)
.
(25.19)
Поскольку выражения (25.18) и (25.19) должны совпадать, получается равенство
![]() ,
(25.20)
,
(25.20)
которое очевидно выполняется при B 1 = B 2 = B , причем A определяется по формуле
A = 1/P (B ), P (B ) = P 1 (B )P 2 (B ). (25.21)
Нетрудно доказать, что верно и обратное, см. ниже упражнение 2.
Таким образом, выяснилось, что при объединении двух систем в одну соответствующие параметры B 1 и B 2 уравниваются. Но точно так же ведет себя температура при вступлении двух тел в тепловой контакт. Если их
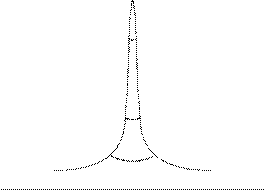
Рис. 15
температуры различны, то начинается процесс теплообмена, и в результате температура выравнивается. Это наводит на мысль отождествить параметр B
с температурой. Параметр B
имеет размерность энергии, поскольку аргумент![]() у экспоненты в распределении Гиббса должен быть безразмерным. Становится понятным, что температура T
есть по своей природе некоторая энергия, а для параметра B
справедливо выражение
у экспоненты в распределении Гиббса должен быть безразмерным. Становится понятным, что температура T
есть по своей природе некоторая энергия, а для параметра B
справедливо выражение
B = kT, (25.22)
где k — постоянный коэффициент, зависящий лишь от выбора единиц измерения энергии и температуры. В частности, измерения дали для постоянной Больцмана k значение
k
= 1.
38 · 10−16
![]() эрг
.
(25.23) град
эрг
.
(25.23) град
Мы можем теперь окончательно записать распределение Больцмана в виде
![]() .
(25.24)
.
(25.24)
Постоянная Больцмана k , как видим, очень мала. Поэтому распределение Гиббса (25.24) оказывается весьма острым, δ-образным (при k → 0 оно стремится к δ-распределению в смысле сходимости обобщенных функций), см. Рис. 15
Плотность ρ максимальна около точки минимума гамильтониана H и очень быстро спадает при отклонении от этой точки (куда быстрее, чем на рисунке!). Поэтому средние, вычисленные относительно этой плотности, оказываются очень близкими к значениям соответствующих функций в точке минимума гамильтониана, а флуктуации в обычных условиях весьма малы. Точнее говоря, большие флуктуации весьма маловероятны.
Далее мы применим изложенные здесь общие результаты к статистической теории идеального газа и твердого тела.
26. Статистическая механика идеального газа
Рассмотрим систему n частиц, двигающихся в пространстве R3 и не взаимодействующих между собой. Обозначим массу i -частицы через mi . Пусть xi — ее положение в R3 , x ˙i — ее скорость. Тогда импульс есть pi = mi x ˙i , а гамильтониан Hi — ее кинетическая энергия, выраженная через импульс
![]() .
(26.1)
.
(26.1)
Поскольку частицы не взаимодействуют, гамильтониан системы H есть сумма частных гамильтонианов
![]() .
(26.2)
.
(26.2)
Далее будем считать, что рассматриваемые частицы двигаются в области D ⊂ R3 , имеющей конечный объем V . Таким образом, конфигурационное пространство данной системы есть Dn = D × ... × D , а фазовое пространство есть (D × R3 )n = Dn × R3n . Мы уже знаем, что для дальнейшего исследования достаточно вычислить статистический интеграл P (B ), где B = kT .
Вычислениестатистическогоинтеграла. В случае гамильтониана (26.2) имеем
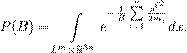 (26.3)
(26.3)
где dx = dq 1 ...dqn dp 1 ...dpn — элемент объема в фазовом пространстве.
Заметим, что подынтегральное выражение не зависит от qi , i = 1,...,n , и представляется в виде произведения множителей, каждый из которых зависит лишь от одного из импульсов pi . Отсюда следует, что интеграл (26.3) можно представить в виде
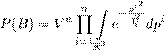 ,
γi
2
= 2mi
B.
(26.4)
,
γi
2
= 2mi
B.
(26.4)
| Общая идея этой выкладки заключается в применении формулы |
|
| Z Z Z f (x )g (y )d µ(x )d ν(y ) = f (x )d µ(x ) · g (y )d ν(y ), |
(26.5) |
X ×Y X Y
которая справедлива для любой пары пространств с мерой (X, µ) и (Y, ν) и обобщается на любое количество таких пространств. Формула (26.4) выражает P (B ) через произведение однотипных интегралов вида
![]() (26.6)
(26.6)
где dp = dp 1 dp 2 dp 3 — элемент объема в R3 . Еще раз применяя ту же идею, получаем
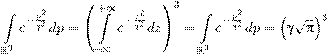 .
(26.7)
.
(26.7)
Здесь использовано хорошо известное значение гауссова интеграла вероятности при γ > 0:
![]() .
(26.8)
.
(26.8)
Применяя формулу (26.7), находим интеграл (26.4) в виде
![]() .
(26.9)
.
(26.9)
Запишем этот результат в виде
![]() ,
(26.10)
,
(26.10)
где не очень существенная константа C определяется равенством
![]() .
(26.11)
.
(26.11)
Применяя формулу (25.16), находим зависимость энергии от параметра B
(по сути, от температуры) в виде
![]() (26.12)
(26.12)
Мы пришли к довольно удивительному выводу, что энергия E зависит лишь от температуры и не зависит от объема V
![]() (26.13)
(26.13)
Еще удивительнее, однако, тот факт, что формула (26.13) великолепно подтверждается экспериментом.
Итак, средняя внутренняя энергия идеального газа — системы n невзаимодействующих частиц — линейно зависит от температуры T и от числа частиц, а от объема не зависит.
Примечательно, что энергия E не зависит и от масс частиц, то есть идеальный газ может быть смесью любого числа различных компонент. Допускается даже, что каждая компонента может быть представлена лишь одной молекулой.
Формула (26.13) позволяет найти теплоемкость
идеального газа. Вообще, теплоемкость c
определяется как производная ![]() . Чтобы избежать недоразумений, сразу скажу, что в общей ситуации теплоемкость не является функцией состояния
, а является, скорее, функцией процесса. Например, приходится различать теплоемкости при постоянном давлении (cp
) и при постоянном объеме (cV
). В данном случае все проще. Дифференцируя равенство (26.13), получаем
. Чтобы избежать недоразумений, сразу скажу, что в общей ситуации теплоемкость не является функцией состояния
, а является, скорее, функцией процесса. Например, приходится различать теплоемкости при постоянном давлении (cp
) и при постоянном объеме (cV
). В данном случае все проще. Дифференцируя равенство (26.13), получаем
![]() (26.14)
(26.14)
Мы пришли к выводу, что теплоемкость идеального газа зависит лишь от числа частиц и не зависит ни от объема, ни от температуры.
Средняя кинетическая энергия частицы.
Вычислим среднюю кинетическую энергию j
-ой частицы. Это означает, что нужно найти математическое ожидание наблюдаемой![]() . Напомню, что для любой наблюдаемой ϕ = ϕ(q,p
) ее среднее определяется равенством
. Напомню, что для любой наблюдаемой ϕ = ϕ(q,p
) ее среднее определяется равенством
![]() (26.15) Соответственно получаем
(26.15) Соответственно получаем
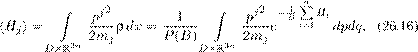
Это выражение, как и интеграл, определяющий P (B ), можно представить в виде произведения интегралов двух типов. Интегралы по области D от 1 дают множитель V n . Остальные интегралы вычисляются по R3 , причем подынтегральное выражение в i -ом множителе зависит лишь от pi . Теперь заметим, что, за исключением j -го множителя в интеграле (26.16), все остальные множители — такие же, как и в интеграле (26.3). Чуть поразмыслив, мы можем написать формулу
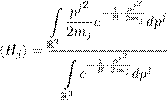 .
(26.17)
.
(26.17)
Знаменатель мы уже вычисляли. Он представляется в виде произведения трех гауссовых интегралов, что дает равенство
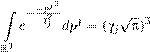 ,
γj
2
= 2mj
B
= 2mj
kT.
(26.18)
,
γj
2
= 2mj
B
= 2mj
kT.
(26.18)
Числитель в (26.17) сначала разбиваем на сумму трех интегралов в соответствии с равенством![]() . Эти слагаемые получаются друг из друга циклической перестановкой индексов компонент
. Эти слагаемые получаются друг из друга циклической перестановкой индексов компонент![]() , а потому одинаковы. Таким образом, имеем
, а потому одинаковы. Таким образом, имеем
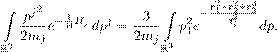 (26.19)
(26.19)
Мы еще заменили pj
на p
— переменную интегрирования можно обозначить как угодно. вещественной оси. Из них два гауссовы, и их произведение естьИнтеграл (26.19) представим в виде произведения трех интегралов по(γj
√
π![]() )2
.
)2
.
Третий множитель имеет вид (p 1 заменяем на z )
![]() .
(26.20)
.
(26.20)
Подставляя полученные значения интегралов в (26.17), имеем
![]() .
(26.21)
.
(26.21)
Окончательно получаем
![]() (26.22)
(26.22)
Мы пришли к важному выводу: средняя кинетическая энергия движения частицы (молекулы) есть температура идеального газа — с точностью до множителя
![]() , отвечающего переходу от механических единиц измерения к тепловым.
, отвечающего переходу от механических единиц измерения к тепловым.
Существенно также, что правая часть в (26.22) не зависит от массы частицы .
И еще один интересный вывод можно сделать, сопоставляя формулы (26.22) и (26.13). Мы видим, что энергия равномерно распределяется по частицам независимо от их масс
. Более того, коэффициент 3 в (26.22) отнюдь не случаен — это размерность пространства R3
, число степеней свободы одной частицы. Фактически мы уже использовали то обстоятельство, что каждая из компонент![]() вносит один и тот же вклад в среднюю кинетическую энергию. (См. также упражнение 3).
вносит один и тот же вклад в среднюю кинетическую энергию. (См. также упражнение 3).
Это частный случай довольно общего закона статистической механики о равнораспределении (equipartition) энергии по степеням свободы. Хотя этот принцип и не всегда выполняется, он имеет немалое эвристическое значение. В том случае, когда гамильтониан представляет собой сумму квадратов параметров, определяющих состояние системы, он превращается в строгую теорему, один частный случай ее мы фактически доказали.
Дальше мы рассмотрим и другие случаи, когда этот принцип работает.
Формула (26.22) является основой (ни более, ни менее!) механической теории теплоты, объясняя механический смысл главной термодинамической величины — температуры.
Флуктуация энергии.
Статистическая механика ставит и решает также принципиально новые задачи, позволяя, в частности, исследовать флуктуации. После того как вычислено математическое ожидание, естественно заняться дисперсией
случайной величины![]() . Согласно определению, дисперсия D(Hj
) дается формулой
. Согласно определению, дисперсия D(Hj
) дается формулой
![]()
D(Hj ) = D(Hj − Hj )2 E . (26.23)
Отсюда непосредственно следует формула
![]() D(Hj
) = DHj
2
E
− H
2
j
.
(26.24)
D(Hj
) = DHj
2
E
− H
2
j
.
(26.24)
Первое слагаемое вычисляем при помощи приема, который был применен
![]()
при вычислении среднего Hj . Имеем (сравните с формулой (26.17))
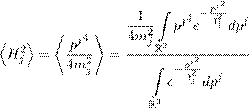 .
(26.25)
.
(26.25)
![]()
Мы уже знаем, что знаменатель в этой формуле есть (γj √ π)3 . Для вычисления числителя вводим сферические координаты (r, ϕ, θ) с центром в нуле и замечаем, что подынтегральное выражение не зависит от ϕ и θ. Поэтому числитель выражается формулой
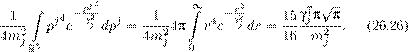
Множитель 4π — площадь единичной сферы (появился после интегрирования по ϕ и θ). Последний интеграл посредством интегрирования по частям сводится к гауссову и легко вычисляется, что и сделано (проверьте!). Подстановка в (26.25) дает равенство
![]() .
(26.27)
.
(26.27)
Теперь из (26.24) получаем
![]() .
(26.28)
.
(26.28)
Средняя квадратичная флуктуация определяется как корень квадрат-
![]()
ный из дисперсии, в данном случае это p D(Hi ). Ее отношение к математическому ожиданию назовем относительной (среднеквадратичной) флуктуацией . Вычисляя ее, получаем
![]() .
(26.29)
.
(26.29)
Как видим, это довольно большая величина: ![]() . Выходит,
. Выходит,
вполне можно ожидать изменения кинетической энергии частицы-молекулы на 80%. Не противоречит ли это нашему заявлению, что флуктуации макроскопических величин весьма малы? Нет, не противоречит, потому что энергия одной молекулы не является макроскопической величиной. Если мы рассмотрим энергию Em выбранного произвольного набора m частиц, то согласно принципу равнораспределения найдем, что
![]() (26.30)
(26.30)
Этот результат не зависит, конечно, от того, какие именно m частиц выбраны. Далее заметим, что для независимых случайных величин, каковыми являются H 1 ,...,Hm , дисперсия суммы равняется сумме дисперсий
![]() .
(26.31)
.
(26.31)
На самом деле, для справедливости этой формулы достаточно несколько более слабого свойства случайных величин, чем независимость, см. упражнение 4.
Применяя формулу (26.28), из (26.31) выводим
![]() (26.32)
(26.32)
Соответственно для среднеквадратичной флуктуации получаем
![]() (26.33)
(26.33)
27 Метод Лапласа асимптотической оценки интегралов
![]()
а для относительной среднеквадратичной флуктуации
![]() .
(26.34)
.
(26.34)
Из этой формулы видим, что для макроскопических количеств газа, скажем, при m ∼ 1020 относительная флуктуация очень мала, вряд ли даже может быть непосредственно измерена в опыте.
27. Метод Лапласа асимптотической оценки интегралов
Малость постоянной Больцмана наводит на мысль применить для вычисления средних (по формуле (26.15)) асимптотический метод Лапласа [42]. Сейчас я, не вдаваясь в доказательства, приведу вывод основных формул метода. Затем мы их применим к задачам статистической механики. Рассмотрим интеграл
![]() (27.1)
(27.1)
Здесь δ — малый положительный параметр, и нас интересует асимптотическое поведение этого интеграла при δ → 0. Будем предполагать, что функция H (x ) — достаточно гладкая, ограничена снизу и растет на бесконечности, например, при больших x имеется оценка снизу
H (x ) ≥ C |x |α , (27.2)
где C и α — известные положительные константы.
Относительно функции ϕ(x ) также предположим, что она гладкая и растет на бесконечности не быстрее, чем степенным образом, так что
|ϕ(x )| ≤ C 1 |x |β , (27.3)
где C 1 и β — известные положительные константы. В принятых условиях интеграл (27.1) существует при любом δ > 0 (возможны, конечно, и иные условия).
Предположим, что x 0 — точка строгого абсолютного минимума функции H . Более того, допустим, что разложение Тейлора функции H в окрестности точки x 0 имеет вид
![]() (27.4)
(27.4)
причем опущены члены порядка 3 и выше, а второй дифференциал положительно определен . В координатах формула (27.4) запишется в виде
![]()
Дальше нам понадобится разложение функции ϕ
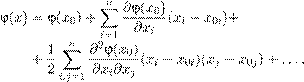 (27.6)
(27.6)
Для вывода асимптотической формулы Лапласа сначала устанавливается, что главный член асимптотики не изменится, если в (27.1) перейти от интегрирования по всему пространству Rn к интегрированию по любой окрестности точки x 0 фиксированного, не зависящего от δ размера.
Это значит, что мы собираемся выбросить из интеграла (27.1) величину
![]() (27.7)
(27.7)
где η — произвольно фиксированное положительное число. Применяя неравенства (27.2) и (27.3), получим оценку
![]() (27.8)
(27.8)
Положим |x − x 0 | = r . Заметим, что dx = rn −1 drdS , где dS — элемент площади единичной сферы Sn −1 с центром в точке x 0 . Поскольку подынтегральное выражение в (27.8) зависит только от r , из (27.8) следует неравенство
![]() (27.9)
(27.9)
где σn −1 есть площадь сферы Sn −1 . Сделаем в последнем интеграле замену r = δ 1/ α ρ. В результате получим
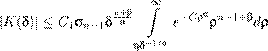 .
(27.10)
.
(27.10)
Интеграл в этом неравенстве при δ → 0 затухает быстрее δ q при любом q > 0. Вы легко убедитесь в этом, применив правило Лапиталя для вычисления предела отношения нитеграла и величины δ q при δ → 0. Получается, что для любого p > 0 имеет место предельное соотношение
![]() .
(27.11)
.
(27.11)
Этот результат справедлив при любом η > 0, лишь бы число η было фиксировано и не зависело от δ.
Положим J(δ) = J1 (δ) + K (δ), где
![]() (27.12)
(27.12)
Дальше мы увидим, что интеграл J 1 (δ) допускает степенную асимптотику при δ → 0, которая к тому же от величины η не зависит. Ввиду (27.11), интеграл J(δ) имеет ту же самую асимптотику, что и J1 (δ).
Пользуясь произволом в выборе η, полагаем его столь малым, чтобы можно было воспользоваться для приближения функций H и ϕ их разложениями Тейлора (27.5) и (27.6). Ограничиваясь первыми членами, в результате получим
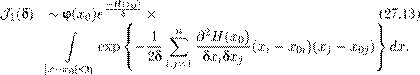
Несложное обоснование того факта, что отбрасывание остаточного члена не влияет на главные члены асимптотики, опущу.
Обозначим через A оператор Гесса функции H в точке x 0 :
![]() .
(27.14)
.
(27.14)
Применяя это обозначение и вновь переходя в (27.13) к интегрированию по Rn , приходим к асимптотике
![]() (27.15)
(27.15)
Мы еще сделали замену x − x 0 → x в последнем интеграле. Неизменность степенной асимптотики при переходе от интегрирования по шару к интегрированию по всему Rn доказывается точно также, как и выше при выводе оценки интеграла K (δ).
Следующий шаг состоит в том, что в последней формуле мы возвращаемся к интегрированию по Rn . Конечно, нужно доказать, что добавление интеграла по внешнему шару не меняет главного члена асимптотики. Предполагая, что это сделано, придем к асимптотике
![]() (27.16)
(27.16)
Здесь для вычисления последнего интеграла применяется следующий стандартный прием. Квадратичную форму можно ортогональным преобразованием привести к сумме квадратов: сделать замену x = Uy , так что в новых переменных
![]() .
(27.17)
.
(27.17)
Здесь λ1 ,..., λn — собственные числа оператора Гесса A (27.14), которые, по предположению, положительны. Ортогональный оператор U сохраняет объемы, так что |detU | = 1. Поэтому dx = dy , и мы приходим к равенству
![]() (27.18)
(27.18)
Последний интеграл представляется в виде произведения гауссовых интегралов
![]() .
(27.19)
.
(27.19)
В результате получаем
![]() .
(27.20)
.
(27.20)
Мы использовали тот факт, что detA = λ1 · ... · λn .
Теперь окончательно приходим к асимптотике при δ → 0:
![]() .
(27.21)
.
(27.21)
В случае, когда ϕ(x 0 ) 6= 0, это асимптотическое равенство означает, что при δ → 0 отношение левой и правой частей выражения (27.21) стремится к единице.
Случай ϕ(x 0 ) = 0. Если же ϕ(x 0 ), то формула (27.19) говорит лишь, что J(δ) → 0 при δ → 0. Мы можем уточнить асимптотическое поведение интеграла J(δ), прибавляя следующие члены разложения функции ϕ(x ). Нетрудно видеть, что члены первой степени на дают вклада в главный член асимптотики. Если привлечь члены второй степени и провести выкладки, аналогичные предыдущим, то получим
![]() (27.22)
(27.22)
где B — матрица Гесса функции ϕ
![]() (27.23)
(27.23)
и через нее выражается второй дифференциал функции ϕ: d 2 ϕ(x 0 )ξ 2 = (B ξ, ξ), где ξ ∈ Rn .
Вычислим интеграл
![]() (27.24)
(27.24)
Снова сделаем замену переменной x = Uy , приводящую форму (Ax,x ) к сумме квадратов, см. (27.17). Интеграл S (δ) запишется тогда в виде
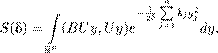 (27.25) Пусть ϕ1
,...,
ϕn
— ортонормальная система собственных векторов оператора A
, так что A
ϕj
= λj
ϕj
, причем собственные значения λj
все положительны. Введем векторы ψj
, полагая ψj
= U
−1
ϕj
. Произвольный вектор x
∈ Rn
допускает разложение
(27.25) Пусть ϕ1
,...,
ϕn
— ортонормальная система собственных векторов оператора A
, так что A
ϕj
= λj
ϕj
, причем собственные значения λj
все положительны. Введем векторы ψj
, полагая ψj
= U
−1
ϕj
. Произвольный вектор x
∈ Rn
допускает разложение
![]() .
(27.26)
.
(27.26)
| Соответственно |
n y = U −1 x = X yj ψj , |
(27.27) |
j =1
и интеграл (27.25) запишется в виде
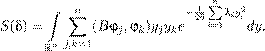 (27.28)
(27.28)
Теперь заметим, что интегралы от слагаемых, отвечающих индексам j 6= k , исчезают. Это происходит потому, что соответствующий интеграл по Rn выражается в виде произведения одномерных интегралов, и при этом целых два множителя — интегралы по yj и yk — нулевые. Это интегралы от нечетных функций. Выражение для S (δ) упрощается и принимает вид
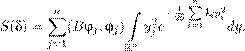 (27.29)
(27.29)
С такими интегралами мы уже умеем обращаться. Действуя так же как при вычислении интеграла (26.16), получаем
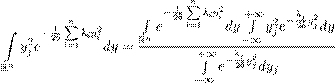 .
(27.30)
.
(27.30)
Для вычисления первого множителя в числителе воспользуемся формулой (27.20). В результате получаем
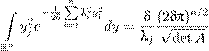 .
(27.31)
.
(27.31)
Окончательно приходим к формуле
![]() .
(27.32)
.
(27.32)
Замечу, что для квадратичных гамильтонианов, с которыми мы до сих пор и имели дело, занимаясь идеальным газом и твердым телом, полученные здесь асимптотические равенства (27.21) и (27.32) превращаются в точные.
Имеется и другой, идейно даже лучший способ вычисления интеграла (27.24). Ради краткости опустим коэффициент ![]() в следующих выкладках
в следующих выкладках
(в окончательном результате заменим потом![]() ). Воспользуемся очевидным равенством
). Воспользуемся очевидным равенством
![]() (27.33)
(27.33)
Для вычисления последнего интеграла воспользуемся формулой (27.20) при 2δ = 1. Имеем
![]() .
(27.34)
.
(27.34)
Заметим, что при малых t оператор A − tB остается положительно определенным, так что наши действия законны. Отметим формулу (см. ниже упражнения 5 и 6)
![]() .
(27.35)
.
(27.35)
При помощи (27.34) и (27.35) получаем
![]() .
(27.36)
.
(27.36)
Возвращаясь к (27.22), с применением (27.36), получаем асимптотическую формулу для интеграла J(δ), определенного равенством (27.1) в случае
ϕ(x
0
) (не забывая заменить![]()
![]() sp(A
−1
B
).
(27.37)
sp(A
−1
B
).
(27.37)
Упражнения
1. Докажите, что максимум энтропии вероятностной системы с n
состояниями достигается при![]() . При этом S
= lnn
.
. При этом S
= lnn
.
2. Докажите, что равенство (25.21) при постоянных B 1 , B 2 , B , A может выполняться для всех p 1 , q 1 , p 2 , q 2 , лишь в случае B 1 = B 2 = B , если оба гамильтониана нетривиальны (не сводятся к постоянным).
3. Докажите, что для идеального газа выполняется равенство
![]() (27.38)
(27.38)
4. Пусть ξ1 ,..., ξm — случайные величины (т.е. функции на пространстве (X, µ) с вероятностной мерой µ). Если условие hξi ξj i = 0 выполнено всякий раз, когда i 6= j , то справедлива формула для дисперсий
![]() .
.
5. Докажите, что для любого линейного оператора B : Rn → Rn справедлива формула
![]()
Для этого припомните, как выводится формула Лиувилля для вронкскиана, и примените правило дифференцирования определителей.
6. Докажите, что если A и B — линейные операторы в Rn , причем, оператор A обратим, то справедлива формула
![]() .
.
Здесь нужно воспользоваться результатом предыдущего упражнения и тем фактом, что определитель произведения операторов равен произведению определителей операторов.
7. Вычислите интеграл
Z
(Bx,x )2e −(Ax,x )dx,
Rn
где A — положительно определенный оператор.
28 Градиентные системы
8. Докажите равенство
Z
(Bx,x )(Cx,x )e −(Ax,x ) dx
Rn
= detA hsp(A −1 B )sp(A −1 C ) − sp(A −1 BA −1 C )i
9. Докажите непосредственно, что выражения (27.28) и (27.36) совпадают.
28. Градиентные системы
Градиентное уравнение в конечномерном евклидовом, или гильбертовом пространстве H имеет вид
x ˙ = grad S (x ) (28.1)
с известной, достаточно гладкой функцией S , называемой потенциалом градиентного уравнения. Поле G (x ) называется потенциальным , если его можно представить в виде G (x ) = grad S (x ) с некоторой функцией S (x ). Основное свойство такого уравнения состоит в том, что для всякого решения x (t ) функция S (x (t )) монотонно возрастает. Для доказательства достаточно вычислить производную S ˙ в силу заданного уравнения движения (28.1). В результате получаем равенство
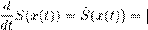 grad S
(x
(t
))|2
≥ 0.
(28.2)
grad S
(x
(t
))|2
≥ 0.
(28.2)
Таким образом, S есть возрастающая функция Ляпунова уравнения (28.1).
Второе начало термодинамики состоит в том, что энтропия замкнутой термодинамической системы со временем возрастает. Поэтому можно сказать, что градиентные уравнения описывают поведение систем типа замкнутых термодинамических, причем потенциал S играет роль энтропии. К этому можно добавить, что формула (28.2) вместе с ее интерпретацией, сохраняется и для более общей системы вида
| x ˙ = grad S (x ) + F (x ), если для всех x ∈ H выполнено соотношение |
(28.3) |
| (grad S (x ),F (x )) = 0. |
(28.4) |
Равенство (28.4) означает, что векторные поля grad S и F образуют косимметрическую пару. Интересный класс уравнений вида (28.3) представляют дифференциальные уравнения
x ˙ = grad S (x ) + A (x )grad S (x ), (28.5)
где линейный оператор A (x ) может зависеть от x нелинейно, однако для каждого x ∈ H является кососимметричным. Напомню, что оператор A : H → H называется кососимметричным, если для всех x ∈ H выполнено равенство (Ax,x ) = 0. В этом случае A ∗ = −A .
Хороший пример уравнения (28.5) дает уравнение в R 3 вида
x ˙ = grad S (x ) + ω(x ) ∧ grad S (x ). (28.6)
Обобщением уравнения (28.5) может служить уравнение
x ˙ = grad S (x ) + Γ(x )grad S (x ), (28.7)
где Γ(x ) есть гироскопический оператор, равенство (Γ(x )ξ, ξ) = 0 выполняется для всех x ∈ H , ξ ∈ H .
Дальше мы рассмотрим некоторые эффекты, производимые дополнительным слагаемым F в уравнении (28.3).
Восстановление потенциала по заданному полю
Если задано автономное дифференциальное уравнение
x ˙ = G (x ) (28.8)
в H , то несложно проверить является ли оно градиентным. Наиболее прямой путь состоит в следующем (см. также упражнения 2–4). Допустим, что G (x ) = grad S (x ). Фиксируем точку x 0 ∈ H , и пусть x — произвольная точка пространства H . Рассмотрим отрезок, соединяющий точки x 0 и x , т.е. множество точек x 0 + ε(x − x 0 ), где ε ∈ [0, 1]. Далее положим x − x 0 = u . Имеем
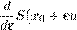 ) = (grad S
(x
0
+ εu
),u
).
(28.9)
) = (grad S
(x
0
+ εu
),u
).
(28.9) 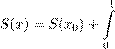 (grad S
(x
0
+ εu
),u
)d
ε (28.10)
(grad S
(x
0
+ εu
),u
)d
ε (28.10)
Интегрируя по ε выводим равенство
Если известно, что поле G потенциально, то потенциал дается формулой
![]() (28.11)
(28.11)
Остается проверить, является ли в действительности построенная функция S (x ) потенциалом данного поля G (x ). Дифференцируя равенство (28.11), получаем
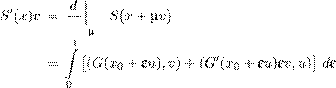
![]() (28.12)
(28.12)
для любого вектора v ∈ H . Это равенство можно также записать в виде
![]() .
(28.13)
.
(28.13)
Мы использовали здесь тот факт, что линейный функционал (в частности, операцию скалярного умножения на вектор v ) можно вносить под знак интеграла.
Отсюда видно, что отвечающее потенциалу S поле имеет вид
grad![]() .
(28.14)
.
(28.14)
Напомню, что градиент grad S (x ) определяется требованием, чтобы для всех v ∈ H выполнялось равенство
(grad S (x ),v ) = S 0 (x )v. (28.15)
В итоге, получается, что поле G (x ) потенциально, и построенная функция S (x ) является потенциалом, в том и только в том случае, когда для любых x 0 и x , принадлежащих H , выполняется равенство:
![]() .
(28.16)
.
(28.16)
В конкретных задачах обычно бывает проще, не используя эту формулу, непосредственно проверить, выполняется ли равенство grad S (x ) = G (x ).
Примеры градиентных систем
Следующий пример показывает, как естественно возникают градиентные системы в механике. Рассмотрим общее уравнение механики Ньютона с рэлеевской силой трения
Mx ¨ = −grad V (x ) − grad v W (v ), v = x, ˙ (28.17)
где W — диссипативная функция Рэлея, а V — потенциальная энергия. Если на систему не действуют потенциальные внешние силы, так что V = const , а grad V (x ) = 0, то для скорости v получится уравнение
Mv ˙ = −grad v W (v ). (28.18)
При M = I уравнение (28.18) является градиентным и совпадает с (28.1), если положить S = −W . Однако и в общем случае положительно определенного оператора M уравнение (28.18) принимает градиентную форму, если ввести в пространстве H новую метрику со скалярным произведением (ξ, η)M = (M ξ, η), см. (11.20):
v ˙ = −grad M W (v ). (28.19)
Уравнение (28.18) обладает двумя функциями Ляпунова: диссипативной функцией W
и кинетической энергией![]() . Справедливы
. Справедливы
соотношения
![]() ,
(28.20)
,
(28.20)
![]() dW
−(grad W
)2
.
(28.21)
dW
−(grad W
)2
.
(28.21)
= dt
Замечу, что выведенное нами ранее уравнение диссипации энергии для системы Навье–Стокса является, по сути, частным случаем уравнения (28.20). Для линеаризованного уравнения (с выброшенным слагаемым (v, ∇)v ) справедливо и уравнение, аналогичное (28.21). Проверить это будет для Вас хорошим упражнением.
Еще один важный пример градиентного уравнения дает уравнение теплопроводности в ограниченной области D ⊂ Rn
![]() (28.22)
(28.22)
где κ > 0 — коэффициент температуропроводности. Пусть на границе выполнено краевое условие первого рода
![]() .
(28.23)
.
(28.23)
Действительно, нетрудно проверить (обязательно проверьте!), что
κ∆u
= Grad ![]() .
(28.24)
.
(28.24)
Здесь Grad означает функциональный градиент.
Равновесия градиентной системы и их устойчивость
Равновесия градиентного уравнения (28.1) определяются уравнением
grad S (x ) = 0. (28.25)
Таким образом, равновесия уравнения (28.1) являются критическими точками потенциала S . Это по сути — вариационный принцип, полезный при исследовании и вычислении равновесий.
![]() Если x
— некоторое равновесие уравнения (28.1), то соответствующее линеаризованное уравнение имеет вид
Если x
— некоторое равновесие уравнения (28.1), то соответствующее линеаризованное уравнение имеет вид
 u
˙ = (grad S
)0
(x
)u.
(28.26)
u
˙ = (grad S
)0
(x
)u.
(28.26)
В случае H = Rn векторное уравнение (28.1) можно записать в координатной форме
![]() (28.27)
(28.27)
Соответственно уравнение (28.26) записывается в виде
![]() (28.28)
(28.28)
Здесь подразумевается суммирование по j = 1,...,n . Матрица этой системы
![]() (28.29)
(28.29)
в случае C 2 –гладкой функции S симметрична. Поэтому все ее собственные значения вещественны и полупросты (являются простыми полюсами резольвенты (λI − A )−1 ), так что присоединенные векторы отсутствуют, и жорданова нормальная форма оператора A диагональна. Общее решение системы (28.28) записывается в виде
![]() ,
(28.30)
,
(28.30)
где ck — произвольные постоянные, λk — вещественные собственные значения, а ϕk — отвечающие им собственные векторы: A ϕk = λk ϕk .
![]()
![]()
![]() Если все λk
<
0, то равновесие x
асимптотически устойчиво по линейному приближению. Теорема Ляпунова о законности линеаризации позволяет в этом случае установить асимптотическую устойчивость равновесия x
и для полной системы (28.27). Нормальные моды — частные решения uk
(t
) = e
λ
k
t
ϕk
— в этом случае монотонно затухают со временем. Говорят, что равновесие x монотонно
асимптотически устойчиво.
Если все λk
<
0, то равновесие x
асимптотически устойчиво по линейному приближению. Теорема Ляпунова о законности линеаризации позволяет в этом случае установить асимптотическую устойчивость равновесия x
и для полной системы (28.27). Нормальные моды — частные решения uk
(t
) = e
λ
k
t
ϕk
— в этом случае монотонно затухают со временем. Говорят, что равновесие x монотонно
асимптотически устойчиво.
![]() Симметричность линейного оператора A
= (grad S
)0
(x
) можно установить и не пользуясь координатами: приводимое ниже доказательство сохраняет силу и для непрерывных операторов grad S
(x
) с C
2
–гладким потенциалом S
, в случае неограниченных операторов потребуются еще рассуждения об области определения оператора A
.
Симметричность линейного оператора A
= (grad S
)0
(x
) можно установить и не пользуясь координатами: приводимое ниже доказательство сохраняет силу и для непрерывных операторов grad S
(x
) с C
2
–гладким потенциалом S
, в случае неограниченных операторов потребуются еще рассуждения об области определения оператора A
.
Пусть x
, u
, v
— произвольные элементы пространства H
, а ε и µ — вещественные параметры. Рассмотрим вторую производную![]()
εu + µv ). Как и в случае функций, заданных на пространстве Rn , эта производная при условии, что S ∈ C 2 (даже при несколько меньших ограничениях), не зависит от порядка дифференцирования по переменным ε, µ.
Вспоминая определение градиента (28.15), выводим
![]() (grad S
(x
+ εu
),v
) =
(grad S
(x
+ εu
),v
) =
(28.31) = ((grad S )0 (x )u,v ) = (u, (grad S )0 (x )v ).
Последнее равенство получается, если сначала продифференцировать по ε, а затем по µ. Оно и означает, что A ∗ = A .
Заметим, что всякое равновесие градиентного уравнения (28.1) является также и равновесием уравнения (28.3) при условии (28.4). Действительно, умножая уравнение равновесий
grad S (x ) + F (x ) = 0 (28.32)
для уравнения (28.3) скалярно на grad S (x ), с учетом условия (28.4) получаем, что |grad S (x )|2 = 0. Таким образом, из уравнения (28.32) следует, что grad S (x ) = 0. Обратное, вообще говоря, неверно (см. упражнение 1). Более того, может случиться, что у уравнения (28.32) вообще нет решений, тогда как уравнение grad S (x ) = 0 имеет много решений.
Колебательная устойчивость и колебательная неустойчивость
![]()
![]()
![]()
![]() Уже в самых простых случаях присутствие дополнительного слагаемого F
в уравнении (28.3) может привести к появлению комплексных собственных значений в спектре линеаризованного на равновесии x
оператора. Рассмотрим например уравнение (28.5), и пусть x
— его равновесие, так что grad S
(x
) = 0. Линеаризованное на x
уравнение имеет вид
Уже в самых простых случаях присутствие дополнительного слагаемого F
в уравнении (28.3) может привести к появлению комплексных собственных значений в спектре линеаризованного на равновесии x
оператора. Рассмотрим например уравнение (28.5), и пусть x
— его равновесие, так что grad S
(x
) = 0. Линеаризованное на x
уравнение имеет вид
 u
˙ = (I
+ A
(x
))(grad S
)0
(x
)u.
(28.33)
u
˙ = (I
+ A
(x
))(grad S
)0
(x
)u.
(28.33)
Для определения показателя σ нормальной моды u (t ) = e σ t ϕ имеем задачу на собственные значения
![]() σϕ = (I
+ A
(x
))B
ϕ,
(28.34)
σϕ = (I
+ A
(x
))B
ϕ,
(28.34)
![]() где B
= (grad S
)0
(x
) — симметричный оператор B
= B
∗
. Если, напри-
где B
= (grad S
)0
(x
) — симметричный оператор B
= B
∗
. Если, напри-
![]() мер,
мер,![]() , то grad S
(x
) = βx
, и x
= 0 — равновесие, которое единственно при β
6= 0. Далее получаем (grad S
)0
(0) = βI
, и уравнение (28.34) принимает вид
, то grad S
(x
) = βx
, и x
= 0 — равновесие, которое единственно при β
6= 0. Далее получаем (grad S
)0
(0) = βI
, и уравнение (28.34) принимает вид
![]() σϕ = β(I
+ A
(x
))ϕ.
(28.35)
σϕ = β(I
+ A
(x
))ϕ.
(28.35)
![]()
![]()
![]() Предположим, что A
(x
) 6= 0. Как известно, спектр всякого ненулевого кососимметрического оператора в Rn
, скажем оператора A
(x
), состоит из некоторого количества пар чисто мнимых собственных значений ∓i
ωk
, ωk
>
0, k
= 1,...,s
и, быть может, собственного значения 0 кратности r
(очевидно, 2s
+ r
= n
). Соответственно, спектр оператора β(I
+ A
(x
)) состоит из собственных значений
Предположим, что A
(x
) 6= 0. Как известно, спектр всякого ненулевого кососимметрического оператора в Rn
, скажем оператора A
(x
), состоит из некоторого количества пар чисто мнимых собственных значений ∓i
ωk
, ωk
>
0, k
= 1,...,s
и, быть может, собственного значения 0 кратности r
(очевидно, 2s
+ r
= n
). Соответственно, спектр оператора β(I
+ A
(x
)) состоит из собственных значений ![]() , а также, возможно, точки β. Собственным значениям σ
∓
k
отвечают нормальные моды e
β
(1∓
ω
k
)t
ϕ
∓
k
. Так как Reσ
∓
k
= β, все они затухают, если β <
0. Это случай колебательной устойчивости.
, а также, возможно, точки β. Собственным значениям σ
∓
k
отвечают нормальные моды e
β
(1∓
ω
k
)t
ϕ
∓
k
. Так как Reσ
∓
k
= β, все они затухают, если β <
0. Это случай колебательной устойчивости.
Многие физики без особых обоснований рассматривают чисто градиентные системы как типичные замкнутые термодинамические системы. Видимо поэтому укрепился предрассудок, что в замкнутой термодинамической системе, если уж равновесие устойчиво, то непременно имеет место монотонная устойчивость. Поэтому, когда Б.П. Белоусов в 1951 году обнаружил, что если слить в пробирку раствор солей церия, малоновой кислоты и серной кислоты, то возникает химическая реакция, при которой достигаемое в конце концов равновесие устойчиво колебательно , ему не поверили. Реакция Б.П. Белоусова, которую сейчас время от времени демонстрируют по телевидению, очень красива — раствор становится, то красным, то голубым.
Неприятно, хотя и поучительно, вспомнить, что рецензенты статьи Белоусова действовали так же, как церковники, которые отказывались взглянуть в зрительную трубу Галилея, чтобы лично убедиться, что на Солнце есть пятна. Зачем глядеть, когда и так было ясно, что никаких пятен нет и быть не может? Рецензенты статьи Белоусова тоже заранее знали, что колебательных реакций не бывает. Они нарушали основной принцип науки: факты — впереди теорий. Ведь только и нужно было подойти к своим полкам с реактивами и, глядя в текст Белоусова, смешать указанные им реагенты в нужных пропорциях. Церковь уже покаялась и оправдала Галилея, что же касается рецензентов Белоусова, то о них ничего неизвестно.
Статья Белоусова так и не была опубликована в серьезных физических и химических журналах. К счастью, С.Э. Шноль в Пущине понял важность этой работы, помог опубликовать реферат статьи в «Рефератах по радиационной медицине», издаваемых Институтом биофизики Министерства здравоохранения СССР, и поручил своему аспиранту А.М. Жаботинскому продолжить работу. За исследование колебательных химических реакций в 1980 году Белоусову и Жаботинскому была присуждена Ленинская премия (Белоусову — посмертно).
Упражнения
1. Пусть H
= R
3
, потенциал![]() , а поле
, а поле![]()
![]() . Проверьте, что уравнение grad S
(x
) = 0 в этом случае имеет решения, которые не являются решениями уравнения grad S
(x
)+F
(x
) = 0. Более того, последнее уравнение, вообще, не имеет решений. Попытайтесь обобщить этот пример.
. Проверьте, что уравнение grad S
(x
) = 0 в этом случае имеет решения, которые не являются решениями уравнения grad S
(x
)+F
(x
) = 0. Более того, последнее уравнение, вообще, не имеет решений. Попытайтесь обобщить этот пример.
2. Докажите, что для потенциальности гладкого поля G (x ) в H необходимо и достаточно, чтобы для любого x производная G 0 (x ) была симметричным оператором, т.е. выполнялось равенство
(G 0 (x )ξ, η) = (ξ,G 0 (x )η), ξ, η ∈ H.
3. Докажите, что для потенциальности гладкого поля G (x ) необходимо и достаточно, чтобы интеграл по любой замкнутой кривой γ в H равнялся нулю:
![]() .
.
Продумайте определение интеграла по кривой в H , заданной параметрическим уравнением x = c (t ), 0 ≤ t ≤ 1. Докажите, что критерием потенциальности может также служить независимость интеграла по кривой, соединяющей две произвольные точки x 0 и x 1 , от вида кривой (он должен зависеть лишь от x 0 , x 1 ).
Замечание. Этот критерий сохраняет силу также для произвольной области в H , тогда как критерий упражнения 2 в части достаточности обобщается лишь на односвязные области в H . Подробности по поводу результатов упражнений смотрите в книге М.М. Вайнберга [6].
4. Пусть H = Rn , и уравнение x ˙ = G (x ) в координатах имеет вид
x ˙i = Gi (x ), i = 1,...,n.
Докажите, что поле G (x ) потенциально в том и только в том случае, когда выполняется равенство
![]()
Приведите пример поля на плоскости R 2 в кольце r 1 < |x | < r 2 , для которого эти условия выполнены, хотя поле не является потенциальным.
5. Выведите градиентное уравнение в частных производных, отвечающее потенциалу
![]()
где K — гладкая функция, D — область в Rn .
6. Докажите, что в случае H = R 3 оператор F (x ) = ω ∧ x (ω — постоянный вектор) — кососимметричен. Докажите, что его собственные значения суть 0 и ∓i |ω |. Исследуйте устойчивость нулевого решения уравнения
u ˙ = βu + ω ∧ u.
7. Каковы будут последствия добавления к правой части уравнения (28.1) слагаемого εF (x ) с малым параметром ε и функцией F , удовлетворяющей условию (28.4)?
8. Напишите общий вид уравнения в H , для которого заданная функция S (x ) является функцией Ляпунова. Найдите также общий вид дифференциального уравнения, для которого функция S (x ) является интегралом.
9. Найдите в Интернете описание истории открытия Белоусова и полюбуйтесь на анимацию реакции Белоусова–Жаботинского.
29. Малые колебания механической системы около
положения равновесия
Уравнения «малых колебаний» системы около положения равновесия получаются посредством линеаризации системы на заданном равновесии. Кавычки я поставил потому, что далеко не всегда, а лишь в случае устойчивого равновесия эти уравнения, действительно, описывают колебания. Вообще, если известно равновесие x 0 ∈ Rn автономной системы
x ˙ = f (x ) (29.1)
в Rn , то линеаризация уравнения (29.1) на равновесии x 0 — это довольно грубая операция. Она состоит в том, что мы полагаем x (t ) = x 0 + u (t ), а затем, подставляем это выражение в уравнение (29.1), и как говорили классики: «разлагаем правую часть уравнения в ряд Тейлора по степеням u , после чего отбрасываем все члены ряда, кроме линейных». Конечно, в этой классической формулировке предполагалась аналитичность векторного поля f (x ), тогда как на самом деле достаточно C 1 –гладкости. Линеаризованное уравнение , называемое также иногда линеаризацией уравнения (29.1), записывается в виде
u ˙ = Au, (29.2)
где A
= f
0
(x
0
) — линейный оператор, не зависящий от времени. В координатах он определяется матрицей![]() . Его правая часть отличается от правой части точного уравнения возмущений
. Его правая часть отличается от правой части точного уравнения возмущений
u ˙ = f (x 0 + u ) (29.3)
на малую величину o (u ) при u → 0, а если f ∈ C 2 , то, точнее, на величину O (u 2 ) при u → 0.
Заметим, что как точное уравнение возмущения (29.3), так и линеаризованное уравнение (29.2) имеют тривиальное решение u (t ) ≡ 0, соответствующее равновесию x 0 уравнения (29.1).
В координатах уравнение (29.2) записывается в виде системы
![]() (29.4)
(29.4)
где fi — компонента поля f (x ) = (f 1 (x ),...,fn (x )).
Вполне аналогично строится уравнение, линеаризованное на произвольном решении x 0 (t ) более общего уравнения
x ˙ = f (x,t ). (29.5)
Предположим, что решение x 0 (t ) определено для всех t ≥ 0. Представим решение x (t ) в виде x (t ) = x 0 (t ) + u (t ), слагаемое u (t ) называется возмущением основного решения x 0 (t ). Подстановка в уравнение (29.5) дает уравнение возмущений в виде
u ˙ = f (x 0 (t ) + u (t ),t ) − f (x 0 (t ),t ). (29.6)
Заранее ясно, что уравнение возмущений имеет тривиальное решение u (t ) ≡ 0. Линеаризация уравнения возмущений дает линейное уравнение, обобщающее (29.4)
u˙ = f0 (x0 (t),t)u. (29.7)
Дальше мы будем, однако, заниматься в основном равновесиями.
Устойчивость по Ляпунову
Если задаться конкретным промежутком времени [0,T ], то из общих результатов теории дифференциальных уравнений о непрерывной зависимости решения задачи Коши от начальных данных можно заключить, что решение задачи Коши для уравнения (29.1), а также и для уравнения (29.2) с начальным условием u (0) = u 0 , будет отличаться не более, чем на ε (ε > 0 и произвольно) от нулевого решения u = 0, если u 0 достаточно мало, точнее, если ku 0 k < δ, где δ = δ(ε).
На самом деле, однако, как это впервые ясно осознал Ляпунов, важно, чтобы малость возмущения u сохранялась на бесконечном промежутке времени [0, ∞).
Определение. Равновесие x 0 уравнения (29.1) называется устойчивым по Ляпунову, если выполнены следующие два условия:
1◦ ) существует окрестность нуля в Rn , скажем, шар B (0, ρ) радиуса ρ > 0 с центром в нуле, что задача Коши для уравнения (29.3) с начальным условием u (0) = u 0 имеет единственное решение u (t ), определенное для всех t ≥ 0 при любом u 0 ∈ B (0, ρ);
2◦ ) для любого ε > 0 существует такое δ > 0, что для любого начального поля u 0 , имеющего столь малую норму, что ku 0 k < δ, решение u (t ) задачи Коши для уравнения (29.3) с начальным условием u (0) = u 0 удовлетворяет неравенству ku (t )k < ε для всех t ≥ 0.
Таким образом, устойчивость по Ляпунову есть непрерывная зависимость решения задачи Коши для уравнения (29.1) от начальных данных (из окрестности точки x 0 ), равномерная по времени t на бесконечном промежутке времени [0, ∞].
Если равновесие x 0 устойчиво по Ляпунову и, кроме того, возмущения затухают при t → +∞, так что ku (t )k → 0 при t → +∞, то скажем, что оно асимптотически устойчиво .
На первый взгляд может показаться, что из свойства притяжения (затухания возмущений) равновесия x 0 следует и его устойчивость. А.М. Ляпунов проявил здесь глубокую проницательность, включив требование устойчивости в определение, хотя примеры решений, обладающих свойством притяжения, но неустойчивых, появились лет через пятьдесят. Возмущения таких решений (по крайней мере, некоторые) при t → +∞ затухают, но сначала их нормы вырастают до фиксированной, немалой величины. При этом можно подобрать решения с таким поведением, отвечающие сколь угодно малым начальным возмущениям.
До Ляпунова многие авторы занимались устойчивостью равновесий и движений. Существовало и несколько определений устойчивости — устойчивость по Лагранжу, устойчивость по Пуассону и т.д. Эти определения применяются иногда до сих пор, но имеют довольно частное значение. Когда говорят, что решение устойчиво, то подразумевается, что оно устойчиво по Ляпунову .
В приложениях теории устойчивости по сути используется, хотя обычно явно и не формулируется, принцип Ляпунова : данный режим движения системы можно наблюдать экспериментально в течение достаточно долгого (неограниченно долгого) времени в том и только в том случае, когда этот режим устойчив по Ляпунову.
Разумеется, устойчивость по Ляпунову есть качественное понятие, как и понятие непрерывности. На практике зачастую оно должно дополняться некоторыми количественными характеристиками. Скажем, интересно бывает уточнить, сколь малым должно быть δ (возмущение в начальный момент), чтобы обеспечить ε-малость возмущения для всех t ≥ 0. Когда некоторое равновесие или движение неустойчиво, возникает ряд новых вопросов. Насколько быстро рост возмущения разрушит основной режим?
Даже и неустойчивый режим (скажем, равновесие карандаша, стоящего на острие) можно наблюдать в течение некоторого времени, и интересно это время оценить. Это время может даже оказаться столь большим, что на практике мы сочтем основной режим устойчивым. Следующий вопрос — каково дальнейшее поведение возмущенных движений, когда они уже достаточно далеко отошли от основного? Думаю, что у Вас возникнет немало подобных вопросов. Замечательно, однако, что на практике принцип Ляпунова работает даже и без всяких количественных уточнений.
Теории устойчивости посвящены многие трактаты [24, 50, 25, 12, 26, 39, 11], начиная со знаменитой диссертации Александра Михайловича Ляпунова (1892). Вначале рассматривались конечномерные системы (обыкновенные дифференциальные уравнения) [24, 50, 25, 12, 26, 39], а затем и бесконечномерные [11].
Если нулевое решение линейного уравнения (29.2) устойчиво (в этом случае, очевидно, все его решения устойчивы, а потому допустимо называть устойчивым уравнение), то говорят, что равновесие x 0 уравнения (29.1) устойчиво по линейному приближению , или что оно устойчиво относительно бесконечно малых возмущений .
А.М. Ляпунов развил методы исследования устойчивости решений, и, в частности, равновесий нелинейных систем дифференциальных уравнений — это знаменитые первый и второй (он же прямой ) методы Ляпунова .
Первый метод Ляпунова основывается на линеаризации дифференциального уравнения на основном решении. А.М. Ляпунов указал условия, при которых исследование устойчивости по линейному приближению оказывается достаточным для решения вопроса об устойчивости основного решения. Он также развил методы исследования устойчивости в критических случаях — когда линейного приближения недостаточно и приходится привлекать следующие (после линейных) члены разложения ряда Тейлора данного дифференциального уравнения в окрестности основного режима. Наиболее полные результаты получаются в проблеме устойчивости равновесия автономной системы или периодического движения периодической системы. Приведу здесь результаты Ляпунова о законности линеаризации в задаче устойчивости (неустойчивости) равновесия автономной системы. Векторное поле f в уравнении (29.1) должно удовлетворять определенным условиям регулярности, достаточно, чтобы оно было C 2 –гладким.
Напомню, что в конечномерном случае спектр σ(A ) линейного оператора A есть набор его собственных значений σ(A ) = {λ1 ,..., λk }. Здесь k — число различных собственных значений, так что k ≤ n .
Теорема 1. Пусть спектр линейного оператора A = f 0 (x 0 ) — коэффициента в линеаризованном уравнении (29.2) — расположен в левой полуплоскости: все его собственные значения λ1 , λ2 ,..., λk имеют отрицательные действительные части. Тогда равновесие x 0 нелинейного уравнения (29.1) асимптотически устойчиво.
Если же хотя бы одно собственное значение, скажем, λj имеет положительную действительную часть ( Reλj > 0), то равновесие неустойчиво.
Эта теорема не охватывает лишь те случаи, когда оператор A не имеет собственных значений в правой полуплоскости, но имеется хотя бы одно собственное число на мнимой оси. Такие случаи и называются критическими , это означает, что выполнено нестрогое неравенство Reλi ≤ 0 при i = 1,...,k , причем хотя бы для одного собственного значения λj имеет место равенство Reλj = 0. В любой книге по теории устойчивости (см., например, [50, 25, 12, 47]) Вы найдете результаты по устойчивости в различных критических случаях, а также формулировки многочисленных нерешенных проблем этой интересной области теории дифференциальных уравнений.
Здесь остается заметить, что в задаче устойчивости равновесия консервативной механической системы, когда не учитываются силы трения и другие факторы диссипации энергии, асимптотическая устойчивость равновесия невозможна (см. упражнение 1). Вместе с тем, результат о законности линеаризации в задаче о неустойчивости из теоремы 29 применим и к таким задачам.
Второй (прямой) метод Ляпунова возник как широкое и содержательное обобщение теоремы Лагранжа об устойчивости равновесия натуральной механической системы в случае, когда оно дает потенциальной энергии строгий минимум . Подробное изложение прямого метода Ляпунова Вы найдете в уже цитированных руководствах по теории устойчивости. Этот метод позволяет получать результаты и об устойчивости, и о неустойчивости, и об асимптотической устойчивости как для автономных, так и для неавтономных дифференциальных уравнений. Здесь я ограничусь лишь теоремой об устойчивости равновесия автономного уравнения. Пусть x 0 — равновесие автономного уравнения в Rn
x ˙ = f (x ). (29.8)
Полагая x (t ) = x 0 + u (t ), где u (t ) — возмущения, запишем соответствующее уравнение возмущений
u ˙ = f (x 0 + u ). (29.9)
Мы помним, что устойчивость равновесия x 0 — то же самое, что и устойчивость тривиального решения u (t ) = 0 уравнения возмущений.
Предположим, что известна функция V (u ), определенная в некоторой окрестности нуля в Rn и такая, что V (0) = 0 и V (u ) > 0 при u 6= 0. Такая функция называется определенно положительной (или положительно определенной ). Будем предполагать, что функция V непрерывно дифференцируема, и вычислим ее производную по времени V ˙ в силу уравнения возмущений (29.9). Имеем
V ˙ = −W ; W = −(grad V (u ),f (x 0 + u )) (29.10)
(см. (5.3)). Знак минус в этой формуле поставлен ради будущих удобств.
Скажем, что функция U неположительна (Ляпунов и некоторые его последователи употребляют термин отрицательная ), если выполняется условие U (0) = 0 и U (u ) ≤ 0 всюду.
Аналогично, функция U называется неотрицательной, если U (0) = 0 и U (u ) ≥ 0 всюду (по терминологии Ляпунова, положительная функция).
Обратите внимание, что во всех этих определениях предполагается выполненным условие U (0) = 0. Замечу, что аргумент 0 появился потому, что речь идет о нулевом решении.
Приведу здесь теорему Ляпунова об устойчивости для рассматриваемого частного случая.
Теорема 2. Пусть функция V определенно положительна, а ее производная неположительна. Тогда равновесие x 0 уравнения (29.8) (или,чтотоже,нулевоерешениеуравнениявозмущений (29.9))устойчиво по Ляпунову.
Сделаем несколько замечаний по поводу этой теоремы. Я не привожу здесь доказательства, но суть теоремы нетрудно усмотреть из рисунка 16, где показано расположение поверхностей уровня функции V в окрестности точки u = 0. Рисунок показывает, что в условиях теоремы, когда значение V не возрастает, движение не может уйти далеко от точки 0.
Далее замечу, что эта теорема не исключает случая, когда функция V является интегралом уравнения (29.8), а производная V ˙ ≡ 0. Чаще всего именно этот случай и возникает в приложениях, в этой ситуации данная теорема незаменима, а метод линеаризации не работает.
Очевидно, в теореме Ляпунова можно взять функцию V определенно отрицательной, если потребовать, чтобы производная V ˙ была неотрицательной. Этот случай сводится к предыдущему заменой V на −V .
Хотя в теории переход к уравнению возмущений удобен и практически всегда проводится, он не является необходимым. Условие определенной
положительности функции V (u ) означает, что она в точке u = 0 достигает строгого минимума . Можно рассматривать функцию V (x ), определенную в окрестности точки x 0 и достигающую в ней строгого минимума. Тогда, та функция, которая фигурирует в теореме, естественно записывается в виде
V (u ) = V (x 0 + u ) − V (x 0 ). (29.11)
Приведу общее определение функции Ляпунова дифференциального уравнения. Это такая функция V (x,t ), что монотонно возрастает (либо убывает) для любого решения x (t ). Функция V , удовлетворяющая условиям теоремы 2, обычно называется функцией Ляпунова первого рода. Пожалуй, вообще, единственный способ узнать что-то о качественном поведении решения дифференциального уравнения, не решая его, состоит в том, чтобы найти его функцию Ляпунова. Сама по себе теорема 2 не содержит указаний о том, каким образом мы можем такую функцию построить. Практически полезных общих методов здесь не существует. Однако для ряда важных классов уравнений надлежащие функции Ляпунова известны. В механике зачастую бывает достаточно в качестве функции Ляпунова использовать полную механическую энергию, быть может, в комбинации с другими интегралами (импульса, момента импульса и т.д.), если они нам известны.
Устойчивость равновесия механической системы
Ограничимся натуральными системами, для которых лагранжиан имеет вид
L = T − V, (29.12)
где V = V (q ) — потенциальная энергия, а кинетическая энергия T есть квадратичная форма относительно скоростей с коэффициентами, зависящими, вообще говоря, от координат:
![]() .
(29.13)
.
(29.13)
Здесь q = (q 1 ,...,qn ) — точка n -мерного конфигурационного пространства. Специфика состоит в том, что мы теперь имеем дело с уравнениями второго порядка — уравнениями Лагранжа второго рода. Пусть q 0 — равновесие, так что q ˙0 = 0. Введем возмущения u , полагая q (t ) = q 0 + u , q ˙ = u ˙ для любого решения q (t ). Линеаризацию уравнений Лагранжа на решении q 0 можно провести, работая с лагранжианом L . Для этого достаточно подставить выражение q = q 0 + u в формулу (29.12) и выделить главную квадратичную часть лагранжиана. Для кинетической энергии имеем
![]() ,
(29.14)
,
(29.14)
где многоточие обозначает слагаемые степени выше второй относительно u , u ˙. Для потенциальной энергии V разложение можем написать в виде
![]() (29.15)
(29.15)
где опущенный остаточный член имеет степень выше второй относительно q ; в случае, когда V ∈ C 3 , он имеет порядок не ниже третьего. Выражение u 2 можно трактовать как тензорный квадрат , для нас сейчас это просто обозначение.
Первое слагаемое в (29.15) есть несущественная константа, и можно положить V (q 0 ) = 0. Второе слагаемое исчезает, потому что q 0 — равновесие и, следовательно, является критической точкой потенциальной энергии.
В результате можем написать
L = T 2 − V 2 + ..., (29.16)
где T 2 дается формулой (29.14), а квадратичная форма V 2 имеет вид
![]() .
(29.17)
.
(29.17)
В (29.16) опущены члены порядка малости выше второго при u → 0. Мы видим, что квадратичная форма (29.17) задается симметричной матрицей Гесса функции V
![]() .
(29.18)
.
(29.18)
Линеаризованные на равновесии q 0 уравнения Лагранжа (полные уравнения нет нужды здесь выписывать) определяются лагранжианом
![]() ,
(29.19)
,
(29.19)
где A — оператор Гесса (29.18), а оператор M задается матрицей с коэффициентами mik (q 0 ). В итоге линеаризованное уравнение, которое является уравнением Лагранжа второго рода с лагранжианом (29.19), принимает вид
Mu ¨ = −Au. (29.20)
Это — общий вид уравнения малых колебаний натуральной механической системы около равновесия q 0 . Мы видим, что уравнение малых колебаний сохраняет форму обобщенного уравнения 2-го закона Ньютона.
Кинетическая энергия есть положительно определенная квадратичная форма относительно скоростей. Поэтому оператор M
положительно определен:![]() . Оператор A
= grad V
2
самосопряжен. Он может быть как знакоопределенным, так и знакопеременным.
. Оператор A
= grad V
2
самосопряжен. Он может быть как знакоопределенным, так и знакопеременным.
Из теоремы 29 непосредственно следует теорема Лагранжа об устойчивости равновесия. Как я уже говорил раньше, исторически теоремы прямого метода Ляпунова возникли как обобщение этой теоремы. Вместе с тем, сама теорема Лагранжа явилась замечательным обобщением принципа Торричелли (1642 г.): механическая система находится в устойчивом равновесии, когда ее центр тяжести занимает наинизшее возможное положение. Разумеется, во времена Торричелли (гениального ученика гениального Галилея), даже во времена Лагранжа понятие устойчивости не было строго оформлено. Поэтому, быть может, правильно было бы говорить о теореме Торричелли–Лагранжа–Ляпунова.
Теорема 3. (Теорема Лагранжа). Равновесие q 0 механической системы (29.20) устойчиво если потенциальная энергия V достигает в точке q 0 (хотя бы локального) строгого минимума.
Доказательство. Нетрудно видеть, что в условиях теоремы Лагранжа полная механическая энергия E = T + V есть функция Ляпунова первого рода. Действительно, для любого q из окрестности q 0 и произвольного q ˙ имеем
E(q,q˙) ≥ V (q) > V (q0 ) = E(q0 ,0). (29.21)
Первое неравенство выполнено потому, что T — положительно определенная квадратичная форма, второе неравенство — в силу условия теоремы. Последнее равенство верно потому, что q ˙0 = 0. Мы доказали, что E достигает строгого минимума в положении равновесия q 0 . Так как E ˙ = 0, условия теоремы (29) выполнены, и теорема Лагранжа доказана
Как известно, достаточным условием строгого минимума служит положительная определенность второго дифференциала V 2 потенциальной энергии V в критической точке q 0 .
Таким образом, из положительной определенности оператора A следует устойчивость равновесия q 0 по Ляпунову . Выходит, что в этой ситуации линеаризация все-таки законна, хотя мы имеем дело с критическим случаем.
Естественно возникает вопрос об условиях неустойчивости равновесия. Это — проблема обращения теоремы Ляпунова, которая до сих пор не решена и остается объектом исследований. Ляпунов доказал, что равновесие q 0 неустойчиво в том случае, когда второй дифференциал d 2 V (q 0 )(ξ, ξ) может для некоторых векторов ξ принимать отрицательные значения . В частности, q 0 — неустойчивое равновесие, когда второй дифференциал отрицательно определен, и функция V в точке q 0 достигает максимума (самая сильная неустойчивость). Случай, когда форма d 2 V (q 0 )(ξ, ξ) неотрицательна, но не положительно определена, является критическим и требует дальнейшего исследования с учетом высших членов разложения Тейлора функции V . Повторюсь, хотя многие авторы продолжали исследования Ляпунова (см. [50, 39, 17]), проблема неустойчивости равновесия полностью не решена.
Если разыскивать частные решения уравнения (29.20) в виде
u ω (t ) = ei ω t ϕ, (29.22)
где ϕ — постоянный вектор, придем к спектральной задаче: найти числа ω (вообще говоря, комплексные) такие, что уравнение
A ϕ = ω2 M ϕ (29.23)
имеет ненулевое решение ϕ. При M = I это обычная задача на собственные значения для оператора A . Имеются различные способы свести общую задачу (29.23) к обыкновенной задаче на собственные значения для самосопряженного оператора. Видимо, лучший из них — попросту обратить в (29.23) оператор M и перейти от стандартной метрики в Rn к новой, порождаемой скалярным произведением
| (ϕ, ψ)M = (M ϕ, ψ). Тогда уравнение (29.23) примет вид |
(29.24) |
| M −1A ϕ = ω2ϕ, |
(29.25) |
и при этом оператор M −1 A оказывается самосопряженным относительно метрики (29.24). Действительно, для любых ϕ и ψ имеется равенство
(M −1 A ϕ, ψ)M = (A ϕ, ψ) = (ψ,A ϕ) = (ϕ,M −1 A ψ)M . (29.26)
Мы уже раньше видели (см. формулу (11.19) и последующий текст), что переход от стандартного скалярного произведения к скалярному произведению (29.24), порождаемому оператором масс M , приводит общее уравнение второго закона Ньютона к его частному случаю с оператором M = I . Как вы знаете, все собственные значения самосопряженного оператора вещественны. Поэтому вещественны все собственные числа оператора M −1 A , и соответственно, частота ω вещественна, если ω 2 > 0, и является чисто мнимой при ω 2 < 0. Это, впрочем, можно установить и непосредственно. Умножим уравнение (29.23) скалярно на ϕ (напомню, что в комплексном случае (ϕ, ψ) = P ϕk ψk ∗ , если ϕ = (ϕ1 ,..., ϕn ) и ψ =
k
(ψ1 ,..., ψn )). В результате получаем
![]() .
(29.27)
.
(29.27)
Поскольку M и A — симметричные операторы, числитель и знаменатель этой дроби вещественны (см. упражнение 3), причем знаменатель положителен.
Как известно из линейной алгебры, симметричный оператор M −1 A всегда имеет ортонормальный собственный базис, состоящий из собственных векторов ϕ1 ,..., ϕn , которым отвечают вещественные собственные значе-
ния ![]() . Выполняются равенства
. Выполняются равенства
Aϕj = ω 2 j Mϕj , j = 1,...,n. (29.28)
Поскольку операторы A и M вещественны, собственные векторы ϕj можно также считать вещественными. Согласно формуле (29.22), каждому собственному значению ω 2 отвечает пара решений e ±i ω t ϕ, называемых нормальными колебаниями , или нормальными модами .
Общее решение уравнения (29.20) можно представить в виде линейной комбинации нормальных колебаний:
n
u (t ) = X cj ei ω j t ϕ j . (29.29)
j =−n
При этом мы полагаем ω−j
= −ωj
, ϕ−j
= ϕj
. Для вещественных решений ![]() . Здесь мы считаем, что c
0
= 0, а ω0
и ϕ0
не определены.
. Здесь мы считаем, что c
0
= 0, а ω0
и ϕ0
не определены.
Решение (29.29) описывает колебания, когда все частоты ωj вещественны, то есть, когда собственные числа ω 2 j положительны. Это соответствует тому случаю, когда оператор A положительно определен. Тогда и квадратичная форма d 2 V (q 0 )(u,u ) = (Au,u ) положительно определена. По теореме Лагранжа–Ляпунова, равновесие q 0 в этом случае устойчиво. Заметим, что и интеграл энергии
![]() (29.30)
(29.30)
есть положительно определенная форма от u и u ˙.
Если разыскивать решение уравнения (29.20) в виде
![]() ,
(29.31)
,
(29.31)
то для координаты xj в собственном базисе получим уравнение гармонического осциллятора
x ¨j + ω 2 j xj = 0. (29.32)
Мы приходим к важному выводу: в случае устойчивого равновесия q 0 , когда второй дифференциал d 2 V (q 0 )(u,u ) = (Au,u ) есть положительно определенная форма, уравнение малых колебаний может быть представлено как набор n независимых гармонических осцилляторов, где n — число степеней свободы системы.
Я уже упоминал раньше, см. 8, о такого рода нетривиальных разбиениях динамической системы на независимые подсистемы. Замечу, что и в неустойчивом случае уравнение «малых колебаний» (29.20) представляется как декартово произведение независимых подсистем, по-прежнему определяемых уравнениями (29.32). В этом случае, однако, те из уравнений (29.32), для которых ω 2 j < 0, описывают не колебания, а экспоненциально растущие или экспоненциально затухающие движения, чему и соответствуют поставленные выше кавычки. В случае ω 2 j = 0 большинство решений уравнения (29.32) линейно растет со временем, лишь решения, отвечающие начальному условию вида x (0) = a , x ˙(0) = 0, — постоянны.
Возможность разбиения динамической системы на невзаимодействующие подсистемы оказывается особенно важной, когда применяются вероятностные методы. Зачастую наличие тех или иных свойств статистической независимости оказывается решающим для успеха исследования. Дальше мы рассмотрим применение статистической механики к теории твердого тела — замечательный пример плодотворности изложенных здесь идей.
Упражнения.
1. Пользуясь теоремой Лиувилля о сохранении фазовых объемов, докажите, что равновесие гамильтоновой системы не может быть асимптотически устойчивым.
2. Докажите, что нулевое равновесие уравнения
x ¨ = −x 3
устойчиво по Ляпунову, хотя условия теоремы Лагранжа нарушены.
3. Пусть линейный оператор A действует в комплексном (унитарном) пространстве Cn . Докажите, что он самосопряжен в том и только в том случае, когда его квадратичная форма (A ϕ, ϕ) при всех ϕ ∈ Cn принимает вещественные значения.
4. При каких условиях решение (29.29) периодично по t ? Вообще говоря, оно лишь квазипериодично .
5. Докажите, что если уравнение
Mu ¨ = Au,
где M
и A
— самосопряженные операторы, причем![]() , имеет экспоненциально растущее решение, то оно имеет также экспоненциально затухающее решение с тем же показателем экспоненты.
, имеет экспоненциально растущее решение, то оно имеет также экспоненциально затухающее решение с тем же показателем экспоненты.
30 Статистическая механика твердого тела
![]()
30. Статистическая механика твердого тела
Теперь речь пойдет о простейшей модели твердого тела в статистической механике. Представим себе кристаллическую решетку, в узлах которой q 1 ,...,qn располагаются частицы — ионы или атомы. Обычно эти частицы несут некоторый электрический заряд — например, в узлах кубической кристаллической решетки поваренной соли находятся ионы натрия и хлора. Более редкий случай — когда в узлах решетки расположены электрически нейтральные атомы — представляет алмаз. Частицы взаимодействуют между между собой, и это взаимодействие описывается потенциальной энергией V (q ). Здесь q = (q 1 ,...,qn ), где qi ∈ R3 — положение i -й частицы. Таким образом, q ∈ R3n . Предположим, что частицы совершают малые колебания около своих равновесных положений q 01 ,q 02 ,...,q 0n . Предполагается, что система натуральна, и ее гамильтониан имеет вид
![]() .
(30.1)
.
(30.1)
Импульс p выражается через оператор масс M (q ) формулой
p = M (q )q. ˙ (30.2)
Здесь q ˙ = (q ˙1 ,...,q ˙n ) — скорость, q ˙ ∈ R3n .
Положим q = q 0 + u , где u — возмущение положения системы. Так как в случае равновесия q 0 = 0, p 0 = 0, можно считать, что q и p суть возмущения.
Простейшая модель получается, когда мы предполагаем колебания частиц около их положений равновесия столь малыми, что можно применить уравнения малых колебаний (см. (29.20))
Mu ¨ = −Au, (30.3)
где M = M (q 0 ), а оператор A (см. (29.18)) определяется матрицей Гесса потенциальной энергии V . Гамильтониан этой системы есть квадратичная относительно возмущений u, u ˙ часть гамильтониана (30.1). Далее будем предполагать, что оператор A положительно определен, так что равновесие q 0 есть точка строгого минимума потенциальной энергии V :
![]() .
(30.4)
.
(30.4)
Как мы уже видели, система (30.3) может быть представлена как декартово произведение 3n экземпляров гармонических осцилляторов. Каждый из них описывается уравнением вида (см. (29.32))
x ¨j + ω 2 j xj = 0, (30.5)
где частоты ωj
отличны от нуля и вещественны в силу предположения ![]() 0 (оператор масс мы всегда считаем положительно определенным). При этом возмущение положения равновесия u
(t
) определяется разложением по нормальным модам (см. (29.31))
0 (оператор масс мы всегда считаем положительно определенным). При этом возмущение положения равновесия u
(t
) определяется разложением по нормальным модам (см. (29.31))
![]() ,
(30.6)
,
(30.6)
где ϕj — собственный вектор оператора M −1 A , отвечающий собственному значению ω 2 j . В переменных xj гамильтониан (30.4) принимает вид
![]() .
(30.7)
.
(30.7)
Пора остановиться и перевести дух. Все предыдущее есть не более, чем некоторые наводящие соображения. Мы можем теперь сказать, что простейшая модель твердого тела есть линейная динамическая система, состоящая из (представляющая собой декартово произведение) 3n невзаимодействующих гармонических осцилляторов. Более того, даже и конкретные значения частот ωj не играют серьезной роли в дальнейшем.
Перейдем к вычислению статистического интеграла
![]() (30.8)
(30.8)
В случае гамильтониана (30.4) интеграл P (B ) представляется в виде произведения 6n гауссовых интегралов:
![]() .
(30.9)
.
(30.9)
Статистическая механика твердого тела
Далее получаем
![]() .
(30.10)
.
(30.10)
Здесь мы считаем (имеем право!), что ωj > 0. Окончательно имеем
![]() .
(30.11)
.
(30.11)
Теперь находим энергию E (B ) по формуле (25.16). Заметим, что P (B ) = CB 3n , где C — константа, зависящая от частот ωj . Поэтому lnP (B ) = 3n lnB + const , и вспоминая, что B = kT , получаем
E = 3nkT. (30.12)
Как и в случае идеального газа, энергия зависит лишь от температуры и числа частиц. Мы можем вычислить также теплоемкость c (точнее, cV — теплоемкость при постоянном объеме):
![]() (30.13)
(30.13)
Таким образом, теплоемкость зависит лишь от числа частиц и не зависит от их природы, а также и от температуры. Это — известный закон Дюлонга и Пти (1819 г.), которые экспериментально обнаружили, что у всех элементов в твердом состоянии атомная удельная теплоемкость (то есть удельная теплоемкость с поправкой на различный атомный вес) одна и та же. В экспериментах нередко наблюдаются большие отклонения от этого закона, но при достаточно высоких температурах. Пока сохраняется твердое состояние, закон, как правило, выполняется. Нужно сразу признать, что статистическая механика оказалась не в состоянии объяснить отклонения от данного закона при низких температурах. Это расхождение между теорией и экспериментом было одним из важнейших стимулов к развитию квантовой механики , точнее, квантовой статистики .
Приложение 1. Типичность единственности и
нетипичность неединственности решения задачи Коши
Здесь мы рассмотрим дифференциальное уравнение
x ˙ = f (x,t ) (A.1)
с непрерывной скалярной функцией f : R 2 → R , заданной на всей плоскости R 2 . На самом деле, следующие рассмотрения можно провести вполне аналогично и для уравнений в Rn . Имеются и дальнейшие обобщения — на уравнения в банаховом пространстве X , на уравнения с многозначными функциями и т. д.
Наша цель — изложить доказательство удивительной теоремы Владислава Орлича (1932, [65]) (исследования Орлича были продолжены в работах [62, 63, 64]). Эта теорема показывает, что в определенном смысле (разъясненном ниже), типичной является ситуация, когда для уравнения
(A.1) с начальным условием вида
![]() (A.2)
(A.2)
решение для всех точек (x 0 ,t 0 ) ∈ R 2 единственно! И это несмотря на то, что одного лишь свойства непрерывности функции√ f , как показывают про-
![]()
стые примеры (вспомните задачу Коши x ˙ = 3 x , x (0) = 0), для единственности недостаточно. Удивительное дело, этот фундаментальный результат польского математика совсем мало известен, не упоминается в трактатах по дифференциальным уравнениям и в учебниках. Более того, весьма распространен предрассудок, что типична как раз неединственность. По-видимому, так получается потому, что многие верят в "принцип хрупкости хорошего". Этот принцип, говорящий, что все хорошее встречается редко и легко портится, применим, к сожалению, ко многим проблемам математики и жизни. Но он, выходит, отказывает применительно к задаче Коши (A.1), (A.2). Не считать же "хорошим" случаем неединственность решения.
В шутку я проводил голосование среди математиков, сначала в России, а затем в нескольких американских университетах, по вопросу о том, что типично — единственность или неединственность. Этот демократический способ решения проблемы дал правильный результат лишь на семинаре в Институте Куранта в Нью-Йорке, причем соотношение голосов за правильный ответ (единственность!) и против него было, кажется, 14:12, многие воздержались. Выдающиеся специалисты по дифференциальным урав-
нениям оказались в разных партиях. Получив, наконец, правильный ответ, я прекратил такие эксперименты.
Дальше нам понадобится ряд понятий из функционального анализа. Вероятно, они вам большей частью известны, а здесь я их лишь кратко напомню.
Категория множества по Бэру. Пусть X — метрическое пространство. Множество M ⊂ X называется всюду плотным в X , если его за-
![]()
мыкание M совпадает с X . Эквивалентное требование таково: в каждом шаре пространства X найдется хотя бы одна точка множества M . Либо так: для любой точки x ∈ X найдется последовательность точек x 1 , x 2 ,... множества M такая, что xn → x , то есть ρ(xn ,x ) → 0. Здесь ρ — метрика, и ρ(x,y ) — расстояние между точками x и y в X .
Множество M ⊂ X называется нигде не плотным в X , если для каждого шара в X найдется расположенный внутри него шар, не содержащий ни одной точки множества M .
Типичные примеры: множество Q всех рациональных чисел всюду плотно в метрическом пространстве R . Множество Qn всевозможных векторов пространства Rn , имеющих рациональные координаты, всюду плотно в Rn . Множество Z всех целых числе нигде не плотно в R . Прямая в R 2 нигде не плотна.
Нетривиальный пример нигде не плотного множества построил Г. Кантор. Рассмотрим сегмент [0,
1]. Выбросим из него интервал![]() . С двумя оставшимися отрезками проделаем такую же процедуру: разделим каждый из них на 3 равных отрезка и выбросим среднюю часть. С оставшимися четырьмя отрезками проделаем то же самое. Продолжим эти действия до бесконечности. Оставшееся канторово множество
K
нигде не плотно на [0,
1]. В этом случае X
= [0,
1], ρ(x,y
) = |x
− y
|. Заметьте, что построенное таким образом канторово множество состоит из всевозможных чисел на отрезке [0,
1], имеющих разложение в троичную дробь, в котором отсутствует цифра 2.
. С двумя оставшимися отрезками проделаем такую же процедуру: разделим каждый из них на 3 равных отрезка и выбросим среднюю часть. С оставшимися четырьмя отрезками проделаем то же самое. Продолжим эти действия до бесконечности. Оставшееся канторово множество
K
нигде не плотно на [0,
1]. В этом случае X
= [0,
1], ρ(x,y
) = |x
− y
|. Заметьте, что построенное таким образом канторово множество состоит из всевозможных чисел на отрезке [0,
1], имеющих разложение в троичную дробь, в котором отсутствует цифра 2.
Канторовы множества долгое время казались математикам абстрактной и вычурной выдумкой. Однако в середине XX века они стали появляться в теории динамических систем и, по сути, во всех областях нелинейной математической физики (конечно, не обязательно в процедуре Кантора делить отрезки на равные части).
Множество M называется множеством 1-ой категории по Бэру, если его можно представить как счетное объединение нигде не плотных множеств. Например, множество Q рациональных чисел в R , а также и Qn в Rn , суть множества 1-й категории, хотя бы по тому, что они сами счетны.
Множества, не являющиеся множествами 1-й категории, называются множествами 2-й категории. Среди них особенный интерес представляют вычеты . Множество M ⊂ X называется вычетом , если оно — 2-й категории, а его дополнение X \ M есть множество 1-й категории. Замечу, что всякое полное метрическое пространство X есть множество второй категории — в себе. В этом случае и всякое непустое открытое множество в X — тоже второй категории, и дополнение всякого множества первой категории имеет вторую категорию, а значит, является вычетом.
Понятно, что множества 1-й категории — это в некотором роде "малые множества зачастую пренебрежимо малые. Напротив, явления, которые происходят для всех точек множества 2-й категории, в аналогичном смысле можно рассматривать как типичные (конечно, типичность явления не означает, что оно происходит всегда, может быть несколько, даже бесконечно много, различных типичных ситуаций, см. упражнение 4).
Конечно, имеются и другие подходы к определению "пренебрежимо малых" и типичных множеств. Напомню два других варианта. Первый из них связан с размерностями. Например, гладкая кривая или гладкая поверхность в R 3 может считаться "пренебрежимым" множеством (замечу, что гладкость здесь очень существенна — как показал Пеано, непрерывная кривая может проходить через все точки куба). Второй подход связан с мерой. Пренебрежимыми считаются множества меры 0, иногда их даже называют нулевыми . Обычно также "пренебрежимо малыми" считаются конечные подмножества бесконечных множеств, или вообще подмножества меньшей мощности . Когда-то математики были поражены результатом Кантора: квадрат и отрезок прямой — множества равномощные (докажите!)
Надо еще подчеркнуть, что понятия плотного, нигде не плотного множества, а также множеств 1-ой и 2-ой категории зависят от выбора метрики. Эти понятия определяются и для более общих топологических пространств, и тоже зависят от выбора топологии . Вполне может случиться, что множество 1-ой категории X станет множеством 2-ой категории, если мы на том же множестве X введем другую метрику или топологию. Точно так же множество, имеющее нулевую меру µ, может оказаться множеством положительной меры µ1 .
Пространство функций C (R 2 ). Каждая функция f : R 2 → R :
(x,t ) 7→ f (x,t ) определяет на всей плоскости R 2 дифференциальное уравнение вида (A.1). Будем рассматривать пространство всевозможных непрерывных функций на плоскости. Чтобы иметь право произносить слово "пространство необходимо определить, что мы понимаем под сходимостью последовательности функций f 1 (x,t ), f 2 (x,t ),... .
Скажем, что fn → f , если для любого компакта в R 2 (а можно сказать проще, для любого круга) имеет место равномерная сходимость fn (x,t ) → f (x,t ), здесь f — предельная функция. Это пространство мы и обозначим через C (R 2 ).
Оказывается, невозможно так определить банахову норму, чтобы сходимость по этой норме совпадала с введенной только что равномерной сходимостью на компактах. Можно однако ввести метрику, определяющую такой тип сходимости. Для этого достаточно положить
![]() .
(A.3)
.
(A.3)
Здесь Bk — круг радиуса k с центром в точке (0, 0), так что Bk = {(x,t ) : x 2 + t 2 ≤ k 2 }. Для любой непрерывной функции f норма в C (Bk ) определяется равенством
![]() .
(A.4)
.
(A.4)
Вам станет понятно, откуда взялся ряд (A.3), если Вы припомните определение метрики в пространстве всевозможных последовательностей S (см.
[23]).
Нетрудно установить (установите!), что введенная равенством (A.3) метрика превращает пространство C (R 2 ) в полное метрическое пространство.
Замечу, что дальнейшее использование пространства C (R 2 ) относится скорее к красивому оформлению, нежели к сути идеи Орлича.
Множество уравнений с точками неединственности. Рассмотрим множество M ⊂ C (R 2 ), состоящее из таких функций f , что задача Коши (A.1), (A.2) хотя бы для одной точки (x 0 ,t 0 ) ∈ R 2 имеет более одного решения. Такую точку (x 0 ,t 0 ) назовем точкой неединственности . Понятно, что дополнение C (R 2 ) \ M состоит из таких функций f , что задача (A.1), (A.2) для всех точек (x 0 ,t 0 ) имеет единственное решение.
Для любой точки (x 0 ,t 0 ) ∈ R 2 и пары положительных чисел τ и a определим множество M (x 0 ,t 0 , τ,a ) ⊂ C (R 2 ), состоящее из таких функций f (x,t ), что в круге B 1 (x 0 ,t 0 ) радиуса 1 с центром (x 0 ,t 0 ) уравнение (A.1) имеет хотя бы одну точку неединственности, скажем, (x ˜0 ,t ˜0 ), и при этом выполняются следующие условия:
1) Существуют два решения x (t ) и x ∗ (t ) уравнения x ˙ = f (x,t ), удовлетворяющие одному и тому же начальному условию x (t ˜0 ) = x ˜0 , x ∗ (t ˜0 ) = x ˜0 ; при этом оба решения определены (по крайней мере) на интервале (t ˜0 − τ,t ˜0 + τ), см. Рис. 17.
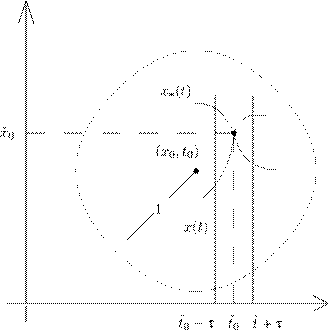
Рис. 17
2) Решения x (t ) и x ∗ (t ) подчинены неравенствам
| |x (t ) − x 0 | ≤ 1, |x ∗ (t ) − x 0 | < 1 для всех t ∈ (t ˜0 − τ,t ˜0 + τ). 3) Выполнена оценка снизу |
(A.5) |
| sup |x (t ) − x ∗ (t )| ≥ a. |
(A.6) |
t ˜0 −τ<t<t ˜0 +τ
Доказательство теоремы Орлича основывается на следующих двух леммах.
Лемма 1. Множество M (x 0 ,t 0 , τ,a ) при любом выборе точки (x 0 ,t 0 ) в R 2 и положительных чисел τ и a замкнуто в C (R 2 ). Доказательство. Суть дела, конечно в том, что все условия, определяющие множество M (x 0 ,t 0 , τ,a ), выдерживают предельный переход в пространстве C (R 2 ). Главным является условие (A.6), которое обеспечивает сохранение неединственности при этом предельном переходе. Небольшая техническая трудность связана с тем, что сама точка неединственности предельного уравнения заранее не определена.
Итак, пусть дана последовательность функций fn ∈ M (x 0 ,t 0 , τ,a ), которая сходится к некоторой функции f ∈ C (R 2 ) в смысле метрики (A.3). Мы должны доказать, что f ∈ M (x 0 ,t 0 , τ,a ).
Согласно определению множества M
(x
0
,t
0
,
τ,a
), для любого n
= 1,
2,...
определена пара решений![]() задачи Коши с начальной точкой
задачи Коши с начальной точкой ![]()
![]() .
(A.7)
.
(A.7)
Здесь ![]() — та самая точка неединственности, которая в общем определении обозначена через x
˜0
,t
˜0
. При этом оба решения определены на интервале
— та самая точка неединственности, которая в общем определении обозначена через x
˜0
,t
˜0
. При этом оба решения определены на интервале ![]() , и, согласно (A.6), выполняются неравенства
, и, согласно (A.6), выполняются неравенства
![]() ,
(A.8)
,
(A.8)
![]() (A.9)
(A.9)
Поскольку все точки неединственности расположены в единичном круге B
1
(x
0
,t
0
), а этот (замкнутый) круг компактен, можно выбрать такую подпоследовательность индексов nk
, что соответствующие точки неединственности ![]() сходятся к некоторой предельной точке
сходятся к некоторой предельной точке ![]() .
.
Ради краткости будем считать, что этот переход к подпоследовательности уже проделан, так что![]() .
.
Теперь наша цель — доказать, что возможно так выбрать подпоследовательность значений индекса n
, что соответствующие подпоследовательности решений xn
(t
) и xn
∗
(t
) будут сходиться соответственно к некоторым решениям ![]() равномерно на любом сегменте, содержащемся в интервале
равномерно на любом сегменте, содержащемся в интервале
![]() . Определим подпоследовательность сегментов
. Определим подпоследовательность сегментов ![]() , где
, где ![]() , m
= 1,
2,...
. Очевидно, что достаточно доказать равномерную сходимость на каждом из сегментов Im
, так как любой сегмент, содержащийся в интервале
, m
= 1,
2,...
. Очевидно, что достаточно доказать равномерную сходимость на каждом из сегментов Im
, так как любой сегмент, содержащийся в интервале ![]() , содержится в каждом сегменте Im
, начиная с некоторого значения m
.
, содержится в каждом сегменте Im
, начиная с некоторого значения m
.
Рассмотрим, например, последовательность функций xn
(t
) (с решениями![]() все аналогично) и докажем, что эта последовательность компактна в
C
(Im
) — в пространстве функций непрерывных на сегменте Im
. Точнее было бы сказать, что речь идет о сужении каждой из функций на сегмент Im
. Для этого, конечно, надо потребовать, чтобы сегмент Im
содержался в интервале задания
все аналогично) и докажем, что эта последовательность компактна в
C
(Im
) — в пространстве функций непрерывных на сегменте Im
. Точнее было бы сказать, что речь идет о сужении каждой из функций на сегмент Im
. Для этого, конечно, надо потребовать, чтобы сегмент Im
содержался в интервале задания ![]() решения xn
(t
). Это верно, возможно, не для всех n
, но для всех n
, начиная с некоторого, такие значения n
и будем рассматривать.
решения xn
(t
). Это верно, возможно, не для всех n
, но для всех n
, начиная с некоторого, такие значения n
и будем рассматривать.
Согласно критерию Арцела (см. [23]), достаточно установить, что последовательность функций xn (t ) на Im равномерно ограничена и равностепенно непрерывна. Равномерная ограниченность непосредственно следует из определения множества M (x 0 ,t 0 , τ,a ): из (A.8) вытекает, что |xn (t )| ≤ |x 0 |+1 для всех n и для всех t . Для доказательства равностепенной непрерывности, как известно, достаточно установить равномерную ограниченность последовательности производных x ˙n (t ) на сегменте Im . Но из уравнения (A.7), которому удовлетворяет xn (t ), следует оценка
![]() ,
(A.10)
,
(A.10)
где Πm — прямоугольник на плоскости R 2 : Πm = J 0 × Im , причем J 0 = [x 0 − 1,x 0 + 1].
Действительно, движущаяся точка xn (t ) при t ∈ Im не выходит из прямоугольника Πm , согласно неравенству (A.8). Поскольку fn сходится к f равномерно на Πm (как и на любом компакте), правая часть в (A.10) ограничена (m — фиксировано) величиной max|f (x,t )| + δ, где δ > 0 — Πm
произвольно фиксировано, равномерно по n для n ≥ N δ . Здесь число N δ определяется по заданному δ.
Таким образом, мы проверили условия критерия Арцела и можем утверждать, что последовательность xn (t ) компактна в C (Im ).
Теперь выберем из последовательности xn
(t
) подпоследовательность, равномерно сходящуюся на сегменте I
1
. Из этой подпоследовательности выберем подпоследовательность, сходящуюся на сегменте I
2
. Продолжая этот процесс неограниченно и применяя диагональную процедуру Георга Кантора, мы получим подпоследовательность последовательности функций xn
(t
), которая равномерно сходится на каждом сегменте Im
(m
= 1,
2,...
), а значит, вообще на любом сегменте, содержащемся в интервале ![]() . Итак, существует предельная функция x
∞
(t
), заданная и непрерывная на всем интервале
. Итак, существует предельная функция x
∞
(t
), заданная и непрерывная на всем интервале ![]() . Аналогично последовательность
. Аналогично последовательность![]() сходится к непрерывной функции
сходится к непрерывной функции ![]() на том же интервале.
на том же интервале.
Докажем теперь, что![]() суть решения предельной задачи Коши
суть решения предельной задачи Коши
![]() .
(A.11)
.
(A.11)
Для этого достаточно заметить, что задача Коши (A.7) (дифференциальное уравнение вместе с начальным условием) эквивалентна интегральному уравнению, которому удовлетворяет xn (t )
t
Z
n n n
x (t ) = x 0 + fn (x (s ),s )ds. (A.12)
t n 0
Перейдем в этом уравнении к пределу, когда n
пробегает выделенную нами подпоследовательность значений. Тогда![]()
равномерно на любом сегменте Im . Поскольку fn → f равномерно на любом компакте, выполнены условия известной Вам теоремы о предельном переходе под знаком интеграла. Таким путем мы приходим к интегральному уравнению
t
Z
x ∞ (t ) = x ∞ 0 + f (x ∞ (s ),s )ds, (A.13)
t ∞0
из которого следует, что x ∞ (t ) является решением задачи Коши
![]() .
(A.14)
.
(A.14)
Аналогично устанавливается, что и функция![]() — решение этой же задачи Коши.
— решение этой же задачи Коши.
Мы уже видели, что ![]() . Переходя к пределу в (A.8) и (A.9), приходим к неравенствам (проделайте подробные доказательства)
. Переходя к пределу в (A.8) и (A.9), приходим к неравенствам (проделайте подробные доказательства)
![]() ,
(A.15)
,
(A.15)
| sup |x ∞ (t ) − x ∞ ∗ (t )| ≥ a. t ∞ 0 −τ<t<t ∞ 0 +τ |
(A.16) |
Мы доказали, что предельная функция принадлежит множеству f ∈ M (x 0 ,t 0 , τ,a ), а вместе с тем и лемму 1.
Лемма 2. Множество M (x 0 ,t 0 , τ,a ) нигде не плотно для любой точки (x 0 ,t 0 ) и любых чисел τ > 0, a > 0.
Доказательство. Рассуждая от противного, допустим, что множество M (x 0 ,t 0 , τ,a ) плотно в некотором шаре пространства C (R 2 ). Ввиду замкнутости, оно целиком содержит этот шар. В каждом шаре пространства C (R 2 ), как известно, плотно также и множество гладких функций C ∞ (нам сейчас достаточно рассматривать сужения функций из C (R 2 ) на круг B 1 (x 0 ,t 0 )). Но для гладкой функции f (x,t ) мы знаем теорему единственности задачи Коши для уравнения x ˙ = f (x,t ). Значит такая функция не может принадлежать множеству M (x 0 ,t 0 , τ,a ) (красиво?). Лемма 2 доказана.
Теорема Орлича. Множество M функций f ∈ C (R 2 ) таких, что уравнение x ˙ = f (x,t )обладаетхотябыоднойточкойнеединственности на плоскости R 2 , является множеством первой категории в C (R 2 ).
Доказательство. Очевидно, что всякая функция f такая, что существует хотя бы одна точка неединственности уравнения x ˙ = f (x,t ), принадлежит некоторому множеству M (x 0 ,t 0 , τ,a ). Более того, ясно, что при этом можно считать числа x 0 , t 0 , τ, a рациональными. Множество Q всех рациональных чисел счетно, множество всех четверок рациональных чисел x 0 , t 0 , τ, a тоже счетно (докажите!). Мы установили, что множество M является счетным объединением
M = [ M(x0 ,t0 ,τ,a) (A.17)
по всем x 0 , t 0 , τ, a ∈ Q . Согласно лемме 2, каждое из множеств M (x 0 ,t 0 , τ,a ) нигде не плотно. Теорема доказана.
В свете этой теоремы ситуация с проблемой единственности решения задачи Коши выглядит драматической. На самом деле, единственность — при любой начальной точке! — имеет место для подавляющего большинства уравнений x ˙ = f (x,t ), f ∈ C (R 2 ). В то же время классическая теорема единственности относится к функциям f , удовлетворяющих условию Липшица, которые в совокупности образуют множество 1-й категории в C (R 2 ). Ситуация с теоремой единственности Осгуда чуть менее ясна. Если зафиксировать в этой теореме функцию g (s ), оценивающую модуль непрерывности функции f , и рассматривать лишь такие f , для которых локально, вблизи каждой точки (x 0 ,t 0 ) ∈ R 2 , выполнено неравенство
|f (x 0 ,t ) − f (x 00 ,t )| ≤ Kg (|x 0 − x 00 |), K > 0, (A.18)
то нетрудно доказать, что соответствующее множество Cg имеет 1-ю категорию.
Вопрос: какова категория множества всех f, удовлетворяющих условиям теоремы Осгуда?
Напомню, что функция g должна лишь подчиняться требованию
![]() .
(A.19)
.
(A.19)
При этом, конечно, предполагается, что g (0) = 0, но g (s ) > 0 для всех s > 0 (или для s достаточно малых). Имеются небольшие обобщения теоремы Осгуда, скажем, в неравенстве (A.18) можно еще допустить множитель ϕ(t ) при достаточной регулярности функции ϕ (см. [35, 49]).
Все это говорит о том, что нужно и интересно искать новые подходы к доказательству теоремы единственности задачи Коши. "Силовые подходы основанные на оценках типа (A.18) абсолютной величины разности f (x 0 ,t ) и f (x 00 ,t ) для пары решений x 0 и x 00 , по-видимому, не приводят к результату для очень многих дифференциальных уравнений, обладающих, на самом деле, свойством единственности.
Надо признаться, что предыдущее утверждение может оказаться "ложной тревогой". В математике не так уж редко случается, что то или иное явление происходит в "подавляющем большинстве" случаев, но установить, что оно происходит в данном конкретном случае, очень трудно, а то и практически невозможно. Например, известно, что в ситуации общего положения линейный оператор A : Rn → Rn имеет ненулевой определитель и обратим, но доказать, что данный определитель отличен от нуля, — непростое дело. Оказалось, что в общей проблеме обратимости оператора A целесообразно изменить постановку вопроса: вместо индивидуального оператора A , рассматривать однопараметрическое семейство операторов A − λI . Тогда можно установить, что обратимость имеет место для всех значений λ, кроме конечного набора собственных значений (в случае банахова пространства и вполне непрерывного оператора A — кроме не более чем счетного множества значений). Это всё, что может дать общая теория. Выяснение того, для каких λ оператор A − λI обратим, и для каких он необратим, распадается на необозримое множество различных частных теорий, которые в совокупности образуют спектральную теорию линейных операторов, и еще, пожалуй, не оформившуюся в самосостоятельную дисциплину бесконечномерную линейную алгебру.
Другой пример — свойства эргодичности и перемешивания динамической системы [48]. Для конкретных систем доказательство эргодичности и перемешивания, как правило, чрезвычайно трудно, хотя доказано, что эргодические системы образуют множество 2-ой категории при определенном выборе топологии. Кстати, это как раз хороший пример зависимости категории по Бэру от выбора топологии.
Если проводить аналогию между проблемой единственности и перечисленными выше проблемами, то с некоторой вероятностью (по-моему, не очень большой) можно опасаться, что для уравнения x ˙ = f (x,t ), где f — всего лишь непрерывная функция, не получится вполне общей теоремы единственности. Интересно, однако, найти пусть частные, условия, обеспечивающие единственность для множества таких уравнений 2-й категории.
О других подходах к проблеме неединственности. Наряду с классификацией множеств по Бэру, имеются и другие подходы к проблеме сравнения множеств по их "массивности". Например, если на рассматриваемом множестве (нас сейчас интересует C (R 2 )) задана некоторая мера, принято и естественно считать "пренебрежимо малыми" множества меры 0. Существенно заметить, что в случае, когда на данном множестве определены и метрика, и мера, эти два подхода могут существенно разойтись. В частности, множество 1-й категории может иметь положительную меру.
В.И. Арнольд не раз обращал внимание на подобное расхождение в ряде важных вопросов теории динамических систем. Поэтому, рассказывая ему о теореме Орлича, я предвидел, что он спросит и о подходе к данной проблеме с точки зрения меры. Это трудный вопрос. Неясно даже, как его корректно сформулировать, поскольку для бесконечномерных метрических пространств не существует естественного аналога меры Лебега в Rn . Какую же меру выбрать? От этого выбора тоже зависит результат. В такой ситуации интересно для начала рассмотреть семейства дифференциальных уравнений, зависящие от конечного числа параметра, например, выбрать в качестве их правых частей конечные линейные комбинации функций из
n
C (R 2 ), скажем, P ck fk (x,t ). Теперь каждому уравнению с такой правой
k =1
частью соответствует точка (c
1
,...,cn
) ∈ Rn
. И резонно спросить, какова мера Лебега множества точек, отвечающих уравнениям, обладающим точками неединственности. При этом можно считать, что коэффициенты ck
ограничены, например, неравенством![]() . Нетрудно привести примеры таких семейств уравнений
. Нетрудно привести примеры таких семейств уравнений
![]() ,
(A.20)
,
(A.20)
для которых точки неединственности присутствуют при любом выборе коэффициентов (например, положим fk (x,t ) = |x |1/ 2k ); тогда (0,t 0 ) — точка неединственности при любом t 0 . Предположим однако, что данное семейство содержит хотя бы одно уравнение, для которого верна теорема единственности решения задачи Коши при любом выборе начальной точки. Что можно тогда сказать о мере множества тех уравнений семейства (я уже отождествил уравнение и определяющую его точку (c 1 ,c 2 ,...,cn )), которые обладают хотя бы одной точкой неединственности?
Поставим вопрос о мере множества тех точек (c 1 ,c 2 ,...,cn ) ∈
n
Rn и удовлетворяющих условию P c 2 k ≤ a 2 (при заданном a > 0),
k =1
для которых уравнение ( A.20) имеет хотя бы одну точку неединственности. При этом предполагается, что для некоторого набора c 0 1 ,...,c 0 n единственность имеет место для всех начальных точек в R 2.
У меня нет полной уверенности, что это уже окончательная постановка задачи. В конце концов, лишь красивый ответ может подтвердить разумность вопроса. Есть однако надежда, что двигаясь в намеченном направлении, возможно прийти к интересным постановкам задач, допускающих содержательные решения.
О глобальной разрешимости. Наряду с единственностью, представляет значительный интерес глобальная разрешимость задачи Коши для дифференциального уравнения x ˙ = f (x,t ). Глобальная разрешимость означает, что для любой начальной точки решение задачи Коши (все решения, если их много) можно продолжить на всю временную ось (или хотя бы на положительную полуось — это другой вариант вопроса).
Типична ли глобальная разрешимость? Какова категория множества глобально разрешимых уравнений? Мне кажется, что в отличие от единственности, глобальная разрешимость нетипична. Может быть, кто-нибудь возьмется подтвердить или опровергнуть эту гипотезу.
Упражнения к Приложению A
1. Доказать, что множество вещественных чисел, в разложении которых в k -ричную дробь какая либо цифра, начиная с некоторого места, отсутствует, есть множество 1-й категории в R .
2. Из результата предыдущего упражнения вывести, что существуют такие числа, что в их разложениях в k -ричную дробь для любого k , каждая значащая цифра присутствует бесконечно много раз. Более того, множество таких чисел является вычетом.
3. Доказать, что множество ограниченных
непрерывных функций есть множество первой категории в C
(R
2
). Доказать, что и множество непрерывных функций f
, таких что ![]() (при фиксированном α) — ограниченная функция на R
2
, — тоже множество 1-й категории в C
(R
2
).
(при фиксированном α) — ограниченная функция на R
2
, — тоже множество 1-й категории в C
(R
2
).
4. Докажите, что как существование у вещественного полинома x 2 + px + q пары вещественных простых корней, так и существование у него пары комплексно сопряженных корней — типичные ситуации, а существование кратного корня — нетипично (в смысле категорий соответствующих множеств точек (p,q ) на плоскости R 2 ). Как обобщить этот вывод на полиномы n -й степени?
5. Рассмотрим пространство функций C (a,b ), непрерывных на интервале (a,b ). Определим сходимость в этом пространстве, считая, что fn → f , если и только если fn (x ) → f (x ) равномерно по x на любом сегменте [α, β] ⊂ (a,b ). По аналогии с метрикой (A.3), определите метрику, отвечающую этому типу сходимости.
6. Докажите, что множество функций из C (R 2 ), удовлетворяющих условию Липшица, есть множество 1-й категории.
7. Останется ли верной теорема Орлича, если в ней заменить пространство C (R 2 ) на банахово пространство MC (R 2 ) непрерывных и ограниченных на R 2 функций? Норма в этом пространстве определяется равенством:
![]() .
.
8. Вспомните доказательство и докажите, что задача Коши x ˙ = f (x ), x (0) = x 0 для одного скалярного дифференциального уравнения имеет, и притом единственное, решение для любой непрерывной функции f (x ) при одном лишь условии, что f (x 0 ) 6= 0.
√![]()
9. Рассмотрите задачу Коши x ˙ = 3 x + εt , x (0) = 0. При ε = 0 решение неединственно. А при ε 6= 0?
10. Рассмотрите уравнение x ˙ = |x +ε |t |β |α , при 0 < α < 1, и 0 < β < 1. При ε = 0 у него есть точка неединственности. Имеются ли точки неединственности при ε 6= 0? (Конечно модули уродуют это уравнение, но их можно опустить, если выбрать в качестве α и β правильные дроби с нечетными знаменателями). Ответ мне в данный момент неизвестен. Теорема Орлича подсказывает гипотезу: при ε 6= 0 — всегда единственность. Любопытно также посмотреть, что дадут стандартные программы решения задачи Коши применительно к уравнениям такого типа.
11. Если физик-экспериментатор покажет Вам матрицу, например, размеров 10×10, элементы которой получены путем измерений, и спросит какова ее жорданова форма, Вы можете уверенно отвечать, что диагональная. Почему?
12. А теперь представьте себе, что Ваш друг, физик-экспериментатор из предыдущего упражнения, попросил Вас привести к диагональному виду два-три десятка матриц 10×10. Еще он Вам сообщил, что каждая из этих матриц многократно проверена независимыми экспериментами. Анализируя диагональные формы этих матриц, он рассчитывает получить важные физические выводы (допустим, об озоновой дыре, либо о строении кристаллов). У Вас имеется несколько стандартных программ диагонализации матриц, все они Вами хорошо проверены и много раз применены для различных матриц 20-го и 30-го порядка. И вот выяснилось, что все Ваши программы отказываются работать для этих матриц. Скорей всего, Вы должны поздравить своего друга-физика с большим успехом. Почему? Что Вы предлагаете делать дальше?
Приложение 2. Изометрии и вращения банахова
пространства. Теорема Мазура и Улама
Здесь изложена замечательная теорема Мазура и Улама о линейности изометрического отображения U : X → Y одного банахова пространства в другое, при условии, что 0 ∈ X переходит в 0 ∈ Y , так что U (0) = 0. Сохраняя основную идею доказательства [5], я попытался прояснить его ход при помощи введения понятия центра множества в метрическом пространстве.
Центрограниченногомножества. Пусть X — метрическое пространство, и M ⊂ X — ограниченное множество в нем. Это означает, что M содержится в некотором шаре пространства X . Определим диаметр d (M ) множества M , полагая
d (M ) = sup ρ(x,y ). (A.1)
x,y ∈M
Очевидно, для ограниченных множеств, и только для них, диаметр конечен. Теперь определим 1-центр C 1 (M ) множества M , полагая
![]() .
(A.2)
.
(A.2)
Таким образом, множество C 1 (M ) состоит из всевозможных точек пространства X , удаленных от произвольной точки множества M не более, чем на половину диаметра множества M .
Например, 1-центр шара в евклидовом пространстве есть попросту множество, состоящее из одной точки — его центра. Бывает, что 1-центр множества пуст: выбросим центр некоторого шара из X , тогда 1-центр шара полученного пространства не будет содержать ни одной точки.
Теперь по индукции определим n -центр Cn (M ) для любого натурального n = 2, 3... , полагая
C 2 (M ) = C 1 (C 1 (M )) ∩ C 1 (M ), ..., Cn (M ) (A.3) = C 1 (Cn −1 (M )) ∩ Cn −1 (M ),...
Заметим, что 1-центр C 1 (M ) конструируется из точек пространства X , в то время как n -центр Cn (M ) при n = 2, 3,... обязан быть подмножеством (n − 1)-центра.
Определим, наконец, центр ограниченного множества M ⊂ X как пересечение всех n -центров
![]() (A.4)
(A.4)
Лемма 1. Центр всякого ограниченного множества M метрического пространства X содержит не более одной точки
Доказательство. Докажем, что диаметр n -центра, по крайней мере, в 2n −1 раз меньше чем d (M ):
![]() .
(A.5)
.
(A.5)
Если x, y ∈ C 1 (M ), то ввиду определения 1-центра (A.2), выполняется неравенство
ρ(x,y) ≤ d(M). (A.6)
Если x, y ∈ Cn (M ), n ≥ 2, то x, y ∈ Cn −1 (M ), поэтому
![]() .
.
Отсюда сразу следует неравенство (A.5) при n = 2, а затем по индукции и для любых n .
Неравенство (A.5) показывает, что диаметр центра C (M ) равен нулю. Это доказывает лемму 1.
Дальше будем считать, что X — банахово пространство, так что ρ(x 1 ,x 2 ) = kx 1 − x 2 kX , где k · kX — норма в пространстве X .
Скажем, что множество M ⊂ X центрально-симметрично , и ξ ∈ X его центр симметрии , если точки x = ξ ± u принадлежат M . Заметим, что преобразование S : M → M , определенное равенством Sx = ¯x = 2ξ − x есть инверсия : S 2 x = x ¯¯ = x , S 2 = I .
Лемма 2. Если множество M в X — центрально-симметрично, то и его n-центры также центрально-симметричны (с тем же центром симметрии ξ), а центр C (M ) либо пуст, либо состоит из одной точки ξ.
Доказательство. Докажем, что 1-центр C 1 (M ) центрально-симметричен относительно точки ξ. Пусть x = ξ + u ∈ C 1 (M ). Это означает, что неравенство
![]() (A.7)
(A.7)
выполнено для любых z ∈ M . Неравенство (A.7) остается верным и при замене z на z ¯, так как z ¯ ∈ M . Поэтому имеем
![]() (A.8)
(A.8)
Таким образом, 1-центр C 1 (M ) центрально-симметричен. Очевидная индукция дает тот же результат и для n -центра Cn (M ). Тогда и центр C (M ) центрально-симметричен, будучи пересечением центрально симметричных множеств. Если теперь допустить, что центр C (M ) содержит точку x = ξ + u , то также и точка x ¯ = ξ − u ему принадлежит. Но, по лемме 1, эти точки должны совпадать. Поэтому u = 0, и лемма 2 доказана.
Следствие.
Пусть множество
M
= {x
1
,x
2
}, где
x
1
и
x
2
произвольные точки в
X. Тогда для множества
M, состоящего из двух точек
x
1
и
x
2
, центр
C
(M
) есть множество, состоящее из одной точки
![]() .
.
Изометрии и вращения. Напомню, что отображение U : X → Y
метрического пространства X в метрическое пространство Y называется изометрическим или изометрией , если для любых x 1 , x 2 ∈ X выполнено равенство
ρY (Ux1 ,Ux2 ) = ρX (x1 ,x2 ). (A.9)
В случае банаховых пространств X и Y равенство (A.9) записывается в виде
kUx1 − Ux2 kY = kx1 − x2 kX . (A.10)
Очевидно, всякое изометрическое отображение непрерывно. Столь же очевидно, что изометрия отображает пространство X на свой образ U (X ) взаимно однозначно.
В любом банаховом пространстве X каждому элементу h можно поставить в соответствие изометрическое отображение Lh : x 7→ x +h , называемое переносом или трансляцией на вектор h . Если U : X → X — изометрия банахова пространства X , то отображение U 0 , определяемое равенством U 0 x = Ux − U (0) — также изометрия. При этом точка 0 ∈ X есть неподвижная точка отображения U 0 , так что U 0 (0) = 0.
Взаимно однозначное отображение U : X → X называется вращением (банахова пространства X ), если оно изометрично и оставляет неподвижной точку ноль.
Подчеркну, что в следующей теореме не требуется, чтобы образ U (X ) пространства X при отображении U совпадал со всем пространством Y .
Теорема Мазура и Улама. Всякое изометрическое отображение U : X → Y банахова пространства X в банахово пространство Y , переводящее 0 пространства X в 0 пространства Y (так что U (0) = 0) — линейно.
Доказательство.
Пусть x
1
и x
2
— произвольные точки в X
. Согласно следствию, центр множества {x
1
,x
2
} есть ![]() .
.
Определения n
-центров и центра множества связаны лишь с метрикой, а изометрия U
ее сохраняет. Поэтому ясно, что отображение U
переводит центр любого множества M
⊂ X
в центр его образа U
(M
) ⊂ Y
. Поскольку центр множества {Ux
1
,Ux
2
} есть ![]() , приходим к равенству
, приходим к равенству
![]() .
(A.11)
.
(A.11)
Полагая здесь x 1 = x и x 2 = 0 и учитывая, что U (0) = 0, для любого x ∈ X получим равенство
![]() (A.12)
(A.12)
Теперь для произвольных x 1 , x 2 ∈ X , полагая в (A.12) x = x 1 + x 2 и применяя (A.11), выводим
![]() (A.13)
(A.13)
.
Это означает, что оператор U аддитивен . Хорошо известно (см. ниже лемму 3), что, вместе с непрерывностью в нуле (а изометрический оператор непрерывен всюду), это свойство влечет линейность оператора U . Теорема доказана.
Лемма 3. Пусть оператор U : X → Y ( X и Y — банаховы) аддитивен и непрерывен в точке 0 ∈ X . Тогда он непрерывен всюду и однороден, то есть U — линейный оператор.
Доказательство. По условию, для любых x 1 , x 2 ∈ X выполняется равенство
U (x 1 + x 2 ) = Ux 1 + Ux 2 . (A.14)
Из него по индукции получается более общее равенство
U(x1 + x2 + ... + xm ) = Ux1 + Ux2 + ... + Uxm . (A.15)
Полагая x 1 = x 2 = ... = xm = x , выводим равенство
U (mx ) = mUx (A.16)
для любого натурального m
и любого x
∈ X
. Заменяя здесь![]() , получим
, получим
![]() (A.17)
(A.17)
Поскольку m ∈ N в (A.16) и (A.17) произвольно, для любого рациональ-
ного числа![]() , выводим равенство
, выводим равенство
![]() (A.18)
(A.18)
Итак, всякое положительное рациональное число можно выносить за знак оператора U . Покажем, что можно выносить и −1. Действительно, если положить в (A.14) x 1 = x 2 = 0, то получится, что U (0) = 2U (0), так что U (0) = 0. Далее, если положить в (A.14) x 1 = x и x 2 = −x , то получим
U (0) = Ux + U (−x ).
Так как U
(0) = 0, выходит, что U
(−x
) = −U
(x
). Теперь ясно, что равенство (A.18) справедлива для любых рациональных![]() .
.
Докажем, что из непрерывности аддитивного оператора в точке 0 следует его непрерывность в произвольной точке x . Действительно, если xn →
x , то ξn = xn − x → 0 и
Uxn −Ux = U (x +ξn )−Ux = Ux +U ξn −Ux = U ξn → 0, (A.19)
ввиду непрерывности оператора U в нуле. Итак, оператор U непрерывен в любой точке x ∈ X .
Если теперь λ
∈ R
— любое вещественное число, то мы возьмем последовательность рациональных чисел вида![]() , сходящуюся к λ, и, переходя к пределу в (A.18), найдем
, сходящуюся к λ, и, переходя к пределу в (A.18), найдем
U (λx ) = λUx. (A.20)
Итак, оператор U непрерывен всюду, аддитивен и однороден, то есть линеен. Лемма 3 доказана.
Как доказал З. Хажинский [61], всякий изометрический оператор, действующий в конечномерном линейном метрическом пространстве также линеен. Для доказательства он построил по данной метрике преднорму (отличается от нормы только тем, что она может обращаться в ноль и на ненулевых векторах) с тем же нулем, инвариантную относительно всех изометрий. Далее, в [61] использована теорема Мазура–Улама и индукция по размерности пространства.
Упражнения к Приложению B
1. Метрическое пространство X состоит из 5-и точек: x 1 , x 2 , x 3 , x 4 ,x 5 . Метрику зададим, полагая ρ(x 1 ,x 2 ) = 1, ρ(x 1 ,x 3 ) = 1, ρ(x 1 ,x 4 ) = 1; ρ(x 1 ,x 5 ) = 2; ρ(x 2 ,x 3 ) = 1/ 2; ρ(x 2 ,x 4 ) = 1/ 2; ρ(x 2 ,x 5 ) = 1; ρ(x 3 ,x 4 ) = 1/ 2; ρ(x 3 ,x 5 ) = 1; ρ(x 4 ,x 5 ) = 1. Проверьте выполнение аксиом метрики. Найдите 1-центр этого пространства, а также его центр.
s x 4
x 1 s s x 3 s x 5
s x 2
2. Докажите, что для всякого шара B в банаховом пространстве X центр C (B ) есть его центр в обычном смысле слова.
3. Пусть U : X → Y — изометрическое отображение метрического пространства X в метрическое пространство Y . Докажите, что для любого множества M ⊂ X с непустым центром C (M ) = {ξ } его образ U (M ) ⊂ Y также имеет центр η ∈ Y и U ξ = η. Докажите также, что U (Cn (M )) = Cn (U (M )).
4. Пусть D
— множество в Rn
, содержащее не менее, чем n
+ 1 точку, среди которых имеется точка 0 ∈ Rn
, а остальные n
точек линейно независимы. Индуцированная на нем метрика пространства Rn
превращает D
в метрическое пространство. Пусть U
: D
→ Rn
— изометрическое отображение, оставляющее точку 0 неподвижной. Докажите, что его можно считать линейным. Точнее, существует линейное изометрическое отображение U
ˆ
: Rn
→ Rn
, однозначно определяемое отображением U
, и такое, что его сужение на D
есть U
, или, в символах:![]() .
.
5. Докажите, что, если в теореме Мазура и Улама отбросить условие сохранения нуля, то можно утверждать, что изометрическое отображение аффинно , то есть U = U 0 +Lh , где Lh — трансляция на постоянный вектор h , а U 0 — линейное изометрическое отображение.
ЛИТЕРАТУРА
[1] Александров П.С., Колмогоров А.И. Введение в теорию функций действительного переменного. М.–Л.: ГТТИ, 1938. 268 с.
[2] Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: Наука, 1984. 271 с.
[3] Арнольд В.И. Математические методы классической механики. М.: Наука, 1989. 472 с.
[4] Бабский В.Г., Копачевский Н.Д., Мышкис А.Д., Слобожанин Л.А., Тюпцов А.Д. Гидромеханика невесомости. М.: Наука, 1976. 504 с.
[5] Банах С. Теория линейных операций. Москва–Ижевск, РХД. 2001. 272 с.
[6] Вайнберг М.М. Вариационные методы исследования нелинейных операторов. — М.: Гостехиздат, 1956. — 344 с.
[7] Ван дер Варден Б.Л. Алгебра. М. Наука, 1976. 648 с.
[8] Ворович И.И. Лекции по динамике Ньютона. Современный взгляд на механику Ньютона и ее развитие — Москва–Ижевск: Инст. комп. исследов., 2004. — 680 с.
[9] Гиббс Дж.В. Термодинамика. Статистическая механика. М.: Наука, 1982. 323 с.
[10] Громол Д., Клингенберг В., Мейер В. Риманова геометрия в целом. М.: Мир, 1971. 343 с.
[11] Далецкий Ю.Л., Крейн М.Г. Устойчивость решений дифференциальных уравнений в банаховом пространстве. М.: Наука, 1970. 534 с.
[12] Демидович Б.П. Лекции по математической теории устойчивости. M.: Наука. 1967. 472 с.
[13] Зеньковская С.М., Юдович В.И. Метод интегро-дифференциальных уравнений и цепных дробей в задаче параметрического возбуждения волн // ЖВМ и МФ. 2004. № 4. С. 370–384.
[14] Зоммерфельд А. Механика. М.: ИЛ, 1947. 391 с.
[15] Зорич В.А. Математический анализ. Т. I, II. М.:Наука, 1984. 642 с.
[16] Козлов В.В. Асимптотические движения и проблема обращения теоремы Лагранжа – Дирихле // ПММ. 1986. Т. 50. Вып. 6. С. 928–937.
[17] Козлов В.В., Паламодов В.П. Об асимптотических решениях уравнений классической механики // ДАН СССР. 1982. Т. 263, № 2. С. 285–
289.
[18] Курант Р., Гильберт Д. Методы математической физики. Т. 1. М.–Л.: Гостехиздат, 1951. 476 с.
[19] Ламб Г. Гидродинамика. М.: Гостехиздат, 1947. 928 с.
[20] Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 1988. 216 с.
[21] Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, 1988. 508 с.
[22] Лионс Ж.-Л. Некоторые методы решения нелинейных краевых задач. М.: Мир, 1972. 588 c.
[23] Люстерник Л.А., Соболев В.И. Элементы функционального анализа. М.: Наука, 1965. 518 с.
[24] Ляпунов А.М. Общая задача об устойчивости движения. М.–Л.: Гостехиздат, 1950. 471 с.
[25] Малкин И.Г. Теория устойчивости движения. М.: Наука. 1966. 532 c.
[26] Меркин Д.Р. Введение в теорию устойчивости движения. М.: Наука. 1987. 304 с.
[27] Миранда К. Уравнения с частными производными эллиптического типа. М.: Изд-во ИЛ, 1957. 256 с.
[28] Михлин С.Г. Вариационные методы в математической физике. М.: ГИТТЛ, 1957. 476 с.
[29] Михлин С.Г. Уравнения математической физики. M.: Наука, 1968. 576 с.
[30] Натансон И.П. Теория функций вещественной переменной. М.: Наука, 1974. 480 с.
[31] Немыцкий В.В., Степанов В.В. Качественная теория дифференциальных уравнений. М.-Л.: ГИТТЛ, 1949. 550 с.
[32] Ньютон И. Математические начала натуральной философии. — М.: Наука, 1989. — 688 с.
Newton I. Philosophiae Naturalis Principia Mathematica, London, 1687;
[33] Олвер П. Приложение групп Ли к дифференциальным уравнениям. М.: Мир, 1989. 640 с.
[34] Паули В. Теория относительности. М.: Наука, 1991. 328 с.
[35] Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: Наука, 1970. 280 с.
[36] Повзнер А.Я. Теорема существования в целом для нелинейной системы и индекс дефекта линейного оператора // Сибирский математический журнал. 1964. Т. 5, № 2. С. 377–386.
[37] Полак Л.С. Вариационные принципы механики. М.: Физ.-мат. лит. 1960. 932 с.
[38] Рудин У. Основы математического анализа. М.: Мир, 1976. 320 с.
[39] Руш Н., Абетс П., Лалуа М. Прямой метод Ляпунова в теории устойчивости. М.: Мир, 1980. 300 с.
[40] Соболев С.Л. Уравнения математической физики. М.: ГИТТЛ, 1954. 444 с.
[41] Степанов В.В. Курс дифференциальных уравнений. — М.: Физматгиз, 1959. 468 c.
[42] Федорюк М.В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений. Наука. 1983. 352 с.
[43] Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Т.12. — M.: Мир, 1976. 439 с.
[44] Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. I, II, III. М.: Наука, 1964.
[45] Фундаментальные и прикладные проблемы теории вихрей. Под ред. Борисова А.В., Мамаева И.С., Соколовского М.А. Москва-Ижевск:
Инcт. комп. исследов. 2003. 704 с.
[46] Хаар Д. Основы гамильтоновой механики. М.: Наука, 1974. 225 c.
[47] Хазин Л.Г., Шноль Э.Э. Устойчивость критических положений равновесия. Пущино: ОНТИ НЦБИ АН СССР, 1985.
[48] Халмош П.Р. Лекции по эргодической теории. Ижевск: Изд. дом "Удмуртский университет 1999. 136 с.
[49] Хартман Ф. Обыкновенные дифференциальные уравнения. — М.: Мир, 1970. 720 с.
[50] Четаев Н.Г. Устойчивость движения. Гостехиздат. 1955. 176 c.
[51] Шарковский А.Н. Сосуществование циклов непрерывного преобразования прямой в себя // Украинский матем. журнал. 1964. Т. XVI, № 1. С. 61–70.
[52] Эйнтштейн А. Собрание научных трудов. Т. 1. М.: Наука, 1965. С. 7–
35.
[53] Юдович В.И. Глобальная разрешимость против коллапса в динамике несжимаемой жидкости // В сб. «математические проблемы XX века». М.: Фазис, 2003. С. 519–548.
[54] Юдович В.И. Динамика нити // Деп. в ВИНИТИ 10.10.95, №2725В95.
[55] Юдович В.И. Косимметрия, вырождение решений операторных уравнений, возникновение фильтрационной конвекции // Мат. заметки. 1991. Т. 49. N. 5. C. 142–148.
[56] Юдович В.И. Лекции об уравнениях математической физики. Изд-во Ростовского ун-та, 1998. 240 с.
[57] Юдович В.И. Лекции об уравнениях математической физики. Часть вторая. Изд-во Ростовского ун-та, 1999. — 255 с.
[58] Юдович В.И. Метод линеаризации в гидродинамической теории устойчивости. Ростов-на-Дону, изд-во РГУ, 1984. 192 с. (Англ. перевод: Yudovich V. I. “The Linearization Method in Hydrodynamical Stability Theory”, Translation of mathematical monographs, 74 ,
American Mathematical Society, Providence, Rhodeisland, 177 p., (1989))
[59] Юдович В.И., Срубщик Л.С. Динамическое прощелкивание и запас устойчивости нелинейной упругой системы // ПММ. Т. 50. 1986. С. 426–435.
[60] Broer L.J.F. On the Dynamics of Strings // J. Engineering Mathematics. 1970. Vol. 4. No. 3. P. 195–202.
[61] Charzinski Z. Sur les transformations isometrique dans les espace du type´ (F), Studia Math., 13, 1953, pp. 94–121.
[62] Janda J. Uber die Kategorie der Menge stetiger Funktionen, welche¨ Differentialgleihungen ohne Eindeutigkeit bestimmen // Czechoslovak Mathematical Journal, 23 (98), no. 1, 1973, 30–33.
[63] Kisielewicz M. Description of a class of differential equations with setvalued solutions // Atti Ac. Naz. Lincei. Rend. Cl. Sci. fis.mat. e natur. 58, no. 2, 1975, 158–162.
[64] Kisielewicz M. Description of a class of differential equations with setvalued solutions // Atti Ac. Naz. Lincei. Rend. Cl. Sci. fis.mat. e natur. 58, no. 3, 1975, 338–341.
[65] Orlicz W. Zur Theorie der Differentialgleichung y 0 = f (t,y ) // Bull. de Acad. Pol. des Sciences, Ser. A, 1932, 221–228.
[66] Verhulst, P. F. Notice sur la loi que la population pursuit dans son accroissement // Correspondance mathe’matique et physique. 1838.
10:113–121.
ОГЛАВЛЕНИЕ
Об авторе и этой книге 2
Предисловие автора 4
Математические модели 8
1 Динамические системы . . . . . . . . . . . . . . . . . . . . 8
2 Автономные дифференциальные уравнения . . . . . . . . . 12
3 О глобальной разрешимости задачи Коши и единственности
решения . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
4 Динамические системы с дискретным временем . . . . . . . 26
5 Интегралы и законы сохранения . . . . . . . . . . . . . . . 38
6 Неавтономные дифференциальные уравнения . . . . . . . . 45
7 Интегро-дифференциальные уравнения . . . . . . . . . . . 48
8 Декартово произведение динамических систем и разбиение
системы на независимые подсистемы . . . . . . . . . . . . . 51
9 Производные и градиенты . . . . . . . . . . . . . . . . . . . 54
Механика 60
10 Принцип Гамильтона и уравнения Лагранжа II рода . . . . . 62
11 Лагранжианы материальных частиц . . . . . . . . . . . . . 75
12 Законы сохранения в механике . . . . . . . . . . . . . . . . 82
13 Принцип Гамильтона для систем со связями . . . . . . . . . 99 14 Принцип наименьшего действия Мопертюи
(Мопертюи–Эйлера–Лагранжа–Якоби) . . . . . . . . . . . 106 15 Применение принципа Гамильтона в механике сплошной среды116
16 Принцип Гамильтона и конечномерные аппроксимации бесконечномерных систем . . . . . . . . . . . . . . . . . . . . . 129 17 Динамика гибкой нерастяжимой нити . . . . . . . . . . . . . 136
18 Уравнение колебаний струны . . . . . . . . . . . . . . . . . 152
19 Специальная теория относительности Эйнштейна . . . . . . 162
20 Каноническая гамильтонова форма уравнений механики . . . 174
21 Силы трения. Диссипация энергии . . . . . . . . . . . . . . 184
Содержание
![]()
Элементы статистической механики 194
22 О законах термодинамики . . . . . . . . . . . . . . . . . . . 195
23 Теоремы Пуанкаре о возвращении . . . . . . . . . . . . . . 198
24 Гидродинамическая интерпретация систем дифференциальных уравнений и теорема Лиувилля . . . . . . . . . . . . . . 205 25 Распределение Гиббса . . . . . . . . . . . . . . . . . . . . . 214
26 Статистическая механика идеального газа . . . . . . . . . . 220
27 Метод Лапласа асимптотической оценки интегралов . . . . . 227
28 Градиентные системы . . . . . . . . . . . . . . . . . . . . . 235
29 Малые колебания механической системы около положения равновесия . . . . . . . . . . . . . . . . . . . . . . . . . . . 244
30 Статистическая механика твердого тела . . . . . . . . . . . 257
Приложение 1. Типичность единственности и нетипичность
неединственности решения задачи Коши 260
Приложение 2. Изометрии и вращения банахова пространства.
Теорема Мазура и Улама 274
ЛИТЕРАТУРА 281
| |||||
| |||||
| |||||
| |||||
|
Смотреть все комментарии (13)
Работы, похожие на Реферат: Математические модели естествознания
Меню |
||||
| Главная Рефераты Благодарности |
||||
Опрос |
||||
|
|
||||




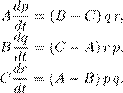 (5.15)
(5.15)
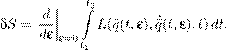 (10.4)
(10.4)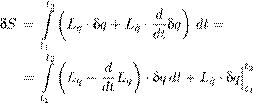 .
(10.9)
.
(10.9)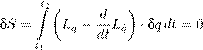 .
(10.12)
.
(10.12)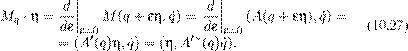
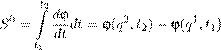 ,
(10.36)
,
(10.36)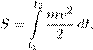 (11.11)
(11.11)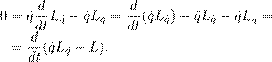 (12.1)
(12.1)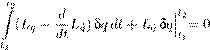 .
(12.21)
.
(12.21)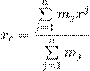 .
(12.32)
.
(12.32)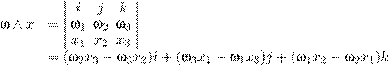 (12.44)
(12.44)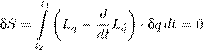 .
(13.20)
.
(13.20)
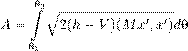 .
(14.9)
.
(14.9)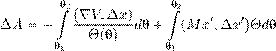 .
(14.11)
.
(14.11)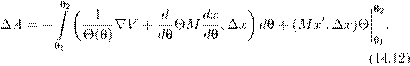
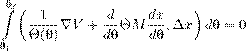 .
(14.13)
.
(14.13)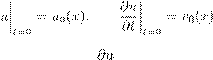 .
(15.3)
.
(15.3)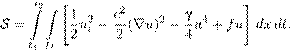 (15.7)
(15.7)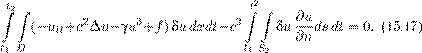
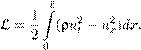 (16.4)
(16.4)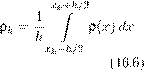
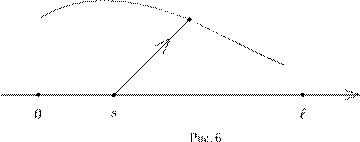 x
(s,t
)
x
(s,t
)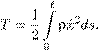 (17.4)
(17.4)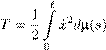 .
(17.5)
.
(17.5)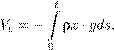 (17.6)
(17.6)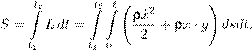 (17.7)
(17.7)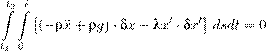 .
(17.19)
.
(17.19) HH
HH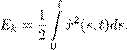 (17.40)
(17.40)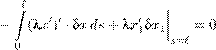 .
(17.50)
.
(17.50)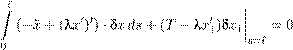 .
(17.51)
.
(17.51)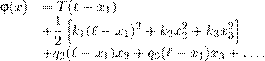 (18.19)
(18.19)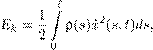 (18.26)
(18.26)