- Неоптолемеевская механика - это не новая механика, а новый язык механики на фундаменте ньютоновской. Аналогично механикам Лагранжа,, Гамильтона и т.п. Разработана применительно к задачам мегамеханики – небесной, звездной, галактической, космологической и космонавтики.

- Для космонавтики коперникианский подход рассмотрения движения в системе Солнца или, вообще, выделенных системах отсчета несодержателен. В ней необходимо рассматривать движение всех объектов – Солнца, Земли, астероидов и метеоритов, планет и лун, иных космических объектов в системе отсчета космического корабля. Фактически, речь идет о возврате к птолемеевскому подходу в механике.

- Для создания неоптолемеевского языка требуется новый анализ основных механических понятий, исходя из практики космонавтики (!!!!! )

Понятие о механическом состоянии механических объектов

- Механическое состояние механических объектов – новое понятие механики.

- Рассматриваются два типа состояний – свободное и несвободное.

- Парашютист в свободном падении, снаряд или боеголовка, космический корабль, космонавт на орбите, Земля, Луна, Солнце, звезды, галактики, рассматриваемые как элементарные механические объекты (ЭМО) – примеры объектов в свободном механическом состоянии .

- Человек или иной предмет на поверхности или внутри Земли, объект на Луне и Солнце, КК и космонавт в нем на активном участке траектории или на орбите при учете «негравитационного торможения», электрон в атоме, частицы солнечного ветра в магнитосфере Земли –примеры объектов в несвободном механическом состоянии .

Весомость как характеристика и мера несвободного механического состояния

- Источник несвободы в механике называется силой . В языке Ньютона именно сила является фундаментальным, первичным, неопределяемым понятием. Для Ньютона сила ассоциировалась с мышцей и тетивой.

- В третьей механике в качестве фундаментального понятия принимается характеристика механического состояния, называемая ВЕСОМОСТЬЮ .

- Весомость есть вектор, приложенный к самому телу.

- Свободные механические объекты находятся в невесомости , т.е. в имеют нулевую весомость.

- Несвободные объекты находятся в весомом состоянии с ненулевой весомостью.

- Устройство для измерения весомости называется ВЕСОМОМЕТР . Весомометрическими устройствами или индикаторами обладают почти все живые организмы. В вестибулярном аппарате целый набор весомометров Это шестой орган чувств.

- Простейший весомометр представляет грузик с пружинкой. Это широко используемый прибор, называемый сейчас (неверно) акселерометром или гравиметром (это вернее) или ньютонометром (тоже неверно).

Весомика

- В системе СИ весомость измеряется в Н/кг. Называется «Галилео» - Гл. Земная весомость 9.81 Гл, лунная – 1.6 Гл, солнечная – 27 Гл.

- Весомость может быть постоянной и переменной, изменяться по величине (болтанка, тряска) или по направлению (качка), быть однородной в пространстве и неоднородной.

- Новый раздел механики – весомика . Это наука о механическом состоянии объектов. Планетная весомика, земная весомика (гравиметрия), космическая и авиационная весомики. Весомика развлечений для парковых аттракционов. Весомика при прочностных расчетах и конструировании космических, авиационных, морских и иных транспортных аппаратов, в ТММ она широко используется под некорректными именами.Медицинская и ветеринарная весомики. И т.д.

- Метрология весомости есть база вообще всей метрологии. Ибо сила эталонируется через весомость и массу.

- Весомика один из важнейших разделов механики, значение которой трудно переоценить. Ее пока нет так как нет терминологии. Это уже первый плод нового языка механики.

- Сейчас в этой области используется нечто типа «перегрузка», «недогрузка», «недоперегрузка» (а что такое «грузка»?), «собственное ускорение» (а это что?). Невнятность языка обуславливает невнятность мысли и невозможность существования науки. Четкость языка есть ясность мысли и дает эффективную науку и практику.

Понятие механического пространства

- Механическое пространство –сцена, на которой играется пьеса механики.

- Перенос практической деятельности человека в космическое пространство требует переосмысления этого понятия. Ведь в космосе нет дорог, городов, островов, континентов, гор и т.д., нет географических карт. В нем все подвижно и динамично. Возникает новая наука – геометрика , которая создает базу геометриизации космического пространства.

- Главное понятие геометрики –понятие системы отсчета . Но предварительно надо ввести главные типы механических объектов. Это элементарный механический объект (ЭМО), механическое тело (МТ) и механическая среда (МС). МТ может быть разделено на ЭМО, МС на отдельные тела и далее на ЭМО.

- Система отсчета это прежде всего механическая среда. Ее описание содержится в описании состояний элементов и их взаимосвязей.

- Вводится понятие абсолютно жесткой связи и прямой как образа напряженной гибкой струны (но не луча света).

- Абсолютно жесткая среда –среда, между элементами которой существует абсолютно жесткая связь. Системы отсчета на абсолютно жестких средах это ньютоновские системы отсчета . В используются и неньютоновские системы отсчета.

- Система координат – совокупность чисел, приписанных элементам отсчета. На одной системе (тел) отсчета можно ввести множество систем координат (декартову, полярную, сферическую и т.д.).

Понятие механического пространства (продолжение)

- Среда, выполненная свободными, невесомыми элементами, называется абсолютно мягкой . Система отсчета на абсолютно мягких средах называется мягкой системой отсчета .

- Мягкая ньютоновская система отсчета (одновременно и мягкая, и жесткая) называется инерциальной системой отсчета . Для инерциальных систем отсчета справедлив принцип Галилея: свободное (невесомое) тело движется в ней равномерно и прямолинейно

- Пространство, в котором можно ввести инерциальную систему отсчета, называется галилеевым .

- Иные пространства называются негалилеевыми . Распределение весомости элементов среды (в ньютоновской системе отсчета) создает весомостное поле негалилеевой системы отсчета.

- Исчисление времени. Идеальные часы. Часы, на ход которые не влияют никакие механические воздействия: Если такие часы синхронизировать в одном месте, а затем их произвольно бросать, кидать, вращать, возить в любое место, то после возврата в одно место и остановки друг относительно друга их показания совпадут.

- Часы размещаются только у наблюдателя. Координатное время определяется законами движения тел. И если предсказания теории и наблюдения совпадают, то и координатное время исчислено верно.

Что такое гравитация

- Гравитация заключается в существовании в окрестности тел области негалилеевости. Гравитация не взаимодействие, а свойство . Его можно изменить исключительно воздействием на источник гравитации.. Носителем свойства является пространство. Гравитация не меняет свободы и невесомости. Проявление этого свойства состоит в том, что свободные тела в нем не двигаются равномерно и прямолинейно.

- Область пространства, в которой проявляется негалилеевость, называется гравитационным полем . На достаточном удалении от источника гравитации поле шарообразно и топологически открыто.

- Величина, пропорциональная квадрату радиуса области негалилеевости объекта характеризует имманентное свойство объекта, называемое массой ..

- Система отсчета, асимптотически инерциальная на бесконечности, называется гармонической . Поле весомости в гармонической системе отсчета является собственно гравитационным полем. Общее весомостное поле аддитивно и состоит из собственно гравитационного поля и поля весомости неинерциальной системы отсчета без учета гравитации (например, связанного с вращением системы отсчета или реактивного воздействия). Локально эти поля неразделимы (принцип Эйнштейна).

Фундамент механики построен.
Начинаем построение
самой механики

Аксиоматика

- Определение силы:

F – сила, W – весомость.

- В новой механике нет гравитационных сил. Все макросилы в ней имеют электромагнитный характер. Например, тело на поверхности Земли имеет весомость, направленную вниз. В нему приложена сила, направленная вверх. Это сила упругости опоры. Она является электромагнитной.

- Закон (аксиома) взаимодействия (третий закон Ньютона) :


.

- Уравнение движения в инерциальной системе отсчета (второй закон (аксиома) Ньютона):

- W – весомость, w – ускорение.

Основные законы

- Полевые уравнения (уравнения поля весомости)

Здесь V (r ) – полевая весомость. U – весомость гравитационная, H –весомость, связанная с неинерциальностью системы отсчета.

- угловая скорость вращения системы отсчета, r - плотность.

Начальные условия: V ₀ = W (r = 0). В этом принципиальное отличие от уравнений электромагнитного поля, в которых задаются граничные условия. Почему волн гравитационной или неинерциальной весомости не существует?

- Уравнение движения произвольного тела в произвольной (ньютоновской) системе отсчета в произвольном пространстве

Это универсальное уравнение движения, так как в него не входят никакие собственные, имманентные характеристики тела.

- Наконец, закон сохранения массы (уравнение неразрывности):

- Все понятия и законы новой механики сформулированы. Они полностью вытекают из ньютоновской механики.

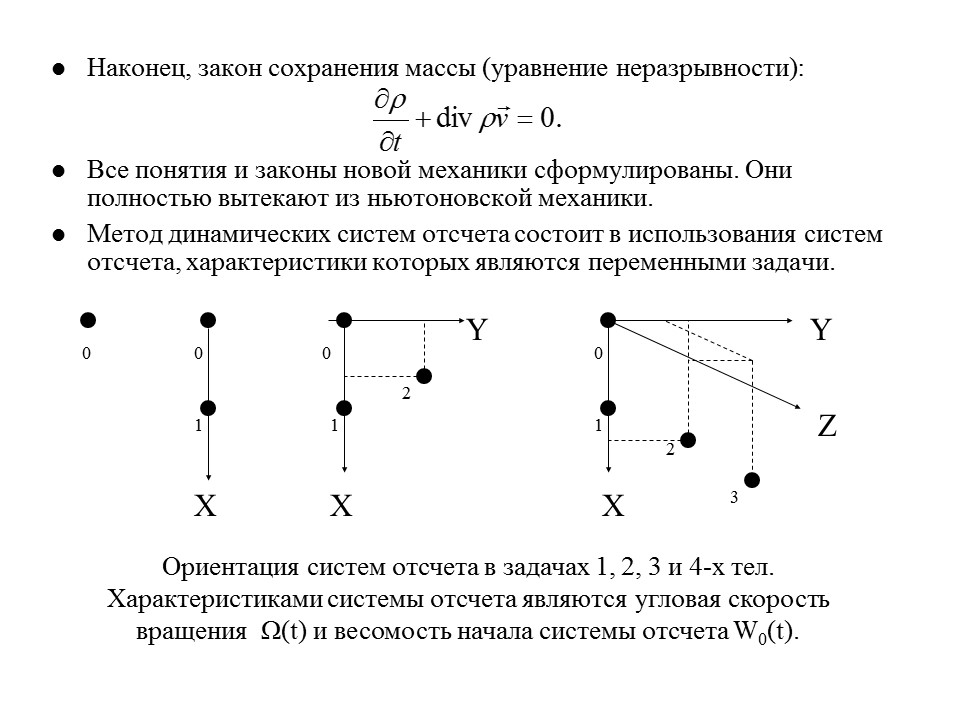
- Метод динамических систем отсчета состоит в использования систем отсчета, характеристики которых являются переменными задачи.