| Ученик 8 В класса
Моусош № 6
Скворцов Сергей
Пифагор
"Следует избегать всеми средствами, отсекая огнем и мечом, и всем, чем только можно, от тела - болезнь, от души - невежество, от желудка - излишнего, от города - смуту, от дома - раздоры, и от всего вместе - неумеренность."
Открытия Пифагора
• • Геометрия. Знаменитая и всеми любимая теорема Пифагора плюс построение некоторых многоугольников и многогранников.
• • География и астрономия. Одним из первых высказал гипотезу о шарообразной форме Земли, считал, что мы – не единственные во Вселенной.
• • Музыка. Зависимость звука от длины струны или флейты.
• • Нумерология. Многие из нас знают, что такое нумерология, но кто первый совместил числа и прогнозы на будущее?
Формулировки теоремы Пифагора
Геометрическая формулировка:
Изначально теорема была сформулирована следующим образом:
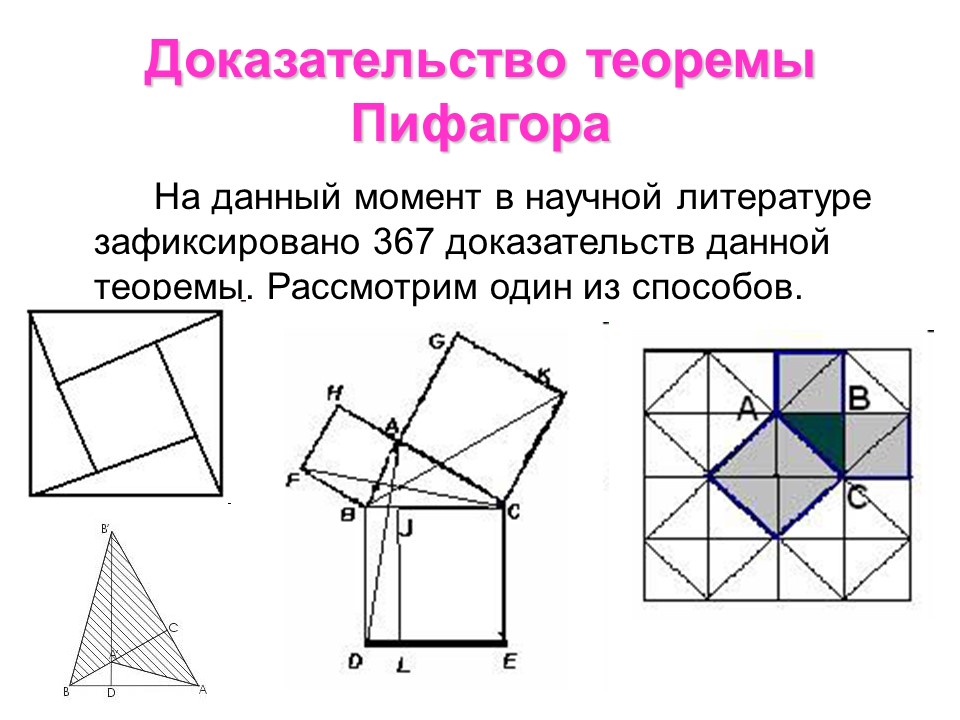
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов
. То есть, обозначив длину гипотенузы треугольника через c
, а длины катетов через a
и b
:
Доказательство теоремы Пифагора
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Рассмотрим один из способов.
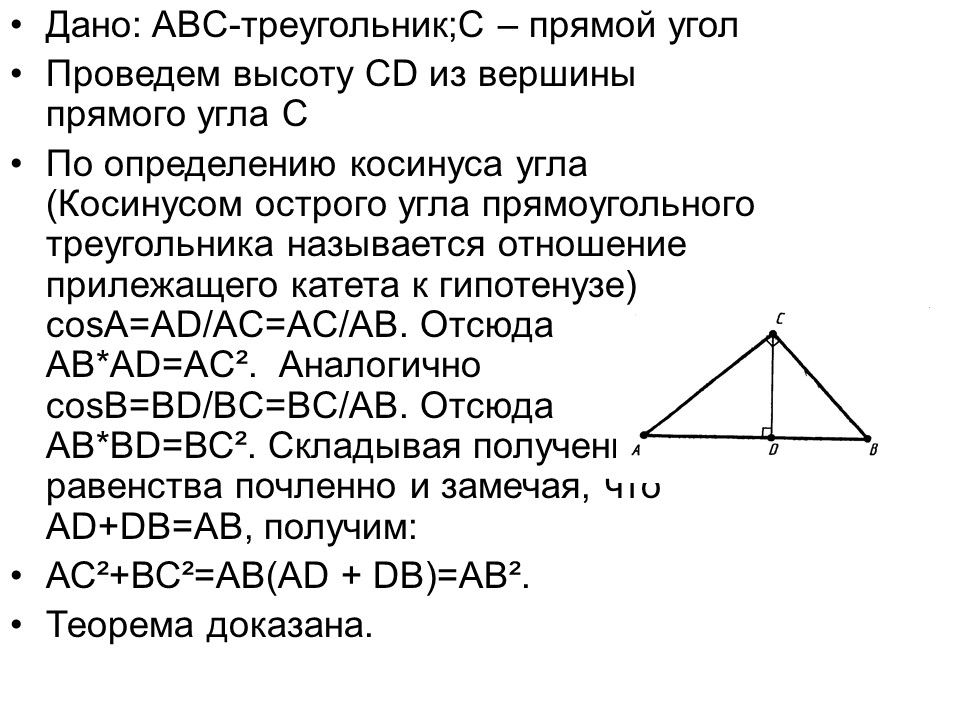
• Дано: ABC-треугольник;C – прямой угол
• Проведем высоту CD из вершины прямого угла С
• По определению косинуса угла (Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе) соsА=AD/AC=AC/AB. Отсюда AB*AD=AC². Аналогично соsВ=BD/BC=BC/AB. Отсюда AB*BD=ВС². Складывая полученные равенства почленно и замечая, что AD+DB=AB, получим:
• АС²+ВС²=АВ(AD + DB)=АВ².
• Теорема доказана.
Следствия из теоремы Пифагора
• В прямоугольном треугольнике любой из катетов меньше гипотенузы
• Для всякого острого угла α cosα<1
Теорема Пифагора.применение
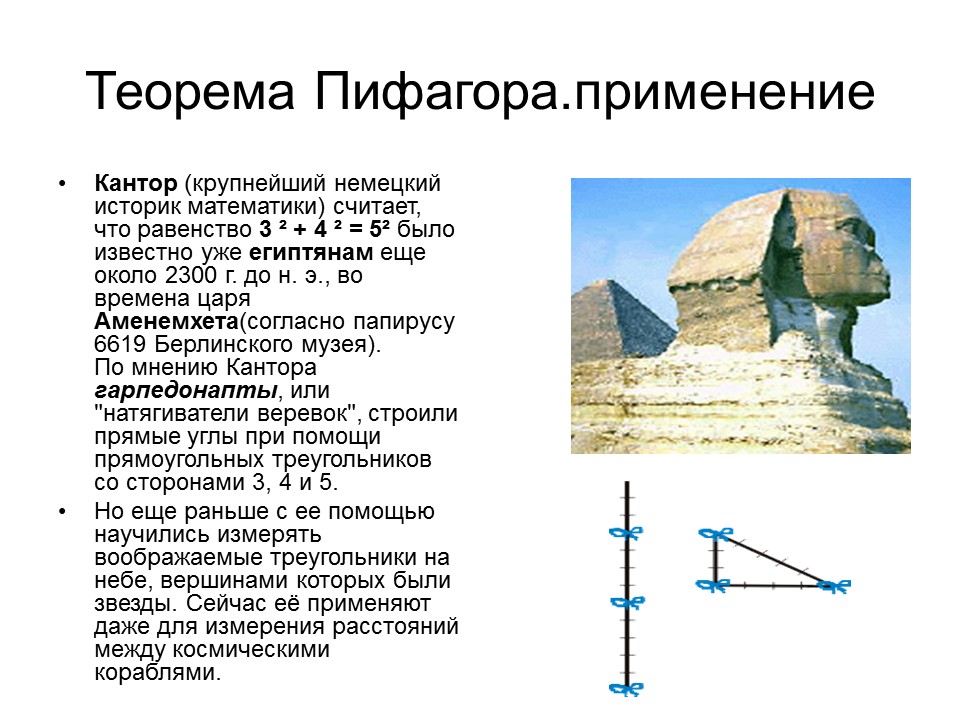
• Кантор
(крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5²
было известно уже египтянам
еще около 2300 г. до н. э., во времена царя Аменемхета
(согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты
, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Реклама

• Но еще раньше с ее помощью научились измерять воображаемые треугольники на небе, вершинами которых были звезды. Сейчас её применяют даже для измерения расстояний между космическими кораблями.
В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли
(открыл на Марсе каналы которые долгое время считались исскуственными) и др.
Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора
.






|