Контрольная работа по эконометрике
«Парная линейная регрессия»
Вариант №6
В таблице приведены значения выручки от экспорта 1 тонны синтетического каучука за 10 кварталов и цены его на внутреннем рынке.
| Период |
Выручка от экспорта 1 тонны, долл. |
Цена внутреннего рынка, долл. За 1 тонну |
| 1-й квартал |
2010 |
1030 |
| 2-й квартал |
1190 |
1550 |
| 3-й квартал |
1340 |
2180 |
| 4-й квартал |
1370 |
2370 |
| 5-й квартал |
1470 |
2380 |
| 6-й квартал |
1510 |
2560 |
| 7-й квартал |
1535 |
2590 |
| 8-й квартал |
1570 |
2700 |
| 9-й квартал |
1540 |
2759 |
| 10-й квартал |
1635 |
2760 |
Линейное уравнение парной регрессии имеет вид:
ŷ = b0
+ b1
· x
где ŷ — оценка условного математического ожидания y;
b0
, b1
— эмпирические коэффициенты регрессии, подлежащие определению.
Эмпирические коэффициенты регрессии b0
, b1
будем определять с помощью инструмента Регрессия надстройки Анализ данных табличного процессора MS Excel.
Из таблицы «Линейн» видно, что эмпирические коэффициенты регрессии соответственно равны:
b0
= 1738,671
b1
= - 0,097
Тогда уравнение парной линейной регрессии, связывающей величину выручки от экспорта yи его цены на внутреннем рынке x, имеет вид:
ŷ = 1739 – 0,097 · x
1.
Рассчитайте параметры уравнения линейной зависимости выручки от экспорта 1тонны синтетического каучука от цены его на внутреннем рынке.
При помощи статистической функции «ЛИНЕЙН» получим:
| Линейн |
| -0,096888247 |
1738,670621 |
| 0,129769731 |
305,1064952 |
| 0,065140593 |
222,2670586 |
| 0,55743649 |
8 |
| 27538,83722 |
395221,1628 |
Где соответственно
| Значение коэффициента b
|
Значение коэффициента a
|
| Среднеквадратическое отклонение b
|
Среднеквадратическое отклонение a
|
| Коэффициент детерминации R2
|
Среднеквадратическое отклонение y
|
| F
-статистика |
Число степеней свободы |
| Регрессионная сумма квадратов |
Остаточная сумма квадратов |
2.
Найти оценки дисперсий
S2
,
D(
b0
),
D(
b1
),
D(ŷ).
а) Найдем S2
S2
=∑ ei
2
/ n-2
| Наблюдение
|
Остатки
ei
|
Квадрат отклонений |
| 1 |
371,1242736 |
137733,2264 |
| 2 |
-398,4938378 |
158797,3387 |
| 3 |
-187,4542419 |
35139,0928 |
| 4 |
-139,0454749 |
19333,64409 |
| 5 |
-38,07659241 |
1449,82689 |
| 6 |
19,36329212 |
374,9370817 |
| 7 |
47,26993954 |
2234,447184 |
| 8 |
92,92764676 |
8635,547532 |
| 9 |
68,64405335 |
4712,006061 |
| 10 |
163,7409416 |
26811,09596 |
| Сумма |
395221,1628 |
Используя данные таблицы, получим S2
= 395221,1628 / 10 – 2 = 395221,1628 / 8 = 49402,64535
б) Найдем D(b0
)
D(b0
) = S2
· (∑ xi
2
/ n ∑ (xi
- x)2
)
| Период |
Цена внутреннего рынка, долл. За 1 тонну, x |
x - x ср. |
квадрат(x - x ср.) |
Квадрат x |
| 1-й квартал |
1030 |
-1257,9 |
1582312,41 |
1060900 |
| 2-й квартал |
1550 |
-737,9 |
544496,41 |
2402500 |
| 3-й квартал |
2180 |
-107,9 |
11642,41 |
4752400 |
| 4-й квартал |
2370 |
82,1 |
6740,41 |
5616900 |
| 5-й квартал |
2380 |
92,1 |
8482,41 |
5664400 |
| 6-й квартал |
2560 |
272,1 |
74038,41 |
6553600 |
| 7-й квартал |
2590 |
302,1 |
91264,41 |
6708100 |
| 8-й квартал |
2700 |
412,1 |
169826,41 |
7290000 |
| 9-й квартал |
2759 |
471,1 |
221935,21 |
7612081 |
| 10-й квартал |
2760 |
472,1 |
222878,41 |
7617600 |
| сумма |
22879 |
1805190,82 |
8678500 |
| Среднее значение x |
2287,9 |
D(b0
) = 49402,64535 · (8678500/ 10 ·1805190,82) = 49402,64535 · (8678500/ 18051908,2) = 49402,64535 · 0,48075 = 23750,32175
в) Найдем D(b1
)
D(b1
) = S2
· (1/ ∑ (xi
- x)2
)
D(b1
) = 49402,64535 · (1/1805190,82) = 49402,64535 · 0,000000554 = 0,02737
г) Найдем D(ŷ)
D(ŷ) = S2
· ( 1 + 1/n + ((xi
- x)2
/∑ (xi
- x)2
)) = 49402,64535 · (1 + 1/10 + )
3.
Постройте таблицу дисперсионного анализа.
Таблица построена при помощи инструмента Регрессия надстройки Анализ данных.
Дисперсионный анализ
|
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия |
1 |
27538,83722 |
27538,83722 |
0,55743649 |
0,476661041 |
| Остаток |
8 |
395221,1628 |
49402,64535 |
| Итого |
9 |
422760 |
4.
Оцените тесноту связи с помощью коэффициента корреляции и детерминации.
В соответствии с заданием, необходимо оценить тесноту статистической связи между величиной выручки от экспорта y и ценой на внутреннем рынке x. Эту оценку можно сделать с помощью коэффициента корреляции rxy
. Величина этого коэффициента в таблице «Регрессионная статистика» обозначена как множественный R и равна 0,255. Поскольку теоретически величина данного коэффициента находится в пределах от –1 до +1, то можно сделать вывод о несущественности статистической связи между величиной выручки от экспорта y и ценой на внутреннем рынке x.
Реклама

Параметр R-квадрат, представленный в таблице «Регрессионная статистика» представляет собой квадрат коэффициента корреляции rxy
2
и называется коэффициентом детерминации. Соответственно величина 1 - rxy
2
характеризует долю дисперсии переменной y, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных. Из таблицы «Регрессионная статистика» видно, что доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет: 1 - 0,06514 = 0,93486 или 93,5%.
Таким образом, при R< 0,3 - связь слабая. В рассматриваемом случае R=0,255, 0,255< 0,3 значит модель строить нельзя.
Регрессионная статистика
|
| Множественный R |
0,255226553 |
| R-квадрат |
0,065140593 |
| Нормированный R-квадрат |
-0,051716833 |
| Стандартная ошибка |
222,2670586 |
| Наблюдения |
10 |
5.
Оцените с помощью средней ошибки аппроксимации качество уравнения.
Определим среднюю ошибку аппроксимации по зависимости:
Для этого исходную таблицу дополняем двумя колонками, в которых определяем значения ŷ, рассчитанные с использованием зависимости и значения разности 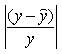 . .
| Период |
Выручка от экспорта 1 тонны, долл. Y |
Цена внутреннего рынка, долл. За 1 тонну x |
ŷ |
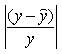 |
| 1-й квартал |
2010 |
1030 |
1639,09 |
0,184532 |
| 2-й квартал |
1190 |
1550 |
1588,65 |
0,335 |
| 3-й квартал |
1340 |
2180 |
1527,54 |
0,13996 |
| 4-й квартал |
1370 |
2370 |
1509,11 |
0,10154 |
| 5-й квартал |
1470 |
2380 |
1508,14 |
0,02595 |
| 6-й квартал |
1510 |
2560 |
1490,68 |
0,012795 |
| 7-й квартал |
1535 |
2590 |
1487,77 |
0,030769 |
| 8-й квартал |
1570 |
2700 |
1477,1 |
0,059172 |
| 9-й квартал |
1540 |
2759 |
1471,377 |
0,04456 |
| 10-й квартал |
1635 |
2760 |
1471,28 |
0,100135 |
| сумма |
15170 |
22879 |
1,034413 |
Тогда средняя ошибка аппроксимации равна:
Практически полагают, что значение средней ошибки аппроксимации не должно превышать 12—15% для грубого приближения регрессии к реальной зависимости. В нашем же случае средняя ошибка аппроксимации, т.е. среднее отклонение расчетных значений от фактических равна 10,34%. Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
6.
Оцените значимость коэффициента корреляции и значимость коэффициента регрессии
b1
с помощью
t-критерия Стьюдента.
На этом этапе необходимо оценить статистическую значимость коэффициентов регрессии с помощью t-критерия Стьюдента. Технология оценки статистической значимости коэффициентов регрессии основывается на проверке нулевой гипотезы о незначимости коэффициентов регрессии. При этом проверяется выполнение условия: если tT
> tКРИТ
, то нулевая гипотеза отвергается и коэффициент регрессии принимается значимым. Из таблицы №3 в приложении видно, что tT
для коэффициента регрессии равен -0,7466. Критическое значение tКРИТ
при уровне значимости α = 0,05 равно 2,3060.
Поскольку tT
<tКРИТ
для коэффициента регрессии (0,7466<2,3060), то нулевая гипотеза не отвергается и объясняющая переменная x является статистически незначимой и ее можно исключить из уравнения регрессии.
Реклама

7.
Оцените с помощью
F-критерия Фишера статистическую надежность результатов регрессионного моделирования.
Из таблицы дисперсионного анализа:
| Дисперсионный анализ |
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия |
1 |
27538,83722 |
27538,837 |
0,5574365 |
0,476661041 |
| Остаток |
8 |
395221,1628 |
49402,645 |
| Итого |
9 |
422760 |
следует, что FT
= 0,56. FКРИТ
определяем с помощью таблицы значений F-критерия Фишера. Для модели парной линейной регрессии число степеней свободы равно 8 и n - k - 1 (где k = 1 - число объясняющих переменных). И второе число степеней свободы равно: 10 - 2 = 8. FКРИТ
= 3,44. Следовательно, FT
<FКРИТ
(0,56<3,44) и уравнение регрессии в целом является незначимым.
|