Глава 1. Уравнения, системы уравнений.
1. Линейные уравнения.
1. Уравнение первой степени вида 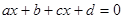 , называется линейным уравнением. Где , называется линейным уравнением. Где 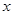 - переменные, числа - переменные, числа 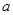 и и 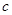 стоящие перед переменными называются коэффициентами, а стоящие перед переменными называются коэффициентами, а 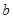 и и 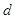 - свободные члены. Запишем линейное уравнение - свободные члены. Запишем линейное уравнение
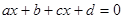 (1) (1)
Для решения уравнения (1) перенесем переменные содержащие коэффициенты, в левую часть уравнения с положительным знаком, а свободные члены в правую часть уравнения с отрицательным знаком, получим уравнение вида
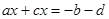 (2) (2)
Пусть 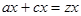 , а , а 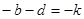 , тогда уравнение (2) будет иметь вид , тогда уравнение (2) будет иметь вид
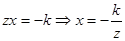 (3) (3)
Примеры.
1) Решить уравнение 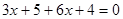
Перенесем неизвестные с коэффициентами в левую часть уравнения , а свободные члены в правую часть, получим
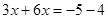
Используя уравнение (3) получим
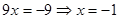
Ответ: 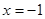
2) Решить уравнение 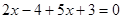
Видно, что в этом уравнении есть один отрицательный свободный член – 4. Но, перенося его в правую часть уравнения еще с одним отрицательным знаком, получим 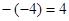 , тогда , тогда
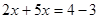
Отсюда
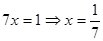
Ответ: 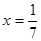
3) Решить уравнение 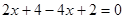
В этом уравнении один коэффициент отрицательный, перенося его и еще с положительным знаком в левую часть нет смысла, т.к. 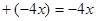 , тогда , тогда
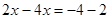
Отсюда
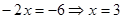
Ответ: 
4) 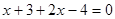
Используя объяснения к уравнению 2), получим
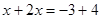
Отсюда
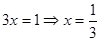
Ответ: 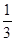
5) 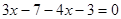
Используя объяснения, приведенные к уравнениям 1), 2), 3), 4), получим
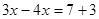
Отсюда
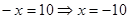
Ответ: 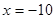
4
2. Пусть дано линейное уравнение вида
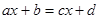 (4) (4)
В отличие от уравнения (1) переменные, содержащие коэффициенты, переносятся в левую часть с отрицательным знаком, в правую часть свободные члены переносятся тоже со знаком отрицательным. Но свободный член 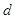 в уравнении (4) и так стоит в правой части, поэтому он не будет менять знак, поменяет знак только член в уравнении (4) и так стоит в правой части, поэтому он не будет менять знак, поменяет знак только член 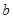 . И так, решим уравнение (4). . И так, решим уравнение (4).
Перенесем переменные с коэффициентами в левую часть с отрицательным знаком, а член 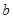 в правую часть тоже с отрицательным знаком, получим в правую часть тоже с отрицательным знаком, получим
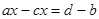 (5) (5)
Отсюда
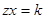
Если 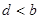 , то , то 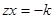
Решение уравнения (4) можно записать в виде системы
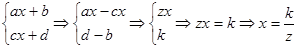 (6) (6)
Пример. Решить уравнение 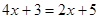
Перенесем неизвестные с коэффициентами в левую часть с отрицательным знаком, а член 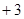 в правую часть со знаком «минус», тогда в правую часть со знаком «минус», тогда
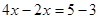
Отсюда
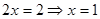
Ответ: 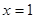
3. Линейное уравнение с двумя переменными имеет вид:
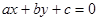 (7) (7)
Для решения уравнения (7) выразим переменную 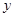 через переменную через переменную 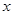 , т.е. получим уравнение вида , т.е. получим уравнение вида
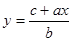 (8) (8)
Для нахождения решения уравнения (7) в уравнении (8) выбирается произвольное (любое) значение 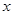 . Таким образом, уравнение (7) обладает множеством решений. . Таким образом, уравнение (7) обладает множеством решений.
Реклама

Пример. Решить уравнение 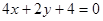
Воспользуемся формулой (8), тогда
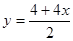
Теперь выберем абсолютно любое значение икса, например, при
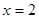 , получим , получим
 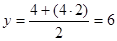
Ответ: 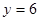
2. Квадратные уравнения.
Уравнение второй степени вида 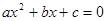 называется квадратным. Для решения такого уравнения воспользуемся следующими формулами: называется квадратным. Для решения такого уравнения воспользуемся следующими формулами:
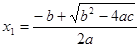 и и 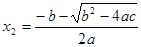 (9) (9)
Где 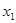 и и 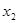 - корни квадратного уравнения - корни квадратного уравнения
Пусть 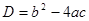 , тогда если , тогда если 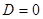 , то можно записать , то можно записать
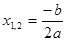 (10) (10)
Если 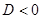 , то уравнение не имеет решений. , то уравнение не имеет решений.
Пример. Решить уравнение 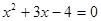
Пользуясь формулами (9) получим
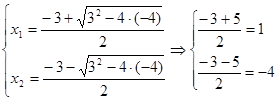
Ответ: 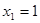 и и 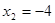
3. Уравнение третей степени.
Уравнение третей степени вида 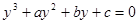 называется кубичным уравнением. Для решения такого уравнения заменим неизвестное - называется кубичным уравнением. Для решения такого уравнения заменим неизвестное - 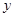 на коэффициент на коэффициент 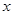 и вводя подстановку и вводя подстановку 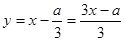
Получим более упрощенное уравнение третей степени
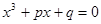 (11) (11)
Поскольку уравнение в третей степени, то соответственно решениями этого уравнения будут три корня, которые сейчас определим из следующей системы
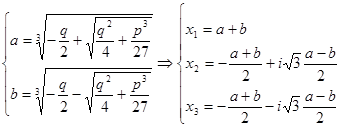 (12) (12)
Корни 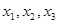 - есть решения уравнения, где - есть решения уравнения, где 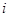 - комплексное число. - комплексное число.
4. Уравнения высших степеней сводящиеся к квадратным.
1.Рассмотрим уравнение, у которого одна переменная находится в четвертой степени, т.е. дано уравнение вида
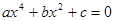 (13) (13)
Для решения такого уравнения, выразим 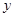 через через 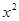 , получим, , получим,
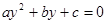 (14) (14)
Решая это уравнение по следующим формулам, имеем
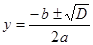 и и 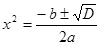 (15) (15)
Пример. Решить уравнение. 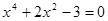
Выразим 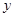 через через 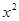 , получим , получим 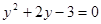 , решая это уравнение по формулам (19) получим , решая это уравнение по формулам (19) получим
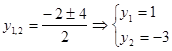
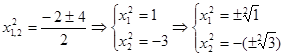
Отсюда получаем множество корней (решений) 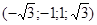
Ответ: 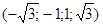
2. Рассмотрим уравнение, у которого одна степень находится в пятой степени, т.е. имеется уравнение вида
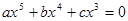 (16) (16)
Для решения такого уравнения выберем переменную, у которой степень самая меньшая, по сравнению с другими степенями, это будет переменная 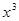 , вынося ее за скобку получим , вынося ее за скобку получим
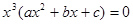 (17) (17)
Отсюда 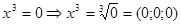 , т.е. мы получили некоторое множество нулей. Уравнение , т.е. мы получили некоторое множество нулей. Уравнение 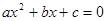 , решается через дискриминант. , решается через дискриминант.
Пример. Решить уравнение 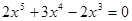
Вынесем 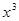 за скобку, получим за скобку, получим 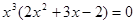 , отсюда , отсюда 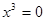 , который имеет множество корней (0; 0; 0). Далее, решая уравнение , который имеет множество корней (0; 0; 0). Далее, решая уравнение 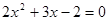 получим получим 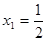 и и 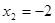 . Таким образом, получили множество решений (0; 0; 0; -2; . Таким образом, получили множество решений (0; 0; 0; -2; 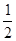 ). ).
5. Системы уравнений.
Пусть дана система уравнений
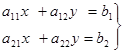 (18) (18)
где 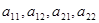 - коэффициенты при неизвестных - коэффициенты при неизвестных 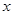 и и 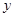 , , 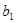 и и 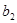 - свободные члены. - свободные члены.
Система (18) решается тремя способами 1) Графический способ; 2) Способ подстановки; 3) Способ сложения. Первый способ рассматривать не будем. Остальные способы рассмотрим при решении следующих систем уравнений.
1) Способ подстановки.
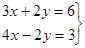
Возьмем первое уравнение системы 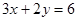 и из этого уравнения выразим и из этого уравнения выразим 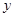 через через 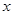 , получим , получим
Реклама

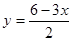
Подставив это выражение во второе уравнение системы, получим
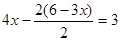
Отсюда,
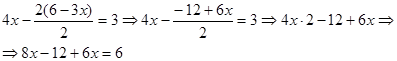
Запишем последнее уравнение и решим его
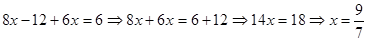
Подставив теперь найденное значение 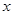 в выражение, стоящее выше, получим в выражение, стоящее выше, получим
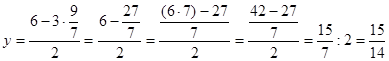
Ответ: 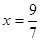 и и 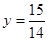
2) Способ сложения.
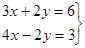
Умножим первое и второе уравнения система на 2, получим
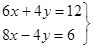
Затем, сложив почленно уравнения системы, получим 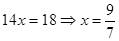 . Найдем значения игрека, для этого найденное значение икса подставим в любое уравнение исходной (первоначальной) системы, получим . Найдем значения игрека, для этого найденное значение икса подставим в любое уравнение исходной (первоначальной) системы, получим
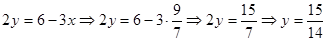
3) Способ сложения.
Запишем систему
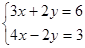
Умножим первое уравнение на 2, а второе на 2, получим:
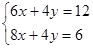
Сложим 6x и 8x, получим 14x и 12+6=18, отсюда 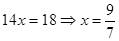 . Подставив теперь значение x в любое уравнение системы, получим . Подставив теперь значение x в любое уравнение системы, получим
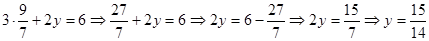
Ответ: 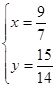
7. Система трех уравнений с тремя переменными.
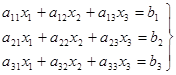 (19) (19)
где 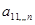 - коэффициенты при неизвестных - коэффициенты при неизвестных 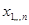 , , 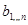 - свободные члены. - свободные члены.
Для решения системы (19) составим определитель
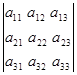 (20) (20)
Первое число у индекса указывает число (номер) строки, второе число – номер столбца. Сам определитель обозначается буквой d.
Для вычисления определителя пользуются правилом Крамера, т.е.
d=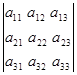 = =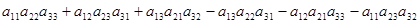
Корни системы (24) находятся по формулам
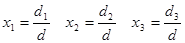
Где 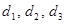 - числа, которые следует определить по следующему правилу - числа, которые следует определить по следующему правилу
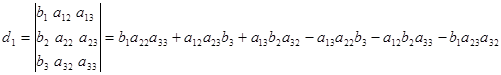
Таким же методом определяются остальные определители
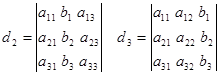
Глава 2. График функции
1. График функции.
Функция 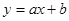 называется линейной функцией. Для нахождения точек пересечения графика функции нужно решить два уравнения: называется линейной функцией. Для нахождения точек пересечения графика функции нужно решить два уравнения:
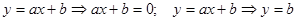
Пример. Функция задана уравнением 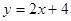 , найти точки пересечения с осями координат. , найти точки пересечения с осями координат.
Решим два уравнения 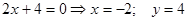
Ответ: точки x =-2 и y = 4 являются точками пересечения с осями координат.
2. Квадратичная функция.
Функция вида 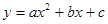 называется квадратичной. Для нахождения точек пересечения графика с осями координат, нужно решить квадратное уравнение называется квадратичной. Для нахождения точек пересечения графика с осями координат, нужно решить квадратное уравнение 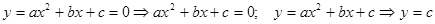
Глава 3 Пределы
1. Предел функции
Пример. Найти предел функции
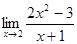
Поскольку икс стремится к двум, т.е. 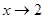 , то в числителе и знаменателе заменяем все иксы на 2, таким образом, получаем , то в числителе и знаменателе заменяем все иксы на 2, таким образом, получаем
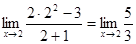
Ответ: 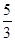
Рассмотрим случай, когда икс стремится к бесконечности. Пусть 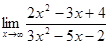
Разделим числитель и знаменатель на высокую степень аргумента 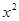 , получим , получим
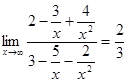
Ответ: 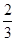
Пусть 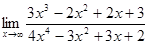 , разделим числитель и знаменатель на , разделим числитель и знаменатель на 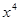 , получим , получим
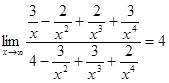
Ответ: 4
Найти предел 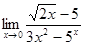
Отсюда 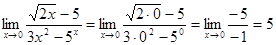
Ответ: 5
Глава 4 Производные
1. Обыкновенные производные
Пусть дана функция 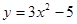 , требуется найти производную. Согласно выражению , требуется найти производную. Согласно выражению 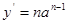 , получим , получим 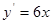 . .
Пример: Найти производную функции
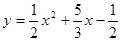
Отсюда
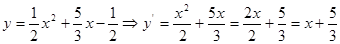
Ответ: 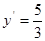
2. Производная функции одной переменной.
Функция одной переменной имеет вид 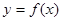 , соответственно функция постоянно изменяется со скоростью, каждой границей изменения этой функции есть предел, который можно записать в виде , соответственно функция постоянно изменяется со скоростью, каждой границей изменения этой функции есть предел, который можно записать в виде
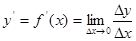 (21) (21)
Функция 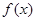 называется дифференцируемой в точке x если предел (21) называется дифференцируемой в точке x если предел (21)
существует.
3. Производные вида 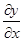
В курсе дифференциальных уравнений часто можно видеть выражение 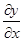 . .
Речь идет о частной производной, в этом выражении переменная x дифференцируется по переменной y. Рассмотрим выражение вида 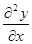 , в таком случае переменную x дифференцируют два раза по переменной y. , в таком случае переменную x дифференцируют два раза по переменной y.
Пример. Найти производную 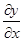 , если , если 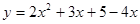
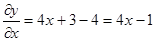
Ответ: 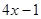
ГЛАВА 5. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
1. Неопределенные и определенные интегралы.
Множество первообразных функции 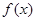 называется неопределенным интегралом. Такой неопределенный интеграл обозначается таким образом: называется неопределенным интегралом. Такой неопределенный интеграл обозначается таким образом:
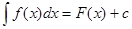
Где 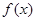 - подынтегральная функция, - подынтегральная функция, 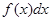 - подынтегральное выражение, - подынтегральное выражение, 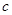 - постоянная интегрирования. - постоянная интегрирования.
Пример: Вычислить интеграл 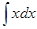
Находим первообразную для функции 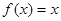 , получим , получим 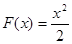 , поэтому , поэтому
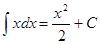
Пример: Найти 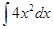
Найдем первообразную для функции 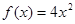 , получим , получим 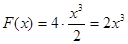 , поэтому , поэтому 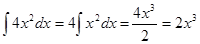
Пример: Найти 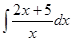
Применяем метод непосредственного интегрирования, получим
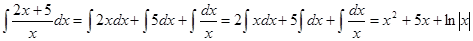
Пример: Найти 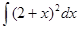
Воспользуемся методом подстановки, получим
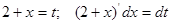
Тогда
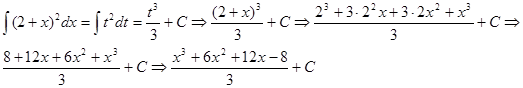
Пример: Найти 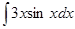
Воспользуемся методом интегрирования по частям, получим
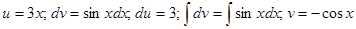
Отсюда 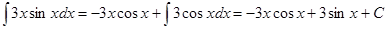
Пример. Найти 
Применим метод интегрирования по частям, получим
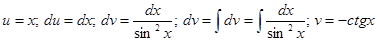
Отсюда
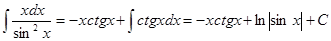
Рассмотрим интеграл вида 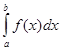 , такой интеграл называется определенным. Число а – называется нижним пределом, а число b – верхним пределом. , такой интеграл называется определенным. Число а – называется нижним пределом, а число b – верхним пределом.
 Пример: Найти Пример: Найти 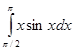
1. Находим неопределенный интеграл, методом интегрирования по частям,
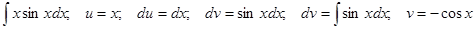
Отсюда,
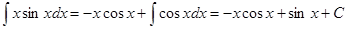
Тогда
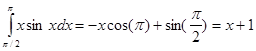
Пример: Найти 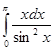
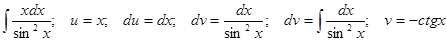
Отсюда,
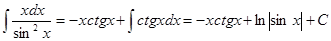
Тогда
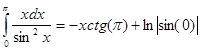
|