| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет
имени Франциска Скорины"
Математический факультет
Кафедра алгебры и геометрии
Курсовая работа
АЛГЕБРАИЧЕСКИЕ ГРУППЫ МАТРИЦ
Исполнитель:
студентка группы H.01.01.01 М-42
Мариненко В.В.
Научный руководитель:
доктор физико-математических наук,
профессор Скиба С.В.
Гомель 2003
Содержание
Введение
1. Алгебраические группы матриц
1.1 Примеры алгебраических групп матриц
1.2 О полугруппах
1.3 Компоненты алгебраической группы
1.4 О 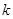 -группах
-группах
2 Ранг матрицы
2.1 Возвращение к уравнениям
2.2 Ранг матрицы
2.3 Критерий совместности
3 Линейные отображения. Действия с матрицами
3.1 Матрицы и отображения
3.2 Произведение матриц
3.3 Квадратные матрицы
Заключение
Список использованных источников
Введение
Множество 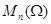 матриц матриц 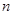 -ой степени над -ой степени над 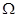 будем рассматривать как аффинное пространство будем рассматривать как аффинное пространство 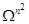 с имеющейся на ней полиномиальной топологией. Алгебраические группы матриц
определяются как невырожденные части алгебраических множеств из с имеющейся на ней полиномиальной топологией. Алгебраические группы матриц
определяются как невырожденные части алгебраических множеств из 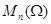 , являющиеся группами относительно обычного матричного умножения. Простейший пример такой группы - общая линейная группа , являющиеся группами относительно обычного матричного умножения. Простейший пример такой группы - общая линейная группа 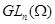 . В настоящем параграфе мы начнем систематическое изучение алгебраических матричных групп. . В настоящем параграфе мы начнем систематическое изучение алгебраических матричных групп.
Все топологические понятия относятся к полиномиальной топологии; черта обозначает замыкание в 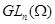 , диез - замыкание в , диез - замыкание в 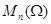 , бемоль - взятие невырожденной части, т. е. , бемоль - взятие невырожденной части, т. е. 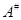 - совокупность всех невырожденных матриц из - совокупность всех невырожденных матриц из 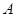 . Иногда, допуская вольность, мы употребляем для групп те же понятия, что и для подлежащих алгебраических множеств, - например, говорим об общих точках групп; это не должно вызывать недоразумений. . Иногда, допуская вольность, мы употребляем для групп те же понятия, что и для подлежащих алгебраических множеств, - например, говорим об общих точках групп; это не должно вызывать недоразумений.
1. Алгебраические группы матриц
1.1 Примеры алгебраических групп матриц
Классические матричные группы - общая, специальная, симплектическая и ортогональная
:
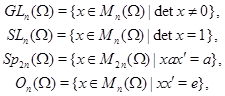
где 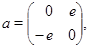
 - единичная матрица и штрих обозначает транспонирование. - единичная матрица и штрих обозначает транспонирование.
Диагональная группа
 , группы клеточно-диагональных матриц данного вида. Треугольная группа , группы клеточно-диагональных матриц данного вида. Треугольная группа
 (для определенности --- с нижним нулевым углом), унитреугольная группа (для определенности --- с нижним нулевым углом), унитреугольная группа 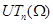 (треугольные матрицы с единичной диагональю), группы клеточно-треугольных матриц данного вида. (треугольные матрицы с единичной диагональю), группы клеточно-треугольных матриц данного вида.
Централизатор произвольного множества из 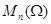 в алгебраической группе в алгебраической группе  , нормализатор замкнутого множества из , нормализатор замкнутого множества из 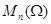 в в 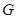 . .
Реклама

Пересечение всех алгебраических групп, содержащих данное множество матриц 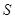 из из 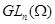 --- алгебраическая группа. Она обозначается --- алгебраическая группа. Она обозначается 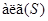 и называется алгебраической группой, порожденной множеством и называется алгебраической группой, порожденной множеством 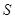 .
.
Каждую алгебраическую линейную группу из 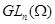 можно изоморфно --- в смысле умножения и полиномиальной топологии --- отождествить с замкнутой подгруппой из можно изоморфно --- в смысле умножения и полиномиальной топологии --- отождествить с замкнутой подгруппой из 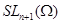 в силу формулы в силу формулы
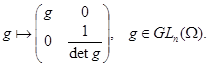
Такое отождествление позволяет при желании ограничиться рассмотрением только таких групп матриц, которые сами являются алгебраическими множествами (а не их невырожденными частями). Это дает другое оправдание тем вольностям в терминологии, которые упоминались в начале параграфа.
Множество всех матриц из 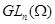 , оставляющих инвариантной заданную невырожденную билинейную форму , оставляющих инвариантной заданную невырожденную билинейную форму 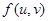 на на 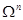 . .
Пусть 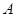 --- алгебра над --- алгебра над 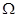 конечной размерности конечной размерности 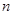 (безразлично, ассоциативная или нет), (безразлично, ассоциативная или нет), 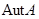 --- группа всех ее автоморфизмов. Фиксируя в --- группа всех ее автоморфизмов. Фиксируя в 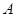 какую-нибудь базу какую-нибудь базу 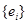 и сопоставляя автоморфизмам алгебры и сопоставляя автоморфизмам алгебры 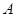 их матрицы в этой базе, мы получим на их матрицы в этой базе, мы получим на 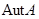 строение алгебраической группы. Действительно, пусть строение алгебраической группы. Действительно, пусть
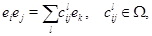
т. е. 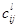 --- структурные константы алгебры --- структурные константы алгебры 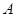 . Пусть далее . Пусть далее
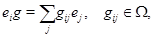
где 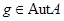 . Тогда . Тогда 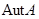 задается в матричных координатах задается в матричных координатах 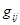 очевидными полиномиальными уравнениями, вытекающими из соотношений очевидными полиномиальными уравнениями, вытекающими из соотношений
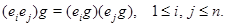
Указать в приведенных выше примерах определяющие уравнения, найти общую точку, если она есть.
В дальнейшем нам встретится еще много примеров и конструкций алгебраических матричных групп.
1.1.1
Если матричная группа 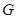 содержит алгебраическую подгруппу содержит алгебраическую подгруппу 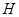 конечного индекса, то конечного индекса, то 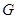 сама алгебраическая. сама алгебраическая.
Доказательство. Пусть 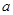 - аннулятор группы - аннулятор группы 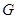 в в 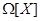 , , 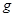 - его корень в - его корень в 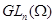 . Надо показать, что . Надо показать, что 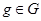 . Пусть, напротив, . Пусть, напротив, 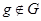 . Пусть . Пусть 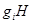 - смежные классы - смежные классы 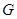 по по 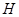 . Для каждого . Для каждого 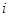 выберем многочлен выберем многочлен
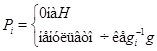
и положим
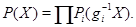
Очевидно, 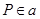 , , 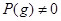 . Получили противоречие. . Получили противоречие.
Пусть 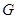 --- алгебраическая группа, --- алгебраическая группа, 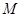 , , 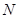 --- подмножество и замкнутое подмножество из --- подмножество и замкнутое подмножество из 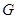 . Тогда множества . Тогда множества
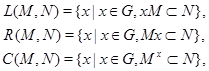
где 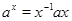 , замкнуты. Если , замкнуты. Если 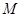 тоже замкнуто и тоже замкнуто и 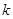 --- общее поле квазиопределения для --- общее поле квазиопределения для 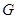 , , 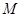 , , 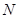 , то , то 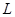 , , 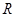 , , 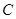 квазиопределены над квазиопределены над 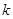 . В частности, если существует хотя бы одно . В частности, если существует хотя бы одно 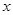 с условием с условием 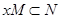 (соответственно, (соответственно, 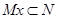 , , 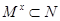 ), то можно считать, что ), то можно считать, что 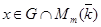 (см. 7.1.5). (см. 7.1.5).
Если на множестве 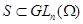 выполняется теоретико-групповое тождество выполняется теоретико-групповое тождество 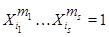 , то оно выполняется и на его замыкании , то оно выполняется и на его замыкании 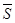 . В частности, коммутативность, разрешимость, нильпотентность матричной группы сохраняются на ее замыкании в полиномиальной топологии. . В частности, коммутативность, разрешимость, нильпотентность матричной группы сохраняются на ее замыкании в полиномиальной топологии.
Определим действие элементов из 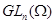 на рациональные функции из на рациональные функции из 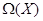 , , 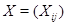 , полагая , полагая
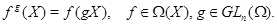
Для каждого 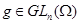 отображение отображение 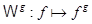 (сдвиг аргумента) есть автоморфизм поля (сдвиг аргумента) есть автоморфизм поля 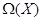 . Отображение . Отображение 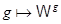 есть изоморфизм полной линейной группы есть изоморфизм полной линейной группы 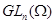 в группу автоморфизмов расширения в группу автоморфизмов расширения 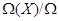 . .
Реклама

Имеет место следующее предложение.
1.2.1
Все замкнутые (в полиномиальной топологии) полугруппы из 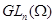 являются группами. Более общно: замыкание являются группами. Более общно: замыкание 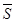 произвольной полугруппы произвольной полугруппы 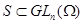 --- группа. Более точно: если --- группа. Более точно: если 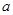 --- аннулятор --- аннулятор 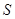 в в 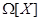 , то , то 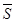 совпадает с совпадает с
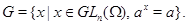
Здесь вместо 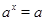 можно написать можно написать 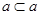 . .
Доказательство. Во-первых, 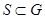 и, значит, и, значит, 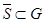 . Действительно, если . Действительно, если 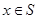 , , 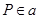 и и 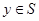 , то , то 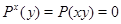 , т. е. , т. е. 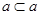 . Подпространство . Подпространство 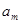 многочленов из многочленов из 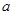 степени степени 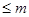 отображается оператором отображается оператором 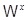 на себя, так как оно конечномерно, а опрератор обратим. Но тогда и всё на себя, так как оно конечномерно, а опрератор обратим. Но тогда и всё 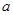 отображается на себя, как объединение всех отображается на себя, как объединение всех 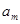 . .
Во-вторых, 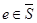 , т. е. , т. е. 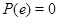 для каждого для каждого 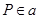 . Действительно, пусть . Действительно, пусть 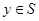 . По уже доказанному, . По уже доказанному,  . Найдём . Найдём 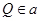 с условием с условием 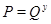 . Тогда . Тогда 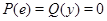 . .
В-третьих, 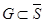 , т. е. , т. е. 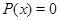 для всех для всех 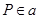 , , 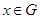 . Действительно, . Действительно, 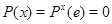 . Предложение доказано. . Предложение доказано.
Таким образом, теория алгебраических полугрупп из 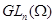 исчерпывается теорией алгебраических групп. исчерпывается теорией алгебраических групп.
Отметим ещё одно полезное предложение.
1.2.2
Пусть алгебраическая группа 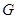 неприводима, т. е. неприводима, т. е. 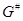 --- многообразие, --- многообразие, 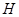 --- густое подмножество, плотное в --- густое подмножество, плотное в 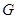 . Тогда каждый элемент . Тогда каждый элемент 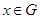 является произведением двух элементов из является произведением двух элементов из 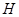 ; в частности, если ; в частности, если 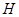 --- подгруппа, то она совпадает с --- подгруппа, то она совпадает с 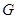 . .
Доказательство. Множества 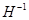 и и 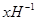 тоже густые и плотные, поэтому пересечение тоже густые и плотные, поэтому пересечение 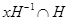 непусто (см. п. 8.2). непусто (см. п. 8.2).
Если 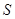 --- полугруппа из --- полугруппа из 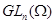 , то , то 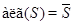 . .
Пусть 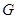 --- алгебраическая группа матриц. Невырожденные части компонент её подлежащего многообразия --- алгебраическая группа матриц. Невырожденные части компонент её подлежащего многообразия 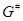 называеются компонентами
группы называеются компонентами
группы 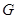 . наличие в . наличие в 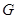 групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия. групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия.
1.3.1
Теорема. Пусть 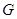 --- алгебраическая группа матриц. Её компонента --- алгебраическая группа матриц. Её компонента 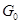 , содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы , содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы 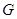 по по 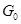 (в частности, они являются связными компонентами группы (в частности, они являются связными компонентами группы 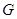 в полиномиальной топологии). в полиномиальной топологии). 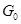 --- единственная связная замкнутая подгруппа конечного индекса в --- единственная связная замкнутая подгруппа конечного индекса в 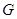 . Аннулятор . Аннулятор 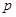 компоненты компоненты 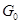 связан с аннулятором связан с аннулятором 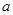 всей группы всей группы 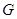 следующим образом: следующим образом:
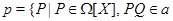 для
некоторого для
некоторого 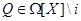 , зависящего от , зависящего от 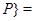
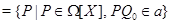 , где , где 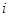 --- аннулятор единицы в --- аннулятор единицы в 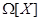 , , 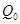 --- некоторый многочлен из --- некоторый многочлен из 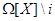 . .
Доказательство. а) Пусть 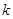 --- общее поле определения всех компонент --- общее поле определения всех компонент 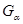 группы группы 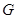 . Пусть . Пусть 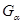 , , 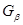 содержат единицу содержат единицу 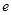 , , 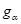 , , 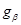 --- их независимые общие точки над --- их независимые общие точки над 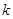 и и 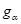 , , 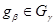 . Имеем специализации . Имеем специализации
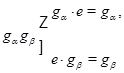
над 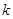 , откуда , откуда 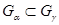 , , 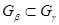 , , 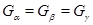 . Этим доказана единственность компоненты . Этим доказана единственность компоненты 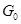 . .
б) Очевидно, что отображения
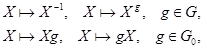
являются гомеоморфизмами пространства 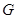 . Так как . Так как 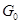 инвариантна относительно них, то инвариантна относительно них, то 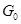 --- нормальная подгруппа группы --- нормальная подгруппа группы 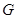 . .
в) Пусть 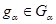 . Тогда . Тогда 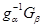 при фиксированном при фиксированном 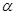 --- снова все компоненты группы --- снова все компоненты группы 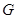 . В частности, . В частности, 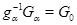 , , 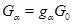 . Этим доказано, что . Этим доказано, что 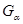 --- смежные классы --- смежные классы 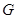 по по 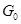 и, значит, связные компоненты группы и, значит, связные компоненты группы 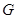 . .
г) Если 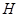 --- связная замкнутая подгруппа группы --- связная замкнутая подгруппа группы 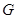 , то, предыдущему, , то, предыдущему, 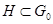 . Если, кроме того, . Если, кроме того, 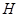 конечного индекса, то она той же размерности, что и конечного индекса, то она той же размерности, что и 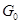 , потому совпадает с , потому совпадает с 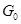 . .
д) Для каждого 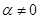 возьмем многочлен возьмем многочлен
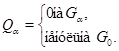
Пусть 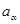 --- точка из --- точка из 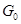 , в которой , в которой 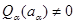 . Рассмотрим многочлен . Рассмотрим многочлен
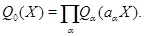
Он искомый. В самом деле, очевидно, 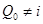 . Оба включения справа налево очевидны (использовать простоту идеала . Оба включения справа налево очевидны (использовать простоту идеала 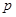 ). Остается доказать включение ). Остается доказать включение
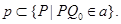
Пусть 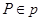 , , 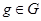 . Имеем: . Имеем:
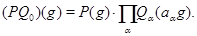
Если 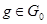 , то , то 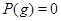 , если же , если же 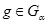 , , 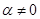 , то , то 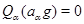 . В любом случае . В любом случае 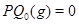 . Следовательно, . Следовательно, 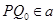 . Теорема доказана. . Теорема доказана.
Мы видим, в частности, что для алгебраической группы неприводимость и связность в полиномиальной топологии --- одно и то же; в дальнейшем мы будем пользоваться только вторым термином, чтобы избежать путаницы с понятием матричной приводимости групп (к полураспавшейся форме).
Доказать, что связанная компонента единицы алгебраической группы содержится в любой замкнутой подгруппе конечного индекса.
Подгруппа 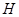 алгебраической группы алгебраической группы 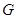 тогда и только тогда замкнута, когда замкнуто её пересечение со связной компонентой единицы тогда и только тогда замкнута, когда замкнуто её пересечение со связной компонентой единицы 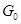 . .
<<Только тогда>> очевидно. <<Тогда>> вытекает из 9.1.9, если заметить, что
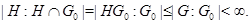
Конечная нормальная подгруппа 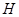 связной алгебраической группы связной алгебраической группы 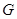 всегда лежит в центре всегда лежит в центре 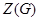 . .
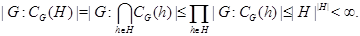
В заключение отметим, что если в качестве универсальной области выбрано поле комплексных чисел 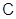 , то в алгебраической группе можно рассматривать две топологии --- полиномиальную и евклидову. Ясно, что вторая тоньше первой, поэтому, в частности, евклидова связная компонента единицы содержится в полиномиальной связной компоненте. Можно было бы доказать и обратное, т. е. на самом деле связные компоненты комплексной алгебраической группы в обеих топологиях одни и те же. Этот результат становится неверным, если рассматривать , то в алгебраической группе можно рассматривать две топологии --- полиномиальную и евклидову. Ясно, что вторая тоньше первой, поэтому, в частности, евклидова связная компонента единицы содержится в полиномиальной связной компоненте. Можно было бы доказать и обратное, т. е. на самом деле связные компоненты комплексной алгебраической группы в обеих топологиях одни и те же. Этот результат становится неверным, если рассматривать 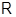 -порцию комплексной алгебраической группы (по поводу определения см. следующий пункт). -порцию комплексной алгебраической группы (по поводу определения см. следующий пункт).
Пусть 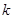 - поле. По определению, алгебраическая - поле. По определению, алгебраическая 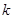 -группа
--- это группа матриц из -группа
--- это группа матриц из 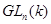 , выделяемая полиномиальными уравнениями с коэффициентами в , выделяемая полиномиальными уравнениями с коэффициентами в 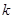 . Иначе можно сказать, что это . Иначе можно сказать, что это 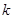 -порция, т. е. пересечение с -порция, т. е. пересечение с 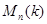 , некоторой алгебраической группы, квазиопределенной над , некоторой алгебраической группы, квазиопределенной над 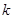 . Обычные алгебраические группы тоже можно трактовать как . Обычные алгебраические группы тоже можно трактовать как 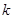 -группы по отношению к некоторой большей универсальной области -группы по отношению к некоторой большей универсальной области 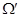 . В этом смысле понятие алгебраической . В этом смысле понятие алгебраической 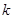 -группы является более общим, так как от -группы является более общим, так как от 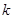 не требуется ни алгебраической замкнутости, ни бесконечной степени трансцендентности над простым полем. не требуется ни алгебраической замкнутости, ни бесконечной степени трансцендентности над простым полем.
В свойствах алгебраических групп и 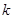 -групп много общего. Имеется сандартный способ перехода от первых ко вторым --- посредством поля определения (в чём и состоит основное значение этого понятия). Нам не раз представится возможность продемонстрировать этот способ. В целом же -групп много общего. Имеется сандартный способ перехода от первых ко вторым --- посредством поля определения (в чём и состоит основное значение этого понятия). Нам не раз представится возможность продемонстрировать этот способ. В целом же 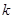 -группы в нашем изложении останутся на заднем плане, лишь иногда выходя на авансцену. -группы в нашем изложении останутся на заднем плане, лишь иногда выходя на авансцену.
Многие результаты о 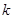 -группах по формулировке и доказательству вполне аналогичны результатам об абсолютных алгебраических группах (в -группах по формулировке и доказательству вполне аналогичны результатам об абсолютных алгебраических группах (в 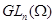 ) и опираются на сведения из алгебраической геометрии для ) и опираются на сведения из алгебраической геометрии для 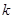 -множеств, (по определению, алгебраическое -множеств, (по определению, алгебраическое 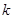 -множество
выделяется в -множество
выделяется в 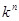 уравнениями с коэффициентами из уравнениями с коэффициентами из 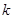 ). ).
2 Ранг матрицы
В арифметическом линейном пространстве 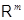 столбцов высоты столбцов высоты 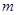 рассмотрим рассмотрим 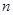 векторов векторов
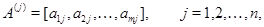
и их линейную оболочку 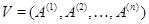 . Пусть дан еще один вектор . Пусть дан еще один вектор 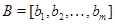 . Спрашивается, принадлежит ли . Спрашивается, принадлежит ли 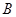 подпространству подпространству 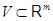 , а если принадлежит, то каким образом его координаты , а если принадлежит, то каким образом его координаты 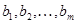 выражаются через координаты векторов выражаются через координаты векторов 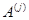 . В случае . В случае 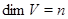 вторая часть вопроса относится к значениям координат вектора вторая часть вопроса относится к значениям координат вектора 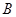 в базисе в базисе 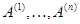 . Мы берем линейную комбинацию векторов . Мы берем линейную комбинацию векторов 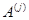 с произвольными коэффициентами с произвольными коэффициентами 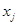 и составляем уравнение и составляем уравнение 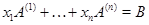 . Наглядный вид этого уравнения . Наглядный вид этого уравнения
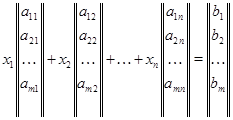
есть лишь иная запись системы из 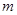 линейных уравнений с линейных уравнений с 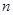 неизвестными: неизвестными:
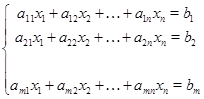
Первое впечатление таково, что мы вернулись к исходным позициям, потеряв время и ничего не выиграв. На самом же деле мы располагаем теперь рядом важных понятий. Осталось приобрести навыки в обращении с ними.
В этом месте удобно условиться в обозначениях. В дальнейшем для сокращения записи мы часто будем обозначать сумму 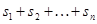 значком значком 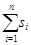 . При этом . При этом 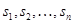 --- величины произвольной природы (числа, векторы-строки и т. д.), для которых выполнены все законы сложения чисел или векторов. Правила --- величины произвольной природы (числа, векторы-строки и т. д.), для которых выполнены все законы сложения чисел или векторов. Правила
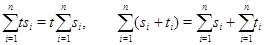
достаточно понятны, чтобы их нужно было разъяснять. Будут рассматриваться также двойные суммы
,
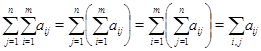
в которых порядок суммирования (по первому и по второму индексу) можно выбирать по своему желанию. Это легко понять, если расположить величины 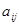 в прямоугольную матрицу размера в прямоугольную матрицу размера 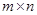 : в нашей воле начинать суммирование элементов матрицы по строкам или по столбцам. : в нашей воле начинать суммирование элементов матрицы по строкам или по столбцам.
Другие возможные типы суммирования будут разъясняться в нужном месте.
Назовем пространством столбцов
прямоугольной матрицы 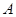 размера размера 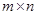 введенное выше пространство введенное выше пространство 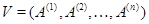 , которое мы будем обозначать теперь символом , которое мы будем обозначать теперь символом 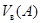 или просто или просто 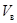 (в --- вертикальный). Его размерность (в --- вертикальный). Его размерность 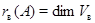 назовем рангом по столбцам матрицы назовем рангом по столбцам матрицы 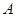 . Аналогично вводится ранг по строкам матрицы . Аналогично вводится ранг по строкам матрицы 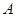 : : 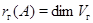 , где , где 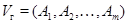 --- подпространство в --- подпространство в 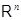 , натянутое на векторы-строки , натянутое на векторы-строки 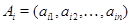 , , 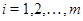 (г --- горизонтальный). Другими словами, (г --- горизонтальный). Другими словами,
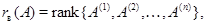
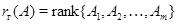
- ранги систем векторов-столбцов и соответственно векторов-строк. По теореме о существовании конечного базиса у подпространства 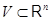 величины величины 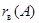 и и 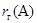 определены правильно. определены правильно.
Будем говорить, что матрица 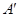 получена из получена из 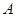 при помощи элементарного преобразования типа
(I), если при помощи элементарного преобразования типа
(I), если 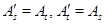 для какой-то пары индексов для какой-то пары индексов 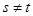 и и 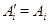 для для 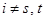 . Если же . Если же 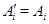 для всех для всех 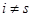 и и 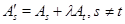 , , 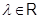 , то говорим, что к , то говорим, что к 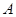 применено элементарное преобразование типа
(II). применено элементарное преобразование типа
(II).
Заметим, что элементарные преобразования обоих типов обратимы, т. е. матрица 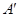 , получающаяся из , получающаяся из 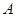 при помощи одного элементарного преобразования, переходит снова в при помощи одного элементарного преобразования, переходит снова в 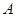 путем применения одного элементарного преобразования, причем того же типа. путем применения одного элементарного преобразования, причем того же типа.
2.2.1
Лемма. Если матрица 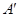 получена из прямоугольной матрицы получена из прямоугольной матрицы 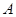 путем применения конечной последовательности элементарных преобразований, то имеют место равенства: путем применения конечной последовательности элементарных преобразований, то имеют место равенства:
(i) 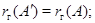
(ii) 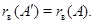
Доказательство. Достаточно рассмотреть тот случай, когда 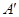 получена из получена из  путем применения одного элементарного преобразования (сокращенно э. п.). путем применения одного элементарного преобразования (сокращенно э. п.).
(i) Так как, очевидно, 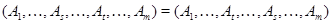 , то э. п. типа (I) не меняет , то э. п. типа (I) не меняет 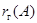 . Далее, . Далее, 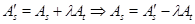 и, следовательно, и, следовательно, 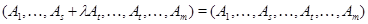 , так что , так что 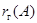 не меняется и при э. п. типа (II). не меняется и при э. п. типа (II).
(ii) Пусть 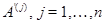 --- столбцы матрицы --- столбцы матрицы 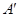 . Нам нужно доказать, что . Нам нужно доказать, что
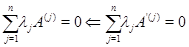
Тогда всякой, в том числе и максимальной, независимой системе столбцов одной матрицы будет отвечать независимая система столбцов с теми же номерами другой матрицы, чем и устанавливается равенство 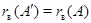 . Заметим еще, что в силу обратимости элементарных преобразований достаточно доказать импликацию в одну сторону. Пусть, например, . Заметим еще, что в силу обратимости элементарных преобразований достаточно доказать импликацию в одну сторону. Пусть, например, 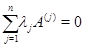 . Тогда, заменяя в (1) . Тогда, заменяя в (1) 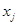 на на 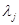 и все и все 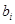 на 0, мы видим, что на 0, мы видим, что 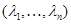 --- решение однородной системы ОС, ассоциированной с линейной системой (2). По соответствующей теореме это решение будет также решением однородной системы --- решение однородной системы ОС, ассоциированной с линейной системой (2). По соответствующей теореме это решение будет также решением однородной системы 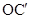 , получающейся из ОС при помощи э. п. типа (I) или (II) и имеющей своей матрицей как раз матрицу , получающейся из ОС при помощи э. п. типа (I) или (II) и имеющей своей матрицей как раз матрицу 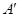 . Так как система . Так как система 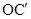 кратко записывается в виде кратко записывается в виде 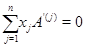 , то мы приходим к соотношению , то мы приходим к соотношению 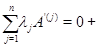
Основным результатом этого параграфа является следующее утверждение:
2.2.2
Теорема. Для любой прямоугольной 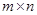 -матрицы -матрицы 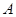 справедливо равенство справедливо равенство 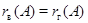 (это число называется просто рангом матрицы (это число называется просто рангом матрицы 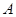 и обозначается символом и обозначается символом 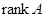 ). ).
Доказательство. Т. к. конечным числом элементарных преобразований, совершаемых над строками 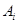 , матрицу , матрицу 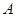 можно привести к ступенчатому виду: можно привести к ступенчатому виду:
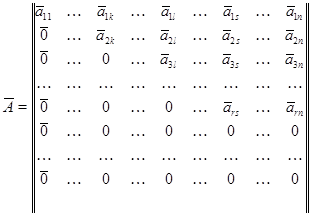
с 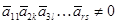 . Согласно лемме . Согласно лемме 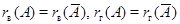 так что нам достаточно доказать равенство так что нам достаточно доказать равенство 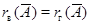 . .
Столбцы матриц 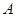 и и 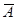 с номерами с номерами 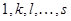 , отвечающими главным неизвестным , отвечающими главным неизвестным 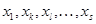 линейной системы (2), будем называть базисными столбцами. Эта терминология вполне оправдана. Предположив наличие соотношения линейной системы (2), будем называть базисными столбцами. Эта терминология вполне оправдана. Предположив наличие соотношения
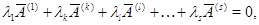
связывающего векторы-столбцы 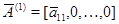 , , 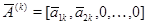 , , 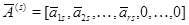 матрицы (3), получим последовательно: матрицы (3), получим последовательно: 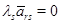 , , 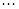 , , 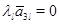 , , 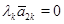 , , 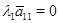 , а так как , а так как 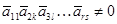 , то , то 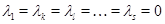 . Значит, . Значит, 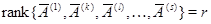 и и 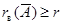 . Но пространство . Но пространство 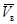 , порожденное столбцами матрицы , порожденное столбцами матрицы 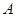 , отождествляется с пространством столбцов матрицы, которая получается из , отождествляется с пространством столбцов матрицы, которая получается из 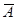 удалением последних удалением последних 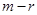 нулевых строк. Поэтому нулевых строк. Поэтому 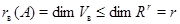 . Сопоставление двух неравенств показывает, что . Сопоставление двух неравенств показывает, что 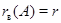 (неравенство (неравенство 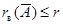 вытекает также из того очевидного соображения, что все столбцы матрицы вытекает также из того очевидного соображения, что все столбцы матрицы 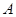 являются линейными комбинациями базисных; проделайте это самостоятельно в качестве упражнения). являются линейными комбинациями базисных; проделайте это самостоятельно в качестве упражнения).
С другой стороны, все ненулевые строки матрицы 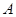 линейно независимы: любое гипотетическое соотношение линейно независимы: любое гипотетическое соотношение
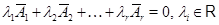
как и в случае со столбцами, дает последовательно 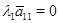 , , 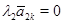 , , 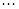 , , 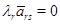 . Откуда . Откуда 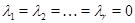 . Стало быть, . Стало быть, 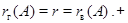
Ступенчатый вид матрицы 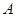 , дающий ответ на ряд вопросов относительно линейных систем, содержит элементы произвола, связанные, например, с выбором базисных столбцов или, что эквивалентно, с выбором главных неизвестных системы (2). В то же время из теоремы 1 и из ее доказательства извлекается , дающий ответ на ряд вопросов относительно линейных систем, содержит элементы произвола, связанные, например, с выбором базисных столбцов или, что эквивалентно, с выбором главных неизвестных системы (2). В то же время из теоремы 1 и из ее доказательства извлекается
Следствие. Число главных неизвестных, линейной системы (2) не зависит от способа приведения ее к ступенчатому виду и равно 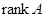 , где , где 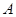 --- матрица системы. --- матрица системы.
Действительно, мы видели, что число главных неизвестных равно числу ненулевых строк матрицы 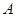 (см. (3)), совпадающему, как мы видели, с рангом матрицы (см. (3)), совпадающему, как мы видели, с рангом матрицы 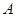 . Ранг определялся нами совершенно инвариантным образом. Этими словами выражается тот факт, что ранг матрицы служит ее внутренней характеристикой, не зависящей от каких-либо привходящих обстоятельств. . Ранг определялся нами совершенно инвариантным образом. Этими словами выражается тот факт, что ранг матрицы служит ее внутренней характеристикой, не зависящей от каких-либо привходящих обстоятельств. 
В следующей главе мы получим эффективное средство для вычисления ранга матрицы 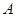 , устраняющее необходимость приведения , устраняющее необходимость приведения 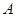 к ступенчатому виду. Это, несомненно, повысит ценность утверждений, основанных на понятии ранга. В качестве простого, но полезного примера сформулируем критерий разрешимости линейной системы. к ступенчатому виду. Это, несомненно, повысит ценность утверждений, основанных на понятии ранга. В качестве простого, но полезного примера сформулируем критерий разрешимости линейной системы.
2.3.3
Теорема. (Кронекер - Капелли) Система линейных уравнений (2) совместна тогда и только тогда, когда ранг ее матрицы совпадает с рангом расширенной матрицы
Доказательство. Совместность линейной системы (2), записанной в виде (1), можно трактовать как вопрос о представлении вектора-столбца 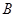 свободных членов в виде линейной комбинации векторов-столбцов свободных членов в виде линейной комбинации векторов-столбцов 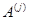 матрицы матрицы 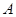 . Если такое представление возможно (т. е. система (2) совместна), то . Если такое представление возможно (т. е. система (2) совместна), то 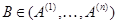 и и 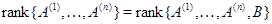 , откуда , откуда 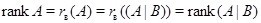 (см. формулировку теоремы 1). (см. формулировку теоремы 1).
Обратно, если ранги матриц 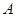 и и 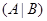 совпадают и совпадают и 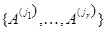 --- какая-то максимальная линейно независимая система базисных столбцов матрицы --- какая-то максимальная линейно независимая система базисных столбцов матрицы 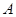 , то расширенная система , то расширенная система 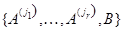 будет линейно зависимой, а это означает, что будет линейно зависимой, а это означает, что 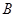 --- линейная комбинация базисных (и тем более всех) столбцов --- линейная комбинация базисных (и тем более всех) столбцов 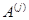 . Стало быть, система (2) совместна. . Стало быть, система (2) совместна. 
3. Линейные отображения. Действия с матрицами
Пусть 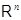 и и 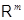 --- арифметические линейные пространства столбцов высоты --- арифметические линейные пространства столбцов высоты 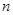 и и 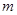 соответственно. Пусть, далее, соответственно. Пусть, далее, 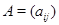 --- матрица размера --- матрица размера 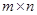 . Определим отображение . Определим отображение 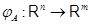 , полагая для любого , полагая для любого 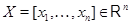
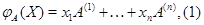
где 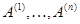 --- столбцы матрицы --- столбцы матрицы 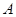 . Так как они имеют высоту . Так как они имеют высоту 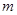 , то в правой части (1) стоит вектор-столбец , то в правой части (1) стоит вектор-столбец 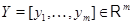 . Более подробно (1) переписывается в виде . Более подробно (1) переписывается в виде
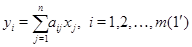
Если 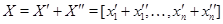 , ,
то 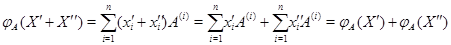 . .
Аналогично 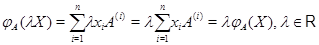 . .
Обратно, предположим, что 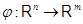 --- отображение множеств, обладающее следующими двумя свойствами: --- отображение множеств, обладающее следующими двумя свойствами:
(i) 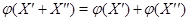 для всех для всех
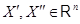 ; ;
(ii) 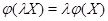 для всех для всех
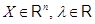 . .
Тогда, обозначив стандартные базисные столбцы пространств 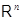 и и 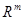 соответственно символами соответственно символами 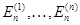 и и 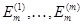 , мы воспользуемся свойствами (i), (ii) в применении к произвольному вектору , мы воспользуемся свойствами (i), (ii) в применении к произвольному вектору
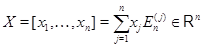 : :
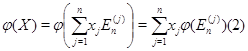
Соотношение (2) показывает, что отображение 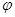 полностью определяется своими значениями на базисных векторах-столбцах. Положив полностью определяется своими значениями на базисных векторах-столбцах. Положив
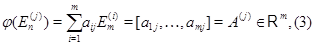
мы обнаруживаем, что задание 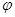 равносильно заданию прямоугольной матрицы равносильно заданию прямоугольной матрицы 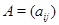 размера размера 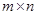 со столбцами со столбцами 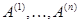 , а соотношения (1) и (2) фактически совпадают. Стало быть, можно положить , а соотношения (1) и (2) фактически совпадают. Стало быть, можно положить 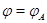 . .
3.1.1 . Определение. Отображение 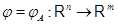 , обладающее свойствами (i), (ii), называется линейным отображением
из , обладающее свойствами (i), (ii), называется линейным отображением
из 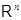 в в 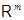 . Часто, в особенности при . Часто, в особенности при 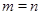 , говорят о линейном преобразовании
. Матрица , говорят о линейном преобразовании
. Матрица 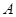 называется матрицей линейного отображения называется матрицей линейного отображения
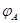 . .
Пусть 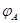 , , 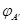 --- два линейных отображения --- два линейных отображения 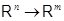 с матрицами с матрицами 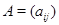 и и 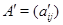 . Тогда равенство . Тогда равенство 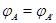 равносильно совпадению значений равносильно совпадению значений 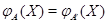 для всех для всех 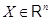 . В частности, . В частности, 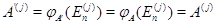 , откуда , откуда 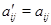 и и 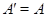 . .
Резюмируем наши результаты:
3.1.2
Теорема. Между линейными отображениями 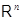 в в 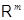 и матрицами размера и матрицами размера 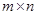 существует взаимно однозначное соответствие. существует взаимно однозначное соответствие.
Следует подчеркнуть, что бессмысленно говорить о линейных отображениях 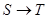 произвольных множеств произвольных множеств 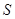 и и 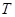 . Условия (i), (ii) предполагают, что . Условия (i), (ii) предполагают, что 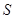 и и 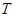 --- подпространства арифметических линейных пространств --- подпространства арифметических линейных пространств 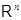 , , 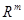 . .
Обратим внимание на специальный случай 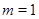 , когда линейное отображение , когда линейное отображение 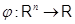 , обычно называемое линейной функцией
от , обычно называемое линейной функцией
от 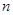 переменных, задается переменных, задается 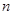 скалярами скалярами 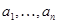 : :
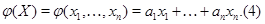
Линейные функции (4), равно как и произвольные линейные отображения 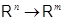 при фиксированных при фиксированных 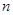 и и 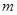 можно складывать и умножать на скаляры. В самом деле, пусть можно складывать и умножать на скаляры. В самом деле, пусть 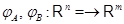 --- два линейных отображения. Отображение --- два линейных отображения. Отображение
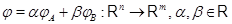
определяется своими значениями:
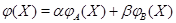
В правой части стоит обычная линейная комбинация векторов-столбцов.
Так как
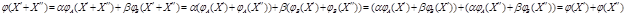
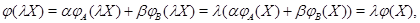
то 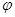 - линейное отображение. По теореме 1 можно говорить о его матрице - линейное отображение. По теореме 1 можно говорить о его матрице 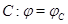 . Чтобы найти . Чтобы найти 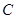 , выпишем, следуя (3), столбец с номером , выпишем, следуя (3), столбец с номером 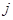 : :
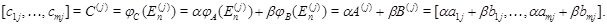
Матрицу 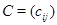 с элементами с элементами 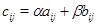 естественно назвать линейной комбинацией матриц естественно назвать линейной комбинацией матриц 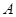 и и 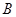 с коэффициентами с коэффициентами 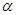 и и 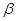 : :
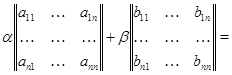
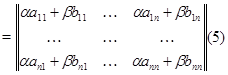
Итак, 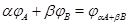 . .
Особенно часто нами будет использоваться тот факт, что линейные комбинации линейных функций снова являются линейными функциями.
Соотношения (5) и (6) выражают согласованность действий сложения и умножения на скаляры в множествах матриц размера 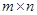 и отображений и отображений  . В случае произвольных множеств имеется еще важное понятие произведения (композиции) отображений. Разумно ожидать, что композиция двух линейных отображений должна выражаться неким согласованным образом в терминах матриц. Посмотрим как это делается. . В случае произвольных множеств имеется еще важное понятие произведения (композиции) отображений. Разумно ожидать, что композиция двух линейных отображений должна выражаться неким согласованным образом в терминах матриц. Посмотрим как это делается.
Пусть 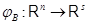 , , 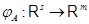 --- линейные отображения, --- линейные отображения, 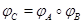 --- их композиция. --- их композиция.
Вообще говоря, нам следовало бы предварительно проверить, что 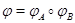 --- линейное отображение, но это довольно ясно: --- линейное отображение, но это довольно ясно:
(i) 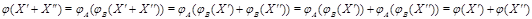 ; ;
(ii) 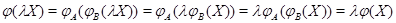 ; ;
поэтому по теореме 1 с 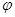 ассоциируется вполне определенная матрица ассоциируется вполне определенная матрица 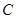 . .
Действие отображений на столбцы в цепочке запишем в явном виде по формуле (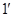 ): ):
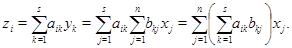
С другой стороны,
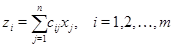
Сравнивая полученные выражения и памятуя о том, что 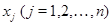 --- произвольные вещественные числа, мы приходим к соотношениям --- произвольные вещественные числа, мы приходим к соотношениям
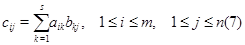
Будем говорить, что матрица 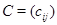 получается в результате умножения
матрицы получается в результате умножения
матрицы 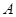 на матрицу на матрицу 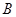 . Принято писать . Принято писать 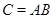 . Таким образом, произведением прямоугольной матрицы . Таким образом, произведением прямоугольной матрицы 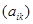 размера размера 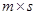 и прямоугольной матрицы и прямоугольной матрицы 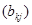 размера размера 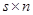 называется прямоугольная матрица называется прямоугольная матрица 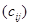 размера размера 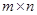 с элементами с элементами 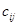 , задающимися соотношением (7). Нами доказана , задающимися соотношением (7). Нами доказана
3.2.1
Теорема. Произведение 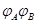 двух линейных отображений с матрицами двух линейных отображений с матрицами 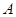 и и 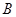 является линейным отображением с матрицей является линейным отображением с матрицей 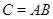 . Другими словами, . Другими словами,
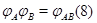
Соотношение (8) - естественное дополнение к соотношению (6).
Мы можем забыть о линейных отображениях и находить произведение 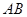 двух произвольных матриц двух произвольных матриц 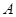 , , 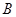 , имея в виду, однако, что символ , имея в виду, однако, что символ 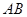 имеет смысл только в том случае, когда число столбцов в матрице имеет смысл только в том случае, когда число столбцов в матрице 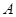 совпадает с числом строк в матрице совпадает с числом строк в матрице 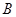 . Именно при этом условии работает правило (7) "умножения
. Именно при этом условии работает правило (7) "умножения 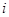 -й строки -й строки 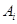 на на 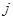 -й столбец -й столбец 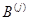 ", согласно которому ", согласно которому
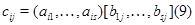
Число строк, матрицы 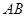 равно числу строк матрицы равно числу строк матрицы 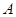 , а число столбцов --- числу столбцов матрицы , а число столбцов --- числу столбцов матрицы 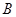 .
В частности, произведение квадратных матриц одинаковых порядков всегда определено, но даже в этом случае, вообще говоря, .
В частности, произведение квадратных матриц одинаковых порядков всегда определено, но даже в этом случае, вообще говоря, 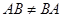 , как показывает хотя бы следующий пример: , как показывает хотя бы следующий пример:
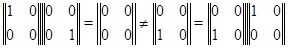
Умножение матриц, конечно, можно было бы вводить многими другими способами (умножать, например, строки на строки), но ни один из этих способов не сравним по важности с рассмотренным выше. Это и понятно, поскольку мы пришли к нему при изучении естественной композиции (суперпозиции) отображений, а само понятие отображения относится к числу наиболее фундаментальных в математике.
Следствие. Умножение матриц ассоциативно:
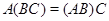
Действительно, произведение матриц соответствует произведению линейных отображений (теорема 2 и соотношение (8)), а произведение любых отображений ассоциативно. К тому же результату можно прийти вычислительным путем, используя непосредственно соотношение (7).
Пусть 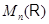 (или (или 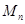 ) --- множество всех квадратных матриц ( ) --- множество всех квадратных матриц (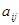 ) порядка ) порядка 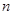 с вещественными коэффициентами с вещественными коэффициентами 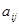 , ,
Единичному преобразованию 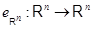 , переводящему каждый столбец , переводящему каждый столбец 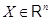 в себя, соответствует, очевидно, единичная матрица в себя, соответствует, очевидно, единичная матрица
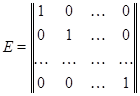
Можно записать 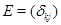 , где , где
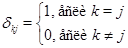
- символ Кронекера
. Правило (7) умножения матриц, в котором следует заменить 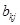 на на 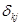 , показывает, что справедливы соотношения , показывает, что справедливы соотношения
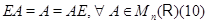
Матричные соотношения (10), полученные вычислительным путем, вытекают, конечно, из соотношений 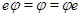 для произвольного отображения для произвольного отображения 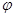 , если воспользоваться теоремой 1 и равенством (8) с , если воспользоваться теоремой 1 и равенством (8) с 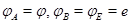 . .
Как мы знаем (см. (5)), матрицы из 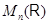 можно умножать на числа, понимая под можно умножать на числа, понимая под 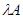 , где , где 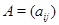 , матрицу , матрицу 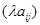 . .
Но умножение на скаляр (число) сводится к умножению матриц:
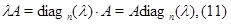
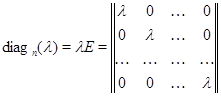
- известная нам скалярная матрица.
В равенстве (11) отражен легко проверяемый факт перестановочности 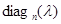 с любой матрицей с любой матрицей 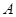 . Весьма важным для приложений является следующее его обращение. . Весьма важным для приложений является следующее его обращение.
3.3.1
Теорема. Матрица из 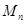 , перестановочная со всеми матрицами в , перестановочная со всеми матрицами в 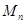 , должна быть скалярной. , должна быть скалярной.
Доказательство. Введем матрицу 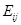 , в которой на пересечении , в которой на пересечении 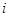 -й строки и -й строки и 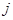 -го столбца стоит 1, а все остальные элементы --- нулевые. Если -го столбца стоит 1, а все остальные элементы --- нулевые. Если 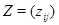 --- матрица, о которой идет речь в теореме, то она перестановочна, --- матрица, о которой идет речь в теореме, то она перестановочна,
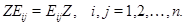
Перемножая матрицы в левой и правой частях этого равенства, мы получим матрицы
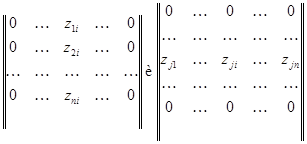
с единственным ненулевым 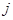 -м столбцом и соответственно с единственной ненулевой -м столбцом и соответственно с единственной ненулевой 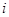 -й строкой. Их сравнение немедленно приводит к соотношениям -й строкой. Их сравнение немедленно приводит к соотношениям 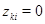 при при 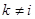 и и 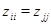 . Меняя . Меняя 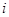 и и 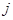 , получаем требуемое. , получаем требуемое. 
Отметим еще соотношения 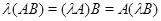 , которые непосредственно вытекают из определения умножения матриц на скаляры или, если угодно, из соотношений (11) и из ассоциативности умножения матриц. , которые непосредственно вытекают из определения умножения матриц на скаляры или, если угодно, из соотношений (11) и из ассоциативности умножения матриц.
Для данной матрицы 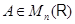 можно попробовать найти такую матрицу можно попробовать найти такую матрицу 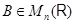 , чтобы выполнялось условие , чтобы выполнялось условие
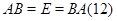
Если матрица 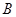 существует, то условию (12) в терминах линейных преобразований отвечает условие существует, то условию (12) в терминах линейных преобразований отвечает условие
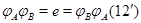
означающее, что 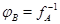 --- преобразование, обратное к --- преобразование, обратное к 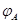 . . 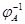 существует тогда и только тогда, когда существует тогда и только тогда, когда 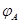 --- биективное преобразование. При этом --- биективное преобразование. При этом 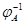 определено однозначно. Так как определено однозначно. Так как 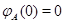 , то биективность , то биективность 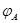 означает, в частности, что означает, в частности, что
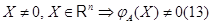
Пусть теперь 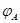 --- какое-то биективное линейное преобразование из --- какое-то биективное линейное преобразование из 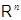 в в 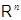 . Обратное к нему преобразование . Обратное к нему преобразование 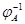 существует, но, вообще говоря, не ясно, является ли оно линейным. Чтобы убедиться в линейности существует, но, вообще говоря, не ясно, является ли оно линейным. Чтобы убедиться в линейности 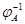 , мы введем векторы-столбцы , мы введем векторы-столбцы
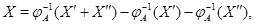
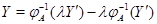
и применим к обеим частям этих равенств преобразование 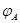 . В силу его линейности получим . В силу его линейности получим
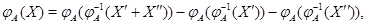
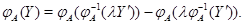
Так как 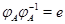 , то , то
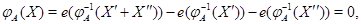
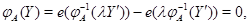
откуда, в соответствии с импликацией (13), находим, что 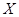 , , 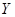 --- нулевые векторы. Таким образом, выполнены свойства (i), (ii) из 3.1, определяющие линейные отображения. Имеем --- нулевые векторы. Таким образом, выполнены свойства (i), (ii) из 3.1, определяющие линейные отображения. Имеем 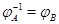 , где , где 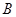 --- некоторая матрица. Переписав условие ( --- некоторая матрица. Переписав условие ( ) в виде ) в виде 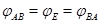 (см. (8)) и снова воспользовавшись теоремой 1, мы придем к равенствам (12). (см. (8)) и снова воспользовавшись теоремой 1, мы придем к равенствам (12).
Итак, матрица, обратная к 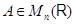 , существует в точности тогда, когда преобразование , существует в точности тогда, когда преобразование 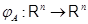 биективно. При этом преобразование биективно. При этом преобразование 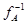 линейно
. Биективность линейно
. Биективность 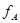 равносильна условию, что любой вектор-столбец равносильна условию, что любой вектор-столбец 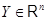 записывается единственным образом в виде (1) записывается единственным образом в виде (1)
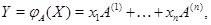
где 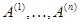 --- столбцы матрицы --- столбцы матрицы 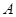 (сюръективность (сюръективность 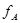 приводит к существованию приводит к существованию 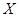 , для которого , для которого 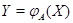 , а инъективность , а инъективность 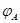 дает единственность дает единственность 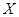 : если : если 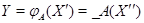 , то , то 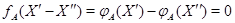 , откуда, согласно (12), , откуда, согласно (12), 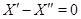 ). Значит, ). Значит, 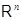 совпадает с пространством столбцов совпадает с пространством столбцов 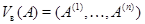 матрицы матрицы 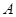 , так что , так что 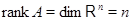 . .
Если матрица, обратная к 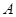 , существует, то, согласно вышесказанному, она единственна. Ее принято обозначать символом , существует, то, согласно вышесказанному, она единственна. Ее принято обозначать символом 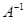 . В таком случае (см. ( . В таком случае (см. ( )) ))
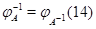
Квадратную матрицу 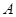 , для которой существует обратная матрица , для которой существует обратная матрица 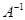 , называют невырожденной
(или неособенной
). Невырожденным называют и соответствующее линейное преобразование , называют невырожденной
(или неособенной
). Невырожденным называют и соответствующее линейное преобразование 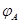 . В противном случае матрицу . В противном случае матрицу 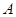 и линейное преобразование и линейное преобразование 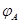 называют вырожденными
(или особенными
). называют вырожденными
(или особенными
).
Резюмируем полученные нами результаты.
3.3.2
Теорема. Квадратная матрица 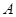 порядка порядка 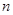 является невырожденной тогда и только тогда, когда ее ранг равен является невырожденной тогда и только тогда, когда ее ранг равен 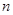 . Преобразование . Преобразование 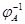 , обратное к , обратное к 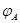 , линейно и задается равенством (14)
. , линейно и задается равенством (14)
.
Следствие. Невырожденность 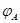 влечет невырожденность влечет невырожденность 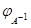 и и 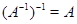 . Если . Если 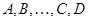 --- невырожденные --- невырожденные 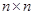 --- матрицы, то произведение --- матрицы, то произведение 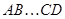 также невырождено и также невырождено и 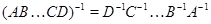 . .
Для доказательства достаточно сослаться на симметричность условия 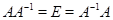 . . 
Нами получено довольно много правил действий с квадратными матрицами порядка 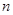 . Имеются в виду, ассоциативность (следствие теоремы 2), (10) и теорема 4. Обратим еще внимание на так называемые законы дистрибутивности
: . Имеются в виду, ассоциативность (следствие теоремы 2), (10) и теорема 4. Обратим еще внимание на так называемые законы дистрибутивности
:
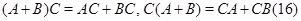
где  , ,  , , 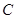 --- произвольные матрицы из --- произвольные матрицы из 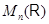 . .
Действительно, полагая 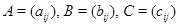 , мы получим для любых , мы получим для любых 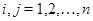 равенство (используется дистрибутивность в равенство (используется дистрибутивность в  ): ):
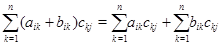
левая часть которого дает элемент 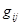 матрицы матрицы 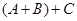 , а правая --- элементы , а правая --- элементы 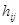 и и 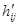 матриц матриц 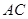 и соответственно и соответственно 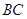 . Второй закон дистрибутивности (16) проверяется совершенно аналогично. Необходимость в нем обусловлена некоммутативностью умножения в . Второй закон дистрибутивности (16) проверяется совершенно аналогично. Необходимость в нем обусловлена некоммутативностью умножения в 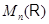 . Законы дистрибутивности . Законы дистрибутивности
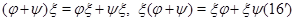
для линейных отображений 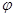 , , 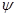 , , 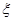 из из 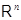 в в 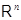 можно не доказывать, ссылаясь на соответствие между отображениями и матрицами, но можно, в свою очередь, выводить (16) из ( можно не доказывать, ссылаясь на соответствие между отображениями и матрицами, но можно, в свою очередь, выводить (16) из (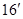 ), поскольку в случае отображений, рассуждение столь же просто. ), поскольку в случае отображений, рассуждение столь же просто.
Заключение
Таким образом, в данной курсовой работе мы доказали, что связанная компонента единицы алгебраической группы содержится в любой замкнутой подгруппе конечного индекса. В работе была доказана теорема: Для любой прямоугольной 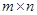 -матрицы -матрицы 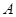 справедливо равенство справедливо равенство 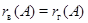 (это число называется просто рангом матрицы (это число называется просто рангом матрицы 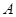 и обозначается символом и обозначается символом 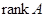 ).А также было
получено эффективное средство для вычисления ранга матрицы ).А также было
получено эффективное средство для вычисления ранга матрицы 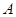 , устраняющее необходимость приведения , устраняющее необходимость приведения 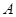 к ступенчатому виду, доказана теорема: Квадратная матрица к ступенчатому виду, доказана теорема: Квадратная матрица 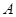 порядка порядка 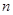 является невырожденной тогда и только тогда, когда ее ранг равен является невырожденной тогда и только тогда, когда ее ранг равен 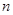 . Преобразование . Преобразование 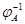 , обратное к , обратное к 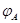 , линейно и задается равенством (14)
и следствие этой теоремы: невырожденность , линейно и задается равенством (14)
и следствие этой теоремы: невырожденность 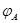 влечет невырожденность влечет невырожденность 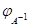 и и 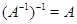 . Если . Если 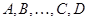 --- невырожденные --- невырожденные 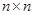 --- матрицы, то произведение --- матрицы, то произведение 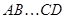 также невырождено и также невырождено и 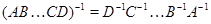 . .
Список использованных источников
1. Шеметков Л.А., Скиба А.Н., Формации алгебраических систем. - М.: Наука, 1989. - 256с.
2. Русаков С.А., Алгебраические 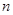 -арные системы. Минск, 1987. - 120с. -арные системы. Минск, 1987. - 120с.
3. Кон П., Универсальная алгебра. М.:Мир, 1968.--351с.
4. Ходалевич А.Д., Свойства централизаторов конгруэнции универсальных алгебр// Вопросы алгебры.-1996.-Вып.10 с.144-152
5. Mонaxов В.С. Произведение конечных групп, близких к нильпотентным.- В кн.: Конечные группы. Мн.: Наука и техника, 1975, с. 70 - 100.
|