|
Задание 1.
По 15 предприятиям, выпускающим один и тот же вид продукции известны значения двух признаков:
х
-
выпуск продукции, тыс. ед.;
у -
затраты на производство, млн. руб.
| x
|
y
|
| 5,3
|
18,4
|
| 15,1
|
22,0
|
| 24,2
|
32,3
|
| 7,1
|
16,4
|
| 11,0
|
22,2
|
| 8,5
|
21,7
|
| 14,5
|
23,6
|
| 10,2
|
18,5
|
| 18,6
|
26,1
|
| 19,7
|
30,2
|
| 21,3
|
28,6
|
| 22,1
|
34,0
|
| 4,1
|
14,2
|
| 12,0
|
22,1
|
| 18,3
|
28,2
|
Требуется:
4. Построить поле корреляции и сформулировать гипотезу о форме связи;
5. Построить модели:
2.1 Линейной парной регрессии;
2.2 Полулогарифмической парной регрессии;
2.3 Степенной парной регрессии; Для этого:
1. Рассчитать параметры уравнений;
2. Оценить тесноту связи с помощью коэффициента (индекса) корреляции;
3. Оценить качество модели с помощью коэффициента (индекса) детерминации и средней ошибки аппроксимации;
4. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом;
5. С помощью F
-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования;
3. По значениям характеристик, рассчитанных в пунктах 2-5 выбрать лучшее уравнение регрессии;
4. Используя метод Гольфрельда-Квандта проверить остатки на гетероскедастичность;
5. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня. Для уровня значимости 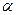 =0,05 определить доверительный интервал прогноза. =0,05 определить доверительный интервал прогноза.
Решение.
1. Строим поле корреляции.
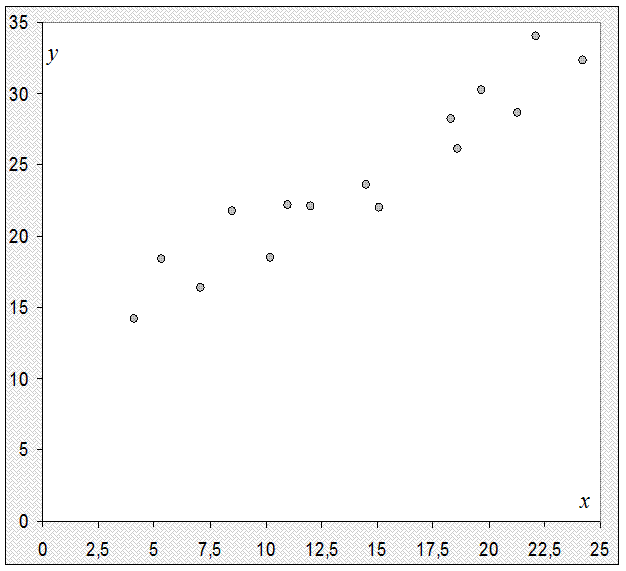
Анализируя расположение точек поля корреляции, предполагаем, что связь между признаками х
и у
может быть линейной, т.е. у=а+
b
х
, или нелинейной вида: у=а+
bln
х, у = ах
b
.
Основываясь на теории изучаемой взаимосвязи, предполагаем получить зависимость у
от х
вида у=а+
b
х,
т. к. затраты на производство y
можно условно разделить на два вида: постоянные, не зависящие от объема производства - a
, такие как арендная плата, содержание администрации и т.д.; и переменные, изменяющиеся пропорционально выпуску продукции b
х,
такие как расход материала, электроэнергии и т.д.
2.1 Модель линейной парной регрессии
2.1.1 Рассчитаем параметры a
и b
линейной регрессии у=а+
b
х
.
Строим расчетную таблицу 1.
Таблица 1
| №
|
x
|
y
|
yx
|
x2
|
y2
|
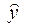
|
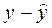
|
Аi
|
| 1
|
5,3
|
18,4
|
97,52
|
28,09
|
338,56
Реклама

|
16,21
|
2,19
|
11,92
|
| 2
|
15,1
|
22,0
|
332,20
|
228,01
|
484,00
|
24,74
|
-2,74
|
12,46
|
| 3
|
24,2
|
32,3
|
781,66
|
585,64
|
1043,29
|
32,67
|
-0,37
|
1,14
|
| 4
|
7,1
|
16,4
|
116,44
|
50,41
|
268,96
|
17,77
|
-1,37
|
8,38
|
| 5
|
11,0
|
22,2
|
244,20
|
121,00
|
492,84
|
21,17
|
1,03
|
4,63
|
| 6
|
8,5
|
21,7
|
184,45
|
72,25
|
470,89
|
18,99
|
2,71
|
12,47
|
| 7
|
14,5
|
23,6
|
342,20
|
210,25
|
556,96
|
24,22
|
-0,62
|
2,62
|
| 8
|
10,2
|
18,5
|
188,70
|
104,04
|
342,25
|
20,47
|
-1,97
|
10,67
|
| 9
|
18,6
|
26,1
|
485,46
|
345,96
|
681,21
|
27,79
|
-1,69
|
6,48
|
| 10
|
19,7
|
30,2
|
594,94
|
388,09
|
912,04
|
28,75
|
1,45
|
4,81
|
| 11
|
21,3
|
28,6
|
609,18
|
453,69
|
817,96
|
30,14
|
-1,54
|
5,39
|
| 12
|
22,1
|
34,0
|
751,40
|
488,41
|
1156,00
|
30,84
|
3,16
|
9,30
|
| 13
|
4,1
|
14,2
|
58,22
|
16,81
|
201,64
|
15,16
|
-0,96
|
6,77
|
| 14
|
12,0
|
22,1
|
265,20
|
144,00
|
488,41
|
22,04
|
0,06
|
0,26
|
| 15
|
18,3
|
28,2
|
516,06
|
334,89
|
795,24
|
27,53
|
0,67
|
2,38
|
| Σ
|
212,0
|
358,5
|
5567,83
|
3571,54
|
9050,25
|
358,50
|
0,00
|
99,69
|
| среднее
|
14,133
|
23,900
|
371,189
|
238,103
|
603,350
|
23,90
|
0,00
|
6,65
|
Параметры a
и b
уравнения
Yx
=
a
+
bx
определяются методом наименьших квадратов:
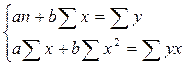
Разделив на n
и решая методом Крамера, получаем формулу для определения b
:
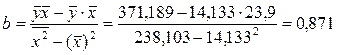
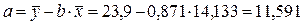
Уравнение регрессии:
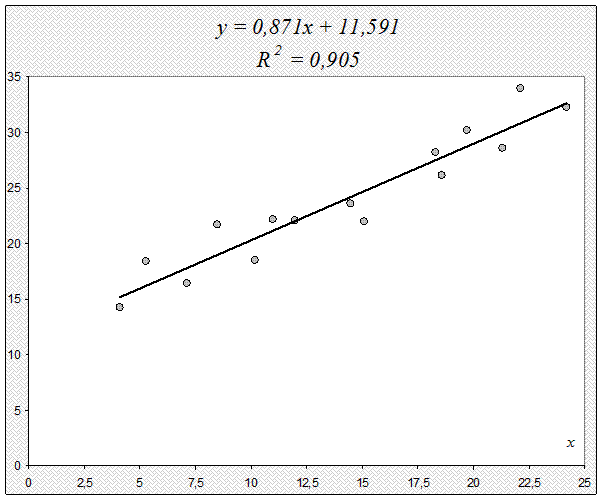
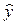 =11,591+0,871
x =11,591+0,871
x
С увеличением выпуска продукции на 1 тыс. руб. затраты на производство увеличиваются на 0,871 млн. руб. в среднем, постоянные затраты равны 11,591 млн. руб.
2.1.2. Тесноту связи оценим с помощью линейного коэффициента парной корреляции.
Предварительно определим средние квадратические отклонения признаков.
Средние квадратические отклонения:
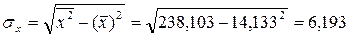
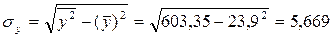
Коэффициент корреляции:
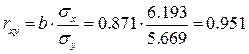
Между признаками X
и Y
наблюдается очень тесная линейная корреляционная связь.
2.1.3 Оценим качество построенной модели.
Определим коэффициент детерминации:
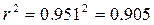
т. е. данная модель объясняет 90,5% общей дисперсии у
, на долю необъясненной дисперсии приходится 9,5%.
Следовательно, качество модели высокое.
Найдем величину средней ошибки аппроксимации А
i
.
Предварительно из уравнения регрессии определим теоретические значения 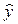 для каждого значения фактора. для каждого значения фактора.
Ошибка аппроксимации А
i
,
i
=1…15:
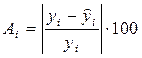
Средняя ошибка аппроксимации:
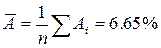
Ошибка небольшая, качество модели высокое.
5.1.4. Определим средний коэффициент эластичности:
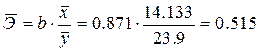
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0,515%.
2.1.5.Оценим статистическую значимость полученного уравнения. Проверим гипотезу H
0
, что выявленная зависимость у
от х
носит случайный характер, т. е. полученное уравнение статистически незначимо. Примем α=0,05. Найдем табличное (критическое) значение F-
критерия Фишера:
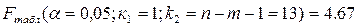
Найдем фактическое значение F
- критерия Фишера:
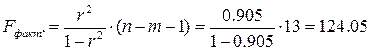
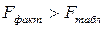
следовательно, гипотеза H
0
отвергается, принимается альтернативная гипотеза H
1
: с вероятностью 1-α=0,95 полученное уравнение статистически значимо, связь между переменными x
и y
неслучайна.
Реклама

Построим полученное уравнение.
2.2. Модель полулогарифмической парной регрессии
.
2.2.1. Рассчитаем параметры а
и b
в регрессии:
у
x
=а +
bln
х
.
Линеаризуем данное уравнение, обозначив:
z=lnx
.
Тогда:
y
=
a
+
bz
.
Параметры a
и b
уравнения
 =
a
+
bz =
a
+
bz
определяются методом наименьших квадратов:
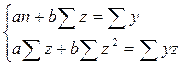 Рассчитываем таблицу 2. Рассчитываем таблицу 2.
Таблица 2
| №
|
x
|
y
|
z
|
yz
|
z2
|
y
2
|
|
|
Аi
|
| 1
|
5,3
|
18,4
|
1,668
|
30,686
|
2,781
|
338,56
|
15,38
|
3,02
|
16,42
|
| 2
|
15,1
|
22,0
|
2,715
|
59,723
|
7,370
|
484,00
|
25,75
|
-3,75
|
17,03
|
| 3
|
24,2
|
32,3
|
3,186
|
102,919
|
10,153
|
1043,29
|
30,42
|
1,88
|
5,83
|
| 4
|
7,1
|
16,4
|
1,960
|
32,146
|
3,842
|
268,96
|
18,27
|
-1,87
|
11,42
|
| 5
|
11,0
|
22,2
|
2,398
|
53,233
|
5,750
|
492,84
|
22,61
|
-0,41
|
1,84
|
| 6
|
8,5
|
21,7
|
2,140
|
46,439
|
4,580
|
470,89
|
20,06
|
1,64
|
7,58
|
| 7
|
14,5
|
23,6
|
2,674
|
63,110
|
7,151
|
556,96
|
25,34
|
-1,74
|
7,39
|
| 8
|
10,2
|
18,5
|
2,322
|
42,964
|
5,393
|
342,25
|
21,86
|
-3,36
|
18,17
|
| 9
|
18,6
|
26,1
|
2,923
|
76,295
|
8,545
|
681,21
|
27,81
|
-1,71
|
6,55
|
| 10
|
19,7
|
30,2
|
2,981
|
90,015
|
8,884
|
912,04
|
28,38
|
1,82
|
6,03
|
| 11
|
21,3
|
28,6
|
3,059
|
87,479
|
9,356
|
817,96
|
29,15
|
-0,55
|
1,93
|
| 12
|
22,1
|
34,0
|
3,096
|
105,250
|
9,583
|
1156,00
|
29,52
|
4,48
|
13,18
|
| 13
|
4,1
|
14,2
|
1,411
|
20,036
|
1,991
|
201,64
|
12,84
|
1,36
|
9,60
|
| 14
|
12,0
|
22,1
|
2,485
|
54,916
|
6,175
|
488,41
|
23,47
|
-1,37
|
6,20
|
| 15
|
18,3
|
28,2
|
2,907
|
81,975
|
8,450
|
795,24
|
27,65
|
0,55
|
1,95
|
| Σ
|
212,0
|
358,5
|
37,924
|
947,186
|
100,003
|
9050,25
|
358,50
|
0,00
|
131,14
|
| Средн.
|
14,133
|
23,900
|
2,528
|
63,146
|
6,667
|
603,350
|
23,90
|
0,00
|
8,74
|
Разделив на n
и решая методом Крамера, получаем формулу для определения b
:
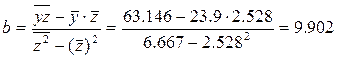
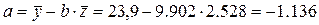
Уравнение регрессии:
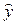 = -1,136 + 9,902
z = -1,136 + 9,902
z
2.2.2. Оценим тесноту связи между признаками у
и х
.
Т. к. уравнение у = а + b
l
n x
линейно относительно параметров а
и b
и его линеаризация не была связана с преобразованием зависимой переменной _у
, то теснота связи между переменными у
и х
, оцениваемая с помощью индекса парной корреляции Rxy
, также может быть определена с помощью линейного коэффициента парной корреляции ryz
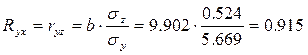
среднее квадратическое отклонение z
:
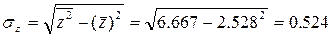
Значение индекса корреляции близко к 1, следовательно, между переменными у
и х
наблюдается очень тесная корреляционная связь вида 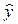 =
a
+
bz
. =
a
+
bz
.
2.2.3 Оценим качество построенной модели.
Определим коэффициент детерминации:
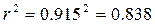
т. е. данная модель объясняет 83,8% общей вариации результата у
, на долю необъясненной вариации приходится 16,2%.
Следовательно, качество модели высокое.
Найдем величину средней ошибки аппроксимации А
i
.
Предварительно из уравнения регрессии определим теоретические значения 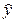 для каждого значения фактора. для каждого значения фактора.
Ошибка аппроксимации А
i
, i
=1…15:
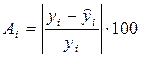
Средняя ошибка аппроксимации:
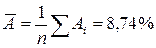
Ошибка небольшая, качество модели высокое.
2.2.4.Определим средний коэффициент эластичности:
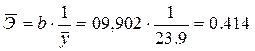
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0,414%.
2.2.5.Оценим статистическую значимость полученного уравнения. Проверим гипотезу H
0
, что выявленная зависимость у
от х
носит случайный характер, т.е. полученное уравнение статистически незначимо. Примем α=0,05.
Найдем табличное (критическое) значение F
-критерия Фишера:
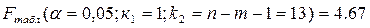
Найдем фактическое значение F
-критерия Фишера:
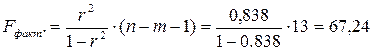
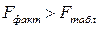
следовательно, гипотеза H
0
отвергается, принимается альтернативная гипотеза H
1
: с вероятностью 1-α=0,95 полученное уравнение статистически значимо, связь между переменными x
и y
неслучайна.
Построим уравнение регрессии на поле корреляции
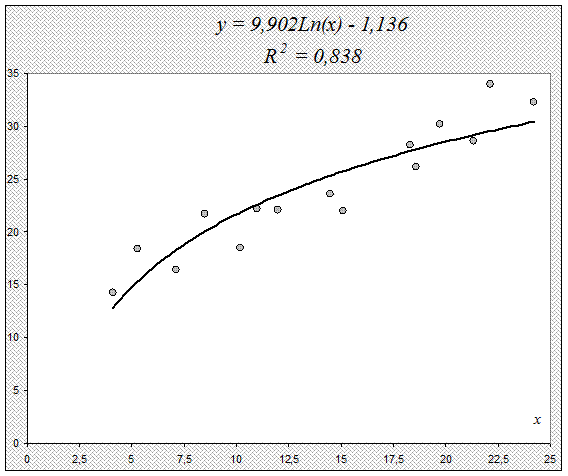
2.3. Модель степенной парной регрессии.
2.3.1. Рассчитаем параметры а
и b
степенной регрессии:
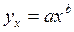
Расчету параметров предшествует процедура линеаризации данного уравнения:
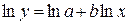
и замена переменных:
Y=lny, X=lnx, A=lna
Параметры уравнения:
Y
=
A
+
bX
определяются методом наименьших квадратов:
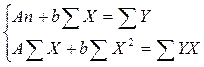 Рассчитываем таблицу 3. Рассчитываем таблицу 3.
Определяем b
:
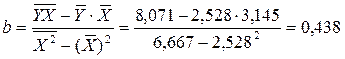
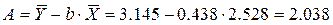
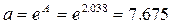
Уравнение регрессии:
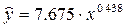
Построим уравнение регрессии на поле корреляции:
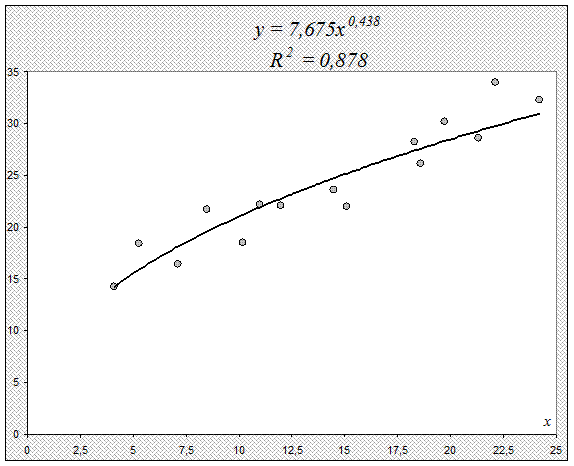
2.3.2. Оценим тесноту связи между признаками у
и х
с помощью индекса парной корреляции Ryx
.
Предварительно рассчитаем теоретическое значение 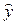 для каждого значения фактора x
,
и для каждого значения фактора x
,
и 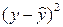 , тогда: , тогда:
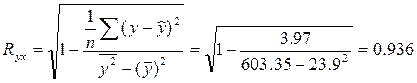
Значение индекса корреляции Rxy
близко к 1, следовательно, между переменными у
и х
наблюдается очень тесная корреляционная связь вида: 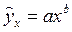
2.3.3.Оценим качество построенной модели.
Определим индекс детерминации:
R
2
=0,9362
=0,878,
т. е. данная модель объясняет 87,6% общей вариации результата у,
а на долю необъясненной вариации приходится 12,4%.
Качество модели высокое.
Найдем величину средней ошибки аппроксимации.
Ошибка аппроксимации А
i
, i
=1…15:
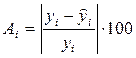
Средняя ошибка аппроксимации:
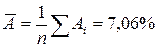
Ошибка небольшая, качество модели высокое.
2.3.4. Определим средний коэффициент эластичности:
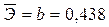
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0,438%.
2.3.5.Оценим статистическую значимость полученного уравнения.
Проверим гипотезу H
0
, что выявленная зависимость у
от х
носит случайный характер, т. е. полученное уравнение статистически незначимо. Примем α=0,05.
табличное (критическое) значение F
-критерия Фишера:
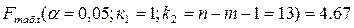
фактическое значение F
-критерия Фишера:
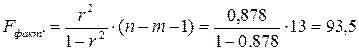
Таблица 3
| №
|
x
|
y
|
X
|
Y
|
YX
|
X2
|
y
2
|
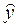
|
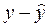
|
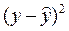
|
Аi
|
| 1
|
5,3
|
18,4
|
1,668
|
2,912
|
4,857
|
2,781
|
338,56
|
15,93
|
2.47
|
6,12
|
13,44
|
| 2
|
15,1
|
22,0
|
2,715
|
3,091
|
8,391
|
7,370
|
484,00
|
25,19
|
-3,19
|
10,14
|
14,48
|
| 3
|
24,2
|
32,3
|
3,186
|
3,475
|
11,073
|
10,153
|
1043,29
|
30,96
|
1,34
|
1,80
|
4,15
|
| 4
|
7,1
|
16,4
|
1,960
|
2,797
|
5,483
|
3,842
|
268,96
|
18,10
|
-1,70
|
2,89
|
10,37
|
| 5
|
11,0
|
22,2
|
2,398
|
3,100
|
7,434
|
5,750
|
492,84
|
21,92
|
0,28
|
0,08
|
1,24
|
| 6
|
8,5
|
21,7
|
2,140
|
3,077
|
6,586
|
4,580
|
470,89
|
19,58
|
2,12
|
4,48
|
9,75
|
| 7
|
14,5
|
23,6
|
2,674
|
3,161
|
8,454
|
7,151
|
556,96
|
24,74
|
-1,14
|
1,30
|
4,84
|
| 8
|
10,2
|
18,5
|
2,322
|
2,918
|
6,776
|
5,393
|
342,25
|
21,21
|
-2,71
|
7,35
|
14,66
|
| 9
|
18,6
|
26,1
|
2,923
|
3,262
|
9,535
|
8,545
|
681,21
|
27,59
|
-1,49
|
2,22
|
5,71
|
| 10
|
19,7
|
30,2
|
2,981
|
3,408
|
10,157
|
8,884
|
912,04
|
28,29
|
1,91
|
3,63
|
6,31
|
| 11
|
21,3
|
28,6
|
3,059
|
3,353
|
10,257
|
9,356
|
817,96
|
29,28
|
-0,68
|
0,46
|
2,37
|
| 12
|
22,1
|
34,0
|
3,096
|
3,526
|
10,916
|
9,583
|
1156,00
|
29,75
|
4,25
|
18,03
|
12,49
|
| 13
|
4,1
|
14,2
|
1,411
|
2,653
|
3,744
|
1,991
|
201,64
|
14,23
|
-0,03
|
0,00
|
0,24
|
| 14
|
12,0
|
22,1
|
2,485
|
3,096
|
7,692
|
6,175
|
488,41
|
22,78
|
-0,68
|
0,46
|
3,06
|
| 15
|
18,3
|
28,2
|
2,907
|
3,339
|
9,707
|
8,450
|
795,24
|
27,40
|
0,80
|
0,65
|
2,85
|
| сумма
|
212,0
|
358,5
|
37,924
|
47,170
|
121,062
|
100,003
|
9050,25
|
358,5
|
0,00
|
59,61
|
105,95
|
| среднее
|
14,133
|
23,900
|
2,528
|
3,145
|
8,071
|
6,667
|
603,350
|
23,90
|
0,00
|
3,97
|
7,06
|
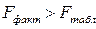
следовательно, гипотеза H
0
отвергается, принимается альтернативная гипотеза H
1
: с вероятностью 1-α=0,95 полученное уравнение статистически значимо, связь между переменными x
и y
неслучайна.
3. Выбор лучшего уравнения.
Составим таблицу полученных результатов исследования.
Таблица 4
| Уравнение
|
Коэффициент (индекс) корреляции
|
Коэффициент (индекс) детерминации
|
Средняя ошибка аппроксимации
|
Коэффициент эластичности
|
| линейное
|
0,951
|
0,905
|
6,65
|
0,515
|
| полулогагифмическое
|
0,915
|
0,838
|
8,74
|
0,414
|
| степенное
|
0,936
|
0,878
|
7,06
|
0,438
|
Анализируем таблицу и делаем выводы.
- Все три уравнения оказались статистически значимыми и надежными, имеют близкий к 1 коэффициент (индекс) корреляции, высокий (близкий к 1) коэффициент (индекс) детерминации и ошибку аппроксимации в допустимых пределах.
- При этом характеристики линейной модели указывают, что она несколько лучше полулогарифмической и степенной описывает связь между признаками x
и у.
- Поэтому в качестве уравнения регрессии выбираем линейную модель.
4.
Для выбранной модели проверим предпосылку МНК о гомоскедастичности остатков, т. е. о том, что остатки регрессии имеют постоянную дисперсию.
Используем метод Гольдфельдта-Квандта.
1. Упорядочим наблюдения по мере возрастания переменной х
.
2. Исключим из рассмотрения 3 центральных наблюдения.
3. Рассмотрим первую группу наблюдений (малые значения фактора х
) и определим 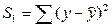 этой группы. этой группы.
4. Рассмотрим вторую группу наблюдений (большие значения фактора х) и определим 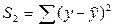 этой группы. этой группы.
5. Проверим, значимо или незначимо отличаются дисперсии остатков этих групп.
Таблица 5
| №
|
x
|
y
|
yx
|
x2
|
y
2
|
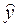
|
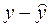
|
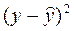
|
| 1
|
4,1
|
14,2
|
58,22
|
16,81
|
201,64
|
15,47
|
-1,27
|
1,60
|
| 2
|
5,3
|
18,4
|
97,52
|
28,09
|
338,56
|
16,50
|
1,90
|
3,61
|
| 3
|
7,1
|
16,4
|
116,44
|
50,41
|
268,96
|
18,05
|
-1,65
|
2,72
|
| 4
|
8,5
|
21,7
|
184,45
|
72,25
|
470,89
|
19,26
|
2,44
|
5,97
|
| 5
|
10,2
|
18,5
|
188,70
|
104,04
|
342,25
|
20,72
|
-2,22
|
4,93
|
| 6
|
11,0
|
22,2
|
244,20
|
121,00
|
492,84
|
21,41
|
0,79
|
0,63
|
| сумма
|
46,2
|
111,4
|
889,53
|
392,60
|
2115,14
|
111,40
|
0,00
|
19,46
|
| среднее
|
7,70
|
18,57
|
148,26
|
65,43
|
352,52
|
18,57
|
0,00
|
3,89
|
Определим параметры уравнения регрессии 1 группы:
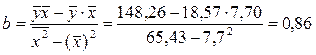
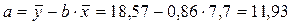
Уравнение регрессии 1 группы:
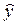 =11,93+0,86
x =11,93+0,86
x
Таблица 6
| №
|
x
|
y
|
yx
|
x2
|
y
2
|
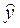
|
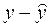
|
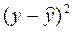
|
| 10
|
18,3
|
28,2
|
516,06
|
334,89
|
795,24
|
27,56
|
0,64
|
0,41
|
| 11
|
18,6
|
26,1
|
485,46
|
345,96
|
681,21
|
27,85
|
-1,75
|
3,06
|
| 12
|
19,7
|
30,2
|
594,94
|
388,09
|
912,04
|
28,92
|
1,28
|
1,63
|
| 13
|
21,3
|
28,6
|
609,18
|
453,69
|
817,96
|
30,49
|
-1,89
|
3,56
|
| 14
|
22,1
|
34,0
|
751,40
|
488,41
|
1156,00
|
31,27
|
2,73
|
7,47
|
| 15
|
24,2
|
32,3
|
781,66
|
585,64
|
1043,29
|
33,32
|
-1,02
|
1,03
|
| сумма
|
124,2
|
179,4
|
3738,70
|
2596,68
|
5405,74
|
179,40
|
0,00
|
17,17
|
| среднее
|
20,70
|
29,90
|
623,12
|
432,78
|
900,96
|
29,90
|
0,00
|
3,43
|
Параметры уравнения регрессии 2 группы:
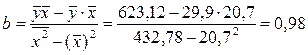
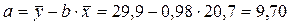
Уравнение регрессии 2 группы:
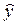 =9,7+0,98
x =9,7+0,98
x
S
1
=
19.46>
S
2
=
17.17
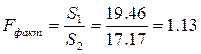
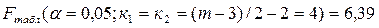
F
факт.
<
F
табл.
следовательно, остатки гомоскедастичны, предпосылки МНК не нарушены.
5. Рассчитаем прогнозное значение результата у, если прогнозное значение фактора х увеличивается на 5% от его среднего уровня.
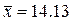
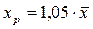
Точечный прогноз:
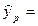 11,59+0,87–1,05–14,13=24,515 млн. руб. 11,59+0,87–1,05–14,13=24,515 млн. руб.
Для данной величины выпуска продукции прогнозное значение затрат на производство составляет 24,515 млн. руб.
Для уровня значимости α= 0,05 определим доверительный интервал прогноза.
Предварительно определим стандартные ошибки коэффициента корреляции и параметра b
.
Стандартная ошибка коэффициента корреляции:
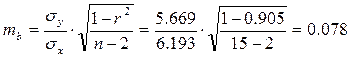
Ошибка прогноза:
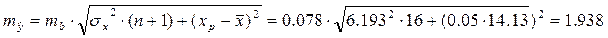 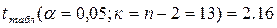
Доверительный интервал прогноза значений y
при 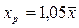 с вероятностью 0,95 составит: с вероятностью 0,95 составит:
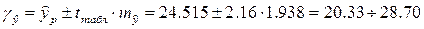
Прогноз надежный, но не очень точный, т. к.
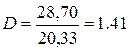
Задание 2
Имеются данные о заработной плате у
(тысяч рублей), возрасте х1
(лет), стаже работы по специальности х2
(лет) и выработке х3
(штук в смену) по 15 рабочим цеха:
| №
|
y
|
х
1
|
х2
|
х
3
|
| 1
|
3,2
|
30
|
6
|
12
|
| 2
|
4,5
|
41
|
18
|
20
|
| 3
|
3,3
|
37
|
11
|
12
|
| 4
|
3,0
|
33
|
9
|
18
|
| 5
|
2,8
|
24
|
4
|
15
|
| 6
|
3,9
|
44
|
19
|
17
|
| 7
|
3,7
|
37
|
18
|
17
|
| 8
|
4,2
|
39
|
22
|
26
|
| 9
|
4,7
|
49
|
30
|
26
|
| 10
|
4,4
|
48
|
24
|
22
|
| 11
|
2,9
|
29
|
8
|
18
|
| 12
|
3,7
|
31
|
6
|
20
|
| 13
|
2,4
|
26
|
5
|
10
|
| 14
|
4,5
|
47
|
19
|
20
|
| 15
|
2,6
|
29
|
4
|
15
|
Требуется:
1. С помощью определителя матрицы парных коэффициентов межфакторной корреляции оценить мультиколлинеарность факторов, исключить из модели фактор, ответственный за мультиколлинеарность.
2. Построить уравнение множественной регрессии в стандартизованной форме:
2.1. Оценить параметры уравнения.
2.2. Используя стандартизованные коэффициенты регрессии сравнить факторы по силе их воздействия на результат.
2.3. Оценить тесноту связи между результатом и факторами с помощью коэффициента множественной корреляции.
2.4. Оценить с помощью коэффициента множественной детерминации качество модели.
2.5. Используя F-критерий Фишера оценить статистическую значимость присутствия каждого из факторов в уравнении регрессии.
3. Построить уравнение множественной регрессии в естественной форме, пояснить экономический смысл параметров уравнения.
4. Найти среднюю ошибку аппроксимации.
5. Рассчитать прогнозное значение результата, если прогнозное значение факторов составит: х1
= 35 лет, х2
=
10 лет, х3
= 20 штук в смену.
Решение.
Для оценки мультиколлинеарности факторов используем определитель матрицы парных коэффициентов корреляции между факторами.
Определим парные коэффициенты корреляции.
Для этого рассчитаем таблицу 7.
Используя рассчитанную таблицу, определяем дисперсию y
,
x
1
,
x
2
,
x
3
.
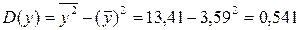
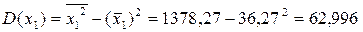
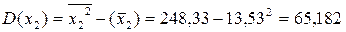
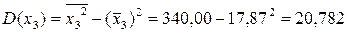
Найдем среднее квадратическое отклонение признаков y
,
x
1
,
x
2
, x
3
, как корень квадратный из соответствующей дисперсии.
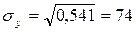
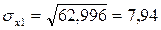
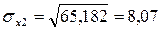
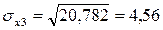
Определим парные коэффициенты корреляции:
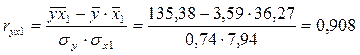

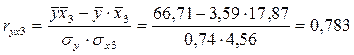
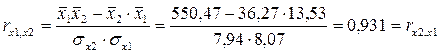
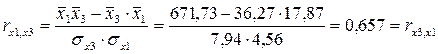
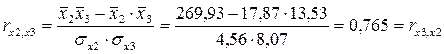
таблица 7
| №
|
y
|
y2
|
x1
|
x1
2
|
x2
|
x2
2
|
x3
|
x3
2
|
yx1
|
yx2
|
yx3
|
x1
x2
|
x1
x3
|
x2
x3
|
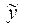
|
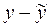
|
А
i
|
| 1
|
3,2
|
10,24
|
30
|
900
|
6
|
36
|
12
|
144
|
96,0
|
19,2
|
38,4
|
180
|
360
|
72
|
2,87
|
0,33
|
10,18
|
| 2
|
4,5
|
20,25
|
41
|
1681
|
18
|
324
|
20
|
400
|
184,5
|
81,0
|
90,0
|
738
|
820
|
360
|
4,00
|
0,50
|
11,03
|
| 3
|
3,3
|
10,89
|
37
|
1369
|
11
|
121
|
12
|
144
|
122,1
|
36,3
|
39,6
|
407
|
444
|
132
|
3,32
|
-0,02
|
0,73
|
| 4
|
3,0
|
9,00
|
33
|
1089
|
9
|
81
|
18
|
324
|
99,0
|
27,0
|
54,0
|
297
|
594
|
162
|
3,38
|
-0,38
|
12,79
|
| 5
|
2,8
|
7,84
|
24
|
576
|
4
|
16
|
15
|
225
|
67,2
|
11,2
|
42,0
|
96
|
360
|
60
|
2,65
|
0,15
|
5,47
|
| 6
|
3,9
|
15,21
|
44
|
1936
|
19
|
361
|
17
|
289
|
171,6
|
74,1
|
66,3
|
836
|
748
|
323
|
4,04
|
-0,14
|
3,54
|
| 7
|
3,7
|
13,69
|
37
|
1369
|
18
|
324
|
17
|
289
|
136,9
|
66,6
|
62,9
|
666
|
629
|
306
|
3,59
|
0,11
|
3,03
|
| 8
|
4,2
|
17,64
|
39
|
1521
|
22
|
484
|
26
|
676
|
163,8
|
92,4
|
109,2
|
858
|
1014
|
572
|
4,19
|
0,01
|
0,20
|
| 9
|
4,7
|
22,09
|
49
|
2401
|
30
|
900
|
26
|
676
|
230,3
|
141,0
|
122,2
|
1470
|
1274
|
780
|
4,83
|
-0,13
|
2,86
|
| 10
|
4,4
|
19,36
|
48
|
2304
|
24
|
576
|
22
|
484
|
211,2
|
105,6
|
96,8
|
1152
|
1056
|
528
|
4,56
|
-0,16
|
3,61
|
| 11
|
2,9
|
8,41
|
29
|
841
|
8
|
64
|
18
|
324
|
84,1
|
23,2
|
52,2
|
232
|
522
|
144
|
3,13
|
-0,23
|
7,82
|
| 12
|
3,7
|
13,69
|
31
|
961
|
6
|
36
|
20
|
400
|
114,7
|
22,2
|
74,0
|
186
|
620
|
120
|
3,36
|
0,34
|
9,17
|
| 13
|
2,4
|
5,76
|
26
|
676
|
5
|
25
|
10
|
100
|
62,4
|
12,0
|
24,0
|
130
|
260
|
50
|
2,51
|
-0,11
|
4,65
|
| 14
|
4,5
|
20,25
|
47
|
2209
|
19
|
361
|
20
|
400
|
211,5
|
85,5
|
90,0
|
893
|
940
|
380
|
4,39
|
0,11
|
2,46
|
| 15
|
2,6
|
6,76
|
29
|
841
|
4
|
16
|
15
|
225
|
75,4
|
10,4
|
39,0
|
116
|
435
|
60
|
2,97
|
-0,37
|
14,17
|
| σ
|
53,8
|
201,08
|
544
|
20674
|
203
|
3725
|
268
|
5100
|
2030,7
|
807,7
|
1000,6
|
8257
|
10076
|
4049
|
53,80
|
0,00
|
91,69
|
| ср.
|
3,59
|
13,41
|
36,27
|
1378,27
|
13,53
|
248,33
|
17,87
|
340,00
|
135,38
|
53,85
|
66,71
|
550,47
|
671,73
|
269,93
|
3,59
|
0,00
|
6,11
|
Матрица парных коэффициентов корреляции:
| |
y
|
x1
|
x2
|
x3
|
| y
|
1,000
|
|
|
|
| x1
|
0,908
|
1,000
|
|
|
| x2
|
0,894
|
0,931
|
1,000
|
|
| x3
|
0,783
|
0,657
|
0,765
|
1,000
|
Анализируем матрицу парных коэффициентов корреляции.
- rx1x2
=0.931, т. е. между факторами x1
и x2
существует сильная корреляционная связь, один из этих факторов необходимо исключить.
- rx1x3
=0.657 меньше, чем rx2x3
=0.765, т.е. корреляция фактора х2
с фактором х3
сильнее, чем корреляция факторов х1
и х3
.
- Из модели следует исключить фактор х2
, т.к. он имеет наибольшую тесноту связи с х3
и, к тому же, менее тесно (по сравнению с x
1
) связан с результатом у
(0.894<0.908).
2.1. Уравнение регрессии в естественной форме будет иметь вид:
y
x
= a + bl
x]
+b3
x3
,
фактор х2
исключен из модели.
Стандартизованное уравнение:
ty
=
β
1
tx
1
+
β
3
tx
3
где:
ty
,
tx
1
,
tx
3
– стандартизованные переменные.
Параметры уравнения β
1
и β
3
определим методом наименьших квадратов из системы уравнений:
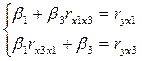
Или:
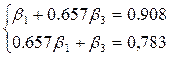
Систему решаем методом Крамера:
| ∆=
|
1
|
0,657
|
= 1-0,6572
= 0,568
|
| 0,657
|
1
|
| ∆β1
=
|
0,908
|
0,657
|
= 0,908-0,657–0,783=0,394
|
| 0,783
|
1
|
| ∆β3
=
|
1
|
0,571
|
=0,833-0,571–0,413= 0,186
|
| 0,413
|
0,833
|
Тогда:
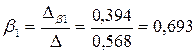
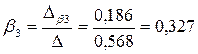
Получили уравнение множественной регрессии в стандартизованном масштабе:
ty
= 0,693
tx
1
+0,327
tx
3
Коэффициенты β1
и β3
сравнимы между собой в отличии от коэффициентов чистой регрессии b
1
и b
3
.
β1
=
0,693 больше β3
=
0,327,
следовательно, фактор x
1
сильнее влияет на результат y
чем фактор x
3
.
Определим индекс множественной корреляции:
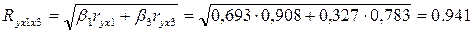
Cвязь между y
и факторами x
1
, x
3
характеризуется как тесная, т. к. значение индекса множественной корреляции близко к 1.
Коэффициент множественной детерминации:
R
2
yx
1
x
3
=(0.941)2
=0.886
Т. е. данная модель объясняет 88,6% вариации y
, на долю неучтенных в модели факторов приходится 100-88,6=11,4%
Оценим значимость полученного уравнения регрессии с помощью F
-критерия Фишера:
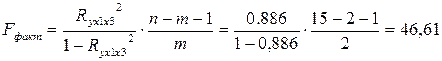
F
табл
(α=
0,05;
k
1
=
2;
k
2
=
15-2-1=12)=
3,88
Табличное значение критерия Фишера (определяем по таблице значений критерия Фишера при заданном уровне значимости α
и числе степеней свободы k
1
и k
2
) меньше фактического значения критерия. следовательно, гипотезу H
0
о том, что полученное уравнение статистически незначимо и ненадежно, отвергаем и принимаем альтернативную гипотезу H
1
: полученное уравнение статистически значимо, надежно и пригодно для анализа и прогноза.
Оценим статистическую значимость включения в модель факторов x
1
и x
2.
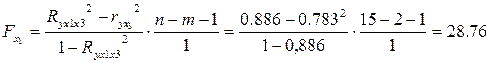
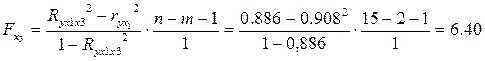
F
табл
(α=
0,05;
k
1
=
1;
k
2
=
15-2-1=12)=
4,75
Fx
1
>
F
табл.
Fx
3
>
F
табл.
Значит, включение в модель факторов x
1
и x
3
статистически значимо.
Перейдем к уравнению регрессии в естественном масштабе:
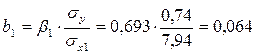
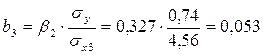
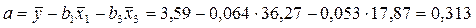
Уравнение множественной регрессии в естественном масштабе:
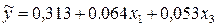
Экономическая интерпретация параметров уравнения:
b1
=0.064, это значит, что с увеличением x1
– возраста рабочего на 1 год заработная плата рабочего увеличивается в среднем на 64 рубля, если при этом фактор x2
- выработка рабочего не меняется и фиксирован на среднем уровне.
b3
=0,053, это значит, что с увеличением x3
– выработки рабочего на 1 шт. в смену, заработная плата рабочего увеличивается в среднем на 53 рубля, если при этом фактор x1
- возраст рабочего не меняется и фиксирован на среднем уровне.
a
=0,313 не имеет экономической интерпретации, формально это значение результата y
при нулевом значении факторов, но факторы могут и не иметь нулевого значения.
Найдем величину средней ошибки аппроксимации, таблица 7.
Ошибка аппроксимации А
i
, i
=1…15:
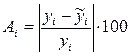
Средняя ошибка аппроксимации:
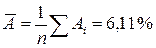
Ошибка небольшая, качество модели высокое.
Используем полученную модель для прогноза.
Если х1
=35, х2
=10, х3
=20, то
ур
= 0,313 + 0,064•35 + 0,053•20 = 3,618 тыс. руб.
т. е. для рабочего данного цеха, возраст которого 35 лет, а выработка 20 шт. в смену, прогнозное значение заработной платы - 3618 руб.
|