 Пермский государственный технический университет Пермский государственный технический университет
Строительный факультет
Кафедра строительной механики и вычислительных технологий
КУРСОВАЯ
РАБОТА
по дисциплине
ИНФОРМАТИКА
Тема: Вычисление площадей криволинейных эпюр изгибающих моментов с использованием численных методов
Работу выполнил:
студент I-го курса
строительного факультета
Лапшин А.М.
Работу принял:
старший преподаватель
Пермь 2009
Решение нелинейного уравнения
Решение некоторых строительных задач сводится к решению достаточно сложных нелинейных уравнений. Корни таких уравнений сравнительно редко удается найти точными методами. Следовательно, сама задача о точном определении корней теряет смысл и важное значении приобретают способы приближенного нахождения корней уравнения и оценки степени их точности.
Любое нелинейное уравнение можно представить в виде:
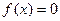 (1.1) (1.1)
где функция f
(x) определена и непрерывна в некотором конечном или бесконечном интервале А<x<B.
Всякое значение х*, обращающее уравнение (1.1) в тождество, называется корнем этого уравнения.
Методы решения нелинейных уравнений делятся на прямые
(точные) и итерационные
(приближенные).
Прямые методы
позволяютзаписатькорни уравнений в аналитическом виде.
Итерационные
методы – методы последовательных приближений.
Алгоритм нахождения приближенных значений корней уравнения (1.1) складывается из двух этапов:
1) определение или локализация корней.
2) Уточнение приближенного корня до заданной степени точности.
Существуют следующие методы решения нелинейных уравнений:
1) метод половинного деления
2) метод хорд
3) метод Ньютона
4) модифицированный метод Ньютона
В данной работе я использовал метод хорд. Рассмотрим его поподробнее.
Сущность метода хорд.
Пусть функция y
=f
(x) на отрезке [a,b] имеет единственный корень х*.
С геометрической точки
зрения
способ состоит в замене кривой y
=f
(x) хордой, проходящей через точки А[a,f
(a)] и B0
[b,f
(b)].
Уравнение хорды АВ запишется, как
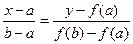 (1.2) (1.2)
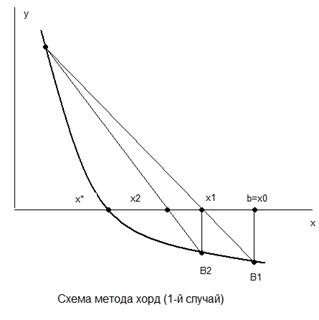
Для построения итерационной последовательности рассмотрим два случая, каждый из которых определен видом графика функции y=f(x) на отрезке [a,b].
Первый случай.
Полагаем f(a)>0, f(b)<0 и f``(x)>0 для x=[a.b].
1) В качестве нулевого приближения корня выбираем правый конец отрезка [a,b], т.е. x0
=b.
Реклама

2) Проводим хорду АВ0
и за первое приближение х1
принимаем абциссу точки пересечения хорды с осью ОХ.
3) Второе приближение х2
получаем как абсциссу точки пересечения хорды АВ1
с осью ОХ.
4) Аналогичным образом строим итерационную последовательность приближений:
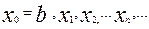 (1.3) (1.3)
Данная итерационная последовательность сводится к корню х
*.
Второй случай.
Полагаем f(a)<0, f(b)>0 и f``(x)>0. В качестве нулевого приближения корня выбираем левый конец отрезка [a,b], x0
=a, в качестве неподвижного конца х=b
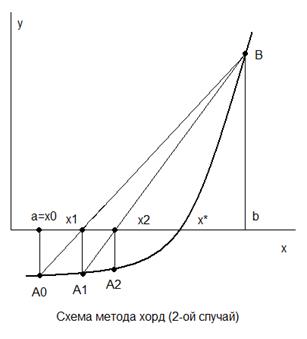
Аналогично первому случаю строим последовательность приближений, сходящуюся к точному х* уравнения (1.1).
Пример решения нелинейного уравнения
Решим нелинейное уравнение
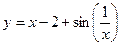
Выберем отрезок, где есть единственное решение уравнения (1.1): 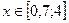 . Протабулируем данную функцию. Разобьем её на 10 частей, тогда шаг будет находиться по формуле: . Протабулируем данную функцию. Разобьем её на 10 частей, тогда шаг будет находиться по формуле: 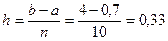 . Составим таблицу табулирования: . Составим таблицу табулирования:
| x
|
y
|
| 0,7 |
-0,310096924 |
| 1,03 |
-0,144620651 |
| 1,36 |
0,030805312 |
| 1,69 |
0,247786078 |
| 2,02 |
0,495075213 |
| 2,35 |
0,762805318 |
| 2,68 |
1,044535871 |
| 3,01 |
1,336148032 |
| 3,34 |
1,634948096 |
| 3,67 |
1,939120346 |
| 4 |
2,247403959 |
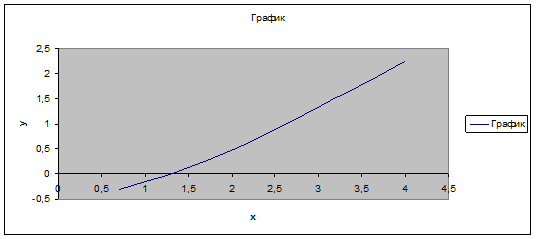
Выбираем начальное приближение. Из условия f``(x)*f(x)<0 выбираем начальное приближение. В нашем случае f``(x)>0, а f(x)<0, данное условие выполняется в точке х
0
=а=0,7
| n
|
x
|
f(x)
|
e
|
| 0
|
0,7 |
-0,310096924 |
- |
| 1
|
1,100124925 |
-0,110993049 |
0,199103875 |
| 2
|
1,236601512 |
-0,040030408 |
0,070962641 |
| 3
|
1,284961356 |
-0,013016136 |
0,027014272 |
| 4
|
1,300595313 |
-0,004074898 |
0,008941238 |
| 5
|
1,305480901 |
-0,001260165 |
0,002814733 |
| 6
|
1,306990925 |
-0,000388218 |
0,000871947 |
| 7
|
1,307456037 |
-0,000119456 |
0,000268761 |
где f(x) это значение функции в данной точке, е – точность, которая равна: 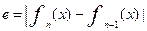 . Из таблицы видно, корнем уравнения будет х*=1,307456037. Корень найден с точностью 0,00268761 на 7-ой итерации. . Из таблицы видно, корнем уравнения будет х*=1,307456037. Корень найден с точностью 0,00268761 на 7-ой итерации.
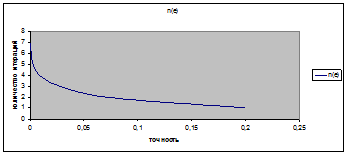
Построим зависимость n(e), из которой будет видно количество итераций для каждого значения е.
| n
|
e
|
| 1
|
0,199103875 |
| 2
|
0,070962641 |
| 3
|
0,027014272 |
| 4
|
0,008941238 |
| 5
|
0,002814733 |
| 6
|
0,000871947 |
| 7
|
0,000268761 |
Построим график зависимости n(e):
Вычисление площадей криволинейных фигур
При решении достаточно большого круга задач приходится сталкиваться с необходимостью вычисления определенного интеграла:
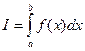 (2.1) (2.1)
Вычисление площадей,
ограниченных кривыми, работы, моментов инерции
и т.д. сводится к вычислению определенного интеграла.
Если непрерывная на отрезке [a,b] функция y=f
(x) имеет на этом отрезке первообразную F
(x), то интеграл (2.1) может быть вычислен по формуле Ньютона-Лейбница:
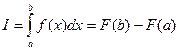 (2.2) (2.2)
Однако только для узкого класса функций y=f
(x) первообразная F
(x) может быть выражена в элементарных функциях. Кроме того, функция y=f
(x) может задаваться графически или таблично. В этих случаях применяют различные формулы для приближенного вычисления интегралов. Такие формулы называют квадратурными формулами или формулами численного интегрирования.
Идея численного интегрирования заключается в замене криволинейной трапеции фигурой, площадь которой вычисляется достаточно просто
.
Для этого отрезок интегрирования [a,b] разбивают на n равных элементарных отрезков [xi
;
xi
+1
] (i
=0,1,2,…,n
-1), с шагом 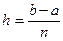 . При этом криволинейная трапеция разобьется на n
элементарных криволинейных трапеций
с основаниями равными h . При этом криволинейная трапеция разобьется на n
элементарных криволинейных трапеций
с основаниями равными h
Реклама

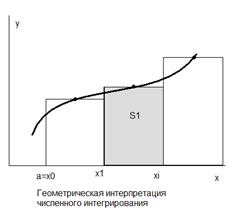
Каждая элементарная криволинейная трапеция заменяется фигурой, площадь которой вычисляется довольно просто. Обозначим эту площадь Si
. Сумма всех этих площадей называется интегральной суммой
и вычисляется по формуле:
σn
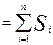 (2.3) (2.3)
Тогда приближённая формула вычисления интеграла (2.1) имеет вид
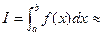 σn
(2.4) σn
(2.4)
Точность вычисления по формуле зависит от числа разбиений n
. С увеличением n
интегральная сумма σn
приближается к точному значению интеграла
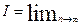 σn
(2.5) σn
(2.5)
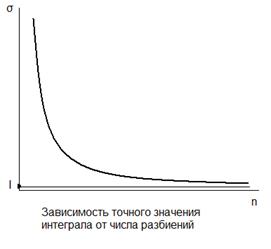
Существуют различные формулы для оценки погрешности выражения (2.4), но, как правило, они достаточно сложны. Будем проводить оценку точности приближения (5.4) методом половинного шага. Для этого циклически повторим следующую последовательность действий:
1) Разбиваем отрезок интегрирования на n
равных отрезков с шагом 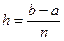
2) Строим σn
по формуле (2.3)
3) Повторяем пункты 1) и 2) для шага h
/2, т.е. для 2n
и строим σ2
n
4) Если два соседних приближения близки, т.е. |σn
– σ2
n
|<e
(2.6), то σ2
n
принимаем за приближённое значение интеграла (2.1) с заданной точностью е:
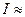 σ2
n
(2.7) σ2
n
(2.7)
5) Если условие (2.6) не выполняется, то надо вернуться на пункт 3).
Способы численного интегрирования
1) Квадратурные формулы прямоугольников.
2) Квадратурная формулы трапеций.
3) Квадратурная формула Симпсона.
Рассмотрим поподробнее способ квадратурных формул прямоугольников.
Квадратурные формулы прямоугольников
Отрезок интегрирования [a,b] разбиваем на n
равных отрезков и получаем n
+1 равноудаленных точек: x
0
=
a
,
xn
=
b
,
xi
+1
=
xi
+
h
,
i
=(0,1,…,
n
-1),
где h
шаг разбивки. При этом обозначим 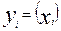 . .
Площадь каждой элементарной криволинейной трапеции заменим площадью прямоугольника с основанием h
и высотой 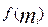 , где , где 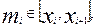 i
=0,1,2,…,n
-1 i
=0,1,2,…,n
-1
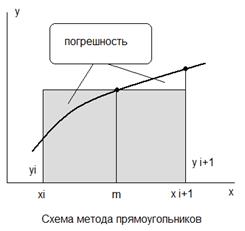
В зависимости от выбора mi
существует несколько формул прямоугольников.
· Формула «левых» (входящих) прямоугольников, когда mi
=
xi
:
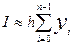 (2.8) (2.8)
· Формула «правых» (выходящих) прямоугольников, когда mi
=
xi
-1
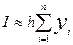 (2.9) (2.9)
· Формула «средних» прямоугольников, когда mi
=
xi
+
h
/2
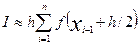 (2.10) (2.10)
Пример нахождения площади криволинейной трапеции
Найдем площадь криволинейной трапеции методом «левых» (входящих) прямоугольников.
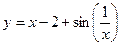
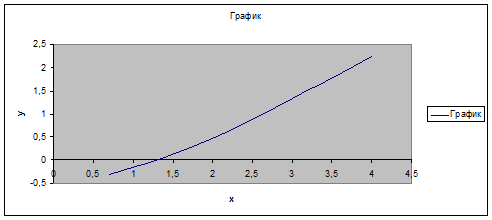
Из графика видно, что искомая площадь будет состоять из 2-х площадей:
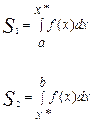 (2.11) (2.11)
В моем случае a
=0,7, b=4, x* - решение нелинейного уравнения (найденное ранее). х*=1,307456037.
Найдем S1.
Для этого, как говорилось ранее, разобьем отрезок от a
до x
*
для начала на 5 частей. Шаг вычислим по формуле 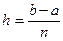 . В нашем случае h
=
0,121491207. Составим таблицу вида: . В нашем случае h
=
0,121491207. Составим таблицу вида:
| x`
|
y
`
|
| 0,821491207 |
-0,240341227 |
| 0,942982415 |
-0,184434792 |
| 1,064473622 |
-0,128303731 |
| 1,185964829 |
-0,067263095 |
| 1,307456037 |
-0,000119456 |
где x`=x+h,
y
`=
y
(
x
`),
т.к. функция до корня x* лежит в отрицательной области, то формула для метода входящих прямоугольников будет выглядеть:
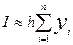
Получаем, что I
=
0,075380714. Теперь уменьшаем шаг в 2 раза, т.е. увеличиваем количество разбиений в 2 раза, тогда получаем h
=0,060745604.
| x`
|
y
`
|
| 0,760745604 |
-0,271918938 |
| 0,821491207 |
-0,240341227 |
| 0,882236811 |
-0,211870637 |
| 0,942982415 |
-0,184434792 |
| 1,003728018 |
-0,156813572 |
| 1,064473622 |
-0,128303731 |
| 1,125219226 |
-0,098518017 |
| 1,185964829 |
-0,067263095 |
| 1,246710433 |
-0,034464413 |
| 1,307456037 |
-0,000119456 |
Получаем значение интеграла: I
=0,08468228, определим е по формуле (2.6). В нашем случае e=0,023936676.
Опять уменьшаем шаг в 2 раза и получаем 20 разбиений с h
=0,030372802.
| x`
|
y
`
|
| 0,730373 |
-0,289886259 |
| 0,760746 |
-0,271918938 |
| 0,791118 |
-0,255565552 |
| 0,821491 |
-0,240341227 |
| 0,851864 |
-0,225872242 |
| 0,882237 |
-0,211870637 |
| 0,91261 |
-0,198114836 |
| 0,942982 |
-0,184434792 |
| 0,973355 |
-0,170700579 |
| 1,003728 |
-0,156813572 |
| 1,034101 |
-0,142699619 |
| 1,064474 |
-0,128303731 |
| 1,094846 |
-0,113585932 |
| 1,125219 |
-0,098518017 |
| 1,155592 |
-0,083080997 |
| 1,185965 |
-0,067263095 |
| 1,216338 |
-0,05105816 |
| 1,24671 |
-0,034464413 |
| 1,277083 |
-0,017483449 |
| 1,307456 |
-0,000119456 |
I
=0,089359684. е=0,004677404, что удовлетворяет заданной точности. Тогда получаем, что
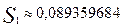
Аналогично рассмотрим участок от x* до b
.
Т.к. функция лежит в положительной области, то вычисляем интеграл по формуле (2.8). Разбиваем участок на 5 частей, тогда h
=
0,538508793
| x`
|
y
`
|
| 1,307456 |
-0,000119456 |
| 1,845965 |
0,361577144 |
| 2,384474 |
0,791667672 |
| 2,922982 |
1,258463933 |
| 3,461491 |
1,746382321 |
| 4 |
2,247403959 |
Получаем, что I
=3,449351066
Уменьшаем шаг в 2 раза, значит увеличиваем число разбиений до 10. получаем шаг h
=
0,269254396
| x`
|
y
`
|
| 1,307456 |
-0,000119456 |
| 1,57671 |
0,169269369 |
| 1,845965 |
0,361577144 |
| 2,115219 |
0,570568282 |
| 2,384474 |
0,791667672 |
| 2,653728 |
1,021701245 |
| 2,922982 |
1,258463933 |
| 3,192237 |
1,500398398 |
| 3,461491 |
1,746382321 |
| 3,730746 |
1,995590368 |
| 4 |
2,247403959 |
Получаем, что I
=3,14028797, e=0,309063096.
Точность не удовлетворяет заданной, поэтому увеличиваем число разбиений до 10. h
=
0,134627198.
| x`
|
y
`
|
| 1,307456 |
-0,000119456 |
| 1,442083 |
0,081270693 |
| 1,57671 |
0,169269369 |
| 1,711338 |
0,262985166 |
| 1,845965 |
0,361577144 |
| 1,980592 |
0,464311544 |
| 2,115219 |
0,570568282 |
| 2,249846 |
0,679830178 |
| 2,384474 |
0,791667672 |
| 2,519101 |
0,905723836 |
| 2,653728 |
1,021701245 |
| 2,788355 |
1,139351027 |
| 2,922982 |
1,258463933 |
| 3,05761 |
1,378863128 |
| 3,192237 |
1,500398398 |
| 3,326864 |
1,622941481 |
| 3,461491 |
1,746382321 |
| 3,596118 |
1,870626018 |
| 3,730746 |
1,995590368 |
| 3,865373 |
2,121203847 |
| 4 |
2,247403959 |
Получаем, что I
=
2,987378894, е=0,152909076. Данная точность не удовлетворяет заданную, поэтому продолжаем разбиение.
Увеличиваем число разбиений до 40. h
=0,134627198
| x
`
|
y
`
|
| 1,307456 |
-0,000119456 |
| 1,37477 |
0,039695527 |
| 1,442083 |
0,081270693 |
| 1,509397 |
0,124499597 |
| 1,57671 |
0,169269369 |
| 1,644024 |
0,215467404 |
| 1,711338 |
0,262985166 |
| 1,778651 |
0,311720214 |
| 1,845965 |
0,361577144 |
| 1,913278 |
0,412467875 |
| 1,980592 |
0,464311544 |
| 2,047906 |
0,517034183 |
| 2,115219 |
0,570568282 |
| 2,182533 |
0,624852304 |
| 2,249846 |
0,679830178 |
| 2,31716 |
0,735450821 |
| 2,384474 |
0,791667672 |
| 2,451787 |
0,848438265 |
| 2,519101 |
0,905723836 |
| 2,586414 |
0,963488964 |
| 2,653728 |
1,021701245 |
| 2,721042 |
1,080331004 |
| 2,788355 |
1,139351027 |
| 2,855669 |
1,198736328 |
| 2,922982 |
1,258463933 |
| 2,990296 |
1,318512697 |
| 3,05761 |
1,378863128 |
| 3,124923 |
1,439497237 |
| 3,192237 |
1,500398398 |
| 3,25955 |
1,561551229 |
| 3,326864 |
1,622941481 |
| 3,394178 |
1,684555937 |
| 3,461491 |
1,746382321 |
| 3,528805 |
1,808409222 |
| 3,596118 |
1,870626018 |
| 3,663432 |
1,933022811 |
| 3,730746 |
1,995590368 |
| 3,798059 |
2,058320067 |
| 3,865373 |
2,121203847 |
| 3,932686 |
2,184234166 |
| 4 |
2,247403959 |
Получаем I
=
2,911333086, e=0,076045808 что удовлетворяет заданной точности. Значит: 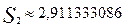
Тогда можем найти искомую площадь, которая будет находиться по формуле:
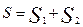
S=
3,000692769.
Вывод
: полученная площадь вычислена с точность e=0,1, при этом количество разбиений до корня равно 10, а полсе корня – 40.
Аппроксимация
Задачи и способы аппроксимации
Большинство численных методов основаны на замене одной функции f
(
x
)
другой функцией φ
(
x
)
. Как правило φ
(
x
)
обладает «хорошими» свойствами и является «удобной» при аналитических и вычислительных операциях. Такую замену называют аппроксимацией.
Таким образом, задача аппроксимации функции f
(
x
)
функций φ
(
x
)
.состоит в построении функции φ
(
x
)
близкой к функции f
(
x
)
на некотором отрезке [a
,
b
].
Для решения этой задачи необходимо ответить на ряд вопросов, а именно:
1. что известно о функции f
(
x
).
Задана она аналитически или таблицей своих значений, какова степень её гладкости.
2. какую функцию φ
(
x
)
выбрать в качестве аппроксимирующей функции.
3. что понимать под близостью между f
(
x
)
иφ
(
x
),
т.е. какова степень приближения.
Термин близости
двух функций понимается по-разному в зависимости от обстоятельств. При этом мы получаем различные задачи теории приближения, из которых рассмотрим интерполирование
и среднеквадратичное отклонение
.
Среднеквадратичное приближение
Исходные данные для построения тех или иных измерений имеют заведомо приближенный характер. Эти данные содержат погрешности измерительной аппаратуры, погрешности условий эксперимента, случайные ошибки и пр.
Предположим, что при обработке результатов какого-либо эксперимента обнаружена некая функциональная зависимость y
=
f
(
x
)
. Эта зависимость представлена в таблице зачтений yi
, полученных в ходе эксперимента yi
| xi
|
x
1
|
x2
|
… |
xn
|
| yi
|
y1
|
y2
|
… |
yn
|
Если аналитическое выражение функции f
(
x
)
неизвестно или весьма сложно, то возникает задача найти функцию y
=
φ
(
x
),
значения которой при x
=
xi
мало отличались бы от опытных данных. Таким образом исследуемая зависимость аппроксимируюется функцией y
=
φ
(
x
)
на отрезке [xi
,
xn
]:
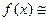 φ
(
x
)
(3.1) φ
(
x
)
(3.1)
Аппроксимирующая функция y
=
f
(
x
)
называется эмпирической формулой
или уравнением регрессии.
Для чего нужна эта зависимость?
Если приближение (3.1) найдено, то можно:
· просчитать значение y
для любого значения аргумента;
· сделать прогноз о поведении функции вне исследуемого отрезка;
· выбрать оптимальное направление развития исследуемого процесса.
Уравнение регрессии может иметь различный вид и различный уровень сложности в зависимости от особенностей исследуемого объекта и необходимости точности представления.
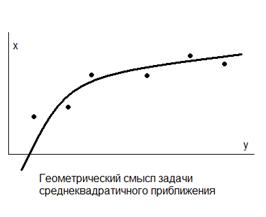
Геометрически
задача построения уравнения регрессии состоит в проведении кривой L
:
y
=
f
(
x
)
«возможно ближе» примыкающей к экспериментальных точек.
Построение уравнения регрессии состоит из 2 этапов:
1. выбор общего вида уравнения регрессии,
2. определения его параметров.
Часто в качестве уравнения регрессии выбирают полином
φ
(
x
)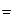 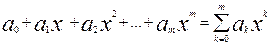 (3.2)
(3.2)
Вторая задача решается методом наименьших квадратов.
Метод наименьших квадратов
Допустим, что результаты эксперимента предоставлены в таблице, представленной выше. И уравнение регрессии записывается в виде (3.2), т.е. зависимость от (m
+1) параметра a
0
,
a
1
,
a
2
,…
an
:
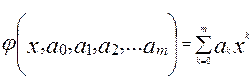 (3.3) (3.3)
Эти параметры и определяют расположение графика эмпирической формулы относительно экспериментальных точек. Однако эти параметры определяются не однозначно. Требуется подобрать параметры так, чтобы график уравнения регрессии был расположен как можно ближе к системе экспериментальных точек.
Введем понятие отклонения
значения уравнения регрессии (3.3) от табличного значения yi
дляxi
:
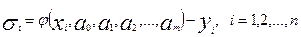 (3.4) (3.4)
Рассмотрим сумму квадратов отклонений
 (3.5) (3.5)
Согласно МНК наилучшими коэффициентами ai
являются те, которые минимизируют функцию S
(3.5)
Используя необходимые условия экстремума функции
нескольких переменных, получим нормальную систему
для определения коэффициентов a
0
,
a
1
,
a
2
,…,
am
:
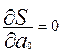 ; ; 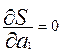 ;…; ;…; 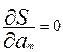 .
(3.6) .
(3.6)
Для аппроксимирующей функции (3.3) система (3.6) является системой линейных алгебраических уравнений относительно неизвестных a
0
,
a
1
,
a
2
,…,
am
.
Если 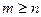 , то существует бесконечно много многочленов (3.3), минимизирующих функцию (3.5). Если , то существует бесконечно много многочленов (3.3), минимизирующих функцию (3.5). Если 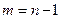 , то существует только один многочлен (3.3), минимизирующий функцию (3.5). Будем считать, что , то существует только один многочлен (3.3), минимизирующий функцию (3.5). Будем считать, что 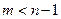 .
.
Чем меньше m
, тем проще тем проще эмпирическая формула, но это не всегда лучше.
Эмпирические формулы с двумя параметрами.
Метод выравнивания
Для описания многих технологических процессов используются эмпирические формулы, содержащие 2 параметра:
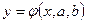 (3.7) (3.7)
Пусть заранее известно, что экспериментальные точки не лежат на одной прямой, для нахождения a
,
b
используется метод выравнивания.
Идея метода.
Вводятся новые переменные
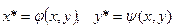 (3.8) (3.8)
так, чтобы преобразованные точки могли быть аппроксимированы линейной зависимостью
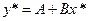 (3.9) (3.9)
Здесь 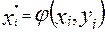 ; ; 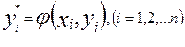
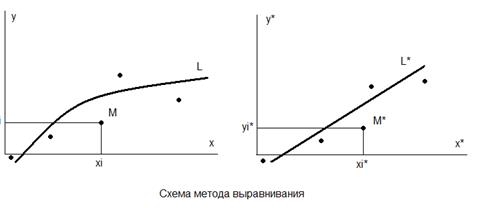
Параметры А и В находятся методом наименьших квадратов.
Аппроксимация экспериментальной зависимость уравнением регрессии 3-го порядка
Поставим задачу аппроксимировать полученную ранее экспериментальную зависимость n(e) уравнением регрессии 3-го порядка, использую надстройку «Поиск решения».
| n
|
e
|
| 1
|
0,199103875 |
| 2
|
0,070962641 |
| 3
|
0,027014272 |
| 4
|
0,008941238 |
| 5
|
0,002814733 |
| 6
|
0,000871947 |
| 7
|
0,000268761 |
Т.е. мы получим функцию вида:
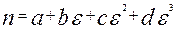 (3.10) (3.10)
В качестве начальных приближений примем a
=
b
=
c
=
d
=1.
Формируем таблицу:
| n
|
e
|
Уравнение регресии
|
Квадрат отклонения
|
| 1 |
0,199103875 |
1,246639174 |
0,567552534 |
| 2 |
0,070962641 |
1,076355684 |
3,700407455 |
| 3 |
0,027014272 |
1,027763757 |
8,834188283 |
| 4 |
0,008941238 |
1,009021899 |
15,92790621 |
| 5 |
0,002814733 |
1,002822678 |
24,97178119 |
| 6 |
0,000871947 |
1,000872708 |
35,98952827 |
| 7 |
0,000268761 |
1,000268833 |
1,000537739 |
| Сумма квадратов:
|
90,99190167
|
где, квадрат отклонения находится по формуле:
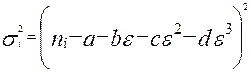 (3.11) (3.11)
Теперь нашей задачей является минимизация суммы квадратов отклонений. Мы можем это сделать путем изменения коэффициентов a
,
b
,
c
,
d
.
Для поиска оптимальных значений выполним команду:
Меню Сервис\Поиск решения
После этого значения a
,
b
,
c
,
d
изменятся на: a
=4,261463435, b
=41,97251008, c
=-1192,303823, d
=4643,463328.
Тогда получаем следующую таблицу измененных значений:
| n
|
e
|
Уравнение регресии
|
Квадрат отклонения
|
| 1 |
0,199103875 |
2,003229556 |
1,043E-05 |
| 2 |
0,070962641 |
2,895188031 |
0,010985549 |
| 3 |
0,027014272 |
4,616753916 |
0,380385393 |
| 4 |
0,008941238 |
4,544749241 |
0,207253253 |
| 5 |
0,002814733 |
4,370262104 |
2,656045611 |
| 6 |
0,000871947 |
4,297157819 |
7,305355855 |
| 7 |
0,000268761 |
4,272657976 |
18,25560618 |
| Сумма квадратов:
|
28,81564227
|
Найдем среднее квадратичное отклонение по формуле:
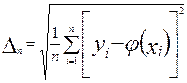 (3.12) (3.12)
В нашем случае 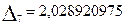
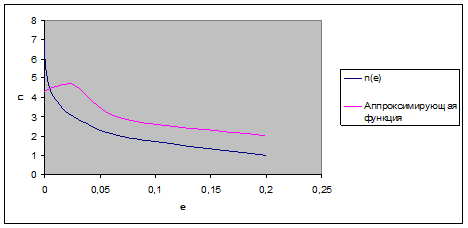
Построим графики обеих функций:
Аппроксимация эмпирической функцией с двумя параметрами
Нам заранее известно, что экспериментальные точки не лежат на одной прямой. А эмпирическая формула имеет вид:
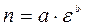 (3.13) (3.13)
Прологарифмируем выражение (3.13)
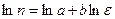
и введем новые переменные:
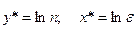 (3.14) (3.14)
Обозначив A
=
lna
;
B
=
b
,
получим вид эмпирической функции в новой системе координат
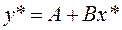
Составим таблицу значений для этой функции:
| y
*
|
x
*
|
| 0 |
-1,61393 |
| 0,693147 |
-2,6456 |
| 1,098612 |
-3,61139 |
| 1,386294 |
-4,71708 |
| 1,609438 |
-5,87289 |
| 1,791759 |
-7,04478 |
| 1,94591 |
-8,22169 |
Неизвестные параметры А, В
находим, используя МНК и строим нормальную систему
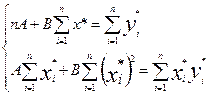 (3.15) (3.15)
Подставив численные значения получаем:
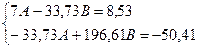
Решаем данную систему методом Крамера:
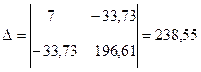
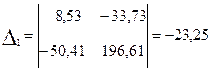
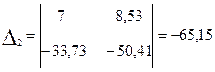
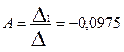
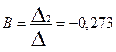
Из (3.14) 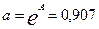 и b
=
B
.
Подставим найденные значения в (3.13) и получим: и b
=
B
.
Подставим найденные значения в (3.13) и получим:
| n
|
e
|
| 1,40915422 |
0,199104 |
| 1,867566864 |
0,070963 |
| 2,430985256 |
0,027014 |
| 3,287575439 |
0,008941 |
| 4,507242556 |
0,002815 |
| 6,206596227 |
0,000872 |
| 8,558355083 |
0,000269 |
Построим обе функции:
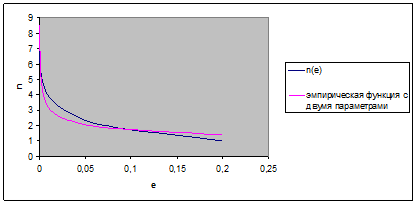
По формуле (3.12) найдем среднее квадратичное отклонение: 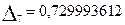
Вывод:
мы получили 2 аппроксимирующие функции для зависимости n(e), но сравнивая среднее квадратичное отклонение видим, что эмпирическая формула с двумя параметрами (3.13) более точная.
Проверка с помощью «линии тренда»
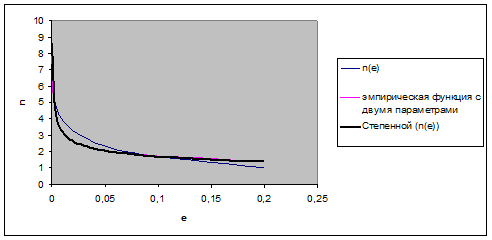
Построив линию тренда видим, что она совпала с эмпирической функцией с двумя переменными
|