|
Всероссийский заочный финансово-экономический институт
Факультет «Менеджмент и маркетинг»
Кафедра «БУАС»
КУРСОВАЯ РАБОТА
по дисциплине «Статистика»
на тему
«Корреляционно-регрессионный анализ взаимосвязи производственных показателей предприятия (организации)»
Вариант №20
Выполнила: студентка 3 курса, МиМ2ВО № студ. билета 09ММД
Проверила: к.э.н. старший преподаватель
Архангельск
2009
Содержание:
| I.
|
Введение
|
3
|
| II.
|
Теоретическая часть
|
|
| 1.
|
Основные производственные показатели предприятия (организации)
|
5
|
| 2.
|
Основные понятия корреляции и регрессии
|
8
|
| 3.
|
Корреляционно-регрессионный анализ
|
11
|
| 4.
|
Пример для теоретической части
|
15
|
| III.
|
Расчетная часть
|
18
|
| IV.
|
Заключение
|
47
|
| V.
|
Список использованной литературы
|
49
|
I.
Введение
Полная и достоверная статистическая информация является тем необходимым основанием, на котором базируется процесс управления экономикой. Принятие управленческих решений на всех уровнях – от общегосударственного или регионального и до уровня отдельной корпорации или частной фирмы – невозможно без должного статистического обеспечения.
Именно статистические данные позволяют определить объемы валового внутреннего продукта и национального дохода, выявить основные тенденции развития отраслей экономики, оценить уровень инфляции, проанализировать состояние финансовых и товарных рынков, исследовать уровень жизни населения и другие социально-экономические явления и процессы.
Статистика – это наука, изучающая количественную сторону массовых явлений и процессов в неразрывной связи с их качественной стороной, количественное выражение закономерностей общественного развития в конкретных условиях места и времени.
Для получения статистической информации органы государственной и ведомственной статистики, а также коммерческие структуры проводят различного рода статистические исследования. Процесс статистического исследования включает три основные стадии: сбор данных, их сводка и группировка, анализ и расчет обобщающих показателей.
От того, как собран первичный статистический материал, как он обработан и сгруппирован, в значительной степени зависят результаты и качество всей последующей работы. Недостаточная проработка программно-методологических и организационных аспектов статистического наблюдения, отсутствие логического и арифметического контроля собранных данных, несоблюдение принципов формирования групп в конечном счете могут привести к абсолютно ошибочным выводам.
Реклама

Не менее сложной, трудоемкой и ответственной является и заключительная, аналитическая стадия исследования. На этой стадии рассчитываются средние показатели и показатели распределения, анализируется структура совокупности, исследуется динамика и взаимосвязи между изучаемыми явлениями и процессами.
Используемые на всех стадиях исследования приемы и методы сбора, обработки и анализа данных являются предметом изучения общей теории статистики
, которая является базовой отраслью статистической науки. Разработанная ею методология применяется в макроэкономической статистике, отраслевых статистиках (промышленности, сельского хозяйства, торговли и прочих), статистике населения, социальной статистике и в других статистических отраслях.
I.
Теоретическая часть
1.
Основные производственные показатели
предприятия (организации)
Статистика промышленности – одна из отраслей экономической статистики. Она изучает промышленность, происходящие в ней явления, процессы, закономерности и взаимосвязи.
На основе статистического изучения производственно-хозяйственной деятельности промышленных предприятий вырабатываются стратегия и тактика развития предприятия, обосновываются производственная программа и управленческие решения, осуществляется контроль за их выполнением, выявляются резервы повышения эффективности производства, оцениваются результаты деятельности предприятий, его подразделений и работников.
В статистике промышленности применяют методологию системного статистического анализа основных экономических показателей результатов деятельности предприятия, характерных для рыночной экономики. Проводят анализ основных статистических показателей по различным направлениям производственно-хозяйственной деятельности предприятия: производство продукции, трудовые ресурсы и уровень их использования, основные фонды и производственное оборудование, оборотные средства и предметы труда, научно-технический прогресс, себестоимость промышленной продукции
.
1. Статистика производства продукции
Продукция промышленности
– прямой полезный результат промышленно-производственной деятельности предприятий, выраженный либо в форме продуктов, либо в форме производственных услуг (работ промышленного характера).
Реклама

Для характеристики результатов деятельности отдельных предприятий, объединений, отраслей промышленности и всей промышленности в целом используется система стоимостных показателей продукции, включающая в себя валовой и внутризаводской обороты, товарную и реализованную продукцию.
2. Статистика рабочей силы и рабочего времени
Использование трудовых ресурсов в промышленности
– одна из основных проблем, значение которой будет возрастать в связи с напряженным трудовым балансом. Вместе с тем, контроль за уровнем использования трудовых ресурсов – одна из важнейших задач статистического анализа результатов деятельности промышленных предприятий.
3. Статистика производительности труда
Производительность труда
– качественная его характеристика, показывающая способность работников к производству материальных благ в единицу времени.
Уровень производительности труда характеризуется количеством продукции, создаваемой в единицу времени (выработка – прямой показатель), или затратами времени на производство единицы продукции (трудоемкость – обратный показатель). Прямые и обратные показатели используются для характеристики уровня производительности труда.
4. Статистика заработной платы
Заработная плата
представляет собой часть общественного продукта, поступающего в индивидуальное распоряжение работников в соответствии с количеством затраченного ими труда. Статистика промышленности рассматривает номинальную заработную плату, выраженную суммой денег, начисленной работнику, без учета их покупательной способности.
5. Статистика основных фондов и производственного оборудования
Основные фонды
представляют собой средства труда, которые целиком и в неизменной натуральной форме функционируют в производстве в течение длительного времени, постепенно перенося свою стоимость на произведенный продукт.
В статистике промышленности различают следующие характеристики стоимости основных фондов: полная первоначальная стоимость; первоначальная стоимость за вычетом износа (остаточная первоначальная стоимость); полная восстановительная стоимость; восстановительная стоимость за вычетом износа (остаточная восстановительная стоимость).
6. Статистика оборотных средств и предметов труда
6.1 Статистика оборотных средств
Оборотные средства
– это выраженные в денежной форме оборотные фонды и фонды обращения, авансируемые в плановом порядке для обеспечения непрерывности производства и реализации продукции.
6.2 Статистика предметов труда
По своему происхождению предметы труда
подразделяются на сырье и материалы. Сырьем называют продукты сельского хозяйства и добывающей промышленности; материалы – продукты обрабатывающей промышленности.
7. Статистика научно-технического прогресса
Основными направлениями научно-технического прогресса
являются: электрификация, механизация, автоматизация и химизация производства; освоение и внедрение новых видов машин, аппаратов, приборов и новых технологических процессов; внедрение изобретений и рационализаторских предложений: углубление специализации и кооперирования.
8. Статистика себестоимости продукции
Под себестоимостью продукции
понимают сумму выраженных в денежной форме затрат, связанных с выпуском определённого объема и состава продукции. Себестоимость – обобщающий качественный показатель работы предприятия. Ее уровень служит основой для определения цен на отдельные виды продукции.
2.
Основные понятия корреляции и регрессии
Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания, так или иначе, определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики.
Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. Достаточно часто функциональная связь проявляется в физике, химии. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и увеличением производства продукции.
Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.
Например, некоторое увеличение аргумента повлечет за собой лишь среднее увеличение или уменьшение (в зависимости от направленности) функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего. Такие зависимости встречаются повсеместно. Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что последние участвуют в формировании урожая. Но для каждого конкретного поля, участка одно и то же количество внесенных удобрений вызовет разный прирост урожайности, так как во взаимодействии находится еще целый ряд факторов (погода, состояние почвы и др.), которые и формируют конечный результат. Однако в среднем такая связь наблюдается – увеличение массы внесенных удобрений ведет к росту урожайности.
По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными.
Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.
Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной. Если изучаются более чем две переменные – множественной.
Указанные выше классификационные признаки наиболее часто встречаются в статистическом анализе. Но, кроме перечисленных различают также непосредственные, косвенные и ложные связи. Собственно, суть каждой из них очевидна из названия. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь – это связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна.
По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнения при интерпретации результатов и др.
Поэтому в данном контексте можно говорить о корреляционном анализе в широком смысле – когда всесторонне характеризуется взаимосвязь. В то же время выделяют корреляционный анализ в узком смысле – когда исследуется сила связи – и регрессионный анализ, в ходе которого оцениваются ее форма и воздействие одних факторов на другие.
Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак.
Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.
Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей.
3.
Корреляционно-регрессионный анализ
Для выявления наличия связи, ее характера и направления в статистике используют методы: приведения параллельных данных; аналитических группировок; графический, корреляции.
Корреляционно-регрессионный анализ включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи (регрессионный анализ).
Одним из методов корреляционно-регрессионного анализа является метод парной корреляции, рассматривающий влияние вариации факторного признака x
на результативный y
.
Аналитическая связь между ними описывается уравнениями:
прямой 
параболы 
гиперболы  и т.д. и т.д.
Оценка параметров уравнения регрессии осуществляется методом наименьших квадратов, в основе которого лежит требование минимальности сумм квадратов отклонений эмпирических данных yi
от выровненных (теоретических) yxi
 (1) (1)
Система нормальных уравнений для нахождения параметров линейной парной регрессии имеет вид:
 (2) (2)
Для оценки типичности параметров уравнения регрессии используется t
-критерий Стьюдента. При этом вычисляются фактические значения t
-критерия для параметров. Полученные фактические значения сравниваются с критическим, которые получают по таблице Стьюдента с учетом принятого уровня значимости и числа степеней свободы.
Полученные при анализе корреляционной связи параметры уравнения регрессии признаются типичными, если t
фактическое больше t
критического.
По приведенным на типичность параметрам уравнения регрессии производится синтезирование (построение) математической модели связи. При этом параметры примененной в анализе математической функции получают соответствующие количественные значения: один параметр показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов, а другой параметр – на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.
Проверка практической значимости синтезированных в корреляционно-регрессионном анализе математических моделей осуществляется посредством показателей тесноты связи между признаками x
и y
.
Для статистической оценки тесноты связи применяются следующие показатели вариации:
1. общая дисперсия результативного признака, отображающая общее влияние всех факторов;
2. факторная дисперсия результативного признака, отображающая вариацию y
только от воздействия изучаемого фактора, которая характеризует отклонение выровненных значений yx
от их общей средней величины y
;
3. остаточная дисперсия, отображающая вариацию результативного признака y
от всех прочих, кроме x
факторов, которая характеризует отклонение эмпирических (фактических) значений результативного признака yi
от их выровненных значений yxi
.
Соотношение между факторной и общей дисперсиями характеризует меру тесноты связи между признаками x
и y
 (3) (3)
Этот показатель называется индексом детерминации (причинности). Он выражает долю факторной дисперсии, т.е. характеризует, какая часть общей вариации результативного признака y
объясняется изменением факторного признака x
. На основе предыдущей формулы определяется индекс корреляции R
:
 (4) (4)
Используя правило сложения дисперсий, можно вычислить индекс корреляции.
 (5) (5)
При прямолинейной форме связи показатель тесноты связи определяется по формуле линейного коэффициента корреляции r:
 (6) (6)
Для оценки значимости коэффициента корреляции r
применяется t
-критерий Стьюдента с учетом заданного уровня значимости  и числа степеней свободы k. и числа степеней свободы k.
Если  , то величина коэффициента корреляции признается существенной. , то величина коэффициента корреляции признается существенной.
Для оценки значимости индекса корреляции R
применяется F
-критерий Фишера. Фактическое значение критерия FR
определяется по формуле:
 , (7) , (7)
где m
– число параметров уравнения регрессии.
Величина FR
сравнивается с критическим значением FK
, которое определяется по таблице F
– критерия с учетом принятого уровня значимости  и числа степеней свободы k
1
=
m
-1
и k
2
=
n
-
m
. и числа степеней свободы k
1
=
m
-1
и k
2
=
n
-
m
.
Если FR
>
FK
, то величина индекса корреляции признается существенной.
По степени тесноты связи различают количественные критерии оценки тесноты связи.
Таблица Чэддока
| Величина коэффициента корреляции
|
Характер связи
|
| до 0,3
|
практически отсутствует
|
| 0,3-0,5
|
слабая
|
| 0,5-0,7
|
умеренная
|
| 0,7-1,0
|
сильная
|
С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности:
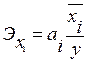 (8) (8)
Он показывает, насколько процентов в среднем изменится значение результативного признака при изменении факторного на 1%.
4. Пример для теоретической части
Имеются следующие данные о производстве молочной продукции и стоимости основных производственных фондов по 15 предприятиям Московской области. Произведем синтез адекватной экономико-математической модели между изучаемыми признаками на базе метода наименьших квадратов. С экономической точки зрения сформулируем выводы относительно исследуемой связи.
Зависимость y
от x
найдем с помощью корреляционно-регрессионного анализа. Рассмотрим прямолинейную форму зависимости y
от x
: 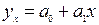
| Таблица 1
|
| Показатели работы предприятий Московской области
|
| Номер предприятия
|
Молочная продукция (млн. руб.)
|
Стоимость ОПФ (млн.руб.)
|
| 1
|
6,0
|
3,5
|
| 2
|
9,2
|
7,5
|
| 3
|
11,4
|
5,3
|
| 4
|
9,3
|
2,9
|
| 5
|
8,4
|
3,2
|
| 6
|
5,7
|
2,1
|
| 7
|
8,2
|
4,0
|
| 8
|
6,3
|
2,5
|
| 9
|
8,2
|
3,2
|
| 10
|
5,6
|
3,0
|
| 11
|
11,0
|
5,4
|
| 12
|
6,5
|
3,2
|
| 13
|
8,9
|
6,5
|
| 14
|
11,5
|
5,5
|
| 15
|
4,2
|
8,2
|
| Итого:
|
120,4
|
66,0
|
Параметры этого уравнения найдем с помощью метода наименьших квадратов и, произведя предварительные расчеты, получим:
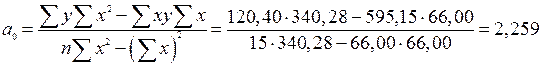
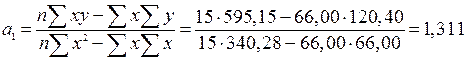
Получаем следующее уравнение регрессии:
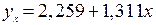
Далее определим адекватность полученной модели. Определим фактические значения t
-критерия для a
0
и a
1
.
для параметра a0
:
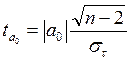
для параметра a1
:
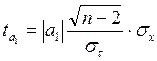
где στ
– среднее квадратическое отклонение результативного признака от выровненных значений ŷ
;
σх
– среднее квадратическое отклонение факторного признака x
от
общей средней 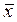 . .
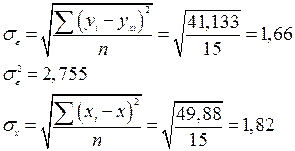
Данные подставляем в формулы и получаем:
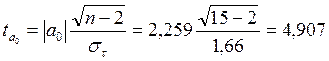
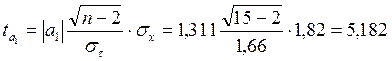
По таблице распределения Стьюдента я нахожу критическое значение t-критерия для ν
= 15-2 = 13 . Вероятность α
я принимаю 0,05. tтабл
равно 2,1604. Так как, оба значения ta
0
и ta
1
больше tтабл
, то оба параметра а0
и а1
признаются значимыми и отклоняется гипотеза о том, что каждый из этих параметров в действительности равен 0 , и лишь в силу случайных обстоятельств оказался равным проверяемой величине.
Из полученного уравнения следует, что с увеличением основных производственных фондов на 1 млн. руб., стоимость молочной продукции возрастает в среднем на 1,311 млн. руб.
II.
Расчетная часть
Имеются исходные выборочные данные по организациям одной из отраслей хозяйствования в отчетном году (выборка 20%-ная, бесповторная) о результатах производственной деятельности организаций:
| Таблица Исходные данные
|
| Исходные данные
|
| № организации
|
Среднесписочная численность работников, чел.
|
Выпуск продукции, млн.руб.
|
Среднегодовая стоимость ОПФ, млн.руб.
|
Уровень производительности труда, млн.руб./чел
|
Фондоотдача, млн.руб./млн.руб.
|
| 1
|
2
|
3
|
4
|
5
|
6
|
| 1
|
162
|
36,450
|
34,714
|
0,225
|
1,050
|
| 2
|
156
|
23,400
|
24,375
|
0,150
|
0,960
|
| 3
|
179
|
46,540
|
41,554
|
0,260
|
1,120
|
| 4
|
194
|
59,752
|
50,212
|
0,308
|
1,190
|
| 5
|
165
|
41,415
|
38,347
|
0,251
|
1,080
|
| 6
|
158
|
26,860
|
27,408
|
0,170
|
0,980
|
| 7
|
220
|
79,200
|
60,923
|
0,360
|
1,300
|
| 8
|
190
|
54,720
|
47,172
|
0,288
|
1,160
|
| 9
|
163
|
40,424
|
37,957
|
0,248
|
1,065
|
| 10
|
159
|
30,210
|
30,210
|
0,190
|
1,000
|
| 11
|
167
|
42,418
|
38,562
|
0,254
|
1,100
|
| 12
|
205
|
64,575
|
52,500
|
0,315
|
1,230
|
| 13
|
187
|
51,612
|
45,674
|
0,276
|
1,130
|
| 14
|
161
|
35,420
|
34,388
|
0,220
|
1,030
|
| 15
|
120
|
14,400
|
16,000
|
0,120
|
0,900
|
| 16
|
162
|
36,936
|
34,845
|
0,228
|
1,060
|
| 17
|
188
|
53,392
|
46,428
|
0,284
|
1,150
|
| 18
|
164
|
41,000
|
38,318
|
0,250
|
1,070
|
| 19
|
192
|
55,680
|
47,590
|
0,290
|
1,170
|
| 20
|
130
|
18,200
|
19,362
|
0,140
|
0,940
|
| 21
|
159
|
31,800
|
31,176
|
0,200
|
1,020
|
| 22
|
162
|
39,204
|
36,985
|
0,242
|
1,060
|
| 23
|
193
|
57,128
|
48,414
|
0,296
|
1,180
|
| 24
|
158
|
28,440
|
28,727
|
0,180
|
0,990
|
| 25
|
168
|
43,344
|
39,404
|
0,258
|
1,100
|
| 26
|
208
|
70,720
|
55,250
|
0,340
|
1,280
|
| 27
|
166
|
41,832
|
38,378
|
0,252
|
1,090
|
| 28
|
207
|
69,345
|
55,476
|
0,335
|
1,250
|
| 29
|
161
|
35,903
|
34,522
|
0,223
|
1,040
|
| 30
|
186
|
50,220
|
44,839
|
0,270
|
1,120
|
Задание 1.
По исходным данным табл. Исходные данные:
1. Построить статистический ряд распределения организаций по уровню производительности труда,
образовав, пять
групп с равными интервалами.
2. Постройте графики полученного ряда распределения.
3. Рассчитайте характеристики ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4. Вычислите среднюю арифметическую
по исходным данным (табл. Х), сравните её с аналогичным показателем, рассчитанным в п. 3 настоящего задания. Объясните причину их расхождения.
Сделайте выводы
по результатам выполнения Задания.
Выполнение Задания 1.
1. Решение:
Для построения интервального ряда распределения определяем величину интервала h
по формуле:
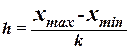 , (
1)
, (
1)
где 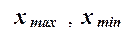 – наибольшее и наименьшее значения признака в исследуемой совокупности, k
–
число групп интервального ряда.
– наибольшее и наименьшее значения признака в исследуемой совокупности, k
–
число групп интервального ряда.
При заданных k
= 5,
xmax
= 360
тыс.руб./чел
и xmin
= 120
тыс.руб./чел
 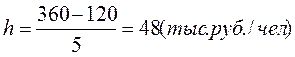
При h
= 48 тыс. руб./чел
границы интервалов ряда распределения имеют следующий вид (табл. 1):
| Таблица 1
|
| Границы интервалов ряда распределения
|
| Номер группы
|
Нижняя граница, тыс.руб./чел
|
Верхняя граница, тыс.руб./чел
|
| 1
|
2
|
3
|
| I
|
120
|
168
|
| II
|
168
|
216
|
| III
|
216
|
264
|
| IV
|
264
|
312
|
| V
|
312
|
360
|
Определяем количество организаций, входящих в каждую группу, используя принцип полуоткрытого интервала
[ )
, согласно которому организации со значениями признаков, служащие одновременно верхними и нижними границами смежных интервалов (168, 216, 264, 312 и 360), будем относить ко второму из смежных интервалов.
Для определения числа организаций в каждой группе строим таблицу 2.
Таблица 2
|
| Разработочная таблица для построения интервального ряда распределения
|
| Группы фирм по уровню производительности труда, тыс.руб.
|
Номер фирмы
|
Уровень производительности труда, тыс. руб./чел
|
Выпуск продукции, тыс.руб.
|
| 1
|
2
|
3
|
4
|
| 120-168
|
15
|
120
|
14 400
|
| 20
|
140
|
18 200
|
| 2
|
150
|
23 400
|
| Всего:
|
3
|
410
|
56 000
|
| 168-216
|
6
|
170
|
26 860
|
| 24
|
180
|
28 440
|
| 10
|
190
|
30 210
|
| 21
|
200
|
31 800
|
| Всего:
|
4
|
740
|
117 310
|
| 216-264
|
14
|
220
|
35 420
|
| 29
|
223
|
35 903
|
| 1
|
225
|
36 450
|
| 16
|
228
|
36 936
|
| 22
|
242
|
39 204
|
| 9
|
248
|
40 424
|
| 18
|
250
|
41 000
|
| 5
|
251
|
41 415
|
| 27
|
252
|
41 832
|
| 11
|
254
|
42 418
|
| 25
|
258
|
43 344
|
| 3
|
260
|
46 540
|
| Всего:
|
12
|
2 911
|
480 886
|
| 264-312
|
30
|
270
|
50 220
|
| 13
|
276
|
51 612
|
| 17
|
284
|
53 392
|
| 8
|
288
|
54 720
|
| 19
|
290
|
55 680
|
| 23
|
296
|
57 128
|
| 4
|
308
|
59 752
|
| Всего:
|
7
|
2 012
|
382 504
|
| 312-360
|
12
|
315
|
64 575
|
| 28
|
335
|
69 345
|
| 26
|
340
|
70 720
|
| 7
|
360
|
79 200
|
| Всего:
|
4
|
1 350
|
283 840
|
| ИТОГО:
|
30
|
7 423
|
1 320 540
|
На основе групповых итоговых строк «Всего» табл. 2 формируем итоговую таблицу 3, представляющую интервальный ряд распределения организаций по уровню производительности труда.
| Таблица 3
|
| Распределение фирм по уровню производительности труда
|
| Номер группы
|
Группы фирм по уровню производительности труда, тыс.руб./чел
|
Число фирм
|
| 1
|
2
|
3
|
| I
|
120-168
|
3
|
| II
|
168-216
|
4
|
| III
|
216-264
|
12
|
| IV
|
264-312
|
7
|
| V
|
312-360
|
4
|
| |
Итого:
|
30
|
Приведем еще три характеристики полученного ряда распределения - частоты групп в относительном выражении, накопленные (кумулятивные) частоты
Sj
,
получаемые путем последовательного суммирования частот всех предшествующих (
j
-1)
интервалов, и накопленные частости
, рассчитываемые по формуле
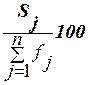 . (2) . (2)
| Таблица 4
|
| Структура фирм по уровню производительности труда
|
| Номер группы
|
Группы фирм по уровню производительности труда, тыс.руб./чел
|
Число фирм
|
Накопленная частота
|
Накопленная частость, %
|
| в абсолютном выражении
|
в % к итогу
|
| 1
|
2
|
3
|
4
|
5
|
6
|
| I
|
120-168
|
3
|
10,00
|
3
|
10,33
|
| II
|
168-216
|
4
|
13,33
|
7
|
23,33
|
| III
|
216-264
|
12
|
40,00
|
19
|
63,33
|
| IV
|
264-312
|
7
|
23,34
|
26
|
86,67
|
| V
|
312-360
|
4
|
13,33
|
30
|
100,00
|
| |
Итого:
|
30
|
100,00
|
|
|
Вывод.
Анализ интервального ряда распределения изучаемой совокупности организаций показывает, что распределение организаций по уровню производительности труда не является равномерным: преобладают организации с уровнем производительности труда от 216 до 264 тыс.руб./чел (это 12 организаций, доля которых составляет 40%); самая малочисленная группа организаций имеет уровень производительности труда от 120 до 168 тыс. руб./чел, которая включает 3 организации, что составляет 10% от общего числа организаций.
2. Решение:
По данным таблицы 3 (графы 2 и 3) строим график распределения организаций по уровню производительности труда.
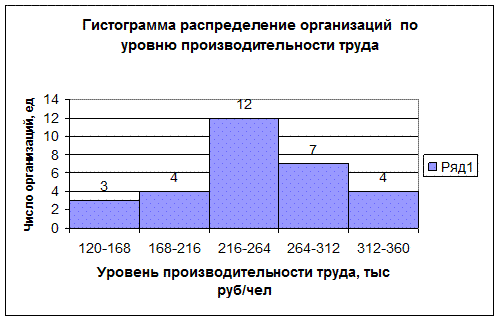
Рис. 1. График полученного ряда распределения
Мода (Мо)
– значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту. Наибольшей частотой является число 12. Этой частоте соответствует модальное значение признака, т.е. количество предприятий. Мода свидетельствует, что в данном примере чаще всего встречаются группы предприятий, входящие в интервал от 216 до 264.
В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
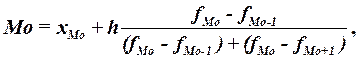 (3) (3)
где хМo
– нижняя граница модального интервала,
h
– величина модального интервала,
fMo
– частота модального интервала,
fMo-1
– частота интервала, предшествующего модальному,
fMo+1
– частота интервала, следующего за модальным.
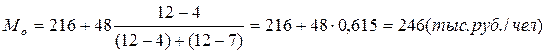
Вывод.
В данном случае наибольший процент предприятий по уровню производительности труда приходится на интервал от 216 до 264, а само значение средней характеризуется 246 (тыс.руб./чел)
Медиана (Ме)
– это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медианы, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда.
Определяем медианный интервал, используя графу 5 табл. 4. Медианным интервалом является интервал 216-264 тыс.руб./чел, т.к. именно в этом интервале накопленная частота S
j
=19
впервые превышает полу-сумму всех частот 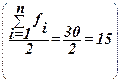 . .
В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности ряды) оказывается в каком-то из интервалов признака х
. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полу-сумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле:
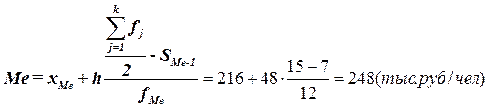 (4) (4)
Вывод:
Полученный результат говорит о том, что из 30 организаций половина организаций имеют уровень производительности труда менее 248 тыс. руб./чел, а вторая свыше.
3. Решение:
Для расчета характеристик ряда распределения 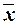 , σ
,
σ
2
, Vσ
на основе табл. 4 строим вспомогательную таблицу 5 (x
’
j
– середина интервала). , σ
,
σ
2
, Vσ
на основе табл. 4 строим вспомогательную таблицу 5 (x
’
j
– середина интервала).
| Таблица 5
|
| Расчетная таблица для нахождения характеристик ряда распределения
|
| Группы уровней производитель-ности труда, тыс.руб.
|
Середина интервала
|
Число органи-заций
|
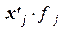
|
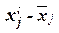
|
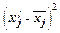
|
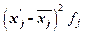
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 120-168
|
144
|
3
|
432
|
-104
|
10 816
|
32 448
|
| 168-216
|
192
|
4
|
768
|
-56
|
3 136
|
12 544
|
| 216-264
|
240
|
12
|
2 880
|
-8
|
64
|
768
|
| 264-312
|
288
|
7
|
2 016
|
40
|
1 600
|
11 200
|
| 312-360
|
336
|
4
|
1 344
|
88
|
7 744
|
30 976
|
| Итого:
|
|
30
|
7 440
|
|
|
87 936
|
Средняя арифметическая взвешенная
– средняя сгруппированных величин x
1
,
x
2
, …,
xn
– вычисляется по формуле:
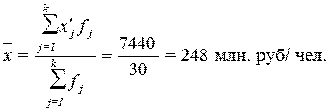 (5) (5)
Среднее квадратическое отклонение
– это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
Рассчитаем среднее квадратическое отклонение, которое равно корню квадратному из дисперсии:
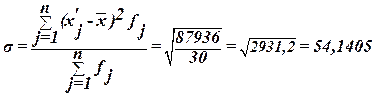 (6) (6)
Рассчитаем дисперсию:
σ2 = 54,14052
=2931,2
Коэффициент вариации представляет собой выраженное в процентах отношение средне квадратического отклонения к средней арифметической.
Рассчитаем коэффициент вариации:
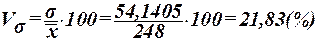 (7) (7)
Вывод
. Анализ полученных значений показателей 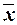 и σ
говорит о том, что средняя величина уровня производительности труда составляет 248 тыс.руб./чел отклонение от этой величины в ту или иную сторону составляет 54,1405 (или 21,83%), наиболее характерный уровень производительности труда находится в пределах от 194 до 302 тыс.руб./чел (диапазон и σ
говорит о том, что средняя величина уровня производительности труда составляет 248 тыс.руб./чел отклонение от этой величины в ту или иную сторону составляет 54,1405 (или 21,83%), наиболее характерный уровень производительности труда находится в пределах от 194 до 302 тыс.руб./чел (диапазон 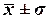 ). ).
Значение Vσ
= 21,83% не превышает 33%, следовательно, вариация уровня производительности труда в исследуемой совокупности организаций незначительна и совокупность по данному признаку однородна. Расхождение между значениями незначительно (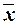 =248 тыс.руб./чел, Мо
=246 тыс.руб./чел, Ме
=248 тыс. руб./чел), что подтверждает вывод об однородности совокупности организаций. Таким образом, найденное среднее значение уровня типичной производительности является типичной, надежной характеристикой исследуемой совокупности организаций. =248 тыс.руб./чел, Мо
=246 тыс.руб./чел, Ме
=248 тыс. руб./чел), что подтверждает вывод об однородности совокупности организаций. Таким образом, найденное среднее значение уровня типичной производительности является типичной, надежной характеристикой исследуемой совокупности организаций.
4. Решение:
Для расчета средней арифметической по исходным данным по уровню производительности труда применяется формула средней арифметической простой:
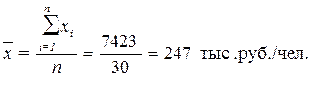 , (8) , (8)
Причина расхождения средних величин, рассчитанных по исходным данным (247 тыс.руб./чел) и по интервальному ряду распределения (248 тыс.руб./чел), заключается в том, что в первом случае средняя определяется по фактическим значениям
исследуемого признака для всех 30-ти организаций, а во втором случае в качестве значений признака берутся середины интервалов
х
j
’
и, следовательно, значение средней будет менее точным. Вместе с тем, при округлении обеих рассматриваемых величин их значения совпадают, что говорит о достаточно равномерном распределении уровня производительности труда внутри каждой группы интервального ряда.
Задание 2.
По исходным данным табл. Исходные данные с использованием результатов выполнения Задания 1 необходимо выполнить следующее:
1. Установить наличие и характер корреляционной связи между признаками фондоотдача
и уровень производительности труда
, образовав пять групп с равными интервалами по каждому из признаков, используя метод аналитической группировки;
2. Измерить тесноту корреляционной связи, между фондоотдачей и уровнем производительности труда с использованием коэффициента детерминации и эмпирического корреляционного отношения
.
3. Оценка значимости (неслучайности) полученных характеристик
связи признаков 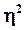 и и 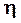
Сделать выводы.
Выполнение Задания 2:
По условию Задания 2 факторным является признак Фондоотдача
, результативным – признак Уровень производительности труда
.
1. Решение:
Аналитическая группировка строится по факторному признаку Х
и для каждой j
-ой группы ряда определяется средне групповое значение 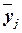 результативного признака Y
. Если с ростом значений фактора Х
от группы к группе средние значения
результативного признака Y
. Если с ростом значений фактора Х
от группы к группе средние значения 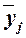 систематически
возрастают (или убывают), между признаками X
и Y
имеет место корреляционная связь.
систематически
возрастают (или убывают), между признаками X
и Y
имеет место корреляционная связь.
Используя разработочную таблицу 2, строим вспомогательную таблицу 6 для проведения в дальнейшем аналитической группировки.
| Таблица 6
|
| Вспомогательная таблица для аналитической группировки
|
| № группы
|
№ организации
|
Выпуск продукции, тыс.руб.
|
Среднегодовая стоимость ОПФ, тыс.руб.
|
Фондоотдача
|
Уровень производительности труда, тыс.руб./чел
|
| А
|
1
|
2
|
3
|
4
|
5
|
| I
|
15
|
14 400,000
|
16 000,000
|
0,900
|
120,000
|
| 20
|
18 200,000
|
19 362,000
|
0,940
|
140,000
|
| 2
|
23 400,000
|
24 375,000
|
0,960
|
150,000
|
| 6
|
26 860,000
|
27 408,000
|
0,980
|
170,000
|
| Всего:
|
4
|
|
|
3,780
|
580,000
|
| II
|
24
|
28 440,000
|
28 727,000
|
0,990
|
180,000
|
| 10
|
30 210,000
|
30 210,000
|
1,000
|
190,000
|
| 21
|
31 800,000
|
31 176,000
|
1,020
|
200,000
|
| 14
|
35 420,000
|
34 388,000
|
1,030
|
220,000
|
| 29
|
35 903,000
|
34 522,000
|
1,040
|
223,000
|
| 1
|
36 450,000
|
34 714,000
|
1,050
|
225,000
|
| 22
|
39 204,000
|
36 985,000
|
1,059
|
242,000
|
| Всего:
|
7
|
|
|
7,189
|
1 480,000
|
| III
|
16
|
36 936,000
|
34 845,000
|
1,060
|
228,000
|
| 9
|
40 424,000
|
37 957,000
|
1,065
|
248,000
|
| 18
|
41 000,000
|
38 318,000
|
1,070
|
250,000
|
| 5
|
41 415,000
|
38 347,000
|
1,080
|
251,000
|
| 27
|
41 832,000
|
38 378,000
|
1,090
|
252,000
|
| 11
|
42 418,000
|
38 562,000
|
1,100
|
254,000
|
| 25
|
43 344,000
|
39 404,000
|
1,100
|
258,000
|
| 3
|
46 540,000
|
41 554,000
|
1,120
|
260,000
|
| 30
|
50 220,000
|
44 839,000
|
1,120
|
270,000
|
| 13
|
51 612,000
|
45 674,000
|
1,130
|
276,000
|
| Всего:
|
10
|
|
|
10,935
|
2 547,000
|
| IV
|
17
|
53 392,000
|
46 428,000
|
1,150
|
284,000
|
| 8
|
54 720,000
|
47 172,000
|
1,160
|
288,000
|
| 19
|
55 680,000
|
47 590,000
|
1,170
|
290,000
|
| 23
|
57 128,000
|
48 414,000
|
1,180
|
296,000
|
| 4
|
59 752,000
|
50 212,000
|
1,190
|
308,000
|
| Всего:
|
5
|
|
|
5,850
|
1 466,000
|
| V
|
12
|
64 575,000
|
52 500,000
|
1,230
|
315,000
|
| 28
|
69 345,000
|
55 476,000
|
1,250
|
335,000
|
| 26
|
70 720,000
|
55 250,000
|
1,280
|
340,000
|
| 7
|
79 200,000
|
60 923,000
|
1,300
|
360,000
|
| Всего:
|
4
|
|
|
5,060
|
1 350,000
|
| Итого:
|
30
|
|
|
32,814
|
7 423,000
|
Используя таблицу 6, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х
– Фондоотдача
и результативным признаком Y
– Уровень производительности труда
.
Групповые средние значения yj
получаем из таблицы 6 (графа 5), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 7.:
| Таблица 7
|
| Зависимость уровня производительности труда от фондоотдачи
|
| Номер группы
|
Фондоотдача
|
Число организаций
|
Уровень производительности труда, тыс. руб./чел
|
| всего
|
в среднем на одну организацию
|
| 1
|
2
|
3
|
4
|
5
|
| I
|
0,900-0,980
|
4
|
580
|
145
|
| II
|
0,980-1,060
|
7
|
1 480
|
211
|
| III
|
1,060-1,140
|
10
|
2 547
|
255
|
| IV
|
1,140-1,220
|
5
|
1 466
|
293
|
| V
|
1,220-1,300
|
4
|
1 350
|
338
|
| |
Итого:
|
30
|
7 423
|
247,4
|
Вывод.
Анализ данных табл. 7 показывает, что с увеличением фондоотдачи от группы к группе систематически возрастает и средний уровень производительности труда по каждой группе организаций, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.
2. Решение:
Коэффициент детерминации
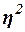 характеризует силу влияния факторного (группировочного) признака Х
на результативный признак Y
и рассчитывается как доля межгрупповой дисперсии
характеризует силу влияния факторного (группировочного) признака Х
на результативный признак Y
и рассчитывается как доля межгрупповой дисперсии 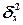 признака Y
в его общей дисперсии признака Y
в его общей дисперсии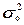 : :
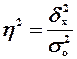 , (9) , (9)
где 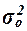 – общая дисперсия признака Y
, – общая дисперсия признака Y
, 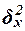 – межгрупповая (факторная) дисперсия признака Y
. – межгрупповая (факторная) дисперсия признака Y
.
Общая дисперсия
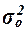 характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y
факторов (систематических и случайных
) и вычисляется по формуле характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y
факторов (систематических и случайных
) и вычисляется по формуле
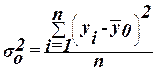 , (10) , (10)
где yi
– индивидуальные значения результативного признака;
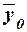 – общая средняя значений результативного признака; – общая средняя значений результативного признака;
n
– число единиц совокупности.
Межгрупповая дисперсия
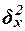 измеряет систематическую вариацию
результативного признака, обусловленную влиянием признака-фактора
Х
(по которому произведена группировка) и вычисляется по формуле: измеряет систематическую вариацию
результативного признака, обусловленную влиянием признака-фактора
Х
(по которому произведена группировка) и вычисляется по формуле:
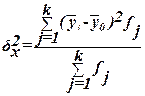 , (11) , (11)
где 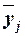 –групповые средние, –групповые средние,
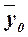 – общая средняя, – общая средняя,
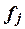 –число единиц в j-ой группе, –число единиц в j-ой группе,
k
– число групп.
Для расчета показателей 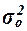 и и 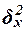 необходимо знать величину общей средней необходимо знать величину общей средней
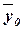 , которая вычисляется как средняя арифметическая простая
по всем единицам совокупности: , которая вычисляется как средняя арифметическая простая
по всем единицам совокупности:
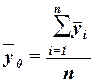 , (12) , (12)
Значения числителя и знаменателя формулы имеются в табл. 7 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую среднюю 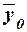 : :
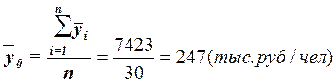
Для расчета общей дисперсии 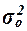 применяется вспомогательная табл. 8. применяется вспомогательная табл. 8.
| Таблица 8
|
| Вспомогательная таблица для расчета общей дисперсии
|
| № организации
|
Уровень производительности труда, тыс.руб./чел
|
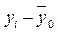
|
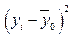
|
| 1
|
2
|
3
|
4
|
| 1
|
225
|
-22
|
484
|
| 2
|
150
|
-97
|
9 409
|
| 3
|
260
|
13
|
169
|
| 4
|
308
|
61
|
3 721
|
| 5
|
251
|
4
|
16
|
| 6
|
170
|
-77
|
5 929
|
| 7
|
360
|
113
|
12 769
|
| 8
|
288
|
41
|
1 681
|
| 9
|
248
|
1
|
1
|
| 10
|
190
|
-57
|
3 249
|
| 11
|
254
|
7
|
49
|
| 12
|
315
|
68
|
4 624
|
| 13
|
276
|
29
|
841
|
| 14
|
220
|
-27
|
729
|
| 15
|
120
|
-127
|
16 129
|
| 16
|
228
|
-19
|
361
|
| 17
|
284
|
37
|
1 369
|
| 18
|
250
|
3
|
9
|
| 19
|
290
|
43
|
1 849
|
| 20
|
140
|
-107
|
11 449
|
| 21
|
200
|
-47
|
2 209
|
| 22
|
242
|
-5
|
25
|
| 23
|
296
|
49
|
2 401
|
| 24
|
180
|
-67
|
4 489
|
| 25
|
258
|
11
|
121
|
| 26
|
340
|
93
|
8 649
|
| 27
|
252
|
5
|
25
|
| 28
|
335
|
88
|
7 744
|
| 29
|
223
|
-24
|
576
|
| 30
|
270
|
23
|
529
|
| Итого:
|
7 423
|
|
101 605
|
Рассчитаем общую дисперсию по формуле (10):
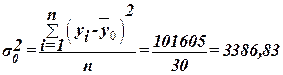
Для расчета межгрупповой дисперсии 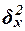 строим вспомогательную таблицу 9. При этом используются групповые средние значения строим вспомогательную таблицу 9. При этом используются групповые средние значения 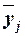 из табл. 7 (графа 5). из табл. 7 (графа 5).
| Таблица 9
|
| Вспомогательная таблица для расчета межгрупповой дисперсии
|
| Номер группы
|
Фондоотдача
|
Число фирм
|
Среднее значение в группе, тыс.руб./чел
|
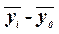
|
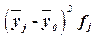
|
|
|
1
|
2
|
3
|
4
|
5
|
| I
|
0,900-0,980
|
4
|
145
|
-102
|
41 616
|
| II
|
0,980-1,060
|
7
|
211
|
-36
|
9 072
|
| III
|
1,060-1,140
|
10
|
255
|
8
|
640
|
| IV
|
1,140-1,220
|
5
|
293
|
46
|
10 580
|
| V
|
1,220-1,300
|
4
|
338
|
91
|
33 124
|
| |
Итого:
|
30
|
247,4
|
|
95 032
|
Рассчитаем межгрупповую дисперсию по формуле (11):
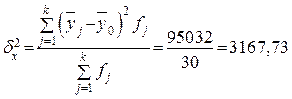
Определяем коэффициент детерминации по формуле (9):
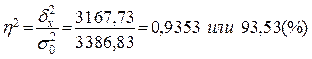
Вывод.
93,53% вариации уровня производительности труда обусловлено вариацией уровня фондоотдачи, а 6,47% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение
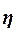 оценивает тесноту связи
между факторным и результативным признаками и вычисляется по формуле: оценивает тесноту связи
между факторным и результативным признаками и вычисляется по формуле:
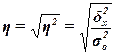 (13) (13)
Рассчитаем показатель 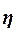 : :
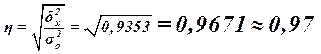
Для оценки тесноты связи с помощью корреляционного отношения используется шкала Чэддока (см. теоретическую часть стр. 14):
Вывод
: согласно шкале Чэддока связь между средним уровнем производительности труда и фондоотдачей по организациям является весьма тесной.
3. Решение:
Показатели 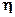 и и 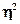 рассчитаны для выборочной совокупности, т.е. на основе ограниченной информации об изучаемом явлении. Поскольку при формировании выборки на первичные данные могли иметь воздействии какие-либо случайные факторы, то есть основание полагать, что и полученные характеристики связи рассчитаны для выборочной совокупности, т.е. на основе ограниченной информации об изучаемом явлении. Поскольку при формировании выборки на первичные данные могли иметь воздействии какие-либо случайные факторы, то есть основание полагать, что и полученные характеристики связи 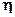 , , 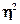 несут в себе элемент случайности. Ввиду этого, необходимо проверить, насколько заключение о тесноте связи, сделанное по выборке, будет правомерными и для генеральной совокупности, из которой была произведена выборка. несут в себе элемент случайности. Ввиду этого, необходимо проверить, насколько заключение о тесноте связи, сделанное по выборке, будет правомерными и для генеральной совокупности, из которой была произведена выборка.
Проверка выборочных показателей на их неслучайность осуществляется в статистике с помощью тестов на статистическую значимость (существенность) показателя.
Для проверки значимости коэффициента детерминации 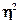 служит дисперсионный
F
-критерий Фишера
, который рассчитывается по формуле служит дисперсионный
F
-критерий Фишера
, который рассчитывается по формуле
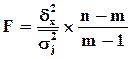 , (14) , (14)
где n – число единиц выборочной совокупности,
m – количество групп,
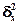 – межгрупповая дисперсия, – межгрупповая дисперсия,
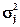 – дисперсия j-ой группы (j=1,2,…,m), – дисперсия j-ой группы (j=1,2,…,m),
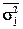 – средняя арифметическая групповых дисперсий. – средняя арифметическая групповых дисперсий.
Величина 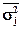 рассчитывается, исходя из правила сложения дисперсий: рассчитывается, исходя из правила сложения дисперсий:
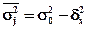 , ,
где 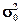 – общая дисперсия. – общая дисперсия.
Для проверки значимости показателя 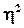 рассчитанное значение F-критерия F
расч
сравнивается с табличным F
тал
для принятого уровня значимости рассчитанное значение F-критерия F
расч
сравнивается с табличным F
тал
для принятого уровня значимости 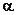 и параметров k
1,
k
2,
зависящих от величин n
и
m
: k
1
=
m
-1,
k
2
=
n
-
m
.
Величина F
табл
для значений и параметров k
1,
k
2,
зависящих от величин n
и
m
: k
1
=
m
-1,
k
2
=
n
-
m
.
Величина F
табл
для значений 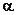 , k
1,
k
2
определяется по таблице распределения Фишера, где приведены критические
(предельно допустимые) величины F-критерия для различных комбинаций значений , k
1,
k
2
определяется по таблице распределения Фишера, где приведены критические
(предельно допустимые) величины F-критерия для различных комбинаций значений 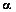 ,
k
1,
k
2
.
Уровень значимости ,
k
1,
k
2
.
Уровень значимости  в социально-экономических исследованиях обычно принимается равным 0,05 (что соответствует доверительной вероятности Р=0,95). в социально-экономических исследованиях обычно принимается равным 0,05 (что соответствует доверительной вероятности Р=0,95).
Если F
расч
>
F
табл
, коэффициент детерминации 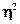 признается статистически значимым
, т.е. практически невероятно, что найденная оценка признается статистически значимым
, т.е. практически невероятно, что найденная оценка 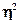 обусловлена только стечением случайных обстоятельств. В силу этого, выводы о тесноте связи изучаемых признаков, сделанные на основе выборки, можно распространить на всю генеральную совокупность. обусловлена только стечением случайных обстоятельств. В силу этого, выводы о тесноте связи изучаемых признаков, сделанные на основе выборки, можно распространить на всю генеральную совокупность.
Если F
расч
<
F
табл
, то показатель 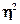 считается статистически незначимым
и, следовательно, полученные оценки силы связи признаков относятся только к выборке, их нельзя распространить на генеральную совокупность. считается статистически незначимым
и, следовательно, полученные оценки силы связи признаков относятся только к выборке, их нельзя распространить на генеральную совокупность.
Фрагмент таблицы Фишера критических величин F-критерия для значений 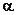 =0,05; k1
=3,4,5; k2
=24-35 представлен ниже: =0,05; k1
=3,4,5; k2
=24-35 представлен ниже:
Таблица 10
| |
k2
|
| k1
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
32
|
33
|
34
|
35
|
| 3
|
3,01
|
2,99
|
2,98
|
2,96
|
2,95
|
2,93
|
2,92
|
2,91
|
2,90
|
2,89
|
2,88
|
2,87
|
| 4
|
2,78
|
2,76
|
2,74
|
2,73
|
2,71
|
2,70
|
2,69
|
2,68
|
2,67
|
2,66
|
2,65
|
2,64
|
| 5
|
2,62
|
2,60
|
2,59
|
2,57
|
2,56
|
2,55
|
2,53
|
2,52
|
2,51
|
2,50
|
2,49
|
2,48
|
Рассчитаем дисперсионный F-критерия Фишера для оценки 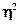 =93,53%, полученной при =93,53%, полученной при 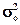 =3386,83; =3386,83; 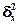 =3167,73 по формуле (14): =3167,73 по формуле (14):
Fрасч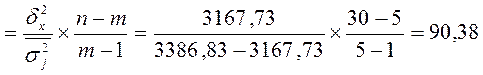
Табличное значение F-критерия при  = 0,05: = 0,05:
| n
|
m
|
k1
=m-1
|
k2
=n-m
|
Fтабл
(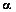 ,4,
25) ,4,
25)
|
| 30
|
5
|
4
|
25
|
2,76
|
ВЫВОД: поскольку F
расч
>
F
табл
, то величина коэффициента детерминации 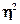 =93,53% признается значимой (неслучайной) с уровнем надежности
95%
и, следовательно, найденные характеристики связи между признаками фондоотдача
и уровнем производительности труда
правомерны не только для выборки, но и для всей генеральной совокупности фирм. =93,53% признается значимой (неслучайной) с уровнем надежности
95%
и, следовательно, найденные характеристики связи между признаками фондоотдача
и уровнем производительности труда
правомерны не только для выборки, но и для всей генеральной совокупности фирм.
Задание 3:
По результатам выполнения Задания 1 с вероятностью 0,683 определите:
1. ошибку выборки среднего уровня производительности труда и границы, в которых будет находиться средний уровень производительности труда в генеральной совокупности.
2. ошибку выборки доли организаций с уровнем производительности труда 264 тыс. руб. и более и границы, в которых будет находиться генеральная доля.
Выполнение Задания 3.
1. Решение:
Применяя выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки репрезентативности), т.к. генеральные и выборочные характеристики, как правило, не совпадают, а отклоняются на некоторую величину ε
.
Принято вычислять два вида ошибок выборки - среднюю
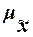 и предельную и предельную
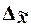 . .
Для расчета средней ошибки выборки 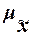 применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную. применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
Для собственно-случайной
и механической
выборки с бесповторным способом отбора
средняя ошибка 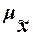 для выборочной средней для выборочной средней 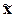 определяется по формуле определяется по формуле
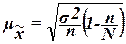 , (15) , (15)
где 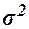 – общая дисперсия изучаемого признака, – общая дисперсия изучаемого признака,
N
– число единиц в генеральной совокупности,
n
– число единиц в выборочной совокупности.
Предельная ошибка выборки 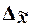 определяет границы, в пределах которых будет находиться генеральная средняя: определяет границы, в пределах которых будет находиться генеральная средняя:
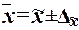 , ,
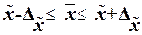 , (16) , (16)
где 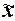 – выборочная средняя, – выборочная средняя,
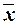 – генеральная средняя. – генеральная средняя.
Предельная ошибка выборки 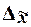 кратна средней ошибке кратна средней ошибке 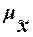 с коэффициентом кратности
t
(
называемым также коэффициентом доверия): с коэффициентом кратности
t
(
называемым также коэффициентом доверия):
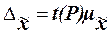 (17) (17)
Коэффициент кратности t
зависит от значения доверительной вероятности
Р
, гарантирующей вхождение генеральной средней в интервал 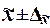 , называемый доверительным интервалом
. , называемый доверительным интервалом
.
Наиболее часто используемые доверительные вероятности Р
и соответствующие им значения t
задаются следующим образом (табл. 11):
Таблица 11
| Доверительная вероятность
P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
| Значение
t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию Задания 2 выборочная совокупность насчитывает 30 организаций, выборка 20% бесповторная, следовательно, генеральная совокупность включает 150 организаций
. Выборочная средняя 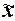 , дисперсия , дисперсия 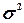 определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 12: определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 12:
Таблица 12
Р
|
t
|
n
|
N
|
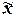
|
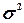
|
| 0,683
|
1,0
|
30
|
150
|
248
|
2931,2
|
Рассчитаем среднюю ошибку выборки по формуле (15):
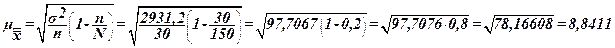
Рассчитаем предельную ошибку выборки по формуле (17):
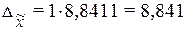 тыс.руб./чел тыс.руб./чел
Определим доверительный интервал для генеральной средней по формуле (16):
248- 8,8411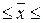 248+8,8411 248+8,8411
239тыс.руб/чел 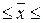 257 тыс.руб./чел 257 тыс.руб./чел
Вывод.
На основании проведенного выборочного обследования с вероятностью 0,683 можно утверждать, что для генеральной совокупности организаций средняя величина среднего уровня производительности труда находится в пределах от 239 до 257 тыс.руб./чел.
2. Решение:
Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой
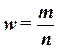 , (18) , (18)
где m
– число единиц совокупности, обладающих заданным свойством;
n
– общее число единиц в совокупности.
Для собственно-случайной
и механической выборки
с бесповторным способом отбора
предельная ошибка выборки 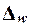 доли единиц, обладающих заданным свойством, рассчитывается по формуле доли единиц, обладающих заданным свойством, рассчитывается по формуле
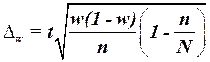 , (19) , (19)
где w
– доля единиц совокупности, обладающих заданным свойством;
(1-
w
)
– доля единиц совокупности, не обладающих заданным свойством,
N
– число единиц в генеральной совокупности,
n
– число единиц в выборочной совокупности.
Предельная ошибка выборки 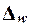 определяет границы, в пределах которых будет находиться генеральная доля р
единиц, обладающих исследуемым признаком: определяет границы, в пределах которых будет находиться генеральная доля р
единиц, обладающих исследуемым признаком:
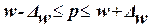 (20) (20)
По условию Задания 3 исследуемым свойством организаций является равенство или превышение среднего уровня производительности труда 264 тыс. руб/чел.
Число организаций с данным свойством определяется из табл. 2 (графа 2):
m=11
Рассчитаем выборочную долю по формуле (18):
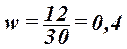
Рассчитаем предельную ошибку выборки для доли по формуле (19):
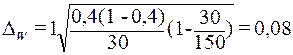
Определим доверительный интервал генеральной доли по формуле (20):
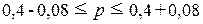
0,32 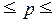 0,48 0,48
или
32% 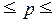 48% 48%
Вывод.
С вероятностью 0,683 можно утверждать, что в генеральной совокупности организаций региона доля организаций с средним уровнем производительности труда 264 тыс.руб./чел и более будет находиться в пределах от 32% до 48%.
Задание 4.
По результатам расчетов заданий 1 и 2 найдите уравнение корреляционной связи между фондоотдачей и производительностью труда, изобразите корреляционную связь графически.
Для определения тесноты корреляционной связи рассчитайте коэффициент корреляции. Сделайте выводы.
Выполнение задания 4.
1. Решение:
Имеются данные по 30 предприятиям по уровню производительности труда и фондоотдачи.
Уравнение корреляционной связи (уравнение регрессии, модели) выражает количественное соотношение между факторным (x – фондоотдача) и результативным (y – уровень производительности труда) признаками. Рассмотрим прямолинейную форму зависимости y
от x
: 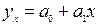
Поскольку для установления наличия корреляционной связи между признаками применялся метод аналитической группировки, то параметры для уравнения регрессии рационально определить по сгруппированным данным (табл. 7). В таком случае система нормальных уравнений для уравнения прямой будет иметь вид:
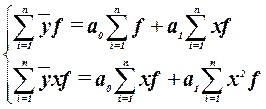 (21) (21)
где 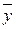 – групповые средние результативного признака, x
– середина интервалов факторного признака. Используя данные табл. 7 строим расчетную таблицу 13, чтобы получить численные значения параметров уравнения регрессии а0
и а1
: – групповые средние результативного признака, x
– середина интервалов факторного признака. Используя данные табл. 7 строим расчетную таблицу 13, чтобы получить численные значения параметров уравнения регрессии а0
и а1
:
| Таблица 13
|
| Расчетная таблица для определения численных значений параметров уравнения регрессии
|
| Середина интер-вала
|
Число органи-заций
|
Групповые средние
|
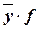
|
xf
|
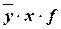
|
x2
f
|
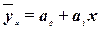
|
xy
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| 0,940
|
4
|
145,000
|
580,000
|
3,760
|
545,200
|
3,534
|
157,61
|
136,300
|
| 1,020
|
7
|
211,000
|
1 477,000
|
7,140
|
1 506,540
|
7,283
|
204,09
|
215,220
|
| 1,100
|
10
|
255,000
|
2 550,000
|
11,000
|
2 805,000
|
12,100
|
250,56
|
280,500
|
| 1,180
|
5
|
293,000
|
1 465,000
|
5,900
|
1 728,700
|
6,962
|
297,04
|
345,740
|
| 1,260
|
4
|
338,000
|
1 352,000
|
5,040
|
1 703,520
|
6,350
|
343,51
|
425,880
|
| Итого:
|
30
|
1 242,000
|
7 424,000
|
32,840
|
8 288,960
|
36,230
|
1252,81
|
1 403,640
|
Данные подставим в систему уравнений (21) и решим:
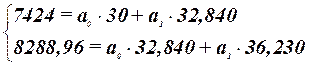
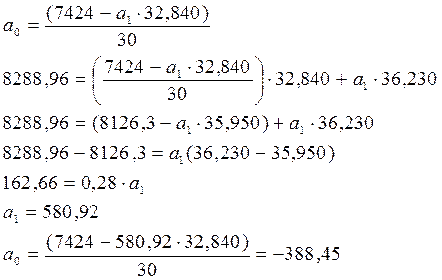
Итак, получилось, что а0
= -388,45
, а а1
=580,92
. Нас интересует именно параметр а1
, показывающий изменение результативного признака при изменении факторного признака на единицу. Коэффициент регрессии показывает, что при увеличении фондоотдачи на единицу значение уровня производительности труда увеличивается в среднем на 580,92 тыс.руб./чел
Итак, уравнение корреляционной связи между фондоотдачей и производительностью труда выглядит так:
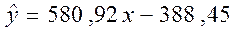
В моей работе графически корреляционная связь выглядит так
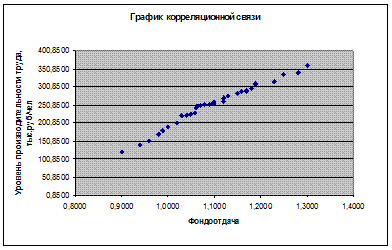
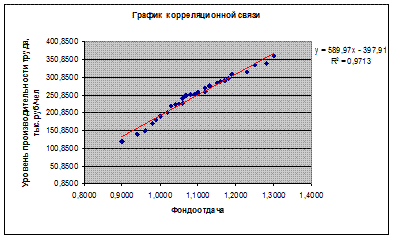
График 2. Графическое изображение корреляционной связи
2. Решение:
Теперь вычислим линейный коэффициент корреляции, который называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, т.е. 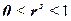 . Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции. . Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.
Составим расчетную таблицу 14, которая будет иметь вид:
| Таблица 14
|
| Расчетная таблица для вычисления коэффициента
|
| Середина интервала
|
Число организаций
|
Групповые средние
|
xy
|
х2
|
у2
|
| 1
|
2
|
3
|
4
|
5
|
6
|
| 0,940
|
4
|
145,000
|
136,300
|
0,884
|
21 025,000
|
| 1,020
|
7
|
211,000
|
215,220
|
1,040
|
44 521,000
|
| 1,100
|
10
|
255,000
|
280,500
|
1,210
|
65 025,000
|
| 1,180
|
5
|
293,000
|
345,740
|
1,392
|
85 849,000
|
| 1,260
|
4
|
338,000
|
425,880
|
1,588
|
114 244,000
|
| 5,500
|
30
|
1 242,000
|
1 403,640
|
6,114
|
330 664,000
|
Для практических вычислений линейный коэффициент корреляции удобнее исчислять по формуле:
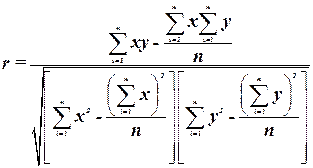 (22) (22)
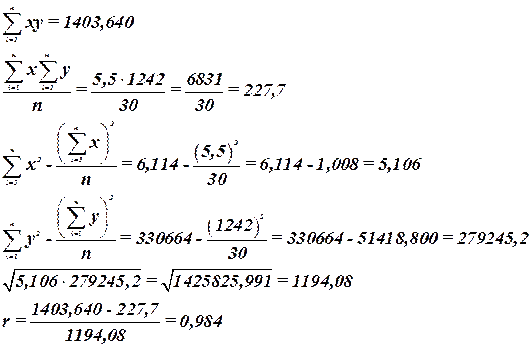
Вывод:
Факт совпадения и несовпадения значений теоретического корреляционного отношения 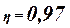 и линейного коэффициента корреляции и линейного коэффициента корреляции 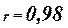 используется для оценки формы связи. В нашем случае несовпадение этих величин говорит о том, что связь между изучаемыми признаками не прямолинейна, а криволинейна. Итак, можно сделать вывод, что связь между уровнем производительности труда и фондоотдачей по организациям является весьма тесной криволинейной. используется для оценки формы связи. В нашем случае несовпадение этих величин говорит о том, что связь между изучаемыми признаками не прямолинейна, а криволинейна. Итак, можно сделать вывод, что связь между уровнем производительности труда и фондоотдачей по организациям является весьма тесной криволинейной.
III.
Заключение
Итак, в заключение хочется отметить, что понятия «корреляция» и «регрессии» тесно связаны между собой. В экономических исследованиях корреляционный и регрессионный анализ нередко объединяют в один – корреляционно-регрессионный анализ. Подразумевается, что в результате такого анализа будет построена регрессионная зависимость и рассчитаны коэффициенты ее тесноты и значимости (т.е. проведен корреляционный анализ).
Практическая реализация корреляционно-регрессионного анализа включает следующие этапы:
1. Постановка задачи – определяются показатели, зависимость между которыми подлежит оценке, формулируется экономически осмысленная и приемлемая гипотеза о зависимости между ними;
2. Формирование перечня факторов, их логический анализ – выбирается оптимальное число наиболее существенных переменных факторов, влияющих на зависимый показатель;
3. Спецификация функции регрессии – дается конкретная формулировка гипотезы о форме зависимости;
4. Оценка функции регрессии и проверка адекватности модели – определяются числовые значения параметров регрессии, вычисляется ряд показателей, характеризующих точность проведенного анализа;
5. Экономическая интерпретация – результаты анализа сравниваются с гипотезами, сформулированными на первом этапе исследования, оценивается их правдоподобие с экономической точки зрения, делаются аналитические выводы.
Следует заметить, что традиционные методы корреляции и регрессии широко представлены в виде разного рода статистических пакетах программ для ЭВМ. Исследователю остается только правильно подготовить информацию, выбрать удовлетворяющий требованиям анализа пакет программ и быть готовым к интерпретации полученных результатов. Алгоритмов вычисления параметров связи существует множество, и в настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов интерпретации результатов является обязательным условием исследования.
Анализ отчетности не замыкается на специфических, разработанных в его рамках приемах, но активно использует самые разнообразные методики, творчески переработав их применительно к собственным требованиям. В частности, использование корреляционно-регрессионного анализа позволяет более эффективно решать задачи прогнозирования доходов организации и планирования ее будущего финансового состояния, в связи с чем, данный математический метод рекомендуется использовать более активно.
IV.
Список использованной литературы
1. Бараз В.Р. Корреляционно-регрессионный анализ связи показателей коммерческой деятельности с использованием программы Exel: Учебное пособие – Екатеринбург: ГОУ ВПО «УГТУ-УПИ», 2005;
2. Курс социально-экономической статистики: Учебник для вузов/Под ред. проф. М.Г. Назарова. — М.: Финстатинформ, ЮНИТИ-ДАНА, 2000;
3. Сергеева С.А. «Применение корреляционно-регрессионного метода в анализе финансового состояния организации» Белгородский университет потребительской кооперации. http://www.rusnauka.com/ONG/Economics/ 8_sergeeva%20s.a..doc.htm
4. Минашкин В.Г., Шмойлова Р.А. и др. Теория статистики/Московская финансово-промышленная академия, М., – 2004
5. Микроэкономическая статистика: Учебник/Под ред. С.Д. Ильенковой. – М.: Финансы и статистика, 2004
6. Герасимов Б.И. В.В.Дробышева, О.В. Воронкова Статистическое исследование в маркетинге: введение в экономический анализ: учебное пособие – Тамбов: Изд-во ТГТУ, 2006
7. Л.С.Хромцова. Корреляционно-регрессионный анализ основных показателей нефтедобывающей промышленности – Журнал "Экономический анализ: теория и практика", 2007, N 7.
8. Мартьянова М.Н., Сафронова Т.П. Основы статистики промышленности: Учебное пособие. – М.: Финансы и статистика, 1983
9. Гусаров В.М. Теория статистики: Учебное пособие для вузов. – М.: Аудит, ЮНИТИ, 1998
|