| Введение
Модель межотраслевого баланса Леонтьева
Рассмотрим n
отраслей промышленности, каждая из которых производит свою продукцию. Обозначим 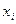 - валовой выпуск продукции отрасли i
, продукция каждой отрасли потребляется в данной отрасли и во всех других отраслях экономики (в противном случае соответствующее значение переменной равно нулю), часть продукции потребляется вне сферы материального производства и называется конечным продуктом. Обозначим - валовой выпуск продукции отрасли i
, продукция каждой отрасли потребляется в данной отрасли и во всех других отраслях экономики (в противном случае соответствующее значение переменной равно нулю), часть продукции потребляется вне сферы материального производства и называется конечным продуктом. Обозначим 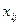 - величина продукта, произведенного в отрасли i
,
потребляемого в отрасли j
, - величина продукта, произведенного в отрасли i
,
потребляемого в отрасли j
, 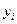 -
величина конечного продукта отрасли i
. Тогда производство и потребление продукции каждой отрасли может быть записано в виде -
величина конечного продукта отрасли i
. Тогда производство и потребление продукции каждой отрасли может быть записано в виде
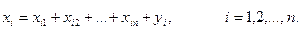
или для всех отраслей экономики региона в виде системы уравнений
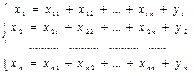 (1.5.1) (1.5.1)
Построенная система линейных уравнений носит название системы балансовых уравнений
, т.к. определяет объемы произведенной и потребляемой продукции по отраслям.
Величина 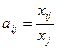 называется коэффициентом прямых затрат
и определяет долю продукции отрасли i
, которая потребляется в отрасли j
.
Тогда называется коэффициентом прямых затрат
и определяет долю продукции отрасли i
, которая потребляется в отрасли j
.
Тогда 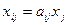 и систему межотраслевого баланса можно представить в виде системы линейных уравнений и систему межотраслевого баланса можно представить в виде системы линейных уравнений
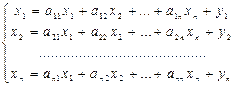 (1.5.2) (1.5.2)
Обозначим матрицы
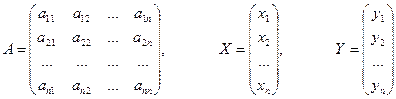
и рассмотрим матричное уравнение (1.5.3), соответствующее системе (1.5.2)
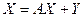 , (1.5.3) , (1.5.3)
в котором матрица (вектор) Х
называется вектором валового выпуска по отраслям, матрица А
называется матрицей прямых затрат или технологической матрицей, матрица (вектор) Y
называется вектором конечного продукта. Матричное уравнение (1.5.3) носит название модели межотраслевого баланса Леонтьева
и позволяет решать задачи трех видов:
1) по известным величинам валового выпуска продукции отраслей Х
и технологической матрице А
можно вычислить величину конечного продукта Y
:
из моде ли
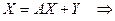 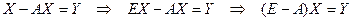
где Е –
единичная матрица. Следовательно,
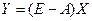 (1.5.4) (1.5.4)
2) по заданным величинам конечного продукта Y
и технологической матрице А
можно определить необходимый выпуск продукции Х:
из модели
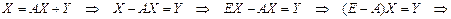 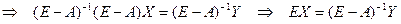
Следовательно,
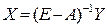 (1.5.5) (1.5.5)
3) по известным величинам валового выпуска некоторых отраслей 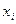 , заданным значениям конечного продукта других отраслей , заданным значениям конечного продукта других отраслей 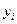 и матрице прямых затрат А
можно определить конечный продукт первых отраслей и валовой выпуск вторых, используя модель Леонтьева в виде системы уравнений (1.5.2). и матрице прямых затрат А
можно определить конечный продукт первых отраслей и валовой выпуск вторых, используя модель Леонтьева в виде системы уравнений (1.5.2).
Реклама

Матрица 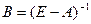 называется матрицей полных затрат
, так как каждый ее элемент называется матрицей полных затрат
, так как каждый ее элемент 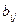 - величина валового выпуска отрасли - величина валового выпуска отрасли 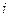 , необходимого для обеспечения выпуска единицы конечного продукта отрасли , необходимого для обеспечения выпуска единицы конечного продукта отрасли 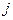 . .
Матрица 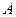 называется продуктивной
, то есть существует решение в модели Леонтьева, если найдется такой вектор (матрица) называется продуктивной
, то есть существует решение в модели Леонтьева, если найдется такой вектор (матрица) 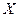 , что , что 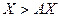 . .
Критерий продуктивности.
Для того, чтобы матрица прямых затрат была продуктивной необходимо и достаточно, чтобы выполнялось одно из условий:
1) существует обратная матрица 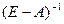 , все элементы которой неотрицательны, , все элементы которой неотрицательны,
2) матричный ряд 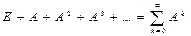 сходится, причем его сумма равна сходится, причем его сумма равна 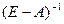 , ,
3) наибольшее по модулю собственное значение 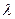 матрицы матрицы 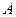 , то есть решение характеристического уравнения , то есть решение характеристического уравнения 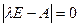 , было строго меньше единицы, , было строго меньше единицы,
4) все главные миноры матрицы положительны.
Цели и задачи курсовой работы
Практическое применение матричных моделей в экономическом анализе и управлении является основной целью данной работы.
Основными задачами курсовой работы являются:
· расширение теоретических знаний по математике и ее применению в экономических исследованиях,
· приобретение практических навыков использования моделей матричного исчисления для решения экономических задач и задач управления,
· проведение анализа исходной и получаемой статистической информации по экономике регионов,
· оценка выбора управленческих решений для моделирования экономической ситуации.
Задание по курсовой работе
1. Среди городов Московской области или регионов России студенту необходимо выбрать административный объект, экономику которого он будет (условно) моделировать. Название города или региона участвует в названии темы курсовой работы, например, «Применение модели межотраслевого баланса Леонтьева для управления экономикой Курской области».
2. Для выбранного региона определить три основных отрасли экономики, участвующие в модели №1 – А1, А2, А3 (например, А1 – самолетостроение, А2 – пищевая промышленность и т.д.) и пять основных отраслей, участвующих в модели №2.
Задача № 1
3. Заполнить выбранными характеристиками (название региона, А1, А2, А3,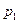 , , 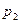 , , 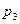 ) таблицу 1: ) таблицу 1:
Таблица 1.
Имеются исходные данные об исполнении баланса за 2005 год в городе N (в условных денежных единицах) (Задача №1)
:
| Отрасль произв-ва
|
Потребление
|
Конечный продукт
|
Валовой выпуск
|
| А1
|
А2
|
А3
|
| А1
|
300
|
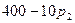
|
200
|
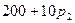
|
1000
|
| А2
|
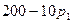
|
480
|
270
|
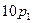
|
950
|
| А3
|
480
|
360
|
200
|
300
|
1340
|
4. Составить балансовые уравнения модели и определить потоки средств производства по отраслям. Оценить имеющийся вклад отраслей в суммарный конечный продукт региона.
Реклама

5. Найти технологическую матрицу коэффициентов прямых затрат А.
6. Исследовать матрицу А на продуктивность и найти матрицу коэффициентов полных затрат В. Сделать вывод о существовании решения в матричной модели Леонтьева.
7. Найти величины конечного продукта отдельно по всем отраслям и в целом по региону, если в его структуре предполагаются следующие изменения:
Вариант 1
: конечный продукт в отрасли А1 увеличится на 10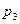 , в отрасли А2 снизится на 15%, в отрасли А3 увеличится в 1,2 раза, , в отрасли А2 снизится на 15%, в отрасли А3 увеличится в 1,2 раза,
Вариант 2
: конечный продукт в отрасли А1 снизится на 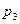 %, в отрасли А2 увеличится на 10%, в отрасли А3 увеличится на ( %, в отрасли А2 увеличится на 10%, в отрасли А3 увеличится на (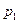 + +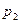 + +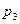 ), ),
Вариант 3
: конечный продукт в отрасли А1 увеличится в 1,3 раза, в отрасли А2 увеличится на (10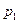 +4 +4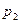 ), в отрасли А3 снизится на ), в отрасли А3 снизится на 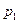 %. %.
Проанализировать полученный объем денежных средств для потребления вне сферы материального производства в целом и по структуре (отдельно по отраслям).
8.
Найти необходимый объем валового выпуска каждой отрасли для каждого из вариантов изменения конечного продукта и оценить преимущества выбора одного из вариантов перед остальными.
 Решение Решение
Название региона – Тульская область.
Основные отрасли, участвующие в модели № 1:
А1 - Машиностроение,
А2 –Энергетика,
А3 –Пищевая промышленность.
Р1-Екатерина-9,
Р2-Роман-5,
Р3-Кравец-6.
Таблица 1.
Имеются исходные данные об исполнении баланса за 2005 год в области:
| Отрасль производства.
|
Потребление.
|
Конечный продукт.
|
Валовой выпуск.
|
| Машиностроение
|
Энергетика
|
Пищевая промышленность
|
| Машиностроение.
|
300
|
350
|
200
|
250
|
1100
|
| Энергетика.
|
110
|
480
|
270
|
90
|
950
|
| Пищевая промышленность.
|
480
|
360
|
200
|
300
|
1340
|
По условию:

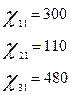 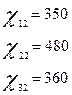 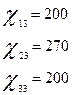 
По формуле 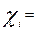 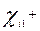 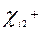 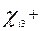 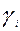 получим систему балансовых уравнений области получим систему балансовых уравнений области
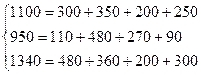
Очевидно, что суммарный конечный продукт равен 250+90+300=640(условных денежных единиц), а наибольший вклад машиностроительной отрасли от общего объема конечный продукт составляет:
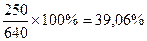
Энергетической отрасли от общего объема конечный продукт составляет:

Пищевой отрасли от общего объема конечный продукт составляет:
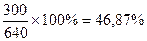
По формуле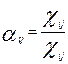 получим: получим:
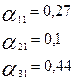 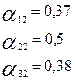 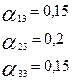
Таким образом, матрица прямых затрат имеет вид:
А=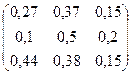
Для исследования матрицы А на продуктивность, воспользуемся критерием продуктивности. Среди всех указанных условий, выберем условие существования обратной матрицы 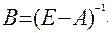 
Для этого, прежде всего, найдем матрицу
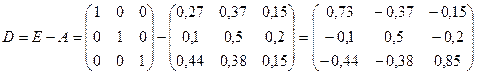
и её определитель
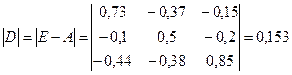
Так как матрица D=(E-A) невырожденная, то у неё существует обратная, 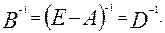 Следовательно, выполнен критерий продуктивности (его первое условие), матрица А продуктивна, а модель Леонтьева имеет решение. Следовательно, выполнен критерий продуктивности (его первое условие), матрица А продуктивна, а модель Леонтьева имеет решение.
Найдем алгебраические дополнения к элементам матрицы D:
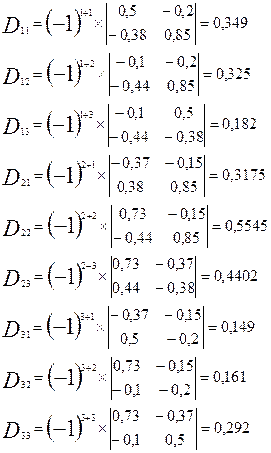
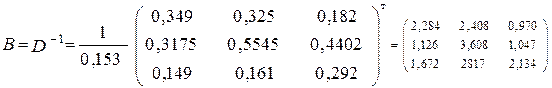 матрица полных затрат. матрица полных затрат.
Вариант 1
: По условию, в отчетном периоде величины конечного продукта составили:
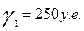 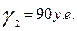 
если конечный продукт в машиностроении увеличится на 60у.е.
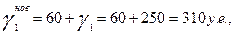
в энергетической отрасли снизится на 15%
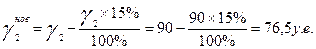
в пищевой отрасли увеличится в 1,2 раза

Тогда вектор конечного продукта 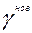 будет иметь вид будет иметь вид
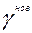 = =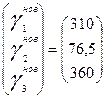
а необходимый для этого валового выпуска по отраслям
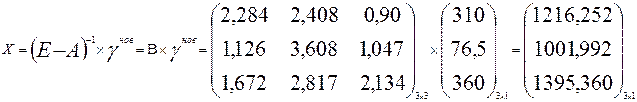
Следовательно, валовой выпуск машиностроения должен составить 1216 у.е.; энергетики 1002 у.е.; пищевой промышленности 1395 условных денежных единиц.
Вариант 2
: По условию, в отчетном периоде величины конечного продукта составили:
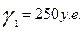 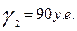 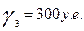
если конечный продукт в машиностроении снизился на 6%
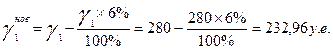
в энергетической отрасли увеличился на 10%
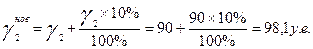
в пищевой отрасли увеличится на 20у.е.
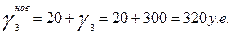
Тогда вектор конечного продукта 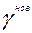 будет иметь вид будет иметь вид
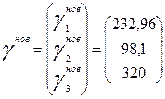
а необходимый для этого валового выпуска по отраслям
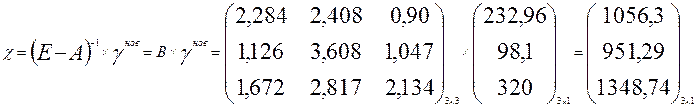 Следовательно, валовой выпуск машиностроения должен составить 1056 у.е.; энергетики 951 у.е.; пищевой промышленности 1349 условных денежных единиц. Следовательно, валовой выпуск машиностроения должен составить 1056 у.е.; энергетики 951 у.е.; пищевой промышленности 1349 условных денежных единиц.
Вариант 3:
По условию, в отчетном периоде величины конечного продукта составили:
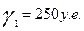 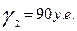 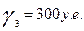
если конечный продукт в отрасли машиностроения увеличился в 1,3 раза
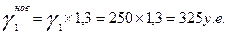
в энергетической отрасли увеличится на 110у.е.
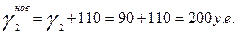
в пищевой отрасли снизится на 6%
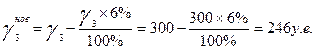
Тогда вектор конечного продукта 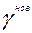 будет иметь вид будет иметь вид
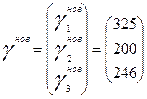
а необходимый для этого валового выпуска по отраслям
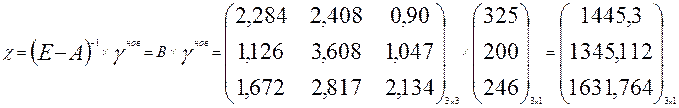
На мой взгляд вариант 3 самый выгодный так как затраты не очень велики по сравнению с 1 и 2 вариантами, а энергетика даже в плюсе, энергетика является одним из основных отраслей ведь не одно производство не обходится без электроэнергии.
Литература
1. Высшая математика для экономистов: Учебн. пособие для вузов/Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фридман; Под ред. проф. Н.Ш.Кремера. - М.: Банки и биржи, ЮНИТИ, 2003.- 471 с.
2. Общий курс высшей математики для экономистов: Учебник / Под ред. В.И.Ермакова. – М.: ИНФРА-М, 2002.- 656с. – (Серия “Высшее образование”).
3. Малыхин В.И. Математика в экономике: Учебное пособие. – М.: ИНФРА-М, 2002. – 352 с. – (Серия “Высшее образование”).
4. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М. МГУ им. М.В.Ломоносова, Издательство “ДИС”, 2004. – 368 с.
5. Колесников А.Н. Краткий курс математики для экономистов: Учебное пособие. – М.: ИНФРА-М, 1997. – 208 с. – (Серия “Высшее образование”).
6. Колемаев В.А. Математическая экономика: Учебник для вузов. – М.: ЮНИТИ, 1998.- 240 с.
7. Красс М.С. Математика для экономических специальностей: Учебник. – 3-е издание, переработанное и дополненное. – М.: Дело, 2002. – 704с.
8. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. – 3-е издание, испр. – М.: Дело, 2002. – 688 с.
9. Кундышева Е.С. Математическое моделирование в экономике: Учебное пособие / Под науч. Ред. Проф. Б.А.Суслакова. – М.: Издательско-торговая корпорация “Дашков и К”, 2004.- 352 с.
|