Федеральное агентство по образованию
ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет Приборостроительный
Кафедра Автоматика и управление
ПРОЕКТ ПРОВЕРЕН ДОПУСТИТЬ К ЗАЩИТЕ
Рецензент Заведующий кафедрой
____________________________ ___________________________
“_____” _____________ 2007__ г. “ _____ “ ____________ 2007__ г.
Синтез алгоритмов согласованного управления пространственным движением беспилотным летательным аппаратом
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К ДИПЛОМНОМУ ПРОЕКТУ
ЮУрГУ-Д.220200 068.000.ПЗ
Консультанты: Руководитель проекта:
______________________________ _______________________________
______________________________ _______________________________
“ _____ “ ______________ 2007 _ г. Автор проекта
студент группы ПС-269м .
______________________________
______________________________ Пушников А.А. .
“ ____ “ ________________ 2007 _ г.
______________________________ Нормоконтролер
______________________________ ______________________________
“ ____ “ _______________ 2007 _ г. “ _____ “ ______________ 2007 __ г.
Челябинск
2007 г.
Аннотация
Пушников А.А. Синтез алгоритмов согласованного управления пространственным движением беспилотным летательным аппаратом. – Челябинск. ЮурГУ. 2007 – 96 стр.
В данном дипломном проекте представлена математическая модель беспилотного летательного аппарата.В модели учтено влияние ветровых и турбулентных возмущений. Это позволяет уже на этапе моделирования предъявлять требования к аэродинамическим характеристикам летательного аппарата.
В работе рассматриваются алгоритмы управления беспилотным летательным аппаратом на сложных траекториях высшего пилотажа.
Ил. 52, библиогр. 6 назв.
Содержание
Введение. 4
1 Описание математической модели летательного аппарата. 6
1.1 Рулевые органы летательного аппарата и системы координат. 7
1.2 Полная нелинейная модель пространственного движения самолета. 13
1.3 Модель двигателя. 18
1.4 Модель атмосферы и воздушных возмущений. 20
1.5 Модель Земли. 23
1.6 Модель рулевых органов. 25
2 Разработка алгоритмов управления беспилотным летательным аппаратом. 27
2.1 Математическое описание полетного задания. 29
2.1.1 Общие положения. 29
2.1.2 Петля Нестерова. 31
2.2 Синтез управления на траекторном уровне. 36
Реклама

2.2.1 Управление движением ЛА.. 41
2.2.2 Управление ориентацией ЛА.. 48
2.3 Синтез управления на пилотажном уровне. 52
2.3.1 Настройка регулятора  .53 .53
2.3.2 Настройка регулятора  .55 .55
2.3.3 Настройка регулятора  .59 .59
2.3.4 Настройка регулятора  .63 .63
2.3.5 Настройка регулятора  .68 .68
2.3.5 Настройка регулятора  .. 74 .. 74
Заключение. 80
Перечень литературы.. 81
Приложение А – Описание параметров модели. 82
Приложение Б - Описание переменных. 86
Приложение В – Исходные map-файлы.. 91
Считается, что первый беспилотный летательный аппарат это “Воздушная торпеда Сперри”, который совершил свой первый полет 6 марта 1918 года. Этот БПЛА стал предшественником современных управляемых ракет, которые можно считать одноразовыми БПЛА. Первый БПЛА, который можно было использовать повторно был “Queen” компании “British Fairey” вариант самолета “Fairey IIIF”, впервые взлетел в сентябре 1932 года.
После многих десятилетий разработок, современная конфигурация БПЛА определенно не такая как у современных управляемых ракет. Фактически БПЛА находят множественное применение в различных областях. Так американское правительство использует их для разведки на поле боя и запуска ракет. Их военный БПЛА “RQ-1 Predator” по сути, стал революционным шагом в приемах ведения боевых действий. Этот БПЛА оснащенный противотанковыми ракетами “Hellfire”. Уже ведутся работы по разработке беспилотного боевого летательного аппарата "Х-45" взлетевшего в 2002 году.
Гражданским примером применения БПЛА может служить проект "Helios". Этот летательный аппарат (ЛА) отличается высокой надежностью и большой высотой полета, его применение это телекоммуникация. Его рабочая высота превышает 60.000 футов, т.е. он не подвержен влиянию погодных условий и не мешает полетам других воздушных судов и используется, по сути, в качестве стационарного спутника, но без временной задержки. В 2001 году БПЛА, работающий на солнечной энергии, поднялся на рекордную высоту 96.863 фута. Другим хорошим примером БПЛА можно считать “Aerosonde”, который уже достаточно известен своими возможностями в метеорологическом мониторинге и продолжительных перелетах. Это первый БПЛА перелетевший Северный Атлантический океан в 1998 году. На рис. 1 приведена модель “Aerosonde”.
За последние годы по всему миру значительно возрос интерес к беспилотным летательным аппаратам (БПЛА). Все больше и больше университетов выпускающие инженеров для аэрокосмической отрасли создают свои собственные программы по разработке БПЛА для исследований в некоторых уникальных областях, а также для целей обучения.
Реклама

Целями работы являются:
· Разработка нелинейных алгоритмов согласованного управления БПЛА.
· Отработка алгоритмов на имитационной модели.
Подобный автопилот может использоваться в качестве основного – для решения задач, где качество управление БПЛА человеком малоэффективно, например посадка или фигуры высшего пилотажа.
Разработка математической модели движения БПЛА относится к одному из первых этапов процесса создания системы управления полетом. При этом их полнота и точность зависит от назначения разрабатываемых моделей.
В данной работе ЛА рассматривается как динамический объект, непрерывное во времени изменение состояния которого описывается дифференциальными уравнениями. В данной работе будут рассматриваться только жесткие БПЛА самолетного типа. В качестве исследуемого БПЛА взят американский беспилотный БПЛА Aerosonde (рис. 1.1).
Процесс разработки и исследования алгоритмического обеспечения системы управления полетом подразумевает наличие математической модели летательного аппарата, используемой для синтеза законов управления и выбора алгоритмов формирования сигналов управления.
1.1 Рулевые органы летательного аппарата и системы координат
Реализация требуемого движения БПЛА основана на возможности создания управляемых по величине и направлению сил и моментов, действующих на БПЛА. Рассматриваемый самолет обладает органом управления тягой двигателя и аэродинамическими рулями, расположение которых показано на рис.1.2. Принцип действия показанных органов различен, но все они при изменении своего положения так или иначе изменяют направление воздушного потока, что приводит к появлению дополнительных аэродинамических сил.
Элероны, руль направления и руль высоты относятся к традиционным рулевым органам самолета и предназначены для создания управляющих моментов вокруг трех ортогональных осей самолета. Закрылки также относятся к традиционным органам управления и предназначены в основном только для увеличения подъемной силы во время взлета и посадки и в отличие от других рулей отклоняются только вниз.
Далее будут использоваться следующие обозначения угловых отклонений управляющих органов:  - отклонение закрылок; - отклонение закрылок;  - отклонение руля высоты; - отклонение руля высоты;  - дифференциальное отклонение левого и правого элерона; - дифференциальное отклонение левого и правого элерона;  - отклонение руля направления; - отклонение руля направления;  - отклонение ручки управления тягой двигателя, нормированный показатель изменяется от 0 до 1. - отклонение ручки управления тягой двигателя, нормированный показатель изменяется от 0 до 1.
При практическом использовании уравнений движения БПЛА их записывают в проекциях на оси выбранных систем координат (СК). В динамике полета получили распространение следующие правые прямоугольные СК [1].
1. Нормальная земная система координат. Начало находится на поверхности земли в любой удобной точке. Оси OoXg (направлена на север) и OoZg (направлена на восток) расположены в горизонтальной плоскости, а ось OoYg направлена вверх (вдоль местной вертикали).
2. Нормальная система координат. Начало находится в центре масс ЛА оси OXg (направлена на север) и OZg (направлена на восток) расположены в горизонтальной плоскости, а ось OYg направлена вверх. В дальнейшем будем полагать, что оси нормальной земной и нормальной СК параллельны. Относительное положение этих СК определяется вектором r между их началами. Проекция вектора r на ось OYg называется геометрической высотой полета.
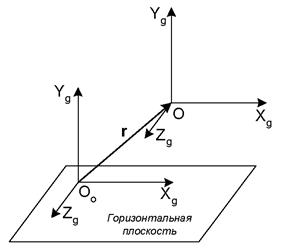
Рис. 1.3. Нормальная земная и нормальная системы координат
3. Связанная система координат. Начало находится в центре масс ЛА. Ось OX направлена вдоль ЛА вперед и называется продольной осью. Ось OZ направлена вправо по ходу самолета и называется поперечной осью. Ось OY лежит в плоскости симметрии самолета, направлена вверх (при нормальном полете) и называется нормальной осью (рис. 1.4).
Относительное положение связанной и нормальной СК определяется в общем случае девятью направляющими косинусами. Часто для определения относительного положения нормальной и связанной СК пользуются углами Эйлера. В этом случае для перехода от нормальной к связанной СК используется следующая последовательность поворотов: поворот на угол рысканья  (вокруг оси OYg), на угол тангажа (вокруг оси OYg), на угол тангажа  (вокруг нового положения оси OZ) и на угол крена (вокруг нового положения оси OZ) и на угол крена  (вокруг оси OX). Использование углов Эйлера опирается на предположение что (вокруг оси OX). Использование углов Эйлера опирается на предположение что  . .

Рис . 1.4. Нормальная и связанная системы координат
Матрица перехода от нормальной к связанной системе координат имеет следующий вид:
 . (1.1.1) . (1.1.1)
Скоростная система координат. Начало находится в центре масс ЛА. Ось OXa направлена вдоль вектора скорости БПЛА относительно воздушной среды и называется скоростной осью. Ось OZa направлена вправо и называется боковой осью. Ось OYa лежит в плоскости симметрии, направлена вверх (при нормальном полете) и называется осью подъемной силы.
Относительное угловое положение связанной и скоростной СК определяется углами атаки  и бокового скольжения и бокового скольжения  (рис. 1.5). (рис. 1.5).

Рис. 1.5. – Связанная и скоростная системы координат
Матрица перехода от связанной СК к скоростной имеет вид:
 . (1.1.2) . (1.1.2)
Траекторная система координат. Начало находится в центре масс ЛА. Ось OXk направлена вдоль вектора земной скорости ЛА (т.е. вдоль вектора скорости ЛА относительно Земли). Ось OZk лежит в горизонтальной плоскости. Ось OYk направлена вверх. Оси этих координат специальных названий не имеют.
Относительное положение траекторной и нормальной СК показано на рис. 1.6. Угол между осью OXg и вертикальной плоскостью, проходящей через ось OXk называется углом пути  . Угол между осью OXk и горизонтальной плоскостью называется углом наклона траектории . Угол между осью OXk и горизонтальной плоскостью называется углом наклона траектории . .

Рис. 1.6. Нормальная и траекторная системы координат
Матрица перехода от траекторной к нормальной системе координат имеет следующий вид:
 . (1.1.3) . (1.1.3)
Правило знаков отклонения управляющих рулей. Положительное отклонение руля высоты  - вниз. Отклонения руля направления - вниз. Отклонения руля направления  и элеронов и элеронов  имеют положительное значение, если при этом самолет начинает отклоняться влево. Причем, результирующее отклонение элеронов определяется как. имеют положительное значение, если при этом самолет начинает отклоняться влево. Причем, результирующее отклонение элеронов определяется как.
 . (1.1.4) . (1.1.4)
Положительное отклонение закрылок  - вниз (при этом увеличивается подъемная сила и сила лобового сопротивления). - вниз (при этом увеличивается подъемная сила и сила лобового сопротивления).
Известно, что одним из основных моментов в составлении или разработке математической модели ЛА является принятие различных допущений, упрощающих, схематизирующих реальный процесс. Принятие допущений это инженерная задача, от правильности, решения которой зависит адекватность полученной модели решаемой проблеме в целом.
При выборе модели исходили из следующего ряда основных допущений:
· конструкция самолета считается жесткой;
· масса самолета изменяется в процессе моделирования, но отсутствует жидкое наполнение;
· масса в плоскостях XZ и YZ распределена равномерно, т.е. пренебрегаем центробежными моментами инерции Jxz и Jyz;
· аэродинамика БПЛА нелинейная по углам атаки и скольжения, обтекание БПЛА квазистационарное;
· атмосфера является стандартной;
· вектор суммарного кинетического момента вращающихся частей двигателя БПЛА направлен вдоль оси OX связанной СК.
Рассмотрим поступательное движение летательного аппарата. Уравнение сил в связанной системе координат имеет следующий вид:
 , (1.2.1) , (1.2.1)
где  - главный вектор сил в связанной СК; m – масса летательного аппарата; - главный вектор сил в связанной СК; m – масса летательного аппарата;  - вектор угловых скоростей в связанной СК. - вектор угловых скоростей в связанной СК.
Главный вектор сил  , представленный в проекции связанной СК , представленный в проекции связанной СК
 , (1.2.2) , (1.2.2)
где  - вектор силы тяжести в связанной СК; - вектор силы тяжести в связанной СК;  - вектор силы тяги двигателя в связанной СК; - вектор силы тяги двигателя в связанной СК;  - равнодействующий вектор аэродинамических сил в связанной СК. - равнодействующий вектор аэродинамических сил в связанной СК.
Вектор силы тяжести в нормальной системе координат
 , (1.2.3) , (1.2.3)
где g = 9.81 м/с2 – ускорение свободного падения.
Вектор силы тяжести в связанной системе координат
 . (1.2.4) . (1.2.4)
Аэродинамические силы, действующие на летательный аппарат, определяются конфигурацией ЛА и характером обтекания его воздушным потоком. В связанной СК
 , (1.2.5) , (1.2.5)
где q – скоростной напор; S – площадь крыла самолета; cx, cy, cz – аэродинамические коэффициенты сил.
 ; (1.2.6) ; (1.2.6)
 ; (1.2.7) ; (1.2.7)
 ; (1.2.8) ; (1.2.8)
 , (1.2.9) , (1.2.9)
где  - плотность воздуха; - плотность воздуха;  , ,  - аэродинамические постоянные (Приложение А); e - коэффициент Освальда; M – число Маха; - аэродинамические постоянные (Приложение А); e - коэффициент Освальда; M – число Маха;  - модуль вектора скорости в связанной СК; - модуль вектора скорости в связанной СК;  , ,  - углы атаки и скольжения. - углы атаки и скольжения.
 ; (1.2.10) ; (1.2.10)
 , (1.2.11) , (1.2.11)
где l – размах крыла;  - скорость звука на текущей высоте. - скорость звука на текущей высоте.
Модуль вектора скорости движения ЛА в связанной СК примет следующий вид:
 . (1.2.12) . (1.2.12)
Углы атаки и скольжения:
 ; (1.2.13) ; (1.2.13)
 . (1.2.14) . (1.2.14)
Положение летательного аппарата в пространстве в нормальной СК
 , (1.2.15) , (1.2.15)
где матрица перехода от связанной к нормальной СК  . .
Рассмотрим вращательное движение летательного аппарата. Вектор момента количества движения L в связанной СК
 , (1.2.16) , (1.2.16)
где  - вектор момента количества движения; J - матрица моментов инерции БПЛА. В соответствии с принятыми допущениями - вектор момента количества движения; J - матрица моментов инерции БПЛА. В соответствии с принятыми допущениями
 . (1.2.17) . (1.2.17)
Вращательное движение БПЛА
 , (1.2.18) , (1.2.18)
где M – главный вектор моментов ЛА. Запишем выражение (1.2.18) в матричном виде
 . (1.2.19) . (1.2.19)
Действующий на летательный аппарат главный вектор моментов представляет собой сумму вектора аэродинамического момента и гироскопического момента двигателя
 , (1.2.20) , (1.2.20)
где  - аэродинамический момент; - аэродинамический момент;  - момент, создаваемый двигателем; - момент, создаваемый двигателем;  - точка приложения аэродинамической силы; - точка приложения аэродинамической силы;  - точка приложения силы двигателя; - точка приложения силы двигателя;  - точка положения центра масс. - точка положения центра масс.
Аэродинамический момент 
 , (1.2.21) , (1.2.21)
где  - диагональная матрица характерных линейных размеров ЛА; l – размах крыла; ba – средняя аэродинамическая хорда крыла; mx, my, mz – аэродинамические коэффициенты моментов, определяемые как - диагональная матрица характерных линейных размеров ЛА; l – размах крыла; ba – средняя аэродинамическая хорда крыла; mx, my, mz – аэродинамические коэффициенты моментов, определяемые как
 ; (1.2.22) ; (1.2.22)
 (1.2.23) (1.2.23)
 , (1.2.24) , (1.2.24)
где  , ,  … - аэродинамические постоянные … - аэродинамические постоянные
Угловые ускорения  , ,  , ,  соответственно соответственно
 (1.2.25) (1.2.25)
Матрица перехода от нормальной к связанной СК характеризуется соотношением (1.1.1).
Рассмотрим модель двигателя летательного аппарата. Модель двигателя состоит из двух частей – пропеллера и поршневого двигателя. Сила и гироскопический момент, создаваемые двигателем, имеют следующий вид:
 ; (1.3.1) ; (1.3.1)
 ; (1.3.2) ; (1.3.2)
 . (1.3.3) . (1.3.3)
где  - радиус пропеллера; - радиус пропеллера;  - угловая скорость вращения пропеллера; - угловая скорость вращения пропеллера;  и и  - коэффициенты силы тяги и мощности. Составляющая гироскопического момента двигателя - коэффициенты силы тяги и мощности. Составляющая гироскопического момента двигателя  , поскольку не совпадает точка приложения силы тяги двигателя и центр масс ЛА. , поскольку не совпадает точка приложения силы тяги двигателя и центр масс ЛА.
Коэффициент, характеризующий режим работы винта
 . (1.3.4) . (1.3.4)
Угловая скорость вращения пропеллера  : :
 , (1.3.5) , (1.3.5)
где  - момент сопротивления вращения пропеллера; - момент сопротивления вращения пропеллера;  - вращающий момент поршневого двигателя; - вращающий момент поршневого двигателя;  - момент инерции вала двигателя; - момент инерции вала двигателя;  - момент инерции пропеллера. - момент инерции пропеллера.
Вращающий момент поршневого двигателя  : :
 , (1.3.6) , (1.3.6)
где  - температура на уровне моря; - температура на уровне моря;  - температура на текущей высоте; - температура на текущей высоте;  - всасывание; - всасывание;  - угловая скорость вращения пропеллера в радиан/минуту. - угловая скорость вращения пропеллера в радиан/минуту.
Всасывание топлива  : :
 , (1.3.7) , (1.3.7)
где p – давление на текущей высоте;  - нормированный показатель ручки управления дроссельной заслонкой двигателя. - нормированный показатель ручки управления дроссельной заслонкой двигателя.
Расход топлива  : :
 , (1.3.8) , (1.3.8)
где  показывает зависимость расхода топлива от всасывания и угловой скорости вращения пропеллера. показывает зависимость расхода топлива от всасывания и угловой скорости вращения пропеллера.
Модель атмосферы включает в себя модель стандартной атмосферы и модель ветровых возмущений.
Стандартная атмосфера. В качестве стандартной атмосферы рассматриваются зависимости следующих параметров от текущей высоты:
статическое давление p = p(H);
температура воздуха T = T(H);
плотность воздуха  = = ; ;
скорость звука Vsnd = Vsnd(H).
Эти зависимости были взяты из описания модели стандартной атмосферы 1976. И представляют собой набор замеров проведенных на разной высоте, промежуточные значения получаем путем линейной аппроксимации этих зависимостей.
Воздушные возмущения. Динамическое воздействие воздушных возмущений на БПЛА может быть формализовано на основе определения воздушной скорости БПЛА, углов атаки и скольжения, с учётом воздействия воздушного потока.
Взаимосвязь между векторами воздушной скорости V, путевой скорости Vk и скорости ветра Vwind определяется соотношением
 . (1.4.1) . (1.4.1)
Полный вектор скорости воздушных возмущений  включает в себя: включает в себя:
· скорость постоянного ветра  ; ;
· турбулентность  . .
 . (1.4.2) . (1.4.2)
Скорость и ускорение постоянной составляющей ветровых возмущений
 ; (1.4.3) ; (1.4.3)
 , (1.4.4) , (1.4.4)
где  , ,  - вектора скоростей и ускорений ветровых возмущений в земной СК. - вектора скоростей и ускорений ветровых возмущений в земной СК.
Турбулентность описывается моделью турбулентности Кармана. Модель представляет собой набор формирующих фильтров продольной, поперечной и вертикальной составляющей для трех источников белого шума. Параметры фильтра зависят от силы ветра и высоты полета.
Общее уравнение для трех фильтров можно записать следующим образом
 ; (1.4.5) ; (1.4.5)
 , (1.4.6) , (1.4.6)
где  - вектор переменных состояний, - вектор переменных состояний,  ; ;  - случайный сигнал с нормальным распределением. Матрицы Ai, Bi и Ci соответственно равны - случайный сигнал с нормальным распределением. Матрицы Ai, Bi и Ci соответственно равны
 ; (1.4.7) ; (1.4.7)
 ; (1.4.8) ; (1.4.8)
 , (1.4.9) , (1.4.9)
где  - опорное расстояние до соответствующего фильтра; - опорное расстояние до соответствующего фильтра;  - интенсивность турбулентности соответствующего фильтра. - интенсивность турбулентности соответствующего фильтра.
Параметры фильтров  и и  определяются как определяются как
 ; (1.4.10) ; (1.4.10)
 ; (1.4.11) ; (1.4.11)
 ; (1.4.12) ; (1.4.12)
 , (1.4.13) , (1.4.13)
где H – высота ЛА над уровнем земли в текущей точке пространства.
Ускорение турбулентности вычисляется дифференцированием по времени скорости турбулентности  , т.е. , т.е.
 . (1.4.14) . (1.4.14)
Ветровой срез характеризуется эффектом изменения вектора скорости ветра во времени по отношению к положению БПЛА в пространстве. В результате возникают дополнительные угловые скорости вращения БПЛА. Эффект ветрового среза влияет только на угловые скорости  и и  . .
 ; (1.4.15) ; (1.4.15)
 , (1.4.16) , (1.4.16)
где  и и  - угловые скорости, обусловленные турбулентностью в связанной СК. - угловые скорости, обусловленные турбулентностью в связанной СК.
Модель Земли включает в себя описание формы и гравитации земли. Расчет локального радиуса земли и гравитации в текущем положении выполняется на основе коэффициентов модели земли WGS-84, следующим образом
 ; (1.5.1) ; (1.5.1)
 ; (1.5.2) ; (1.5.2)
 (1.5.3) (1.5.3)
 , (1.5.4) , (1.5.4)
где  - экваториальный радиус Земли; - экваториальный радиус Земли;  - первый эксцентриситет; - первый эксцентриситет;  - текущая широта; - текущая широта;  - ускорение свободного падения на экваторе; - ускорение свободного падения на экваторе;  - гравитационная постоянная; - гравитационная постоянная;  - радиус меридиана; - радиус меридиана;  - нормальный радиус Земли; - нормальный радиус Земли;  - эквивалентный радиус Земли. - эквивалентный радиус Земли.
Для определения положения ЛА в географической системе координат при известной скорости движения в нормальной системе координат  имеем имеем
 ; (1.5.5) ; (1.5.5)
 ; (1.5.6) ; (1.5.6)
 , (1.5.7) , (1.5.7)
где  и и  - скорость по широте и долготе соответственно. - скорость по широте и долготе соответственно.
Еще одной из основных характеристик модели земли является высота над средним уровнем моря, т.к. на основе этого параметра вычисляются все характеристики стандартной атмосферы. Этот параметр вычисляется с учетом эллиптичности поверхности земли описываемой моделью WGS-84, используя модель гиоидной неровности поверхности земли EGM-96 [2]. Таким образом, необходимо вычислить высоту между эллипсоидной формой и действительным положением среднего уровня моря (гиоидная неровность), что связанно с неравномерностью гравитационного потенциала земли. Коррекция полученной высота выполняется на основе корректирующей двумерной таблицы Широта-Долгота, с разрешением в 1 градус в обоих направлениях. Гиоидная неровность поверхности земли учитывается прибавлением корректирующего значения -0.53 метра модели WGS-84 к высоте вычисленной на основе уравнений движения БПЛА.
Неотъемлемой частью систем автоматического управления движением БПЛА являются исполнительные устройства - отклоняющие рулевые органы БПЛА в соответствии с реализуемыми законами управления.
Естественным и широко распространенным способом учета при моделировании динамических и статических свойств исполнительных устройств (приводов) а также их случайных ошибок является включение математических моделей этих устройств в модель обобщенного объекта управления.
Исполнительные приводы рулевых органов выбираются из условия, чтобы их нагрузочные характеристики обеспечивали необходимую динамику процессов управления, другими словами, от них требуется обеспечение перемещения с заданной скоростью рулевого органа, нагруженного внешними силами или внешними моментами.
По принципу построения и характеру используемой энергии авиационные приводы рулевых органов делятся на электромеханические, электрогидравлические и электропневматические. Каждый из этих типов приводов обладает динамическими особенностями, и, кроме того, встречаются различные количества каскадов преобразования энергии в приводах. Все это обуславливает различие математических моделей этих приводов.
В упрощенной постановке можно полагать, что электромеханические и электропневматические приводы при наличии обратной связи по положению рулевого органа описываются моделью вида
 . (1.6.1) . (1.6.1)
Следует отметить, что рулевой орган может отклоняться с определенной скоростью в пределах  и на определенных углах в пределах и на определенных углах в пределах  . Таким образом, предельные технически реализуемые отклонения и скорости отклонения рулевых органов для входного сигнала . Таким образом, предельные технически реализуемые отклонения и скорости отклонения рулевых органов для входного сигнала 
 ; (1.6.2) ; (1.6.2)
 . (1.6.3) . (1.6.3)
Полагаем, что предельные скорости отклонения рулевых органов составляют соответственно  и и  , а предельные углы отклонения рулевых органов , а предельные углы отклонения рулевых органов  и и  соответственно. Постоянная времени привода соответственно. Постоянная времени привода  . .
Общая задача управления движением ЛА традиционно подвергается декомпозиции (разделению) на различные подзадачи или частные задачи. Эти задачи по своему физическому содержанию могут либо соотноситься как соподчиненные, либо носить автономный характер. Каждая из таких задач требует проработки специфических вопросов построения и функционирования алгоритмов управления.
Одной из характерных черт современного уровня развития теории управления движением ЛА является стремление к интеграции систем управления, решающих частные задачи. Предполагается, что интеграция систем этих систем даст потенциальные возможности улучшения всей системы управления ЛА.
Задача интегрированного управления движением ЛА неизбежно сталкивается с проблемой управления многомерными, в общем случае взаимосвязанными процессами. Высокие порядки уравнений движения ЛА (с учетом, например, упругих деформаций) и уравнений его отдельных систем, учитываемых при управлении (двигательные установки, приводы и т.д.), могут являться серьезным препятствием на пути практической реализации разрабатываемых алгоритмов управления.
Методы распределенной обработки информации могут снизить необходимость в передаче всех данных в один процессор и могут позволить распределить вычислительную загрузку по формированию управления между несколькими процессорами. Известны два основных варианта декомпозиции управления:
· иерархическое управление, в котором процессоры объединены в функциональном порядке;
· децентрализованное управление, в котором процессоры взаимодействуют на одинаковом уровне.
Возможны также различные комбинации этих вариантов. В целом же организация обмена информацией и вычислений в процессорной управляющей системе тесно связана с особенностями алгоритмического обеспечения управления. Создание распределенной системы управления ЛА требует разработки специальных алгоритмов, ориентированных на решение этой задачи.
Для задачи управления движением ЛА существует традиционное разделение на ряд подзадач различного уровня. В качестве таких уровней можно указать:
1. уровень выбора и расчета маршрута движения ЛА, на котором по целевой установке использования ЛА определяется оптимальная или предпочтительная траектория движения ЛА от начального пункта такой траектории к конечному или формируются условия текущего формирования такой траектории (программирование летного задания);
2. уровень траекторного управления, на котором ЛА, как правило, полагается твердым телом, без учета аэродинамики, и определяется отклонение действительной траектории ЛА от заданной или формируемой по установленным правилам, а также синтезируются команды сокращения этого отклонения;
3. уровень пилотирования, для которого характерно управление движением ЛА как твердым телом, с учетом аэродинамики, с целью реализации команд траекторного уровня.
2.1.1 Общие положения
Полетное задание представим как траекторию движения самолета, известную до 3 производной:
 (2.1.1) (2.1.1)
Зная траекторию можно получить угловые скорости ЛА до 2 производной:
 (2.1.2) (2.1.2)
 (2.1.3) (2.1.3)
 (2.1.4) (2.1.4)
Если углы атаки и скольжения близки к нулю, то по заданной траектории ЛА, можно найти производные угловой скорости.
 (2.1.5) (2.1.5)
 (2.1.6) (2.1.6)
 (2.1.7) (2.1.7)
Аналогично вычисляются вторые производные угловой частоты:
 , ,  , ,  . .
Если при полете изменяются углы атаки и скольжения, функции их изменения учитываются при формировании каждой траектории индивидуально.
Петля Нестерова - фигура пилотажа, при которой самолет выполняет полет по криволинейной траектории в вертикальной плоскости с сохранением направления полета после вывода.
Петля была обоснована Н. Е. Жуковским и впервые выполнена 9 сентября 1913 года русским летчиком П. Н. Нестеровым, который является основоположником фигур высшего пилотажа.
Петля применяется не только как фигура пилотажа, а также имеет широкое применение для обучения управлению самолетом в условиях интенсивного изменения угла тангажа, перегрузки, скорости и высоты полета. Кроме того, элементы петли составляют основу других эволюции в полете, а также фигур пилотажа: переворот, вертикальные восьмерки и др.
Петля считается правильной, если все точки ее траектории лежат в одной вертикальной плоскости, а нормальная перегрузка  на протяжении всего маневра остается положительной. на протяжении всего маневра остается положительной.
Петля - это не установившееся движение самолета по криволинейной траектории в вертикальной плоскости под действием постоянно существующей центростремительной силы. Первая половина петли осуществляется за счет запаса скорости и тяги силовой установки. Вторая - за счет веса самолета и тяги силовой установки.
Схема сил, действующих на самолет в наиболее характерных точках петли, показана на рисунке 2.1.
Допустим, самолет летит горизонтально со скоростью, необходимой для ввода в петлю. Для ввода в петлю необходимо отклонить ручку управления на себя, увеличивая тем самым угол атаки. Подъемная сила увеличивается и становится больше веса самолета (при малом угле искривления траектории) или составляющей силы веса самолета Gcos (при больших углах траектории). Под действием возникающей центростремительной силы, в начале она равна Fay-G >0 (при малых углах (при больших углах траектории). Под действием возникающей центростремительной силы, в начале она равна Fay-G >0 (при малых углах  ) и Fay-Gcos ) и Fay-Gcos (при больших углах (при больших углах  ), самолет искривляет траекторию полета вверх. ), самолет искривляет траекторию полета вверх.
Уравнения движения при вводе имеют вид (положение 1):
условие уменьшения скорости
 (2.1.8) (2.1.8)
условие искривления траектории в вертикальной плоскости
 (2.1.9) (2.1.9)
Другая составляющая силы веса самолета Gsin совместно с лобовым сопротивлением тормозит движение, так как становится больше силы тяги Fdсиловой установки. В результате скорость уменьшается. совместно с лобовым сопротивлением тормозит движение, так как становится больше силы тяги Fdсиловой установки. В результате скорость уменьшается.
По мере искривления траектории самолет увеличивает угол наклона траектории, при этом составляющая силы веса самолета Gcos уменьшается и центростремительная сила, равная Fay-Gcos уменьшается и центростремительная сила, равная Fay-Gcos , должна увеличиваться, но она уменьшается, так как скорость падает в большей степени. Составляющая веса Gsin , должна увеличиваться, но она уменьшается, так как скорость падает в большей степени. Составляющая веса Gsin . увеличивается, что приводит к интенсивному уменьшению скорости. . увеличивается, что приводит к интенсивному уменьшению скорости.
В положении 2 центростремительной силой является подъемная сила.
Уравнения движения в положении 2 имеют вид:
условие уменьшения скорости
 (2.1.10) (2.1.10)
условие искривления траектории в вертикальной плоскости
 (2.1.11) (2.1.11)

Рис.
2.1 Схема сил, действующих на самолет при выполнении петли
После перехода вертикального положения самолет переходит в перевернутый полет. При этом составляющая силы веса Gcos совместно с подъемной силой Fay создают центростремительную силу, искривляющую траекторию полета: Fay+Gcos совместно с подъемной силой Fay создают центростремительную силу, искривляющую траекторию полета: Fay+Gcos >0. Составляющая веса самолета Gsin >0. Составляющая веса самолета Gsin уменьшается. В самой верхней точке петли скорость будет наименьшей, поэтому наименьшей будет подъемная сила. Она будет направлена вниз и совместно с силой веса самолета создаст центростремительную силу, имеющую также положительную величину (Fay+G>0). Так как вес самолета и поFayдъемная сила направлены вниз, то самолет легко переходит в пикирование (положение 3). уменьшается. В самой верхней точке петли скорость будет наименьшей, поэтому наименьшей будет подъемная сила. Она будет направлена вниз и совместно с силой веса самолета создаст центростремительную силу, имеющую также положительную величину (Fay+G>0). Так как вес самолета и поFayдъемная сила направлены вниз, то самолет легко переходит в пикирование (положение 3).
При переходе в пикирование обороты двигателя уменьшаются до минимума. Далее при увеличении угла обратного пикирования центростремительная сила, искривляющая траекторию, состоит из подъемной силы Fay и составляющей веса Gcos (Fay+Gcos (Fay+Gcos ). Составляющая веса самолета Gsin ). Составляющая веса самолета Gsin совместно с тягой силовой установки увеличивают скорость (Fd+Gsin совместно с тягой силовой установки увеличивают скорость (Fd+Gsin -Fax>0). -Fax>0).
В вертикальном положении вниз искривляющей силой является подъемная сила Fay (положение 4), а вес самолета и тяга двигателя Fd направлены в одну сторону и больше силы лобового сопротивления, что способствует дальнейшему разгону скорости (G+Fd-Fax>0).
Уравнения движения в положении 3 имеют вид:
условие искривления траектории
 (2.1.12) (2.1.12)
условие увеличения скорости
 (2.1.13) (2.1.13)
Уравнения движения в положении 4 имеют вид:
условие искривления траектории
 (2.1.14) (2.1.14)
 (2.1.15) (2.1.15)
Траектория полета в вертикальной плоскости искривляется центростремительной силой Fay-Gcos . .
Составляющая веса Gsin совместно с тягой силовой установки больше лобового сопротивления, что способствует дальнейшему увеличению скорости Fd+Gcos совместно с тягой силовой установки больше лобового сопротивления, что способствует дальнейшему увеличению скорости Fd+Gcos -Fax>0. -Fax>0.
Для быстрого увеличения скорости обороты силовой установки необходимо увеличить до максимальных.
Уравнения движения на выводе (положение 5) имеют вид:
условие увеличения скорости
 (2.1.16) (2.1.16)
условие искривления траектории
 (2.1.17) (2.1.17)
Форма петли получается не круглой, а несколько вытянутой вверх. Объясняется это тем, что скорость при подъеме и при снижении непрерывно изменяется, что приводит к изменению подъемной силы, также изменяется величина составляющей силы веса Gcos . На восходящем участке скорость падает, поэтому радиус кривизны траектории уменьшается. На нисходящем участке петли скорость нарастает и радиус кривизны увеличивается. В верхней точке кривизна траектории наибольшая. . На восходящем участке скорость падает, поэтому радиус кривизны траектории уменьшается. На нисходящем участке петли скорость нарастает и радиус кривизны увеличивается. В верхней точке кривизна траектории наибольшая.
Рассматриваемый подход предусматривает, что задача сформулирована с помощью голономных соотношений выходов системы и для ее решения используется метод согласованного управления [3]. В нем используется преобразование к системе задачно-ориентированных координат, характеризирующее линейные и угловые отклонения от требуемых соотношений, что дает возможность свести многоканальную задачу управления к ряду простых задач компенсации указанных отклонений и найти решение с помощью приемов нелинейной стабилизации и программного управления.
На траекторном уровне формируются команды для пилотажного комплекса в виде заданных компонент сил, угловых моментов и их производных. На этом уровне используется как текущая информация о траектории движения ЛА, так и информация о требованиях, предъявляемых к траектории. Задачей системы управления на траекторном уровне является формирование сил и угловых моментов ЛА в связанной системе координат, обеспечивающих движение ЛА вдоль заданной пространственной траектории.
На траекторном уровне ЛА рассматривается как симметричное, твердое тело. Его динамика в нормальной системе координат  задается уравнениями поступательного движения: задается уравнениями поступательного движения:
 , (2.2.1) , (2.2.1)
 (2.2.2) (2.2.2)
и вращательного движения
 (2.2.3) (2.2.3)
где  и и  - векторы декартовых координат и их скоростей, - векторы декартовых координат и их скоростей,  - вектор мгновенной угловой скорости, - вектор мгновенной угловой скорости,  - вектор внешних действующих сил, - вектор внешних действующих сил,  - вектор внешних моментов, m и J – постоянные массо-инерционные параметры. - вектор внешних моментов, m и J – постоянные массо-инерционные параметры.
Положение тела в пространстве  характеризуется парой характеризуется парой
 (2.2.4) (2.2.4)
где  - ортогональная матрица, которая представляет собой базис, связанный с центром тела (рис. 2.2). - ортогональная матрица, которая представляет собой базис, связанный с центром тела (рис. 2.2).

Рисунок 2.2 – Кривая  в декартовом пространстве в декартовом пространстве
Эта матрица характеризует повороты тела относительно главных осей пространства  при переходе из связной системы координат в нормальную. Она известна так же как матрица направляющих косинусов и удовлетворяет следующему дифференциальному уравнению: при переходе из связной системы координат в нормальную. Она известна так же как матрица направляющих косинусов и удовлетворяет следующему дифференциальному уравнению:
 (2.2.5) (2.2.5)
где  косо-симметричная матрица вида косо-симметричная матрица вида
 (2.2.6) (2.2.6)
где  - вектор мгновенных угловых скоростей, заданный в системе координат твердого тела и связанный с внешним вектором скоростей - вектор мгновенных угловых скоростей, заданный в системе координат твердого тела и связанный с внешним вектором скоростей  как: как:
 (2.2.7) (2.2.7)
Уравнения (2.2.1)-(2.2.3) и (2.2.5) описывают 3-канальную динамическую систему 6-го порядка, состояние которой определяется координатами векторов R,V,w, выходы – векторами  , ,  (рис. 2.2). (рис. 2.2).

Рисунок 2.3 – ЛА под воздействием внешних и внутренних сил
Так же целесообразно ввести внутренние (в связной системе координат) сило-моментные воздействия (рис. 2.3):
 (2.2.8) (2.2.8)
 (2.2.9) (2.2.9)
Они будут рассматриваются как управляющие воздействия.
Таким образом ставиться задача поиска таких  , ,  , ,  , ,  , которые сведут R,V,w к R*,V*,w*. , которые сведут R,V,w к R*,V*,w*.
Будем изучать движение твердого тела в декартовом пространстве относительно некоторого отрезка гладкой кривой  (рис. 2.2), заданной уравнениями согласования (рис. 2.2), заданной уравнениями согласования
 (2.2.10) (2.2.10)
полагая, что на данном отрезке длина пути определяется как
 (2.2.11) (2.2.11)
Выберем функции  так, что на кривой так, что на кривой  матрица Якоби матрица Якоби
 (2.2.12) (2.2.12)
ортогональна. Матрица  соответствует базису кривой (рис. 2.2), называемому базисом Френе, и подчиняется следующему уравнению [5]: соответствует базису кривой (рис. 2.2), называемому базисом Френе, и подчиняется следующему уравнению [5]:
 (2.2.13) (2.2.13)
где  - кососимметричная матрица вида - кососимметричная матрица вида
 , ,
 - кривизна кривой, - кривизна кривой,  - кручение. - кручение.
По аналогии, введем гладкую кривую вращения твердого тела  , заданную уравнениями согласования , заданную уравнениями согласования
 (2.2.14) (2.2.14)
полагая, что на данном отрезке длина пути определяется как
 (2.2.15) (2.2.15)
Выберем функции  так, что на кривой так, что на кривой  матрица Якоби матрица Якоби
 (2.2.16) (2.2.16)
ортогональна. Матрица  подчиняется следующему уравнению [5]: подчиняется следующему уравнению [5]:
 (2.2.17) (2.2.17)
где  - кососимметричная матрица вида - кососимметричная матрица вида
 , ,
 - кривизна кривой, - кривизна кривой,  - кручение. - кручение.
Таким образом, общая задача управления пространственным движением твердого тела становиться как задача поддержания условий согласования, представленных голономными соотношениями переменных системы, которые должны выполняться в ходе движения тела в декартовом пространстве. При этом уравнение (2.2.10) вводит необходимые связи декартовых координат R, а уравнение (2.2.15) – связи угловых координат  , соответствующие требуемой ориентации тела относительно кривой. Эти задачи дополнены описанием желаемого режима продольного движения тела , соответствующие требуемой ориентации тела относительно кривой. Эти задачи дополнены описанием желаемого режима продольного движения тела  и вращения и вращения  . .
Рассмотрим поведение ЛА, описываемое уравнениями (2.2.1) и (2.2.2), относительно кривой (2.2.10). Уравнения кривой вводят связи между декартовыми координатами R, а ортогональные отклонения от S
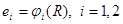 (2.2.18) (2.2.18)
характеризуют нарушения условий (2.2.10). Задача устранения отклонения  и стабилизации установившегося решения и стабилизации установившегося решения  за счет соответствующих воздействий F составляют основной предмет задачи траекторного управления ЛА. Дополнительные требования, касающиеся режима движения вдоль кривой (продольной динамики), устанавливаются в виде задачи поддержания продольной скорости за счет соответствующих воздействий F составляют основной предмет задачи траекторного управления ЛА. Дополнительные требования, касающиеся режима движения вдоль кривой (продольной динамики), устанавливаются в виде задачи поддержания продольной скорости  на постоянном уровне на постоянном уровне
 (2.2.19) (2.2.19)
Процедура синтеза управления траекторным движением ЛА заключается в выводе задачно-ориентированной модели движения ЛА, преобразование управляющих воздействий и синтез локальных регуляторов, соответствующих основной задаче управления.
Дифференцируя по времени уравнения (2.2.12) и (2.2.13) и принимая во внимание (2.2.1), выводим скоростные соотношения:
 (2.2.20) (2.2.20)
Продолжив дифференцирование и подставив уравнения (2.2.2), (2.2.13) и (2.2.20) получим:
 (2.2.21) (2.2.21)
Еще раз продифференцировав, получим:
 (2.2.22) (2.2.22)
Введем в рассмотрение преобразование входных воздействий
 , (2.2.23) , (2.2.23)
где  - продольное, а - продольное, а  - относительное управляющие воздействия. - относительное управляющие воздействия.
Запишем (2.2.22) в виде задачно-ориентированной модели пространственного движения
 (2.2.24) (2.2.24)
Приведем уравнение (2.2.24) к виду:
 (2.2.25) (2.2.25)
Локальные алгоритмы управления (регуляторы) выбирается как:
 (2.2.26) (2.2.26)
Исходя из условия сходимости были выбраны коэффициенты в уравнении (2.2.26):

Было проведено моделирование ЛА в среде Vissimна 3 траекториях:
1. движение по прямой со скоростью 30 м/с;
2. набор высоты с 1000м до 1200м за 30с на скорости 50 м/с;
3. мертвая петля радиусом 500м и начальной скоростью 50 м/с.
Моделирование проводилось при скорости ветра (1;1;5) м/с
2.2.2 Управление ориентацией ЛА
Аналогично предыдущему разделу рассмотрим поведение ЛА, описываемое уравнением (2.2.3), относительно кривой (2.2.15). Уравнения кривой вводят связи между координатами w, а ортогональные отклонения от 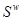
 (2.2.27) (2.2.27)
характеризуют нарушения условий (2.2.15). Задача устранения отклонения  и стабилизации установившегося решения и стабилизации установившегося решения  за счет соответствующих воздействий M составляют основной предмет задачи управления ориентаций ЛА. Дополнительные требования, касающиеся режима движения вдоль кривой (продольной динамики), устанавливаются в виде задачи поддержания продольной скорости за счет соответствующих воздействий M составляют основной предмет задачи управления ориентаций ЛА. Дополнительные требования, касающиеся режима движения вдоль кривой (продольной динамики), устанавливаются в виде задачи поддержания продольной скорости  на постоянном уровне на постоянном уровне
 (2.2.28) (2.2.28)
Процедура синтеза управления траекторным движением ЛА заключается в выводе задачно-ориентированной модели движения ЛА, преобразование управляющих воздействий и синтез локальных регуляторов, соответствующих основной задаче управления.
Дифференцируя по времени уравнения (2.2.16) и (2.2.17), выводим скоростные соотношения:
 (2.2.29) (2.2.29)
Продолжив дифференцирование и подставив уравнения (2.2.3), (2.2.5), (2.2.7), (2.2.9) и (2.2.29), получим:
 (2.2.30) (2.2.30)
Еще раз продифференцировав, получим:
 (2.2.31) (2.2.31)
Введем в рассмотрение преобразование входных воздействий
 , (2.2.32) , (2.2.32)
где  - продольное, а - продольное, а  - относительное управляющие воздействия. - относительное управляющие воздействия.
Запишем (2.2.31) в виде задачно-ориентированной модели пространственного движения
 (2.2.33) (2.2.33)
Приведем уравнение (2.2.33) к виду:
 (2.2.34) (2.2.34)
Локальные алгоритмы управления (регуляторы) выбирается как:
 (2.2.35) (2.2.35)
Исходя из условия сходимости были выбраны коэффициенты в уравнении (2.2.35):

Было проведено моделирование ЛА в среде Vissimна 2 траекториях:
1. движение по прямой со скоростью 30 м/с;
2. набор высоты с 1000м до 1200м за 30с на скорости 50 м/с;
Моделирование проводилось при скорости ветра (1;1;5) м/с
Предполагается, что в пилотажный комплекс из более высокого уровня иерархии управления поступает командный сигнал. Например командным сигналом могут быть силы действующие на ЛА и угловые моменты его движения
Задачей управления на пилотажном уровне является формирование управляющих сигналов для рулевых органов ЛА, обеспечивающих достижение и выдерживание заданных сил и моментов. Критерии оптимизации управляющих сигналов пилотажного комплекса формируются в отклонениях действительного состояния ЛА от заданного (эталонного). Пилотажный комплекс, построенный по изложенным выше принципам, обеспечивает оптимальное, в смысле этого критерия, слежение управляемым ЛА за заданным состоянием или состоянием эталонной модели.
Рассмотрим задачу, в которой используемые рулевые органы характеризуются непрерывным во времени изменением положения. В число таких рулевых органов, как правило, входит большинство аэродинамических рулей.
С траекторного уровня приходят 6 переменных (3 силы и 3 угловых момента), которые необходимо отследить с помощью 5 управляющих воздействий  , ,  , ,  , ,  , ,  . Чтобы получить 6 управляющее воздействие, будем управлять левым и правым элероном независимо, т.е.: . Чтобы получить 6 управляющее воздействие, будем управлять левым и правым элероном независимо, т.е.:
 . (2.3.1) . (2.3.1)
Запишем уравнение (1.2.2) в проекции на ось ОХ в виде
 . (2.3.2) . (2.3.2)
Для построения алгоритма управления необходимо найти оценки функций  и и  . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции  найдем значения найдем значения  и и  . .
 (2.3.3) (2.3.3)

 (2.3.4) (2.3.4)
 (2.3.5) (2.3.5)
Для построения контроллера используем алгоритм пропорционального управления.
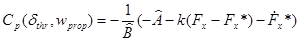 (2.3.6) (2.3.6)
 (2.3.7) (2.3.7)
Исходя из условия сходимости был выбран коэффициент в уравнении (2.3.7):

Было проведено ЛА в среде Vissim на 3 траекториях:
1. движение по прямой со скоростью 30 м/с;
2. набор высоты с 1000м до 1200м за 30с на скорости 50 м/с;
3. мертвая петля радиусом 500м и начальной скоростью 50 м/с.
Моделирование проводилось при скорости ветра (1;1;5) м/с
Запишем уравнение (1.2.2) в проекции на ось ОY в виде
 . (2.3.8) . (2.3.8)
Для построения алгоритма управления необходимо найти оценки функций  и и  . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции  найдем значения найдем значения  и и  . .
 (2.3.9) (2.3.9)


(2.3.10)
 (2.3.11) (2.3.11)
Для построения контроллера используем алгоритм пропорционального управления.
 (2.3.12) (2.3.12)
Исходя из условия сходимости был выбран коэффициент в уравнении (2.3.12):

Было проведено ЛА в среде Vissim на 3 траекториях:
1. движение по прямой со скоростью 30 м/с;
2. набор высоты с 1000м до 1200м за 30с на скорости 50 м/с;
3. мертвая петля радиусом 500м и начальной скоростью 50 м/с.
Запишем уравнение (1.2.2) в проекции на ось ОZ в виде
 . (2.3.13) . (2.3.13)
Для построения алгоритма управления необходимо найти оценки функций  и и  . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции  найдем значения найдем значения  и и  . .
 (2.3.14) (2.3.14)

 (2.3.15) (2.3.15)
 (2.3.16) (2.3.16)
Для построения контроллера используем алгоритм пропорционального управления.
 (2.3.17) (2.3.17)
Исходя из условия сходимости был выбран коэффициент в уравнении (2.3.17):

Было проведено ЛА в среде Vissim на 3 траекториях:
1. движение по прямой со скоростью 30 м/с;
2. набор высоты с 1000м до 1200м за 30с на скорости 50 м/с;
3. мертвая петля радиусом 500м и начальной скоростью 50 м/с.
2.3.4 Настройка регулятора  . .
Запишем уравнение (1.2.20) в проекции на ось ОX в виде
 . (2.3.18) . (2.3.18)
Для построения алгоритма управления необходимо найти оценки функций  и и  . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции  найдем значения найдем значения  и и  . .
 (2.3.19) (2.3.19)
 (2.3.20) (2.3.20)
 (2.3.21) (2.3.21)
 (2.3.22) (2.3.22)
Для построения контроллера используем алгоритм пропорционального управления.
 (2.3.23) (2.3.23)
Исходя из условия сходимости был выбран коэффициент в уравнении (2.3.23):

Было проведено ЛА в среде Vissim на 3 траекториях:
1. движение по прямой со скоростью 30 м/с;
2. набор высоты с 1000м до 1200м за 30с на скорости 50 м/с;
3. мертвая петля радиусом 500м и начальной скоростью 50 м/с.
Запишем уравнение (1.2.20) в проекции на ось ОY в виде
 . (2.3.24) . (2.3.24)
Для построения алгоритма управления необходимо найти оценки функций  и и  . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции  найдем значения найдем значения  и и  . .
 (2.3.25) (2.3.25)
 (2.3.26) (2.3.26)
 (2.3.27) (2.3.27)
 (2.3.28) (2.3.28)
Для построения контроллера используем алгоритм пропорционального управления.
 (2.3.29) (2.3.29)
Исходя из условия сходимости был выбран коэффициент в уравнении (2.3.29):

Было проведено ЛА в среде Vissim на 3 траекториях:
1. движение по прямой со скоростью 30 м/с;
2. набор высоты с 1000м до 1200м за 30с на скорости 50 м/с;
3. мертвая петля радиусом 500м и начальной скоростью 50 м/с.
Запишем уравнение (1.2.20) в проекции на ось ОZ в виде
 . (2.3.30) . (2.3.30)
Для построения алгоритма управления необходимо найти оценки функций  и и  . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции . Так как модель беспилотного летательного аппарата нам полностью известна, то при дифференцировании функции  найдем значения найдем значения  и и  . .
 (2.3.31) (2.3.31)
 (2.3.32) (2.3.32)

(2.3.33)
 (2.3.34) (2.3.34)
Для построения контроллера используем алгоритм пропорционального управления.
 (2.3.35) (2.3.35)
Исходя из условия сходимости был выбран коэффициент в уравнении (2.3.35):

Было проведено ЛА в среде Vissim на 3 траекториях:
1. движение по прямой со скоростью 30 м/с;
2. набор высоты с 1000м до 1200м за 30с на скорости 50 м/с;
3. мертвая петля радиусом 500м и начальной скоростью 50 м/с.
В ходе проделанной работы были достигнуты следующие результаты:
· Синтезированы нелинейные законы согласованного управления летательным аппаратом для пилотажного и траекторного уровня;
· Проведенные имитационные испытания алгоритмов управления показали высокую надежность и точность регулирования.
Математическая модель является универсальной и может быть настроена на любой летательный аппарат путем выставки соответствующих коэффициентов и начальных условий. Разработанная математическая модель может рассматриваться как инструмент для исследования динамики жестких летательных аппаратов.
1. Буков В.Н. Адаптивные прогнозирующие системы управления полетом. –М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 232с.
2. Aerosim Blockset v. 1.1. User’s Guide., 2003. -192с.
3. Мирошник И. В., Никифоров В. О., Фрадков А.Л. Нелинейное и адаптивное управление сложными динамическими системами. – СПб.: Наука, 2000. – 549 с.
4. Дорф Р. Современные системы управления. Р.Дорф, Р.Бишоп. Пер. с англ. Б.И. Копылова. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.
5. Мищенко А.С., Фоменко А.Т. Курс дифференциальной геометрии и топологии. – М.: Изд-во Моск. ун-та, 1980 – 439 с.
6. Висленов Б.В., Кузьменко Д.В. Теория авиации. Москва – 1939.
| Описание параметра модели |
Величина / ед. измерения |
| Аэродинамические справочные параметры |
| Средняя аэродинамическая хорда крыла, ba |
0.189941, м |
| Размах крыла, l |
2.8956, м |
| Площадь крыла, S |
0.55, м2 |
| Точка приложения аэродинамической силы, rAC |
[0.1425; 0; 0], м |
| Аэродинамические коэффициенты |
| Коэффициент лобового сопротивления |
Минимальное лобовое сопротивление,  |
0.0434 |
Производная по управлению креном (элероны),  |
0.0302 |
Производная по управлению тангажем (руль высоты),  |
0.0135 |
Производная по управлению подъемом (закрылки),  |
0.1467 |
Производная по управлению рысканьем (руль направления),  |
0.0303 |
Производная по числу Маха,  |
0 |
| Коэффициент Освальда, e |
0.75 |
| Коэффициент подъема |
Коэффициент подъема при нулевом угле тангажа,  |
-0.23 |
Производная первого порядка по углу атаки,  |
-5.6106 |
Производная по управлению подъемом (закрылки),  |
-0.74 |
Производная по управлению тангажем (руль высоты),  |
-0.13 |
Производная второго порядка по углу атаки,  |
-1.9724 |
Производная по угловой скорости тангажа,  |
-7.9543 |
Производная по числу Маха, |
0 |
| Коэффициент боковой силы |
Производная по углу скольжения,  |
-0.83 |
Производная по управлению креном (элероны),  |
-0.075 |
Производная по управлению рысканьем (руль направления),  |
0.1914 |
Производная по угловой скорости крена,  |
0 |
Производная по угловой скорости рысканья,  |
0 |
Производная по числу Маха, |
0 |
| Коэффициент момента крена |
Производная первого порядка по углу скольжения,  |
-0.13 |
Производная по управлению креном (элероны),  |
-0.1695 |
Производная по управлению рысканьем (руль направления),  |
0.0024 |
Производная по угловой скорости крена,  |
-0.5051 |
Производная по угловой скорости рысканья,  |
0.2519 |
Производная по числу Маха, |
0 |
| Коэффициент момента рысканья |
Производная первого порядка по углу скольжения,  |
-0.0726 |
Производная по управлению креном (элероны),  |
-0.0108 |
Производная по управлению рысканьем (руль направления),  |
0.0693 |
Производная по угловой скорости крена,  |
0.069 |
Производная по угловой скорости рысканья,  |
0.0946 |
Производная по числу Маха, |
0 |
| Коэффициент момента тангажа |
Коэффициент подъема при нулевом угле тангажа,  |
0.135 |
Производная первого порядка по углу атаки,  |
-2.7397 |
Производная по управлению подъемом (закрылки),  |
0.0467 |
Производная по управлению тангажем (руль высоты),  |
-0.9918 |
Производная второго порядка по углу атаки,  |
-10.3796 |
Производная по угловой скорости тангажа,  |
-38.2067 |
Производная по числу Маха, |
0 |
| Инерция |
| Масса самолета при пустых баках, mempty |
8.5, кг |
| Масса самолета при полных баках, mgross |
13.5, кг |
| Положение центра масс при пустых баках, CGempy |
[0.156; -0.079; 0], м |
| Положение центра масс при полных баках, CGgross |
[0.159; -0.090; 0], м |
| Моменты инерции при пустых баках, Jempy |
[0.7795; 1.752; 1.122; 0.1211], кг·м2 |
| Моменты инерции при полных баках, Jgross |
[0.8244; 1.759; 1.135; 0.1204],
кг·м2
|
| Двигатель |
| Точка приложения силы тяги двигателя, rPC |
[0; 0; 0], м |
| Радиус пропеллера, Rprop |
0.254, м |
| Момент инерции пропеллера, Jprop |
0.002, кг·м2 |
| Момент инерции вала двигателя, Jeng |
0.001, кг·м2 |
| Зажигание, ign |
1 |
| Прочие параметры |
Число пи,  |
3.14 |
Радиус экватора,  |
6378137, м |
Первая эксцентричность,  |
0.081819191 |
Ускорение свободного падения на экваторе,  |
9.780327 м/c2 |
Гравитационная постоянная,  |
0.00193185 |
Давление на уровне моря,  |
102300, Па |
Температура на уровне моря,  |
291.15, К |
| Начальные значения |
Начальное положение в пространстве по OXg,  |
0, м |
Начальное положение в пространстве по OYg,  |
1000, м |
Начальное положение в пространстве по OZg,  |
0, м |
Начальная скорость по OX,  |
25, м/c |
Начальная скорость по OY,  |
0, м/c |
Начальная скорость по OZ,  |
0, м/c |
| Начальная загрузка топлива, fl |
2, кг |
1) Давление во всасывающем коллекторе двигателя
pd = [60 70 80 90 92 94 96 98 100]T, кПа
2) Расход топлива на уровне моря
Расход топлива на уровне моря Qff ( , pd), грамм/час: , pd), грамм/час:
 |
60 |
70 |
80 |
90 |
92 |
94 |
96 |
98 |
100 |
| 1500 |
31 |
32 |
46 |
53 |
55 |
57 |
65 |
73 |
82 |
| 2100 |
40 |
44 |
54 |
69 |
74 |
80 |
92 |
103 |
111 |
| 2800 |
50 |
63 |
69 |
92 |
95 |
98 |
126 |
145 |
153 |
| 3500 |
66 |
75 |
87 |
110 |
117 |
127 |
150 |
175 |
190 |
| 4500 |
89 |
98 |
115 |
143 |
148 |
162 |
191 |
232 |
246 |
| 5100 |
93 |
102 |
130 |
159 |
167 |
182 |
208 |
260 |
310 |
| 5500 |
100 |
118 |
137 |
169 |
178 |
190 |
232 |
287 |
313 |
| 6000 |
104 |
126 |
151 |
184 |
191 |
206 |
253 |
326 |
337 |
| 7000 |
123 |
144 |
174 |
210 |
217 |
244 |
321 |
400 |
408 |
3) Мощность двигателя на уровне моря
Мощность двигателя на уровне моря power( , pd), Вт , pd), Вт
 |
60 |
70 |
80 |
90 |
92 |
94 |
96 |
98 |
100 |
| 1500 |
18.85 |
47.12 |
65.97 |
67.54 |
69.12 |
67.54 |
67.54 |
69.12 |
86.39 |
| 2100 |
59.38 |
98.96 |
127.55 |
149.54 |
151.74 |
160.54 |
178.13 |
200.12 |
224.31 |
| 2800 |
93.83 |
149.54 |
187.66 |
237.5 |
249.23 |
255.1 |
307.88 |
366.52 |
398.77 |
| 3500 |
109.96 |
161.27 |
245.57 |
307.88 |
326.2 |
351.86 |
421.5 |
491.14 |
531.45 |
| 4500 |
164.93 |
245.04 |
339.29 |
438.25 |
447.68 |
494.8 |
565.49 |
673.87 |
772.83 |
| 5100 |
181.58 |
245.67 |
389.87 |
496.69 |
528.73 |
571.46 |
662.25 |
822.47 |
993.37 |
| 5500 |
184.31 |
293.74 |
403.17 |
535.64 |
570.2 |
622.04 |
748.75 |
956.09 |
1059.76 |
| 6000 |
163.36 |
276.46 |
420.97 |
565.49 |
609.47 |
691.15 |
860.8 |
1130.97 |
1193.81 |
| 7000 |
124.62 |
249.23 |
417.83 |
586.43 |
645.07 |
762.36 |
996.93 |
1246.17 |
1429.42 |
4) Коэффициент, характеризующий режим работы винта
Коэффициент, характеризующий режим работы винта  : :
 = [-1 0 0.1 0.2 0.3 0.35 0.4 0.45 0.5 0.6 0.7 0.8 0.9 1 1.2 2]T = [-1 0 0.1 0.2 0.3 0.35 0.4 0.45 0.5 0.6 0.7 0.8 0.9 1 1.2 2]T
5) Коэффициент тяги
Коэффициент тяги CT( ) )
 |
-1 |
0 |
0.1 |
0.2 |
0.3 |
0.35 |
0.4 |
0.45 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
1.2 |
2 |
| CT, 10-2 |
4.92 |
2.86 |
2.66 |
2.32 |
3.43 |
3.4 |
3.72 |
3.14 |
2.54 |
1.17 |
-0.5 |
-1.6 |
-2 |
-3 |
-4 |
-11.2 |
6) Коэффициент мощности
Коэффициент мощности CP( ) )
 |
-1 |
0 |
0.1 |
0.2 |
0.3 |
0.35 |
0.4 |
0.45 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
1.2 |
2 |
| CT, 10-2 |
1.99 |
2.07 |
1.91 |
1.69 |
2.17 |
2.23 |
2.54 |
2.35 |
2.12 |
1.46 |
0.4 |
-0.5 |
-1 |
-1.8 |
2.7 |
-7.4 |
|