Курсовая работа
Тема: Разработка приложений на С,
Pascal
,
Delphi
Оглавление
Оглавление
Введение
Глава 1. Нахождение значения интеграла с заданной точностью
1.1Способы нахождения значения определённого интеграла
1.1.1Методы прямоугольников
1.1.2Метод трапеций
1.2Программные средства языка C
1.2.1Основы объектно-ориентированного программирования
1.2.2Функции в C++
1.3Программные средства языка Pascal (версия 7.0)
1.3.1 Объекты в Pascal
1.3.2 Оператор выбора в Pascal
1.4Алгоритм программы вычисления определённого интеграла
1.5Тестирование программы
Глава 2. Обработка результатов измерений
2.1 Теоретическая часть. Метод наименьших квадратов
2.2 Алгоритм программы обработки данных
2.3Тестирование программы
Листинги программ
Вычисление интегралов С
Вычисление интегралов Pascal
Обработка измерений
Выводы
Список литературы
Приложение
Введение
Целью написания курсовой работы является обобщение практических знаний, полученных по курсу «Программирование на языках высокого уровня». Она содержит программные алгоритмы, которые служат для решения практических задач в области высшей математики и химии, написанные на языках, освоенных мной за время чтения курса: С++, BorlandPascal 7.0, Delphi 7.0.
В данной записке я поясняю теоретические основы использованных в курсовой работе языков программирования и некоторые теоретические основы математического анализа и химии, которые позволили мне разработать системные программы.
Глава 1. Нахождение значения интеграла с заданной точностью
Численные методы основаны на замене интеграла
I=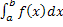
конечной суммой
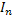 = =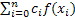
где 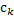 – числовые коэффициенты, – числовые коэффициенты, 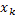 – точки отрезка [a; b], k=0, 1, …, n. Приближённое равенство – точки отрезка [a; b], k=0, 1, …, n. Приближённое равенство 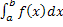 ≈ ≈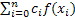 , «называется квадратурной формулой, коэффициенты , «называется квадратурной формулой, коэффициенты 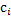 - коэффициентами квадратурной формулы, - коэффициентами квадратурной формулы, 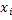 - узлами квадратурной формулы» [5]. Отклонение от точно значения зависит от расположения узлов формулы, выбора коэффициентов и характера функции. - узлами квадратурной формулы» [5]. Отклонение от точно значения зависит от расположения узлов формулы, выбора коэффициентов и характера функции.
1.1.1 Методы прямоугольников
Методы прямоугольников основаны на представлении фигуры под графиком функции в виде ступенчатой фигуры, состоящей из прямоугольников. Отрезок интегрирования делится точками 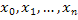 на отрезки длиной на отрезки длиной 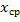 = =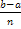 . Затем получают значения функции в узлах формулы: . Затем получают значения функции в узлах формулы: 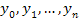 и считают значение сумм и считают значение сумм 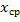 ( (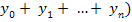 . .
Реклама

Отличие формул нахождения значения интеграла по методам левых, правых и средних прямоугольников состоит в том, в какой части отрезка 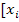 ; ; 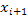 ] считается значение ] считается значение 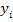 : если в точке : если в точке 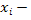 метод левых прямоугольников, если в метод левых прямоугольников, если в 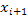 – метод правых прямоугольников, если в середине отрезка – метод средних прямоугольников. – метод правых прямоугольников, если в середине отрезка – метод средних прямоугольников.
1.1.2 Метод трапеций
Данный метод состоит в аппроксимации графика функции прямой, проходящей через конечные значения. Площадь трапеции на отрезке 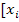 ; ; 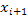 ] вычисляется по формуле ] вычисляется по формуле
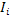 = =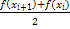 ( (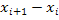 ) )
Тогда значение интеграла на этом отрезке вычисляется по формуле
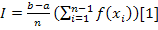
1.2.1 Основы объектно-ориентированного программирования
В языке С++ класс – это тип. «Класс – это собрание связанной информации, которая включает в себя данные и функции (программы для работы с данными). Эти функции в калассах называются методами. Класс – это дальнейшее развитие структур: в них так же объединяются данные разных типов. Это такой же шаблон, под который (как и под структуру) память выделяется только тогда, когда мы создаём «переменную типа этого шаблона». Класс – это конструкция, параметрически определяющая некоторую категорию объектов»[3].
Основные принципы построения классов – инкапсуляция, наследование, полиморфизм.
Инкапсуляция – принцип объединения в едином объекте данных и программ, обрабатывающих их. При этом Данные называются данными-членами, а построенные в виде функций программы, обрабатывающие их, - членами-функциями или методами.
Наследование предполагает, что все характеристики класса-родителя присваиваются классу-потомку. Некоторые из них могут переопределяться. После этого потомку добавляются новые характеристики.
Полиморфизм понимает под собой то, что «родственные объекты (происходящие от родителя) могут вести себя по-разному в зависимости от ситуации, возникающей при выполнении программы. Полиморфизм становится возможным потому, что функциям класса-родителя позволено выполняться в классе-потомке.»[3]
Структура объявления класса:
Class <имя класса>
{Private: /Имя секции. Данные и методы, помещённые в эту секцию, будут доступны только методам этого класса. Доступ к ним производным классам запрещён*/
<Приватные данные>
<Приватные конструкторы>
<Приватные методы>
Protected: /Имя секции. Данные и методы, помещённые в эту секцию, будут доступны методам этого класса и производным от него*/
<Защищённые данные>
< Защищённые конструкторы>
< Защищённые методы>
Реклама

Public: /Имя секции. Данные и методы, помещённые в эту секцию, будут доступны методам всех классов*/
< Общедоступные данные>
< Общедоступные конструкторы>
< Общедоступные методы>};
1.2.2 Функции в C++
Как было написано выше, методы классов представляют собой функции. Рассмотрим объявление функций в C++.
Функция – независимое множество операторов для выполнения некоторой задачи. Структура функций в С/С++:
Заголовок_функции
{Тело_функции}
В заголовке функции указываются описатель типа, имя, список параметров. Описатель типа определяет тип возвращаемого значения в вызываемую функцию. Если функция не возвращает никакого значения, то используется производный тип void. По умолчанию применяется тип int.
«Описатель типа в заголовке должен соответствовать описателю типа, используемому при объявлении данной функции.
Имя представляет собой любой идентификатор языка Си. После имени обязательны круглые скобки, независимо от того, имеет ли функция параметры.»[2]
Список параметров – это список имён переменных, которым будут ставиться в соответствие значения аргументов при обращении к функции.
Пример функции:
float spf1(float x)
{return x*x;}
Обращение к функции происходит следующим образом:
s=s+spf1(x)*h;
В данном разделе моей пояснительно записки использованы далеко не все программные средства С и С++, а только самые новые и наиболее сложные на мой взгляд.
1.3.1 Объекты в Pascal
Принципы использования и построения объектов ОПП схожи у разных языков. В Pascal, как и в С. Это наследование, инкапсуляция и полиморфизм. Поэтому я опишу только структуру объекта, который является аналогом класса в С.
Для описания объекта служит зарезервированное слово object. Описание объектов находится в разделе описания типов.
type
LevPr = object
Private
{экземпляры скрыты от пользователя}
Public
{экземпляры доступны пользователю}
end;
Как можно заметить, использование объектов в Pascal очень похоже на использование классов в С.
1.3.2 Оператор выбора в
Pascal
Если предстоит выбор из нескольких (трёх и более случаев) удобно использовать не операцию if, а оператор выбора case. Операторимеетвид
case expression of
values_l: statement_l;
values_2: statement_2;
...
values_n: statement_n;
else
statement;
end;
Рассмотрим элементы этой конструкции. Во-первых, это три зарезервированных слова: case, of и end. Между case и of находится выражение expression, принимающее значение, которое, возможно, имеется в одном из списков значений, находящихся слева от двоеточий. Данное выражение называется селектором оператора case. Каждый оператор, идущий за двоеточием, отделяется от следующего списка значений точкой с запятой. Ветвь else, отвечающая всем не перечисленным значениям выражения expression, необязательна. При выполнении данного оператора вначале вычисляется значение селектора. Затем выбирается тот список значений, которому принадлежит полученное значение, и выполняется соответствующий оператор.
В списках значений оператора case допустимыми являются типы переменных, называемые скалярными, включая целые и исключая вещественные типы. Любое заданное значение селектора может входить в список значений неоднократно, но выполняться будет лишь первая подходящая ветвь. Если значение селектора отсутствует в списках значений, ни одна из альтернатив выполняться не будет. В этом случае выполняется ветвь else оператора case или (если эта ветвь отсутствует) следующий за case оператор.[4]
1.4 Алгоритм программы вычисления определённого интеграла
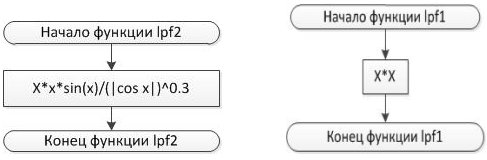
Блок-схема 1 Функция lpf1 Блок-схема 2 Функция lpf2
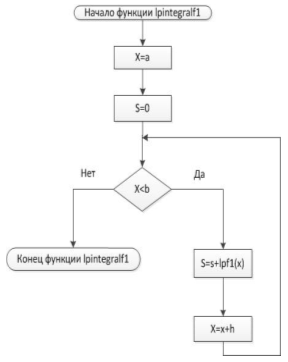
Блок-схема 4Функция lpintegra1
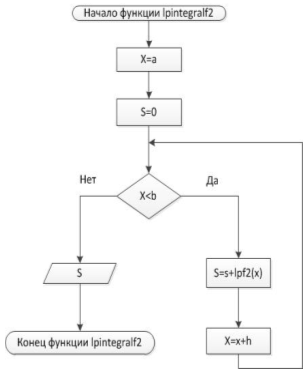
Блок-схема 5Функция lpintegralf2
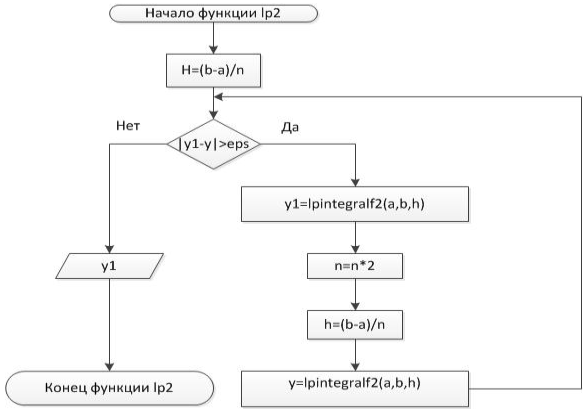
Блок-схема 6. Функцияlp2
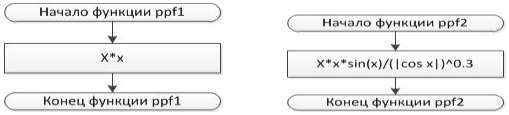
Блок-схема 8 Функция ppf1 Блок-схема 7 Функция ppf2
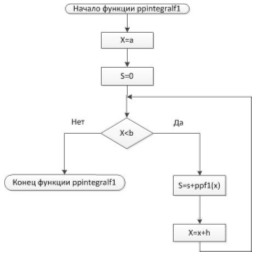
Блок-схема 6Функция ppintegralf1
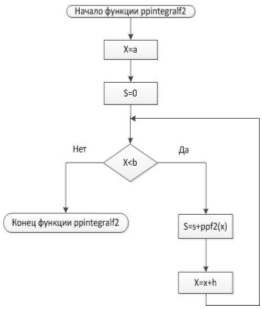
Блок-схема 10 Функция ppintegralf2
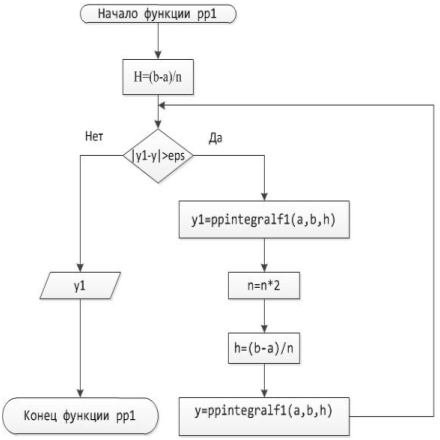
Блок-схема 10 Функция pp1
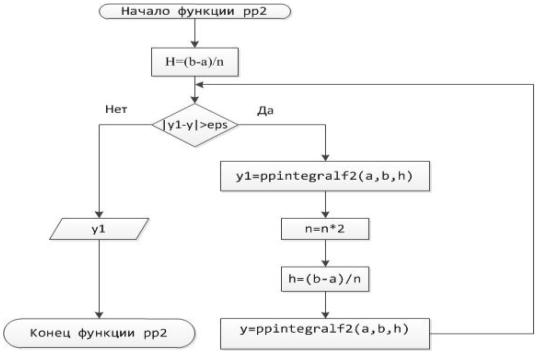
Блок-схема 9Функция pp2

Блок-схема 11 Функция spf1 Блок-схема 13 Функция spf2
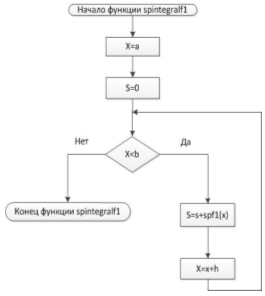
Блок-схема 14Функция spintegralf1
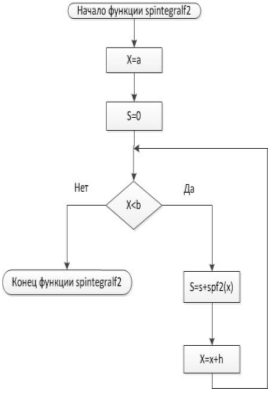
Блок-схема 12Функция spintegralf2
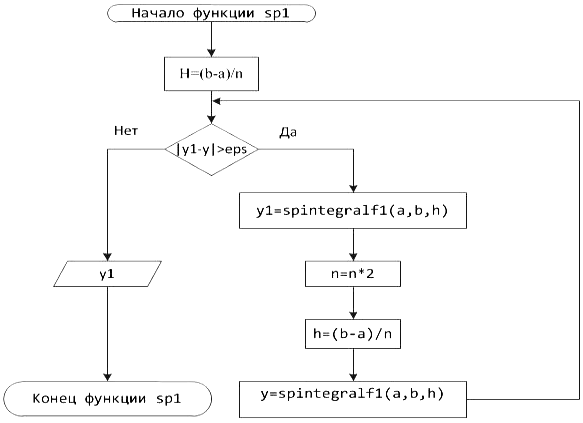
Блок-схема 15 Функция sp1
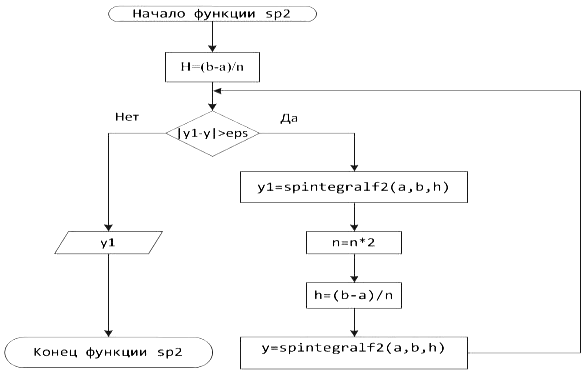
Блок-схема 16Функция sp2
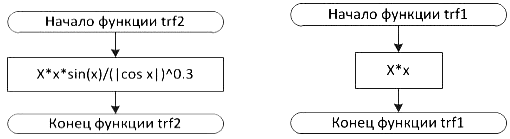
Блок-схема 20 Функция trf1Блок-схема 17 Функция trf2
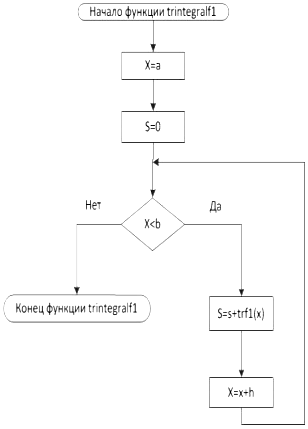
Блок-схема 18 Функция trintegralf1
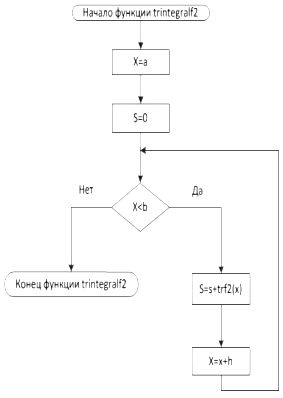
Блок-схема 19 Функция trintegralf2
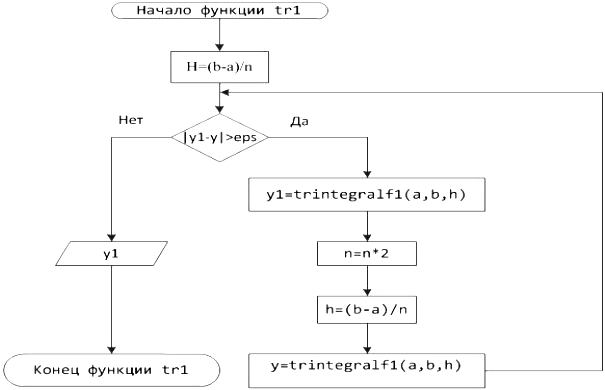
Блок-схема 22Функция tr1
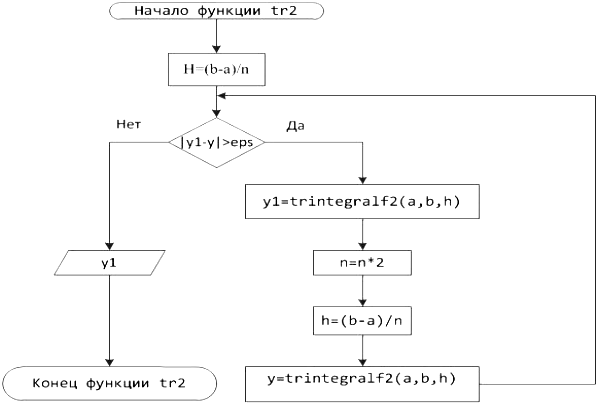
Блок-схема 21 Функция tr2
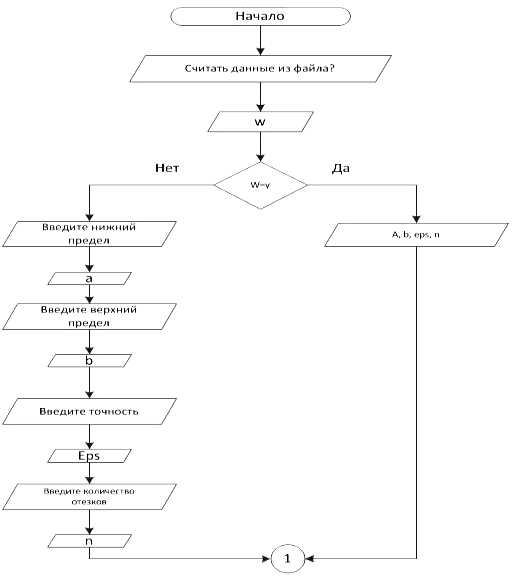
Блок-схема 23 Главная функция
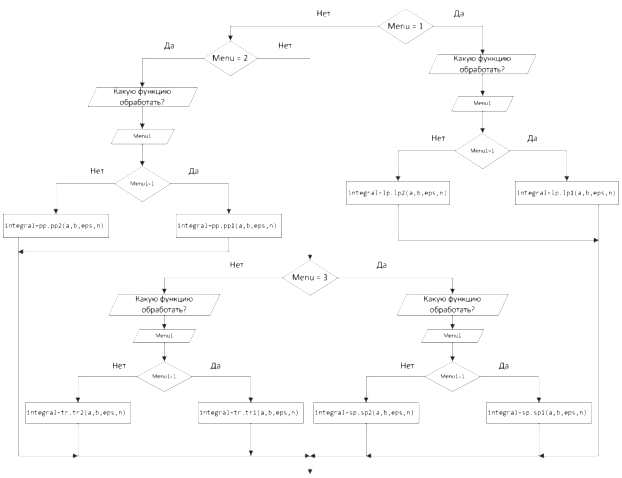
Блок-схема 24 Главная функция
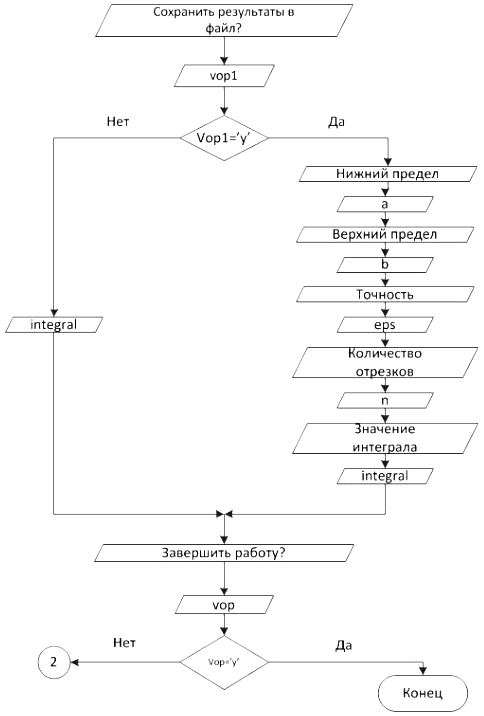
Блок-схема 25 Главная функция
Для тестирования проведём интегрирование обеих функций всеми четырьмя методами и рассмотри интерфейс программы при интегрировании одной из функций одним из 4 методов.
При запуске программа задаёт вопрос пользователю, откуда взять обрабатываемые данные:
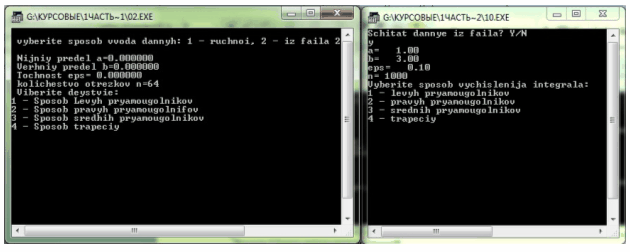
Рисунок 1 Запрос источника данных
Когда пользователь выберет необходимый источник, ему будет предложено выбрать способ интегрирования:
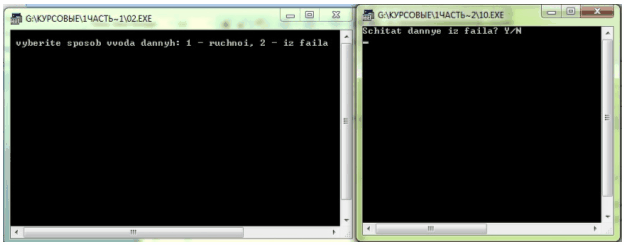
Рисунок 2 Запрос метода интегрирования
Когда выбран метод вычисления интеграла, выдаётся запрос о функции, которую следует проинтегрировать:
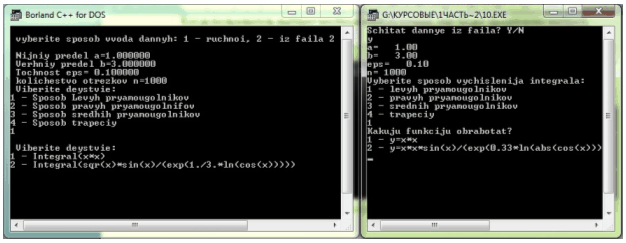
Рисунок 3 Запрос интегрируемой функции
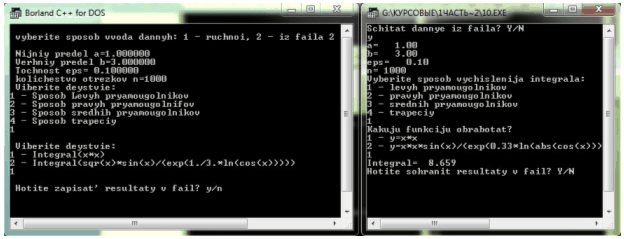
Рисунок 4 Запрос на сохранение результатов в файл
После этого пользователю будет предложено сохранить результаты в файл. В самом конце работы программы будет задан вопрос, продолжить ли работу. Если пользователь согласится, то программа вернётся к началу – вопросу об источнике данных, если нет, то завершит свою работу.
Глава 2. Обработка результатов измерений
2.1 Теоретическая часть. Метод наименьших квадратов
Рассмотрим случай линейной функции одного аргумента. Пусть из опыта получены точки:
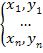 (1) (1)
Требуется найти уравнение прямой y=ax+b (2), наилучшим образом согласующейся с опытными точками. Пусть мы нашли такую прямую. Обозначим через 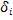 расстояние опытной точки от этой прямой (измеренное параллельно оси y). Из уравнения (2) следует, что расстояние опытной точки от этой прямой (измеренное параллельно оси y). Из уравнения (2) следует, что 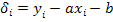 (3) Чем меньше числа (3) Чем меньше числа 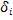 , тем лучше подобрана прямая. Характеристикой точности подбора может служить сумма квадратов этих расстояний , тем лучше подобрана прямая. Характеристикой точности подбора может служить сумма квадратов этих расстояний 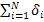 .(4). Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов S была минимальной. Из уравнений (3) и (4) получаем: S= .(4). Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов S была минимальной. Из уравнений (3) и (4) получаем: S=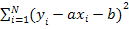 (5) (5)
Условия минимума:
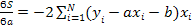 =0 (6) =0 (6)
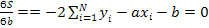 (7) (7)
Уравнения (6) и (7) можно записать в виде (8) и (9):
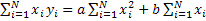 (8) (8)
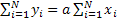 +n +n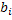 (9) (9)
Из уравнений (8) и (9) легко найти a и b по опытным значениям 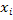 и и 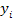 . Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями. . Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями.
Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки (1) и уравнение (2), можно записать систему уравнений для a и b:
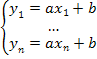 (10) (10)
Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на 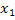 , … , , … ,  ) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8). Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9). Решая его, получим коэффициенты искомой прямой a, b. ) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8). Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9). Решая его, получим коэффициенты искомой прямой a, b.
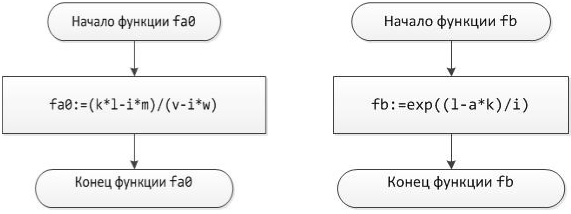
Блок-схема 28 Функция fa0 Блок-схема 29 Функция fb
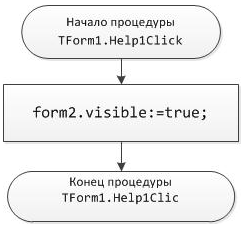
Блок-схема 31 Процедура TForm1.Help1Click
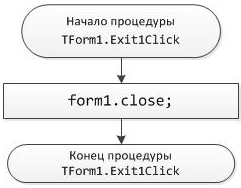
Блок-схема 32 Процедура TForm1.Exit1Click
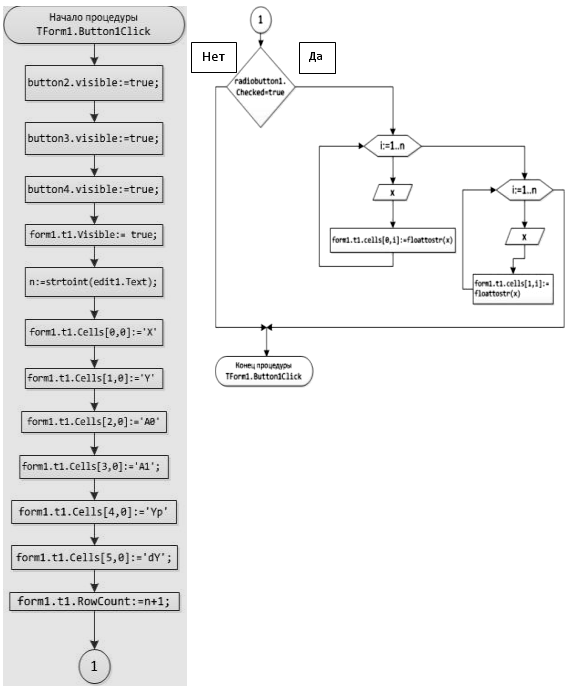
Блок-схема 33 Процедура TForm1.Button1Click
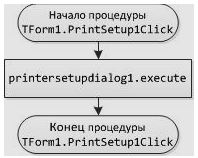
Блок-схема34 Процедура TForm1.Print1Click

Блок-схема 35 Процедура TForm1.PrintSetup1Click
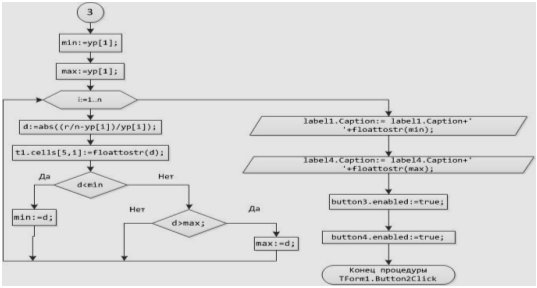
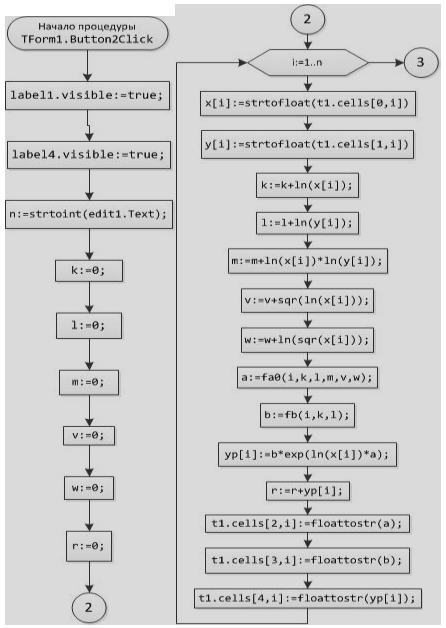
Блок-схема 36 Процедура TForm1.Button2Click
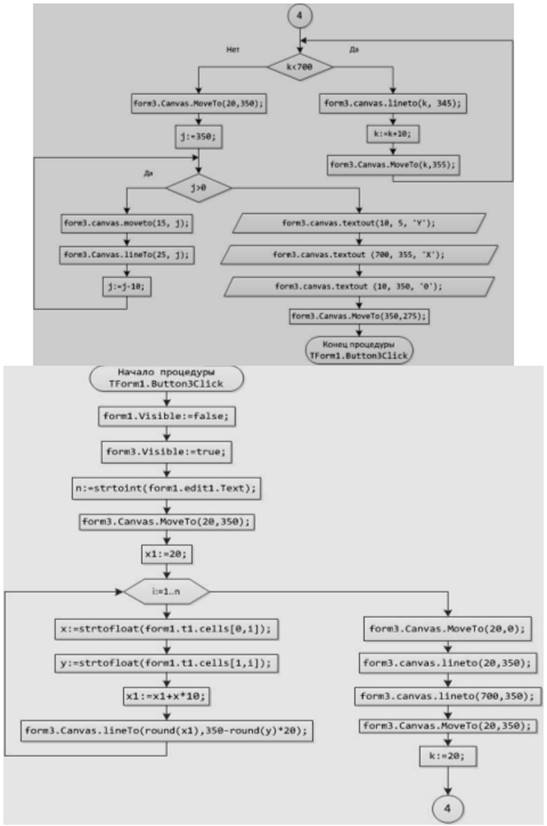
Блок-схема 37 Процедура TForm1.Button3Click
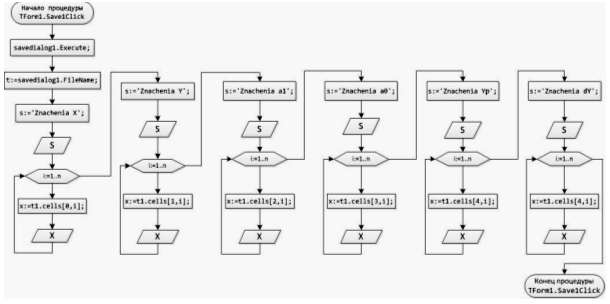
Блок-схема 38 Процедура TForm1.Save1Click
При запуске программы на экране появляется форма:
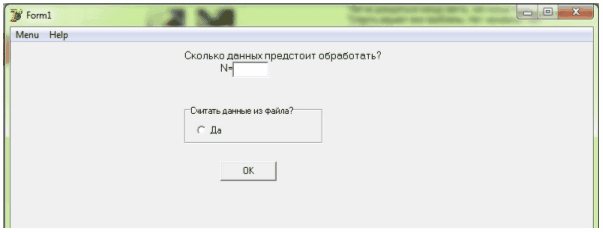
Рисунок 5 Форма запуска
При нажатии на кнопку Menu, пользователь получает доступ к главному меню программы:
Назначение его пунктов и общие принципы пользования программой описаны в окне, выпадающем при нажатии кнопки Help.
Рисунок 6 Главное меню
Рисунок 7 Окно Help
Если пользователь выберет количество результатов для обработки и способ их введения, то на экране появится таблица измерений. Для проведения расчетов следует нажать кнопку Рассчитать. Для получения наглядного представления данных следует нажать одну из кнопок y=f(x) или Yp=f1(x). Построенные графики были проверены в программе MicrosoftExcel 2007.
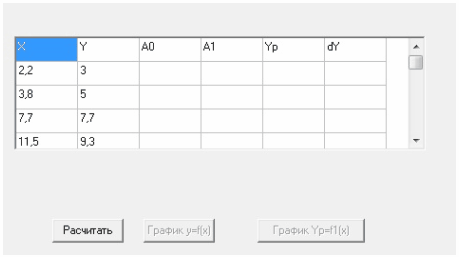
Рисунок 8 Таблица измерений
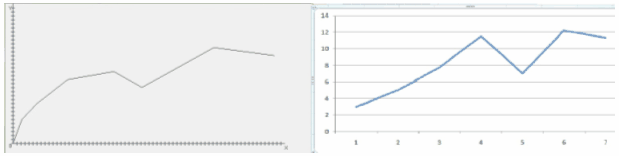
Рисунок 9 Сравнение графиков у=f(x)
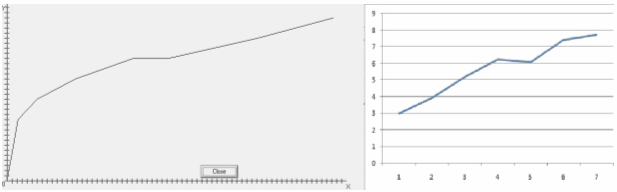
Рисунок 10 Сравнение графиков Yp=f1(x)
После завершения расчетов программа позволяет сохранить результаты в файл, используя соответствующую кнопку главного меню.
Листинги программ
(главная функция main)
void main ()
{/*opisanie peremennyh*/
float x,a,b,h,y,integral,eps;
int n;
char vop,vop1;
LevPr lp;
PravPr pp;
SrPr sp;
Trapeciy tr;
FILE *in;
FILE *out;
int i,j,menu,menu1,w;
vop='n';
in=fopen("in.txt","rt");
out=fopen("out.txt","w");
do
{clrscr();
/*zapros, schitat' li dannye iz faila*/
printf("\n vyberite sposob vvoda dannyh: 1 - ruchnoi, 2 - iz faila ");
scanf("%d", &w);
switch(w)
{case 1:
{/*vvod dannyh v ruchuju*/
printf("\n Vvedite nijniy predel a= ");
scanf("%f", &a);
printf("\n Vvedite verhniy predel b= ");
scanf("%f", &b);
printf("\n Vvedite tocnost ");
scanf("%f", &eps);
printf("\n Vvedite kolichestvo otrezkov n= ");
scanf("%d", &n);
break;}
case 2:
{/*schityvanie dannyh iz faila*/
fscanf(in, "%f",&a);
printf("\n Nijniy predel a=%f", a);
fscanf(in, "%f",&b);
printf("\n Verhniy predel b=%f", b);
fscanf(in, "%f",&eps);
printf("\n Tochnost eps= %f", eps);
fscanf(in, "%d",&n);
printf("\n kolichestvo otrezkov n=%d", n);
break;}
}
/*zapros u polzovatelia metoda vychislenija*/
printf("\n Viberite deystvie:\n1 - Sposob Levyh pryamougolnikov\n2 - Sposob pravyh pryamougolnifov\n3 - Sposob sredhih pryamougolnikov\n4 - Sposob trapeciy\n");
scanf("%d", &menu);
switch(menu)
{case 1:
{/*zapros, kakuju funkciju obrabotat'*/
printf("\n Viberite deystvie:\n1 - Integral(x*x)\n2 - Integral(sqr(x)*sin(x)/(exp(1./3.*ln(cos(x)))))\n");
scanf("%d", &menu1);
switch(menu1)
{case 1:
{integral=lp.lp1(a,b,eps,n);
break;}
case 2:
{integral=lp.lp2(a,b,eps,n);
break;}
}
break;}
case 2:
{
printf("\n Viberite deystvie:\n1 - Integral(x*x)\n2 - Integral(sqr(x)*sin(x)/(exp(1./3.*ln(cos(x)))))\n");
scanf("%d", &menu1);
switch(menu1)
{
case 1:
{
integral=pp.pp1(a,b,eps,n);
break;
}
case 2:
{
integral=pp.pp2(a,b,eps,n);
break;
}
}
break;}
case 3:
{printf("\n Viberite deystvie:\n1 - Integral(x*x)\n2 - Integral(sqr(x)*sin(x)/(exp(1./3.*ln(cos(x)))))\n");
scanf("%d", &menu1);
switch(menu1)
{
case 1:
{
integral=sp.sp1(a,b,eps,n);
break;
}
case 2:
{
integral=sp.sp2(a,b,eps,n);
break;
}
}
break;}
case 4:
{
printf("\n Viberite deystvie:\n1 - Integral(x*x)\n2 - Integral(sqr(x)*sin(x)/(exp(1./3.*ln(cos(x)))))\n");
scanf("%d", &menu1);
switch(menu1)
{
case 1:
{
integral=tr.tr1(a,b,eps,n);
break;
}
case 2:
{
integral=tr.tr2(a,b,eps,n);
break;
}
}
break;
}
}
/*zapros na sohranenie resultatov v fail*/
printf("\n Hotite zapisat' resultaty v fail? y/n");
vop1=getch();
if (vop1=='y')
{
/*zapis' v fail*/
fputs( "\n Nijniy predel ", out );
fprintf(out, " %f", a);
fputs( "\n Verhniy predel ", out );
fprintf(out, "%f", b);
fputs( "\n Tochnost' ", out );
fprintf(out, "%f", eps);
fputs( "\n kolichestvo otrezkov ", out );
fprintf(out, "%d", n);
fputs( "\n Integral", out );
fprintf(out, " %f", integral);
fclose(out);
fclose(in);
}
/*vyvod resultatov na ekran*/
printf("\n Znachenie integrala = %f", integral);
/*zapros polzovatelu, zavershit' li rabotu programmy*/
printf("\n Hotite zavershit' zadachy?");
vop=getch();
} while (vop!='y');
printf("vypolnila studentka 895 gruppy Araztaganova Alina");
}
(примерыописанияобъекта)
type LevPr = object {opredelenie klassa, kotoriy realizuet metod levyh pryamougolnikov}
Public
function f1(x:real):real;
function f2(x:real):real;
function integralf1(a:real; b: real; h:real):real;
function integralf2(a:real; b: real; h:real):real;
function levprf1(a:real; b:real; eps: real; n:integer):real;
function levprf2(a:real; b:real; eps: real; n:integer):real;
end;
type PravPr = object {opredelenie klassa, kotoriy realizuet metod pravyh pryamougolnikov}
Public
function f1(x:real):real;
function f2(x:real):real;
function integralf1(a:real; b: real; h:real):real;
function integralf2(a:real; b: real; h:real):real;
function Pravprf1(a:real; b:real; eps: real; n:integer):real;
function Pravprf2(a:real; b:real; eps: real; n:integer):real;
end;
type SRPr = object {opredelenie klassa, kotoriy realizuet metod srednih pryamougolnikov}
Public
function f1(x:real):real;
function f2(x:real):real;
function integralf1(a:real; b: real; h:real):real;
function integralf2(a:real; b: real; h:real):real;
function Srprf1(a:real; b:real; eps: real; n:integer):real;
function Srprf2(a:real; b:real; eps: real; n:integer):real;
end;
type Trap = object {opredelenie klassa, kotoriy realizuet metod trapeciy}
Public
function f1(x:real):real;
function f2(x:real):real;
function integralf1(a:real; b: real; h:real):real;
function integralf2(a:real; b: real; h:real):real;
function Trapf1(a:real; b:real; eps: real; n:integer):real;
function Trapf2(a:real; b:real; eps: real; n:integer):real;
end;
{opisaniya motodov klassov}
function LevPr.f1(x: real):real;
begin
f1:=sqr(x);
end;
function LevPr.f2(x: real):real;
begin
f2:=sqr(x)*sin(x)/(exp(0.3*ln(abs(cos(x)))));
end;
function LevPr.integralf1(a:real; b: real; h:real):real;
var s, x: real;
begin
x:=a;
s:=0;
while x<b do begin
s:=s+LevPr.f1(x)*h;
x:= x+h;
end;
integralf1:=s;
end;
function LevPr.integralf2(a:real; b: real; h:real):real;
var s, x: real;
begin
x:=a;
s:=0;
while x<b do begin
s:=s+LevPr.f2(x)*h;
x:= x+h;
end;
integralf2:=s;
end;
function LevPr.levprf1(a:real; b:real;eps: real; n:integer):real;
label l1;
var
i: integer;
x, y, h, y1:real;
begin
h:=(b-a)/n;
y1:=LevPr.integralf1(a, b, h);
l1: n:=n*2;
h:=(b-a)/n;
y:=LevPr.integralf1(a, b, h);
if (abs(y-y1)>eps) then begin y1:=y; goto l1; end;
levprf1:=y1;
end;
function LevPr.levprf2(a:real; b:real; eps: real; n:integer):real;
label l1;
var
i: integer;
x, y, h, y1:real;
begin
h:=(b-a)/n;
y1:=LevPr.integralf2(a, b, h);
l1: n:=n*2;
h:=(b-a)/n;
y:=LevPr.integralf2(a, b, h);
if (abs(y-y1)>eps) then begin y1:=y; goto l1; end;
levprf2:=y1;
end;
(процедура, подсчитывающая коэффициенты)
begin
label1.visible:=true;
label4.visible:=true;
n:=strtoint(edit1.Text);
k:=0; l:=0; m:=0;
v:=0; w:=0; r:=0;
for i:=1 to n do begin
x[i]:=strtofloat(t1.cells[0,i]);
y[i]:=strtofloat(t1.cells[1,i]);
k:=k+ln(x[i]);
l:=l+ln(y[i]);
m:=m+ln(x[i])*ln(y[i]);
v:=v+sqr(ln(x[i]));
w:=w+ln(sqr(x[i]));
a:=fa0(i,k,l,m,v,w);
b:=fb(i,k,l);
yp[i]:=b*exp(ln(x[i])*a);
r:=r+yp[i];
t1.cells[2,i]:=floattostr(a);
t1.cells[3,i]:=floattostr(b);
t1.cells[4,i]:=floattostr(yp[i]);
end;
min:=yp[1];
max:=yp[1];
for i:=1 to n do begin
d:=abs((r/n-yp[i])/yp[i]);
t1.cells[5,i]:=floattostr(d);
if d<min then min:=d;
if d>max then max:=d;
end;
label1.Caption:= label1.Caption+' '+floattostr(min);
label4.Caption:= label4.Caption+' '+floattostr(max);
button3.enabled:=true;
button4.enabled:=true;
end;
Выводы
Компьютеры стали неотъемлемой частью нашей жизни. Но без хороших программ компьютер – это просто груда железа. Поэтому так важно осваивать языки программирования, чтобы не оказаться за бортом жизни и цивилизации.
Данная курсовая работа является завершающим этапом работы по предмету «Программирование на языках высокого уровня». Она является прекрасной возможностью закрепить свои практические знания по предмету, а также получить новые, которые не входили в программу курса.
Данная работа состоит из двух частей. В первой было необходимо разработать приложения на языках Pascal и С++ для вычисления численного значения определённого интеграла с заданной степенью точности. Выполнение задачи получилось не сразу, но после некоторого времени, потраченного на работу с программными кодами и их исправление, программы стали работать.
Вторая часть требовала составить программу обработки полученных прямых измерений, основанную на методе наименьших квадратов. Следует отметить практическую пользу такой обработки. Она позволяет не только найти аппроксимированную прямую, наиболее близко подходящую к результатам, но и увидеть ее графическое исполнение.
Таким образом, после выполнения поставленных задач я завершаю свою работу.
1. Калитки Н.Н. Численные методы: Учеб. пособие для вузов. – М. : Наука., 1978 г. – 512 с.
2. Котлинская Г.П., Галиновский О.И. Программирование на языке Си : Справочное пособие. – Минск. : Высшая школа., 1991. – 156 с.
3. Пахомов Б.И. C/C++ и MSVisualC++ 2005 для начинающих: Пособие для начинающих. – СПб. : БХВ – Петербург, 2007. – 464 с.
4. Программирование Учебник Turbo Pascal [электронный ресурс] Оператор case...of...end <http://www.cyberguru.ru/programming/pascal/pascal-introduction-page8.html> 22.05.2010
5. Самарский А. А., Гулин А. В. Численные методы : Учеб. пособие для вузов. — М.: Наука. Гл. ред. физ-мат. лит., 1989. — 432 с.
Приложения
Иллюстрации методов интегрирования
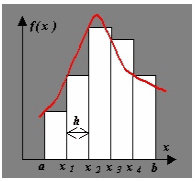
Рисунок 10 Метод левых прямоугольников
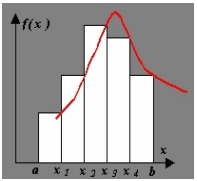
Рисунок 11 Метод правых прямоугольников

Рисунок 12 Метод средних Рисунок 13 Метод трапеций
прямоугольников
|