Косинов Николай Васильевич, кандидат технических наук
Проведенные исследования показали, что используемые в современной физике фундаментальные физические константы непосредственно происходят от перечисленных ниже констант вакуума [5...15].
hu
= 7,69558071(63)·10–37
Дж·с.
Gu
= 2,56696941(21)·10–45
Н·с2
.
Ru
= 29,9792458 Ом.
tu
= 0,939963701(11)·10–23
с.
lu
= 2,817940285(31)·10–15
м.
Установлено, что современные фундаментальные физические постоянные имеют вторичный статус по отношению к найденным константам и представляют собой различные комбинации констант hu
, tu
, lu
и чисел π и α. Константам, входящим в hu
-tu
-lu
-π-α-базис, определен специальный статус – они определены как универсальные суперконстанты [6, 8, 13, 15]. На основе универсальных суперконстант получено новое значение гравитационной постоянной Ньютона, планковских констант и найдена универсальная формула силы. Новые фундаментальные физические константы дают широкие возможности для установления новых физических законов и поиска констант взаимодействия для различных физических законов.
Введение
Физика входит в 21-й век с большим клубком нерешенных проблем. Если в конце 19-го века в физике было «все благополучно» за исключением отрицательных результатов опыта Майкельсона и непонятной зависимости излучения абсолютно черного тела от температуры, то к концу 20-го века физика накопила невиданное количество нерешенных проблем. Наиболее важные из них можно найти в недавно опубликованном В.Л.Гинзбургом списке 1999 года [4].
Если только две проблемы конца 19-го века привели к радикальному изменению ситуации в физике, то клубок нерешенных проблем конца 20-го века способен привести к обвальному пересмотру понимания устройства мира, за которым может последовать перекраивание сложившейся научной картины мира. Обилие неудачных попыток в создании новых физических теорий говорит о том, что правильное стратегическое направление исследований до сих пор не выявлено. Среди нерешенных фундаментальных проблем еще не обозначена та важнейшая проблема, решение которой даст ключ к решению других проблем. Усилия ученых направлены как на теоретические, так и на экспериментальные исследования. Поиск новых подходов активно проводится в области исследования новых физических полей на основе концепции физического вакуума. Для описания новых видов полей и новых взаимодействий необходимо проводить поиск констант взаимодействий. Весьма вероятно, что это должны быть новые еще неизвестные физике константы.
Реклама

В настоящей работе затронута проблема, которая, на мой взгляд, незаслуженно выпала из поля зрения физиков и до сих пор не была обозначена в числе важнейших фундаментальных проблем. Я имею в виду проблему фундаментальных физических констант. Она должна стоять на первом месте, поскольку именно в ней содержится ключ к решению других проблем физики. Как будет показано ниже на некоторых примерах, эта проблема действительно является ключевой, а ее решение открывает большие возможности для поиска новых физических законов и новых физических констант.
1. Проблема фундаментальных физических констант
Проблема фундаментальных физических констант естественным образом возникла на основе большого количества накопленных результатов исследований в области физики элементарных частиц. Благодаря этому направлению исследований появилось большое количество новых фундаментальных физических постоянных, которые уже выделены в отдельный класс – «атомные и ядерные константы» [1]. Следует отметить, что их количество уже намного превышает количество всех других констант вместе взятых [1]. В общей сложности в физике используются уже сотни физических констант. Список фундаментальных физических констант рекомендованный CODATA 1998 насчитывает около 300 фундаментальных физических констант [1]. То, что количество констант достигло уже нескольких сотен, и все они фундаментальные – явно ненормально. Если к ним подходить как к истинно фундаментальным, то их слишком много. Если исходить из того, что в основе мира лежит единая сущность, и что механические, электрические и гравитационные явления должны иметь единую природу, то для описания всех физических явлений и законов не нужно такое большое количество констант. Если же подходить к понятию фундаментальности по полной мере, то истинной фундаментальностью должны обладать совсем минимальное количество констант, а никак не сотни. Таким образом, существует большое противоречие между минимально необходимым количеством фундаментальных констант и их реальным обилием.
Можно предположить, что известные на сегодня константы являются составными константами и статус фундаментальных они носят лишь в силу исторических особенностей их появления. Тогда возникают вопросы: «из каких новых неприводимых констант они могут состоять и как они связаны между собой?». Если такие первичные константы существуют, то они могли бы претендовать на роль фундаментальных физических суперконстант и заменить собой существующие константы. Существуют ли такие суперконстанты, которые в состоянии заменить такое большое количество столь различных фундаментальных физических констант и сколько их? На эти вопросы в рамках современных знаний ответов пока нет.
Реклама

Наиболее важные современные физические теории оперируют константами G, h, c в их различных комбинациях [3]. Так, например, теорию тяготения Ньютона можно условно назвать G-теорией [3]. Общая теория относительности является классической (G, c)-теорией. Релятивистская квантовая теория поля является квантовой (h, c)-теорией [3]. Каждая из этих теорий оперирует одной или двумя размерными константами. Открытие планковских единиц длины, массы и времени породили надежду на возможность создания новой квантовой теории на основе трех констант. Однако, попытки создать единую теорию электромагнитных полей, частиц и гравитации на основе трех размерных констант – (G, c, h)-теорию, окончились неудачей. Такой теории до сих пор нет, хотя на ее появление возлагали большие надежды [3]. На G-c-h-базис все еще возлагают надежды как на основополагающую тройку констант для будущей теории. И действительно, многое указывает на то, что трех размерных констант должно быть достаточно для создания единой теории. Ведь неспроста только из трех основных единиц – метра, килограмма и секунды можно получить все производные единицы, имеющие механическую природу. Однако до сих пор неясно, какие три константы должны составить основу будущей непротиворечивой теории? Задача эта оказалась очень сложной. Я считаю, что причины сложности кроются в невыясненной сущности многих фундаментальных констант и в невыясненных истоках их происхождения. Проведенные исследования [5...15] позволяют сказать, что минимальное количество первичных констант, из которых состоят современные фундаментальные физические константы, действительно существует. При этом в минимальный константный базис входят как уже известные физические постоянные, так и новые константы.
2. Константы физического вакуума
При исследовании свойств физического вакуума, из соотношения для плотности энергии получена следующая формула для полной энергии, заключенной в динамическом объекте вакуума [5, 14]:
E = 1
/2
·q2
νπc·10–7
. (1)
Это соотношение напоминает по своему виду формулу Планка E=h·ν. Только роль кванта действия выполняет в ней не постоянная Планка, а новая константа:
hu
= e2
cμ v
, (2)
где: μ v
– магнитная постоянная вакуума.
Новая физическая константа названа фундаментальным квантом действия [6...10, 13...15]. Ее значение равно [6]:
hu
= 7,69558071(63)·10–37
Дж·с.
Из формулы для фундаментального кванта действия (2) следуют еще две новые физические константы:
Gu
= hu
/c, (3)
Ru
= hu
/e2
. (4)
Значение константы Gu
равно [6]:
Gu
= 2,56696941(21)·10–45
Н·с2
.
Константа Ru
получила название фундаментальный квант сопротивления [6]. Ее значение равно [6]:
Ru
= 29,9792458 Ом.
Эти три константы hu
, Gu
, Ru
являются основными константами вакуума. Примечательным является то, что они непосредственно следуют из непрерывного поля Максвелла [5, 12, 15].
С константой вакуума Gu
связан новый динамический закон, свойственный физическому вакууму. Этот закон имеет вид [6]:
mэ
·l = Gu
, (5)
где: mэ
– электромагнитная масса, l – метрическая характеристика.
Из динамического закона следует, что электромагнитная масса принимает значения от некоторого минимального значения до некоторой предельной величины:
0 < mэ
< mmax
.
Это приводит к тому, что метрическая характеристика изменяется от некоторого максимального значения до некоторой предельной величины:
lmin
< l < ∞ .
Уравнение (5) представляет собой динамический закон, который отображает динамическую симметрию вакуума. D-инвариантность вакуума является новым видом симметрии и отражает наиболее фундаментальное свойство Природы. С D-инвариантностью вакуума связан важнейший закон сохранения, который не нарушается при всех видах взаимодействий.
D-инвариантность вакуума является симметрией более высокого порядка, чем известные на сегодня симметрии. Нарушения симметрии, которые наблюдаются в Природе, вплоть до несохранения CP-инвариантности, не затрагивают D-инвариантность вакуума. Границей D-инвариантности являются фундаментальные константы me
и lu
, что и отражает динамический закон вакуума. Таким образом, динамическая симетрия вакуума не противоречит идее развития, поскольку D-инвариантность сохраняется и тогда, когда нарушаются другие виды симметрии. В вакууме реализуется реальный физический процесс, обязанный своим существованием динамической симметрии, который приводит к появлению дискретных частиц из непрерывного физического объекта, что в математическом описании представлено как достижение физическими величинами своих предельных квантованных значений [5...14].
Из соотношений (2) и (4) следует, что:
Ru
= c μ v
, (6)
где: μ v
– магнитная константа вакуума.
Из формулы для фундаментального кванта действия (2) следует новая формула для элементарного заряда e:
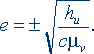 (7) (7)
В системе СГСЭ соотношение для элементарного заряда примет вид:
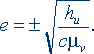 (8) (8)
Соотношения (7) и (8) представлены квадратным корнем. Из них непосредственно следует бинарность зарядов, т.е. то, что заряды имеют два знака. Поскольку заряды определяются только константами, то из этих соотношений следует также и квантованность зарядов.
Рассмотривая динамику невещественных объектов вакуума, легко видеть, что первым фиксированным значением энергии, которая соответствует устойчивому физическому объекту, является энергия электрона или позитрона Ee
. Тогда значение частоты, которое соответствует этой величине энергии будет равно:
ν = Ee
/hu
= 1,063870869·1023
Гц.
Отсюда следует четвертая физическая константа вакуума – фундаментальный квант времени:
tu
= 0,939963701(11)·10–23
с.
Используя константу скорости света c, получим пятую константу вакуума – фундаментальный квант длины:
lu
= 2,817940285(31)·10–15
м.
Отметим, что значение этой константы в точности совпадает с классическим радиусом электрона. Все пять констант вакуума hu
, Gu
, Ru
, tu
, lu
получены на основе нового подхода к пониманию физической сущности полевых структур. Проведенные исследования этих констант показали, что используемые в современной физике фундаментальные физические константы непосредственно происходят от констант физического вакуума [6...8, 14]. Приведенные выше основные константы вакуума позволяют получить ряд вторичных констант, которые являются производными константами и также относятся к физическому вакууму.
Константы фундаментальной метрики tu
и lu
образуют новую константу b, названную фундаментальным ускорением [5]:
b = lu
/tu
2
.
Значение этой константы равно:
b = 3,189404629(36)·1031
м/с2
.
Эта константа позволила получить новый закон силы [6, 8, 10, 15]
F = m·b.
Этот закон отражает связь силы с дефектом массы.
Исследования констант вакуума привели к выводу, что для динамических объектов вакуума можно определить константу магнитного момента. Такой магнитный момент был найден в [6]. Он получил название фундаментальный магнетон вакуума. Приводим соотношение для фундаментального магнетона вакуума:
μu
= lu
(hu
c)1/2
/2π.
Значение этой константы равно:
μu
= 2,15418485(11)·10–26
Дж/Тл.
Фундаментальный магнетон μu
и магнетон Бора μB
связаны между собой следующим соотношением:
μu
= μB
α/π.
3. Универсальные суперконстанты
В [6, 8...10] получены новые результаты, показывающие, что группа констант вакуума hu
, tu
, lu
совместно с числами π и α, обладает уникальной особенностью. Эта особенность состоит в том, что используемые в физике фундаментальные константы представляют собой различные комбинации перечисленных констант. Таким образом, названные константы вакуума имеют первичный статус и могут выполнять роль онтологического базиса физических констант. Константы, входящие в hu
-tu
-lu
-π-α-базис, названы универсальными суперконстантами [6, 8, 13, 15].
Их значения следующие:
фундаментальный квант действия hu
= 7,69558071(63)·10–37
Дж·с;
фундаментальный квант длины lu
= 2,817940285(31)·10–15
м;
фундаментальный квант времени tu
= 0,939963701(11)·10–23
с;
постоянная тонкой структуры α = 7,297352533(27)·10–3
;
число π = 3,141592653589...
Константы этой группы позволили выявить совершенно неожиданную всеобщую взаимозависимость и глубокую взаимную связь всех фундаментальных физических констант. Ниже, в качестве примера, показано как некоторые фундаментальные постоянные связаны с универсальными суперконстантами. Для основных констант эти функциональные зависимости оказались следующими:
элементарный заряд: e = f (hu
, lu
, tu
);
масса электрона: me
= f (hu
, lu
, tu
);
постоянная Ридберга: R∞
= f (lu
, α, π);
гравитационная постоянная: G = f (hu
, lu
, tu
, α, π);
отношение масс протона-электрона: mp
/me
= f (α, π);
постоянная Хаббла: H = f (tu
, α, π);
планковская масса: mpl
= f (hu
, lu
, tu
, α, π);
планковская длина: lpl
= f (lu
, α, π);
планковское время: tpl
= f (tu
, α, π);
квант магнитного потока: Ф0
= f (hu
, lu
, tu
, α, π);
магнетон Бора: μB
= f (hu
, lu
, tu
, α,).
Как видим, между физическими константами существует глобальная связь на фундаментальном уровне. Из приведенных зависимостей видно, что наименее сложными являются константы h, c, R∞
, mp
/me
. Это указывает на то, что эти постоянные наиболее близки к первичным константам, однако сами таковыми не являются. Как видим, константы, которые традиционно носят статус фундаментальных констант, не являются первичными и независимыми постоянными. К первичным и независимым можно отнести только суперконстанты вакуума. Подтверждением этому явилось то, что использование суперконстантного базиса позволило получить все основные фундаментальные физические константы расчетным путем [5...15]. То, что известные сегодня фундаментальные физические константы не имеют статуса первичных и независимых постоянных, а на их основе пытались построить физические теории, и явилось причиной многих проблем физики. Фундаментальные теории невозможно построить на вторичных константах.
Размерные суперконстанты hu
, lu
, tu
определяют физические свойства пространства-времени. Суперконстанты π и α определяют геометрические свойства пространства-времени. Таким образом, подтверждается подход А.Пуанкаре, согласно которому утверждается дополнительность физики и геометрии [16]. Согласно этому подходу в реальных экспериментах мы всегда наблюдаем некую «сумму» физики и геометрии [17]. Группа универсальных суперконстант своим составом подтверждает это.
4. Новое значение константы G
Зависимость константы G от первичных суперконстант указывает на то, что эту важнейшую постоянную можно получить посредством математических расчетов. Как известно, сама форма закона всемирного тяготения Ньютона – прямая пропорциональность силы массам и обратная пропорциональность квадрату расстояния, проверена с гораздо большей точностью, чем точность определения гравитационной постоянной G. Поэтому, основное ограничение на точное определение гравитационных сил накладывает константа G. Кроме того, со времен Ньютона остается открытым вопрос о природе гравитации и о сущности самой гравитационной постоянной G. Эта константа определена экспериментально. Науке пока неизвестно существует ли аналитическое соотношение для определения гравитационной константы. Науке также не была известна связь между постоянной G и другими фундаментальными физическими константами. В теоретической физике эту важнейшую постоянную пытаются использовать совместно с постоянной Планка и скоростью света для создания квантовой теории гравитации и для разработки единых теорий. Поэтому, вопросы о первичности и независимости константы G, а также необходимость знать ее точное значение, выходят на первый план.
Численное значение G было определено впервые английским физиком Г.Кавендишем в 1798г. на крутильных весах путем измерения силы притяжения между двумя шарами.
Современное значение константы G, рекомендуемое CODATA 1998 [1]:
G = 6,673(10)·10–11
м3
кг–1
с–2
.
Из всех универсальных физических постоянных точность в определении G является самой низкой. Среднеквадратическая погрешность для G на несколько порядков превышает погрешность других констант.
Совершенно неожиданным оказалось то, что G может быть выражена посредством электромагнитных констант. Это становится важным, так как точность констант электромагнетизма намного больше точности постоянной G.
Открытая группа универсальных суперконстант, имеющих первичный статус, и выявленная глобальная связь фундаментальных констант позволили получить математические формулы для вычисления гравитационной постоянной G [6, 9, 10, 15]. Таких формул оказалось несколько. В качестве подтверждения этому, ниже приведены 9 эквивалентных формул:

Из приведенных формул видно, что константа G выражается с помощью других фундаментальных констант очень компактными и красивыми соотношениями. При этом, все формулы для гравитационной константы сохраняют когерентность. В числе физических постоянных, с помощью которых представлена гравитационная константа, находятся такие константы как фундаментальный квант hu
, скорость света c, постоянная тонкой структуры α, постоянная Планка h, число π, фундаментальная метрика пространства-времени (lu
, tu
), элементарная масса me
, элементарный заряд e, большое число Дирака D0
, энергия покоя электрона Ee
, планковские единицы длины lpl
, массы mpl
, времени tpl
, постоянная Хаббла H, константа Ридберга R∞
. Это указывает на единую сущность электромагнетизма и гравитации и на наличие фундаментального единства у всех физических констант. Из приведенных формул видно, что связь между электромагнетизмом и гравитацией действительно существует и проявляется даже на уровне гравитационной константы G.
Теперь, по прошествии 200 лет после первого измерения G, появилась возможность на основе полученных формул вычислить ее точное значение, используя константы электромагнетизма. Поскольку точность в определении констант электромагнетизма высокая, то точность гравитационной постоянной можно приблизить к точности электромагнитных констант. Все приведенные выше формулы дают новое значение G, которое по точности почти на пять порядков (!) выше известного на сегодня значения. Новое значение G вместо четырех цифр содержит 9 цифр [6, 9, 10, 15]:
G = 6,67286742(94)·10–11
м3
кг–1
с–2
.
С помощью универсальных суперконстант удалось получить новые формулы для планковских констант [6, 8, 9, 15]:
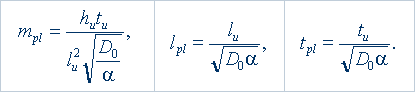
На основе этих формул получены новые значения планковских констант:
mpl
= 2,17666772(25)·10–8
кг.
lpl
= 1,616081388(51)·10–35
м.
tpl
= 5,39066726(17)·10–44
с.
Эти новые значения планковских констант по точности почти на пять порядков точнее известных на сегодня значений [1].
Универсальные суперконстанты позволили получить новое точное значение параметра Хаббла:
H = 53,98561(87) (км/с)/Мпс.
5. Фундаментальная константа силы
Особенности констант физического вакуума привели к выводу, что силы взаимодействия также должны выражаться через константы вакуума. Покажем это. Из закона Кулона для взаимодействующих элементарных зарядов следует:
F = e2
/l 2
.
На основании формулы (8) представим это соотношение следующим образом:
F = hu
c/l 2
= hu
ν2
/c.
Значение hu
/c с учетом формулы (3) будет равно Gu
. Исходя из этого, получим соотношение для закона универсального взаимодействия [5...15]:
F = Gu
·ν2
.
Для предельного значения метрики из закона универсального взаимодействия получим следующее соотношение для константы силы:
Fu
= hu
/lu
tu
.
Эта новая физическая константа названа фундаментальной константой силы. Ее значение равно:
Fu
= 29,0535047(31) Н.
Она является универсальной константой силы для всех известных на сегодня видов взаимодействий. Как показано в [6, 9, 10, 13], эта константа присутствует не только в законе Кулона, но и в законах Ньютона, в законе Галилея, в законе Ампера и в законе всемирного тяготения.
6. Универсальная формула силы
Поиск единого взаимодействия, сводящего воедино четыре фундаментальных взаимодействия, – одна из сложнейших нерешенных задач физики. Современные попытки объединения сильного, слабого, электромагнитного и гравитационного взаимодействий основаны на поиске условий, при которых константы взаимодействий совпадают по своим величинам. Считается, если существует такая единая константа, то объединение взаимодействий возможно. Однако такой подход пока не привел к обнадеживающим результатам. Не раскрыта взаимосвязь четырех фундаментальных взаимодействий, не ясны истоки их появления.
Я считаю, что решение проблемы единого взаимодействия нужно искать на другом направлении.
Вместо поиска условий, при которых константы взаимодействий могут совпадать, целесообразно исследовать генезис фундаментальных взаимодействий и вести поиск новой константы единого взаимодействия. Есть все основания полагать, что такая константа существует. Единство фундаментальных физических констант указывает на существование единства у электромагнитных и гравитационных сил. В частности, к решению этой проблемы может подтолкнуть выяснение следующего вопроса. Почему так схожи по своему виду формулы законов Кулона и всемирного тяготения Ньютона? Столь разные взаимодействия оказались такими похожими в математическом представлении формулы силы. В одном – заряды, в другом – массы, но формулы одинаковы. Что скрывается за этим поразительным сходством? Есть несколько путей решения этой проблемы. Первый путь состоит в том, чтобы выяснить какая существует связь между массой и зарядом. Практически это означает, что необходимо вести поиск ответа на вопрос: существует ли электромагнитная масса и что это такое? Второй путь состоит в выяснении сущности гравитационной константы G. Возможно, что и в ней скрыта связь между электричеством и гравитацией. Третий путь основан на предположении о том, что и закон Кулона, и закон Ньютона являются фрагментами какого-то универсального фундаментального закона силы. Если это сходство не случайно, то должен существовать единый закон силы, который лишь проявляется для электричества как закон Кулона, а для гравитации – как закон Ньютона. Как показано в [6, 9, 10, 15] единый закон силы действительно существует. Закон Кулона и законы Ньютона действительно являются его частными проявлениями. Используя универсальные суперконстанты, у нас представилась возможность не просто выявить сходство в форме записи у этих законов, а установить их связь на фундаментальном уровне. На основе суперконстант удалось получить новую формулу силы, которая названа универсальной формулой силы [6, 10, 15]. Она имеет следующий вид:
F = (hu
/lu
·tu
)·(N1
·N2
/N3
2
).
В универсальную формулу силы входят суперконстанты hu
, lu
, tu
и безразмерные коэффициенты N1
, N2
, N3
. Коэффициенты N1
и N2
единым образом представляют или отношения взаимодействующих масс к элементарной массе, или отношение зарядов к элементарным зарядам, или отношение токов к элементарному току. Коэффициент N3
представляет собой отношение длины к фундаментальному кванту длины. Универсальная формула силы превращается в формулу F=ma при N1
= m/me
, N2
= 1/lu
, N3
= 1/lu
:
F = (hu
/lu
tu
) (N1
·N2
/N3
2
) = ma.
Универсальная формула силы превращается в формулу закона Кулона при N1
= q1
/e, N2
= q2
/e, N3
= 1/lu
:
F = (hu
/lu
·tu
) (N1
·N2
/N3
2
) = q1
q2
/l 2
.
В универсальной формуле силы первый сомножитель представляет собой новую физическую константу, имеющую размерность силы. Это есть фундаментальная константа силы Fu
, полученная выше.
Соотношение для этой константы определяется исключительно размерными суперконстантами вакуума.
При N1
= m1
/me, N2
= m2
/me
, N3
= 1/lu
и при замене фундаментального кванта действия hu
на гравитационный квант действия hg
= hu
/D0
универсальная формула силы превращается в следующую формулу:
F = (hg
/lu
·tu
)(N1
·N2
/N3
2
) = (hu
·lu
/tu
·me
2
D0
)·(m1
·m2
/l 2
).
Комбинация констант в первом сомножителе в правой части соотношения в точности совпадает с формулой для вычисления гравитационной константы G:
hu
·lu
/tu
·me
2
D0
= G.
Таким образом, универсальная формула силы превращается в формулу закона всемирного тяготения:
F = (hg
/lu
·tu
)·(N1
·N2
/N3
2
) = G·m1
·m2
/l 2
.
В этой формуле физическая константа, имеющая размерность силы, определяется аналогично фундаментальной константе силы. Соотношение для этой константы имеет вид:
Fug
= hg
/lu
·tu
.
Ее значение равно 6,9731134·10–42
·Н.
Тот факт, что и законы механики, и закон гравитации, и закон электростатики выражаются единой формулой – универсальной формулой силы, указывает на единую природу всех взаимодействий. Такая связь выявлена с законом Ньютона, законом Галилея, законом Кулона и даже с законом Ампера для взаимодействующих проводников с током.
Исследования показали, что из универсальной формулы силы следуют два новых закона [6, 7, 9, 10]:
F = mb и F = Gu
ν2
.
Формула F = mb определяет связь силы с дефектом массы. Константой в этой формуле является фундаментальное ускорение b = 3,189404629(36)·1031
м/с2
[6, 7]. Формула F = Gu
ν2
представляет новое универсальное взаимодействие [6,7, 9, 10]. Константой в этой формуле является новая физическая постоянная вакуума Gu
= 2,56696941(21)·10–45
Н·с2
. В [6,7, 9, 10] показано, что из закона универсального взаимодействия непосредственно следуют и закон Кулона и закон всемирного тяготения Ньютона и закон Ампера.
По генетической связи все взаимодействия можно расположить в такой последовательности: универсальное, электромагнитное, сильное, слабое, гравитационное. Как видим, корни всех взаимодействий следует искать в универсальном взаимодействии. Это пятое взаимодействие характерно для физического вакуума и не связано с взаимодействием каких бы то ни было частиц, в том числе частиц вещества. В то же время, из него проистекают законы относящиеся к взаимодействиям частиц.
Универсальная формула силы показывает, что значения электрических, магнитных, механических и гравитационных сил зависят не столько от абсолютных значений масс, зарядов, токов и расстояний, сколько от их соотношения с фундаментальными константами – массой электрона, элементарным зарядом, элементарным током и фундаментальным квантом длины. Это указывает на необходимость нового подхода к пониманию сущности фундаментальных взаимодействий.
Таким образом, причина поразительного сходства формул в законах Кулона и всемирного тяготения Ньютона проистекает от фундаментального единства сил инерции, гравитации и электромагнетизма. Это единство сил удалось установить на основе выявленного фундаментального единства физических констант и найденных новых физических постоянных.
7. Выводы
Получены новые фундаментальные физические константы hu
, Gu
, Ru
, tu
, lu
, относящиеся к физическому вакууму. Выявлена группа констант, которым определен специальный статус универсальных суперконстант. С помощью универсальных суперконстант, которые являются константами вакуума, можно представить все законы и формулы классической и квантовой физики, а также все фундаментальные константы, в том числе постоянную Планка h и гравитационную постоянную G. Группа, состоящая из пяти универсальных суперконстант hu
, tu
, lu
, π, α, позволяет описывать физические законы, относящиеся как к полю, так и к веществу. Известные на сегодня фундаментальные физические постоянные имеют вторичный статус по отношению к найденным универсальным суперконстантам вакуума. Открытие группы из пяти независимых универсальных суперконстант, которых совершенно достаточно для получения других физических констант, указывает на глубокую взаимосвязь констант различной природы. Найденные новые фундаментальные константы открывают перспективное направление для выявления новых физических законов и для поиска новых констант взаимодействий.
Список литературы
PeterJ.Mohr and BarryN.Taylor. «CODATA Recommended Values of the Fundamental Physical Constants: 1998»; NIST Physics Laboratory. Constants in the category «All constants»; Reviews of Modern Physics, (2000), v.72, No.2.
D.C.Cole and H.E.Puthoff, «Extracting Energy and Heat from the Vacuum», Phys. Rev. E, v.48, No.2, 1993.
Ю.И.Манин. Математика и физика. М.:«Знание», 1979.
В.Л.Гинзбург. «Какие области физики и астрофизики представляются важными и интересными». УФН, №4, т.169, 1999.
Н.В.Косинов. «Электродинамика физического вакуума». Физический вакуум и природа, №1, 1999.
Н.В.Косинов. «Физический вакуум и гравитация». Физический вакуум и природа, №4, 2000.
Н.В.Косинов. «Законы унитронной теории физического вакуума и новые фундаментальные физические константы». Физический вакуум и природа, №3, 2000.
N.Kosinov. «Five Fundamental Constants of Vacuum, Lying in the Base of all Physical Laws, Constants and Formulas». Physical Vacuum and Nature, №4, 2000.
Н.В.Косинов. «Пять универсальных физических констант, лежащих в основе всех фундаментальных rонстант, законов и формул физики». Шестая Международная конференция «Современные проблемы естествознания». Программа и тезисы. С-Петербург, август, 2000г.
Н.В.Косинов. «Разгадка причин поразительного сходства формул законов Кулона и всемирного тяготения Ньютона». Шестая Международная конференция «Современные проблемы естествознания». Программа и тезисы. С-Петербург, август, 2000г.
Н.В.Косинов. «Эманация вещества вакуумом и проблема структурогенеза». Идея, №2, 1994.
Н.В.Косинов. «Энергия вакуума». Энергия будущего века, №1, 1998.
Н.В.Косинов. «Универсальные физические суперконстанты».
Н.В.Косинов. «Новая фундаментальная физическая константа, лежащая в основе постоянной Планка».
N.V.Kosinov, Z.N.Kosinova. «Tie of Gravitational Constant G and Planck Constanth». 51st
International Astronautical Congress 2...6 Oct. 2000 / Rio de Janeiro, Brazil.
A. Пуанкаре. Наука и гипотеза. A. Пуанкаре. О науке. М., 1983.
В.А.Фирсов. «Философско-методологический анализ проблемы единства физики в концепции калибровочных полей». Философия науки, №1(3), 1997.
|