Л. Курляндчик, Г. Розенблюм
Какое иррациональное число самое «старое»? Несомненно, √2. Мы не знаем точно, кто первый доказал иррациональность этого числа, однако мы убеждены, что сделано было это примерно так.
Доказательство первое
Допустим, что число √2 рационально. Геометрически это означает, что диагональ квадрата длины c соизмерима с его стороной длины a, то есть найдутся отрезок длины d и целые числа m и n такие, что c = dm, a = dn. Отметим m–1 точек на диагонали AC и n–1 точек на стороне DC, делящие эти отрезки на кусочки длины d. Отложим на [AC] отрезок AK: |AK| = |AD|; на [DC] — отрезок DE: |DE| = |KC|. Точки K и E попадут в отмеченные точки (см. рис.). Докажем, что треугольники ACD и KEC подобны. Угол C у них общий. Достаточно, значит, проверить равенство
Заметим, что |KC| = c – a, |EC| = 2a – c. Поэтому
|KC|2
|EC|2
|
= |
c2 + a2 – 2ac
c2 + 4a2 – 4ac
|
. |
Поскольку c2 = 2a2, то
|KC|2
|EC|2
|
= |
3a2 – 2ac
6a2 – 4ac
|
= |
1
2
|
= |
|AD|2
|AC|2
|
. |
Таким образом, треугольник KEC, подобный треугольнику ACD, — прямоугольный равнобедренный, и мы можем проделать на его сторонах такое же построение, как на сторонах треугольника ACD. Отложим на [EC] отрезок EK1: |EK1| = |KC|; на [KC] — отрезок KE1: |KE1| = |K1C|. Точки K1 и E1 вновь попадут в точки деления. Треугольник K1CE1 снова окажется прямоугольным равнобедренным. Для него мы тем же способом построим треугольник K2CE2; эту процедуру можно продолжать без конца. При этом треугольники KjCEj становятся всё мельче, но всякий раз точки Kj и Ej будут попадать в первоначальные точки деления отрезков AC и CD. Но ведь этих точек только конечное число! А треугольников KjCEj бесконечно много. Это противоречие и доказывает иррациональность √2.
Прошли века... Появилось алгебраическое доказательство, пожалуй, более простое.
Доказательство второе
Иррациональность √2 означает, что у уравнения x2 = 2y2 нет решений в натуральных числах x, y. Допустим, что такие решения есть, и x = m, y = n — одно из них.
Из уравнения следует, что m — чётное число, m = 2m1. Подставляя m = 2m1 в уравнение, получаем n2 = 2m12, то есть x = n, y = m1 — тоже решение. Отметим при этом, что n < m, m1 < n. Теперь видно, что n — чётное число, n = 2n1, следовательно, m12 = 2n12. Таким образом, x = m1, y=n1 — решение уравнения, при этом m1 < n, n1 < m1. Мы можем поступать так же и дальше, получая всё меньшие и меньшие решения уравнения. Но здесь-то уже и есть противоречие. Ведь все числа m, n, m1, n1, ... — натуральные, m > n > m1 > n1 > ..., а бесконечной убывающей последовательности натуральных чисел быть не может! Значит, наше предположение было ошибочно, и число √2 иррационально.
Реклама

Оба рассуждения по существу проходили по одной схеме: предположив, что у задачи есть решение, мы строили некоторый бесконечный процесс, в то время как по самому смыслу задачи этот процесс должен на чём-то кончаться. Подобный метод и называется методом бесконечного спуска *.
Часто метод спуска применяется в более простой форме. Предположив, что мы уже добрались до естественного конца процесса, мы видим, что «остановиться» не можем.
Доказательство третье
Пусть x = m, y = n — решение уравнения x2 = 2y2 с наименьшим возможным x. Число m должно быть чётным, m = 2m1, следовательно, x = m, y = m1 — тоже решение нашего уравнения. Однако m > n, что противоречит выбору решения m, n как «наименьшего».
Из этого варианта доказательства видно, что метод спуска сродни методу математической индукции. Оба метода основаны на том факте, что любое непустое множество натуральных чисел имеет минимальный элемент. Метод спуска наиболее удобен для доказательства «отрицающих» теорем.
Метод спуска в задачах
Задача 1. Доказать неразрешимость в натуральных числах уравнения
8x4 + 4y4 + 2z4 = t4.
Решение. Допустим, что решения есть, и x = m, y = n, z = p, t = r — решение с наименьшим возможным x. Из уравнения видно, что r — чётное число, r = 2r1.
Подставляя это решение в уравнение и деля на 2, получаем
4m4 + 2n4 + p4 = 8r14.
Теперь ясно, что p — чётное, p = 2p1, следовательно,
2m4 + n4 + 8p14 = 4r14.
Далее действуем так же: n = 2n1,
m4 + 8n14 + 4p14 = 2r14.
Наконец, m = 2m1,
8m14 + 4n14 + 2p14 = r14.
Таким образом, x = m1, y = n1, z = p1, t = r1 — решение нашего уравнения. Но ведь m1 < m! Мы получили противоречие с выбором решения m, n, r, p как «наименьшего».
Рассмотрим задачу чуть сложнее.
Задача 2. Доказать неразрешимость в натуральных числах уравнения
x2 + y2 + z2 + t2 = 2xyzt.
Решение. Пусть x, y, z, t — решение.
Так как x2 + y2 + z2 + t2 — чётное число, то среди чисел x, y, z, t — чётное число нечётных, то есть либо четыре, либо два, либо нуль. Если все числа нечётные, то x2 + y2 + z2 + t2 делится на 4, а 2xyzt не делится. Если же только два нечётных числа, то x2 + y2 + z2 + t2 не делится на 4, a 2xyzt делится. Поэтому все числа чётные, то есть x = x1, y = y1, z = z1, t = t1. Подставив эти значения в уравнение, получаем
Реклама

x12 + y12 + z12 + t12 = 8x1 y1 z1 t1.
Как и прежде, видим, что все четыре числа нечётными быть не могут, иначе x12 + y12 + z12 + t12 не делится на 8. Также не могут быть нечётными ровно два числа, ибо и тогда x12 + y12 + z12 + t12 не делится на 8. Итак, мы получаем, что все числа чётные, то есть
x1 = 2x2, y1 = 2y2, z1 = 2z2, t1 = 2t2.
Поэтому
x22 + y22 + z22 + t22 = 32x2 y2 z2 t2.
Рассуждая как и раньше, получаем, что x2, y2, z2, t2 — чётные числа и так далее. Легко понять, что при всяком натуральном s
xs2 + ys2 + zs2 + ts2 = 22s+1xs ys zs ts,
причём
xk = 2xk+1, yk = 2yk+1, zk = 2zk+1, tk = 2tk+1, k ≥ 1.
То есть при любом натуральном s числа
x
2s
|
, |
y
2s
|
, |
z
2s
|
, |
t
2s
|
— целые. Ну, а это невозможно ни при каких натуральных x, y, z, t.
А вот уравнение, у которого бесконечно много решений, но которое исследуется тем же методом.
Задача 3. Найти все решения в натуральных числах уравнения
x2 – 2y2 = 1.
Решение. Очевидно, что x1 = 3, y1 = 2 — решение данного уравнения. Докажем, что если пара (x, y) — решение, то пара (3x + 4y, 2x + 3y) — тоже решение. Это следует из тождества
(3x + 4y)2 – 2(2x + 3y)2 = x2 – 2y2.
Таким образом,
x2 = 3·3 + 4·2 = 17;
y2 = 2·3 + 3·2 = 12;
x3 = 99, y3 = 70, и так далее.
|
Мы указали бесконечную последовательность решений (x1, y1), (x2, y2), ... Докажем теперь, что других чисел, удовлетворяющих уравнению, нет.
Пусть (x, y) — некоторое решение. В таком случае (3x – 4y, 3y – 2x) — также решение, ибо
(3x – 4y)2 – 2(3y – 2x)2 = x2 – 2y2.
Из условия 9 = 9x2 – 18y2 > – 2y2 следует, что 3x > 4y; а при y > 2 из условия 4 = 4x2 – 8y2 < y2 следует, что 3y > 2x. То есть при y > 2 мы из решения (x, y) получаем решение (x(1), y(1)) в натуральных числах, причем x(1) < x, y(1) < y. Так как этот процесс не может продолжаться бесконечно (в любом непустом множестве натуральных чисел есть наименьший элемент!), то когда-нибудь мы получим решение (x(n), y(n)), где y(n) ≤ 2. Так как y(n), очевидно, не может равняться 1, то y(n) = 2. Значит, x(n) = 3. А это и означает, что числа x и y принадлежат построенной ранее последовательности.
До сих пор мы рассматривали только уравнения. Теперь решим нашим методом «текстовую» задачу.
Задача 4. Имеется 2N+1 гирь, каждая из которых весит целое число граммов. Известно, что любые 2N из них можно так разложить на чашки весов, по N на каждую, что наступит равновесие. Доказать, что все гири имеют одинаковый вес.
Решение. Ясно, что все гири одновременно имеют или чётный или нечётный вес: вес любых 2N гирь чётен. Вычтем теперь из весов всех гирь вес самой лёгкой гири (или самых лёгких, если их несколько). Новая система гирь, очевидно, также удовлетворяет условию задачи, причём среди гирь есть «гири» нулевого веса. Поэтому веса всех гирь новой системы чётны. Разделив веса всех гирь пополам, мы снова получаем систему гирь, удовлетворяющую условиям задачи, среди которых есть «гири» нулевого веса. Поэтому опять же получаем, что вес всех гирь чётен, и так далее. Из «бесконечного спуска» следует, что все «гири» нулевые, а это и означает, что все исходные гири имеют одинаковый вес.
Идея бесконечного спуска позволяет решать некоторые задачи комбинаторной геометрии.
Задача 5. Можно ли куб разрезать на несколько различных кубиков?
Решение. Сделаем сначала одно очевидное замечание. Пусть квадрат P разбит на конечное число различных квадратов. Тогда самый маленький квадрат не прилегает к границе квадрата P.
Допустим теперь, что куб Q удалось разрезать на различные кубы Qj, пусть P — одна из граней Q. Кубы Qj, прилегающие к P, порождают разбиение P на попарно различные квадраты. Пусть P1 — самый маленький из этих квадратов, Q1 — соответствующий куб. P1 не прилегает к границе P, следовательно, он окружен большими квадратами. Соответствующие кубы образуют «колодец», в котором лежит кубик Q1.
Пусть P'1 — «верхняя» грань (противоположная грани P1) куба Q1. Кубы, прилегающие к P'1, порождают разбиение P'1 на различные квадраты. Вновь самый маленький из них, P2, расположен внутри P'1, следовательно, кубы, окружающие соответствующий кубик Q2, больше Q2 и снова образуют «колодец». Продолжая построение и дальше, мы получим бесконечную «башню», состоящую из все уменьшающихся кубов, а это невозможно.
В заключение — задача на клетчатой бумаге.
Задача 6. Дан лист клетчатой бумаги. Доказать, что при n ≠ 4 не существует правильного n-угольника с вершинами в узлах решётки.
Решение. Вначале докажем, что не существует правильного треугольника с вершинами в узлах. Действительно, пусть a — длина стороны этого треугольника; тогда a2 — целое число по теореме Пифагора. Площадь треугольника равна a2√3/4, то есть иррациональна. С другой стороны, очевидно, что площадь любого многоугольника с вершинами в узлах рациональна.
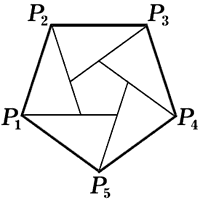 Поскольку в правильный шестиугольник можно вписать правильный треугольник с вершинами в его вершинах, для n = 6 утверждение тоже доказано. Поскольку в правильный шестиугольник можно вписать правильный треугольник с вершинами в его вершинах, для n = 6 утверждение тоже доказано.
Пусть n ≠ 3, 4, 6. Допустим, что P1, P2, ..., Pn — n-угольник с вершинами в узлах. Отложим от точек P1, P2, ..., Pn векторы, соответственно равные векторам P2P3, P3P4, ..., P1P2 (см. рис.). Новые точки вновь попадут в узлы решётки и образуют правильный n-угольник внутри первоначального. С новым n-угольником можно поступить так же, и так далее, без конца. Однако квадрат длины стороны n-угольника — целое число, а при наших постороениях оно всё время уменьшается!
|