Фун 2 числовых аргументов.
Пусть имеется Е (х1
;у1
) – элементы принадлеж точке Е
Сущ закон или правило по которому каж точке (xi
;yi
) ставится в соот-е число Wi
или любой точке (xi
;yi
) или паре чисел ставится в соот-е zi
след-но zi
=F(х;у), где Е-обл опред-я F(х;у).
Если рассмот-ть точку (хi
;уi
) и нашли соот-е значения zi
=F(хi
;уi
).
Пусть точка (х0
;у0
)ÎЕ дельта окрест-ю точки (х0
;у0
) наз множество точек
(х;у) удовлетвор-х нерав-у
Ö[(х-х0
)+(y-y0
)] <d.
Точка (х0
;у0
) наз внутренней точкой множества Е,
если сущ-ет некоторая окрест этой точки, которая вместе с точкой Î этому множеству.
Точка (х0
;у0
) наз граничной точкой
множ-ва Е, если в любой ее окрест-и сущ точка кроме самой этой точки, которая Î множ Е.
Совокупность всех граничных точек множ-а Е наз границей множ-а
Е.
Множ-во, все точки которого внутренние, наз открытыми,
т.е. безграничным.
Точка (х0
;у0
)Î множ-ву Е наз изолированной точкой,
если сущ-ет окрест этой точки в которой кроме этой точки нет ни одной точки из множества Е.
Фун 2 переменных.
Опр: Если каж паре (х;у) значений 2, не завис др от друга, переменных величин х и у, из некоторой обл их знач-я D, соот-ет опр-е знач-е величины z, то мы говорим, что z есть фун 2 независимых пременных х и у,
определ-ся в обл D.
Геом. Смысл: Геометрическое место точек Р, коор-ты которых удовлет-т ур-ю z=f(х;у), где коор-ы точки Р х и у, z=f(х;у), наз графиком фун 2 переменных.
Графиком фун 2 переменных яв-ся поверхность, проектирующая на плоскость Оху в обл опред-я фун. Каж перпендик-р к плоскости Оху пересекает поверхность z=f(х;у) не более чем в одной точке. Фун z=f(х;у) опред-ся в обл G.
Обл опред-я фун 2 переменных
– это совокупность пар (х;у) значений х и у при котором определяется фун-я z=f(х;у).
Совокупность точек на плоскости также наз-ся обл определения.
Предел фун 2 переменных.
Опр: Число А наз пределом фун
z=
f(х;у)
при х®х0
, у®у0
, М(х;у)®М0
. limх
®х0 (у
®у0)
f(х;у)=A
Если для любого e>0 сущ-ет d окрест-ть точки (х0
;у0
) такая, что при всех (х;у)Îd окрест-ти будет выполн нерав-во Ö[(х-х0
)2
+(y-y0
)2
] <d. êА-f(х;у)ê<e, A-e<f(х;у)<A+e.
Реклама

Основные теоремы о пределах:
1)lim Xn=a, lim Yn=b => lim (Xn±Yn)=a±b (n®¥)
Док-во: lim Xn=a => Xn=a+an
; lim Yn=b => Yn=b+bn
;
Xn ± Yn = (a + an
) ± (b + bn
) = (a ± b) + (an
± bn
) => lim(Xn±Yn)=a±b (n®¥).
2)limXnYn = lim Xn * lim Yn (n®¥).
3)lim Xn=a, lim Yn=b (n®¥) => lim Xn/Yn =
(lim Xn)/(lim Yn) = a/b.
Док-во: Xn/Yn – a/b = (a+an
)/(b+bn
) – a/b = (ab+an
b–ab–abn
)/b(b+bn
) =(ban
-abn
)/b(b+bn
)=gn
=> Xn/Yn=a/b+gn
=> $ lim Xn/Yn = a/b = (lim Xn)/(lim Yn) (n®¥).
Все св-ва и правила вычисл-я такие же как для 1 переменной.
Непрерывность фун в точке.
Опр: Пусть точка М0
(х0
;у0
) Î обл опр-я фун-и f(х;у). Фун-я z=f(х;у) наз непрерывной в точке
М0
(х0
;у0
), если имеет место равенство limх
®х0(у
®у0)
f(х;у)=f(х0
;у0
) или limDх
®0(
Dу
®0)
f(х0
+Dх;у0
+Dу)= f(х0
;у0
), где х=х0
+Dх и у=у0
+Dу, причем точка М(х;у) стремиться к точке М0
(х0
;у0
) произвольным образом, оставаясь в области определения фун-и.
Условия:1)f(х;у) – опред ф-ия; 2) Сущ-ют конечные пределы со всех сторон; 3)Эти пределы равны между собой; 4)Конечные пределы со всех сторон =f(x0
;у0
).
Если (х0
;у0
) точка разрыва и выполняется условие 2, то (х0
;у0
)–1 род.
Если (х0
;у0
)–1 род и выполняется условие 3, то разрыв устранимый.
Если (х0
;у0
) точка разрыва и не выполняется условие 2, то (х0
;у0
) – 2 рода.
Св-ва непрерывности в точке:1)Если фун f1
(х;у) и f2
(х;у) непрерывны в точке (х0
;у0
), то сумма (разность) f(х;у)=f1
(х;у)±f2
(х;у), произведение f(х;у)=f1
(х;у)*f2
(х;у), а также отношение этих функций f(х;у)=f1
(х;у)/f2
(х;у), есть непрер-я фун в точке х0
;у0
.
Док-во (суммы): По определению получаем, что limх
®х0(у
®у0)
f1
(х;у)=f1
(х0
;у0
), limх
®х0(у
®у0)
f2
(х;у)=f2
(х0
;у0
) на основании св-ва: limXn=a, limYn=b => lim(Xn±Yn)=a±b (n®¥), можем написать: limх
®х0(у
®у0)
f(х;у)=limх
®х0(у
®у0)
[f1
(х;у)+f2
(х;у)]=
=limх
®х0(у
®у0)
f1
(х;у)+limх
®х0(у
®у0)
f2
(х;у)=
=f1
(х0
;у0
)+f2
(х0
;у0
)=f(х0
;у0
). Итак сумма есть непрерывная функция.· 2)Всякая непрерывная фун непрерывна в каждой точке, в которой она определена. 3) Если фун z=j(m) непрерывна в точке m=х0
;у0
, а фун y=f(z) непрерывна в соот-й точке z0
=j(х0
;у0
), то фун y=f(j(х;у)) непрер-а в точке (х0
;у0
).
Реклама

Если фун непрерывна в каждой точке некоторого интервала (а,в), где а<в, то говорят, что фун непреывна на этом интервале.
Если фун непрерывна в каждой точке некоторого интервала (а,в) и непрерывна на концах интервала, то говорят, что f(x;у) непрерывна на замкнутом интервале или отрезке (а,в).
Точки разрыва.
Если в некоторой точке N(х0
;у0
) не выполняется условие limх
®х0(у
®у0)
f(х;у)= f(х0
;у0
), то точка N(х0
;у0
) наз точкой разрыва
фун z=f(х;у).
Условие limDх
®0(
Dу
®0)
f(х0
+Dх;у0
+Dу)=f(х0
;у0
) может не выпол-ся в след-х случаях: 1)z=f(х;у) определена во всех точках некоторой окрестности точки N(х0
;у0
), за исключением самой точки N(х0
;у0
); 2)фун z=f(х;у) определена во всех точках некоторой окрестности точки N(х0
;у0
), но не сущ-ет предела limх
®х0(у
®у0)
f(х;у); 3)фун z=f(х;у) определена во всех точках некоторой окрестности точки N(х0
;у0
) и сущ-ет предел limх
®х0(у
®у0)
f(х;у), но limх
®х0(у
®у0)
f(х;у)¹f(х0
;у0
).
Классификация точек разрыва:
Если (х0
;у0
) точка разрыва и сущ-ют конечные пределы со всех сторон, то (х0
;у0
) – 1 род.
Если (х0
;у0
) – 1 род, сущ-ют конечные пределы со всех сторон и эти пределы равны между собой, то разрыв устранимый.
Если (х0
;у0
) точка разрыва и не сущ-ют конечные пределы со всех сторон, то (х0
;у0
) – 2 рода.
Непрерывность фун нескольких (или 2) переменных в замкнутой области.
Опр: Фун-я, непрерывная в каж точке некоторой замкнутой области, наз непрерывной в этой замкнутой области.
Св-ва: 1)Если фун f(x;y…) определена и непрерывна в замкнутой и ограниченной области D, то в обл D найдется по крайней мере одна точка N(х0
;у0
…) такая, что для всех др точек обл будет выплн-ся соот-е f(х0
;у0
…)³f(х;у) и по крайней мере одна точка `N(`х0
;`у0
…) такая, что для всех др точек обл будет выпол соот-е f(`х0
;`у0
…)£f(х;у…). Фориулируется так: Непрерывная фун в замкнутой огранич обл
D достигает по крайней мере один раз наиболь значения М и наимень значения
m.
2)Если фун f(x;y…) непрерывна в замкнутой и ограниченной обл D и если M и m – наиб и наим значения фун f(x;y…) в обл, то для любого числа m, удовл усл m<m<М, найдется в обл такая точка N*
(x*
;y*
…), что будет выполн рав-во f(x*
0
;y*
0
…)=m. Следствие из св2: Если фун f(x;y…) непрерывна в замкнутой огран обл и принимает как положит, так и отрицательные значения, то внутри области найдутся точки, в которых функция f(x;y…) обращается в нуль.
Частное приращ-е, произв-ные, диф-лы фун-и.
Пусть имеем функцию z=f(х;у). Дадим независимой переменной х приращение ∆х, тогда z получит приращение, кот. наз. частным приращением
z по x.
∆x
z=f(x+∆x,y)-f(x,y) Аналогично частное приращение по y ∆y
z=f(x,y+∆y)-f(x,y).
Частные производные. Опр: Частной производной по x от функции z=f(x,y)
наз. предел отношения частного приращения ∆x
z к приращ-ю ∆x при ∆x®0.
∂z/∂x=lim(∆x
®0)
∆x
z/∆x=lim(∆x
®0)
(f(x+∆x,y)-f(x,y))/∆x. Аналогично частная производная по y.
∂z/∂y=lim(∆y
®0)
∆y
z/∆y=lim(∆y
®0)
(f(x,y+∆y)-f(x,y))/∆y.
Част диф-л фун: dx
z(x;y)=[(¶z/¶x)*Dx] и dу
z(x;y)=[(¶z/¶у)*Dу].
Полное приращ-е, полный диф-л. Диф-ть фун.
Пусть имеем функцию z=f(х;у). Сообщив аргументу x приращение ∆x, а аргументу y приращение ∆y, получим для z новое приращение ∆z , кот наз. полным приращением.
∆z=f(x+∆x,y+∆y)-f(x,y).
Полный дифференциал: Если фун z=f(x;y) имеет непрерывные частные производные в данной точке, то она диф-ма в этой точке и имеет полный диф-л dz=(∂f/∂x)*∆x+(∂f/∂y)*∆y.
Дифференцируемость ф-и: Ф-я z=f(x,y) наз. дифференцируемой в т. (x0
,y0
),
если её полное приращение ∆z можно представить в виде суммы 2 слагаемых ∆z=(A*∆x+B*∆y)+0(r), где r=Ö(∆x2
+∆y2
), т.е. lim(
Dх
®0,
Dу
®0,
r
®0)
0(r)/r=0 бесконечная величина более высокого порядка малости, чем r. (A*∆x+B*∆y) линейное относительно ∆x ,∆y.
Полный диф-л в приближенных вычислениях:
f(x+∆x0
,y+∆y)»f(x,y)+[¶f(x,y)/¶x]*Dx+[¶f(x,y)/¶y]*Dy.
Необходимое усл диф-ти:
Если z=f(x,y) диффер-ема в т.(x0
,y0
), то сущ. конечные частные производные (∂z/∂х;∂z/∂y) при x=x0
, y=y0
. A=∂z(х0
;у0
)/∂x; B=∂z(х0
;у0
)/∂y.
Достаточное усл диф-ти:
Если функция z=f(x,y) в т.(x0
,y0
) и в нек. окресности непрерывна и имеет непрерывные частные производные (∂z/∂х;∂z/∂y), то ф-ия диф-ма.
Производные высших порядков.
∂z/∂x=φ(x,y); ∂z/∂y=φ(x,y); Вторая производная: ∂φ/∂x=∂2
z/∂x2
;z``
xx
здесь фун диф-я посл-но 2раза по х;
∂φ/∂y=∂z/∂x∂y;z``
xy
;∂φ/∂x=∂z/∂y∂x;z``
yx
; ∂φ/∂y=∂2
z/∂y2
;z``
yy
;
Третья производная: ∂3
z/∂x3
; ∂3
z/∂x2
∂y; ∂3
z/∂x∂y¶х; ∂3
z/∂y∂x2
; ∂3
z/∂y∂x∂y; ∂3
z/∂y2
∂x; ∂3
z/∂y3
.
Производная сложной ф-ии.
z=f(u,v)=F(x;y), u=j(х;у) и v=y(х;у). Если ф-ия f диф-ма по u и v, а u и v диф-ы по x и y, то выполняется след равенство ¶z/¶x=(∂z/∂u)(¶u/¶x)+(∂z/∂v)(¶v/¶x); ¶z/¶y=(∂z/∂u)(¶u/¶y)+(∂z/∂v)(¶v/¶y).
z=f(x;u;v)=F(x)
Полная производная по х:
dz/dx=¶z/¶x+(∂z/∂u)(du/dx)+(∂z/∂v)(dv/dx);
Полная производная по
у:
dz/dу=¶z/¶у+(∂z/∂u)(du/dу)+(∂z/∂v)(dv/dу);
Экстремумы фун 2 переменных.
Ф-ия z=f(x,y) имеет максимум (минимум)
в точке M0
(x0
,y0
), если f(x0
,y0
)> f(x,y) {f(x0
,y0
)<f(x,y)}для всех точек (x,y) достаточно близких к точке (x0
,y0
)и отличных от неё.
Определение max и min при предположении, что х=х0
+Dх и у=у0
+Dу, тогда
f(x;y)-f(x0
;y0
)=f(х0
+Dх;у0
+Dу)-f(x0
;y0
)=Df. 1)Если Df<0 при всех достаточно малых приращениях независимых переменных, то фун f(x;y) достигает max в точке М0
(х0
;у0
); 2)Если Df>0 при всех достаточно малых приращениях независимых переменных, то фун f(x;y) достигает min в точке М0
(х0
;у0
);
Необходимое усл экстремум:
Если функция z=f(x,y) достигает экстремума при x=x0
, y=y0
, то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не сущ.
Док-во: Действительно, дадим переменному y определённое значение, а именно y=y0
. Тогда ф-ия f(x,y0
) будет функцией одного переменного x. Т.к. при x=x0
она имеет экстремум, то следовательно (∂z/∂x) при x=x0
,y=y0
или равно нулю или не сущ. Аналогично доказ, что (∂z/∂у) при x=x0
, y=y0
или равно нулю или не сущ.
Достаточное усл экстемум:
Пусть в нек. Области, содержащей т.M(x0
,y0
), функция f(x,y) имеет непрерывные частные производные до третьего порядка включительно, пусть, кроме того т.M(x0
,y0
) является критической точкой функции f(x,y) т.е. ∂f(x0
,y0
)/∂x=0, ∂f(x0
,y0
)/∂y=0.
Тогда при x=x0
, y=y0
:
1)f(x,y) имеет максимум, если
∂2
f(x0
,y0
)/¶x2
*∂2
f(x0
,y0
)/¶y2
-(∂2
f(x0
,y0
)/∂x∂y)2
>0 и ∂2
f(x0
,y0
)/¶x2
<0
2)f(x,y) имеет максимум, если
∂2
f(x0
,y0
)/¶x2
*∂2
f(x0
,y0
)/¶y2
-(∂2
f(x0
,y0
)/∂x∂y)2
>0 и ∂2
f(x0
,y0
)/¶x2
>0
3)f(x,y) не имеет ни макс. ни мин.
∂2
f(x0
,y0
)/¶x2
*∂2
f(x0
,y0
)/¶y2
-(∂2
f(x0
,y0
)/∂x∂y)2
<0
4)Если ∂2
f(x0
,y0
)/¶x2
*∂2
f(x0
,y0
)/¶y2
-(∂2
f(x0
,y0
)/∂x∂y)2
=0, то экстремум может быть, а может и не быть.
Неявнозаданная функция и нахождение ее производной.
Задана фун F(x,y,z)=0 наз заданная неявно,
если существует z=j (x,y) в некоторой области D что при подстановке получаем тождественно нуль. F(x,y,z)º0. Продифф. по x: F(x,y,z)º0, F¢x
=0, ¶F/¶x+(¶F/¶z)*(¶z/¶x) ¶z/¶x=--[(¶F/¶x)/(¶F/¶z)];
Продифф. аналогично по у ¶z/¶y=--[(¶F/¶y)/(¶F/¶z)]
Двойной интеграл.
Рассмотрим в плоскости ОХУ замкнутую область D ограниченную линией L. Пусть в области D задана непрерывная функция z=f(x,y). Разобьем D на n частей(DS1
,DS2
,DS3
…DSn
). На каждой площадке возьмем по точке Pi
(P1
,P2
,P3
…Pn
). f(Pi
) – значение функции в заданной точке. Возмем сумму произведений вида: f(Pi
)DSi
. Vn
=n
åi=1
f(Pi
)DSi
– это интегральная сумма для функции f(x,y) по обл D.
  Опр: Предел limmax
di
®0
n
åi=1
f(Pi
)DSi
интегральной суммы n
åi=1
f(Pi
)DSi
, если он сущ-ет независимо от способа разбиения обл D на DDi
и от выбора точек Pi
ÎDi
наз двойным интегралом зад фун
z=
f(
x;
y) по обл
D. Опр: Предел limmax
di
®0
n
åi=1
f(Pi
)DSi
интегральной суммы n
åi=1
f(Pi
)DSi
, если он сущ-ет независимо от способа разбиения обл D на DDi
и от выбора точек Pi
ÎDi
наз двойным интегралом зад фун
z=
f(
x;
y) по обл
D.
Теорема: Если сущ-ет фун z=f(x;y) непрерывна в заданной обл `D, то сущ-ет предел limmax
di
®0
n
åi=1
f(Pi
)DSi
т.е. сущ-ет двойной интеграл для данной фун по данной области. limmax
di
®0
n
åi=1
f(Pi
)DSi
=óóD
f(x;y)dxdy=(или)= =óóD
f(x;y)dS/¶
Св-ва:
1)óóD
(f1(x,y)+f2(x,y))dxdy=óóD
f1(x,y)dxdy+óóD
f2(x,y)dxdy
2) óóD
a f(x,y)dxdy=aóóD
f(x,y)dxdy.
3) Если область D=D1
ÈD2
, то
óóD
f(x,y)=óóD
1
f(x,y))+óóD
2
f(x,y).
Док-во: Инегральную сумму по обл D можно представить в виде D1
и D2
.
óóD
f(Pi
)DSi
=óóD
1
f(Pi
)DSi
+óóD
2
f(Pi
)DSi
, где превая сумма содержит слагаемые, соот-е площади обл D1
, вторая – соот-е площадкам обл D2
. В самом деле, т.к. двойной интеграл не зависит от способа разбиения, то мы производим разбиение области D так, что общая граница областей D1
и D2
яв-ся границей площадок DSi
. Переходя в равенство
óóD
f(Pi
)DSi
=óóD
1
f(Pi
)DSi
+óóD
2
f(Pi
)DSi
к пределу при DSi
®0, получаем равенство
óóD
f(x,y)=óóD
1
f(x,y))+óóD
2
f(x,y).·
4) Если фун f(x,y)=1, то óóD
1dxdy=SD
5) Если фун в данной области f(x,y)³(£)0, то интегр от этой фун отриц (полож) не может быть
óóD
f(x,y)dxdy³(£)0
6) Если f1(x,y)³f2(x,y), то
óóD
f1(x,y)dxdy³óóD
f2(x,y)dxdy
7)Теорема о среднем: Двукратный интеграл ID
от f(x,y) по области D с площадью S равен произведению площади S на значение функции в некоторой точке P области D.
в
óа
( j
2(x)
ój
1(x)
f(x,y)dy)dx=f(P)*S.
Док-во: Из соот-я
mS£в
óа
(j
2(x)
ój
1(x)
f(x,y)dy)dx=f(P)*S£MS получаем mS£1/S*ID
£MS. Число 1/S*ID
заключено между наиболь и наимень знач f(x,y) в области D. В силу непрерывности фун f(x,y) принимает в некоторой точке P обл D принимает значение равное 1/S*ID
.
Двукратный интеграл
Пусть дана область D такая, что любая прямая параллельная одной из осей пересекает эту область в двух точках. Пусть область D ограничена линиями y=f1(x), y=f2(x), y=a, y=b (a<b, f1(x)<f2(x)). Пусть f(x,y) непрерывна в области D.
Рассмотрим ID
=в
óа
f
2(
x
)
óf
1(
x
)
f(x,y)dydx=в
óа
Ф(х)dx
-это двукратный интеграл
.
Вычисление двойного интеграла есть вычисление двукратного интеграла.
Вычисление двойного интеграла в полярных координатах:
óóD
f(x,y)dxdy=½x=pcosj, y=psinj , I=p½=
=óóD
f(pcosj;psinj)pdpdj=
=j2
ój1
dj p2(
j
)
óp1(
j
)
(pcosj ;psinj)pdp.
Геометрическое приложение двойного интеграла.
Площадь плоской поверхности.
óóD
f(x,y)dxdy=SD
2) Объем цилиндроидов. z=f(x,y)>0. По определению область D разбивается на элементарные кусочки DDi; выбрать в этих кусочках точку принадлежащую DDi и найти значение функции в этой точке. DVi=f(xi,yi)*DSi. Сумма
DVi=n
åi
=1
f(xi,yi)*DSi – это объем фигуры состоящей из элементарных параллелепипедов. Основания параллелепипедов заполняют область D.
limmax
di
®
0
n
åi
=1
f(xi,yi)*DSi=VТ
если этот предел сущ-ет, то это V тела (цилиндройда).óó f(x,y)dxdy=Vцил
Площадь поверхности.
Sпов.
= óó[Ö1+(dz/dx)2
+(dz/dy)2
dxdy].
Диф-е ур-я (осн понятия).
Общий вид диф ур F(x;y;y’;у”…уn
)=0. Наивысший порядок производ-й в ур-и F(x;y;y’;у”…уn
)=0 наз порядковым ур-ем.
Решением ур
F(
x;
y;
y’;у”…у
n
)=0
наз любая фун вида у=j(х), которая будучи подставленная в F(x;y;y’;у”…уn
)=0 вместе со своими произ-ми обращает в тождество. F(x;j(х);j(х)’;j(х)”… j(х)n
)=0.
Фун вида у=j(х;С1
;С2
;…Сn
) наз общим решением ур
F(x;y;y’;у”…уn
)=0, если выполняется: 1) эта фун-я яв-ся решением при любых С1
;С2
;…Сn
; 2) для любых начальных усл х0
, у0
, у’
0
, уn
0
можно найти конкретную совокупность С1 0
;С2 0
;С3 0
;…Сn 0
при которых фун у=j(х;С1 0
;С2 0
;С3 0
;…Сn 0
), что эта фун будет удвл начальному условиям.
Соот-е вида j(х;С1
;С2
;С3
;…Сn
)=0 полученная при решении ур F(x;y;y’;у”…уn
)=0 наз общим интегралом ур
F(x;y;y’;у”…уn
)=0 (т.е. решение ур находиться в неявной форме).
Дифф. ур. 1-го порядка
Общий вид F(x;y;y’)=0 Решением данного ур
. наз. любая фун.=j(x), кот. обращает ур. в тождество.
Опр-е: Фун. y=j(x;C) наз-ся общим решением
, если она удов.:1)данная фун. яв-ся реш-м при любых C; 2)при любых x0;y0 можно найти такое C0, что фун. y= j(x,C0) удов. начальным усл-ям.
Рав-во вида Ф(x;y;C)=0, неявно задающее общее реш-е, наз-ся общим интегралом дифф. ур-я.
Опр: Частным реш-м
наз-ся любая фун. y=j(x;C0), кот. получается из общего реш. y=j(x;C), если в последнем произ. постоянному С придать опред. значение С=С0. Соотн. Ф(x;y;C0)=0 наз-ся в этом случае частным интегралом ур.
Методы интегрирования диф-я уравнений 1 порядка:
1). Ур-е с разделенными переменными
f1(x)y’=f2(y) f1(x)dy=f2(y)dx, dy/f2(y)=dx/f1(x), ∫dy/f2(y)=∫dx/f1(x) 2).Ур-е с разделяющимися переменными
f(x;y)y’+j(x;y)=0, f1(x)f2(y)dy+j1(x)j2(y)dx=0 все разделим на j2(y)*f1(x)
{f2(y)/j2(y)}dy+{j1(x)/f1(x)}dx=0
∫{f2(y)/j2(y)}dy+∫{j1(x)/f1(x)}dx=C – общий интеграл 3).Линейные диффер. ур.
y’+p(x;y)=Q(x) – общий вид, Если Q(x)º0, то линейное уравнение y’+p(x;y)=0.
Методы решений: 1) Метод вариации постоянной;
2)Решение этого ур будем искать как y=U(x)V(x) (диффер-ем) dy/dx=UdV/dx+VdU/dx (подставим) UdV/dx+VdU/dx+PUV=Q
U(dV/dx+PV)+VdU/dx=Q, dV/dx+PV=0, dV/V=-PdxlnC1+lnV=-∫Pdx
V= C1e–
∫
Pdx
и подставляем в UdV/dx+VdU/dx+PUV=Q
V(x)= e–∫
Pdx
, где ∫Pdx - какая-нибудь первообразная
V(x)dU/dx=Q(x), dU/dx=Q(x)/V(x), U=∫Q(x)/V(x)dx+C, y=V(x) ∫ Q(x)/V(x)dx+CV(x)
Уравнения приводящиеся к линейным(Бернулли)
y’+P(x)y=Q(x)yn
, P(x) и Q(x) – непрерывные фун. от x (или пост.) n¹0,1. Это ур-е наз ур Бернулли
, приводится к линейному следующим преобразованием.
Разделим на yn
с наибольшим значением n, получим
(y–
n
)y’+P(y–
n+1
)=Q, Сделаем далее замену z=(y–
n+1
), тогда dz/dx=(-n+1)(y-
n
)y’. Подставляя эти значения в ур-е
(y–
n
)y’+P(y–
n+1
)=Q, будем иметь линейное ур-е
dz/dx=(1-n)Pz=(1-n)Q
Найдя его общий интеграл и подставив вместо z выражение (y–
n+1
), получим общий инт. ур.Бернулли
Однородные ур-я
Ур-е вида y’=f(x;y) наз-ся однор.ур-ем,
если фун. f(x;y)
–однородная нулевого измерения или порядок однородности равен 0, т.е. f(tx;ty)=(t0
)f(x;y).
Фун. f(x;y) наз-ся однор.ур-ем
k-го порядка однородности
, если вып. усл. f(tx;ty)=(tk
)f(x;y); f(tx;ty)=(t0
)f(x;y), где k=0; f(tx;ty)=f(x;y), где t=1/x; f[(1/x)*x;(1/y)*x)]=f(1;y/x), обозначим y/x=U(x) след-но y=U(x)x, y’=U’x+U подставим в исходное ур-е U’x+U=f(1;U), U’x+U=j(U) (dU/dx)*x=j(U)-U, dx/x=dU/(j(U)-U), ln|x|=[∫dU/(j(U)-U)] + CÞ вместо U подст. y/x и получим общий инт.
Замеч. Однор.ур. может выгл. так M(x;y)dx+N(x;y)dy=0 если обе фун. M(x;y) и N(x;y) однородные k-го порядка.
Дифф. ур. 2-го порядка
Общий вид дифф. ур.2-го порядка F(x;y;y’;y’’)=0. Решением урав
. наз. любая фун.y=j(x), кот. обращает это ур. в тождество F(x;j(x);j’(x);j’’(x))=0
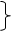 Общим решением
наз. ур. вида y=(x;C1;C2), кот. яв-ся 1)реш. при любых знач. C1,C2,Cn; 2)для любых x0,y0,y0’,y0’’ можно найти С10,С20, при кот. заданная фун. y=j(x1; С10;С20) будет удов. заданному нач. ур-ю, т.е. Общим решением
наз. ур. вида y=(x;C1;C2), кот. яв-ся 1)реш. при любых знач. C1,C2,Cn; 2)для любых x0,y0,y0’,y0’’ можно найти С10,С20, при кот. заданная фун. y=j(x1; С10;С20) будет удов. заданному нач. ур-ю, т.е.
j(x0;С10;С20)=y0 ,
j’(x0; С10;С20)=y0’
Линейные дифф. ур-я 2-го порядка
Общий вид линейн. диф. ур. 2-го порядка y’’+P(x)y’+q(x)y=f(x). (1)
Если f(x)=0 следовательно y’’+P(x)y’+q(x)y=0 (2)
– линейное однородное урав.
Структура реш. лин. одн.ур.2-го пор.
1)Если 2 реш. ур (2) y1(x) и y2 (x) – линейно-независ, т.е. нельзя одну вырозить через др, т.е.
y1(x)/y2(x)¹const, то общим решением ур (2) y=C1y1+C2y2
2) Если известно одно реш. y1, то др. найдем по форм. y2= y1∫[(e–∫
P(
x)
dx
)]/(y1
2
)dx. Общее реш. y=C1y1+C2y2
3) y1 находим подбором.
Структура общего реш. неоднородного ур.
1)Общее реш.y(x)=y(-)+y*, где y(-)=C1y1+C2y2 общее реш.(2), y*- нек. частное реш. самого ур.
2)Метод вариации произ. постоянной
y*= C1(x)y1+C2(x)y2
3)Для нахождения C1(x) и C2(x) созд.
сист. ур-ий. 0 y2
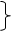 C1’(x)y1+ C2’(x) y2=0 Þ C1’(x)= f(x) y2’ C1’(x)y1+ C2’(x) y2=0 Þ C1’(x)= f(x) y2’
C1’(x)y1’+ C2’(x) y2’=f(x) y1 y2
y1’ y2’
Þ C1(x)=∫(--)/(--)dx
y1 0
C2’(x)= y1’ f(x) Þ C2(x)=∫(--)/(--)dx
y1 y2
y1’ y2’
Лин. дифф. ур-ия со спец. правой частью.
Рассмотрим случай: y’’
+py’
+qy=f(x), p,q – числа. y=c1
y1
+c2
y2
+y*
, где y1
, y2
– два лин-но незав. реш.
(1) y’’
+ py’
+qy=0 – лин. однород дифф. ур-ие 2ого порядка.
y=ekx
k2
+pk+q=0 – характерист. ур-ие ур-ия (1).
Рассмотрим 3 случия:
1. D>0, k1,2
=(-p±Ö(p2
-4q))/2, k1
¹k2
y1
=ek
1
x
, y2
=ek
2
x
.
Т.к. y1
/y2
¹const, то y=c1
ek
1
x
+c2
ek
2
x
.
2. D=0 k1,2
=-p/2
y1
=e-px/2
, y2
=y1
∫(e--
∫
pdx
)/y1
2
dx=e-px/2
, y=e-px/2
(c1
+c2
x).
3.Когда корни комплексные, т.е. D<0, k1,2
=a±bi, y1
=ea
x
Cosbx, y2
=ea
x
Sinbx, y1
/y2
¹const, y=ea
x
(c1
Cosbx+c2
Sinbx)
Неоднородные ур-ия со спец. правой частью.
1. f(x)=Pn
(x)ea
x
1) a - не явл-ся корнем хар. ур-ия
y*
=(A0
xn
+A1
xn-1
++...+An
)=Qn
(x)ea
x
.
a - однократный корень y*
=xQn
(x)ea
x
.
3) a - двукрат. корень y*
=x2
Qn
(x)ea
x
.
2. f(x)=p(x)ea
x
Cosbx+q(x)ea
x
Sinbx
1) a+bi – не корень y*
=U(x)ea
x
Cosbx+V(x)ea
x
Sinbx.
2) a+bi – корень y*
=x[U(x)ea
x
Cosbx+V(x)ea
x
Sinbx].
3. f(x)=MCosbx+NSinbx
1)bi – не корень, y*
=ACosbx+BSinbx.
2)bi – корень, y*
=x(ACosbx+BSinbx).
РЯДЫ
Числовые ряды. Основные определения.
Пусть дана бесконечная послед-ть чисел U1
, U2
...Un
,... Выражение U1
+U2
+...+Un
+... наз-ся числовым рядом
,
U1
, U2
...Un
– члены ряда.
Сумма конечного числа n первых членов ряда наз-ся
n-ой частичной суммой ряда
: Sn
= U1
+U2
+...+Un
.
Если сущ-ет конечный предел limn
®
¥
Sn
=S, то этот предел наз суммой ряда.
Если предел limn
®
¥
Sn
равен ¥ или не сущ-ет, то говорят , что ряд расходится.
Если сущ-ет предел limn
®
¥
Sn
,
то ряд сходится.
Некоторые очевидные свойства числовых рядов:
1)Теорема 1. На сходимость ряда не влияет отбрасывание конечного числа его членов.
Док-во
: Sn
– сумма n первых членов ряда, Ck
– сумма k отброшенных членов, Dn
-
k
– сумма членов ряда, входящих в сумму Sn
и не входящих в Ck
. Тогда имеем: Sn
=Ck
+Dn
-
k
, где Ck
– постоянное число, не зависящее от n. Из последнего соотношения следует, что если сущ-ет limDn
-
k
, то сущ-ет и limSn
; если сущ-ет limSn
, то сущ-ет limDn
-
k
, а это доказ-ет справедливость теоремы.
2)Теорема 2. Если ряд a1
+a2
+...(1) сходится, и его сумма равна S, то ряд ca1
+ca2
+...(2), где c=const, также сходится и его сумма равна сS.
Док-во:
обозначим n-ю частичн сумму ряда (1) через Sn
, а ряда (2) – через Dn
. Тогда Dn
=ca1
+...+can
=c(a1
+...+an
)=cSn
. Отсюда ясно, что передел n-ой частичной суммы ряда (2) сущ-ет, т.к.
lim Dn
=lim(cSn
)=climSn
=cS. ч.т.д.
3)Теорема 3. Если ряды a1
+a2
+...(5) и b1
+b2
+...(6) сходятся, и их суммы, соответственно, равны S1
и S2
, то ряды (a1
+b1
)+(a2
+b2
)+...(7) и (a1
–b1
)+(a2
–b2
)+...(8) также сходятся, и их суммы, соответственно, равны S1
+S2
и
S1
–S2
.
Док-во:
док-ем сходимость ряда (7). Обозначая его n-ую частичную сумму через Dn
, а n-е частичные суммы рядов (5) и (6) соответственно через S1
n
и S2
n
, получим: Dn
=(a1
+b1
)+...+(an
+bn
)=(a1
+...+an
)+(b1
+...+bn
)=S1
n
+S2
n
. Переходя к в этом равенстве к пределу при n®¥:, получим limDn
=lim(S1
n
+S2
n
)= limS1
n
+limS2
n
=S1
n
+S2
n
.
Т.о., ряд (7) сходится и его сумма равна S1
n
+S2
n
.
4)Необходимый признак сходимости ряда. Если ряд сходится, то limUn
=0 n®¥.
Док-во:
пусть ряд U1
+U2
+...+Un
+... сходится, т.е. limSn
=Sn®¥, тогда имеет место равенство limSn
-1
=S.
limSn
–limSn-1
=0, lim(Sn
–Sn-1
)=0. Но Sn
–Sn
-1
=Un
следов-но limUn
=0 ч.т.д.
Достат. призаки сходимости знакоположит. рядов.
1)Признак сравнения. Пусть дан ряд U1
+U2
+...+Un
+...(1), S1
n
; V1
+V2
+...+Vn
+...(2) S2
n
; Известно,что Vn
³Un
при n³N0
.
если ряд (2) сходится, то ряд (1) также сходится;
если ряд (1) расходится, то ряд (2) расходится.
Док-во:
Из сходимости ряда (2) следует, что $limS2
n
=S. S1
n
=U1
+U2
+...+UN
0
+UN
0+1
+...+Un
=SN
0
+VN
0+1
+...+Vn
. limS1
n
=lim(SN
0
+Dn
-
N0
)=SN
0
+D. S1
n
– возраст. послед-ть, ограниченная числом SN
0
+D => $limS1
n
=Sn
1
.
2) Предельный признак сравнения. Если сущ-ет limUn
/Vn
=L, но L¹0,¥ при n®¥, то ряды ведут себя одинаково.
3) Признак Даламбера.
Если $lim(Un
+1
/Un
)=L(2) при n®¥, то: 1) ряд сходится, если L<1; 2) расходится, если L>1. Док-во:
1) пусть L<1. Рассмотрим число q, удовл. соотнош L<q<1. Из определения предела и соотношения (2) следует, что для всех n, n³N, будет иметь место нер-во (Un
+1
/Un
)<q (2’
). Действительно, т.к. величина Un
+1
/Un
стремится к пределу L, то разность м/у этой величиной и числом L м.б.сделана (начиная с некоторого номера N) по абсолютному значению меньше любого положит числа, в частности, меньше, чем q–L, т.е.
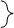 |Un
+1
/Un
– L|<q–L. из последнего нер-ва и следует нер-во (2’). Записывая нер-во (2’
) для различных значений n, начиная с номера N, получим UN
+1
<qUN
, |Un
+1
/Un
– L|<q–L. из последнего нер-ва и следует нер-во (2’). Записывая нер-во (2’
) для различных значений n, начиная с номера N, получим UN
+1
<qUN
,
UN
+2
<qUN
+1
< q2
UN
Рассмотрим теперь два ряда:
U1
+U2
+...+UN
+Un+1
+... (1)
UN
+qUN
+q2
UN
+... (1’
). Ряд (1’
) есть геом прогрессия с положит знаменат q<1. Следоват-но, этот ряд сходится. Члены ряда (1), начиная с UN
+1
, меньше членов ряда (1’
), следоват-но, ряд (1) сходится. Ч.т.д. 2) Пусть L>1. тогда из равенства lim(Un
+1
/Un
)=L следует, что, начиная с некот. N, т.е. для n³N, будет иметь место нер-во (Un
+1
/Un
)>1, или Un
+1
>Un
для всех n³N. Но это озн-ет, что члены ряда возрастают, начиная с номера N+1, и поэтому общий член ряда не стремится к нулю. Значит, ряд расходится.
4)Признак Коши. Если для ряда с положит членами limn
ÖUn
=L, то: 1) ряд сходится, если L<1; 2)расходится, если L>1.
Док-во:
1) пусть L<1. Рассмотр число q, L<q<1. Начиная с некот n=N, будет иметь место соотношение
|n
ÖUn
–L|<q–L; осюда следует, что n
ÖUn
<q или Un
<qn
для всех n³N. Рассмотрим теперь два ряда: U1
+U2
+...+UN
+UN
+1
+... (1) и qN
+qN
+1
+qN
+2
+... (1’
). Ряд (1’
) сходится, т.к. его члены обр-ют убыв. геом прогр. Члены ряда (1), начиная с UN
, меньше членов ряда (1’
). Значит, ряд (1) сходится. 2) Пусть L>1. Тогда, начиная с некот номера n=N, будем иметь: n
ÖUn
>1 или Un
>1. но если все члены рассматр ряда, начиная с UN
, больше 1, то ряд расходится, т.к. его общий член не стремится к нулю.
5)Интегральный признак сходимости. Имеем ряд ¥
ån=1
Un
, где члены ряда убывают Un
>Un
+1
>0. Есть фун f(x)>0, хÎ[1;¥] непрерывная и убывающая и такая, что при целых значениях х=n значение фун-и f(n)=Un
.
Если не собственный интеграл ¥
ò1
f(x)dx – сходиться, то ряд сходится. Если не собственный интеграл ¥
ò1
f(x)dx – расходиться, то ряд расходится.
Знакочередующиеся ряды.
Под знакочередующимся
рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны.
Т.Лейбница: Если члены знакочередующегося ряда убывают по абсолютной величине U1
>U2
>U3
… и предел его общего члена при n®¥ равен 0
(Lim n
®
¥
Un
=0), то ряд сходится, а его сумма не превосходит первого члена: U1
³S.
Д: Рассмотрим последовательность частичных сумм четного числа членов при n=2m:
S2m
=(U1
-U2
)+(U3
-U4
)+…+(U2m-1
-U2m
). Эта последовательность возрастающая и ограниченная. На основании признака существования придела последовательность S2
m
имеет предел Limm
®
¥
S2
m
=S. Переходя к пределу в неравенстве S2
m
<U1
при m®¥, получим, что U1
³S. Рассмотрим последовательность частичных сумм нечетного числа членов при n= 2m+1. Очевидно, что S2
m+1
=S2
m
+A2
m+1
; Поэтому учитывая необходимый признак сходимости ряда, Limm
®
¥
S2
m+1
=
=Limm
®
¥
S2
m
+ Limm
®
¥
А2
m+1
=S+0=S. Итак, при любом n (четном и нечетном) Limn
®
¥
Sn=S, т.е. ряд сходится.
Знакопеременные ряды.
Пусть U1
+U2
+U3
….+Un
+ знакопеременный ряд (*), в котором любой его член Un
может быть как положительным, так и отрицательным.
Т.(Достаточный признак сходимости знакопеременного ряда): Если ряд, составленный из абсолютных величин членов данного ряда (*) и если ряд ¥
ån=1
½Un
½; |U1
|+|U2
|+…+|Un
|+…(1), сходится и наз абс. сходящимся.
Обратное утверж не справедливо.
Д: Обозначим Sn
+
и Sn
-
суммы абсолютных величин членов данного ряда (*), входящих со знаком плюс и минус. Тогда частичная сумма данного ряда Sn
1
=Sn
+
-Sn
-
, а ряда составленного из абсолютных величин его членов Sn
2
= Sn
+
+Sn
-
. По условию ряд (1) сходится, значит сущ-т конечный предел Limn
®
¥
Sn
2
=S. Последовательности Sn
+
и Sn
-
являются возрастающими и ограниченными (Sn
+
≤ SSn
-
≤ S ), значит существуют пределы
Limn
®
¥
Sn
+
и Limn
®
¥
Sn
-
, и соответственно предел частичной суммы данного ряда
Limn
®
¥
Sn1
=Limn
®
¥
Sn
+
-Limn
®
¥
Sn
-
, т.е. ряд (*) сходится.·
Если ряд |U1
|+|U2
|+…+|Un
|+…сходиться, то ряд U1
+U2
+U3
….+Un
+ наз абс. сходящимся.
Если ряд U1
+U2
+U3
….+Un
+ сходиться, а ряд |U1
|+|U2
|+…+|Un
|+…расходиться, то ряд U1
+U2
+U3
….+Un
+ наз усл. сходящимся.
Св-ва абс сход рядов: Если ряд U1
+U2
+U3
….+Un
+ абс сходиться, то на сходимость не влияет перестановка членов ряда и группировка.
Степенные ряды.
C0
+C1
X+C2
X2
+…+Cn
Xn
..-степенной ряд (*)
Св-ва: 1)Т. Абеля: 1)Если степенной ряд сходится при значении X=X0
≠0, то он сходится и, притом абсолютно, при всех значениях Х таких что |Х|<|X0
|, 2)Если степенной ряд расходится при Х=Х1
, то он расходится при всех значениях Х таких что |Х|>|Х1
|.
Д: 1)По условию ряд (*) сходится при Х=Х0
≠0, следовательно, выполняется необходимый признак сходимости Limn
®
¥
Un
=Limn
®
¥
Cn
X0
n
=0. Значит последовательность |Cn
X0
n
| Оганичена, т.е. сущ. Такое число М>0, что для всех n выполняется неравенство |Cn
X0
n
|<M. Рассмотрим ряд, составленный из абсолютных величинчленов ряда(*)
|С0
|+ |C1
X0
||Х/X0
|+…+ |Cn
X0
n
||X/X0
|n
+…(1). Члены ряда (1) меньше соответствующих членов ряда М+М|Х/X0
|+…+М|X/X0
|n
+… представляющего геометрический ряд, к-й сходится, когда его знаменатель q=|X/X0
|<1, т.е. при|X|<|X0
|, на основании признака сравнения ряд (*) сходится. 2)Предположим противное, т.е. при|X|>|X1
| ряд (*) сходится. Тогда по доказанному выше он должен сходится и в точке Х1
(т.к. |X|>|X1
|), что противоречит условию.·
Из теоремы Абеля следует, что сущ. Такое число R≥0, что при │Х│<R ряд сходится, а при │Х│>R – расходится. Число R получило название радиуса сходимости
, а интервал (-R;R)-интервала сходимости
степенного ряда.
2) и 3) на любом отрезке [a,b], целиком принадлежащем интервалу сходимости(-R;R), ф-я F(x) является непрерывной, а следовательно степенной ряд можно почленно интегрировать и дифференцировать на этом отрезке.
4) Степенные ряды вида а0
+а1
х+а2
х2
+…+аn
х2
+…+аn+1
хn+1
+… и
а0
+а1
(х-х0
)+а2(х-х0
)2
+…+аn(х-х0
)2
+… сходяться равномерно.
5) Степенные ряды сход к фун S(x), которая непрерывна в обл сходимости.
Функциональные ряды
Ряд U1
+U2
+..+Un+.. называется функциональным,
если его члены являются функциями от Х. Рассмотрим функциональный ряд U1
(Х)+U2
(Х)+..+Un(Х)+...(1) Совокупность тех значений Х, при которых функциональный ряд сходится, называют областью сходимости
этого ряда.
Обозначим через Sn
(Х) сумму первых n членов ряда (1). Если этот ряд сходится и сумма его равна S(x), то S(x)=Sn
(x)+rn
(x), где rn
(x) есть сумма ряда Un
+1
(x)+Un
+2
(x) +…, т.е. rn
(x)= Un+1
(x)+Un+2
(x) +… В этом случае величина rn
(x) называется остатком ряда (1). Для всех значений Х в области сходимости ряда имеет место соотношение Limn
→∞
rn
(x)= Limn
→∞
[S(x)-Sn
(x)]=0, т.е. остаток rn
(x) сходящегося ряда стремится к нулю при n→∞.
Функциональный ряд U1
(Х)+U2
(Х)+..+Un(Х)+.. (1) называется мажорируемым
в нек-й области изменения Х, если существует такой сходящийся числовой ряд а1
+а2
+а3
+…+аn
..(2) с положительными членами, что для всех значений Х из данной области выполняются соотношения │U1
(x)│≤a1,
…,│Un
(x)│≤an
,… Иначе, ряд называется мажорируемым,
если каждый его член по абсолютной величине не больше соответствующего члена нек-го сход. ряда с полож. членами.
Ряд Тейлор.
Для ф-и F(x) имеющей все производные до (n-1) порядка включительно, в окрестности точки х=а справедлива формула Тейлора: f(x)=f(a)+f¢(a)(x-a)+f¢¢(a)[(x-a)2
/2!]+…
…+fn
(a)[(x-a)n
/n!]+Rn
(x), (1) где остаточный член Rn
(х)={[(x-a)n+
1]/[(n+1)!]}f(
n+1)
[a+q(x-a)], где 0<q<1. Для того, чтобы ряд сходился к ф-и, необходимо и достаточно, чтобы при n®¥ остаток ряда стремился к 0, т.е. Rn
(x)®o. Переходя в формуле (1) к пределу при n®¥, получим справа бесконечный ряд, котороый наз рядом Тейлора:
f(x)=f(a)+f¢(a)(x-a)+…+fn
(a)[(x-a)n
/n!]+…
Если в ряде Тейлора предположим а=0, то получим ряд Маклорена: f(x)=f(0)+f¢(0)x+f¢¢(0)[x2
/2!]+…
…+fn
(0)[xn
/n!]+….
Разложение нек-х ф-й в ряд Маклорена:
ex
=1+x+x2
/2!+…+xn
/n!+… (-¥;¥)
sinX=x-x3
/3!+x5
/5!+…+(-1)n-1
[X2n-1
]/(2n-1)!+… (-¥;¥)
cosX=1-x2
/2!+x4
/4!-…+[(-1)n
X2n
]/(2n)!+… (-¥;¥)
(1+x)m
=1+mx+[m(m-1)x2
]/2!+[m(m-1)*
*(m-2)x3
]/3!+[m(m-1)(m-n+1)xn
]/n!+… (-1;1)
ln(1+x)=x-x2
/2+x3
/3-..+[(-1)n
xn+1
]/(n+1)+.. (-1;1]
1/(1-x)=1+x+x2
+…+xn
+..
1/(1+X2
)=1-x2
+x4
-x6
+…
arctgX=x-x3
/3+x5
/5-x7
/7+…+[(-1)n+1
x2n-1
]/2n-1+…
|