КЛАСТЕРНЫЙ АНАЛИЗ В ЗАДАЧАХ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО ПРОГНОЗИРОВАНИЯ
Введение в кластерный анализ.
При анализе и прогнозировании социально-экономических явлений исследователь довольно часто сталкивается с многомерностью их описания. Это происходит при решении задачи сегментирования рынка, построении типологии стран по достаточно большому числу показателей, прогнозирования конъюнктуры рынка отдельных товаров, изучении и прогнозировании экономической депрессии и многих других проблем.
Методы многомерного анализа - наиболее действенный количественный инструмент исследования социально-экономических процессов, описываемых большим числом характеристик. К ним относятся кластерный анализ, таксономия, распознавание образов, факторный анализ.
Кластерный анализ наиболее ярко отражает черты многомерного анализа в классификации, факторный анализ – в исследовании связи.
Иногда подход кластерного анализа называют в литературе численной таксономией, численной классификацией, распознаванием с самообучением и т.д.
Первое применение кластерный анализ нашел в социологии. Название кластерный анализ происходит от английского слова cluster – гроздь, скопление. Впервые в 1939 был определен предмет кластерного анализа и сделано его описание исследователем Трионом. Главное назначение кластерного анализа – разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы или кластеры. Это означает, что решается задача классификации данных и выявления соответствующей структуры в ней. Методы кластерного анализа можно применять в самых различных случаях, даже в тех случаях, когда речь идет о простой группировке, в которой все сводится к образованию групп по количественному сходству.
Большое достоинство кластерного анализа в том, что он позволяет производить разбиение объектов не по одному параметру, а по целому набору признаков. Кроме того, кластерный анализ в отличие от большинства математико-статистических методов не накладывает никаких ограничений на вид рассматриваемых объектов, и позволяет рассматривать множество исходных данных практически произвольной природы. Это имеет большое значение, например, для прогнозирования конъюнктуры, когда показатели имеют разнообразный вид, затрудняющий применение традиционных эконометрических подходов.
Реклама

Кластерный анализ позволяет рассматривать достаточно большой объем информации и резко сокращать, сжимать большие массивы социально-экономической информации, делать их компактными и наглядными.
Важное значение кластерный анализ имеет применительно к совокупностям временных рядов, характеризующих экономическое развитие (например, общехозяйственной и товарной конъюнктуры). Здесь можно выделять периоды, когда значения соответствующих показателей были достаточно близкими, а также определять группы временных рядов, динамика которых наиболее схожа.
Кластерный анализ можно использовать циклически. В этом случае исследование производится до тех пор, пока не будут достигнуты необходимые результаты. При этом каждый цикл здесь может давать информацию, которая способна сильно изменить направленность и подходы дальнейшего применения кластерного анализа. Этот процесс можно представить системой с обратной связью.
В задачах социально-экономического прогнозирования весьма перспективно сочетание кластерного анализа с другими количественными методами (например, с регрессионным анализом).
Как и любой другой метод, кластерный анализ имеет определенные недостатки и ограничения: В частности, состав и количество кластеров зависит от выбираемых критериев разбиения. При сведении исходного массива данных к более компактному виду могут возникать определенные искажения, а также могут теряться индивидуальные черты отдельных объектов за счет замены их характеристиками обобщенных значений параметров кластера. При проведении классификации объектов игнорируется очень часто возможность отсутствия в рассматриваемой совокупности каких-либо значений кластеров.
В кластерном анализе считается, что:
а) выбранные характеристики допускают в принципе желательное разбиение на кластеры;
б) единицы измерения (масштаб) выбраны правильно.
Выбор масштаба играет большую роль. Как правило, данные нормализуют вычитанием среднего и делением на стандартное отклоненение, так что дисперсия оказывается равной единице.
Задача кластерного анализа.
Задача кластерного анализа заключается в том, чтобы на основании данных, содержащихся во множестве Х, разбить множество объектов G на m (m – целое) кластеров (подмножеств) Q1, Q2, …, Qm, так, чтобы каждый объект Gj принадлежал одному и только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время, как объекты, принадлежащие разным кластерам были разнородными.
Реклама

Например, пусть G включает n стран, любая из которых характеризуется ВНП на душу населения (F1), числом М автомашин на 1 тысячу человек (F2), душевым потреблением электроэнергии (F3), душевым потреблением стали (F4) и т.д. Тогда Х1 (вектор измерений) представляет собой набор указанных характеристик для первой страны, Х2 - для второй, Х3 для третьей, и т.д. Задача заключается в том, чтобы разбить страны по уровню развития.
Решением задачи кластерного анализа являются разбиения, удовлетворяющие некоторому критерию оптимальности. Этот критерий может представлять собой некоторый функционал, выражающий уровни желательности различных разбиений и группировок, который называют целевой функцией. Например, в качестве целевой функции может быть взята внутригрупповая сумма квадратов отклонения:

где xj - представляет собой измерения j-го объекта.
Для решения задачи кластерного анализа необходимо определить понятие сходства и разнородности.
Понятно то, что объекты i-ый и j-ый попадали бы в один кластер, когда расстояние (отдаленность) между точками Хi и Хj было бы достаточно маленьким и попадали бы в разные кластеры, когда это расстояние было бы достаточно большим. Таким образом, попадание в один или разные кластеры объектов определяется понятием расстояния между Хi и Хj из Ер, где Ер - р-мерное евклидово пространство. Неотрицательная функция d(Хi , Хj) называется функцией расстояния (метрикой), если:
а) d(Хi , Хj) ³ 0, для всех Хi и Хj из Ер
б) d(Хi, Хj) = 0, тогда и только тогда, когда Хi = Хj
в) d(Хi, Хj) = d(Хj, Хi)
г) d(Хi, Хj) £ d(Хi, Хk) + d(Хk, Хj), где Хj; Хi и Хk - любые три вектора из Ер.
Значение d(Хi, Хj) для Хi и Хj называется расстоянием между Хi и Хj и эквивалентно расстоянию между Gi и Gj соответственно выбранным характеристикам (F1, F2, F3, ..., Fр).
Наиболее часто употребляются следующие функции расстояний:
1. Евклидово расстояние d2(Хi , Хj) = 
2. l1 - норма d1(Хi , Хj) = 
3. Сюпремум - норма d¥ (Хi , Хj) = sup
k = 1, 2, ..., р
4. lp - норма dр(Хi , Хj) = 
Евклидова метрика является наиболее популярной. Метрика l1 наиболее легкая для вычислений. Сюпремум-норма легко считается и включает в себя процедуру упорядочения, а lp - норма охватывает функции расстояний 1, 2, 3,.
Пусть n измерений Х1, Х2,..., Хn представлены в виде матрицы данных размером p ´n:

Тогда расстояние между парами векторов d(Хi , Хj) могут быть представлены в виде симметричной матрицы расстояний:

Понятием, противоположным расстоянию, является понятие сходства между объектами Gi. и Gj. Неотрицательная вещественная функция S(Хi ; Хj) = Sij называется мерой сходства, если :
1) 0£ S(Хi , Хj)<1 для Хi¹ Хj
2) S(Хi , Хi) = 1
3) S(Хi , Хj) = S(Хj , Хi)
Пары значений мер сходства можно объединить в матрицу сходства:

Величину Sij называют коэффициентом сходства.
1.3. Методы кластерного анализа.
Сегодня существует достаточно много методов кластерного анализа. Остановимся на некоторых из них (ниже приводимые методы принято называть методами минимальной дисперсии).
Пусть Х - матрица наблюдений: Х = (Х1, Х2,..., Хu) и квадрат евклидова расстояния между Хi и Хj определяется по формуле:

1) Метод полных связей.
Суть данного метода в том, что два объекта, принадлежащих одной и той же группе (кластеру), имеют коэффициент сходства, который меньше некоторого порогового значения S. В терминах евклидова расстояния d это означает, что расстояние между двумя точками (объектами) кластера не должно превышать некоторого порогового значения h. Таким образом, h определяет максимально допустимый диаметр подмножества, образующего кластер.
2) Метод максимального локального расстояния.
Каждый объект рассматривается как одноточечный кластер. Объекты группируются по следующему правилу: два кластера объединяются, если максимальное расстояние между точками одного кластера и точками другого минимально. Процедура состоит из n - 1 шагов и результатом являются разбиения, которые совпадают со всевозможными разбиениями в предыдущем методе для любых пороговых значений.
3) Метод Ворда.
В этом методе в качестве целевой функции применяют внутригрупповую сумму квадратов отклонений, которая есть ни что иное, как сумма квадратов расстояний между каждой точкой (объектом) и средней по кластеру, содержащему этот объект. На каждом шаге объединяются такие два кластера, которые приводят к минимальному увеличению целевой функции, т.е. внутригрупповой суммы квадратов. Этот метод направлен на объединение близко расположенных кластеров.
4) Центроидный метод.
Расстояние между двумя кластерами определяется как евклидово расстояние между центрами (средними) этих кластеров:
d2 ij = (`X –`Y)Т(`X –`Y) Кластеризация идет поэтапно на каждом из n–1 шагов объединяют два кластера G и p, имеющие минимальное значение d2ij Если n1 много больше n2, то центры объединения двух кластеров близки друг к другу и характеристики второго кластера при объединении кластеров практически игнорируются. Иногда этот метод иногда называют еще методом взвешенных групп.
1.4 Алгоритм последовательной кластеризации.
Рассмотрим Ι = (Ι1, Ι2, … Ιn) как множество кластеров {Ι1}, {Ι2},…{Ιn}. Выберем два из них, например, Ι i и Ι j, которые в некотором смысле более близки друг к другу и объединим их в один кластер. Новое множество кластеров, состоящее уже из n-1 кластеров, будет:
{Ι1}, {Ι2}…, {Ι i , Ι j}, …, {Ιn}.
Повторяя процесс, получим последовательные множества кластеров, состоящие из (n-2), (n-3), (n–4) и т.д. кластеров. В конце процедуры можно получить кластер, состоящий из n объектов и совпадающий с первоначальным множеством Ι = (Ι1, Ι2, … Ιn).
В качестве меры расстояния возьмем квадрат евклидовой метрики di j2. и вычислим матрицу D = {di j2}, где di j2 - квадрат расстояния между
Ι i и Ι j:
| Ι1 |
Ι2 |
Ι3 |
…. |
Ιn |
| Ι1 |
0 |
d122 |
d132 |
…. |
d1n2 |
| Ι2 |
0 |
d232 |
…. |
d2n2 |
| Ι3 |
0 |
…. |
d3n2 |
| …. |
…. |
…. |
| Ιn |
0 |
Пусть расстояние между Ι i и Ι j будет минимальным:
di j2 = min {di j2, i ¹ j}. Образуем с помощью Ι i и Ι j новый кластер
{Ι i , Ι j}. Построим новую ((n-1), (n-1)) матрицу расстояния
| {Ι i , Ι j} |
Ι1 |
Ι2 |
Ι3 |
…. |
Ιn |
| {Ι i ; Ι j} |
0 |
di j21 |
di j22 |
di j23 |
…. |
di j2n |
| Ι1 |
0 |
d122 |
d13 |
…. |
d12n |
| Ι2 |
0 |
di j21 |
…. |
d2n |
| Ι3 |
0 |
…. |
d3n |
| Ιn |
0 |
(n-2) строки для последней матрицы взяты из предыдущей, а первая строка вычислена заново. Вычисления могут быть сведены к минимуму, если удастся выразить di j2k,k = 1, 2,…, n; (k ¹ i ¹ j) через элементы первоначальной матрицы.
Исходно определено расстояние лишь между одноэлементными кластерами, но надо определять расстояния и между кластерами, содержащими более чем один элемент. Это можно сделать различными способами, и в зависимости от выбранного способа мы получают алгоритмы кластер анализа с различными свойствами. Можно, например, положить расстояние между кластером i + j и некоторым другим кластером k, равным среднему арифметическому из расстояний между кластерами i и k и кластерами j и k:
di+j,k = ½ (di k + dj k).
Но можно также определить di+j,k как минимальное из этих двух расстояний:
di+j,k = min (di k + dj k).
Таким образом, описан первый шаг работы агломеративного иерархического алгоритма. Последующие шаги аналогичны.
Довольно широкий класс алгоритмов может быть получен, если для перерасчета расстояний использовать следующую общую формулу:
di+j,k = A(w) min(dik djk) + B(w) max(dik djk), где
A(w) =  , если dik £ djk , если dik £ djk
A(w) =  , если dik > djk , если dik > djk
B(w) = , если dik £ djk , если dik £ djk
B(w) =  , если dik > djk , если dik > djk
где ni и nj - число элементов в кластерах i и j, а w – свободный параметр, выбор которого определяет конкретный алгоритм. Например, при w = 1 мы получаем, так называемый, алгоритм «средней связи», для которого формула перерасчета расстояний принимает вид:
di+j,k = 
В данном случае расстояние между двумя кластерами на каждом шаге работы алгоритма оказывается равным среднему арифметическому из расстояний между всеми такими парами элементов, что один элемент пары принадлежит к одному кластеру, другой - к другому.
Наглядный смысл параметра w становится понятным, если положить w®¥. Формула пересчета расстояний принимает вид:
di+j,k = min (di,k djk)
Это будет так называемый алгоритм «ближайшего соседа», позволяющий выделять кластеры сколь угодно сложной формы при условии, что различные части таких кластеров соединены цепочками близких друг к другу элементов. В данном случае расстояние между двумя кластерами на каждом шаге работы алгоритма оказывается равным расстоянию между двумя самыми близкими элементами, принадлежащими к этим двум кластерам.
Довольно часто предполагают, что первоначальные расстояния (различия) между группируемыми элементами заданы. В некоторых задачах это действительно так. Однако, задаются только объекты и их характеристики и матрицу расстояний строят исходя из этих данных. В зависимости от того, вычисляются ли расстояния между объектами или между характеристиками объектов, используются разные способы.
В случае кластер анализа объектов наиболее часто мерой различия служит либо квадрат евклидова расстояния

(где xih, xjh - значения h-го признака для i-го и j-го объектов, а m - число характеристик), либо само евклидово расстояние. Если признакам приписывается разный вес, то эти веса можно учесть при вычислении расстояния

Иногда в качестве меры различия используется расстояние, вычисляемое по формуле:

которые называют: "хэмминговым", "манхэттенским" или "сити-блок" расстоянием.
Естественной мерой сходства характеристик объектов во многих задачах является коэффициент корреляции между ними

где mi ,mj ,di ,dj - соответственно средние и среднеквадратичные отклонения для характеристик i и j. Мерой различия между характеристиками может служить величина 1 - r. В некоторых задачах знак коэффициента корреляции несуществен и зависит лишь от выбора единицы измерения. В этом случае в качестве меры различия между характеристиками используется ô1 - ri j ô
1.5 Число кластеров.
Очень важным вопросом является проблема выбора необходимого числа кластеров. Иногда можно m число кластеров выбирать априорно. Однако в общем случае это число определяется в процессе разбиения множества на кластеры.
Проводились исследования Фортьером и Соломоном, и было установлено, что число кластеров должно быть принято для достижения вероятности a того, что найдено наилучшее разбиение. Таким образом, оптимальное число разбиений является функцией заданной доли b наилучших или в некотором смысле допустимых разбиений во множестве всех возможных. Общее рассеяние будет тем больше, чем выше доля b допустимых разбиений. Фортьер и Соломон разработали таблицу, по которой можно найти число необходимых разбиений. S(a,b) в зависимости от a и b (где a - вероятность того, что найдено наилучшее разбиение, b - доля наилучших разбиений в общем числе разбиений) Причем в качестве меры разнородности используется не мера рассеяния, а мера принадлежности, введенная Хользенгером и Харманом. Таблица значений S(a,b) приводится ниже.
Таблица значений S(a,b)
| b \ a |
0.20 |
0.10 |
0.05 |
0.01 |
0.001 |
0.0001 |
| 0.20 |
8 |
11 |
14 |
21 |
31 |
42 |
| 0.10 |
16 |
22 |
29 |
44 |
66 |
88 |
| 0.05 |
32 |
45 |
59 |
90 |
135 |
180 |
| 0.01 |
161 |
230 |
299 |
459 |
689 |
918 |
| 0.001 |
1626 |
2326 |
3026 |
4652 |
6977 |
9303 |
| 0.0001 |
17475 |
25000 |
32526 |
55000 |
75000 |
100000 |
Довольно часто критерием объединения (числа кластеров) становится изменение соответствующей функции. Например, суммы квадратов отклонений: 
Процессу группировки должно соответствовать здесь последовательное минимальное возрастание значения критерия E. Наличие резкого скачка в значении E можно интерпретировать как характеристику числа кластеров, объективно существующих в исследуемой совокупности.
Итак, второй способ определения наилучшего числа кластеров сводится к выявлению скачков, определяемых фазовым переходом от сильно связанного к слабосвязанному состоянию объектов.
1.6 Дендограммы.
Наиболее известный метод представления матрицы расстояний или сходства основан на идее дендограммы или диаграммы дерева. Дендограмму можно определить как графическое изображение результатов процесса последовательной кластеризации, которая осуществляется в терминах матрицы расстояний. С помощью дендограммы можно графически или геометрически изобразить процедуру кластеризации при условии, что эта процедура оперирует только с элементами матрицы расстояний или сходства.
Существует много способов построения дендограмм. В дендограмме объекты располагаются вертикально слева, результаты кластеризации – справа. Значения расстояний или сходства, отвечающие строению новых кластеров, изображаются по горизонтальной прямой поверх дендограмм.

Рис1
На рисунке 1 показан один из примеров дендограммы. Рис 1 соответствует случаю шести объектов (n=6) и k характеристик (признаков). Объекты А и С наиболее близки и поэтому объединяются в один кластер на уровне близости, равном 0,9. Объекты D и Е объединяются при уровне 0,8. Теперь имеем 4 кластера:
(А, С), (F), (D, E), (B).
Далее образуются кластеры (А, С, F) и (E, D, B), соответствующие уровню близости, равному 0,7 и 0,6. Окончательно все объекты группируются в один кластер при уровне 0,5.
Вид дендограммы зависит от выбора меры сходства или расстояния между объектом и кластером и метода кластеризации. Наиболее важным моментом является выбор меры сходства или меры расстояния между объектом и кластером.
Число алгоритмов кластерного анализа слишком велико. Все их можно подразделить на иерархические и неиерархические.
Иерархические алгоритмы связаны с построением дендограмм и делятся на:
а) агломеративные, характеризуемые последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров;
б) дивизимные (делимые), в которых число кластеров возрастает, начиная с одного, в результате чего образуется последовательность расщепляющих групп.
Алгоритмы кластерного анализа имеют сегодня хорошую программную реализацию, которая позволяет решить задачи самой большой размерности.
1.7 Данные
Кластерный анализ можно применять к интервальным данным, частотам, бинарными данным. Важно, чтобы переменные изменялись в сравнимых шкалах.
Неоднородность единиц измерения и вытекающая отсюда невозможность обоснованного выражения значений различных показателей в одном масштабе приводит к тому, что величина расстояний между точками, отражающими положение объектов в пространстве их свойств, оказывается зависящей от произвольно избираемого масштаба. Чтобы устранить неоднородность измерения исходных данных, все их значения предварительно нормируются, т.е. выражаются через отношение этих значений к некоторой величине, отражающей определенные свойства данного показателя. Нормирование исходных данных для кластерного анализа иногда проводится посредством деления исходных величин на среднеквадратичное отклонение соответствующих показателей. Другой способ сводиться к вычислению, так называемого, стандартизованного вклада. Его еще называют Z-вкладом.
Z-вклад показывает, сколько стандартных отклонений отделяет данное наблюдение от среднего значения:
 , где xi – значение данного наблюдения, – среднее, S – стандартное отклонение. , где xi – значение данного наблюдения, – среднее, S – стандартное отклонение.
Среднее для Z-вкладов является нулевым и стандартное отклонение равно 1.
Стандартизация позволяет сравнивать наблюдения из различных распределений. Если распределение переменной является нормальным (или близким к нормальному), и средняя и дисперсия известны или оцениваются по большим выборным, то Z-вклад для наблюдения обеспечивает более специфическую информацию о его расположении.
Заметим, что методы нормирования означают признание всех признаков равноценными с точки зрения выяснения сходства рассматриваемых объектов. Уже отмечалось, что применительно к экономике признание равноценности различных показателей кажется оправданным отнюдь не всегда. Было бы, желательным наряду с нормированием придать каждому из показателей вес, отражающий его значимость в ходе установления сходств и различий объектов.
В этой ситуации приходится прибегать к способу определения весов отдельных показателей – опросу экспертов. Например, при решении задачи о классификации стран по уровню экономического развития использовались результаты опроса 40 ведущих московских специалистов по проблемам развитых стран по десятибалльной шкале:
обобщенные показатели социально-экономического развития – 9 баллов;
показатели отраслевого распределения занятого населения – 7 баллов;
показатели распространенности наемного труда – 6 баллов;
показатели, характеризующие человеческий элемент производительных сил – 6 баллов;
показатели развития материальных производительных сил – 8 баллов;
показатель государственных расходов – 4балла;
«военно-экономические» показатели – 3 балла;
социально-демографические показатели – 4 балла.
Оценки экспертов отличались сравнительно высокой устойчивостью.
Экспертные оценки дают известное основание для определения важности индикаторов, входящих в ту или иную группу показателей. Умножение нормированных значений показателей на коэффициент, соответствующий среднему баллу оценки, позволяет рассчитывать расстояния между точками, отражающими положение стран в многомерном пространстве, с учетом неодинакового веса их признаков.
Довольно часто при решении подобных задач используют не один, а два расчета: первый, в котором все признаки считаются равнозначными, второй, где им придаются различные веса в соответствии со средними значениями экспертных оценок.
1.8. Применение кластерного анализа.
Рассмотрим некоторые приложения кластерного анализа.
Деление стран на группы по уровню развития.
Изучались 65 стран по 31 показателю (национальный доход на душу населения, доля населения занятого в промышленности в %, накопления на душу населения, доля населения, занятого в сельском хозяйстве в %, средняя продолжительность жизни, число автомашин на 1 тыс. жителей, численность вооруженных сил на 1 млн. жителей, доля ВВП промышленности в %, доля ВВП сельского хозяйства в %, и т.д.)
Каждая из стран выступает в данном рассмотрении как объект, характеризуемый определенными значениями 31 показателя. Соответственно они могут быть представлены в качестве точек в 31-мерном пространстве. Такое пространство обычно называется пространством свойств изучаемых объектов. Сравнение расстояния между этими точками будет отражать степень близости рассматриваемых стран, их сходство друг с другом. Социально-экономический смысл подобного понимания сходства означает, что страны считаются тем более похожими, чем меньше различия между одноименными показателями, с помощью которых они описываются.
Первый шаг подобного анализа заключается в выявлении пары народных хозяйств, учтенных в матрице сходства, расстояние между которыми является наименьшим. Это, очевидно, будут наиболее сходные, похожие экономики. В последующем рассмотрении обе эти страны считаются единой группой, единым кластером. Соответственно исходная матрица преобразуется так, что ее элементами становятся расстояния между всеми возможными парами уже не 65, а 64 объектами – 63 экономики и вновь преобразованного кластера – условного объединения двух наиболее похожих стран. Из исходной матрицы сходства выбрасываются строки и столбцы, соответствующие расстояниям от пары стран, вошедших в объедение, до всех остальных, но зато добавляются строка и столбец, содержащие расстояние между кластером, полученным при объединении и прочими странами.
Расстояние между вновь полученным кластером и странами полагается равным среднему из расстояний между последними и двумя странами, которые составляют новый кластер. Иными словами, объединенная группа стран рассматривается как целое с характеристиками, примерно равными средним из характеристик входящих в него стран.
Второй шаг анализа заключается в рассмотрении преобразованной таким путем матрицы с 64 строками и столбцами. Снова выявляется пара экономик, расстояние между которыми имеет наименьшее значение, и они, так же как в первом случае, сводятся воедино. При этом наименьшее расстояние может оказаться как между парой стран, так и между какой-либо страной и объединением стран, полученным на предыдущем этапе.
Дальнейшие процедуры аналогичны описанным выше: на каждом этапе матрица преобразуется так, что из нее исключаются два столбца и две строки, содержащие расстояние до объектов (пар стран или объединений – кластеров), сведенных воедино на предыдущей стадии; исключенные строки и столбцы заменяются столбцом и строкой, содержащими расстояния от новых объединений до остальных объектов; далее в измененной матрице выявляется пара наиболее близких объектов. Анализ продолжается до полного исчерпания матрицы (т. е. до тех пор, пока все страны не окажутся сведенными в одно целое). Обобщенные результаты анализа матрицы можно представить в виде дерева сходства (дендограммы), подобного описанному выше, с той лишь разницей, что дерево сходства, отражающее относительную близость всех рассматриваемых нами 65 стран, много сложнее схемы, в которой фигурирует только пять народных хозяйств. Это дерево в соответствии с числом сопоставляемых объектов включает 65 уровней. Первый (нижний) уровень содержит точки, соответствующие каждых стране в отдельности. Соединение двух этих точек на втором уровне показывает пару стран, наиболее близких по общему типу народных хозяйств. На третьем уровне отмечается следующее по сходству парное соотношение стран (как уже упоминалось, в таком соотношении может находиться либо новая пара стран, либо новая страна и уже выявленная пара сходных стран). И так далее до последнего уровня, на котором все изучаемые страны выступают как единая совокупность.
В результате применения кластерного анализа были получены следующие пять групп стран:
афро-азиатская группа;
латино-азиатская группа;
латино-среднеземнаморская группа;
группа развитых капиталистических стран (без США)
США
Введение новых индикаторов сверх используемого здесь 31 показателя или замена их другими, естественно, приводят к изменению результатов классификации стран.
2. Деление стран по критерию близости культуры.
Как известно маркетинг должен учитывать культуру стран (обычаи, традиции, и т.д.).
Посредством кластеризации были получены следующие группы стран:
арабские;
ближневосточные;
скандинавские;
германоязычные;
англоязычные;
романские европейские;
латиноамериканские;
дальневосточные.
3. Разработка прогноза конъюнктуры рынка цинка.
Кластерный анализ играет важную роль на этапе редукции экономико-математической модели товарной конъюнктуры, способствуя облегчению и упрощению вычислительных процедур, обеспечению большей компактности получаемых результатов при одновременном сохранении необходимой точности. Применение кластерного анализа дает возможность разбить всю исходную совокупность показателей конъюнктуры на группы (кластеры) по соответствующим критериям, облегчая тем самым выбор наиболее репрезентативных показателей.
Кластерный анализ широко используется для моделирования рыночной конъюнктуры. Практически основное большинство задач прогнозирования опирается на использование кластерного анализа.
Например, задача разработки прогноза конъюнктуры рынка цинка.
Первоначально было отобрано 30 основных показателей мирового рынка цинка:
Х1 - время
Показатели производства:
Х2 - в мире
Х3 - США
Х4 - Европе
Х5 - Канаде
Х6 - Японии
Х7 - Австралии
Показатели потребления:
Х8 - в мире
Х9 - США
Х10 - Европе
Х11 - Канаде
Х12 - Японии
Х13 - Австралии
Запасы цинка у производителей:
Х14 - в мире
Х15 - США
Х16 - Европе
Х17 - других странах
Запасы цинка у потребителей:
Х18 - в США
Х19 - в Англии
Х10 - в Японии
Импорт цинковых руд и концентратов (тыс. тонн)
Х21 - в США
Х22 - в Японии
Х23 - в ФРГ
Экспорт цинковых руд и концентратов (тыс. тонн)
Х24 - из Канады
Х25 - из Австралии
Импорт цинка (тыс. тонн)
Х26 - в США
Х27 - в Англию
Х28 - в ФРГ
Экспорт цинка (тыс. Тонн)
Х29 - из Канады
Х30 - из Австралии
Для определения конкретных зависимостей был использован аппарат корреляционно-регрессионного анализа. Анализ связей производился на основе матрицы парных коэффициентов корреляции. Здесь принималась гипотеза о нормальном распределении анализируемых показателей конъюнктуры. Ясно, что rij являются не единственно возможным показателем связи используемых показателей. Необходимость использования кластерного анализа связано в этой задаче с тем, что число показателей влияющих на цену цинка очень велико. Возникает необходимость их сократить по целому ряду следующих причин:
а) отсутствие полных статистических данных по всем переменным;
б) резкое усложнение вычислительных процедур при введении в модель большого числа переменных;
в) оптимальное использование методов регрессионного анализа требует превышения числа наблюдаемых значений над числом переменных не менее, чем в 6-8 раз;
г) стремление к использованию в модели статистически независимых переменных и пр.
Проводить такой анализ непосредственно на сравнительно громоздкой матрице коэффициентов корреляции весьма затруднительно. С помощью кластерного анализа всю совокупность конъюнктурных переменных можно разбить на группы таким образом, чтобы элементы каждого кластера сильно коррелировали между собой, а представители разных групп характеризовались слабой коррелированностью.
Для решения этой задачи был применен один из агломеративных иерархических алгоритмов кластерного анализа. На каждом шаге число кластеров уменьшается на один за счет оптимального, в определенном смысле, объединения двух групп. Критерием объединения является изменение соответствующей функции. В качестве функции такой были использованы значения сумм квадратов отклонений вычисляемые по следующим формулам:

(j = 1, 2, …, m),
где j - номер кластера, n - число элементов в кластере.
rij - коэффициент парной корреляции.
Таким образом, процессу группировки должно соответствовать последовательное минимальное возрастание значения критерия E.
На первом этапе первоначальный массив данных представляется в виде множества, состоящего из кластеров, включающих в себя по одному элементу. Процесс группировки начинается с объединения такой пары кластеров, которое приводит к минимальному возрастанию суммы квадратов отклонений. Это требует оценки значений суммы квадратов отклонений для каждого из возможных 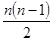 объединений кластеров. На следующем этапе рассматриваются значения сумм квадратов отклонений уже для объединений кластеров. На следующем этапе рассматриваются значения сумм квадратов отклонений уже для 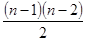 кластеров и т.д. Этот процесс будет остановлен на некотором шаге. Для этого нужно следить за величиной суммы квадратов отклонений. Рассматривая последовательность возрастающих величин, можно уловить скачок (один или несколько) в ее динамике, который можно интерпретировать как характеристику числа групп «объективно» существующих в исследуемой совокупности. В приведенном примере скачки имели место при числе кластеров равном 7 и 5. Далее снижать число групп не следует, т.к. это приводит к снижению качества модели. После получения кластеров происходит выбор переменных наиболее важных в экономическом смысле и наиболее тесно связанных с выбранным критерием конъюнктуры - в данном случае с котировками Лондонской биржи металлов на цинк. Этот подход позволяет сохранить значительную часть информации, содержащейся в первоначальном наборе исходных показателей конъюнктуры. кластеров и т.д. Этот процесс будет остановлен на некотором шаге. Для этого нужно следить за величиной суммы квадратов отклонений. Рассматривая последовательность возрастающих величин, можно уловить скачок (один или несколько) в ее динамике, который можно интерпретировать как характеристику числа групп «объективно» существующих в исследуемой совокупности. В приведенном примере скачки имели место при числе кластеров равном 7 и 5. Далее снижать число групп не следует, т.к. это приводит к снижению качества модели. После получения кластеров происходит выбор переменных наиболее важных в экономическом смысле и наиболее тесно связанных с выбранным критерием конъюнктуры - в данном случае с котировками Лондонской биржи металлов на цинк. Этот подход позволяет сохранить значительную часть информации, содержащейся в первоначальном наборе исходных показателей конъюнктуры.
|