Выпускная квалификационная работа
Выполнила студентка V курса математического факультета Кощеева Анна Сергеевна
Вятский Государственный Гуманитарный университет (ВятГГУ)
Киров 2005
Введение
Функциональный анализ – мощное средство для решения математический задач, возникающих в реальных ситуациях, он имеет множество приложений в различных областях математики, его методы проникают в смежные технические дисциплины.
Многие задачи математической физики, теории упругости, гидродинамики сводятся к отысканию решения дифференциального линейного уравнения, что, в свою очередь, приводит к задаче отыскания решения уравнения Аx = y с линейным оператором А. В данной работе рассмотрены два метода решения операторных уравнений.
Цель данной работы: рассмотреть основы теории линейных операторов и методы решения операторных уравнений – метод малого параметра и метод продолжения по параметру, показать применение этих методов к решению задач.
Изучив имеющийся материал по данной теме, я поставила перед собой следующие задачи:
раскрыть некоторые основы теории линейных операторов, необходимые для освоения методов решения операторных уравнений;
проиллюстрировать на конкретных примерах способы решения операторных уравнений и дать пояснения по ходу решения конкретных задач.
Так как выделение из функционального анализа его прикладной части, содержащей конструктивные методы получения решений задач, преследует методическую цель – сделать эти методы доступнее тем, кто занимается приложениями математики. Поэтому данная работа разделена на две главы, в первой содержатся необходимые теоретические обоснования способов решения операторных уравнений и суть обоих методов, а во второй – решения конкретных задач.
Глава 1. Операторные уравнения
§1.Определение линейного оператора
Пусть X и Y – линейные пространства, оба вещественные или оба комплексные.
Оператор А: X → Y с областью определения D(А) называется линейным, если
А(λ1x1 + λ2x2) = λ1А(x1) + λ2А(x2)
для любых x1,x2 Î D и любых скаляров λ1 и λ2.
Пусть X и Y – нормированные пространства и А: X → Y, где А – линейный оператор, всюду заданный в X (т.е. D(А) = X).
Реклама

Оператор А называется непрерывным в точке x0 Î X, если Аx → Аx0 при x → x0. Но судить о непрерывности линейного оператора в различных точках x0 Î X можно по непрерывности его в нуле пространства X.
Теорема 1. Пусть линейный оператор А всюду задан в банаховом пространстве X и со значениями в банаховом пространстве Y непрерывен в точке 0 Î X; тогда А непрерывен в любой точке x0 Î X.
Доказательство. Рассмотрим равенство Аx – Аx0 = А (x – x0). Если x → x0, то z = x – x0 → 0. По непрерывности в нуле Аz → 0, но тогда Аx – Аx0 → 0, что и требовалось доказать.
Линейный оператор А называется непрерывным, если он непрерывен в точке x = 0.
Пусть S1(0) – замкнутый шар ||x|| ≤ 1 в банаховом пространстве X.
Будем называть линейный оператор А: X → Y ограниченным, если он ограничен на единичным шаре S1(0), т.е. если ограничено множество
{ ||Аx||, ||x|| ≤ 1}.
Согласно определению, если А ограничен, то существует постоянная с > 0 такая, что для любых x с ||x|| ≤ 1 справедливо неравенство
||Аx|| ≤ с (1)
Теорема 2. А ограничен тогда и только тогда, когда справедлива оценка
||Аx|| ≤ с ||x|| (2)
для любых x Î X, где с – постоянная.
Теорема 3. Пусть А: X → Y, А – линейный оператор, X, Y – банаховы пространства. Для того чтобы А был непрерывным, необходимо и достаточно, чтобы он был ограниченным.
§2. Норма линейного оператора
В линейном пространстве непрерывных линейных операторов зададим норму следующим образом:
 . (1) . (1)
Поясним, почему существует конечное число ||А||, определяемое для любого ограниченного оператора равенством (1). Так как А – ограничен, то множество

ограничено сверху. По теореме о верхней грани существует  . .
Из свойства sup M следует, что ||Аx|| ≤ ||А|| для всех x Î S1(0). Отсюда
||Аx|| ≤ ||А|| ||x||, (2)
справедливое для всех x Î X, включая x = 0. таким образом, ||А|| является наименьшей из констант в неравенстве ||Аx|| ≤ ||А||, и, значит, оценка (2) является наилучшей.
Пространство нормированных непрерывных линейных операторов, действующих из X в Y, будем обозначать L(X, Y).
§3.Обратные операторы
Системы линейных алгебраических уравнений, интегральные уравнения, а также различные задачи для обыкновенных дифференциальных уравнений и уравнений с производными часто могут быть записаны в виде линейного уравнения

Если существует обратный оператор  , то решение задачи записывается в явном виде: , то решение задачи записывается в явном виде:
Реклама


Важное значение приобретает теперь выявление условий, при выполнении которых обратный оператор существует и обладает теми или иными свойствами.
Пусть задан линейный оператор: А: X → Y, где X,Y – линейные пространства, причем его область определения D(A) X, а область значений R(A) X, а область значений R(A) Y. Y.
Введем множество  - множество нулей оператора А. заметим, что N(A) не пусто, так как 0 Î N(A) - множество нулей оператора А. заметим, что N(A) не пусто, так как 0 Î N(A)
Теорема 4. Оператор А переводит D (А) в R (А) взаимно однозначно тогда и только тогда, когда N(A)= , (т.е. множество А нулей состоит только из элемента 0) , (т.е. множество А нулей состоит только из элемента 0)
Теорема 5. Оператор А-1 существует и ограничен на R(A) тогда и только тогда, когда для некоторой постоянной m>0 и любого x Î D(A) выполняется неравенство
 . (1) . (1)
Введем теперь следующее важное понятие.
Будем говорить, что линейный оператор А: X → Y непрерывно обратим, если R(A)=Y , оператор обратим и A-1 Î L(Y, X), (т.е. ограничен).
Обращаясь к теореме 5, мы сможем сформулировать следующее утверждение.
Теорема 6. Оператор А непрерывно обратим тогда и только тогда, когда R(A)=Y и для некоторой постоянной m>0 и для всех  выполняется неравенство (1). выполняется неравенство (1).
В случае определенного и ограниченного на всем множестве оператора A Î L(X,Y) имеется теорема Банаха об обратном операторе.
Теорема 7. Если А – ограниченный линейный оператор, отображающий взаимно однозначно банахово пространство X на банахово пространство Y, то обратный оператор А-1 ограничен.
Иными словами, если А Î L(X,Y), где X и Y банаховы, R(A)=Y и А обратим, то А непрерывно обратим.
Взглянем на понятие непрерывно обратимого оператора с точки зрения разрешимости линейного уравнения
Ax = y (2)
Если А непрерывно обратим, то уравнение это имеет единственное решение x = A-1y для любой правой части у. Если при этом  (решение того же уравнения с правой частью (решение того же уравнения с правой частью  ), то ), то  . Это означает, что малое изменение правой части y влечет малое изменение решения, или, как принято говорить, задача (2) корректно разрешима. . Это означает, что малое изменение правой части y влечет малое изменение решения, или, как принято говорить, задача (2) корректно разрешима.
Пусть А Î L(X,Y). Оператор U Î L(X,Y) будем называть правым обратным к А, если AU = Iy. Оператор V Î L(X,Y) будем называть левым обратным к А, если VA = Ix.
Здесь через Iy (Ix) обозначен тождественный оператор в пространстве Y (X). Ниже для правого обратного к А используем обозначение Аr–1, а для левого – АL–1.
Лемма 1. Если существует правый обратный Аr–1 к А, то уравнение (2) имеет решение
x = Аr–1 y
Если существует левый обратный оператор к А, то уравнение (2) может иметь не более одного решения.
Доказательство.
А(Аr–1 y) = (А Аr–1)y = y,
т.е. x = Аr–1 y обращает (2) в тождество и, значит, является решением.
Далее, пусть существует АL–1. рассмотрим N(A). Пусть x Î N(A), тогда Аx = 0. применим к этому равенству оператор АL–1, тогда АL–1Аx = 0, откуда x = 0. итак, всякое x Î N(A) оказывается равным 0. Значит, N(A) = {0} и, по теореме 4, А взаимно однозначен, т.е. для уравнения (2) справедлива теорема единственности. Что и требовалось доказать.
Пусть X – банахово пространство. Рассмотрим банахово пространство L(X) – пространство линейных, ограниченных и заданных на всем множестве операторов. Пусть I – тождественный оператор в L(X). Очевидно, что I непрерывно обратим. Ниже доказывается, что вместе с I непрерывно обратимы все операторы  - единичного шара в L(X), т.е. все такие А, для которых справедливо неравенство - единичного шара в L(X), т.е. все такие А, для которых справедливо неравенство  . .
Для краткости положим C = I – A. Ниже мы будем ссылаться на признак Вейерштрасса: пусть X – банахово пространство, тогда всякий абсолютно сходящийся в X ряд сходится.
Теорема 8. Пусть  и и  ; тогда оператор I – C непрерывно обратим. При этом справедливы оценки ; тогда оператор I – C непрерывно обратим. При этом справедливы оценки
 (1) (1)
 (2) (2)
Доказательство. Рассмотрим в L(X) ряд
I+C+C2+C3+… (3)
Так как  , то ряд (3) оценивается сходящимся числовым рядом – геометрической прогрессией , то ряд (3) оценивается сходящимся числовым рядом – геометрической прогрессией

По признаку Вейерштрасса ряд (3) сходится равномерно, т.е.
 . .
Где S – сумма ряда (3). Далее простой проверкой убеждаемся, что
 , ,
 . .
Но при этом  (ибо (ибо  и и  ), а ), а  . Поэтому, в пределе имеем равенства (I – C)S = I и S(I – C) = I. По лемме 1 отсюда заключаем, что I – C непрерывно обратим и S=(I – C)-1. Далее, . Поэтому, в пределе имеем равенства (I – C)S = I и S(I – C) = I. По лемме 1 отсюда заключаем, что I – C непрерывно обратим и S=(I – C)-1. Далее,
 , ,
 . .
Переходя в этих неравенствах к пределу при  , получаем оценки (1) и (2). Теорема доказана. , получаем оценки (1) и (2). Теорема доказана.
Теперь рассмотрим более общий случай пространства L(X,Y). Пусть А Î L(X,Y) непрерывно обратим.
Теорема 9. Пусть A, B Î L(X,Y), А непрерывно обратим и выполнено неравенство  . Тогда B непрерывно обратим и справедливы оценки . Тогда B непрерывно обратим и справедливы оценки
 , ,  . .
§4. Абстрактные функции
Пусть S – некоторое множество на числовой оси или в комплексной плоскости, а X – нормированное пространство.
Рассмотрим функцию x( ) с областью определения S и с областью значений в X. Такие функции принято называть абстрактными функциями числовой переменной или векторными функциями числовой переменной, поскольку элементы линейного (иначе – векторного) пространства мы называем также векторами. На абстрактные функции числовой переменной переносятся многие понятия и факты математического анализа. Далее рассмотрим сведения о пределах и непрерывности таких функций, о разложении в степенные ряды, а также понятие аналитической абстрактной функции. ) с областью определения S и с областью значений в X. Такие функции принято называть абстрактными функциями числовой переменной или векторными функциями числовой переменной, поскольку элементы линейного (иначе – векторного) пространства мы называем также векторами. На абстрактные функции числовой переменной переносятся многие понятия и факты математического анализа. Далее рассмотрим сведения о пределах и непрерывности таких функций, о разложении в степенные ряды, а также понятие аналитической абстрактной функции.
Пусть x( ) определена в окрестности точки ) определена в окрестности точки  0, за исключением, быть может, самой точки 0, за исключением, быть может, самой точки  0. Элемент а Î X будем называть пределом функции x( 0. Элемент а Î X будем называть пределом функции x( ) при ) при  → → 0 и записывать 0 и записывать
 при при  → → 0, 0,
если  при при  → → 0. 0.
Степенные ряды – это специальный случай рядов в нормированном пространстве, когда члены ряда зависят от параметра . .
Рассмотрим в нормированном пространстве X ряд вида  , где xк Î X, а , где xк Î X, а  – вещественное или комплексное переменное. Поскольку можно ввести новую переменную – вещественное или комплексное переменное. Поскольку можно ввести новую переменную  – – 0 = 0 =  , то в дальнейшем мы полагаем , то в дальнейшем мы полагаем  0 = 0 и рассматриваем степенные ряды вида 0 = 0 и рассматриваем степенные ряды вида
 (1) (1)
Конечная сумма  называется частичной суммой степенного ряда (1). называется частичной суммой степенного ряда (1).
Пусть  – множество всех точек – множество всех точек  , для которых ряд (1) сходится. , для которых ряд (1) сходится.  называется областью сходимости ряда (1). называется областью сходимости ряда (1).
Сумму ряда (1) при  Î Î обозначим через S( обозначим через S( ) (это абстрактная функция, определенная на ) (это абстрактная функция, определенная на  со значениями в X), при этом будем писать со значениями в X), при этом будем писать
 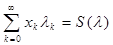 , при , при  Î Î . .
Последнее равенство означает, что Sn( ) → S( ) → S( ) при n→∞ для всех ) при n→∞ для всех  Î Î . .
Очевидно, область сходимости любого степенного ряда (1) не пуста, так как 0 Î . Как и в случае скалярных функций, справедлива следующая теорема. . Как и в случае скалярных функций, справедлива следующая теорема.
Теорема 10 (Абель). Пусть 0 ≠ 0 и 0 ≠ 0 и  0 Î 0 Î , тогда круг , тогда круг 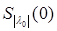 содержится в содержится в  . Во всяком круге Sr(0), где r < . Во всяком круге Sr(0), где r < 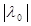 , ряд (1) сходиться абсолютно и равномерно относительно , ряд (1) сходиться абсолютно и равномерно относительно  . .
Теорема 11. Пусть два степенных ряда равны в круге SR(0), R>0:
 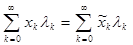 ; ;
тогда равны все их коэффициенты: 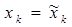 (k=0, 1, 2, …) (k=0, 1, 2, …)
Дифференцирование абстрактных функций
Пусть функция 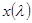 числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0. числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0.
По определению производной x’(λ0) функции x(λ) в точке λ0 называется предел
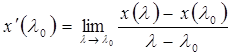 , ,
если этот предел существует (и конечен). Если 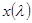 имеет производную в точке λ0, то она называется дифференцируемой в этой точке. имеет производную в точке λ0, то она называется дифференцируемой в этой точке.
§5. Аналитические абстрактные функции и ряды Тейлора
Абстрактную функцию x( ) будем называть аналитической при ) будем называть аналитической при  =0, если она представима в некоторой окрестности точки =0, если она представима в некоторой окрестности точки  =0 сходящимся степенным рядом: =0 сходящимся степенным рядом:
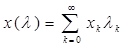 (1) (1)
с ненулевым радиусом сходимости.
Теорема 12. Если x( ) – аналитическая абстрактная функция при ) – аналитическая абстрактная функция при  =0, то x( =0, то x( ) непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1). ) непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1).
Теорема 13. Если x( ) – аналитическая абстрактная функция при ) – аналитическая абстрактная функция при  =0, то x( =0, то x( ) дифференцируема в круге SR(0) сходимости своего степенного разложения. ) дифференцируема в круге SR(0) сходимости своего степенного разложения.
Пусть x( ) бесконечно дифференцируема в точке 0. Ряд вида ) бесконечно дифференцируема в точке 0. Ряд вида
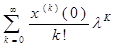
называется рядом Тейлора функции x( ). ).
Если x( ) аналитична при ) аналитична при  =0, то ее ряд Тейлора, в силу теоремы 10, является ее степенным разложением и, значит, сходится к ней в SR(0). =0, то ее ряд Тейлора, в силу теоремы 10, является ее степенным разложением и, значит, сходится к ней в SR(0).
Понятие абстрактной аналитической функции используется в широко применяемом на практике методе малого параметра.
§6. Метод малого параметра в простейшем случае
Рассмотрим следующее уравнение:
Аx – Сx=y. (1) Сx=y. (1)
Здесь А, С Î L(X,Y) и y Î Y заданы,  - скалярный параметр, - скалярный параметр, 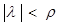 , а неизвестное x разыскивается в X. Если , а неизвестное x разыскивается в X. Если 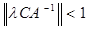 , т.е. , т.е.
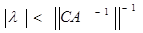 , (2) , (2)
то, согласно теореме 9, оператор А– С непрерывно обратим, и тогда решение уравнения (1) существует, единственно и задается явной формулой С непрерывно обратим, и тогда решение уравнения (1) существует, единственно и задается явной формулой
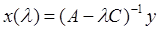 . (3) . (3)
Отсюда видно, что в круге (2) решение является аналитической функцией параметра  и, следовательно, может быть найдено в виде и, следовательно, может быть найдено в виде
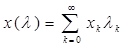 (4) (4)
На этой идее основывается метод малого параметра для уравнения (1). Подставим ряд (4) в уравнение (1) и, согласно теореме единственности разложения в степенной ряд, приравниваем коэффициенты при одинаковых степенях  в правой и левой частях получившегося тождества: в правой и левой частях получившегося тождества:
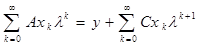 . .
Таким образом, мы приходим к следующей рекуррентной системе уравнений для определения x0, x1, …:
Аx0=y, Аx1=Сx0, …, Аxк=Сxк-1, …
Так как А непрерывно обратим, то отсюда последовательно находим
x0=А–1y, x1= А–1(СА–1)y, …, xк= А–1(СА–1)кy, …
Следовательно,
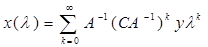 . (5) . (5)
Мы получили решение (3), разложенное в степенной ряд. Если мы хотим оборвать степенной ряд и ограничиться приближенным решением
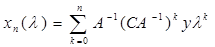
то можно оценить ошибку. Вычитая из ряда (5) его частичную сумму (6) и оценивая разность по норме, получим
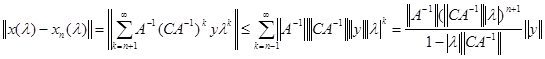 . .
§7. Метод малого параметра в общем случае
Пусть дано уравнение
А( )х = у( )х = у( ). (1) ). (1)
Здесь А( )Î L(X,Y) задана при каждом )Î L(X,Y) задана при каждом  , , 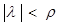 , или, как говорят, А( , или, как говорят, А( ) – оператор-функция. Пусть А( ) – оператор-функция. Пусть А( ) аналитична при ) аналитична при  =0, а оператор А(0) непрерывно обратим, у( =0, а оператор А(0) непрерывно обратим, у( ) – заданная аналитическая функция ) – заданная аналитическая функция  при при  =0 со значениями в Y. Неизвестное x разыскивается в X. =0 со значениями в Y. Неизвестное x разыскивается в X.
Аналитичность А( ) и у( ) и у( ) в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны ) в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны 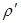 и и 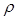 соответственно: соответственно:
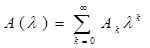 , , 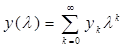 . (2) . (2)
Из аналитичности А( ) следует непрерывность А( ) следует непрерывность А( ) при ) при  =0. следовательно, найдется число r > 0 такое, что в круге =0. следовательно, найдется число r > 0 такое, что в круге 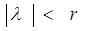
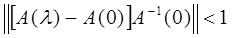 . .
Отсюда вытекает, что в круге 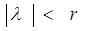 оператор-функция А( оператор-функция А( ) непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение ) непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение
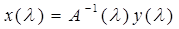 , ,
при этом x( ) аналитична в точке ) аналитична в точке  =0 и радиус сходимости соответствующего степенного ряда равен min( =0 и радиус сходимости соответствующего степенного ряда равен min(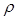 , r). Для фактического построения x( , r). Для фактического построения x( ) удобно воспользоваться методом малого параметра. Будем разыскивать x( ) удобно воспользоваться методом малого параметра. Будем разыскивать x( ) в виде ) в виде
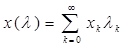 . (3) . (3)
Подставляя ряд (3) в уравнение (1) и учитывая разложения (2), приходим к следующей системе для неопределенных коэффициентов x0, x1, x2, …:
А0x0 = y0, А0x1+А1x0 = y1,
А0x2 + А1x1 + А2x0 = y2, (4)
. . . . . . . . . . .
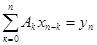 , … , …
Здесь А0 = А(0) непрерывно обратим. Решая последовательно уравнения получившейся системы, находим
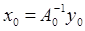 , , 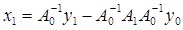 , … (5) , … (5)
Возникающие здесь формулы довольно громоздки, однако этим путем можно найти решение уравнения с любой степенью точности. Метод малого параметра особенно удобен в тех случаях, когда обращение оператора А(0) – задача более простая, чем задача обращения оператора А( ). ).
§8. Метод продолжения по параметру
8.1. Формулировка основной теоремы
В качестве еще одного приложения теорем об обратных операторах рассмотрим один из вариантов метода продолжения по параметру. Пусть 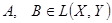 и А непрерывно обратим. Если и А непрерывно обратим. Если 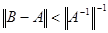 , то, согласно теореме 9 §3, В также непрерывно обратим. Оказывается, при определенных условиях можно доказать, что В будет непрерывно обратим и в том случае, когда он очень далек от А. Идея заключается в следующем. Рассмотрим непрерывную на отрезке [0, 1] оператор - функцию , то, согласно теореме 9 §3, В также непрерывно обратим. Оказывается, при определенных условиях можно доказать, что В будет непрерывно обратим и в том случае, когда он очень далек от А. Идея заключается в следующем. Рассмотрим непрерывную на отрезке [0, 1] оператор - функцию 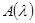 такую, что А(0)=А, А(1)=В. Иначе говоря, в L(X, Y) рассматривается непрерывная кривая, соединяющая точки А и В. Будем предполагать, что для оператор – функции такую, что А(0)=А, А(1)=В. Иначе говоря, в L(X, Y) рассматривается непрерывная кривая, соединяющая точки А и В. Будем предполагать, что для оператор – функции 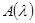 выполняется следующее условие: выполняется следующее условие:
Существует постоянная 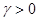 такая, что при всех такая, что при всех 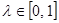 и при любых и при любых 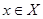 справедливо неравенство справедливо неравенство
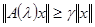 . (1) . (1)
Ниже будет доказана следующая теорема.
Теорема 14. Пусть А(λ) – непрерывная на [0, 1] оператор-функция (при каждом 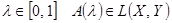 ), причем оператор А(0) непрерывно обратим. Если для А(λ)выполняется условие I, то А(I)непрерывно обратим, причем ), причем оператор А(0) непрерывно обратим. Если для А(λ)выполняется условие I, то А(I)непрерывно обратим, причем 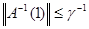 . .
Замечание к теореме 14. Если выполнено условие I при 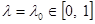 и оператор и оператор 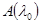 непрерывно обратим, то непрерывно обратим, то
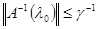 . (2) . (2)
Действительно, пусть 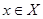 , а , а 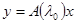 , т.е. , т.е.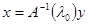 . тогда условие I дает . тогда условие I дает 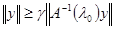 или или 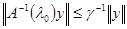 , что означает справедливость неравенства (2). , что означает справедливость неравенства (2).
8.2. Простейший случай продолжения по параметру
Приведем здесь доказательство теоремы 14 для случая, когда 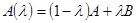 . Согласно условию этой теоремы . Согласно условию этой теоремы  . По замечанию 14 . По замечанию 14 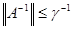 . Имеем следующую оценку: . Имеем следующую оценку:
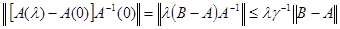 . .
Пусть 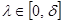 , где , где 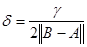 . На [0, δ] имеем . На [0, δ] имеем 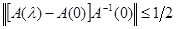 , и, следовательно, по теореме 9 А(λ) при всяком , и, следовательно, по теореме 9 А(λ) при всяком 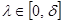 непрерывно обратим. Если окажется, то непрерывно обратим. Если окажется, то 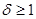 , то теорема доказана. , то теорема доказана.
Пусть δ < 1. Возьмем А(δ). Согласно замечанию п.14.1 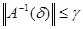 . Повторяем наши рассуждения при λ>δ. Имеем оценку . Повторяем наши рассуждения при λ>δ. Имеем оценку
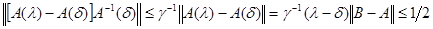 , ,
если 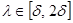 , откуда А(λ) непрерывно обратим при каждом , откуда А(λ) непрерывно обратим при каждом 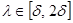 . Если . Если  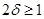 , то теорема доказана. Если же 2δ < 1, то , то теорема доказана. Если же 2δ < 1, то 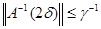 и рассуждение можно повторить. После конечного числа шагов мы достигаем точки λ=1, и, следовательно, А(1) непрерывно обратим. и рассуждение можно повторить. После конечного числа шагов мы достигаем точки λ=1, и, следовательно, А(1) непрерывно обратим.
Доказательство теоремы в общем случае
Рассмотренный выше частный случай отрезка в L(X,Y) не всегда удобен в приложениях. Общий случай основывается на следующем элементарном предложении.
Лемма. Пусть М – некоторое непустое множество на [0,1], одновременно открытое и замкнутое на [0.1]. тогда М=[0, 1].
Замечание 1. условие открытости М на [0,1] понимается так: для любого 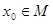 существует δ > 0 такое, что существует δ > 0 такое, что 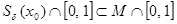 . .
Доказательство леммы. Пусть N = [0, 1] \ M (дополнение к М на [0, 1]). Нужно доказать, что N = Æ – пустое множество. Допустим противное, что N ¹Æ. Поскольку М ¹Æ и ограничено сверху, то существует b = supM, причем b Î M вследствие замкнутости. Покажем, что b = 1. Если b <1, то вследствие открытости M на [0, 1] найдется x > b, x Î M. Это противоречит определению supM. Следовательно, b >1 невозможно. Итак, 1Î М.
Теперь рассмотрим множество N. Как дополнение к М, оно также открыто и замкнуто на [0, 1], и, значит, к нему применимо рассуждение с supM . мы получаем, что 1 Î N. Это невозможно, ибо N – дополнение к М. полученное противоречие доказывает, что допущение N ¹Æ неверно. Итак, N= Æ, т.е. М = [0, 1]. Лемма доказана.
Вернемся к доказательству теоремы. Пусть М – множество тех точек λÎ[0, 1], для которых оператор А(λ) непрерывно обратим. Согласно замечанию 1 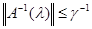 для всех λ Î М. М не пусто, поскольку 0 Î [0, 1]. для всех λ Î М. М не пусто, поскольку 0 Î [0, 1].
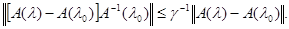
воспользуемся непрерывностью оператор–функции А(λ) в метрике L(X,Y). Для любого e > 0 найдется δ = δ(e)>0 такое, что при всех λ Î [0, 1] таких, что 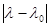 < δ выполняется неравенство < δ выполняется неравенство 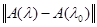 <e. <e.
Возьмем e = γ, тогда при 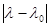 < δ(γ), λ Î [0, 1] < δ(γ), λ Î [0, 1]
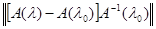 <1. <1.
По теореме 9 §3 А(λ) непрерывно обратим для всех таких λ. Итак, вместе с λ0 М содержит 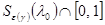 , т.е. М открыто на [0, 1]. , т.е. М открыто на [0, 1].
Докажем, что М замкнуто на [0, 1]. Пусть 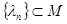 и и 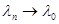 при при  . Надо доказать, что λ0 М. воспользуемся неравенством . Надо доказать, что λ0 М. воспользуемся неравенством 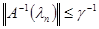 и получим и получим
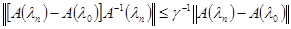 . .
Вследствие непрерывности А(λ) по λ для любого e > 0 находим номер N = N(e) такой, что при n > N будет 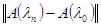 <e. Возьмем e = γ, тогда для n = N(γ)+1 <e. Возьмем e = γ, тогда для n = N(γ)+1 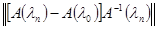 <1. <1.
По теореме 9 А(λ0) непрерывно обратим, т.е. λ0 Î М, и, значит, М замкнуто на [0, 1]. По лемме М = [0, 1] . в частности, 1Î М и 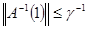 . Теорема полностью доказана. . Теорема полностью доказана.
Замечание. Рассмотрим уравнение с параметром:
А(λ)х = у, λÎ [0, 1]. (1*)
Пусть для всех возможных решений этого уравнения при всяком λÎ [0, 1] справедлива оценка
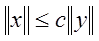 , (2*) , (2*)
где с – некоторая постоянная, не зависящая от х, у и λ. Оценка такого рода называется априорной оценкой для решения уравнения (1*). Очевидно, априорная оценка (2*) представляет собой лишь иначе записанное условие (1): 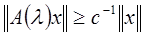 . .
Доказанная выше теорема свидетельствует о важности априорных оценок для доказательства теорем существования и единственности решений.
Глава 2. Приложение
Пример 1. Рассмотрим интегральное уравнение с малым вещественным параметром λ:
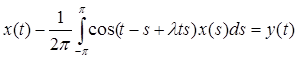 (1) (1)
Это уравнение вида А( )х = у( )х = у( ) – операторное уравнение в С[-π; π], где ) – операторное уравнение в С[-π; π], где
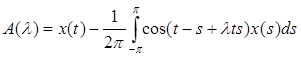
Покажем, что А( ) аналитична в т. 0, т.е. разлагается в ряд вида ) аналитична в т. 0, т.е. разлагается в ряд вида 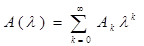 . Разложим функцию А( . Разложим функцию А( ) в ряд Тейлора: ) в ряд Тейлора: 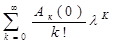 . .
Найдем к – ую производную:
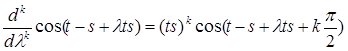
Разложим функцию в ряд Тейлора в т. 0:
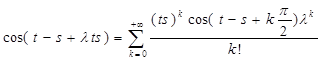
Таким образом, функция аналитична, следовательно, непрерывна при  = 0, а значит, уравнение имеет единственное решение. = 0, а значит, уравнение имеет единственное решение.
Операторные коэффициенты имеют вид:
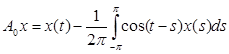 ; ; 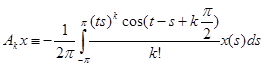 (2) (2)
I. Начнем с уравнения А0x0 = y системы (4) §7, где у нас теперь y0=y, yк=0, к ≥ 1.
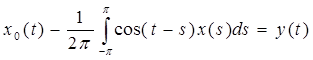
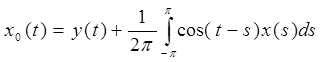
Заменим, 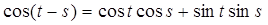 , поэтому , поэтому 
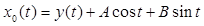 , (4) , (4)
где
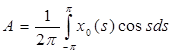 , , 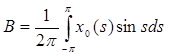
Для того, чтобы найти коэффициент А в уравнении (4), умножим его на cos t и, интегрируем по t от –π до π:
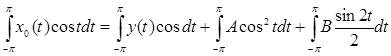 , ,
подсчитаем интегралы:
 , , 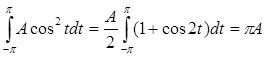 , , 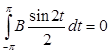
Тогда, подставив в уравнение, получаем: 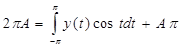 . Отсюда: . Отсюда:
 . (5) . (5)
Найдем коэффициент В уравнения (4), умножив это уравнение на sin t и интегрируя по t от –π до π:
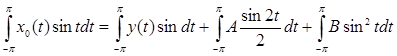 . .
Подсчитав соответствующие интегралы:
  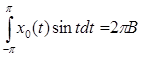 , , 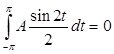 , , 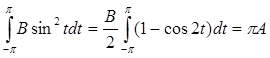 , подставив и выразив В, получаем: , подставив и выразив В, получаем:
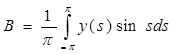 . (6) . (6)
Подставим найденные коэффициенты (5) и (6) в уравнение (4):
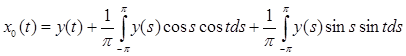
и свернем по формуле:
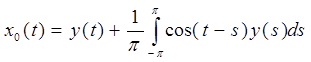
II. Найдем теперь x1(t), для этого необходимо решить следующее уравнение системы (4) §7: А0x1+А1x0 = y1. Так как y1=0 в нашем случае, то мы будем решать уравнение А0x1= – А1x0.
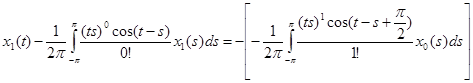
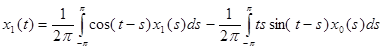
Обозначим 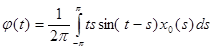 , т.к. мы знаем теперь x0(s), следовательно φ(t) можно вычислить. Имеем: , т.к. мы знаем теперь x0(s), следовательно φ(t) можно вычислить. Имеем:
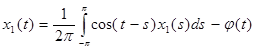
Как в предыдущем случае заменим, 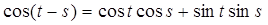 , поэтому , поэтому 
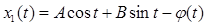 . (7) . (7)
где 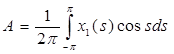 , , 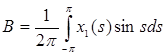 . .
Умножим уравнение (7) на cos t и проинтегрируем по t от –π до π – получим коэффициент А:
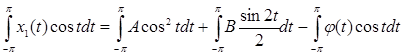
Подсчитав: 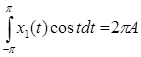 , , 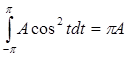 , , 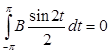 , ,
имеем 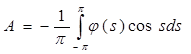 . .
Аналогично умножив уравнение (7) на sin t и проинтегрируем по t от –π до π – получим коэффициент В: 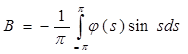 . .
Составляем функцию x1(t), подставив коэффициенты А и В в уравнение и свернув равенство по формуле косинуса разности:
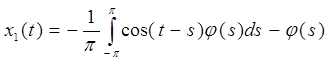 . .
Таким способом мы можем найти все остальные решения уравнения с любой степенью точности.
Пример 2. Применим метод продолжения по параметру для оценки разрешимости краевой задачи для дифференциального уравнения, а потом решим ее методом малого параметра.
–x'' + b(t)x' +c(t)x = y(t), 0< t <1, (1)
x(0) = x(1) = 0 (2)
Здесь c(t) непрерывна на [0, 1], b(t) непрерывно дифференцируема на [0, 1]. Предположим еще, что на [0, 1] c(t) – b(t)'/2 ≥ α > –8/π (*).
Покажем методом продолжения по параметру, что в этих условиях при всякой правой части y ÎY = С [0, 1] существует единственное решение задачи x Î X = С2 [0, 1] – пространству, состоящему из дважды непрерывно дифференцируемых на [0, 1] функций x(t), удовлетворяющих граничным условиям (2), и с нормой 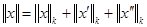 , где , где 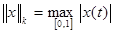 . .
Запишем задачу (1) – (2) в операторном виде: Вx = y
Здесь 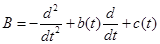 определен всюду на X со значениями в Y. В качестве оператора А примем определен всюду на X со значениями в Y. В качестве оператора А примем 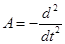 ÎL(X, Y). ÎL(X, Y).
Соединим операторы А и В отрезком
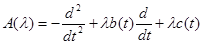 , λ Î [0, 1]. , λ Î [0, 1].
Теперь необходимо установить априорную оценку для решений краевой задачи
–x'' + λb(t)x' + λc(t)x = y(t), 0< t <1, (3)
x(0) = x(1) = 0 (4)
Как только такая оценка будет получена, из теоремы п.8.1. будет следовать однозначная разрешимость краевой задачи (3) – (4).
Умножим уравнение (3) на x(t) и проинтегрируем полученное равенство по t от 0 до 1:
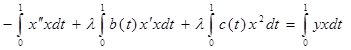 . .
Заметим, с учетом граничных условий:
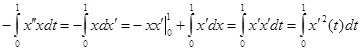
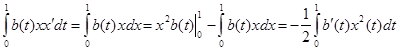
Подставим полученные интегралы и сгруппируем относительно λ:
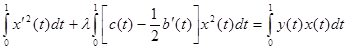 (5) (5)
Произведем оценку всех трех слагаемых в этом равенстве.
Докажем, что 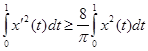 . (6) . (6)
Заметим, что 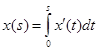 , и значит по неравенству Коши – Буняковского: , и значит по неравенству Коши – Буняковского:
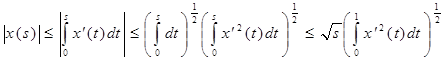 . .
Точно так же:
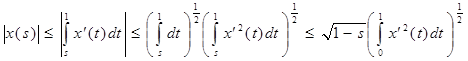 . .
Перемножим эти неравенства:
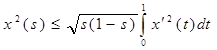 . (6*) . (6*)
Отсюда, замечая, что 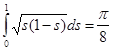 , получим , получим
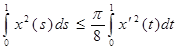 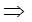 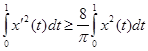 . .
Далее 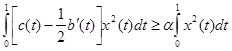 (7) (7)
– это следует из предположения (*).
Последний интеграл равенства (5) можно оценить, используя скалярный квадрат:
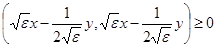 , где , где 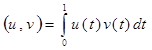 . .
Для любого ε > 0 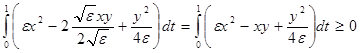 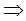
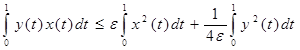 . (8) . (8)
Используя полученные неравенства (6), (7), (8) и подставляя их в равенство (5), получаем:
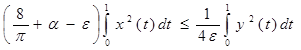 , ,
считая ε > 0 достаточно малым, имеем
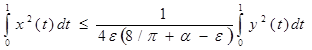 . .
Выберем 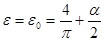 и получим и получим
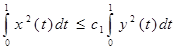 , где , где 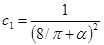 . .
Возвращаясь снова к равенству (5), получим следующую оценку:
 , где , где 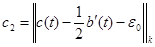 , а , а 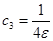 . .
Теперь с помощью оценки (6*) имеем 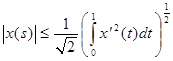 и, значит, учитывая, что и, значит, учитывая, что 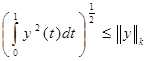 , получим , получим
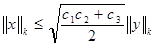 (9) (9)
Из уравнения (3) можем получить оценки для 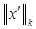 и и 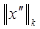 : :
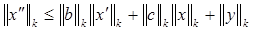 . (10) . (10)
Здесь 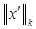 оценивается через оценивается через 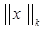 и и 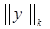 . Действительно, x(0) = x(1) = 0. по теореме Роля на (0, 1) найдется точка ξ, в которой x'(ξ) = 0. Тогда, запишем уравнение (3) в виде . Действительно, x(0) = x(1) = 0. по теореме Роля на (0, 1) найдется точка ξ, в которой x'(ξ) = 0. Тогда, запишем уравнение (3) в виде
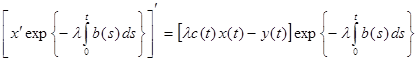 , ,
(в этом можно убедиться, взяв производную:
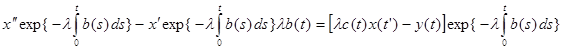
и сократив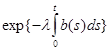 ) )
интегрируем его от ξ до θ и получим
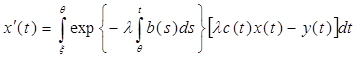 . .
Отсюда имеем оценку
 , (11) , (11)
где 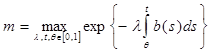 . .
Теперь подставим полученные результаты в (10):
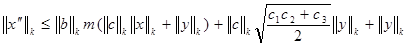 . (12) . (12)
Теперь (9), (11) и (12) дают искомую априорную оценку:
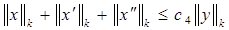
(постоянную с4 нетрудно подсчитать, сложив неравенства(9), (11), (12)и выполнив преобразования).
Таким образом, доказательство разрешимости задачи получено, теперь приступим к ее решению методом малого параметра.
Итак, рассмотрим операторное уравнение:
А(λ)x = y(λ),
где 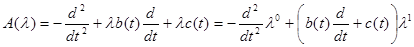 . .
I. Начнем с уравнения А0x0 = y (где А0 – коэффициент при нулевой степени λ) системы (4) §7, причем y0 = y, yк = 0, к ≥ 1.
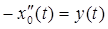 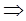 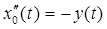 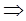 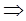 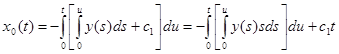 , причем с1 подбирается так, чтобы выполнялось краевое условие: x0(1) = 0. , причем с1 подбирается так, чтобы выполнялось краевое условие: x0(1) = 0.
II. Найдем x1(t), для этого необходимо решить следующее уравнение: А0x1+А1x0 = y1. Так как y1=0, то мы будем решать уравнение А0x1= – А1x0.
Из того, что 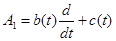 следует следующее уравнение: следует следующее уравнение:
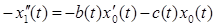 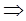 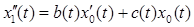 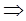
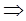 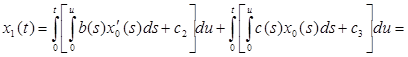 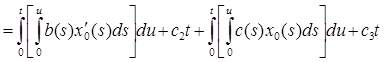 . .
По аналогии c2 и c3 подбираем так, чтобы выполнялось краевое условие: x0(1) = 0.
Таким образом, решения нашей краевой задачи выглядит так:
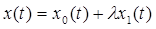 , ,
подставляя найденные решения, имеем:
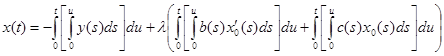
или
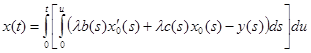
Список литературы
Данфорд Н., Шварц Дж. Линейные операторы. М., 1962
Талдыкин А.Т. Элементы прикладного функционального анализа: Учеб. пособие. – М.: Высшая школа, 1982.
Треногин В.А. Функциональный анализ. М., 1993.
Функциональный анализ./Под. ред. С. Г. Крейна. М., 1972
Хатсон В., Пим Дж. С. Приложения функционального анализа и теория операторов. Пер. с англ. – М.: Мир, 1983.
|