1. Постановка задачи и анализ исходных данных
Основная цель фирмы заключается в максимизации прибыли путем рационального распределения затрачиваемых ресурсов.
Данный курсовой проект ставит перед собой цель выяснить насколько эффективна деятельность фирмы в долгосрочном периоде при выборе вектора х=(х1
,х2
) затрат из пространства затрат.
Поэтому задача максимизации прибыли в долговременном промежутке имеет следующий вид;
 PR=p(x1
,x2
)*
f(x1
,x2
)-c(x1
,x2
) max (х1
,х2
> 0),где PR=p(x1
,x2
)*
f(x1
,x2
)-c(x1
,x2
) max (х1
,х2
> 0),где
p(х1
,х2
) -
функция спроса;
f(х1
,х2
) -
производственная функция выпуска;
с(х1
,х2
) -
функция затрат.
Будут использоваться данные:
| КАПИТАЛ
|
ТРУД
|
ВЫПУСК
|
ЦЕНА
|
ЗАТРАТЫ
|
| 1,05 |
1,03 |
1,50 |
25,44 |
5,10 |
| 2,00 |
2,90 |
4,20 |
15,11 |
10,20 |
| 3,00 |
6,00 |
7,43 |
10,60 |
19,40 |
| 4,00 |
9,00 |
9,60 |
8,57 |
27,00 |
| 5,00 |
12,00 |
12,15 |
7,34 |
36,00 |
| 6,00 |
15,30 |
15,75 |
6,45 |
42,60 |
| 7,00 |
18,00 |
18,45 |
5,87 |
50,00 |
| 8,00 |
21,00 |
21,45 |
5,39 |
58,00 |
| 9,00 |
24,00 |
24,30 |
5,00 |
66,00 |
| 10,00 |
27,00 |
26,85 |
4,67 |
74,00 |
| 11,00 |
30,00 |
30,15 |
4,40 |
82,00 |
| 12,00 |
33,00 |
33,00 |
4,17 |
90,00 |
| 13,00 |
36,00 |
36,75 |
3,97 |
99,00 |
| 14,00 |
39,00 |
41,28 |
3,79 |
107,00 |
| 15,00 |
42,00 |
42,30 |
3,63 |
120,00 |
Зависимые переменные : выпуск, цена, затраты.
Независимые переменные: капитал (х1
) и труд (х2
), которые удовлетворяют выше приведенным условиям.
Исходя из заданных данных необходимо определить вид и параметры функций спроса, затрат и производственной функции выпуска.
| Определение вида и параметров функции спроса, достоверности параметров, качества регрессии.
|
| Функция спроса - функция цены выпускаемой продукции в зависимости от объемов затрачиваемых ресурсов.
|
| КАПИТАЛ
|
ТРУД
|
ЦЕНА
|
LN x1
|
LN x2
|
LN y
|
| 1,05 |
1,03 |
25,44 |
0,05 |
0,03 |
3,24 |
| 2,00 |
2,90 |
15,11 |
0,69 |
1,06 |
2,72 |
| 3,00 |
6,00 |
10,60 |
1,10 |
1,79 |
2,36 |
| 4,00 |
9,00 |
8,57 |
1,39 |
2,20 |
2,15 |
| 5,00 |
12,00 |
7,34 |
1,61 |
2,48 |
1,99 |
| 6,00 |
15,30 |
6,45 |
1,79 |
2,73 |
1,86 |
| 7,00 |
18,00 |
5,87 |
1,95 |
2,89 |
1,77 |
| 8,00 |
21,00 |
5,39 |
2,08 |
3,04 |
1,68 |
| 9,00 |
24,00 |
5,00 |
2,20 |
3,18 |
1,61 |
| 10,00 |
27,00 |
4,67 |
2,30 |
3,30 |
1,54 |
| 11,00 |
30,00 |
4,40 |
2,40 |
3,40 |
1,48 |
| 12,00 |
33,00 |
4,17 |
2,48 |
3,50 |
1,43 |
| 13,00 |
36,00 |
3,97 |
2,56 |
3,58 |
1,38 |
| 14,00 |
39,00 |
3,79 |
2,64 |
3,66 |
1,33 |
| 15,00 |
42,00 |
3,63 |
2,71 |
3,74 |
1,29 |
| 12,62 |
-38,59 |
50,48 |
-0,36 |
-0,23 |
3,26 |
26,00 |
| 3,19 |
9,51 |
8,90 |
0,00 |
0,00 |
0,00 |
1,00 |
| 0,83
|
2,60 |
#Н/Д |
1,00
|
0,00 |
#Н/Д |
| 29,14 |
12,00 |
#Н/Д |
8736032,75 |
12,00 |
#Н/Д |
| 393,61 |
81,06 |
#Н/Д |
4,35 |
0,00 |
#Н/Д |
| значение распределения Стьюдента
|
значение распределения Стьюдента
|
| 3,95 |
-4,06 |
5,67 |
-280,59
|
-132,26
|
7866,80 |
25,99
|
| Критическое значение Стьюдента
|
критич. Знач. Стьюдента=стьюдраспобр
|
| 2,18
|
2,18
|
| Достоверен |
достоверен |
достоверен |
достоверен |
достоверен |
достоверен |
| Критическое распределение Фишера
|
критическое распределение Фишера
|
| 0,00002 |
1,04959E-37 |
| 29,14>0,00002
|
8736032,75>1,04959Е-37
|
| R2
-достоверен
|
R2
-достоверен
|
| Выбираем степенную ф-ю т.к. у степенной ф-ции три достоверных параметра. Коэф. Детерминации равен 1 (1>0,83), Fстатистика больше, чем у линейной (8736032,75>29,14). |
| p(x1
,x2
)=P=b0*
x1
-b1
*
x2
-b2
|
Параметры: |
b0
|
b1
|
b2
|
| 26,00 |
-0,23 |
-0,36 |
| Определение вида и параметров функции затрат, достоверности параметров, качества регрессии.
|
| Функция затрат - функция от двух переменных - факторов производства - капитала и труда.
|
| КАПИТАЛ
|
ТРУД
|
ЗАТРАТЫ
|
| 1,05 |
1,03 |
5,10 |
| 2,00 |
2,90 |
10,20 |
| 3,00 |
6,00 |
19,40 |
| 4,00 |
9,00 |
27,00 |
| 5,00 |
12,00 |
36,00 |
| 6,00 |
15,30 |
42,60 |
| 7,00 |
18,00 |
50,00 |
| 8,00 |
21,00 |
58,00 |
| 9,00 |
24,00 |
66,00 |
| 10,00 |
27,00 |
74,00 |
| 11,00 |
30,00 |
82,00 |
| 12,00 |
33,00 |
90,00 |
| 13,00 |
36,00 |
99,00 |
| 14,00 |
39,00 |
107,00 |
| 15,00 |
42,00 |
120,00 |
| 1,96 |
2,21 |
0,00 |
| 0,30 |
0,82 |
#Н/Д |
| 1,00
|
1,54 |
#Н/Д |
| 3818,56 |
13,00 |
#Н/Д |
| 18116,82 |
30,84 |
#Н/Д |
| значение распределения Стьюдента
|
| 6,54 |
2,70 |
#Н/Д |
| критическое значение Стьюдента
|
| 2,16
|
| достоверен |
достоверен |
| критическое распределение Фишера
|
| 9,92626E-19 |
| 3818,56>9,92626Е-19
|
| R2
-достоверен
|
| Функция затрат имеет вид линейной функции. |
c(x1
,x2
)=C=c1*
x1
+c2*
x2
|
| Параметры: |
c1
|
c2
|
| 2,21 |
1,96 |
| Оптимизация
|
| Общая постановка задачи:
|
| Определив вид и параметры функций спроса, производственной функции и функции затрат ,мы можем преобразовать уравнение прибыли соответственно с нашим решением. |
| a0
|
1,54
|
b0
|
26,00
|
КАПИТАЛ
|
ТРУД
|
f(x1
,x2
)=F
|
| a1
|
0,43
|
b1
|
-0,23
|
c1
|
2,21
|
1,05 |
1,03 |
1,60 |
| a2
|
0,57
|
b2
|
-0,36
|
c2
|
1,96
|
2,00 |
2,90 |
3,81 |
| 3,00 |
6,00 |
6,86 |
| PR=p(x1
,x2
)*
f(x1
,x2
)-c(x1
,x2
)
|
прибыль (1) |
4,00 |
9,00 |
9,78 |
| Найденные уравнения регрессии: |
5,00 |
12,00 |
12,68 |
| p(x1
,x2
)=P=b0*
x1
-b1
*
x2
-b2
|
ф-я спроса (5) |
6,00 |
15,30 |
15,75 |
| f(x1
,x2
)=F=a0*
x1
a1
*
x2
a2
|
произв. ф-я (6) |
7,00 |
18,00 |
18,47 |
| c(x1
,x2
)=C=c1*
x1
+c2*
x2
|
ф-я затрат (7) |
8,00 |
21,00 |
21,36 |
| из этого следует, что |
9,00 |
24,00 |
24,24 |
| PR=a0*
b0*
x1
(a1+b1)
*
x2
(a2+b2)
-c1
x1
-c2
x2
|
10,00 |
27,00 |
27,13 |
| далее решим систему уравнений |
11,00 |
30,00 |
30,01 |
| qPR/qx1
=0
|
(2) |
12,00 |
33,00 |
32,89 |
| qPR/qx2
=0
|
13,00 |
36,00 |
35,78 |
| 14,00 |
39,00 |
38,66 |
| Решение : |
15,00 |
42,00 |
41,54 |
| a0*
b0*
(а1
+в1
)*
x1
(a1+b1-1)
*
x2
(a2+b2)
-c1
=0
|
| a0*
b0*
x1
(a1+b1)
*
(а2
+в2
)*
x2
(a2+b2-1)
-c2
=0
|
| При упрощении выражения получается уравнение вида: |
| x2
/x1
=(c1*
(a2
+b2
))/(c2
(a1
+b1
)) |
| Обозначим правую часть уравнения через коэффициент К: |
| x2
/x1
=K
|
К=
|
1,18 |
| Cледовательно: |
| x2
/x1
=1,18
|
х1
=х2
/1,18 , х2
=х1*
1,18 |
| Выразив х1
через х2
и решив систему уравнений получаем оптимальные значения х1опт
и х2опт
|
| x1o
=
|
9,48 |
| x2o
=
|
11,20 |
| Для проверки правильности нахождения экстремума необходимо произвести расчет по формулам ( 3) и ( 4 ): |
| q2
PR(x1
,x2
)/qx1
2
<0
|
для оптимальных значений х1
,х2
|
( 3 )
|
| Подставив свои значения получаю формулу: |
| а0
*в0
*(а1
+в1
)*(а1
+в1
-1)*х1
(а1+в1-2)
*х2
(а2+в2)
<0
|
-0,19
|
<0
|
| (q2
PR(x1
,x2
)/qx1
2
)*(q2
PR(x1
,x2
)/qx2
2
)-(q2
PR(x1
,x2
)/qx1
х2
)2
>0
|
( 4 )
|
| Представим формулу в виде: |
А*В-D2
>0
|
| А=а0
*в0
*(а1
+в1
)*(а1
+в1
-1)*х1
(а1+в1-2)
*х2
(а2+в2)
|
| В=а0
*в0
*(а2
+в2
)*(а2
+в2
-1)*х1
(а1+в1)
*х2
(а2+в2-2)
|
| D=а0
*в0
*(а1
+в1
)*(а2
+в2
)*х1
(а1+в1-1)
*х2
(а2+в2-1)
|
| Найдем значения А,В
и D
: |
| А =
|
-0,19
|
| B =
|
-0,14
|
| D =
|
0,04
|
| Подставим эти значения в формулу: |
0,024
|
>0
|
| Вывод:
|
Найденные значения х1опт
и х2опт
являются оптимальным решением системы уравнений . |
| При подстановке этих значений мы получим максимум прибыли(1) и максимум выпуска (5) |
61,37
|
| 6,50
|
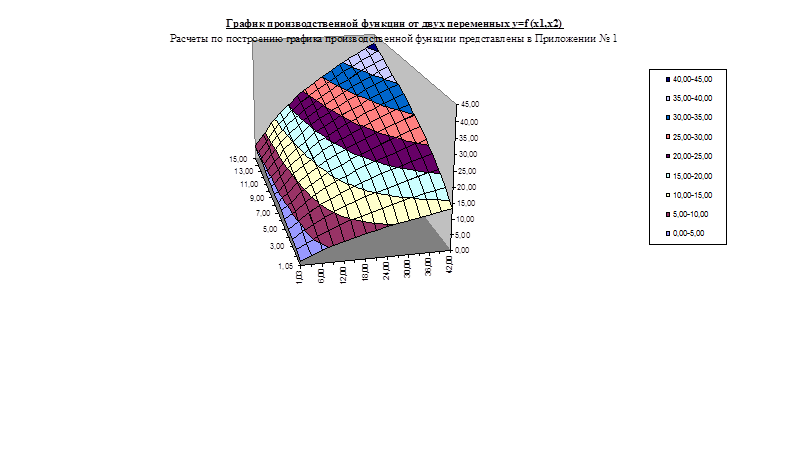
| График прибыли от двух переменных
|
| PR=f(х1
,х2
)
|
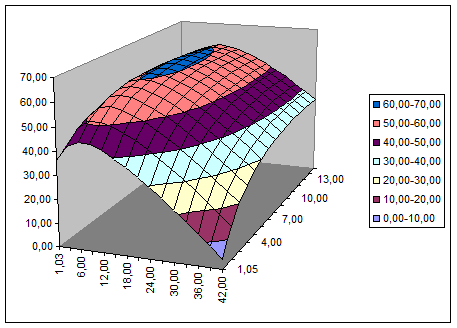
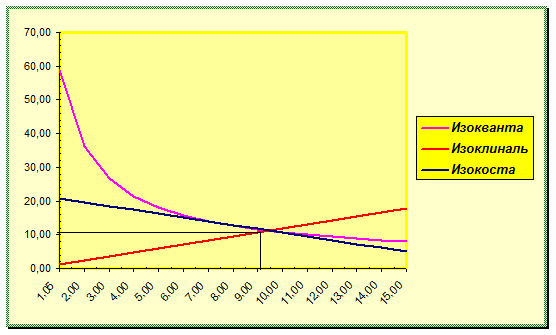
| Построение графиков изоквант и изокост.
|
| Капитал |
Труд |
Изокванта |
Изоклиналь |
Изокоста |
Параметры |
| 1,05 |
1,03 |
58,90 |
1,24 |
20,71 |
| 2,00 |
2,90 |
36,23 |
2,36 |
19,63 |
а0
|
1,54
|
| 3,00 |
6,00 |
26,68 |
3,54 |
18,51 |
а1
|
0,43
|
| 4,00 |
9,00 |
21,47 |
4,73 |
17,38 |
а2
|
0,57
|
| 5,00 |
12,00 |
18,15 |
5,91 |
16,25 |
с1
|
2,21
|
| 6,00 |
15,30 |
15,82 |
7,09 |
15,12 |
с2
|
1,96
|
| 7,00 |
18,00 |
14,08 |
8,27 |
14,00 |
yо
|
16,05 |
| 8,00 |
21,00 |
12,73 |
9,45 |
12,87 |
| 9,00 |
24,00 |
11,65 |
10,63 |
11,74 |
g опт
|
0,89 |
| 10,00 |
27,00 |
10,76 |
11,81 |
10,61 |
| 11,00 |
30,00 |
10,01 |
13,00 |
9,49 |
с0
|
42,90 |
| 12,00 |
33,00 |
9,38 |
14,18 |
8,36 |
| 13,00 |
36,00 |
8,83 |
15,36 |
7,23 |
х1опт
|
9,48 |
| 14,00 |
39,00 |
8,35 |
16,54 |
6,10 |
х2 опт
|
11,20 |
| 15,00 |
42,00 |
7,92 |
17,72 |
4,98 |
в0
|
26,00
|
| в1
|
-0,23
|
| в2
|
-0,36
|
| Для построения графиков используются расчеты по следующим формулам: |
| Изокванта |
х2
(х1
)=(у0
/(а0
*х1
a1
)^(1/a2
) |
| Изоклиналь |
x2
(x1
)=gопт
.*(a2
/a1
)*x1
|
| Изокоста |
x2
(x1
)=(c0
-c1
*x1
)/c2
|
| а также: |
| Оптимальный выпуск |
у0
=а0
*х1опт
.a1
*x2опт
.a2
|
| Предельная норма замещения |
gопт
.=(a1
*x2опт
)/(а2
*х1опт
) |
| Затраты оптимального варианта |
с0
=с1
*х1опт.
+с2
*х2опт.
|
| Анализ свойств производственной функции и возможности замещения ресурсов.
|
| a0
|
1,54
|
Капитал x1
|
Труд x2
|
ПЭ по х1
|
ПЭ по х2
|
F |
Е х1
|
Е х2
|
ПНЗ g |
| a1
|
0,43
|
1,05 |
1,03 |
0,65 |
0,89 |
1,60 |
0,43 |
0,57 |
0,74 |
| a2
|
0,57
|
2,00 |
2,90 |
0,82 |
0,75 |
3,81 |
0,43 |
0,57 |
1,09 |
| b0
|
26,00
|
3,00 |
6,00 |
0,98 |
0,65 |
6,86 |
0,43 |
0,57 |
1,51 |
| b1
|
-0,23
|
4,00 |
9,00 |
1,05 |
0,62 |
9,78 |
0,43 |
0,57 |
1,70 |
| b2
|
-0,36
|
5,00 |
12,00 |
1,09 |
0,60 |
12,68 |
0,43 |
0,57 |
1,81 |
| c1
|
2,21
|
6,00 |
15,30 |
1,13 |
0,59 |
15,75 |
0,43 |
0,57 |
1,92 |
| c2
|
1,96
|
7,00 |
18,00 |
1,13 |
0,58 |
18,47 |
0,43 |
0,57 |
1,94 |
| 8,00 |
21,00 |
1,15 |
0,58 |
21,36 |
0,43 |
0,57 |
1,98 |
| x1o
=
|
9,48 |
9,00 |
24,00 |
1,16 |
0,58 |
24,24 |
0,43 |
0,57 |
2,01 |
| x2o
=
|
11,20 |
10,00 |
27,00 |
1,17 |
0,57 |
27,13 |
0,43 |
0,57 |
2,04 |
| 11,00 |
30,00 |
1,17 |
0,57 |
30,01 |
0,43 |
0,57 |
2,06 |
| 12,00 |
33,00 |
1,18 |
0,57 |
32,89 |
0,43 |
0,57 |
2,07 |
| 13,00 |
36,00 |
1,18 |
0,57 |
35,78 |
0,43 |
0,57 |
2,09 |
| 14,00 |
39,00 |
1,19 |
0,57 |
38,66 |
0,43 |
0,57 |
2,10 |
| 15,00 |
42,00 |
1,19 |
0,56 |
41,54 |
0,43 |
0,57 |
2,11 |
| оптима
|
9,48
|
11,20
|
0,73
|
0,82
|
16,05
|
0,43
|
0,57
|
0,89
|
| Оптимальное
расчитано для оптимальных значений х1
,х2
|
| Предельная эффективность
характеризует отношение прироста выпуска продукции к малому приросту количества производственного ресурса . |
| ПЭ1
-Предельная эффективность ресурса х1
|
qf/qx1
>=0
|
| ПЭ1
=а0
*а1
*х1
(а1-1)
*х2
а2
|
| ПЭ2
-Предельная эффективность ресурса х2
|
qf/qx2
>=0
|
| ПЭ2
=а0
*а2
*х1
а1
*х2
(а2-1)
|
| Вывод:
Проанализировав расчеты в таблице можно увидеть , что малый прирост капитала ведет к увеличению прироста выпуска , а прирост труда ведет к его уменьшению . |
| F-Функция выпуска |
F=а0
*х1
а1
*х2
а2
|
| Помимо предельной эффективности в качестве характеристики изменения выпуска продукции при увеличении затрат ресурсов используют также отношение этих величин , которое принято называть эластичностью выпуска
по отношению изменения затрат i-го ресурса. |
| Эластичность выпуска
показывает на сколько процентов возрастет объем продукции при увеличении затрат ресурсов на 1 % по отношению к изменению затрат. |
| Еi
-Эластичность выпуска по ресурсу хi
|
Ei
(x)=xi
/f(x)*qf/qxi
|
| Е1
-Эластичность выпуска по ресурсу х1
|
E1
=(х1
/F)*а0
*а1
*х1
(а1-1)
*х2
а2
|
| Е2
-Эластичность выпуска по ресурсу х2
|
E2
=(х2
/F)*а0
*а2
*х1
а1
*х2
(а2-1)
|
| Вывод:
Наша производственная функция характеризуется постоянной эластичностью выпуска по отношению к изменению ресурсов. |
| Предельная норма
замещения одного ресурса другим ( величина g) показывает сколько второго ресурса может быть высвобождено при увеличении затрат первого ресурса , если выпуск продукции остается неизменным. |
| g-Предельная норма замещения |
g=qx2
/qx1
=(qf/qx1
)/(qf/qx2
)
|
| g=(а1
*х2
)/(а2
*х1
)
|
| Производственная функция характеризуется определенной отдачей от расширения масштабов производства.Последняя характеризует изменение выпуска продукции при пропорциональном изменении затрат ресурсов и выражена математически в умножении всех компонентов вектора х на скаляр t.Скалярная функция f(x) является однородной функцией степени d ,если для любого вектора х и любого скаляра t она удовлетворяет соотношению : |
| 0<t<1
|
f(tx)=td
f(x)
|
| f(x)=а0
*х1
а1
*х2
а2
|
f(tx)=а0
*(t*х1
)а1
*(t*х2
)а2
=t(a1+a2)
*а0
*х1
а1*
х2
а2
|
d=a1
+a2
|
| d=
|
1,00
|
, т.е. d=1 |
| Вывод
:Функция характеризуется постоянной отдачей от расширения масштаба производства. |
| Для характеристики последствий изменения масштаба производства вводят показатель Е(х) , называемый эластичностью производства
и определяемый следующим образом: |
| E(x)=
|
lim
|
t
|
qf(tx)
|
| t 1
|
f(tx)
|
qt
|
| Этот показатель характеризует процентное изменение выпуска продукции при изменении масштаба производства на 1% при данной структуре ресурсов х. |
| т.к. f(tx)=td
f(x),то |
Е(х)=d=1 |
|