|
ЧУЗ-ИДА
Кривой Рог PEI-IBM
Частное Учебное Заведение
Институт Делового Администрирования
Private Educational Institution
Institute of Business Managment
Основы теории систем и
системного анализа
Конспект лекций для специальности
УЧЕТ И АУДИТ
·
95
сентябрь-декабрь 1996 г.
Термины теория систем
и системный анализ
или, более кратко — системный подход,
несмотря на период более 25 лет их использования, все еще не нашли общепринятого, стандартного истолкования.
Причина этого факта заключается, скорее всего, в динамичности процессов в области человеческой деятельности и, кроме того, в принципиальной возможности использовать системный подход практически в любой решаемой человеком задаче.
Даже в определении самого понятия система
можно обнаружить достаточно много вариантов, часть из которых базируется на глубоко философских подходах, а другая использует обыденные обстоятельства, побуждающие нас к решению практических задач системного плана.
Выберем золотую середину и будем далее понимать термин система
как совокупность (множество) отдельных объектов
с неизбежными связями
между ними. Если мы обнаруживаем хотя бы два таких объекта: учитель и ученик в процессе обучения, продавец и покупатель в торговле, телевизор и передающая станция в телевидении и т. д. — то это уже система
. Короче, с некоторой претензией на высокопарность, можно считать системы способом существования окружающего нас мира
.
Более важно понять преимущество взгляда на этот мир с позиций системного подхода
: возможность ставить и решать, по крайней мере, две задачи:
· расширить и углубить собственные представления о “меха-низме” взаимодействий объектов в системе; изучить и, возможно, открыть новые её свойства;
· повысить эффективность системы в том плане ее функционирования, который интересует нас больше всего.
Хотя хронология науки относит момент зарождения теории систем и системного анализа
(далее ТССА
) к средине текущего столетия, тем не менее, можно понять, что возраст ТССА
[ГАсГ1]
составляет ровно столько, сколько существует Homo Sapiens.
Другое дело, что по мере развитие науки, прежде всего — кибернетики, эта отрасль прикладной науки сформировалась в самостоятельный раздел. Ветви ТССА прослеживаются во всех “ведомственных кибернетиках”: биологической, медицинской, технической и, конечно же, экономической. В каждом случае объекты, составляющие систему, могут быть самого широкого диапазона — от живых существ в биологии до механизмов, компьютеров или каналов связи в технике.
Реклама

Но, несмотря на это, задачи и принципы системного подхода остаются неизменными, не зависящими от природы объектов в системе.
Для лиц вашей будущей профессии наибольший интерес представляют, естественно, экономические системы
, а глобальной задачей системного подхода — совершенствование процесса управления экономикой.
Поэтому для нас с вами предметом системного анализа будут являться вопросы сбора, хранения и обработки информации об экономических объектах и, возможно, технологических процессах.
Используя классическое определение кибернетики как науки об общих законах получения, хранения, передачи и преобразования информации (кибернетика
в дословном переводе — искусство управлять
), можно считать ТССА фундаментальным разделом экономической кибернетики.
ТССА, как отрасль науки, может быть разделена на две, достаточно условные части:
·
теоретическую
: использующую такие отрасли как теория вероятностей, теория информации, теория игр, теория графов, теория расписаний, теория решений, топология, факторный анализ и др.;
·
прикладную
, основанную на прикладной математической статистике, методах исследовании операций, системотехнике и т. п. Таким образом, ТССА широко использует достижения многих отраслей науки и этот “захват” непрерывно расширяется.
Вместе с тем, в теории систем имеется свое “ядро”, свой особый метод — системный подход
к возникающим задачам. Сущность этого метода достаточно проста: все элементы
системы и все операции
в ней должны рассматриваться только
как одно целое, только в совокупности, только во взаимосвязи
друг с другом.
Плачевный опыт попыток решения системных вопросов с игнорированием этого принципа, попыток использования "местечкового" подхода достаточно хорошо изучен. Локальные решения, учет недостаточного числа факторов, локальная оптимизация — на уровне отдельных элементов почти всегда приводили к неэффективному в целом, а иногда и опасному по последствиям, результату.
· Итак, первый принцип
ТССА — это требование рассматривать совокупность элементов системы как одно целое
или, более жестко, — запрет на рассмотрение системы как простого объединения элементов.
Реклама

· Второй принцип
заключается в признании того, что свойства системы не просто сумма
свойств ее элементов. Тем самым постулируется возможность того, что система обладает особыми свойствами, которых может и не быть у отдельных элементов.
· Весьма важным атрибутом системы является ее эффективность.
Теоретически доказано, что всегда существует функция ценности
системы — в виде зависимости ее эффективности (почти всегда это экономический показатель) от условий построения и функционирования. Кроме того, эта функция ограничена, а значит можно и нужно искать ее максимум. Максимум эффективности
системы может считаться третьим
ее основным принципом.
·Четвертый принцип
запрещает рассматривать данную систему в отрыве от окружающей ее среды — как автономную, обособленную. Это означает обязательность учета внешних связей
или, в более общем виде, требование рассматривать анализируемую систему как часть (подсистему) некоторой более общей системы.
· Согласившись с необходимостью учета внешней среды, признавая логичность рассмотрения данной системы как части некоторой, большей ее, мы приходим к пятому принципу
ТССА — возможности (а иногда и необходимости) деления данной системы на части, подсистемы
. Если последние оказываются недостаточно просты для анализа, с ними поступают точно также. Но в процессе такого деления нельзя нарушать предыдущие принципы — пока они соблюдены, деление оправдано, разрешено в том смысле, что гарантирует применимость практических методов, приемов, алгоритмов решения задач системного анализа.
Все изложенное выше позволяет формализовать определение термина система
в виде — многоуровневая конструкция из взаимо-действующих элементов, объединяемых в подсистемы нескольких уровней для достижения единой цели функционирования (целевой функции).
Как уже отмечалось, в большинстве случаев (в экономических системах — повсеместно), показателем полноты достижения цели “жизни” системы служит стоимостной показатель. Разумеется, что выбор показателя — критерия
эффективности системы
, является заключитель-ным этапом формулировки целей и задач системы. Но нельзя упускать из виду, что от этого этапа будут зависеть наши представления о свойствах системы и результаты самого системного анализа.
Предположим, что по отношению к некоторой системе все формальные вопросы описания уже благополучно разрешены. Что же дальше?
А дальше надо системой управлять
— точнее решать вопрос об алгоритме или тактике управления для достижения наибольшей эффективности. Скорее всего, именно в этой области и лежит поле профессиональной деятельности в вашей будущей профессии — делового администрирования, решения задач организационно-управленческого характера.
Вроде бы все очень просто — имеется предприятие, выделены его подсистемы (отделы), определены функции каждой подсистемы и каждого элемента в них, описаны связи внутри системы и по отношению к внешней среде. Так пусть каждый элемент функционирует оптимально — наиболее эффективно делает свое дело.
Но здесь почти всегда возникают противоречия, суть которых можно определить с помощью примера, ставшего классическим.
Рассмотрим деятельность некоторой фирмы, производящей определенные виды продукции и, естественно, стремящейся получить мак-симальную прибыль от ее продажи. Пусть решается простой вопрос — сколько готовой продукции хранить на складе предприятия и сколько разновидностей ее должно производиться? Посмотрим на “частные” интересы различных отделов фирмы и сразу же обнаружим их несовпадение.
Да, каждый из отделов заинтересован в достижении глобальной цели — максимуме прибыли фирмы (если это не так, то системный подход здесь бессилен). Но!
· Производственный отдел
будет заинтересован в длительном и непрерывном производстве одного и того же вида продукции. Только в этом случае будут наименьшими расходы на наладку оборудования.
· Отдел сбыта
, наоборот, будет отстаивать идею производства максимального числа видов продукции и больших запасов на складах.
· Финансовый отдел
, конечно же, будет настаивать на минимуме складских запасов — то, что лежит на складе, не может приносить прибыли!
· Даже отдел кадров
будет иметь свою
локальную целевую функцию — производить продукцию всегда (даже в периоды делового спада) и в одном и том же ассортименте, так как в этом случае не будет проблем текучести кадров.
Вот и представьте себе сложность задачи управления такой большой системой
с достижением глобальной цели — максимума прибыли.
Ясно, что придется ставить и решать задачи согласования целей
отдельных подсистем и хорошо еще, если показатели эффективности подсистем имеют ту же размерность, что и показатель (критерий) эффективности системы в целом. Ведь вполне может оказаться, что эффективность работы некоторых подсистем приходится измерять не в денежном выражении, а с помощью других, не числовых, показателей.
Рассмотрим теперь вопрос о связях системы — между отдельными элементами подсистем, подсистемами разных уровней и связях с внешней средой. Хотя бы умозрительно можно полагать наличие каналов,
по которым эти связи производятся. Но чем же “наполнены” такие каналы? Скорее всего, в экономических системах можно обнаружить и выделить только три типа наполнителей
· продукция
;
· деньги
;
· информация
.
Нет нужды объяснять принципиальные различия продукции и денег. Что же касается информации, то можно вспомнить ответ отца кибернетики Н.Винера на вопрос — так что же такое информация: это НЕ материя и НЕ энергия!
Возникает вопрос о том, как же согласовывать эти совершенно несопоставимые по размерностям показатели, как привести их к “общему знаменателю”? Ведь без такого согласования невозможно будет установить единый показатель эффективности системы в целом.
Вторая проблема оценки связей в системе станет понятной, если мы примем условное деление систем на естественные и искусственные. Никто не станет отрицать, что в природе все взаимосвязано — все “имеет свой конец, свое начало”. И, тем не менее, все согласятся с тем, что “поведение” природы (а тем более — человека) невозможно предсказать со 100% уверенностью.
Таким образом, вторая проблема оценки связей при системном анализе заключается в том, что количества продукции, суммы денег и показатели информационных потоков в каналах связи системы имеют стохастичную, вероятностную
природу — их значения в данный момент времени нельзя предсказать абсолютно надежно.
Поэтому при системном анализе часто приходится иметь дело не с конкретными значениями величин, не с заранее определенными событиями, а с их оценками
по прошлым наблюдениям или по прогнозам на будущее. Отсюда возникает необходимость использования специальных, большей частью прикладных, методов математической ста-тистики.
Если теперь вспомнить основное назначение системного анализа — получить рекомендации по вопросам управления системой или, по крайней мере, по совершенствованию этого управления, то возникает вопрос — а всегда ли оправдан системный подход? Ведь ясно, что для его реализации потребуются определенные и возможно немалые затраты времени и средств. Но, если выводы системного анализа, полу-ченные на его основе рекомендации, почти всегда не полностью достоверны, то выходит, что мы рискуем
? Да, это так и есть.
Без риска ошибки в реальном, окружающем нас мире просто жить, а уж тем более действовать, — практически невозможно. Надо осознать, что даже самое точное следование рекомендациям науки не дает гарантии получить именно то, что мы задумали, проектировали, планировали. В утешение лишь скажем, что можно рисковать без попыток просчитать возможные последствия и можно рисковать в условиях, когда использованы все научные методы оценки этих последствий.
Это совершенно противоположные подходы, но нельзя считать ни один из них "юридически законным" или вытекающим из каких ни будь законов природы, нельзя считать стиль управления системой на основе системного анализа "правильным", "современным", "куль-турным". Другое дело — не знать
о возможности применения системного подхода к вопросам управления — вот это неправильно, некультурно.
Для закрепления темы введения в курс, с целью хотя бы частично осветить не затронутые еще вопросы системного анализа, рассмотрим конкретный пример из собственного практического опыта лектора.
В конце 70 г. г. украинский МинВуз принял решение глобального учета информации о текущей успеваемости студентов всех вузов Украины. Дело было поставлено с поистине советским размахом — каж-дые две недели семестра все
студенты вуза проходили аттестацию по всем
учебным дисциплинам. Вся эта лавина информации (конечно же, недостоверной — в виде прогноза будущей оценки на экзамене) передавалась в Киев. Сейчас дело не в том как она использовалась (в конце этой эпопеи оказалось — никак!).
Мы, в Криворожском горнорудном институте (теперь — технический университет) попытались использовать ситуацию для совершен-ствования управления учебным процессом, благо что процесс сбора информации был обусловлен приказом по министерству.
На первом этапе системного подхода к задаче был решен вопрос о выделении подсистем и их элементов. В качестве основных подсистем рассматривались всего три их разновидности:
· подсистема “Студенты”;
· подсистема “Кафедры”;
· подсистема “Деканаты”.
Было понятно, что локальные цели каждой из подсистем отличались друг от друга (в первом случае это учеба, во втором — обучение, в третьем — управление обучением на уровне факультета).
Вместе с тем имелась и единая цель функционирования вуза — подготовка специалистов с высшим образованием по отдельным профи-лям. Была определена и мера оценки эффективности системы в целом, пусть даже в таком примитивном виде, как экзаменационные оценки знаний. Принималась во внимание иерархия
подсистем в плане подчинения, направленность потоков знаний и информации о них в каналах связи между звеньями.
Были содержательно сформулированы две задачи:
· как по результатам текущего контроля знаний оценить эффективность процесса обучения на данном интервале семестра, обнаружить “узкие места” этого процесса;
· как оценить эффективность управляющих воздействий на систему обучения на конечном его этапе — после подведения итогов сессии.
При этом заранее предполагалось, что “виновниками” недостаточной эффективности обучения могут оказаться элементы любой из подсистем.
В самом деле, низкая успеваемость может быть обусловлена разными причинами:
· слабой предварительной подготовкой студентов;
· малоэффективными в данных условиях методами обучения;
· промахами в организации обучения.
Заметим, что эти выводы пока никакого отношения к системному анализу не имеют, они сформулированы на основании понимания
особенностей процесса
обучения.
Здесь, на этом этапе системного подхода в любой сфере всегда необходимо обращаться к “технологии” процессов, происходящих в системе. А это означает, что в предварительной части системного анализа в равной степени должны участвовать как специалисты в области ТССА, так и знатоки процессов данной системы. Участие одного из них — лица, принимающего решения (далее — ЛПР) совершенно обязательно.
На следующем этапе в рассматриваемом примере были разработаны методы сбора, хранения и обработки информации. И здесь, как в любом случае системного подхода к задачам управления, пришлось решать проблему представительности собираемых данных.
Прежде всего, пришлось поставить и решить вопрос об оценках текущего контроля знаний, Поскольку это не метры, литры или килобайты, поскольку не существует шкалы
знаний, то что должна означать оценка текущего контроля?
После обсуждения этих вопросов в среде специалистов (экспертов в области обучения в высшей школе) было принято решение — оценка текущего контроля знаний рассматривается как прогноз
экзаменационной оценки.
И снова обратим внимание на тот факт, что такая договоренность между ЛПР и специалистами ТССА была бы необходима и в том случае, когда речь бы шла не о знаниях, а о будущих прибылях или надоях!
Здесь возможно различие в достоверности прогноза и то далеко не всегда, но со стохастичным характером данных системного анализа приходится мириться — такова природа явлений в реальной жизни.
Но и это еще не всё об информации, используемой при системном анализе. Далеко не всегда “измерения” чего-то можно производить без ощутимых последствий. И пусть даже сбор информации не приносит прямого морального или материального ущерба, что иногда вполне возможно, хотя и не всегда очевидно. Главное в другом — если мы хотим иметь информацию об элементе системы, то надо стремиться получить ее с наименьшими, информационными же, потерями.
В рассматриваемом примере не использовались никакие приборы, лишенные разума и эмоций, — источниками данных и “измерителями” являлись люди! В самом деле, необходимость предсказать свои собственные достижения в условиях, когда они не только от тебя зависят (прогнозировать итог экзамена студента), вне всяких сомнений, хоть чуть-чуть, но всё же меняет один из элементов, то есть преподавателя.
Одной из проблем, с которой сталкиваются почти всегда при проведении системного анализа, является проблема эксперимента
в системе или над системой. Очень редко это разрешено моральными законами или законами безопасности, но сплошь и рядом связано с материальными затратами и (или) значительными потерями информации.
Опыт всей человеческой деятельности учит — в таких ситуациях надо экспериментировать не над объектом, интересующим нас предметом или системой, а над их моделями
. Под этим термином надо понимать не обязательно модель физическую,
т. е. копию объекта в уменьшенном или увеличенном виде. Физическое моделирование очень редко применимо в системах, хоть как то связанных с людьми. В частности в социальных системах (в том числе — экономических) приходится прибегать к математическому моделированию.
Буквально через минуту станет ясно, что математическим моделированием мы овладеваем еще на школьной скамье. В самом деле, пусть требуется найти площадь прямоугольника со сторонами 2 и 8 метров. Измерение сторон произведено приближенно — других измерений расстояний не бывает! Как решить эту задачу? Конечно же — не путем рисования прямоугольника (даже в уменьшенном масштабе) и последующем разбиении его на квадратики с окончательным подсчетом их числа. Да, безусловно, мы знаем формулу S = B
·H
и воспользуемся ею — применим математическую модель
процесса определения площади.
Возвращаясь к начатому ранее примеру системного анализа обучения, можно заметить, что там собственно нечего вычислять по фор-мулам — где же их взять. Это так и есть, не существует методов расчета в такой сфере как “прием-передача” знаний и сомнительно, чтобы эти методы когда-либо появились.
Но ведь не существует формулы пищеварения, а люди все таки едят, планируют процесс питания, управляют им и иногда даже успешно.....
Так что же? Если нет математических моделей — не выдумывать же их самому? Ответ на этот вопрос самый простой: всем
это уметь и делать — не обязательно, а вот тому, кто взялся решать задачи системного анализа — приходится и очень часто. Иногда здесь возможна подсказка природы, знание технологии системы; в ряде случаев может выручить эксперимент над реальной системой или ее элементами (т. н. методы планирования экспериментов
) и, наконец, иногда приходится прибегать к методу “черного ящика”, предполагая некоторую статистическую связь между его входом и выходом.
Таким “ящиком” в рассматриваемом примере считался не только студент (с вероятностью такой-то получивший
знания), но и все остальные элементы системы — преподаватели и лица, организующие обучение.
Конечно, возможны ситуации, когда все процессы в большой системе описываются известными законами природы и когда можно надеяться, что запись уравнений этих законов даст нам математическую модель хотя бы отдельных элементов или подсистем. Но и в этих, редких, случаях возникают проблемы не только в плане сложности урав-нений, невозможности их аналитического решения (расчета по формулам). Дело в том, что в природе трудно обнаружить примеры “чистого” проявления ее отдельных законов — чаще всего сопутствующие явление факторы “смазывают” теоретическую картину.
Еще одно важное обстоятельство приходится учитывать при математическом моделировании. Стремление к простым, элементарным моделям и вызванное этим игнорирование ряда факторов может сделать модель неадекватной реальному объекту, грубо говоря — сделать ее неправдивой. Снова таки, без активного взаимодействия с технологами, специалистами в области законов функционирования систем данного типа, при системном анализе не обойтись.
В системах экономических, представляющих для вас основной интерес, приходится прибегать большей частью к математическому моделированию, правда в специфическом виде — с использованием не только количественных, но и качественных, а также логических показателей.
· Из хорошо себя зарекомендовавших на практике можно упомянуть модели: межотраслевого баланса; роста; планирования эко-номики; прогностические; равновесия и ряд других.
Завершая вопрос о моделировании при выполнении системного анализа, резонно поставить вопрос о соответствии
используемых моделей реальности
.
Это соответствие или адекватность
могут быть очевидными или даже экспериментально проверенными для отдельных элементов системы. Но уже для подсистем, а тем более системы в целом существует возможность серьезной методической ошибки, связанная с объективной невозможность оценить адекватность модели большой системы на логическом уровне.
Иными словами — в реальных системах вполне возможно логическое
обоснование моделей элементов. Эти модели мы как раз и стремимся строить минимально достаточными
, простыми настолько, насколько это возможно без потери сущности процессов. Но логически осмыслить взаимодействие десятков, сотен элементов человек уже не в состоянии. И именно здесь может “сработать” известное в математике следствие из знаменитой теоремы Гёделя — в сложной системе, полностью изолированной от внешнего мира, могут существовать истины, положения, выводы вполне “допустимые
” с позиций самой системы, но не имеющие никакого смысла
вне
этой системы.
То есть, можно построить логически безупречную модель реальной системы с использованием моделей элементов и производить анализ такой модели. Выводы этого анализа будут справедливы для каждого элемента, но ведь система — это не простая сумма элементов, и ее свойства не просто сумма свойств элементов.
Отсюда следует вывод — без учета внешней среды выводы о поведении системы, полученные на основе моделирования, могут быть вполне обоснованными при взгляде изнутри системы. Но не исключена и ситуация, когда эти выводы не имеют никакого отношения к системе — при взгляде на нее со стороны внешнего мира.
Для пояснения вернемся к рассмотренному ранее примеру. В нем почти все элементы были построены на вполне оправданных логических постулатах
(допущениях) типа: если студент Иванов получил оценку “знает” по некоторому предмету, и посетил все занятия по этому предмету, и управление его обучением было на уровне “Да” — то вероятность
получения им оценки “знает” будет выше, чем при отсутствии хотя бы одного из этих условий.
Но как на основании системного анализа такой модели ответить на простейший вопрос; каков вклад (хотя бы по шкале “больше-меньше”) каждой
из подсистем в полученные фактические результаты сессии? А если есть числовые
описания этих вкладов, то каково доверие к ним? Ведь управляющие воздействия на систему обучения часто можно производить только через семестр или год.
Здесь приходит на помощь особый способ моделирования — метод статистических испытаний (Монте Карло). Суть этого метода проста — имитируется достаточно долгая “жизнь” модели, несколько сотен семестров для нашего примера. При этом моделируются и регистрируются случайно меняющиеся внешние (входные)
воздействия на систему. Для каждой из ситуации по уравнениям модели просчитываются выходные (системные)
показатели. Затем производится обратный расчет — по заданным выходным показателям производится расчет входных. Конечно, никаких совпадений мы не должны ожидать — каждый элемент системы при входе “Да” вовсе не обязательно будет “Да” на выходе.
Но существующие современные методы математической статистики позволяют ответить на вопрос — а можно ли и, с каким доверием, использовать данные моделирования. Если эти показатели доверия для нас достаточны, мы можем использовать модель для ответа на поставленные выше вопросы.
Пусть построена модель системы с соблюдением всех принципов системного подхода, разработаны и “обкатаны” алгоритмы необходимых расчетов, приготовлены варианты управляющих воздействий на систему. Надо понять, что эти воздействия не всегда заключаются в изменениях уровня некоторых входных параметров — это могут быть варианты структурных перестроек системы.
Так вот — все это есть. И что же дальше? Пора и управлять, управлять с единой целью — повышения эффективности функционирования системы (однокритериальная задача) или с одновременным достижением нескольких целей (многокритериальная задача).
Естественно, мы ставим вопрос: “А что будет, если …
?” и ожидаем ответа. Но здесь не следует ожидать чуда, нельзя надеяться на однозначный ответ. Если к примеру, мы интересуемся вопросом — “к чему приведет увеличение на 20% закупок цемента?”, то мы должны не удивляться, получив ответ — “Это приведет к увеличению рентабельности производства кирпича на величину, которая с вероятностью 95% не
будет ниже 6% и не
будет выше 14%”. И это еще очень содержательный ответ, могут быть и более “расплывчатые”!
Здесь уместно в последний раз обратиться к примеру с анализом системы обучения и ответить на возможный вопрос — а как же были использованы выводы системного анализа обучения в КГРИ? Ответ одного из соавторов системного анализа, пишущего эти строки, очень краткий — никак
.
Можно теперь открыть еще одну (не последнюю) тайну ТССА. Дело в том, что судьбу разработок по управлению большими системами должно решать только ЛПР, и только этот человек (или коллективный орган) решает вопрос дальнейшей судьбы итогов системного анализа. Важно отметить, что это правило никак не связано ни с “важностью” конкретной отрасли промышленности, торговли или образования, ни с политическими обстоятельствами, ни с государственным строем. Все намного проще — мудрость отцов-основателей ТССА проявилась, прежде всего, в том, что неполнота достоверности
выводов системного анализа была ими заранее оговорена
.
Поэтому те, кто ведет системный анализ, не должны претендовать на обязательное использование своих разработок; факты отказа от их использования не есть показатель непригодности этих разработок.
С другой стороны, те, кто принимают решения, должны столь же четко понимать, что расплывчатость выводов ТССА есть неизбежность, она может быть обусловлена не промахами анализа, а самой природой или ошибкой постановки задачи, например, попытки управлять такой гигантской системой, как экономика бывшего СССР.
Как уже говорилось, при анализе больших систем наполнителем каналов связи между элементами, подсистемами и системы в целом могут быть:
· продукция, т. е. реальные, физически ощутимые предметы с заранее заданным способом их количественного и качественного описания;
· деньги, с единственным способом описания — суммой;
· информация, в виде сообщений о событиях в системе и значениях описывающих ее поведение величин.
Начнем с того, что обратим внимание на тесную (системную!) связь показателей продукции и денег с информацией об этих показателях. Если рассматривать некоторую физическую величину, скажем — количество проданных за день образцов продукции, то сведения об этой величине после продажи могут быть получены без проблем и достаточно точно или достоверно. Но, уже должно быть ясно, что при системном анализе нас куда больше интересует будущее — а сколько этой продукции будет продано за день? Этот вопрос совсем не праздный — наша цель управлять, а по образному выражению “управлять — значит предвидеть”.
Итак, без предварительной информации, знаний о количественных показателях в системе нам не обойтись. Величины, которые могут принимать различные значения в зависимости от внешних по отношению к ним условий, принято называть случайными (стохастичными
по природе). Так, например: пол встреченного нами человека может быть женским или мужским (дискретная случайная величина); его рост также может быть различным, но это уже непрерывная случайная величина — с тем или иным количеством возможных значений (в зависимости от единицы измерения).
Для случайных величин (далее — СВ
) приходится использовать особые, статистические
методы их описания. В зависимости от типа самой СВ — дискретная или непрерывная это делается по разному.
Дискретное описание заключается в том, что указываются все
возможные значения данной величины (например - 7 цветов обычного спектра) и для каждой из них указывается вероятность
или частота наблюдений именного этого значения при бесконечно большом числе всех наблюдений.
Можно доказать (и это давно сделано), что при увеличении числа наблюдений в определенных условиях за значениями некоторой дискретной величины частота
повторений данного значения будет все больше приближаться к некоторому фиксированному значению — которое и есть вероятность
этого значения.
К понятию вероятности значения дискретной СВ можно подойти и иным путем — через случайные события
. Это наиболее простое понятие в теории вероятностей и математической статистике — событие с вероятностью 0.5 или 50% в 50 случаях из 100 может произойти или не произойти, если же его вероятность более 0.5 - оно чаще происходит, чем не происходит. События с вероятностью 1
 называют достоверными
, а с вероятностью 0
— невозможными
. называют достоверными
, а с вероятностью 0
— невозможными
.
Отсюда простое правило: для случайного события X
вероятности P(X)
(событие происходит) и P(X
)
(событие не происходит), в сумме для простого события дают 1
.
Если мы наблюдаем за сложным событием — например, выпадением чисел 1..6 на верхней грани игральной кости, то можно считать, что такое событие имеет множество исходов и для каждого из них вероятность составляет 1/6 при симметрии кости.
Если же кость несимметрична, то вероятности отдельных чисел
будут разными, но сумма их равна 1
.
Стоит только рассматривать итог бросания кости как дискретную случайную величину и мы придем к понятию распределения вероятностей
такой величины.
Пусть в результате достаточно большого числа наблюдений за игрой с помощью одной и той же кости мы получили следующие данные:
Таблица 2.1
| Грани
|
1
|
2
|
3
|
4
|
5
|
6
|
Итого
|
| Наблюдения
|
140
|
80
|
200
|
400
|
100
|
80
|
1000
|
Подобную таблицу наблюдений за СВ часто называют выборочным распределением
, а соответствующую ей картинку (диаграмму) — гистограммой
.
Рис. 2.1
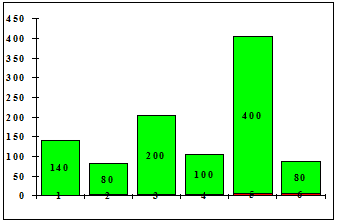
Какую же информацию несет такая табличка или соответствующая ей гистограмма?
Прежде всего, всю
— так как иногда и таких данных о значениях случайной величины нет и их приходится либо добывать (эксперимент, моделирование), либо считать исходы такого сложного события равновероятными — по 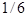 на любой из исходов. на любой из исходов.
С другой стороны — очень мало
, особенно в цифровом, численном описании СВ. Как, например, ответить на вопрос: — а сколько в среднем
мы выигрываем за одно бросание кости, если выигрыш соответствует выпавшему числу на грани?
Нетрудно сосчитать:
1•0.140+2•0.080+3•0.200+4•0.400+5•0.100+6•0.080= 3.48
То, что мы вычислили, называется средним значением
случайной величины, если нас интересует прошлое.
Если же мы поставим вопрос иначе — оценить по этим данным наш будущий выигрыш, то ответ 3.48 принято называть математическим ожиданием
случайной величины, которое в общем случае определяется как
Mx =
å
Xi
· P(Xi
)
; {2 - 1}
где P(Xi
)
— вероятность того, что X
примет свое i-е очередное значение.
Таким образом, математическое ожидание случайной величины (как дискретной, так и непрерывной)— это то, к чему стремится
ее среднее значение при достаточно большом числе наблюдений.
Обращаясь к нашему примеру, можно заметить, что кость несимметрична, в противном случае вероятности составляли бы по 1/6 каждая, а среднее и математическое ожидание составило бы 3.5.
Поэтому уместен следующий вопрос - а какова степень асимметрии кости - как ее оценить по итогам наблюдений?
Для этой цели используется специальная величина — мера рассеяния
— так же как мы "усредняли" допустимые значения СВ, можно усреднить ее отклонения от среднего. Но так как разности (Xi
- Mx)
всегда будут компенсировать друг друга, то приходится усреднять не отклонения от среднего, а квадраты этих отклонений
. Величину
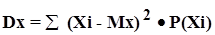 {2 - 2} {2 - 2}
принято называть дисперсией
случайной величины X.
Вычисление дисперсии намного упрощается, если воспользоваться выражением
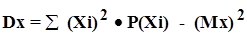 {2 - 3} {2 - 3}
т. е. вычислять дисперсию случайной величины через усредненную
разность квадратов ее значений и квадрат ее среднего значения.
Выполним такое вычисление для случайной величины с распределением рис. 1.
Таблица 2.2
| Грани(X)
|
1
|
2
|
3
|
4
|
5
|
6
|
Итого
|
| X2
|
1
|
4
|
9
|
16
|
25
|
36
|
|
| Pi
|
0.140
|
0.080
|
0.200
|
0.400
|
0.100
|
0.080
|
1.00
|
| Pi•X2
•1000
|
140
|
320
|
1800
|
6400
|
2500
|
2880
|
14040
|
Таким образом, дисперсия составит 14.04 - (3.48)2
= 1.930.
Заметим, что размерность дисперсии не совпадает с размерностью самой СВ и это не позволяет оценить величину разброса. Поэтому чаще всего вместо дисперсии используется квадратный корень из ее значения — т. н. среднеквадратичное отклонение
или отклонение от среднего значения:
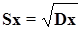 {2 - 4}
{2 - 4}
составляющее в нашем случае 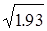 = 1.389. Много это или мало? = 1.389. Много это или мало?
Сообразим, что в случае наблюдения только одного из возможных значений (разброса нет) среднее было бы равно именно этому значению, а дисперсия составила бы 0. И наоборот - если бы все значения наблюдались одинаково часто (были бы равновероятными), то среднее значение составило бы (1+2+3+4+5+6) / 6 = 3.500; усредненный квадрат отклонения — (1 + 4 + 9 + 16 + 25 + 36) / 6 =15.167; а дисперсия 15.167-12.25 = 2.917.
Таким образом, наибольшее
рассеяние значений СВ имеет место при ее равновероятном
или равномерном распределении.
Отметим, что значения Mx
и SX
являются размерными и их абсолютные значения мало что говорят. Поэтому часто для грубой оценки "случайности" данной СВ используют т. н. коэффициент вариации
или отношение корня квадратного из дисперсии к величине математического ожидания:
Vx
= SX
/MX
.
{2 - 5}
В нашем примере эта величина составит 1.389/3.48=0.399.
Итак, запомним, что неслучайная, детерминированная
величина имеет математическое ожидание равное ей самой
, нулевую
дисперсию и нулевой
коэффициент вариации,
в то время как равномерно распределенная
СВ имеет максимальную
дисперсию и максимальный
коэффициент вариации.
В ряде ситуаций приходится иметь дело с непрерывно распределенными
СВ - весами, расстояниями и т. п. Для них идея оценки среднего значения (математического ожидания) и меры рассеяния (дисперсии) остается той же, что и для дискретных СВ. Приходится только вместо соответствующих сумм вычислять интегралы. Второе отличие — для непрерывной СВ вопрос о том какова вероятность принятия нею конкретного значения обычно не имеет смысла — как проверить, что вес товара составляет точно 242 кг - не больше и не меньше?
Для всех СВ — дискретных и непрерывно распределенных, имеет очень большой смысл вопрос о диапазоне
значений. В самом деле, иногда знание вероятности того события
, что случайная величина не превзойдет заданный рубеж, является единственным способом использовать имеющуюся информацию для системного анализа и системного подхода к управлению. Правило определения вероятности попадания в диапазон очень просто — надо просуммировать вероятности отдельных дискретных значений диапазона или проинтегрировать кривую распределения на этом диапазоне.
Вернемся теперь к вопросу о случайных событиях. Здесь методически удобнее рассматривать вначале простые события (может произойти или не произойти). Вероятность события X
будем обозначать P(X)
и иметь ввиду, что вероятность того, что событие не произойдет, составляет
P(X
)
= 1
-
P(X)
. {2 - 6}
Самое важное при рассмотрении нескольких случайных событий (тем более в сложных системах с развитыми связями между элементами и подсистемами) — это понимание способа определения вероятности одновременного наступления нескольких событий или, короче, — совмещения
событий.
Рассмотрим простейший пример двух событий X
и Y,
вероятности которых составляют P(X)
и P(Y).
Здесь важен лишь один вопрос — это события независимые или, наоборот взаимозависимые и тогда какова мера связи между ними? Попробуем разобраться в этом вопросе на основании здравого смысла.
Оценим вначале вероятность одновременного
наступления двух независимых
событий.
Элементарные рассуждения приведут нас к выводу: если события независимы, то при 80%-й вероятности X
и 20%-й вероятности Y
одновременное их наступление имеет вероятность всего лишь 0.8 • 0.2 = 0.16 или 16% .
Итак — вероятность наступления двух независимых событий определяется произведением
их вероятностей:
P(XY) = P(X) 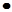 P(Y).
{2 - 7} P(Y).
{2 - 7}
Перейдем теперь к событиям зависимым. Будем называть вероятность события X
при условии, что событие Y
уже произошло условной вероятностью
P(X/Y)
, считая при этом P(X)
безусловной
или полной
вероятностью. Столь же простые рассуждения приводят к так называемой формуле Байеса
P(X/Y)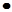 P(Y) = P(Y/X) P(Y) = P(Y/X)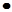 P(X)
{2 - 8} P(X)
{2 - 8}
где слева и справа записано одно и то же — вероятности одновременного наступления двух "зависимых" или коррелированных
событий.
Дополним эту формулу общим выражением безусловной вероятности события X
:
P(X)
= P(X/Y)
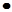 P(Y)
+ P(X/Y
) P(Y)
+ P(X/Y
)
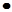 P(Y
)
, {2 - 9} P(Y
)
, {2 - 9}
означающей, что данное событие X
может произойти либо после того как событие Y
произошло, либо после того, как оно не произошло (Y
)
— третьего не дано!
Формулы Байеса или т. н. байесовский подход
к оценке вероятностных связей для простых событий и дискретно распределенных СВ играют решающую роль в теории принятия решений в условиях неопределенности последствий этих решений или в условиях противо-действия со стороны природы, или других больших систем (конкуренции). В этих условиях ключевой является стратегия управления, основанная на прогнозе т. н. апостериорной (послеопытной) вероятности события
P(X/Y)
 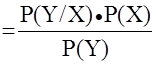 .
{2 - 10} .
{2 - 10}
Прежде всего, еще раз отметим взаимную
связь событий X
и Y
— если одно не зависит от другого, то данная формула обращается в тривиальное тождество. Кстати, это обстоятельство используется при решении задач оценки тесноты связей — корреляционном анализе. Если же взаимосвязь событий имеет место, то формула Байеса позволяет вести управление путем оценки вероятности достижения некоторой цели на основе наблюдений над процессом функционирования системы — путем перерасчета вариантов стратегий с учетом изменившихся представлений, т. е. новых значений вероятностей.
Дело в том, что любая стратегия управления будет строиться на базе определенных представлений о вероятности событий в системе — и на первых шагах эти вероятности будут взяты "из головы" или в лучшем случае из опыта управления другими системами. Но по мере "жизни" системы нельзя упускать из виду возможность "коррекции" управления - использования всего накапливаемого опыта.
Большую роль в теории и практике системного анализа играют некоторые стандартные распределения непрерывных и дискретных СВ.
Эти распределения иногда называют "теоретическими", поскольку для них разработаны методы расчета всех показателей распределения, зафиксированы связи между ними, построены алгоритмы расчета и т. п.
Таких, классических законов распределений достаточно много, хотя "штат" их за последние 30..50 лет практически не пополнился. Необходимость знакомства с этими распределениями для специалистов вашего профиля объясняется тем, что все они соответствуют некоторым "теоретическим" схемам случайных (большей частью — элементарных) событий.
Как уже отмечалось, наличие больших массивов взаимосвязанных событий и обилие случайных величин в системах экономики приводит к трудностям априорной оценки законов распределений этих событий или величин. Пусть, к примеру, мы каким-то образом установили математическое ожидание спроса некоторого товара. Но этого мало - надо хотя бы оценить степень колебания этого спроса, ответить на вопрос — а какова вероятность того, что он будет лежать в таких-то пределах? Вот если бы установить факт принадлежности данной случайной величины к такому классическому распределению как т. н. нормальное
, то тогда задача оценки диапазона, доверия к нему (доверительных интервалов) была бы решена безо всяких проблем.
Доказано, например, что с вероятностью более 95% случайная величина X
с нормальным законом распределения лежит в диапазоне — математическое ожидание Mx
плюс/минус три среднеквадратичных отклонения SX
.
Так вот — все дело в том к какой из схем случайных событий классического образца ближе всего схема функционирования элементов вашей большой системы. Простой пример - надо оценить показатели оплаты за услуги предоставления времени на междугородние переговоры - например, найти вероятность того, что за 1 минуту осуществляется ровно N
переговоров, если заранее известно среднее число поступающих в минуту заказов. Оказывается, что схема таких случайных событий прекрасно укладывается в т. н. распределение Пуассона
для дискретных случайных величин. Этому распределению подчинены почти все дискретные величины, связанные с так называемыми "редкими" событиями.
Далеко не всегда математическая оболочка классического закона распределения достаточно проста. Напротив — чаще всего это сложный математический аппарат со своими, специфическими приемами. Но дело не в этом, тем более при "повальной" компьютеризации всех областей деятельности человека. Разумеется, нет необходимости знать в деталях свойства всех или хоть какой-то части классических распределений - достаточно иметь в виду саму возможность воспользоваться ими.
Из личного опыта - очень давно, в до_компьютерную эру автору этих строк удалось предложить метод оценки степени надежности энергоснабжения, найти по сути дела игровой
метод принятия решения о необходимости затрат на резервирование линий электропередач в условиях неопределенности — игры с природой.
Таким образом, при системном подходе к решению той или иной задачи управления (в том числе и экономического) надо очень взвешено отнестись к выбору элементов системы или отдельных системных операций. Не всегда "укрупнение показателей" обеспечит логическую стройность структуры системы — надо понимать, что заметить близость схемы событий в данной системе к схеме классической чаще всего удается на самом "элементарном" уровне системного анализа.
Завершая вопрос о распределении случайных величин обратим внимание на еще одно важное обстоятельство: даже если нам достаточно одного единственного показателя — математического ожидания данной случайной величины, то и в этом случае возникает вопрос о надежности данных об этом показателя.
В самом деле, пусть нам дано т. н. выборочное
распределение случайной величины X
(например — ежедневной выручки в $) в виде 100 наблюдений за этой величиной. Пусть мы рассчитали среднее Mx
и оно составило $125 при колебаниях от $50 до $200. Попутно мы нашли SX
,
равное $5. Теперь уместен вопрос: а насколько правдоподобным будет утверждение о том, что в последующие дни выручка составит
точно $125? Или будет лежать в интервале $120..$130? Или окажется более некоторой суммы — например, $90?
Вопросы такого типа чрезвычайно остры - если это всего лишь элемент некоторой экономической системы (один из многих), то выводы на финише системного анализа, их достоверность, конечно же, зависят от ответов на такие вопросы.
Что же говорит теория, отвечая на эти вопросы? С одной стороны очень много, но в некоторых случаях — почти ничего. Так, если у вас есть уверенность в том, что "теоретическое" распределение данной случайной величины относится к некоторому классическому (т. е. полностью описанному в теории) типу, то можно получить достаточно много полезного.
· С помощью теории можно найти доверительные
интервалы для данной случайной величины. Если, например, уже доказано (точнее — принята гипотеза) о нормальном
распределении, то зная среднеквадратичное отклонение можно с уверенностью в 5% считать, что окажется вне диапазона (Mx
- 3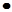 Sx
)......(Mx Sx
)......(Mx
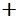 3 3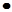 Sx
)
или в нашем примере выручка с вероятностью 0.05 будет <$90 или >$140. Надо смириться со своеобразностью теоретического вывода — утверждается не тот факт, что выручка составит от 90 до 140 (с вероятностью 95%), а только то, что сказано выше. Sx
)
или в нашем примере выручка с вероятностью 0.05 будет <$90 или >$140. Надо смириться со своеобразностью теоретического вывода — утверждается не тот факт, что выручка составит от 90 до 140 (с вероятностью 95%), а только то, что сказано выше.
· Если у нас нет теоретических оснований принять какое либо классическое распределение в качестве подходящего для нашей СВ, то и здесь теория окажет нам услугу — позволит проверить гипотезу о таком распределении на основании имеющихся у нас данных. Правда - исчерпывающего ответа "Да" или "Нет" ждать нечего. Можно лишь получить вероятность ошибиться, отбросив верную
гипотезу (ошибка 1 рода) или вероятность ошибиться приняв ложную
(ошибка 2 рода).
· Даже такие "обтекаемые" теоретические выводы в сильной степени зависят от объема выборки
(количества наблюдений), а также от "чистоты эксперимента" — условий его проведения.
Использование классических распределений случайных величин обычно называют "параметрической статистикой" - мы делаем предположение о том, что интересующая нас СВ (дискретная или непрерывная) имеет вероятности, вычисляемые по некоторым формулам или алгоритмам. Однако не всегда у нас имеются основания для этого. Причин тому чаще всего две:
· некоторые случайные величины просто не имеют количественного описания, обоснованных единиц измерения (уровень знаний, качество продукции и т. п.);
· наблюдения над величинами возможны, но их количество слишком мало для проверки предположения (гипотезы) о типе распределения.
В настоящее время в прикладной статистике все большей популярностью пользуются методы т. н. непараметрической
статистики — когда вопрос о принадлежности распределения вероятностей данной величины к тому или иному классу вообще не подымается, но конечно же — задача оценки самой СВ, получения информации о ней, остается.
Одним из основных понятий непараметрической статистики является понятие ШКАЛЫ или процедуры шкалирования
значений СВ. По своему смыслу процедура шкалирования суть решение вопроса о "единицах измерения" СВ. Принято использовать четыре вида шкал.
Nom
.
Первой из них рассмотрим НОМИНАЛЬНУЮ шкалу — применяемую к тем величинам, которые не имеют природной единицы измерения. Если некоторая величина может принимать на своей номинальной шкале значения X
, Y
или Z
, то справедливыми считаются только выражения типа: (X#Y), (X#Z), (X=Z),
а выражения типа (X>Y), (X<Z), (X+Z)
не имеют никакого смысла. Примеры СВ, к которым применимы только номинальные шкалы — пол, цвет, марка автомобиля и т. п.
Ord.
Второй способ шкалирования - использование ПОРЯД-КОВЫХ шкал. Они незаменимы для СВ, не имеющих природных единиц измерения, но позволяющих применять понятия предпочтения одного значения другому. Типичный пример: оценки знаний (даже при нечисловом описании), служебные уровни и т. п.; для таких величин разрешены не только отношения равенства (= или #), но и знаки предпочтения (> или <). Иногда говорят о рангах
значений таких величин.
Int & Rel.
Еще два способа шкалирования используются для СВ, имеющих натуральные размерности — это ИНТЕРВАЛЬНАЯ и ОТНОСИТЕЛЬНАЯ шкала. Для таких величин, кроме отношений равенства и предпочтения, допустимы операции сравнения - т. е. все четыре действия арифметики. Главная особенность таких шкал заключается в том, что разность двух значений на шкале (36 и 12) имеет один смысл для любого места шкалы (28 и 4). Различие между интервальной шкалой и относительной — только в понятии нуля
— на интервальной шкале 0 Кг веса означает отсутствие веса, а на относительной шкале температур 0 градусов не означает отсутствие теплоты — поскольку возможны температуры ниже 0 градусов (Цельсия).
Можно теперь заметить еще одно преимущество, которое мы получаем при использовании методов непараметрической статистики — если мы сталкиваемся со случайной величиной непрерывной природы, то использование интервальной или относительной шкалы позволит нам иметь дело не со случайными величинами, а со случайными событиями — типа "вероятность того, что вес продукции находится в интервале 17 Кг". Поэтому можно предложить единый подход к описанию всех
показателей функционирования сложной системы — описание на уровне простых случайных событий
(с вероятностью P(X)
может произойти событие X
). При том под событием придется понимать то, что случайная величина займет одно из допустимых для нее положений на шкале Nom, Ord, Int
или Rel.
Конечно — такой, “микроскопический”
подход резко увеличивает объем информации, необходимой для системного анализа. Частично этот недостаток смягчается при использовании компьютерных методов системного анализа, но более важно другое — преимущество на начальных этапах анализа, когда решаются вопросы дезинтеграции большой системы (выделение отдельных ее элементов) и последующей ее интеграции для разработки стратегии управления системой.
Не будет большим преувеличением считать, что методы непараметрической статистики - наиболее мощное средство
для решения задач системного анализа во многих областях деятельности человека и, в частности, в экономике.
Прямое токование термина корреляция
— стохастическая, вероятная, возможная связь
между двумя (парная) или несколькими (множественная) случайными величинами.
Выше говорилось о том, что если для двух СВ (X
и Y
) имеет место равенство P(XY) =P(X) 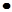 P(Y)
, то величины X
и Y
считаются независимыми. Ну, а если это не так!? P(Y)
, то величины X
и Y
считаются независимыми. Ну, а если это не так!?
Ведь всегда важен вопрос — а как сильно
зависит одна СВ от другой? И дело в не присущем людям стремлении анализировать что-либо обязательно в числовом измерении. Уже понятно, что системный анализ означает непрерывные выЧИСЛ
ения, что использование компьютера вынуждает нас работать с числами
, а не понятиями.
Для числовой оценки возможной связи между двумя случайными величинами: Y
(со средним My
и среднеквадратичным отклонением Sy
) и — X
(со средним Mx
и среднеквадратичным отклонением Sx
) принято использовать так называемый коэффициент корреляции
Rxy
=
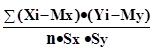 . {2 - 11} . {2 - 11}
Этот коэффициент может принимать значения от -1 до +1 — в зависимости от тесноты связи между данными случайными величинами.
Если коэффициент корреляции равен нулю, то X
и Y
называют некоррелированными
. Считать их независимыми обычно нет оснований — оказывается, что существуют такие, как правило — нелинейные связи величин, при которых Rxy
= 0
, хотя величины зависят друг от друга. Обратное всегда верно — если величины независимы
, то Rxy
= 0
. Но, если модуль Rxy
= 1, то есть все основания предполагать наличие линейной
связи между Y
и X
. Именно поэтому часто говорят о линейной корреляции
при использовании такого способа оценки связи между СВ.
Отметим еще один способ оценки корреляционной связи двух случайных величин — если просуммировать произведения отклонений каждой из них от своего среднего значения, то полученную величину —
Сxy
=
S
(X - Mx
)
·(Y - My
)
или ковариацию
величин X
и Y
отличает от коэффициента корреляции два показателя:
во-первых, усреднение
(деление на число наблюдений или пар X
, Y
) и, во-вторых, нормирование
путем деления на соответствующие среднеквадратичные отклонения.
Такая оценка связей между случайными величинами в сложной системе является одним из начальных этапов системного анализа, поэтому уже здесь во всей остроте встает вопрос о доверии к выводу о наличии или отсутствии связей между двумя СВ.
В современных методах системного анализа обычно поступают так. По найденному значению R
вычисляют вспомогательную величину:
W = 0.5 Ln[(1 + R)/(1-R)]
{2 - 12}
и вопрос о доверии к коэффициенту корреляции сводят к доверительным интервалам для случайной величины W, которые определяются стандартными таблицами или формулами.
В отдельных случаях системного анализа приходится решать вопрос о связях нескольких (более 2) случайных величин или вопрос о множественной корреляции
.
Пусть X
, Y
и Z
- случайные величины, по наблюдениям над которыми мы установили их средние Mx
, My
,Mz
и среднеквадратичные отклонения Sx
, Sy
, Sz
.
Тогда можно найти парные
коэффициенты корреляции Rxy
, Rxz
, Ryz
по приведенной выше формуле. Но этого явно недостаточно - ведь мы на каждом из трех этапов попросту забывали о наличии третьей случайной величины! Поэтому в случаях множественного корреляционного анализа иногда требуется отыскивать т. н. частные
коэффициенты корреляции — например, оценка виляния Z
на связь между X
и Y
производится с помощью коэффициента
Rxy.z
=
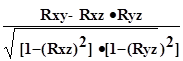 {2 - 13}
{2 - 13}
И, наконец, можно поставить вопрос — а какова связь между данной СВ и совокупностью остальных? Ответ на такие вопросы дают коэффициенты множественной
корреляции Rx.yz
, Ry.zx
, Rz.xy
,
формулы для вычисления которых построены по тем же принципам — учету связи одной из величин со всеми остальными в совокупности.
На сложности вычислений всех описанных показателей корреляционных связей можно не обращать особого внимания - программы для их расчета достаточно просты и имеются в готовом виде во многих ППП современных компьютеров.
Достаточно понять главное — если при формальном описании элемента сложной системы, совокупности таких элементов в виде подсистемы или, наконец, системы в целом, мы рассматриваем связи
между отдельными ее частями, — то степень тесноты этой связи в виде влияния одной СВ на другую можно и нужно оценивать на уровне корреляции.
В заключение заметим еще одно — во всех случаях системного анализа на корреляционном уровне обе случайные величины при парной корреляции или все при множественной считаются "равноправными" — т. е. речь идет о взаимном влиянии СВ друг на друга.
Так бывает далеко не всегда - очень часто вопрос о связях Y
и X
ставится в иной плоскости — одна из величин является зависимой (функцией) от другой (аргумента).
В тех случаях, когда из природы процессов в системе или из данных наблюдений над ней следует вывод о нормальном законе распределения двух СВ - Y
и X
, из которых одна является независимой, т. е. Y
является функцией X
, то возникает соблазн определить такую зависимость “формульно”, аналитически.
В случае успеха нам будет намного проще вести системный анализ — особенно для элементов системы типа "вход-выход”. Конечно, наиболее заманчивой является перспектива линейной зависимости типа Y = a + b
·X .
Подобная задача носит название задачи регрессионного анализа
и предполагает следующий способ решения.
Выдвигается следующая гипотеза
:
H0
:
случайная величина Y
при фиксированном значении величины X
распределена нормально
с математическим ожиданием
My
= a + b
·
X
и дисперсией Dy
, не зависящей от X
. {2 - 14}
При наличии результатов наблюдений над парами Xi
и Yi
предварительно вычисляются средние значения My
и Mx
, а затем производится оценка коэффициента b
в виде
b = 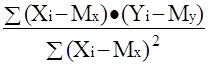 = Rxy = Rxy 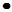 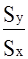 {2 - 15}
{2 - 15}
что следует из определения коэффициента корреляции {2 - 11}.
После этого вычисляется оценка для a
в виде
a = My
- b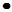 MX
{2 - 16} MX
{2 - 16}
и производится проверка значимости полученных результатов. Таким образом, регрессионный анализ является мощным, хотя и далеко не всегда допустимым расширением корреляционного анализа, решая всё ту же задачу оценки связей в сложной системе.
Что такое - статистическое решение? В качестве простейшего примера рассмотрим ситуацию, в которой вам предлагают сыграть в такую игру:
· вам заплатят 2 доллара, если подброшенная монета упадет вверх гербом;
· вы заплатите 1 доллар, если она упадет гербом вниз.
Скорее всего, вы согласитесь сыграть, хотя понимаете степень риска. Вы сознаете, "знаете
" о равновероятности появления герба и "вычисляете
" свой выигрыш 0.5 · 1- 0.5 · 1= + $0.5.
Усложним игру — вы видите, что монета несколько изогнута и возможно будет падать чаще одной из сторон. Теперь решение играть или не играть по-прежнему зависит от вероятности выигрыша, которая не может быть заранее (по латыни — apriori
) принята равной 0.5.
Человек, знакомый со статистикой, попытается оценить
эту вероятность с помощью опытов, если конечно они возможны и стоят не очень дорого. Немедленно возникает вопрос - сколько таких бросаний вам будет достаточно?
Пусть с вас причитается 5 центов за одно экспериментальное бросание, а ставки в игре составляют $2000 против $1000. Скорее всего, вы согласитесь сыграть, заплатив сравнительно небольшую сумму за 100..200 экспериментальных бросков. Вы, наверное, будете вести подсчет удачных падений и, если их число составит 20 из 100, прекратите эксперимент и сыграете на ставку $2000 против $1000, так как ожидаемый
выигрыш оценивается в 0.8·2000 + 0.2·1000 -
100·0.05=$1795.
В приведенных примерах главным для принятия решения была вероятность благоприятного исхода падения монетки. В первом случае — априорная вероятность, а во втором — апостериорная. Такую информацию принято называть данными о состоянии природы
.
Приведенные примеры имеют самое непосредственное отношение к существу нашего предмета. В самом деле — при системном управлении приходится принимать решения в условиях, когда последствия таких решений заранее достоверно неизвестны. При этом вопрос: играть или не играть — не стоит! "Играть" надо, надо управлять
системой. Вы спросите - а как же запрет на эксперименты? Ответ можно дать такой — само поведение системы в обычном ее состоянии может рассматриваться как эксперимент, из которого при правильной организации сбора и обработки информации о поведении системы можно ожидать получения данных для выяснения особенности системного подхода к решению задач управления.
В большинстве случаев практического применения системного анализа для исследования свойств и последующего оптимального управления системой можно выделить следующие основные этапы: · Содержательная постановка задачи
· Построение модели изучаемой системы
· Отыскание решения задачи с помощью модели
· Проверка решения с помощью модели
· Подстройка решения под внешние условия
· Осуществление решения
Остановимся вкратце на каждом из этих этапов. Будем выделять наиболее сложные в понимании этапы и пытаться усвоить методы их осуществления на конкретных примерах.
Но уже сейчас отметим, что
в каждом конкретном случае этапы системного занимают различный “удельный вес” в общем объеме работ по временным, затратным и интеллектуальным показателям. Очень часто трудно провести четкие границы — указать, где оканчивается данный этап и начинается очередной.
Уже упоминалось, что в постановке задачи системного анализа обязательно участие двух сторон: заказчика (ЛПР) и исполнителя данного системного проекта. При этом участие заказчика не ограничивается финансированием работы - от него требуется (для пользы дела) произвести анализ системы, которой он управляет, сформулированы цели и оговорены возможные варианты действий. Так, — в упомянутом ранее примере системы управления учебным процессом одной из причин тихой кончины ее была та, что одна из подсистем руководство Вузом практически не обладала свободой действий по отношению к подсистеме обучаемых.
Конечно же, на этом этапе должны быть установлены и зафиксированы понятия эффективности деятельности системы. При этом в соответствии с принципами системного подхода необходимо учесть максимальное число связей как между элементами системы, так и по отношению к внешней среде. Ясно, что исполнитель-разработчик не всегда может, да и не должен иметь профессиональные знания именно тех процессов, которые имеют место в системе или, по крайней мере, являются главными. С другой стороны совершенно обязательно наличие таких знаний у заказчика — руководителя или администратора системы. Заказчик должен знать что
надо сделать, а исполнитель — специалист в области системного анализа — как
это сделать.
Обращаясь к будущей вашей профессии можно понять, что вам надо научиться и тому и другому. Если вы окажетесь в роли администратора, то к профессиональным знаниям по учету и аудиту весьма уместно иметь знания в области системного анализа — грамотная постановка задачи, с учетом технологии решения на современном уровне будет гарантией успеха. Если же вы окажетесь в другой категории — разработчиков, то вам не обойтись без “технологических" знаний в области учета и аудита. Работа по системному анализу в экономических системах вряд ли окажется эффективной без специальных знаний в области экономики. Разумеется, наш курс затронет только одну сторону — как использовать системный подход в управлении экономикой.
Модель изучаемой системы в самом лаконичном виде можно представить в виде зависимости
E = f(X,Y)
{3 - 1}
где:
E
— некоторый количественный показатель эффективности системы в плане достижения цели ее существования T
, будем называть его — критерий эффективности
.
X
— управляемые переменные системы — те, на которые мы можем воздействовать или управляющие воздействия
;
Y
— неуправляемые, внешние по отношению к системе воздействия; их иногда называют состояниями природы
.
Заметим, прежде всего, что возможны ситуации, в которых нет никакой необходимости учитывать состояния природы. Так, например, решается стандартная задача размещения запасов нескольких видов продукции и при этом можем найти E
вполне однозначно, если известны значения Xi
и, кроме того, некоторая информация о свойствах анализируемой системы.
В таком случае принято говорить о принятии управляющих решений или о стратегии управления
в условиях определенности
.
Если же с воздействиями окружающей среды, с состояниями природы мы вынуждены считаться, то приходится управлять системой в условиях неопределенности
или, еще хуже — при наличии противодействия. Рассмотрим первую, на непросвещенный взгляд — самую простую, ситуацию.
Классическим примером простейшей задачи системного анализа в условиях определенности может служить задача производства и поставок товара. Пусть некоторая фирма должна производить и поставлять продукцию клиентам равномерными партиями в количестве N
=24000 единиц в год. Срыв поставок недопустим, так как штраф за это можно считать бесконечно большим.
Запускать в производство приходится сразу всю партию, таковы условия технологии. Стоимость хранения единицы продукции Cx
=10 копеек в месяц, а стоимость запуска одной партии в производство (независимо от ее объема) составляет Cp
=400 гривен.
Таким образом, запускать в год много партий явно невыгодно, но невыгодно и выпустить всего 2 партии в год — слишком велики затраты на хранение! Где же “золотая середина”, сколько партий в год лучше всего выпускать?
Будем строить модель такой системы. Обозначим через n
размер партии и найдем количество партий за год — p
= N / n
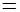 24000 / n
. 24000 / n
.
Получается, что интервал времени между партиями составляет
t
= 12 / p
(месяцев), а средний запас изделий на складе — n
/2 штук.
Сколько же нам будет стоить выпуск партии в n штук за один раз?
Сосчитать нетрудно — 0.1 · 12 · n / 2 гривен на складские расходы в год и 400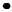 p
гривен за запуск партий по n
штук изделий в каждой. p
гривен за запуск партий по n
штук изделий в каждой.
В общем виде годовые затраты составляют
E = 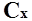 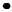 T T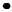 n / 2 + n / 2 + 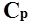 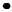 N / n
{3 - 2} N / n
{3 - 2}
где T =
12 — полное время наблюдения в месяцах.
Перед нами типичная вариационная
задача: найти такое n0
, при котором сумма E
достигает минимума.
Решение этой задачи найти совсем просто — надо взять производную по n
и приравнять эту производную нулю. Это дает
n0
=
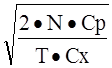 , {3 - 3} , {3 - 3}
что для нашего примера составляет 4000 единиц в одной партии и соответствует интервалу выпуска партий величиной в 2 месяца.
Затраты при этом минимальны и определяются как
E0
= 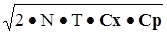 , {3 - 4} , {3 - 4}
что для нашего примера составляет 4800 гривен в год.
Сопоставим эту сумму с затратами при выпуске 2000 изделий в партии или выпуске партии один раз в месяц (в духе недобрых традиций социалистического планового хозяйства):
E1
= 0.1·12·2000/2 + 400·24000/ 2000 = 6000 гривен в год.
Комментарии, как говорится, — излишни!
Конечно, так просто решать задачи выработки оптимальных стратегий удается далеко не всегда, даже если речь идет о детерминированных
данных для описания жизни системы — ее модели. Существует целый класс задач системного анализа и соответствующих им моделей систем, где речь идет о необходимости минимизировать одну
функции многих переменных следующего типа:
E = a1
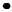 X1
+ a2 X1
+ a2
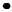 X2
+ ..... an X2
+ ..... an
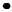 Xn
{3 - 5} Xn
{3 - 5}
где Xi
— искомые переменные, ai
— соответствующие им коэффициенты или “веса переменных
” и при этом имеют место ограничения
как на переменные, так и на их веса.
Задачи такого класса достаточно хорошо исследованы в специальном разделе прикладной математики — линейном программировании
. Еще в докомпьютерные времена были разработаны алгоритмы поиска экстремумов таких функций E = f(a,X)
, которые так и назвали — целевыми
. Эти алгоритмы или приемы используются и сейчас — служат основой для разработки прикладных компьютерных программ системного анализа.
Системный подход к решению практических задач управления экономикой, особенно для задач со многими десятками сотен или даже тысячами переменных привел к появлению специализированных, типовых направлений как в области теории анализа, так и в практике.
Наиболее “старыми” и, следовательно, наиболее обкатанными являются методы решения специфичных задач, которые давно уже можно называть классическими
.
Специалистам в области делового администрирования надо знать эти задачи хотя бы на уровне постановки и, главное, в плане моделирования соответствующих систем.
· Задачи управления запасами
Первые задачи управления запасами были рассмотрены еще в 1915 году — задолго не только до появления компьютеров, но и до употребления термина “кибернетика”. Был обоснован метод решения простейшей задачи — минимизация затрат на заказ и хранение
запасов при заданном спросе
на данную продукцию и фиксированном уровне цен
. Решение — размер оптимальной партии обеспечивало наименьшие суммарные затраты за заданный период времени.
Несколько позже были построены алгоритмы решения задачи управления запасами при более сложных условиях — изменении уровня цен (наличие “скидок за качество” и / или “скидок за количество”); необходимости учета линейных ограничений на складские мощности и т. п.
· Задачи распределения ресурсов
В этих задачах объектом анализа являются системы, в которых приходится выполнять несколько операций с продукцией (при наличии нескольких способов выполнения этих операций) и, кроме того, не хватает ресурсов или оборудования для выполнения всех этих операций.
Цель системного анализа — найти способ наиболее эффективного выполнения операций
с учетом ограничений на ресурсы.
Объединяет все такие задачи метод их решения — метод математического программирования, в частности, — линейного программирования
. В самом общем виде задача линейного программирования формулируется так:
требуется обеспечить минимум выражения (целевой функции)
E(X) = C1
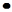 X1
+ C2 X1
+ C2
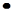 X2
+ ......+ Ci X2
+ ......+ Ci
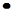 Xi
+ ... Cn Xi
+ ... Cn
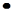 Xn
{3 - 6} при следующих условиях: Xn
{3 - 6} при следующих условиях:
все Xi
положительны и, кроме того, на все Xi
налагаются m
ограничений (m < n)
 A11
·
X1
+ A12
·
X2
+ ......+ Aij
·
Xj
+ ... A1n
·
Xn
= B1; A11
·
X1
+ A12
·
X2
+ ......+ Aij
·
Xj
+ ... A1n
·
Xn
= B1;
.....................................................................................
   Ai1
·
X1
+ Ai2
·
X2
+ ......+ Aij
·
Xj
+ ... Ain
·
Xn
= Bi;
{3 - 7} Ai1
·
X1
+ Ai2
·
X2
+ ......+ Aij
·
Xj
+ ... Ain
·
Xn
= Bi;
{3 - 7}
.....................................................................................
 Am1
·
X1
+ Am2
·
X2
+ .....+ Amj
·
Xj
+ ... Amn
·
Xn
= Bm . Am1
·
X1
+ Am2
·
X2
+ .....+ Amj
·
Xj
+ ... Amn
·
Xn
= Bm .
Начала теоретического обоснования и разработки практических методов решения задач линейного программирования были положены Д.Данцигом (по другой версии — Л.В.Канторовичем).
Для большинства конкретных приложений универсальным считается т. н. симплекс-метод
поиска цели, для него и смежных методов разработаны специальные пакеты прикладных программ (ППП) для компьютеров.
Весьма часто этап содержательной постановки задачи системного анализа приводит нас к выводу о наличии нескольких целей функционирования системы. В самом деле, если некоторая экономическая система может иметь “главную цель” — достижение максимальной прибыли, то почти всегда можно наблюдать ситуацию наличия ограничений или условий. Нарушение этих условий либо невозможно (тогда не будет самой системы), либо заведомо приводит к недопустимым последствиям для внешней cреды. Короче говоря, ситуация, когда цель всего одна и достичь ее требуется любой ценой, практически невероятна.
Пусть имеется самая простая ситуация многокритериальности — существуют только две цели системы T1
и T2
и только две возможных стратегии S1
, S2
.
Пусть мы как-то оценили эффективность E11
стратегии S1
по отношению к T1
и эффективность эта оказалась равной 0.4 (по некоторой шкале 0..1). Проделав такую же оценку для всех стратегий и всех целей, мы получили табличку (матрицу эффективностей):
Таблица 3.1
| E
|
T1
|
T2
|
| S1
|
0.4
|
0.6
|
| S2
|
0.7
|
0.3
|
Какую же из стратегий считать наилучшей? Пока мы не оговорим значимость каждой из целей, не укажем их веса
, — спорить бесполезно! Вот если бы нам было известно, что первая цель, к примеру, в 3 раза важнее второй, то тогда
можно учесть их относительные веса
— скажем величинами 0.75 для первой и 0.25 для второй. При таких условиях суммарные эффективности
стратегий (по отношению ко всем целям) составят:
для первой E1
= 0.4 · 0.70 + 0.6 · 0.30 = 0.28 + 0.18 = 0.46;
для второй E2
= 0.8 · 0.70 + 0.2 · 0.25 = 0.56 + 0.05 = 0.61;
так что ответ на вопрос о выборе стратегии далеко не очевиден.
Итак, критерий эффективности системы при наличии нескольких целей приходится выражать через эффективности отдельных стратегий виде: Es
=
S
St
· Ut
{3 - 8}
т. е. учитывать веса отдельных целей Ut
.
Если вы внимательно следили за рассуждениями при рассмотрении примера {3-2}, то сейчас можете сообразить, что по сути дела там речь шла о двух целях. С одной стороны, мы хотели бы иметь как можно меньшие
партии — их дешевле хранить (мал срок хранения). с другой стороны, нам были желательны большие
партии, поскольку при этом меньше затраты на запуск партий в производство. Если бы мы перебирали все 365 возможных стратегий (от смены партии каждый день до одной в год), то, конечно же, нашли бы оптимальную стратегию со сменой партий каждые два месяца. Другое дело, что в нашем распоряжении была аналитическая модель
системы (формула суммарных затрат).
Так вот — весовые коэффициенты целей в той модели были равными
и мы их могли не замечать при поиске минимума затрат. Ну, а что делать, если “важность” целей приходится измерять не по шкале Int
или Rel,
т. е. в числовом виде,
а по шкале Ord
? Иными словами — откуда берутся весовые коэффициенты целей?
Очень редко весовые коэффициенты определяются однозначно по “физическому смыслу” задачи системного анализа. Чаще же всего их отыскание можно называть “назначением”, “придумыванием”, “предсказанием” — т. е. никак не "научными" действиями.
Иногда, как ни странно это звучит, весовые коэффициенты назначаются путем голосования — явного или тайного. Дело в том, что в ситуациях, когда нет числового метода оценки веса цели, реальным выходом из положения является использование накопленного
опыта
.
Нередко задает весовые коэффициенты непосредственно ЛПР, но чаще его опыт управления подсказывает: одна голова — хорошо, а много умных голов — куда лучше. Принимается особое решение — использовать метод экспертных оценок..
Суть этого метода достаточно проста. Требуется четко оговорить все цели функционирования системы и предложить группе лиц, высоко компетентных в данной отрасли (экспертов
) хотя бы расположить все цели по значимости, по “призовым местам” или, на языке ТССА, по рангам.
Высший ранг (обычно 1) означает наибольшую важность (вес) цели, следующий за ним — несколько меньший вес и т. д. Специальный раздел непараметрической статистики — теория ранговой корреляции
, позволяет проверить гипотезы о значимости полученной от экспертов информации. Развитие ранговой корреляции, ее другой раздел, позволяет устанавливать согласие, согласованность мнений экспертов или ранговую конкордацию.
Это особо важно в случаях, когда не только возникла нужда использовать мнения экспертов, но и существует сомнение в их компетентности.
Пусть в процессе системного анализа нам пришлось учитывать некоторую величину U
, измерение которой возможно лишь по порядковой шкале (Ord).
Например, нам приходится учитывать 10 целей функционирования системы и требуется выяснить их относительную значимость, удельные веса.
Если имеется группа лиц, компетентность которых в данной области не вызывает сомнений, то можно опросить каждого из экспертов,
предложив им расположить цели по важности или “проранжировать” их. В простейшем случае можно не разрешать повторять ранги, хотя это не обязательно — повторение рангов всегда можно учесть.
Результаты экспертной оценки в нашем примере представим таблицей рангов целей:
Таблица 3.2
| Эксперты
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Сумма
|
| A
|
3
|
5
|
1
|
8
|
7
|
10
|
9
|
2
|
4
|
6
|
55
|
| B
|
5
|
1
|
2
|
6
|
8
|
9
|
10
|
3
|
4
|
7
|
55
|
| Сумма рангов
|
8
|
6
|
3
|
14
|
15
|
19
|
19
|
5
|
8
|
13
|
|
| Суммарный ранг
|
4.5
|
3
|
1
|
7
|
8
|
9.5
|
9.5
|
2
|
4.5
|
6
|
55
|
Итак, для каждой из целей Ti
мы можем найти сумму рангов, определенных экспертами, и затем суммарный или результирующий
ранг цели Ri
. Если суммы рангов совпадают — назначается среднее значение.
Метод ранговой корреляции позволяет ответить на вопрос — насколько коррелированны, неслучайны ранжировки каждого из двух экспертов, а значит — насколько можно доверять результирующим рангам? Как обычно, выдвигается основная гипотеза — об отсутствии связи
между ранжировками и устанавливается вероятность справедливости этой гипотезы. Для этого можно использовать два подхода: определение коэффициентов ранговой корреляции Спирмэна или Кендэлла.
Более простым в реализации является первый — вычисляется значение коэффициента Спирмэна
Rs =
1
-
 ;
{3 - 9} ;
{3 - 9}
где di
определяются разностями рангов первой и второй ранжировок по n
объектов в каждой.
В нашем примере сумма квадратов разностей рангов составляет 30, а коэффициент корреляции Спирмэна около 0.8, что дает значение вероятности гипотезы о полной независимости двух ранжировок всего лишь 0.004.
При небходимости можно воспользоваться услугами группы из m
экспертов, установить результирующие ранги целей, но тогда возникнет вопрос о согласованности мнений этих экспертов или конкордации.
Пусть у нас имеются ранжировки 4 экспертов по отношению к 6 факторам, которые определяют эффективность некоторой системы.
Таблица 3.3
| Факторы -->
Эксперты
|
1
|
2
|
3
|
4
|
5
|
6
|
Сумма
|
| A
|
5
|
4
|
1
|
6
|
3
|
2
|
21
|
| B
|
2
|
3
|
1
|
5
|
6
|
4
|
21
|
| C
|
4
|
1
|
6
|
3
|
2
|
5
|
21
|
| D
|
4
|
3
|
2
|
3
|
2
|
5
|
21
|
| Сумма рангов
Сум. ранг
|
15
4
|
11
2
|
10
1
|
19
6
|
12
3
|
17
5
|
84
|
| Отклонение суммы
от среднего
|
+1
1
|
-3
9
|
-4
16
|
+5
25
|
-2
4
|
+3
9
|
0
64
|
Заметим, что полная сумма рангов составляет 84, что дает в среднем по 14 на фактор.
Для общего случая n
факторов и m
экспертов среднее значение суммы рангов для любого фактора определится выражением
D
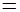 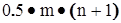 {3 - 10}
{3 - 10}
Теперь можно оценить степень согласованности мнений экспертов по отношению к шести факторам. Для каждого из факторов наблюдается отклонение суммы рангов, указанных экспертами, от среднего значения такой суммы. Поскольку сумма этих отклонений всегда равна нулю, для их усреднения разумно использовать квадраты значений.
В нашем случае сумма таких квадратов составит S=
64, а в общем случае эта сумма будет наибольшей только при полном совпадении мнений всех экспертов по отношению ко всем факторам:
S
max
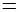 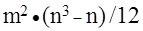 {3 - 11}
{3 - 11}
М. Кэндэллом предложен показатель согласованности или коэффициент конкордации
,
определяемый как
 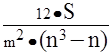 {3 - 12} {3 - 12}
В нашем примере значение коэффициента конкордации составляет около 0.229, что при четырех экспертах и шести факторах достаточно, чтобы с вероятностью не более 0.05 считать мнения экспертов несогласованными. Дело в том, что как раз случайность
ранжировок, их некоррелированность просчитывается достаточно просто. Так для нашего примера указанная вероятность соответствует сумме квадратов отклонений S= 143.3 , что намного больше 64.
В заключение вопроса об особенностях метода экспертных оценок в системном анализе отметим еще два обстоятельства.
 В первом примере мы получили результирующие ранги 10 целей функционирования некоторой системы. Как воспользоваться этой результируюзей ранжировкой? Как перейти от ранговой (Ord
) шкалы целей к шкале весовых коэффициентов — в диапазоне от 0 до 1?
В первом примере мы получили результирующие ранги 10 целей функционирования некоторой системы. Как воспользоваться этой результируюзей ранжировкой? Как перейти от ранговой (Ord
) шкалы целей к шкале весовых коэффициентов — в диапазоне от 0 до 1?
Здесь обычно используются элементарные приемы нормирования. Если цель 3 имеет ранг 1, цель 8 имеет ранг 2 и т. д., а сумма рангов составляет 55, то весовой коэффициент для цели 3 будет наибольшим и сумма весов всех 10 целей составит 1.
Вес цели
придется определять как
(11-1) / 55 для 3 цели;
(11-2) / 55 для 8 цели и т. д.
 При использовании групповой экспертной оценки можно не только выяснять мнение экспертов о показателях, необходимых для системного анализа. Очень часто в подобных ситуациях используют так называемый метод Дельфы
(от легенды о дельфийском оракуле).
При использовании групповой экспертной оценки можно не только выяснять мнение экспертов о показателях, необходимых для системного анализа. Очень часто в подобных ситуациях используют так называемый метод Дельфы
(от легенды о дельфийском оракуле).
Опрос экспертов проводят в несколько этапов, как правило — анонимно. После очередного этапа от эксперта требуется не просто ранжировка, но и ее обоснование. Эти обоснования сообщаются всем экспертам перед очередным этапом без указания авторов обоснований.
Имеющийся опыт свидетельствует о возможностях существенно повысить представительность, обоснованность и, главное, достоверность суждений экспертов. В качестве “побочного эффекта” можно составить мнение о профессиональности каждого эксперта.
Как уже отмечалось в первой части нашего курса, в большинстве реальных больших систем не обойтись без учета “состояний природы” — воздействий стохастического
типа, случайных величин или случайных событий. Это могут быть не только внешние
воздействия на систему в целом или на отдельные ее элементы. Очень часто и внутренние
системные связи имеют такую же, “случайную” природу.
Важно понять, что стохастичность связей между элементами системы и уж тем более внутри самого элемента (связь “вход-выход”) является основной причиной риска выполнить вместо системного анализа
совершенно бессмысленную работу, получить в качестве рекомендаций по управлению системой заведомо непригодные решения.
Выше уже оговаривалось, что в таких случаях вместо самой случайной величины X
приходится использовать ее математическое ожи-дание Mx
.
Все вроде бы просто — не знаем,
так ожидаем
. Но насколько оправданы наши ожидания? Какова уверенность или какова вероятность ошибиться?
Такие вопросы решаются, ответы на них получить можно — но для этого надо иметь информацию о законе распределения СВ. Вот и приходится на данном этапе системного анализа (этапе моделирования) заниматься статистического исследованиями, пытаться получить ответы на вопросы:
· А не является ли данный элемент системы и производимые им операции “классическими”?
· Нет ли оснований использовать теорию для определения типа распределения СВ (продукции, денег или информационных сообщений)? Если это так — можно надеяться на оценки ошибок при принятии решений, если же это не так, то приходится ставить вопрос иначе.
· А нельзя ли получить искомое распределение интересующей нас СВ из данных эксперимента? Если этот эксперимент обойдется дорого или физически невозможен, или недопустим по моральным причинам, то может быть “для рагу из зайца использовать хотя бы кошку” — воспользоваться апостериорными данными, опытом прошлого или предсказаниями на будущее, экспертными оценками?
Если и здесь нет оснований принимать положительное решение, то можно надеяться еще на один выход из положения.
Не всегда, но все же возможно использовать текущее состояние уже действующей большой системы, ее реальную “жизнь” для получения глобальных показателей
функционирования системы.
Этой цели служат методы планирования эксперимента, теоретической и методологической основой которых является особая область системного анализа — т. н. факторный анализ, сущность которого будет освещена несколько позже.
Достаточно часто при анализе экономических систем приходится решать т. н. задачи массового обслуживания, возникающие в следующей ситуации. Пусть анализируется система технического обслужи-вания автомобилей, состоящая из некоторого количества станций различной мощности. На каждой из станций (элементе системы) могут возникать, по крайней мере, две типичных ситуации:
· число заявок слишком велико для данной мощности станции, возникают очереди и за задержки в обслуживании приходится платить;
· на станцию поступает слишком мало заявок и теперь уже приходится учитывать потери, вызванные простоем станции.
Ясно, что цель системного анализа в данном случае заключается в определении некоторого соотношения между потерями доходов по причине очередей
и потерями по причине простоя
станций. Такого соотношения, при котором математическое ожидание суммарных потерь окажется минимальным.
Так вот, специальный раздел теории систем — теория массового обслуживания,
позволяет
· использовать методику определения средней длины очереди и среднего времени ожидания заказа в тех случаях, когда скорость поступления заказов и время их выполнения заданы;
· найти оптимальное соотношение между издержками по причине ожидания в очереди и издержками простоя станций обслуживания;
· установить оптимальные стратегии обслуживания.
Обратим внимание на главную особенность такого подхода к задаче системного анализа — явную зависимость результатов анализа и получаемых рекомендаций от двух внешних факторов: частоты поступления и сложности заказов (а значит — времени их исполнения).
Но это уже связи
нашей системы с внешним миром
и без учета этого факта нам не обойтись. Потребуется провести исследования потоков заявок по их численности и сложности, найти статистические показатели этих величин, выдвинуть и оценить достоверность гипотез о законах их распределения. Лишь после этого можно пытаться анализировать — а как будет вести себя система при таких внешних воздействиях, как будут меняться ее показатели (значение суммарных издержек) при разных управляющих воздействиях или стратегиях управления.
Очень редко при этом используется сама система, производится натуральный эксперимент над ней. Чаще всего такой эксперимент связан с риском потерь заказчиков или неоправданными затратами на создание дополнительных станций обслуживания.
Поэтому следует знать о таком особом подходе к вопросу моделирования систем как метод статистических испытаний или метод Монте Карло.
Вернемся к примеру с анализом работы станций обслуживания. Пусть у нас всего лишь одна такая станция и заранее известны:
l
—
средняя скорость поступления заказов и
m
—
средняя скорость выполнения заказов (штук в единицу времени), и таким образом задана величина b
=
l
/
m
— интенсивность нагрузки станции.
Уже по этим данным оказывается возможным построить простейшую модель системы. Будем обозначать X
число заказов, находящихся в очереди на обслуживании в единицу времени, и попытаемся построить схему случайных событий для определения вероятности P(X)
.
Событие
— в очереди находятся точно X
заказов
может наблюдаться в одной из четырех ситуаций.
· В очереди было X
заказов (A1)
, за это время не поступило ни одного нового заказа (A2)
и за это же время не был выполнен ни один заказ из находящихся в работе (A3)
.
· В очереди было X - 1
заказов (B1)
, за это время поступил один новый заказ (B2)
и за это же время не был выполнен ни один заказ из находящихся в работе (B3)
.
· В очереди было X + 1
заказов (C1)
, за это время не поступило ни одного нового заказа (C2)
и за это же время был выполнен один заказ из находящихся в работе (C3)
.
· В очереди было X
заказов (D1)
, за это время поступил один новый заказа (D2)
и за это же время был выполнен один заказ из находящихся в работе (D3)
.
Такая схема событий предполагает особое свойство "технологии" нашей системы — вероятность поступления более одного заказа за рассматриваемую единицу времени и вероятность выполнения более одного заказа за то же время считаются равными 0
.
Это не такое уж "вольное" допущение — длительность отрезка времени всегда можно уменьшить до необходимых пределов.
А далее все очень просто. Перемножая вероятности событий A1..3, B1..3, C1..3, D1..3
, мы определим вероятности каждого из вариантов интересующего нас события — в течение заданного нами интервала времени длина очереди не поменялась.
.
Несложные преобразования суммы вероятностей всех четырех вариантов такого события приведут нас к выражению для вероятности длины очереди в X
заказов:
P(X)
= b
x
· (1-
b
),
{3-13}
а также для математического ожидания длины очереди:
MX
= b
/ (1-
b
).
{3-14}
Оценить полезность такого моделирования позволят простые примеры. Пусть мы решили иметь всего лишь 50%-ю интенсивность нагрузки станции, то есть вдвое "завысили" ее пропускную способность по отношению к потоку заказов.
Тогда для b
= 0.5
имеем следующие данные:
Таблица 3.4
| Очередь
|
0
|
1
|
2
|
3
|
4 и более
|
| Вероятность
|
0.5
|
0.25
|
0.125
|
0.0625
|
0.0625
|
Обобщим полученные результаты:
· вероятность отсутствия очереди оказалась точно такой же, как и ее наличия;
· очередь в 4 и более заказа практически невероятна;
· математическое ожидание очереди составляет ровно 1 заказ.
Наше право (если мы и есть ЛПР!) — принять такую интенсивность или отказаться от нее, но все же у нас есть определенные показатели последствий такого решения.
Полезно проанализировать ситуации с другими значениями интенсивности нагрузки станции.
Таблица 3.5
| b
|
1 / 2
|
3 / 4
|
7 / 8
|
15 / 16
|
| Mx
|
1
|
3
|
7
|
15
|
Обратим теперь внимание еще на одно обстоятельство — мы полагали известной информацию только о средней скорости (ее математического ожидания) выполнения заказов. Иными словами, мы считали время выполнения очередного заказа независящим ни от его "содержания" (помыть автомобиль или ликвидировать следствия аварии), ни от числа заказов, "стоящих в очереди".
В реальной жизни это далеко не всегда так и хотелось бы хоть как-то учесть такую зависимость. И здесь теория приходит на помощь (тому, кто понимает ее возможности).
Если нам представляется возможность установить не только само m
(среднюю или ожидаемую скорость обработки заказа), но и разброс этой величины D
m
(дисперсию), то можно будет оценить среднее число заказов в очереди более надежно
(именно так — не точнее, а надежнее!):
Mx
= 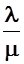 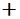 0.5
· 0.5
· 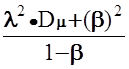 . {3 - 15} . {3 - 15}
Как уже неоднократно отмечалось, системный анализ невозможен без учета взаимодействий данной системы с внешней средой. Ранее упоминалась необходимость учитывать состояния природы
— большей частью случайных, стохастических воздействий на систему.
Конечно, природа не мешает (но и не помогает) процессам системы осознанно,
злонамеренно или, наоборот, поощряюще. Поэтому учет внешних природных воздействий можно рассматривать как "игру с природой
", но в этой игре природа — не противник, не оппонент, у нее нет цели существования вообще, а тем более — цели противодействия нашей системе.
Совершенно иначе обстоит дело при учете взаимодействий данной системы с другими, аналогичными или близкими по целям
своего функционирования. Как известно, такое взаимодействие называют конкуренцией
и ситуации жизни больших систем-монополистов крайне редки, да и не вызывают особого интереса с позиций теории систем и системного анализа.
Особый раздел науки — теория игр
позволяет хотя бы частично разрешать затруднения, возникающие при системном анализе в условиях противодействия. Интересно отметить, что одна из первых монографий по этим вопросам называлась "Теория игр и экономического поведения" (авторы — Нейман и Моргенштерн, 1953 г., имеется перевод) и послужила своеобразным катализатором развития методов линейного программирования и теории статистических решений.
В качестве простого примера использования методов теории игр в экономике рассмотрим следующую задачу.
Пусть вы имеете всего три варианта стратегий в условиях конкуренции S1
,S2
и S3
(например — выпускать в течение месяца один из 3 видов продукции). При этом ваш конкурент имеет всего два варианта стратегий C1
и C2
(выпускать один из 2 видов своей продукции, в каком то смысле заменяющей продукцию вашей фирмы). При этом менять вид продукции в течение месяца невозможно ни вам, ни вашему конкуренту.
Пусть и вам, и вашему конкуренту достоверно известны последствия каждого из собственных вариантов поведения, описываемые следующей таблицей.
Таблица 3.6
| C1
|
C2
|
| S1
|
-2000
|
+ 2000
|
| S2
|
-1000
|
+3000
|
| S3
|
+1000
|
+2000
|
Цифры в таблице означают следующее:
· вы несете убытки в 2000 гривен, а конкурент имеет ту же сумму прибыли, если вы приняли стратегию S1
, а конкурент применил C1
;
· вы имеете прибыль в 2000 гривен, а конкурент теряет ту же сумму, если вы приняли S1
против C2
;
· вы несете убытки в сумме 1000 гривен, а конкурент получает такую прибыль, если ваш вариант S2
оказался против его варианта C1
,
и так далее.
Предполагается, что обе стороны имеют профессиональную подготовку в области ТССА и действуют разумно, соблюдая правила — вариант поведения принимают один раз на весь месяц, не зная, конечно, что предпринял на этот же месяц конкурент.
По сути дела, в чисто житейском смысле — это обычная "азартная" игра, в которой существует конечный результат, цель игры — выигрыш
.
Этой цели добивается каждый игрок, но не каждый может ее добиться. Варианты поведения игроков можно считать ходами
, а множество ходов — рассматривать как партию
.
Пусть партия состоит всего лишь из одного хода с каждой стороны. Попробуем найти этот наилучший ход сначала для вашего конкурента — порассуждаем за него.
Так как таблица известна как вам, так и конкуренту, то его рассуждения можно промоделировать.
Вашему конкуренту вариант C2
явно невыгоден — при любом вашем ходе вы будете в выигрыше, а конкурент в проигрыше. Следовательно, со стороны вашего противника будет, скорее всего, принят вариант C1
, доставляющий ему минимум потерь.
Теперь можно порассуждать за себя. Вроде бы вариант S2
принесет нам максимальный выигрыш в 3000 гривен, но это при условии выбора C2
вашим конкурентом, а он, скорее всего, выберет C1
.
Значит наилучшее, что мы можем предпринять — выбрать вариант S3
, рассчитывая на наименьший из возможных выигрышей — в 1000 гривен.
Ознакомимся с рядом общепринятых терминов теории игр:
· поскольку в таблице игры наш возможный выигрыш всегда равен проигрышу конкурента и наоборот, то эту специфику отображают обычно в названии — игра с нулевой
суммой
;
· варианты поведения игроков-конкурентов называют чистыми стратегиями
игры, учитывая независимость их от поведения конкурента;
· наилучшие стратегии для каждого из игроков называют решением игры
;
· результат игры, на который рассчитывают оба игрока (1000 гривен прибыли для вас или столько же в виде проигрыша для конкурента) называют ценой игры
; она в игре с нулевой суммой однакова для обеих сторон;
· таблицу выигрышей (проигрышей) называют матрицей игры
, в данном случае — прямоугольной
.
Рассмотренный выше ход рассуждений по поиску наилучшего плана игры в условиях конкуренции — не единственный способ решения задач. Очень часто намного короче и, главное, более логически стройным оказывается другой принцип поиска оптимальных игровых стратегий — принцип минимакса.
Для иллюстрации этого метода рассмотрим предыдущий пример игры с несколько видоизмененной матрицей.
| C1
|
C2
|
| S1
|
-2000
|
- 4000
|
| S2
|
-1000
|
+3000
|
| S3
|
+1000
|
+2000
|
Таблица 3.7
Повторим метод рассуждений, использованный для предыдущего примера.
· Мы никогда не выберем стратегию S1
, поскольку она при любом ответе конкурента принесет нам значительные убытки.
· Из двух оставшихся разумнее выбрать S3
, так как при любом ответе конкурента мы получим прибыль.
· Выбираем в качестве оптимальной стратегии S3
.
Рассуждения нашего конкурента окажутся примерно такими же по смыслу. Понимая, что мы никогда не примем S1
и выберем, в конце концов, S3
, он примет решение считать оптимальной для себя стратегию C1
— в этом случае он будет иметь наименьшие убытки.
Можно применить и иной метод рассуждений, дающий, в конце концов, тот же результат. При выборе наилучшего плана игры для нас можно рассуждать так:
· при стратегии S1
минимальный (min
) "выигрыш" составит - 4000
гривен;
· при стратегии S2
минимальный (min
) "выигрыш" составит - 1000
гривен;
· при стратегии S3
минимальный (min
) выигрыш составит + 1000
гривен.
Выходит, что наибольший (max
) из наименьших (min)
выигрышей — это 1000 гривен и сам бог велел полагать стратегию S3
оптимальной, с надеждой на ответный ход конкурента его стратегией C1
. Такую стратегию и называют стратегией MaxiMin
.
Если теперь попробовать смоделировать поведение конкурента, то для него:
· при стратегии C1
максимальный (max)
проигрыш составит 1000
гривен;
· при стратегии C2
максимальный (max)
проигрыш составит 2000
гривен.
Значит, наш конкурент, если он будет рассуждать здраво, выберет стратегию C1
, поскольку именно она обеспечивает наименьший (min)
из наибольших (max)
проигрышей. Такую стратегию и называют стратегией MiniMax
.
Легко заметить, что это одно и то же — вы делаете ход S3
в расчете на ответ C1
, а ваш конкурент — ход C1
в расчете на S3
.
Поэтому такие стратегии называют минимаксными
— мы надеемся на минимум максимальных убытков или, что одно и то же, на максимум минимальной прибыли.
В двух рассмотренных примерах оптимальные стратегии "противников" совпадали, принято говорить — они соответствовали седловой точке
матрицы игры.
Метод минимакса отличается от стандартного пути логических рассуждений таким важным показателем как алгоритмичность.
В самом деле, можно доказать, что если седловая точка существует, то она находится на пересечении некоторой строки S
и некоторого столбца C
. Если число в этой точке самое
большое для данной строки
и, одновременно, самое малое в данном столбце
, то это и есть седловая точка
.
Конечно, далеко не все игры обладают седловой точкой, но если она есть, то поиск ее при числе строк и столбцов в несколько десятков (а то и сотен) по стандартному логическому плану — дело практически безнадежное без использования компьютерных технологий.
Но, даже при использовании компьютера, писать программу для реализации всех возможных If ... Then
придется на специальных языках программирования (например — язык Prolog
). Эти языки велико-лепны для решения логических задач, но практически непригодны для обычных вычислений. Если же использовать метод минимакса, то весь алгоритм поиска седловой точки займет на языке Pascal
или C++
не более 5...10 строк программы.
Рассмотрим еще один простой пример игры, но уже без седловой точки
.
| C1
|
C2
|
| S1
|
-3000
|
+7000
|
| S2
|
+6000
|
+1000
|
Таблица 3.8
Задача в этом случае для нас (и для нашего разумного конкурента) будет заключаться в смене стратегий, в надежде найти такую их комбинацию, при которой математическое ожидание выигрыша или средний выигрыш за некоторое число ходов будет максимальным.
Пусть мы приняли решение половину ходов в игре делать с использованием S1
, а другую половину — с S2
. Конечно, мы не можем знать, какую из своих двух стратегий будет применять конкурент, и поэтому придется рассматривать два крайних случая его поведения.
Если наш конкурент все время будет применять C1
, то для нас выигрыш составит 0.5·(-3000)+0.5·(+6000) = 1500
гривен.
Если же он все время будет применять C2
, то на выигрыш составит 0.5·(+7000)+0.5·(+1000) = 4000
гривен.
Ну, это уже повод для размышлений, для анализа. В конце концов, можно прикинуть, а что мы будем иметь в случае применения конкурентом также смешанной стратегии? Ответ уже готов — мы будем иметь выигрыш не менее 1500 гривен, поскольку выполненные выше расчеты охватили все
варианты смешанных стратегий конкурента.
Поставим вопрос в более общем виде — а существует ли наилучшая
смешанная стратегия (комбинация S1
и S2
) для нас в условиях применения смешанных стратегий (комбинации C1
и C2
) со стороны конкурента? Математическая теория игр позволяет ответить на этот вопрос утвердительно — оптимальная смешанная стратегия всегда существует, но она может гарантировать минимум
математического ожидания выигрыша
. Методы поиска таких стратегий хорошо разработаны и отражены в литературе.
Таким образом, мы снова оказались в роли ЛПР — системный подход не может
дать рецепта для безусловного
получения выигрыша.
Нам и только нам, решать — воспользоваться ли рекомендацией и применить оптимальную стратегию игры, но при этом считаться с риском возможного проигрыша (выигрыш окажется гарантированным лишь при очень большом числе ходов).
Завершим рассмотрение последнего примера демонстрацией поиска наилучшей смешанной стратегии.
Пусть мы применяем стратегию S1
с частотой e
, а стратегию S2
с частотой (1 -
e
)
.
Тогда мы будем иметь выигрыш
W(C1) =
e
·
(-3000) + (1-
e
)
·
(+6000) = 6000 - 9000
·
e
при применении конкурентом стратегии C1
или будем иметь выигрыш
W(C2) =
e
·
(+7000) + (1-
e
)
·
(+1000) = 1000 + 6000
·
e
при применении конкурентом стратегии C2
.
Теория игр позволяет найти наилучшую стратегию для нас из условия W(C1) = W(C2);
{3 - 16}
что приводит к наилучшему значению e
=1/3 и математическому ожиданию выигрыша величиной в (-3000)·(1/3)+(+6000)·(2/3)=3000 гривен.
К этому классу относятся задачи анализа систем с противодействием (конкуренцией), также игровых по сути, но с одной особенностью — "правила игры" не постоянны в одном единственном пункте — цены за то, что продается.
При небольшом числе участников торгов вполне пригодны описанные выше приемы теории игр, но когда число участников велико и, что еще хуже, заранее неизвестно, — приходится использовать несколько иные методы моделирования ситуаций в торгах.
Наиболее часто встречаются два вида торгов:
· закрытые торги
, в которых два или более участников независимо друг от друга предлагают цены (ставки) за тот или иной объект; при этом участник имеет право лишь на одну ставку, а ведущий торги принимает высшую (или низшую) из предложенных;
· открытые торги
или аукционы,
когда два или более участников подымают цены до тех пор, пока новой надбавки уже не предлагается.
Рассмотрим вначале простейший пример закрытых торгов. Пусть мы (A
) и наш конкурент (B
) участвуем в закрытых торгах по двум объектам суммарной стоимости C1
+
C2
.
Мы располагаем свободной суммой S
и нам известно, что точно такой же суммой располагает наш конкурент. При этом S< C1
+
C2
, то есть купить оба объекта без торгов не удастся.
Мы должны назначить свои цены A1, A2
за первый и второй объекты в тайне от конкурента, который предложит за них же свои цены B1, B2.
После оглашения цен объект достанется предложившему большую цену, а если они совпали — по жребию. Предположим, что и мы и наш конкурент владеем методом выбора наилучшей стратегии (имеем соответствующее образование).
Так вот — можно доказать, что при равных
свободных суммах с нашей и с противоположной стороны существует одна, оптимальная
для обеих сторон стратегия назначения цен.
Сущность ее (скажем, для нас) определяется из следующих рассуждений. Если нам удастся купить первый объект, то наш доход составит (C1
- A1
)
или же, при покупке второго, мы будем иметь доход (C2
- A2
).
Значит, в среднем мы можем ожидать прибыль
d = 0.5
·(C1
+ C2
— A1
— A2
) = 0.5
·(C1
+ C2
— S).
{3 - 17}
Таким образом, нам выгоднее всего назначить цены
A1
= C1
— d = 0.5
·
(C1
— C2
+ S);
A2
= C2
— d = 0.5
·
(C2
— C1
+ S).
{3 - 18}
Если же одна из них по расчету окажется отрицательной — выставим ее нулевой и вложим все деньги в цену за другой объект.
Но и наш конкурент, имея ту же свободную сумму и рассуждая точно так же, назначит за объекты точно такие же цены. Как говорится, боевая ничья! Ну, если конкурент не владеет
профессиональными
знаниями? Что ж, тем хуже для него — мы будем иметь доход больше, чем конкурент.
Конкретный пример. Сумма свободных средств составляет по 10000 гривен у каждого, цена первого объекта равна 7500, второго 10000 гривен.
Назначим цену за первый объект в 0.5·(7500-10000+10000)=3750 гривен, а за второй 0.5·(10000-7500+10000) = 6250 гривен.
Наш доход при выигрыше первого или второго объекта составит 3750 гривен. Такой же доход ожидает и конкурента, если он выбрал такую же, оптимальную стратегию. Но, если он так не поступил и назначил цену за первый объект 3500, а за второй 6000 гривен (пытаясь сэкономить!), то в таком случае мы можем выиграть торги по двум объектам сразу и будем иметь доход уже в 7500 гривен — приобретая имущество общей стоимостью в 17500 за цену в 10000 гривен!
Конечно, если стартовые суммы участников торгов неодинаковы, число объектов велико и велико число участников, то задача поиска оптимальной стратегии становится более сложной, но все же имеет аналитическое решение.
Рассмотрим теперь второй вид задачи — об открытых торгах
(аукционах). Пусть все те же два объекта (с теми же стоимостями) продаются с аукциона, в котором участвуем мы и наш конкурент.
В отличие от первой задачи свободные суммы различны и составляют SA
и SB
, причем каждая из них меньше (C1
+ C2
)
и, кроме того, отношение нашей суммы к сумме конкурента более 0.5, но менее 2.
Пусть мы знаем "толщину кошелька" конкурента и, поскольку ищем оптимальную стратегию для себя, нам безразлично — знает ли он то же о наших финансовых возможностях.
Задача наша заключается в том, что мы должны знать — когда надо прекратить подымать цену за первый объект. Эту задачу не решить, если мы не определим цель своего участия в аукционе (системный подход, напомним, требует
этого).
Здесь возможны варианты:
· мы хотим иметь максимальный доход;
· мы стремимся минимизировать доход конкурента;
· мы желаем максимизировать разницу в доходах — свой побольше, а конкурента поменьше.
Наиболее интересен третий вариант ситуации — найти нашу стратегию, обеспечивающую
DA
— DB
=
Max. {3-19}
Поскольку объектов всего два, то все решается в процессе торгов за первый объект. Будем рассматривать свой ход в ответ на очередное предложение цены X
за этот объект со стороны конкурента.
Мы можем использовать две стратегии поступить двумя способами:
· стремиться уступить первый объект конкуренту — за наибольшую цену, надеясь купить второй;
· стремиться купить первый объект — за минимальную цену, уступив конкуренту второй.
Пусть конкурент назначил за первый объект очередную сумму X.
Если мы не добавим небольшую сумму (минимальную надбавку D
), то первый объект достанется конкуренту. При этом у конкурента в запасе останется сумма SB
- X
. Доход конкурента составит при этом (без учета D
) DB
= С1
- X.
Мы наверняка купим второй объект, если у нас в кармане
SA
= (SB
- X) +
D
, то есть немного больше, чем осталось у конкурента.
Значит, мы будем иметь доход DA
= C2
- (SB
- X)
и разность доходов в этом случае составит
DA
- DB
= C2
- C1
- SB
+ 2
·
X .
{3-20}
Ясно, что эта разность будет положительна только тогда, когда мы уступим первый объект за цену
X >  ,
{3-21} ,
{3-21}
но никак не меньше.
· Будем повышать цену за первый объект до суммы X+
D
с целью купить
его.
Наш доход составит при этом
DA
= C1
- (X +
D
).
В
торой объект достанется конкуренту за сумму
SA
- (X +
D
) +
D
,
так как ему придется поднять цену за этот объект до уровня, чуть большего остатка денег у нас.
Доход конкурента составит
DB
= C2
- (SA
- (X +
D
) +
D
),
а разность доходов составит (без учета D
)
DA
- DB
= (C1
- X) - (C2
- SA
+ X) = С1
- С2
+ SA
- 2X .
{3-22}
Эта разность будет положительна при условии
X < 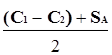 , {3-23} , {3-23}
Мы нашли две "контрольные" суммы для того, чтобы знать — когда надо пользоваться одной из двух доступных нам стратегий — выражения {3-21} и
{3-23}. Среднее этих величин составит
K = 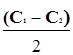 + + 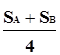 {3-24}
{3-24}
и определяет разумную границу для смены стратегий нашего участия в аукционе с целью одновременно получить доход себе побольше, а конкуренту — поменьше.
Интересно сосчитать свой доход и разность доходов на этой границе.
· Если мы уступили первый объект на этой границе, то по {3-20}
DA
- DB
= C2
- C1
- SB
+ 2K = 0.5(SA
- SB
).
· Если же мы купили первый объект на этой границе, то по {3-22}
DA
- DB
= С1
- С2
+ SA
- 2K = 0.5(SA
- SB
).
Для удобства сопровождения числовыми данными зададимся свободными суммами и ценами объектов (по нашему представлению об этих объектах): SA
=
100 < 175; SB
=
110 < 175; C1
=
75; C2
=
100;
0.5 <
(SA
/ SB
<
2 и примем разрешенную надбавку к цене равной 1.
В этом конкретном случае граница "сражения" за первый объект проходит через сумму
K = 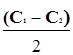 + + 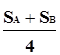 = -12.5 + 52.5 = 40 $ = -12.5 + 52.5 = 40 $
Если наш конкурент считает, что объекты для него
стоят столько же (он знает нашу свободную сумму, а мы знаем его свободную сумму, но другой информации мы и он не обладаем), то он вычислит эту же границу и мы будем довольствоваться разностью доходов не в свою пользу: DA
- DB
= С1
- С2
+ SA
- 2K = 0.5(SA
- SB
)
= -5
.
Что делать — у конкурента больший стартовый капитал.
Но, возможно, наш конкурент (играя за себя) будет считать стоимости объектов совсем иными и для него граница будет совсем другой. Или же — цель конкурента в данном аукционе совершенно не такая как наша, что также обусловит другую граничную сумму участия в торгах за первый объект. Иными словами — оптимальная стратегия для конкурента нам совершенно неизвестна.
Тогда все зависит от того, на какой сумме он "отдаст" нам первый объект или, наоборот, до какой границы он будет "сражаться" за него . Следующая таблица иллюстрирует этот вывод.
Таблица 3.9
| Граница 1 торга за объект
|
Владелец
1 объекта
|
Доход DA
|
Доход DB
|
Разность
DA
- DB
|
| 20
|
A
|
55
|
20
|
35
|
| 30
|
A
|
45
|
30
|
10
|
| 35
|
A
|
40
|
35
|
5
|
| 40
|
A
|
35
|
40
|
-5
|
| 40
|
B
|
25
|
35
|
-5
|
| 45
|
B
|
35
|
30
|
5
|
| 50
|
B
|
40
|
25
|
15
|
| 55
|
B
|
45
|
20
|
25
|
| 60
|
B
|
50
|
15
|
40
|
| 75
|
B
|
75
|
0
|
75
|
Заканчивая вопрос об открытых торгах — аукционах, отметим, что в реальных условиях задача моделирования и выбора оптимальной стратегии поведения оказывается весьма сложной.
Дело не только в том, число объектов может быть намного больше двух, а что касается числа участников, то оно также может быть большим и даже не всегда известным заранее. Это приведет к чисто количественным трудностям при моделировании "вручную", но не играет особой роли при использовании компьютерных программ моделирования.
Дело в другом — большей частью ситуация усложняется неопределенностью, стохастичностью поведения наших конкурентов. Что ж, прийдется иметь дело не с самими величинами (заказываемыми ценами, доходами и т. д.), а с их математическими ожиданиями
, вычисленными по вероятностным моделям, или со средними значениями
, найденными по итогам наблюдений или статистических экспериментов.
Еще в начале рассмотрения вопросов о целях и методах системного анализа мы обнаружили ситуации, в которых нет возможности описать элемент системы, подсистему и систему в целом аналитически
, используя системы уравнений или хотя бы неравенств.
Иными словами — мы не всегда можем построить чисто математическую модель на любом уровне — элемента системы, подсистемы или системы в целом.
Такие системы иногда очень метко называют "плохо организованными" или "слабо структурированными".
Так уж сложилось, что в течение почти 200 лет после Ньютона в науке считалось незыблемым положение о возможности "чистого" или однофакторного
эксперимента. Предполагалось, что для выяснения зависимости величины Y=f(X)
даже при очевидной зависимости Y
от целого ряда других переменных всегда можно стабилизировать все переменные, кроме X
, и найти "личное" влияние X
на Y
.
Лишь сравнительно недавно (см. работы В. В. Налимова) плохо организованные или, как их еще называют — большие системы
вполне "законно" стали считаться особой средой, в которой неизвестными являются не то что связи внутри системы, но и самые элементарные процессы.
Анализ таких систем (в первую очередь социальных, а значит и экономических) возможен при единственном, научно обоснованном подходе — признании скрытых, неизвестных нам причин и законов процессов. Часто такие причины называют латентными
факторами
, а особые свойства процессов — латентными признаками
.
Обнаружилась и считается также общепризнанной возможность анализа таких систем с использованием двух, принципиально различных подходов или методов.
· Первый из них может быть назван методом многомерного статистического анализа
. Этот метод был обоснован и применен видным английским статистиком Р.Фишером в 20..30 годы этого столетия. Дальнейшее развитие многомерной математической статистики как науки и как основы многих практических приложений считается причинно связанным с появлением и совершенствованием компьютерной техники. Если в 30-е годы, при ручной обработке данных удавалось решать задачи с учетом 2..3 независимых переменных, то 1965 году решались задачи с 6 переменными, а к 70..80 годам их число уже приближалось к 100.
· Второй метод принято называть кибернетическим
или "винеровским",
связывая его название с отцом кибернетики Н.Винером. Краткая сущность этого метода — чисто логический анализ процесса
управления
большими системами. Рождение этого метода было вполне естественным — коль скоро мы признаем существование плохо организованных систем, то логично ставить вопрос о поиске методов и средств управления ими. Совершенно нелепо ставить вопрос о распределении токов в электрической цепи — это процессы в хорошо организованной (законами природы) системе.
Интересно, что оба метода, несмотря на совершенное различие между собой, могут применяться и с успехом применяются при системном анализе одних и тех же систем.
Так, например, интеллектуальная деятельность человека изучается "фишеровским" методом — многие психологи, как иронически замечает В.В.Налимов, "уверены, что им удастся разобраться в результатах многочисленных тестовых испытаний ".
С другой стороны, построение т.н. систем искусственного интеллекта
представляет собой попытки создания компьютерных программ, имитирующих поведение человека в области умственной деятельности, т.е. применение "винеровского" метода.
Нетрудно понять, что экономические системы, скорее всего, следует отнести именно к плохо организованным — прежде всего, потому, что одним из видов элементов в них является человек. А раз так, то неудивительно, что при системном анализе в экономике потребуется "натурный" эксперимент.
В простейшем случае речь может идти о некотором элементе экономической системы, о котором нам известны лишь внешние воздействия (что нужно для нормального функционирования элемента) и выходные его реакции (что должен "делать" этот элемент).
В каком то смысле спасительной является идея рассмотрения такого элемента как "черного ящика". Используя эту идею, мы признаемся, что не в состоянии проследить процессы внутри элемента и надеемся построить его модель без таких знаний.
Напомним классический пример — незнание процессов пищеварения в организме человека не мешает нам организовывать свое питание по "входу" (потребляемые продукты, режим питания и т. д.) с учетом "выходных" показателей (веса тела, самочувствия и других).
Так вот, наши намерения вполне конкретны в части "что делать" — мы собираемся подавать на вход элемента разные
внешние, управляющие воздействия и измерять его реакции на эти воздействия.
Теперь надо столь же четко решить — а зачем мы это будем делать, что мы надеемся получить. Вопрос этот непростой — очень редко можно позволить себе просто удовлетворить свою любознательность. Как правило, эксперименты над реальной экономической системой являются вынужденной процедурой, связанной с определенными затратами на сам эксперимент и, кроме того, с риском непоправимых отрицательных последствий.
Теоретическое обоснование и методика действий в таких ситуациях составляют предмет особой отрасли кибернетики — теории планирования эксперимента.
Договоримся о терминологии:
· все, что подается на вход элемента, будем называть управляющими воздействиями
или просто воздействиями;
· все, что получается на выходе элемента, будем называть реакциями
;
· если мы можем выделить в системе (или подсистеме) несколько в некотором смысле однотипных
элементов, то их совокупность будем называть блоком
;
· содержательное описание своих действий по отношению к элементам блока будем называть планом
эксперимента.
Очень важно понять цель планируемого эксперимента. В конце концов, мы можем и не получить никакой информации о сущности процессов в цепочке "вход-выход" в самом элементе.
Но если мы обнаружим полезность некоторых, доступных нам воздействий на элемент и убедимся в надежности полученных результатов, то достигнем главной цели эксперимента — отыскания опти-мальной
стратегии управления элементом. Нетрудно сообразить, что понятие "управляющее воздействие" очень широко — от самых обычных приказов до подключения к элементу источников энергетического или информационного "питания".
Оказывается, что уже само составление плана эксперимента требует определенных познаний и некоторой квалификации.
Опыт доказывает целесообразность включения в план следующих четырех компонентов:
· Описание множества стратегий
управления, из которого мы надеемся выбрать наилучшую.
· Спецификацию
или детальное сравнительное описание элементов
блока.
· Правила размещения стратегий
на блоке элементов.
· Спецификацию выходных данных
, позволяющих оценивать эффективность элементов.
Внимательное рассмотрение компонентов плана эксперимента позволяет заметить, что для его реализации требуются знания в раз-личных областях науки, даже если речь идет об экономической системе — той области, в которой вы приобретаете профессиональную подготовку. Так, при выборе управляющих воздействий не обойтись без минимальных знаний в области технологии
(не всегда это — чистая экономика), очень часто нужны знания в области юридических законов, экологии. Для реализации третьего компонента совершенно необходимы знания в области математической статистики, так как при-ходится использовать понятия распределений случайных величин, их математических ожиданий и дисперсий. Вполне могут возникнуть ситуации, требующие применения непараметрических методов статистики.
Для демонстрации трудностей составления плана эксперимента и необходимости понимания методов использования результатов эксперимента, рассмотрим простейший пример.
Пусть мы занимаемся системным анализом фирмы, осуществляющей торговлю с помощью сети "фирменных" магазинов и имеем возможность наблюдать один и тот же выходной показатель элемента такой системы (например, дневную выручку магазина фирмы).
Естественным является стремление найти способ повышения этого показателя, а если таких способов окажется несколько — выбрать наилучший. Предположим, что в соответствии с первым пунктом правил планирования эксперимента, мы решили испытать четыре стратегии управления магазинами. Коль скоро такое решение принято, то неразумно ограничить эксперимент одним элементом, если их в системе достаточно много и у нас нет уверенности в "эквивалентности" условий работы всех магазинов фирмы.
Пусть мы имеем N
магазинов — достаточно много, чтобы провести "массовый" эксперимент, но их нельзя отнести к одному и тому же типу. Например, мы можем различать четыре типа магазинов: А, Б, В
и Г
(аптечные, бакалейные, водочные и галантерейные).
Ясно также (хотя и для этого надо немножко разбираться в технологии торговли), что выручка магазина вполне может существенно зависеть от дня недели — пусть рабочие дни всех магазинов: Ср
, Пт, Сб, Вс
.
Первое, "простое" решение, которое приходит в голову — выбрать из N
несколько магазинов наугад (применив равновероятное распределение их номеров) и применять некоторое время новую стратегию управления ими. Но столь же простые рассуждения приводят к мысли, что это будет не лучшее решение.
В самом деле — мы рассматриваем элементы системы как "равноправные" по нескольким показателям:
· мы ищем единую и наилучшую для фирмы в целом стратегию управления;
· мы используем единый для всех элементов показатель эффективности (дневную выручку).
И, в то же время, мы сами разделили объекты на группы и тем самым признаем различие во внешних условиях работы для различных групп. На языке ТССА это означает, что профессиональные знания в области управления торговлей помогают нам предположить наличие, по крайней мере, двух
причин или факторов,
от которых может зависеть выручка: профиль товаров магазина и день недели. Ни то, ни другое не может быть стабилизировано — иначе мы будем искать нечто другое: стратегию для управления только
водочными магазинами и только
по пятницам! А наша задача — поиск стратегии управления всеми
магазинами и по любым
дням их работы.
Хотелось бы решить эту задачу так: выбирать случайно как группы магазинов, так и дни недели, но иметь гарантию (уже не случайно!) представительности выходных данных испытания стратегии.
Теория планирования эксперимента предлагает особый метод решения этой проблемы, метод обеспечения случайности или рандомизации
плана эксперимента.
Этот метод основан на построении
специальной таблицы, которую принято называть латинским квадратом,
если число факторов равно двум.
Для нашего примера, с числом стратегий 4, латинский квадрат может иметь вид табл. 3.10 или табл. 3.11.
Таблица 3.10 Таблица 3.11
| 1
|
2
|
3
|
4
|
| Ср
|
А
|
Б
|
В
|
Г
|
| Пт
|
В
|
Г
|
А
|
Б
|
| Сб
|
Б
|
А
|
Г
|
В
|
| Вс
|
Г
|
В
|
Б
|
А
|
| Ср
|
Пт
|
Сб
|
Вс
|
| А
|
1
|
2
|
3
|
4
|
| Б
|
3
|
4
|
1
|
2
|
| В
|
2
|
1
|
4
|
3
|
| Г
|
4
|
3
|
2
|
1
|
В ячейках первой таблицы указаны номера стратегий для дней недели и магазинов данного профиля, причем такой план эксперимента гарантирует проверку каждой из стратегий в каждом профиле торговли и в каждый день работы магазина.
Конечно же, таких таблиц (квадратов) можно построить не одну — правила комбинаторики позволяют найти полное число латинских квадратов типа "4·4" и это число составляет 576. Для квадрата "3·3" имеется всего 12 вариантов, для квадрата "5·5" — уже 161 280 вариантов.
В общем случае, при наличии t
стратегий и двух
факторах, определяющих эффективность, потребуется N=a
·
t2
элементов для реализации плана эксперимента, где a
в простейшем случае равно 1.
Это означает, что для нашего примера необходимо использовать 16 "управляемых" магазинов, так как данные, скажем второй строки и третьего столбца, нашего латинского квадрата означают, что по субботам в одном из выбранных наугад
бакалейных магазинов будет применяться стратегия номер 1.
Отметим, что латинский квадрат для нашего примера может быть помтроен совершенно иначе — в виде таблицы 3.11, но по-прежнему будет определять все тот же, рандомизированный план эксперимента.
Пусть мы провели эксперимент и получили его результаты в виде следующей таблицы, в ячейках которой указаны стратегии и результаты их применения в виде сумм дневной выручки:
Таблица 3.12
| Дни
|
Магазины
А Б В Г
|
Сумма
|
| Вс
|
2: 47
|
1: 90
|
3: 79
|
4: 50
|
266
|
| Ср
|
4: 46
|
3: 74
|
2: 63
|
1: 69
|
252
|
| Пт
|
1: 62
|
2: 61
|
4: 58
|
3: 66
|
247
|
| Сб
|
3: 76
|
4: 63
|
1: 87
|
2: 59
|
285
|
| Сумма
|
231
|
288
|
287
|
244
|
1050
|
| Итого по
стратегиям
|
1
308
|
2
230
|
3
295
|
4
217
|
1050/4=
262.5
|
Если вычислить, как и положено, средние значения, дисперсии и среднеквадратичные отклонения для четверок значений дневной выручки (по дням, магазинам и стратегиям), то мы будем иметь следующие данные:
Таблица 3.12А
| Дни недели
|
Магазины
|
Стратегии
|
| Среднее
|
262.5
|
262.5
|
262.5
|
| Дисперсия
|
217.3
|
646.3
|
1563.3
|
| СКО
|
14.74
|
25.42
|
39.5
|
| Коэф.вариации
|
0.056
|
0.097
|
0.151
|
Уже такая примитивная статистическая обработка данных эксперимента позволяет сделать ряд важных выводов:
· сравнительно малые значения рассеяния данных по дням недели и по категориям магазинов в какой то мере вселяют надежду на правильный выбор плана эксперимента;
· разброс значений по стратегиям на этом фоне, скорее всего свидетельствует о большей зависимости дневной выручки от стратегии, чем от дней недели или категории магазина;
· заметное отличие средних по 1-й и 3-й стратегиям от средних по 2-й и 4-й, может быть основой для принятия решения — искать наилучшую стратегию, выбирая между 1-й и 3-й.
В этом — прямой практический результат использования рандомизированного плана, построения латинского квадрата.
Но это далеко не все. Теория планирования эксперимента дает, кроме способов построения планов с учетом возможных влияний на интересующую нас величину других факторов, еще и особые методы обработки полученных экспериментальных данных.
Самая суть этих методов может быть представлена так.
Пусть Wis
есть выручка в i-
м магазине при применении к нему s
-й стратегии управления. Предполагается рассматривать эту выручку в виде суммы составляющих
Wis
= W0
+
D
s
+
e
i;
{3-25}
где:
·
W0
определяет среднюю выручку для всех
магазинов при условии применения к каждому из них всех
стратегий по очереди с соблюдением постоянными всех других условий, влияющих на выручку;
· W0
+
D
s
есть средняя выручка при применении ко всем
магазинам s
-й стратегии;
· e
i
рассматривается как "ошибка измерения" — случайная величина с нулевым математическим ожиданием и нормальным законом распределения.
Несмотря на явную нереальность соблюдения постоянными внешних влияющих факторов, мы можем получить оценку каждого из слагаемых Wis
и искать оптимальную стратегию через прибавку от ее применения D
s
с учетом ошибки наблюдения. Можно считать доказанной "нормальность" распределения величины e
i
и использовать "правило трех сигм" при принятии решений по итогам эксперимента.
Данный параграф является заключительным и более не будет возможности осветить еще одну особенность методов системного анализа, показать вам еще один путь к достижению профессионального уровня в области управления экономическими системами.
Уже ясно, что ТССА большей частью основывает свои практические методы на платформе математической статистики. Несколько упреждая ваш рабочий учебный план (курс математической статистики — предмет нашего сотрудничества в следующем семестре), обратимся к современным постулатам этой науки.
Общепризнанно, что в наши дни можно выделить три подхода к решению задач, в которых используются статистические данные.
· Алгоритмический подход
, при котором мы имеем статистические данные о некотором процессе и по причине слабой изученности процесса его основная характеристика (например, эффективность экономической системы) мы вынуждены сами строить “разумные” правила обработки данных, базируясь на своих собственных представлениях об интересующем нас показателе.
· Аппроксимационный подход
, когда у нас есть полное представление о связи данного показателя с имеющимися у нас данными, но неясна природа возникающих ошибок — отклонений от этих представлений.
· Теоретико-вероятностный подход
, когда требуется глубокое проникновение в суть процесса для выяснения связи показателя со статистическими данными.
В настоящее время все эти подходы достаточно строго обоснованы научно и “снабжены” апробированными методами практических действий.
Но существуют ситуации, когда нас интересует не один, а несколько показателей процесса и, кроме того, мы подозреваем наличие нескольких, влияющих на процесс,
воздействий — факторов,
которые являются не наблюдаемыми, скрытыми или латентными
.
Наиболее интересным и полезным в плане понимания сущности факторного анализа
— метода решения задач в этих ситуациях, является пример использования наблюдений при эксперименте, который ведет природа, Ни о каком планировании здесь не может идти речи — нам приходится довольствоваться пассивным экспериментом
.
Удивительно, но и в этих “тяжелых” условиях ТССА предлагает методы выявления таких факторов, отсеивания слабо проявляющих себя, оценки значимости полученных зависимостей показателей работы системы от этих факторов.
Пусть мы провели по n
наблюдений за каждым из k
измеряемых показателей эффективности некоторой экономической системы и данные этих наблюдений представили в виде матрицы (таблицы).
Матрица исходных данных E
[n·k] {3-26}
| E 11
|
E12
|
…
|
E1i
|
…
|
E1k
|
| E 21
|
E22
|
…
|
E2i
|
…
|
E2k
|
| …
|
…
|
…
|
…
|
…
|
…
|
| E j1
|
Ej2
|
…
|
Eji
|
…
|
Ejk
|
| …
|
…
|
…
|
…
|
…
|
…
|
| E n1
|
En2
|
…
|
Eni
|
…
|
Enk
|
Пусть мы предполагаем, что на эффективность системы влияют и другие — ненаблюдаемые, но легко интерпретируемые (объяснимые по смыслу, причине и механизму влияния) величины — факторы.
Сразу же сообразим, что чем больше n
и чем меньше таких число факторов m
(а может их и нет вообще!),
тем больше надежда оценить их влияние на интересующий нас показатель E.
Столь же легко понять необходимость условия m < k,
объяснимого на простом примере аналогии — если мы исследуем некоторые предметы с использованием всех 5 человеческих чувств, то наивно надеяться на обнаружение более пяти “новых”, легко объяснимых, но неизмеряемых признаков у таких предметов, даже если мы “испытаем” очень большое их количество.
Вернемся к исходной матрице наблюдений E[n
·k]
и отметим, что перед нами, по сути дела, совокупности по n
наблюдений над каждой из k
случайными величинами E1
, E2
, … E k
. Именно эти величины “подозреваются” в связях друг с другом — или во взаимной коррелированности.
Из рассмотренного ранее метода оценок таких связей следует, что мерой разброса случайной величины E
i
служит ее дисперсия, определяемая суммой квадратов всех зарегистрированных значений этой величины S
(
Eij
)2
и ее средним значением (суммирование ведется по столбцу).
Если мы применим замену переменных в исходной матрице наблюдений, т.е. вместо Ei j
будем использовать случайные величины
Xij
= 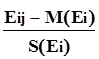 ,
{3-27} ,
{3-27}
то мы преобразуем исходную матрицу в новую
X[n
·
k]
{3-28}
| X 11
|
X12
|
…
|
X1i
|
…
|
X1k
|
| X 21
|
X22
|
…
|
X2i
|
…
|
X2k
|
| …
|
…
|
…
|
…
|
…
|
…
|
| X j1
|
Xj2
|
…
|
Xji
|
…
|
Xjk
|
| …
|
…
|
…
|
…
|
…
|
…
|
| X n1
|
Xn2
|
…
|
Xni
|
…
|
Xnk
|
Отметим, что все элементы новой матрицы X[n
·
k]
окажутся безразмерными, нормированными величинами и, если некоторое значение Xij
составит, к примеру,
+2, то это будет означать только одно - в строке j
наблюдается отклонение от среднего по столбцу i
на два среднеквадратичных отклонения (в большую сторону).
Выполним теперь следующие операции.
· Просуммируем квадраты всех значений столбца 1 и разделим результат на (n - 1)
— мы получим дисперсию (меру разброса) случайной величины X1
,
т.е. D1
.
Повторяя эту операцию, мы найдем таким же образом дисперсии всех наблюдаемых (но уже нормированных) величин.
· Просуммируем произведения соответствующих строк (от j =1 до j = n) для столбцов 1,2 и также разделим на (n -1)
. То, что мы теперь получим, называется ковариацией
C12
случайных величин X1
, X2
и служит мерой их статистической связи.
· Если мы повторим предыдущую процедуру для всех пар столбцов, то в результате получим еще одну, квадратную матрицу C[k
·k],
которую принято называть ковариационной.
Эта матрица имеет на главной диагонали дисперсии случайных величин X
i
, а в качестве остальных элементов — ковариации этих величин ( i
=1…k).
Ковариационная матрица C
[k·k] {3-29}
| D1
|
C12
|
C13
|
…
|
…
|
C1k
|
| C21
|
D2
|
C23
|
…
|
…
|
C2k
|
| …
|
…
|
…
|
…
|
…
|
…
|
| Cj1
|
Cj2
|
…
|
Cji
|
…
|
Cjk
|
| …
|
…
|
…
|
…
|
…
|
…
|
| Cn1
|
Cn2
|
…
|
Cni
|
…
|
Dk
|
Если вспомнить, что связи случайных величин можно описывать не только ковариациями, но и коэффициентами корреляции, то в соответствие матрице {3-29} можно поставить матрицу парных коэффициентов корреляции или корреляционную
матрицу
R
[k·k] {3-30}
| 1
|
R12
|
R13
|
…
|
…
|
R1k
|
| R21
|
1
|
R23
|
…
|
…
|
R2k
|
| …
|
…
|
…
|
…
|
…
|
…
|
| Rj1
|
Rj2
|
…
|
Rji
|
…
|
Rjk
|
| …
|
…
|
…
|
…
|
…
|
…
|
| Rn1
|
Rn2
|
…
|
Rni
|
…
|
1
|
в которой на диагонали находятся 1, а внедиагональные элементы являются обычными коэффициентами парной корреляции.
Так вот, пусть мы полагали наблюдаемые переменные E
i независящими друг от друга,
т.е. ожидали увидеть матрицу R
[k·k] диагональной, с единицами в главной диагонали и нулями в остальных местах. Если теперь это не так, то наши догадки о наличии латентных факторов в какой-то мере получили подтверждение.
Но как убедиться в своей правоте, оценить достоверность нашей гипотезы — о наличии хотя бы одного латентного фактора, как оценить степень его влияния на основные (наблюдаемые) переменные? А если, тем более, таких факторов несколько — то как их проранжировать по степени влияния?
Ответы на такие практические вопросы призван давать факторный анализ. В его основе лежит все тот же “вездесущий” метод статистического моделирования (по образному выражению В.В.Налимова — модель вместо теории
).
Дальнейший ход анализа при выяснению таких вопросов зависит от того, какой из матриц мы будем пользоваться. Если матрицей ковариаций C
[k·k], то мы имеем дело с методом главных компонент
,
если же мы пользуемся только матрицей R
[k·k],
то мы используем метод факторного анализа
в его “чистом” виде.
Остается разобраться в главном — что позволяют оба эти метода, в чем их различие и как ими пользоваться. Назначение обоих методов одно и то же — установить сам факт наличия латентных переменных (факторов), и если они обнаружены, то получить количественное описание
их влияния на основные переменные Ei
.
Ход рассуждений при выполнении поиска главных компонент
заключается в следующем. Мы предполагаем наличие некоррели-рованных переменных Zj
( j=1…k), каждая из которых представляется нам комбинацией основных переменных (суммирование по i =1…k):
Z
j
=
S
A
j i
·X
i
{3-31}
и, кроме того, обладает дисперсией, такой что
D(Z
1
)
³
D(Z
2
)
³
…
³
D(Z
k
).
Поиск коэффициентов A
j i
(их называют весом j
-й компонеты в содержании i
-й переменной)
сводится к решению матричных уравнений и не представляет особой сложности при использовании компьютерных программ. Но суть метода весьма интересна и на ней стоит задержаться.
Как известно из векторной алгебры, диагональная матрица [2·2] может рассматриваться как описание 2-х точек (точнее — вектора) в двумерном пространстве, а такая же матрица размером [k·k]—
как описание k
точек k
-мерного пространства.
Так вот, замена реальных, хотя и нормированных переменных X
i
на точно такое же количество переменных Z
j
означает не что иное, как поворот k
осей многомерного пространства.
“Перебирая” поочередно оси, мы находим вначале ту из них, где дисперсия вдоль оси наибольшая. Затем делаем пересчет дисперсий для оставшихся k-1
осей и снова находим “ось-чемпион” по дисперсии и т.д.
Образно говоря, мы заглядываем в куб (3-х мерное пространство) по очереди по трем осям и вначале ищем то направление, где видим наибольший “туман” (наибольшая дисперсия говорит о наибольшем влиянии чего-то постороннего); затем “усредняем” картинку по оставшимся двум осям и сравниваем разброс данных по каждой из них — находим “середнячка” и “аутсайдера”. Теперь остается решить систему уравнений — в нашем примере для 9 переменных, чтобы отыскать матрицу коэффициентов (весов) A
[k·k].
Если коэффициенты A
j i
найдены, то можно вернуться к основным переменным, поскольку доказано, что они однозначно выражаются в виде (суммирование по j=1…k)
X
i
=
S
A
ji·Z
j
.
{3-32}
Отыскание матрицы весов A[k
·
k]
требует использования ковариационной матрицы и корреляционной матрицы.
Таким образом, метод главных компонент
отличается прежде все тем, что дает всегда единственное решение задачи. Правда, трактовка этого решения своеобразна.
· Мы решаем задачу о наличии ровно стольких факторов, сколько у нас наблюдаемых переменных, т.е. вопрос о нашем согласии на меньшее число латентных факторов невозможно поставить;
· В результате решения, теоретически всегда единственного, а практически связанного с громадными вычислительными трудностями при разных физических размерностях основных величин, мы получим ответ примерно такого вида — фактор такой-то (например, привлекательность продавцов при анализе дневной выручки магазинов) занимает третье место по степени влияния на основные переменные.
Этот ответ обоснован — дисперсия этого фактора оказалась третьей по крупности среди всех прочих. Всё… Больше ничего получить в этом случае нельзя. Другое дело, что этот вывод оказался нам полезным или мы его игнорируем — это наше право решать, как использовать системный подход!
Несколько иначе осуществляется исследование латентных переменных в случае применения собственно факторного анализа
. Здесь каждая реальная переменная рассматривается также как линейная комбинация ряда факторов F
j , но в несколько необычной форме
X i
=
S
B ji
·
Fj +
D
i
.
{3-33} причем суммирование ведется по j=1…m , т.е. по каждому фактору.
Здесь коэффициент B
ji
принято называть нагрузкой
на j
-й фактор со стороны i
-й переменной, а последнее слагаемое в {3-33} рассматривать как помеху, случайное отклонение для Xi
.
Число факторов m
вполне может быть меньше числа реальных переменных n
и ситуации, когда мы хотим оценить влияние всего одного фактора (ту же вежливость продавцов), здесь вполне допустимы.
Обратим внимание на само понятие “латентный”, скрытый, непосредственно не измеримый фактор. Конечно же, нет прибора и нет эталона вежливости, образованности, выносливости и т.п. Но это не мешает нам самим “измерить” их — применив соответствующую шкалу для таких признаков, разработав тесты для оценки таких свойств по этой шкале и применив эти тесты к тем же продавцам. Так в чем же тогда “ненаблюдаемость”? А в том, что в процессе эксперимента (обязательно) массового мы не можем непрерывно сравнивать все эти признаки с эталонами и нам приходится брать предварительные, усредненные, полученные совсем не в “рабочих” условиях данные.
Можно отойти от экономики и обратиться к спорту. Кто будет спорить, что результат спортсмена при прыжках в высоту зависит от фактора — “сила толчковой ноги”. Да, это фактор можно измерить
и в обычных физических единицах (ньютонах или бытовых килограммах), но когда?! Не во время же прыжка на соревнованиях!
А ведь именно в это, рабочее
время фиксируются статистические данные, накапливается материал для исходной матрицы.
Несколько более сложно объяснить сущность самих процедур факторного анализа простыми, элементарными понятиями (по мнению некоторых специалистов в области факторного анализа — вообще невозможно). Поэтому постараемся разобраться в этом, используя достаточно сложный, но, к счастью, доведенный в практическом смысле до полного совершенства, аппарат векторной или матричной алгебры.
До того как станет понятной необходимость в таком аппарате, рассмотрим так называемую основную теорему факторного анализа. Суть ее основана на представлении модели факторного анализа {3-33} в матричном виде
X
[k·1] = B
[k·m] · F
[m·1] + D
[k·1] {3-34}
и на последующем доказательстве истинности выражения
R
[k·k] = B
[k·m] · B*
[m·k], {3-35}
для “идеального” случая, когда невязки D
пренебрежимо малы.
Здесь B*
[m
·k]
это та же матрица B [k
·m],
но преобразованная особым образом (транспонированная).
Трудность задачи отыскания матрицы нагрузок на факторы очевидна — еще в школьной алгебре указывается на бесчисленное множество решений системы уравнений, если число уравнений больше числа неизвестных. Грубый подсчет говорит нам, что нам понадобится найти k
·m
неизвестных элементов матрицы нагрузок, в то время как только около k2
/ 2
известных коэффициентов корреляции. Некоторую “помощь” оказывает доказанное в теории факторного анализа соотношение между данным коэффициентом парной корреляции (например R
12
) и набором соответствующих нагрузок факторов:
R
12
= B
11
· B
21
+ B
12
· B
22
+ … + B
1m
· B
2m
. {3-36}
Таким образом, нет ничего удивительного в том утверждении, что факторный
анализ (а, значит, и системный
анализ в современных условиях) — больше искусство
, чем наука. Здесь менее важно владеть “навыками” и крайне важно понимать как мощность, так и ограниченные возможности этого метода.
Есть и еще одно обстоятельство, затрудняющее профессиональную подготовку в области факторного анализа — необходимость быть профессионалом в “технологическом” плане, в нашем случае это, конечно же, экономика.
Но, с другой стороны, стать экономистом высокого уровня вряд ли возможно, не имея хотя бы представлений о возможностях анализировать и эффективно управлять экономическими системами на базе решений, найденных с помощью факторного анализа.
Не следует обольщаться вульгарными обещаниями популяризаторов факторного анализа, не следует верить мифам о его всемогущности и универсальности. Этот метод “на вершине” только по одному показателю — своей сложности, как по сущности, так и по сложности практической реализации даже при “повальном” использовании компьютерных программ. К примеру, есть утверждения о преимуществах метода главных компонент — дескать, этот метод точнее расчета нагрузок на факторы. По этому поводу имеется одна острота известного итальянского статистика Карло Джинни, она в вольном пересказе звучит примерно так: “ Мне надо ехать в Милан, и я куплю билет на миланский поезд, хотя поезда на Неаполь ходят точнее и это подтверждено надежными статистическими данными. Почему? Да потому, что мне надо в Милан…”.
Выражая благодарность каждому, кто дочитал до этого места или прослушал все лекции и посетил все семинары, автор считает своим долгом сделать ряд пояснений, раскрыть свою позицию и свои взгляды на курс “Основы теории систем и системного анализа”.
· Место курса ТССА в ряду учебных дисциплин специальности “Учет и аудит” обусловлено прежде всего общим учебным планом, в первую очередь — разумной дисцпозицией всех дисциплин, с учетом их содержания и отводимого числа часов. Анализ (разумеется — системный!) общего рабочего плана специальности показывает, что курс ТССА должен излагаться после
курса “Высшая математика” или, по крайней мере, в том семестре, в котором излагаются вопросы матричной алгебры
. Кроме того, слушатели должны иметь представления о сути методов математической статистики, элементарных положениях теории вероятностей и иметь хотя бы начальные навыки обработки статистических данных. Отсюда второй вывод — данному курсу должно предшествовать
изучение хотя бы введения в математическую статистику (в объеме не менее 2 час. лекций и 1 часа семинаров в неделю).
· Курс ТССА является теоретической и, главное, методолгической основой большинства специальных, экономических дисциплин (если, конечно, они излагаются на уровне современных информационных технологий). Поэтому данный курс должен читаться до
таких дисциплин как “Экономическая статистика”, “Экономическо-математические методы и модели”, “Эконометрия”, “Экономический риск” и т.д.
· Несомненна целесообразность связей курса ТССА с такими дисциплинами как “Компъютерная техника и программирование”, а также
“Информационные системы учета”. Первая из них может считаться необходимой базой для знакомства слушателей с практикой решения задач системного анализа на ЭВМ, вторая — может служить естественным продолжением ТССА в такой специфической области как информатика.
· И, наконец, — о данном материале. Решение о необходимости его создания было принято кафедрой не только в связи с известными, временными трудностями только что созданного ВУЗа в вопросах обеспечения учебными и методическими пособиями. Сыграли роль и предвидимые кафедрой трудности восприятия курса слушателями, не имеющими “платформы знаний” в области статистики и необходимых вопросов математики.
Всё это и обусловило столь нестандартный, причудливый подход к изложению данного курса (1 час лекций в неделю и 1 час семинаров): основные узловые точки, фундаментальные понятия излагались на лекциях и, затем, движение по таким же вопросам продолжалось на семинарах, с акцентом на практических примерах.
· В заключение несколько слов о роли “практических” занятий по данному курсу. По мнению автора эти занятия могут быть полезны только в чистом виде “семинара” (группового занятия с коллективным обсуждением проблем системного анализа), но при этом не занимать половину аудиторного времени.
Профессор кафедры
информационных систем
и высшей математики ИДА
Г.И.Корнилов
12.12.96
Общие вопросы системного анализа
| Методы поиска экстремума
|
Уайлд Д.Дж.
|
| Наука об управлении. Байесовский подход
|
Моррис У.
|
| Введение в минимакс
|
Демьянов В.Ф., …
|
| Целочисленные методы оптимизации
|
Саати Т.
|
| Численные методы оптимизации
|
Полак Э.
|
| Методы оптимизации - вводный курс
|
Банди Б.
|
Системы массового обслуживания
| Элементы теории массового обслуживания
|
Саати Т.Л.
|
| Очереди с приоритетами
|
Джейсуол Н.
|
Экономические системы
| Математическая экономика
|
Аллен Р.
|
| Теория линейных экономических моделей
|
Гейл Д.
|
| Экономическая теория и исследование операций
|
Баумоль У.
|
| Применение математики в экономических исследованиях
|
Монография
в 3 томах
|
| Введение в экономическую кибернетику
|
Ланге О.
|
| Экономико-математические модели
|
Канторович Л.В.
|
| Основы экономической кибернетики
|
Кобринский Н.Е.
|
| Теория игр и экономическое поведение
|
Нейман Дж.,
Моргенштерн О.
|
| Математика-управление-экономика
|
Моисеев Н.Н.
|
| Критерии математической статистики в эко-номических исследованиях
|
Головач А.В., …
|
| Комбинаторные планы в задачах медицины, финансов и экономики
|
Маркова Е.В.,
Лисенков А.Н.
|
| Многомерные статист. методы экономики
|
Болч Б.У., Хуань К.Д.
|
| Байесовские методы в эконометрии
|
Зельнер А.
|
| Эконометрия структурных изменений
|
Пуарье Д.
|
Комбинаторика
| Введение в комбинаторный анализ
|
Риордан Дж.
|
| Прикладная комбинаторная математика
|
Беккенбах Э.(ред.)
|
| Комбинаторика
|
Виленкин Н.Я.
|
| Математическое открытие
|
Пойа Д.
|
Теория вероятностей
| Сборник задач по теории вероятностей, математической статистике и случайным функциям
|
Свешников А.А.
|
| Вероятность
|
Мостеллер Ф.
|
| Теория вероятностей
|
Прохоров Ю.В.,
Розанов Ю.А.
|
Теория игр
| Матричные игры
|
Воробьев Н.Н.(ред.)
|
| Игры и решения
|
Льюс Р., Райфа Х.
|
| Бесконечные антагонистические игры
|
Воробьев Н.Н. (ред)
|
| Стратегические игры
|
Дрешер М.
|
| Математические методы в теории игр, программировании и экономике
|
Карлин С.
|
| Позиционные игры
|
Воробьев Н.Н. (ред.)
|
| Игровые задачи о встрече движений
|
Красовский Н.Н.
|
| Теория игр
|
Оуэн Г.
|
Математическое программирование
| Линейное программирование
|
Гасс С.
|
| Элементы линейной алгебры и линейного программирования
|
Карпелевич Ф.И.
Садовский Л.Е.
|
| Динамическое программирование и современная теория управления
|
Беллман Р.,
Калаба Р.
|
| Геометрическое программирование
|
Даффин Р. и др.
|
Общие вопросы
| Метод наименьших квадратов
|
Линник Ю.В.
|
| Теория распределений
|
Кендалл М.,СтьюартА.
|
| Математическая статистика
|
Уилкс С.
|
| Основные понятия мат.статистики
|
Барра Ж.-Р.
|
| Математические методы статистики
|
Крамер Г.
|
| Теоретическая статистика
|
Кокс Д., Хинкли Д.
|
Статистическое моделирование
| Статистические модели в инженерных задачах
|
Хан Г., Шапиро С.
|
| Стохастическая аппроксимация
|
Вазан М.
|
| Метод Моте-Карло и смежные вопросы
|
Ермаков С.М.
|
| Статистические методы в имитационном моделировании
|
Клейнен Дж.
|
Статистические выводы и решения
| Элементарная теория статистических решений
|
Чернов Г., Мозес Л.
|
| Статистические выводы и связи
|
Кендалл М.,
Стьюарт А.
|
| Оптимальные статистические решения
|
Де Гроот М.
|
| Теория статистических выводов
|
Закс Л.
|
| Статистическое оценивание
|
Закс Л.
|
| Анализ решений
|
Райфа Г.
|
| Теория полезности для принятия решений
|
Фишберн П.
|
| Проверка значимости
|
Колкот Э.
|
| Введение в теорию статистически ненадежных решений
|
Федулов А.А., …
|
| Принятие решений при многих критериях
|
Гафт М.Г.
|
| Принятие решений при многих критериях
|
Кини Р.Л., Райфа Х.
|
| Проверка статистических гипотез
|
Леман Э.
|
| Статистические выводы, основанные на рангах
|
Хеттманспергер Т.
|
| Прикладная теория статистических решений
|
Райфа Г.,Шлейфер Р.
|
| Статистическое оценивание и проверка гипотез на ЭВМ
|
Петрович М.Л.,
Давидович М.И.
|
Статистический эксперимент
| Введение в планирование эксперимента
|
Финни Д.
|
| Теория эксперимента
|
Налимов В.В.
|
| Теория оптимального эксперимента
|
Федоров В.В.
|
| Теория инженерного эксперимента
|
Шенк Х.
|
Статистический анализ
| Последовательный анализ
|
Вальд А.
|
| Статистический анализ последовательностей событий
|
Кокс Д.,
Льюис П.
|
| Анализ временных рядов:
Прогноз и управление
|
Бокс Дж.,
Дженкинс Г.
|
| Статистический последовательный анализ
|
Ширяев А.Н.
|
| Многомерный статистический анализ и временные ряды
|
Кендалл М.,
Стьюарт А.
|
| Дисперсионный анализ
|
Шеффе Г.
|
| Многомерный дисперсионный анализ
|
Аренс Х., Лейтер Ю.
|
| Нелинейное оценивание параметров
|
Бард Й.
|
| Стохастические модели социальных процессов
|
Бартоломью Д.
|
| Математическая статистика вып.1,2
|
Бикел П., Доксам М.
|
| Методы анализа данных
|
Дидэ Э. , …
|
| Прикладной регрессионный анализ кн. 1,2
|
Дрейпер Н., Смит Г.
|
| Факторный анализ
|
Иберла К.
|
| Статический анализ неэкспериментальных данных
|
Лимер Э.
|
| Анализ данных и регресия вып.1,2
|
МостеллерФ.ТьюкиДж
|
| Динамическая регрессия: теория и алгоритмы
|
Песаран М., Слейтер Л.
|
| Анализ данных типа времени жизни
|
Кокс Д.Р., Оукс Д.
|
| Факторный анализ с обобщениями
|
Благуш П.
|
Методы непараметрической статистики
| Теория ранговых критериев
|
Гаек Я., Шидак З.
|
| Математические методы в социальных науках
|
Лазарсфельд П.,
Генри Н.
|
| Ранговые корреляции
|
Кэндэл М.
|
| Непараметрические методы статистики
|
Тюрин Ю.Н.
|
| Справочник по непараметрической статистике
|
Рунион Р.
|
| Непараметрические методы статистики
|
Холлендер М., Вулф Д.
|
| Многомерное шкалирование
|
Дейвисон М.
|
Вопросы прикладной статистики
| Таблицы математической статистики
|
Большев Л.Н.,
Смирнов Н.В.
|
| Теория вероятностей, математическая статистика, статистический контроль
|
Шторм Р.
|
| Прикладная Статистика: Основы моделирования и обработка данных
|
Айвазян С.А. и др.
|
| Вычислительные алгоритмы в прикладной статистике
|
Мэйндоналд Дж.
|
| Справочник по прикладной статистике т.1
|
Ллойд Э., Ледерман У.
|
| Справочник по прикладной статистике т.2
|
Ллойд Э., Ледерман У.
|
Экспертные оценки
| Математико-статистические методы экспертных оценок
|
Бешелев С.Д.,
Гурвич Ф.Г.
|
| Руководство по экспертным системам
|
Уотермен Д.
|
| Экспертные оценки в педаг. исследованиях
|
Черепанов В.С.
|
Оглавление
1. Особенности системного подхода к решению задач управления...........................
1.1 Общие понятия теории систем и системного анализа.............................................
1.2 Сущность и принципы системного подхода............................................................
1.3 Проблемы согласования целей...................................................................................
1.4 Проблемы оценки связей в системе...........................................................................
1.5 Пример системного подхода к задаче управления...................................................
1.6 Моделирование как метод системного анализа......................................................
1.7 Процессы принятия управляющих решений..........................................................
2. Основные понятия математической статистики.................................................
2.1 Случайные события и величины, их основные характеристики.........................
2.2 Взаимосвязи случайных событий............................................................................
2.3 Схемы случайных событий и законы распределений случайных величин........
2.4 Методы непараметрической статистики.................................................................
2.5 Корреляция случайных величин..............................................................................
2.6 Линейная регрессия...................................................................................................
2.7 Элементы теории статистических решений...........................................................
3. Этапы системного анализа..........................................................................................
3.1 Общие положения......................................................................................................
3.2 Содержательная постановка задачи.........................................................................
3.3 Построение модели изучаемой системы в общем случае......................................
3.4 Моделирование в условиях определенности..........................................................
3.5 Наличие нескольких целей — многокритериальность системы.......................
3.6 Экспертные оценки, ранговая корреляция и конкордация...................................
3.7 Моделирование системы в условиях неопределенности......................................
3.8 Моделирование систем массового обслуживания.................................................
3.9 Моделирование в условиях противодействия, игровые модели..........................
3.10 Моделирование в условиях противодействия, модели торгов...........................
3.11 Методы анализа больших систем, планиров. экспериментов.............................
3.12 Методы анализа больших систем, факторный анализ......................................
4. От автора.........................................................................................................................
5. Литература......................................................................................................................
5.1 Теория систем и системный анализ.........................................................................
5.2 Общие вопросы математики.....................................................................................
5.3 Математическая статистика.............................................................................
[ГАсГ1]
|