Методы и алгоритмы построения элементов систем
статистического моделирования
Содержание
Введение
1. Метод статистического моделирования систем
2. Моделирование случайных величин и процессов
3. Основные понятия марковских процессов
4. Математический аппарат дискретных марковских цепей
Введение
В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно это относится к сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации.
Метод моделирования широко применяют в таких областях, как автоматизация проектирования и организации в автоматизированных системах научных исследований, в системах исследования и проектирования, в системах массового обслуживания, анализ различных сторон деятельности человека, автоматизированное управление производственными и другими процессами. Важно подчеркнуть, что моделирование используется при проектировании, создании, внедрении, эксплуатации систем, а также на различных уровнях их изучения, начиная от анализа работы элементов и кончая исследованием системы в целом при их взаимодействии с окружающей средой.
1. Метод статистического моделирования систем
На этапе исследования и проектирования систем при построении и реализации машинных моделей (аналитических и имитационных) широко используется метод статистического моделирования (Монте-Карло), который базируется на использовании случайных чисел, т.е. возможных значений некоторой случайной величины с заданным распределением вероятностей. Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемой системе. Для получения представляющих интерес оценки характеристик моделируемой системы S
с учетом воздействий внешней среды Е
статистические данные обрабатываются и классифицируются с использованием методов математической статистики,
Сущность метода статистического моделирования сводится к построению для процесса функционирования исследуемой системы S
некоторого моделирующего алгоритма, имитирующего поведение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды Е,
и реализации этого алгоритма с использованием программно-технических средств ЭВМ.
Реклама

Различают две области применения метода статистического моделирования:
- для изучения стохастических систем;
- для решения детерминированных задач.
Основной идеей, которая используется для решения детерминированных задач методом статистического моделирования, является замена детерминированной задачи эквивалентной схемой некоторой стохастической системы, выходные характеристики последней совпадают с результатом решения детерминированной задачи. При такой замене погрешность уменьшается с увеличением числа испытаний (реализации моделирующего алгоритма) N.
В результате статистического моделирования системы S
получается серия частных значений искомых величин или функций, статистическая обработка которых позволяет получить сведения о поведении реального объекта или процесса в произвольные моменты времени. Если количество реализации N
достаточно велико, то полученные результаты моделирования системы приобретают статистическую устойчивость и с достаточной точностью могут быть приняты в качестве оценок искомых характеристик процесса функционирования системы S.
При статистическом моделировании систем одним из основных вопросов является учет стохастических воздействий. Количество случайных чисел, используемых для получения статистически устойчивой оценки характеристики процесса функционирования системы S
при реализации моделирующего алгоритма на ЭВМ, колеблется в достаточно широких пределах в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. Для метода статистического моделирования на ЭВМ характерно, что большое число операций, а соответственно большая доля машинного времени расходуются на действия со случайными числами. Кроме того, результаты статистического моделирования существенно зависят от качества исходных (базовых) последовательностей случайных чисел. Поэтому наличие простых и экономичных способов формирования последовательностей случайных чисел требуемого качества во многом определяет возможность практического использования машинного моделирования системы.
Понятие “статистическое моделирование” тесно связано с понятием “метод Монте-Карло” и почти ему тождественно.
Для решения задач методом Монте-Карло необходимо получать на ЭВМ последовательность выборочных значений случайной величины с заданным распределением. Такой процесс принято называть моделированием случайной величины. Случайные величины обычно моделируют с помощью преобразований одного или нескольких независимых значений случайной величины а, равномерно распределенной в интервале (0,1). Независимые случайные величины, равномерно распределенные в интервале (0,1).
Реклама

Можно выделить следующие этапы моделирования случайных величин:
· генерирование N
реализации случайной величины с требуемой функцией распределения;
· преобразование полученной величины, определяемой математической моделью;
· статистическая обработка реализации.
Особенностью первого этапа является то, что все методы для получения заданного распределения используют преобразование равномерно распределенной величины.
Конструктивно задаются случайная величина, равномерно распределенная в интервале (0,1),  (0,l), далее производится отображение (0,l), далее производится отображение   и получается новая случайная величина и получается новая случайная величина  с распределением, определяемым решаемой задачей, в общем случае с распределением, определяемым решаемой задачей, в общем случае  может быть довольно сложным. может быть довольно сложным.
Далее следует получение некоторых характеристик. При параметрических оценках вычисляется некоторая функция  . При непараметрическом задании функций распределения обычно вычисляются плотности или функции распределения. Чаще всего находят оценки математической ожидания. Погрешность оценки определяется дисперсией (если она известна) по числу экспериментов N. . При непараметрическом задании функций распределения обычно вычисляются плотности или функции распределения. Чаще всего находят оценки математической ожидания. Погрешность оценки определяется дисперсией (если она известна) по числу экспериментов N.
В результате можно выделить следующие этапы (рис. 4.1):
- подготовка исходных данных (блок 1),
- генерирование равномерно распределенных случайных чисел (блок 2),
- преобразования для получения заданного закона распределения (блок 3);
- выполнение дополнительных преобразований в соответствии с проблем ной областью (блок 4);
- статистическая обработка (блок 5).Рис. 4.1. Технологический процесс в Монте-Карло системах
где:
- ПИД - подготовка исходных данных,
- ГРРСЧ - генерирование равномерно распределенных случайных чисел;
- ГПЗ - генерирование произвольного (заданного) закона распределения;
- ДПр - дополнительные преобразования;
- СО - статистическая обработка.
Имитационные системы имеют следующие функциональные блоки:
- имитации входных процессов;
- имитации правил переработки входной информации исследуемой системы;
- накопления информации в результате моделирования;
- анализа накопленной информации;
- управления имитирующей системы.
Традиционный подход использует все классы задач, что и в методе Монте-Карло. Рассмотрим подробнее аналитический подход задания экзогенных переменных (первый случай). Они являются выходными другой подсистемы макросистемы и сами представляют собой макромодель. В рассматриваемом случае характеристики заданы аналитически.
Информационно технологическая блок-схема представлена на рис. 4.2.
Рис. 4.2. Технологический процесс имитационной системы
ГСП - генерирование случайных (входных) процессов;
ИС - имитационная система.
На первом этапе находят наиболее подходящие методы и алгоритмы для описания аналитических функций распределения и проводят вычисления (блок 1) для определения исходных данных, например, при аппроксимационных методах - координаты узлов, коэффициентов и т.п.
Во втором и третьем блоках производится генерирование случайных чисел с равномерным распределением x, и экзогенных случайных процессов z.
Блок 4 имитирует работу исследуемой системы, результаты его работы накапливаются для последующей статистической обработки. В последнем, пятом, блоке осуществляется статистическая обработка.
При моделировании систем на ЭВМ программная имитация случайных воздействий любой сложности сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. В качестве базового может быть принят любой удобный в случае моделирования конкретной системы S процесс (например, пуассоновский поток при моделировании Q-схемы). Однако при дискретном моделировании базовым процессом является последовательность чисел  , представляющих собой реализации независимых, равномерно распределенных на интервале (0,1) случайных величин , представляющих собой реализации независимых, равномерно распределенных на интервале (0,1) случайных величин  или – в статистических терминах- повторную выборку из равномерно распределенной на (0,1) генеральной совокупности значений величины x. или – в статистических терминах- повторную выборку из равномерно распределенной на (0,1) генеральной совокупности значений величины x.
Непрерывная случайная величина x имеет равномерное распределение в интервале (а,b), если ее функция плотности (рис. 4.3,а) и распределение (рис. 4.3,6) соответственно примут вид:
Рис. 4.3. Равномерное распределение случайной величины
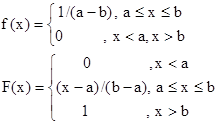
2. Моделирование случайных величин и процессов
Под статистическим моделированием понимается воспроизведение с помощью ЭВМ функционирования вероятностной модели некоторого объекта.
Задачи статистического моделирования состоят в том, чтобы научиться воспроизводить с помощью ЭВМ поведение таких моделей, например:
- с помощью специальных методов и средств вырабатывать программы реализации случайных чисел;
- с помощью этих чисел получать реализацию случайных величин или случайных процессов с более сложными законами распределения;
- с помощью полученных реализации вычислять значения величин, характеризующих модель, и производить обработку результатов экспериментов;
Устанавливать связь алгоритмов моделирования с алгоритмами решения задач вычислительной математики с помощью метода Монте-Карло и строить так называемые “фиктивные” модели, т.е. модели, не имеющие связи с объектом моделирования, но удобные в вычислительном отношении и позволяющие вычислять нужные нам характеристики объекта.
Моделирование случайных процессов строится на основе базовых распределений случайных величин.
Одним из таких процессов является марковские процессы.
3. Основные понятия марковских процессов
Марковские случайные процессы названы по имени выдающегося русского математика А.А. Маркова (1856-1922), впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать “динамикой вероятностей”. В дальнейшем основы этой теории явились исходной базой общей теории случайных процессов, а также таких важных прикладных наук, как теория диффузионных процессов, теория надежности, теория массового обслуживания и т.д. В настоящее время теория марковских процессов и ее приложения широко применяются в самых различных областях таких наук, как механика, физика, химия и др.
Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений особое внимание марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений.
Несмотря на указанную выше простоту и наглядность, практическое применение теории марковских цепей требует знания некоторых терминов и основных положений, на которых следует остановиться перед изложением примеров.
Как указывалось, марковские случайные процессы относятся к частным случаям случайных процессов (СП). В свою очередь, случайные процессы основаны на понятии случайной функции (СФ).
Случайной функцией называется функция, значение которой при любом значении аргумента является случайной величиной (СВ). По- иному, СФ можно назвать функцию, которая при каждом испытании принимает какой-либо заранее неизвестный вид.
Такими примерами СФ являются: колебания напряжения в электрической цепи, скорость движения автомобиля на участке дороги с ограничением скорости, шероховатость поверхности детали на определенном участке и т.д.
Как правило, считают, что если аргументом СФ является время, то такой процесс называют случайным. Существует и другое, более близкое к теории принятия решений, определение СП. При этом под случайным процессом понимают процесс случайного изменения состояний какой-либо физической или технической системы по времени или какому-либо другому аргументу.
Нетрудно заметить, что если обозначить состояние 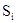 и изобразить зависимость и изобразить зависимость 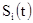 , то такая зависимость и будет случайной функцией. , то такая зависимость и будет случайной функцией.
СП классифицируются по видам состояний 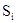 и аргументу t. При этом СП могут быть с дискретными или непрерывными состояниями или временем. Например, любой выборочный контроль продукции будет относиться к СП с дискретными состояниями ( и аргументу t. При этом СП могут быть с дискретными или непрерывными состояниями или временем. Например, любой выборочный контроль продукции будет относиться к СП с дискретными состояниями (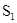 - годная, - годная, 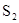 - негодная продукция) и дискретным временем ( - негодная продукция) и дискретным временем (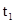 , , 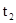 - времена проверки). С другой стороны, случай отказа любой машины можно отнести к СП с дискретными состояниями, но непрерывным временем. Проверки термометра через определенное время будут относиться к СП с непрерывным состоянием и дискретным временем. В свою очередь, например, любая осциллограмма будет записью СП с непрерывными состояниями и временем. - времена проверки). С другой стороны, случай отказа любой машины можно отнести к СП с дискретными состояниями, но непрерывным временем. Проверки термометра через определенное время будут относиться к СП с непрерывным состоянием и дискретным временем. В свою очередь, например, любая осциллограмма будет записью СП с непрерывными состояниями и временем.
Кроме указанных выше примеров классификации СП существует еще одно важное свойство. Это свойство описывает вероятностную связь между состояниями СП. Так, например, если в СП вероятность перехода системы в каждое последующее состояние зависит только от предыдущего состояния, то такой процесс называется процессом без последействия (рис.1).
Зависимость 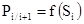 называют переходной вероятностью, часто говорят, что именно процесс называют переходной вероятностью, часто говорят, что именно процесс без последействия обладает марковским свойством, однако, строго говоря, здесь есть одна неточность. Дело в том, что можно представить себе СП, в котором вероятностная связь существует не только с предшествующими, но и более ранними ( без последействия обладает марковским свойством, однако, строго говоря, здесь есть одна неточность. Дело в том, что можно представить себе СП, в котором вероятностная связь существует не только с предшествующими, но и более ранними (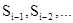 ) состояниями, т.е. ) состояниями, т.е.
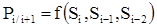 (1) (1)Рис. 1. Схема процесса без последействия
Такие процессы также рассматривались А.А. Марковым, который предложил называть их в отличие от первого случая (простой цепи) - сложной цепью. В настоящее время теория таких цепей разработана слабо и обычно применяют так называемый процесс укрупнения состояний путем математических преобразований, объединяя предшествующие состояния в одно.
Это обстоятельство должно обязательно учитываться при составлении математических моделей принятия решений.
Выше мы совершили незаметный терминологический переход от понятия СП к “марковской цепи”. Теперь эту неясность следует устранить. Отметим, во-первых, что случайный процесс с дискретными состояниями и временем называется случайной последовательностью.
Если случайная последовательность обладает марковским свойством, то она называется цепью Маркова.
С другой стороны, если в случайном процессе состояния дискретны, время непрерывно и свойство последействия сохраняется, то такой случайный процесс называется марковским процессом с непрерывным временем.
Марковский СП называется однородным, если переходные вероятности 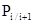 остаются постоянными в ходе процесса. остаются постоянными в ходе процесса.
Цепь Маркова считается заданной, если заданы два условия.
1. Имеется совокупность переходных вероятностей в виде матрицы:
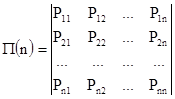 . (2) . (2)
2. Имеется вектор начальных вероятностей
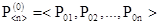 , ….. (3) , ….. (3)
описывающий начальное состояние системы.
Матрица (2) называется переходной матрицей (матрицей перехода). Элементами матрицы являются вероятности перехода из i-го в j-е состояние за один шаг процесса. Переходная матрица (2) обладает следующими свойствами:
a) 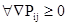 , (3a) , (3a)
б) 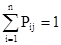 . .
Матрица, обладающая свойством (3a), называется стохастической. Кроме матричной формы модель марковской цепи может быть представлена в виде ориентированного взвешенного графа (рис. 2).
Рис. 2. Ориентированный взвешенный граф
Вершины графа обозначают состояние 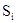 , а дуги- переходные вероятности. , а дуги- переходные вероятности.
Множество состояний системы марковской цепи, определенным образом классифицируется с учетом дальнейшего поведения системы.
1. Невозвратное множество
(рис. 3).
Рис. 3. Невозвратное множество
В случае невозвратного множества возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может вернуться в него.
2. Возвратное множество
(рис. 4).
Рис. 4. Возвратное множествоВ этом случае также возможны любые переходы внутри множества. Система может войти в это множество, но не может покинуть его.
3. Эргодическое множество
(рис. 5).
Рис. 5. Эргодическое множество
В случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него.
4. Поглощающее множество
(рис. 6)
Рис. 6. Поглощающее множество
При попадании системы в это множество процесс заканчивается.
Кроме описанной выше классификации множеств различают состояния системы:
а) существенное состояние
(рис.7): возможны переходы из 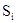 в в 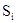 и обратно. и обратно.Рис. 7. Существенное состояние
б) несущественное состояние
(рис. 8): возможен переход из 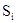 в в 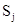 , но невозможен обратный. , но невозможен обратный.
Рис. 8. Несущественное состояние
В некоторых случаях, несмотря на случайность процесса, имеется возможность до определенной степени управлять законами распределения или параметрами переходных вероятностей. Такие марковские цепи называются управляемыми. Очевидно, что с помощью управляемых цепей Маркова (УЦМ) особенно эффективным становится процесс принятия решений, о чем будет сказано впоследствии.
Основным признаком дискретной марковской цепи (ДМЦ) является детерминированность временных интервалов между отдельными шагами (этапами) процесса. Однако часто в реальных процессах это свойство не соблюдается и интервалы оказываются случайными с каким-либо законом распределения, хотя марковость процесса сохраняется. Такие случайные последовательности называются полумарковскими.
Кроме того, с учетом наличия и отсутствия тех или иных, упомянутых выше, множеств состояний марковские цепи могут быть поглощающими, если имеется хотя бы одно поглощающее состояние, или эргодическими, если переходные вероятности образуют эргодическое множество.
В свою очередь, эргодические цепи могут быть регулярными или циклическими. Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (циклов) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают. Если просуммировать все вышесказанные определения, то можно дать следующую классификацию марковских процессов (рис. 9):
Рис. 9. Классификация марковских процессов
4. Математический аппарат дискретных марковских цепей
В дальнейшем рассматриваются простые однородные марковские цепи с дискретным временем. Основным математическим соотношением для ДМЦ является уравнение, с помощью которого определяется состояние системы на любом ее k-м шаге. Это уравнение имеет вид:
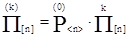 (4) (4)
и называется уравнением Колмогорова-Чепмена
.
Уравнение Колмогорова-Чепмена относится к классу рекуррентных соотношений, позволяющих вычислить вероятность состояний марковского случайного процесса на любом шаге (этапе) при наличии информации о предшествующих состояниях.
Дальнейшие математические соотношения зависят от конкретного вида марковской цепи.
4.1. Поглощающие марковские цепи
Как указывалось выше, у поглощающих ДМЦ имеется множество, состоящее из одного или нескольких поглощающих состояний.
Для примера рассмотрим переходную матрицу, описывающую переходы в системе, имеющей 4 возможных состояния, два из которых являются поглощающими. Матрица перехода такой цепи будет иметь вид:
 (5) (5)
Практически важным является вопрос о том, сколько шагов сможет пройти система до остановки процесса, то есть поглощения в том или ином состоянии. Для получения дальнейших соотношений путем переименования состояний матрицу (8.5) переводят к блочной форме:
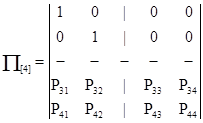 (6) (6)

Такая форма позволяет представить матрицу (6) в каноническом виде:
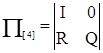 (6а) (6а)
где 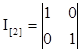 - единичная матрица; - единичная матрица;
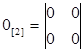 - нулевая матрица; - нулевая матрица;
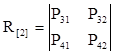 - матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество; - матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество;
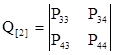 - матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний. - матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний.
На основании канонической формы (6а) получена матрица, называемая фундаментальной:
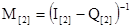 (7) (7)
В матрице (7) символ (-1) означает операцию обращения, то есть
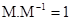 (8) (8)
После соответствующих преобразований матрица (7) примет вид:
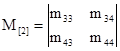 (7а) (7а)
Каждый элемент матрицы (7а) соответствует среднему числу раз попадания системы в то или иное состояние до остановки процесса (поглощения).
Если необходимо получить общее среднее количество раз попадания системы в то или иное состояние до поглощения, то фундаментальную матрицу М необходимо умножить справа на вектор-столбец, элементами которого будут единицы, то есть
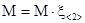 (8а) (8а)
где 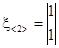 . .
Для иллюстрации приведем конкретный числовой пример: пусть известны значения переходных вероятностей матрицы 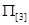 с одним поглощающим состоянием: с одним поглощающим состоянием: 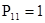 ; ; 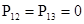 ; ; 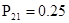 ; ; 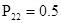 ; ; 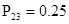 ; ; 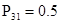 ; ; 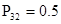 ; ; 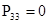 . .
Переходная матрица в блочной системе будет выглядеть так:
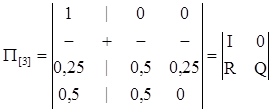
В данном случае
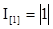 ; ; 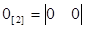 ; ; 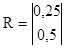 ; ; 
Проделаем необходимые вычисления:
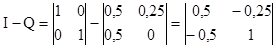 ; ;
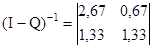 ; ;
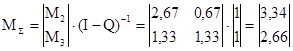 . .
В данном случае компоненты вектора 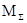 означают, что если процесс начинается с состояния означают, что если процесс начинается с состояния 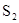 , то общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния , то общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния 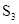 , то - 2,26. , то - 2,26.
В конкретных задачах, конечно, более информативным результатом будет не количество шагов, а какие-либо временные или экономические показатели. Этот результат легко получить, если связать пребывание в каждом состоянии с соответствующими характеристиками. Очевидно, набор этих характеристик составит вектор, на который нужно умножить 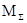 слева. слева.
Так, если задать в нашем примере время пребывания в состоянии 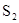 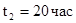 , а в состоянии , а в состоянии 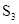 - - 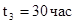 , то общее время до поглощения будет равно: , то общее время до поглощения будет равно:
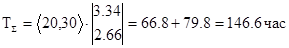
В случаях, когда марковская цепь включает несколько поглощающих состояний, возникают такие вопросы: в какое из поглощающих состояний цепь попадет раньше (или позже); в каких из них процесс будет останавливаться чаще, а в каких - реже? Оказывается, ответ на эти вопросы легко получить, если снова воспользоваться фундаментальной матрицей.
Обозначим через 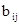 вероятность того, что процесс завершится в некотором поглощающем состоянии вероятность того, что процесс завершится в некотором поглощающем состоянии 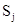 при условии, что начальным было состояние при условии, что начальным было состояние 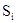 . Множество состояний . Множество состояний 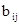 снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы - всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом: снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы - всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом:
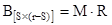 (8.9) (8.9)
где
М - фундаментальная матрица с размерностью S;
R - блок фундаментальной матрицы с размерностью r.
Рассмотрим конкретный пример системы с четырьмя состояниями 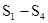 , два из которых- , два из которых- 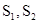 - поглощающие, а два - - поглощающие, а два - 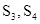 - невозвратные (рис.10): - невозвратные (рис.10):Рис. 8.10. Система с четырьмя состояниями
Для наглядности и простоты вычислений обозначим переходные вероятности следующим образом:
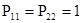 ; ; 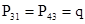 ; ; 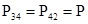
Остальные значения вероятностей будут нулевыми. Каноническая форма матрицы перехода в этом случае будет выглядеть так:
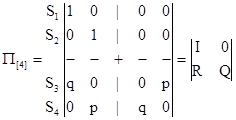
Фундаментальная матрица после вычислений примет вид:
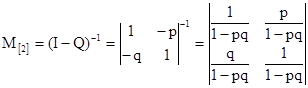
Тогда, согласно формуле (9), матрица вероятностей поглощения вычисляется так:
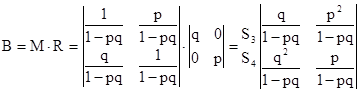 . .
Поясним вероятностный смысл полученной матрицы с помощью конкретных чисел. Пусть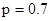 , а , а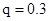 . Тогда после подстановки полученных значений в матрицу . Тогда после подстановки полученных значений в матрицу 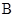 получим: получим:
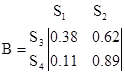
Таким образом, если процесс начался в 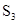 , то вероятность попадания его в , то вероятность попадания его в 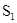 равна равна 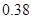 , а в , а в 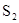 - - 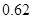 . Отметим одно интересное обстоятельство: несмотря на то, что, казалось бы, левое поглощающее состояние (“левая яма”) находится рядом с . Отметим одно интересное обстоятельство: несмотря на то, что, казалось бы, левое поглощающее состояние (“левая яма”) находится рядом с 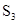 , но вероятность попадания в нее почти в два раза меньше, чем в “удаленную яму” - , но вероятность попадания в нее почти в два раза меньше, чем в “удаленную яму” - 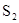 . Этот интересный факт подмечен в теории ДМЦ, и объясняется он тем, что . Этот интересный факт подмечен в теории ДМЦ, и объясняется он тем, что 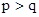 , то есть процесс имеет как бы “правый уклон”. Рассмотренная выше модель называется в теории ДМЦ моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр. , то есть процесс имеет как бы “правый уклон”. Рассмотренная выше модель называется в теории ДМЦ моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр.
В частности, в рассмотренном примере объясняется тот факт, что более сильный игрок может дать заранее значительное преимущество (“фору”) слабому противнику и все равно его шансы на выигрыш будут более предпочтительными.
Кроме указанных выше средних характеристик вероятностного процесса с помощью фундаментальной матрицы можно вычислить моменты и более высоких порядков. В частности, дисперсия числа пребывания в том или ином состоянии - D определяется с помощью следующей матрицы:
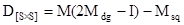 (10) (10)
где
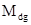 - диагональная матрица, т.е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (7а) будет иметь вид: - диагональная матрица, т.е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (7а) будет иметь вид:
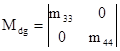
В свою очередь, матрица М представляет собой матрицу, полученную из М путем возведения в квадрат каждого ее элемента, то есть для (7а) будем иметь:
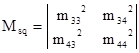
Аналогичным образом определяема и дисперсия для общего количества раз пребывания в том или ином состоянии 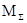 . Обозначим ее . Обозначим ее 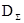 : :
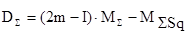 (11) (11)
4.2. Эргодические цепи
Как указывалось выше под эргодической ДМЦ понимается цепь, не имеющая невозвратных состояний. Таким образом, в такой цепи возможны любые переходы между состояниями. Напомним, что эргодические цепи могут быть регулярными и циклическими. Ранее определение таких цепей было дано.
Поскольку согласно данному выше определению в эргодической ДМЦ на любом шаге должны быть возможными любые переходы, то очевидно при этом, что переходные вероятности не должны равняться нулю. Оказывается, из этого условия вытекают некоторые замечательные свойства регулярных ДМЦ:
1. Степени 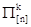 при при 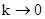 стремятся к стохастической матрице стремятся к стохастической матрице 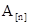 . .
2. Каждая строка матрицы 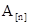 представляет один и тот же вероятностный вектор представляет один и тот же вероятностный вектор
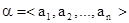 (12) (12)
все компоненты которого положительны.
Вектор (12) в теории ДМЦ занимает особое место из-за наличия многих приложений и называется вектором предельных или финальных вероятностей (иногда - стационарным вектором). Финальные вероятности определяют с помощью векторно-матричного уравнения
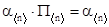 (13) (13)
которое в развернутом виде будет выглядеть так:
 (13а) (13а)
К уравнениям (8.13а) можно дополнительно добавить условие нормировки:
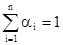 (14) (14)
Тогда любое из уравнений в (8.14) можно исключить.
Так же, как и в случае поглощения ДМЦ многие характеристики эргодических цепей определяются с помощью фундаментальной матрицы, которая в этом случае будет иметь вид:
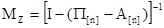 (15) (15)
Для эргодических цепей характеристикой, имеющей важное практическое значение, является продолжительность времени, за которое процесс из состояния 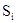 впервые попадает в впервые попадает в 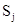 , так называемое время первого достижения. Матрица средних времен достижения определяется по формуле: , так называемое время первого достижения. Матрица средних времен достижения определяется по формуле:
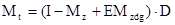 (16) (16)
где
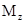 - фундаментальная матрица (15); - фундаментальная матрица (15);
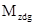 - диагональная матрица, образованная из фундаментальной заменой всех элементов, кроме диагональных, нулями; - диагональная матрица, образованная из фундаментальной заменой всех элементов, кроме диагональных, нулями;
D - диагональная матрица с диагональными элементами, 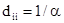 ; ;
Е - матрица, все элементы которой равны единице.
Матрица дисперсий времени первого достижения имеет несколько более сложный вид:
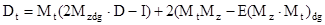 (17) (17)
где кроме уже упомянутых обозначений встречается новое - (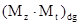 , обозначающее диагональную матрицу, полученную из матричного произведения матриц , обозначающее диагональную матрицу, полученную из матричного произведения матриц 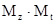 . .
4.3. Управляемые марковские цепи
Как указывалось выше, под управляемыми марковскими процессами понимают такие, у которых имеется возможность до определенной степени управлять значениями переходных вероятностей. В качестве примеров таких процессов можно привести любые торговые операции, у которых вероятность сбыта и получения эффекта может зависеть от рекламы, мероприятий по улучшению качества, выбора покупателя или рынка сбыта и т.д.
Очевидно, что при создании математических моделей в данном случае должны фигурировать следующие компоненты:
- конечное множество решений (альтернатив) 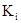 , где , где 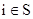 - номер состояния системы; - номер состояния системы;
- матрицы переходов 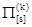 соответствующие тому или иному принятому k-му решению; соответствующие тому или иному принятому k-му решению;
- матрицы доходов (расходов) 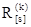 , также отражающие эффективность данного решения. , также отражающие эффективность данного решения.
Управляемой цепью Маркова (УЦМ) называется случайный процесс, обладающий марковским свойством и включающий в качестве элемента математической модели конструкцию (кортеж) 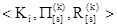 . Решение, принимаемое в каждый конкретный момент (шаг процесса), назовем частным управлением. . Решение, принимаемое в каждый конкретный момент (шаг процесса), назовем частным управлением.
Таким образом, процесс функционирования системы, описываемой УЦМ, выглядит следующим образом:
- если система находится в состоянии 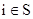 и принимается решение и принимается решение 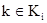 , то она получает доход , то она получает доход 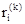 ; ;
- состояние системы в последующий момент времени (шаг) определяется вероятностью 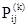 , то есть существует вероятность того, что система из состояния , то есть существует вероятность того, что система из состояния 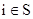 перейдет в состояние перейдет в состояние 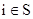 , если выбрано решение , если выбрано решение 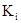 . .
Очевидно, общий доход за n шагов является случайной величиной, зависящей от начального состояния и качества принимаемых в течение хода процесса решений, причем это качество оценивается величиной среднего суммарного дохода (при конечном времени) или среднего дохода за единицу времени (при бесконечном времени).
Стратегией
p называется последовательность решений:
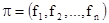 (18) (18)
где
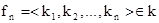 - вектор управления. - вектор управления.
Задание стратегии означает полное описание конкретных решений, принимаемых на всех шагах процесса в зависимости от состояния, в котором находится в этот момент процесс.
Если в последовательности (векторе) p все 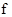 одинаковы, то такая стратегия называется стационарной
, т.е. не зависящей от номера шага. Стратегия одинаковы, то такая стратегия называется стационарной
, т.е. не зависящей от номера шага. Стратегия 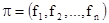 называется марковской
, если решение называется марковской
, если решение 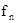 , принимаемое в каждом конкретном состоянии, зависит только от момента времени n, но не зависит от предшествующих состояний. , принимаемое в каждом конкретном состоянии, зависит только от момента времени n, но не зависит от предшествующих состояний.
Оптимальной будет такая стратегия, которая максимизирует полный ожидаемый доход для всех i и n. В теории УМЦ разработаны два метода определения оптимальных стратегий: рекуррентный
и итерационный
.
Первый, рекуррентный, метод применяется чаще всего при сравнительно небольшом числе шагов n. Его идея основана на применении принципа Беллмана и заключается в последовательной оптимизации дохода на каждом шаге с использованием рекуррентного уравнения следующего вида:
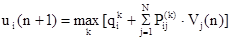 (19) (19)
где
 - полный ожидаемый доход; - полный ожидаемый доход;
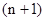 шагов, если система находится в состоянии i; шагов, если система находится в состоянии i;
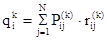 - непосредственно ожидаемый доход, т.е. доход на одном шаге, если процесс начался с i-го состояния; - непосредственно ожидаемый доход, т.е. доход на одном шаге, если процесс начался с i-го состояния;
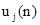 - величина полного ожидаемого дохода за n прошедших шагов, если процесс начинался с j-го состояния (i¹j). - величина полного ожидаемого дохода за n прошедших шагов, если процесс начинался с j-го состояния (i¹j).
Таким образом, данный метод, по существу, аналогичен методу динамического программирования, отличием является лишь то, что на каждом шаге учитывается вероятность попадания системы в то или иное состояние. Поэтому этот метод называют стохастическим динамическим программированием.
Конкретное применение метода будет рассмотрено далее на примере.
Второй - итерационный метод оптимизации применяется при неограниченном числе этапов (шагов) процесса. Этот метод использует свойство эргодичности марковской цепи и заключается в последовательном уточнении решения путем повторных расчетов (итераций). При этих уточнениях находят решение, обеспечивающее в среднем минимум дохода при большом числе шагов. Оно уже не будет зависеть от того, на каком шаге производится оценка оптимальной стратегии, то есть является справедливым для всего процесса, независимо от номера шага. Важным достоинством метода является, кроме того, и то, что он дает возможность определить момент прекращения дальнейших уточнений.
Главное отличие итерационного метода от рассмотренного ранее, рекуррентного, заключается в том, что в данном случае используется матрица предельных (финальных) вероятностей, где вследствие свойства эргодичности переходные вероятности постоянны на всех шагах процесса. Поскольку матрица доходов состоит также из постоянных, не зависимых от n величин, то можно предположить, что с ростом n общая величина доходов будет возрастать линейно.
Представим графически линейную зависимость суммарного дохода от числа шагов 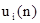 (рис. 11). (рис. 11).
Для наглядности график (см. рис. 11) изображен для УМЦ с двумя состояниями 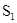 и и 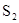 . На графике прямая . На графике прямая 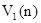 показывает зависимость суммарного дохода, если система “стартовала” из состояния показывает зависимость суммарного дохода, если система “стартовала” из состояния 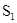 . Соответственно, прямая . Соответственно, прямая 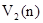 изображает ту же зависимость для состояния изображает ту же зависимость для состояния 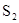 . Обе прямые могут быть описаны линейными уравнениями . Обе прямые могут быть описаны линейными уравнениями 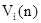 : :
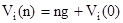 (20) (20)
где
g - угловой коэффициент прямой 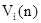 ; ;
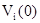 - доход в i-том состоянии в конце процесса. - доход в i-том состоянии в конце процесса.
Легко заметить, что при таком представлении зависимости 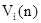 величина непосредственно ожидаемого дохода q (см. формулу (19)) заменяется g. Отличие здесь лишь в том, что g является величиной постоянной для всего процесса, в то время как q меняется на каждом шаге. Величина величина непосредственно ожидаемого дохода q (см. формулу (19)) заменяется g. Отличие здесь лишь в том, что g является величиной постоянной для всего процесса, в то время как q меняется на каждом шаге. Величина 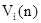 показывает, на сколько в среднем отличается доход, когда процесс заканчивается в том или ином состоянии. В теории марковских цепей показывает, на сколько в среднем отличается доход, когда процесс заканчивается в том или ином состоянии. В теории марковских цепей 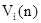 называют весом, так как разница называют весом, так как разница 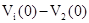 при двух состояниях показывает средний выигрыш от того, в каком состоянии мы находимся в конце процесса (независимо от выбранной стратегии). при двух состояниях показывает средний выигрыш от того, в каком состоянии мы находимся в конце процесса (независимо от выбранной стратегии).

Рис. 11. Зависимость суммарного дохода от числа шагов
Таким образом, подводя итоги общих рассуждений, можно сказать, что свойство эргодичности позволяет нам считать справедливым приближенное равенство:
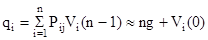 (21) (21)
На этом предположении и основан итерационный метод. Суть его сводится к тому, что при разных стратегиях путем последовательных приближений определяются значения сумм
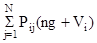 (22) (22)
Таким образом, если ранее (при рекуррентном методе) искалась стратегия, обеспечивающая на каждом шаге максимум суммы непосредственно ожидаемого дохода и дохода на предшествующих шагах, то здесь находится стратегия, обеспечивающая максимум средней прибыли и относительного веса сразу для всего процесса. При этом производятся последовательные расчеты - итерации, на каждом этапе которых уточняются значения угловых коэффициентов и весов, обеспечивающие максимум доходов.
|