Содержание:
Постулаты Евклида
Попытки доказательства V постулата Евклида
Кант об априорных понятиях
Появление неевклидовой геометрии
Янош Бояи.
Геометрия Лобачевского
Непротиворечивость геометрии Лобачевского
Развитие евклидовой геометрии
Список литературы:
Постулаты Евклида
Евклид – автор первого дошедшего до нас строгого логического построения геометрии. В нем изложение настолько безупречно для своего времени, что в течение двух тысяч лет с момента появления его труда “Начал” оно было единственным руководством для изучающих геометрию.
“Начала” состоят из 13 книг, посвященных геометрии и арифметике в геометрическом изложении.
Каждая книга “Начал” начинается определением понятий, которые встречаются впервые. Так, например, первой книге предпосланы 23 определения. В частности,
Определение 1. Точка есть то, что не имеет частей.
Определение 2. Линия есть длины без ширины
Определение 3. Границы линии суть точки.
Вслед за определениями Евклид приводит постулаты и аксиомы, то есть утверждения, принимаемые без доказательства.
Постулаты
I. Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию.
II . И чтобы каждую прямую можно было неопределенно продолжить.
III. И чтобы из любого центра можно было описать окружность любым радиусом.
IV. И чтобы все прямые углы были равны.
V. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние внутренние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.
Аксиомы
I. Равные порознь третьему равны между собой.
II. И если к ним прибавим равные, то получим равные.
III. И если от равных отнимем равные, то получим равные.
IV. И если к неравным прибавим равные, то получим неравные.
V. И если удвоим равные, то получим равные.
VI. И половины равных равны между собой.
VII. И совмещающиеся равны.
VIII. И целое больше части.
IX. И две прямые не могут заключать пространства.
Иногда IV и V постулаты относят к числу аксиом. Поэтому пятый постулат иногда называют XI аксиомой. По какому принципу одни утверждения относятся к постулатам, а другие к аксиомам, неизвестно.
Реклама

Никто не сомневался в истинности постулатов Евклида, что касается и V постулата. Между тем уже с древности именно постулат о параллельных привлек к себе особое внимание ряда геометров, считавших неестественным помещение его среди постулатов. Вероятно, это было связано с относительно меньшей очевидностью и наглядностью V постулата: в неявном виде он предполагает достижимость любых, как угодно далеких частей плоскости, выражая свойство, которое обнаруживается только при бесконечном продолжении прямых.
Попытки доказательства
V постулата Евклида
Возможно, что уже сам Евклид пытался доказать постулат о параллельных. В пользу этого говорит то обстоятельство, что первые 28 предложений “Начал” не опираются на V постулат. Евклид как бы старался отодвинуть применение этого постулата до тех пор, пока использование его не станет настоятельно необходимым.
Одни математики старались доказать постулат о параллельных, применяя только другие постулаты и те теоремы, которые можно вывести из последних, не используя сам V постулат. Все такие попытки оказались неудачными. Их общий недостаток в том, что в доказательстве неявно применялось какое-нибудь предположение, равносильное доказываемому постулату.
Другие предлагали по-новому определить параллельные прямые или же заменить V постулат каким-либо, по их мнению, более очевидным предложением. Так, например, в XI веке Омар Хайям ввел вместо V постулата “принцип”, согласно которому две лежащие в одной плоскости сходящиеся прямые пересекаются и не могут расходиться в направлении схождения. С помощью этого принципа Хайям доказывает, что в четырехугольнике ABCD, в котором углы при основании А и В – прямые и стороны АС, ВD равны, углы С и D так же прямые, а из этого предложения о существовании прямоугольника выводится V постулат. Рассуждения Хайяма получили оригинальное развитие в XIII веке у Насирэдинна ат-Туси, работы которого в свою очередь стимулировали исследования Д. Валлиса. В 1663 году Валлис доказал постулат о параллельных, исходя из явного допущения, что для каждой фигуры существует подобная ей фигура произвольной величины. Это допущение он считал вытекающим из существа пространственных отношений.
С логической точки зрения результаты Хайяма или Валлиса лишь выявляли равносильность V постулата и некоторых других предложений геометрии. Так, Хайям, по существу, установил эквивалентность постулата и предложения о сумме углов треугольника, а Валлис показал, что не только из V постулата можно вывести учение о подобии, но и обратно – их евклидова учения о подобии следует V постулат.
Реклама

Один из обнадеживающих способов подхода к доказательству пятого постулата, которым пользовались многие геометры XVIII и первой половины XIX веков, состоит в том, что пятый постулат заменяется его отрицанием или каким-либо утверждением, эквивалентным отрицанию. Опираясь на измененную таким образом систему постулатов и аксиом, доказываются всевозможные предложения, логически из нее вытекающие. Если пятый постулат действительно вытекает из остальных постулатов и аксиом, то измененная указанным образом система постулатов ми аксиом противоречива. Поэтому рано или поздно мы придем у двум взаимно исключающим выводам. Этим и будет доказан пятый постулат.
Именно таким путем пытались доказать пятый постулат Д. Саккери (1667-1733), И. Г. Ламберт (1728-1777) и А.М. Лежандр (1752-1833).
 Исследования Саккери были опубликованы в 1733 году под названием “Евклид, очищенный от всяких пятен, или опыт, устанавливающий самые первые принципы универсальной геометрии”. Исследования Саккери были опубликованы в 1733 году под названием “Евклид, очищенный от всяких пятен, или опыт, устанавливающий самые первые принципы универсальной геометрии”.
Саккери исходил из рассмотрения четырехугольника  с двумя прямыми углами при основании с двумя прямыми углами при основании и с двумя равными боковыми сторонами и с двумя равными боковыми сторонами  и и  . Из симметрии фигуры относительно перпендикуляра . Из симметрии фигуры относительно перпендикуляра  к середине основания к середине основания  следует, что углы при вершинах следует, что углы при вершинах  и и  равны. Если принять пятый постулат и, следовательно, евклидову теорию параллельных, то можно установить, что углы равны. Если принять пятый постулат и, следовательно, евклидову теорию параллельных, то можно установить, что углы  и и  прямые и прямые и  - прямоугольник. Обратно, как доказывает Саккери, если хотя бы в одном четырехугольнике указанного вида углы при верхнем основании окажутся прямыми, то будет иметь место евклидов постулат о параллельных. Желая доказать этот постулат Саккери делает три возможных предположения: либо углы - прямоугольник. Обратно, как доказывает Саккери, если хотя бы в одном четырехугольнике указанного вида углы при верхнем основании окажутся прямыми, то будет иметь место евклидов постулат о параллельных. Желая доказать этот постулат Саккери делает три возможных предположения: либо углы  и и  прямые, либо тупые, либо острые (гипотезы прямого, острого и тупого угла). Для доказательства пятого постулата необходимо опровергнуть гипотезы острого и тупого угла. Совершенно точными рассуждениями Саккери приводит к противоречию гипотезу тупого угла. Вслед за тем, приняв гипотезу острого угла, он выводит весьма далеко идущие ее следствия с тем, чтобы и здесь получить противоречие. Развивая эти следствия Саккери строит сложную геометрическую систему, не заключая о противоречии только потому, что полученные им выводы не соответствуют привычным представлениям о расположении прямых. В результате он “находит” логическое противоречие, но в результате вычислительной ошибки. прямые, либо тупые, либо острые (гипотезы прямого, острого и тупого угла). Для доказательства пятого постулата необходимо опровергнуть гипотезы острого и тупого угла. Совершенно точными рассуждениями Саккери приводит к противоречию гипотезу тупого угла. Вслед за тем, приняв гипотезу острого угла, он выводит весьма далеко идущие ее следствия с тем, чтобы и здесь получить противоречие. Развивая эти следствия Саккери строит сложную геометрическую систему, не заключая о противоречии только потому, что полученные им выводы не соответствуют привычным представлениям о расположении прямых. В результате он “находит” логическое противоречие, но в результате вычислительной ошибки.
Идеи Ламберта, развитые им в сочинении “теория параллельных линий” (1766г.), близко примыкают к соображениям Саккери.
Он рассматривает четырехугольник с тремя прямыми углами. Относительно четвертого угла так же возникают три гипотезы: этот угол прямой, тупой или острый. Доказав эквивалентность пятого постулата гипотезе прямого угла и сведя к противоречию гипотезу тупого угла, Ламберт, подобно Саккери, вынужден заниматься гипотезой острого угла. Она приводит Ламберта к сложной геометрической системе, в которой ему не удалось встретить логического противоречия. Ламберт нигде в своем сочинении не утверждает, что V постулат им доказан, и приходит к твердому заключению, что и все другие попытки в этом направлении не привели к цели.
“Доказательства евклидова постулата, - пишет Ламберт, - могут быть доведены столь далеко, что остается, по-видимому, ничтожная мелочь. Но при тщательном анализе оказывается, что в этой кажущейся мелочи и заключается вся суть вопроса; обыкновенно она содержит либо доказываемое предложение, либо равносильный ему постулат”.
Более того, развивая систему гипотезы острого угла, Ламберт обнаруживает аналогию этой системы со сферической геометрией и в этом усматривает возможность ее существования.
“Я склонен даже думать, что третья гипотеза справедлива на какой-нибудь мнимой сфере. Должна же быть причина, вследствие которой она на плоскости далеко не поддается опровержению, как это легко может быть сделано со второй гипотезой”.
Лежандр в своем доказательстве пятого постулата рассматривает три гипотезы относительно суммы углов треугольника.
1. Сумма углов треугольника равна двум прямым.
2. Сумма углов треугольника больше двух прямых.
3. Сумма углов треугольника меньше двух прямых.
Он доказал, что первая гипотеза эквивалентна пятому постулату, вторая гипотеза невозможна; и приняв третью гипотезу приходит к противоречию, неявно воспользовавшись в доказательстве пятым постулатом через один из его эквивалентов.
В результате проблема параллельных оставалась к началу XIX века неразрешенной и положение казалось безвыходным. Большой знаток вопроса венгерский математик Фаркаш Бояи в 1820 году писал своему сыну Яношу: “Молю тебя, не делай только и ты попыток одолеть теорию параллельных линий: ты затратишь на это все свое время, а предложения этого вы не докажете все вместе. Не пытайся одолеть теорию параллельных линий ни тем способом, который ты сообщаешь мне, ни каким-либо другим. Я изучил все пути до конца: я не встретил ни одной идеи, которой бы я не разрабатывал. Я прошел весь беспросветный мрак этой ночи, и всякий светоч, всякую радость жизни я в ней похоронил… Этот беспросветный мрак… никогда не прояснится на земле, и никогда несчастный род человеческий не будет владеть чем-либо совершенным даже в геометрии. Это большая и вечная рана в моей душе…”. Беспросветный мрак, о котором с горечью писал старший Бойяи, рассеял Лобачевский и, несколько позднее, Я. Бояи.
Кант об априорных понятиях
В то время многие математики с воодушевлением восприняли философскую теорию Иммануила Канта о человеческом познании. В “Пролегоменах ко всякой будущей метафизике, могущей появиться как наука” (1783) он писал: “Мы можем с достоверностью сказать, что некоторые чистые априорные синтетические познания имеются и нам даны, а именно чистая математика
и чистое естествознание
, потому что оба содержат положения, частью аподиктически достоверные на основе одного только разума, частью же на основе общего согласия из опыта и тем не менее повсеместно признанные независимыми от опыта”.
“Критика чистого разума” (1781) Канта начинается еще более обнадеживающими словами. Кант утверждает, что все аксиомы и теоремы математики истинны. Он говорит, что наш разум сам по себе владеет формами пространства и времени. Пространство и время представляют собой разновидности восприятия (называемые Кантом интуитивными представлениями), посредством которых разум созерцает опыт. Мы воспринимаем, организуем и осознаем опыт в соответствии с этими формами созерцания разум накладывает формы созерцания на полученные им чувственные восприятия, вынуждая те подстраиваться под заложенные в нем схемы. Так как интуитивное представление о пространстве берет свое начало в разуме, некоторые свойства пространства разум автоматически. Такие утверждения, как “прямая – кратчайший путь между двумя точками”, “через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну”, или как постулат Евклида о параллельных, Кант называет априорными искусственными истинами. Они составляют неотъемлемую часть нашего умственного багажа. Геометрия занимается изучением лишь логических следствий из таких утверждений. Уже одно то, что наш разум созерцает опыт через изначально присущие ему “пространственные структуры”, означает, что опыт согласуется с априорными синтетическими истинами и теоремами. Порядок и рациональность, которые мы, как нам кажется, воспринимаем во внешнем мире, в действительности проецируется на внешний мир нашим разумом и формами нашего мышления.
Конструируя пространство на основе работы клеток головного мозга человека, кант не видел причин для отказа от евклидова пространства. Собственную неспособность представить другие геометрии Кант счел достаточным основанием, чтобы утверждать, что другие геометрии не могут существовать.
Появление неевклидовой геометрии
Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в России носит имя Лобачевского, который впервые опубликовал работу с ее изложением.
И одной из предпосылок геометрических открытий Н. И. Лобачевского (1792-1856) был как раз его материалистический подход к проблемам познания. Лобачевский Он был твердо уверен в объективном и не зависящем от человеческого сознания существовании материального мира и в возможности его познания. В речи “О важнейших предметах воспитания” (Казань, 1828) Лобачевский сочувственно приводит слова Ф. Бэкона: “оставьте трудиться напрасно, стараясь извлечь из одного разума всю мудрость; спрашивайте природу, она хранит все истины и на все вопросы ваши будет отвечать вам непременно и удовлетворительно”. В своем сочинении “О началах геометрии”, являющемся первой публикацией открытой им геометрии, Лобачевский писал: “первые понятия, с которых начинается какая-нибудь наука, должны быть ясны и приведены к самому меньшему числу. Тогда только они могут служить прочным и достаточным основанием учения. Такие понятия приобретаются чувствами; врожденным – не должно верить”. Тем самым Лобачевский отвергал идею об априорном характере геометрических понятий, поддерживавшуюся И. Кантом.
Первые попытки Лобачевского доказать пятый постулат относятся к 1823 году. К 1826 году он пришел к убеждению в том, что V постулат не зависит от остальных аксиом геометрии Евклида и 11(23) февраля 1826 года сделал на заседании факультета казанского университета доклад “Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных”, в котором были изложены начала открытой им “воображаемой геометрии”, как он называл систему, позднее получившую название неевклидовой геометрии. Доклад 1826г. вошел в состав первой публикации Лобачевского по неевклидовой геометрии – статьи “О началах геометрии”, напечатанной в журнале Казанского университета “Казанский вестник” в 1829-1820гг. дальнейшему развитию и приложениям открытой им геометрии были посвящены мемуары “Воображаемая геометрия”, “Применение воображаемой геометрии к некоторым интегралам” и “Новые начала геометрии с полной теорией параллельных”, опубликованные в “Ученых записках” соответственно в 1835, 1836 и 1835-1838 гг. Переработанный текст “Воображаемой геометрии” появился во французском переводе в Берлине, там же в 1840г. вышли отдельной книгой на немецком языке “Геометрические исследования по теории параллельных линий” Лобачевского. Наконец, в 1855 и 1856 гг. он издал в Казани на русском и французском языках “Пангеометрию”.
Высоко оценил “Геометрические исследования” Гаусс, который провел Лобачевского (1842) в члены-корреспонденты Геттингенского ученого общества, бывшего по существу Академией наук ганноверского королевства. Однако в печати в оценкой новой геометрической системы Гаусс не выступил.
Исследования Гаусса по неевклидовой геометрии
Высокая оценка гауссом открытия Лобачевского была связана с тем, что Гаусс, еще с 90-х годов XVIII в. занимавшийся теорией параллельности линий ,пришел к тем же выводам, что и Лобачевский. Свои взгляды по этому вопросу Гаусс не публиковал, они сохранились только в его черновых записках и в немногих письмам к друзьям. В 1818 г. в письме к австрийскому астроному Герлингу (1788-1864) он писал: “Я радуюсь, что вы имеете мужество высказаться так, как если бы Вы признавали ложность нашей теории параллельных, а вместе с тем и всей нашей геометрии. Но осы, гнездо которых Вы потревожите, полетят Вам на голову”; по-видимому, под “потревоженными осами” Гаусс имел в виду сторонников традиционных взглядов на геометрию, а также априоризма математических понятий.
Янош Бояи.
Независимо от Лобачевского и гаусса к открытию неевклидовой геометрии пришел венгерский математик Янош Бояи (1802-1860), сын Ф. Бояи.
Когда Я. Бояи пришел к тем же идеям, что Лобачевский и гаусс, отец не понял его, однако предложил напечатать краткое изложение его открытия в виде приложения к своему руководству по математике, вышедшему в 1832г. Полное название труда Я. Бояи – “Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)” и его обычно коротко называют просто “Аппендикс”. Открытие Я. Бояи не было признано при его жизни; Гаусс, которому Ф. Бояи послал "Аппендикс", понял его, но никак не способствовал признанию открытия Я. Бояи.
Геометрия Лобачевского
В мемуаре “О началах геометрии” (1829) Лобачевский прежде всего воспроизвел свой доклад 1826г.
Он определяет основные понятия геометрии, не зависящие от V постулата, и заметив, что сумма углов прямолинейного треугольника не может быть 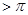 , как это имеет место у сферических треугольников, Лобачевский заявляет: “Мы видели, что сумма углов прямолинейного треугольника не может быть , как это имеет место у сферических треугольников, Лобачевский заявляет: “Мы видели, что сумма углов прямолинейного треугольника не может быть 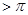 . Остается предполагать эту сумму . Остается предполагать эту сумму 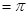 или или 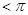 . То и другое может быть принято без всякого противоречия впоследствии, от чего и происходят две Геометрии: одна, употребительная доныне по своей простоте, соглашается со всеми измерениями на самом деле; другая, воображаемая, более общая и потому затруднительная в своих вычислениях, допускает возможность зависимости линий от углов”. . То и другое может быть принято без всякого противоречия впоследствии, от чего и происходят две Геометрии: одна, употребительная доныне по своей простоте, соглашается со всеми измерениями на самом деле; другая, воображаемая, более общая и потому затруднительная в своих вычислениях, допускает возможность зависимости линий от углов”.
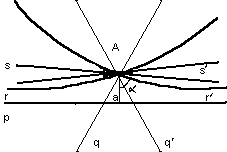 Лобачевский указывает, что в “воображаемой геометрии” сумма углов треугольника всегда Лобачевский указывает, что в “воображаемой геометрии” сумма углов треугольника всегда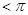 и две прямые могут не пересекаться в случае, когдаони образуют с секущей углы, в сумме меньшие и две прямые могут не пересекаться в случае, когдаони образуют с секущей углы, в сумме меньшие 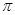 . Параллельные прямые определяются как такие, которые не пересекаются, но могут быть получены предельным переходом из пересекающихся. Через каждую точку плоскости проходят две прямые, параллельные данной прямой, лежащей в этой плоскости; эти прямые делят пучок прямых, проходящих через данную точку, на четыре области, в двух из которых проходят прямые, пересекающие данную прямую, а в двух – прямые, которые не пересекают эту прямую и не могут быть получены предельным переходом из пересекающихся – такие прямые называются расходящимися; параллельные прямые разграничивают пресекающие прямые от расходящихся (на рис. условно изображены прямые . Параллельные прямые определяются как такие, которые не пересекаются, но могут быть получены предельным переходом из пересекающихся. Через каждую точку плоскости проходят две прямые, параллельные данной прямой, лежащей в этой плоскости; эти прямые делят пучок прямых, проходящих через данную точку, на четыре области, в двух из которых проходят прямые, пересекающие данную прямую, а в двух – прямые, которые не пересекают эту прямую и не могут быть получены предельным переходом из пересекающихся – такие прямые называются расходящимися; параллельные прямые разграничивают пресекающие прямые от расходящихся (на рис. условно изображены прямые 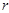 и и 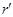 , проведенные через точку А параллельно прямой , проведенные через точку А параллельно прямой 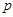 , прямые , прямые 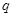 и и 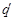 , проведенные через точку А и пресекающие прямую , проведенные через точку А и пресекающие прямую 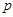 , и прямые , и прямые 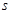 и и 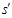 , расходящиеся с прямой , расходящиеся с прямой 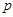 ). Угол ). Угол 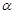 между прямой, проведенной через точку А параллельно прямой между прямой, проведенной через точку А параллельно прямой 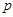 , и перпендикуляром, опущенным из А на , и перпендикуляром, опущенным из А на 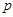 , Лобачевский называет “углом параллельности” и показывает, что функция , Лобачевский называет “углом параллельности” и показывает, что функция 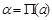 , выражающая зависимость этого угла от длины а
перпендикуляра, может быть (в современных обозначениях) записана в виде , выражающая зависимость этого угла от длины а
перпендикуляра, может быть (в современных обозначениях) записана в виде
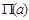 =2arctg =2arctg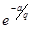 , (1) , (1)
где q
– некоторая постоянная. При а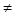 0 угол параллельности всегда острый, причем он стремится к
0 угол параллельности всегда острый, причем он стремится к 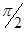 при при 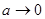 , постоянная же q
может служить на плоскости Лобачевского абсолютной единицей длины, аналогичной абсолютной единицей длины, аналогичной единице угла в евклидовом пространстве. Лобачевский устанавливаеттакже, что расходящиеся прямые обладают общим перпендикуляром и удаляются друг от друга по обе стороны от него, а две параллельные прямые приближаются друг к другу и расстояния точек одной из них от другой стремится к 0 при неограниченном удалении этих точек. Сумма углов треугольника в геометрии Лобачевского всегда меньше , постоянная же q
может служить на плоскости Лобачевского абсолютной единицей длины, аналогичной абсолютной единицей длины, аналогичной единице угла в евклидовом пространстве. Лобачевский устанавливаеттакже, что расходящиеся прямые обладают общим перпендикуляром и удаляются друг от друга по обе стороны от него, а две параллельные прямые приближаются друг к другу и расстояния точек одной из них от другой стремится к 0 при неограниченном удалении этих точек. Сумма углов треугольника в геометрии Лобачевского всегда меньше 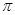 , и если , и если 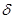 - “угловой дефект” треугольника, то есть разность между - “угловой дефект” треугольника, то есть разность между 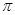 и суммой его углов, то площадь треугольникаS
равна и суммой его углов, то площадь треугольникаS
равна
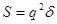 , (2) , (2)
где q
– та же постоянная, что и в формуле (1).
Круг при стремлении его радиуса к бесконечности переходит в системе Лобачевского не в прямую, а в особого рода кривую “предельного круга” - в настоящее время такие кривые называют орициклами. Сфера при тех же обстоятельствах переходит не в плоскость, а в кривую поверхность, которую Лобачевский назвал “предельной сферой”, а в настоящее время именуют орисферой. Лобачевский отмечает, что на орисфере имеет место евклидова геометрия, причем роль прямых на ней играют орициклы. Это позволяет Лобачевскому, опираясь на евклидову тригонометрию на орисфере, вывести тригонометрию на плоскости в его геометрической системе. Название “воображаемая геометрия” подчеркивает, что эта геометрия относится к евклидовой, “употребительной”, по терминологии Лобачевского, как мнимые числа, “воображаемые”, по его терминологии, к действительным.
Лобачевский сразу же поставил вопрос об экспериментальной проверке того, какая геометрия имеет место в реальном мире – “употребительная” или “воображаемая”, для чего он решил измерить сумму углов треугольника, образованного двумя диаметрально противоположными положениями Земли на ее орбите и Сириусом и считая один из углов этого треугольника прямым, а другой – равным углу параллельности, Лобачевский нашел, что эта сумма отличается от 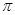 на разность, меньшую ошибки угломерных инструментов в его время. “После того, - пишет Лобачевский, - можно вообразить, сколько эта разность, на которой основана наша теория параллельных, оправдывает точность всех вычислений обыкновенной геометрии и дозволяет принятые начала рассматривать как бы строго доказанными”. на разность, меньшую ошибки угломерных инструментов в его время. “После того, - пишет Лобачевский, - можно вообразить, сколько эта разность, на которой основана наша теория параллельных, оправдывает точность всех вычислений обыкновенной геометрии и дозволяет принятые начала рассматривать как бы строго доказанными”.
Это объясняет, что под “строгим доказательством теоремы о параллельных” в докладе 1826 г. Лобачевский понимал невозможность установить экспериментальным путем ,какая из двух геометрий имеет место в реальном мире, откуда вытекает, что на практике можно пользоваться “употребительной геометрией”, не рискуя впасть в ошибку.
Наиболее полно изложена система Лобачевского в его “Новых началах с полной теорией параллельных” (1835-1838). Изложение геометрии у Лобачевского основывается на чисто топологических свойствах прикосновения и сечения, конгруэнтность тел и равенство отрезков определяются по существу с помощью движения.
В позднейших работах Лобачевский ввел координаты и вычислил из геометрических соображений целый ряд новых определенных интегралов, которым он специально посвятил работу “Применение воображаемой геометрии к некоторым интегралам” (Учен. зап. Казан. ун-та, 1836), многие из которых были включены в дальнейшие справочники.
Непротиворечивость геометрии Лобачевского
Выведя уже в своей первой работе “О началах геометрии” формулы тригонометрии своей новой системы, Лобачевский заметил, что “эти уравнения переменяются в… (уравнения) сферической Тригонометрии, как скоро вместо боков a, b, c
ставим в 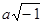 , , 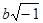 , , 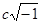 , но в обыкновенной Геометрии и сферической Тригонометрии везде входят одни содержания (т. е. отношения) линий: следовательно, обыкновенная Геометрия, Тригонометрия и эта новая геометрия всегда будут согласованы между собой”. Это означает,что если мы запишем теорему косинусов, теорему синусов и двойственную теорему косинусов сферической тригонометрии для сферы радиуса r
в виде , но в обыкновенной Геометрии и сферической Тригонометрии везде входят одни содержания (т. е. отношения) линий: следовательно, обыкновенная Геометрия, Тригонометрия и эта новая геометрия всегда будут согласованы между собой”. Это означает,что если мы запишем теорему косинусов, теорему синусов и двойственную теорему косинусов сферической тригонометрии для сферы радиуса r
в виде
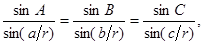
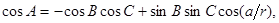
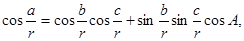
то формулы тригонометрии Лобачевского можно записать в том же виде, заменив стороны a, b, c
треугольника произведениямиai, bi, ci
; так как умножение сторон a, b, c
на i
равносильно умножению на i
радиуса сферы, то, полагая r=qi
и воспользовавшись известными соотношениями
cos(ix
) = ch x
, sin(ix
) = i
sh x
,
мы можем переписать соответственные формулы тригонометрии Лобачевского в виде
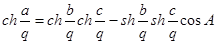 , ,
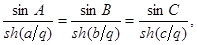
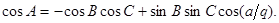
Сам Лобачевский пользовался не функциями ch x
и sh x
, акомбинациями введенной им функции 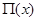 с тригонометрическими функциями; постоянная q
в этих формулах – та же, что и в формулах (1) и (2). с тригонометрическими функциями; постоянная q
в этих формулах – та же, что и в формулах (1) и (2).
Фактически Лобачевский доказал непротиворечивость своей системы тем, что ввел как на плоскости, так и в пространстве координаты и таким образом построил арифметическую модель плоскости и пространства Лобачевского. Однако сам Лобачевский видел свидетельство непротиворечивости открытой им геометрии в указанной связи формул его тригонометрии с формулами сферической тригонометрии. Этот вывод Лобачевского неправомерен. В своем мемуаре он доказал, что формулы сферической тригонометрии вытекают из его геометрии, между тем, чтобы утверждать, что из непротиворечивости тригонометрических формул вытекает непротиворечивость геометрии Лобачевского, надо было бы доказать, что все предложения последней можно вывести из ее тригонометрических формул и “абсолютной геометрии” - предложений, не зависящих от пятого постулата. Лобачевский попытался провести такое доказательство, но в его рассуждения вкралась ошибка.
Развитие евклидовой геометрии
Новая система геометрии не получила признания при жизни ее творцов.
Коллега Лобачевского по Казанскому университету П.И. Котельников (1809-1879) в своей актовой речи 1842 г. открыто заявил: “не могу умолчать о том, что тысячелетние тщетные попытки доказать со всей математической строгостью одну из основных теорем геометрии, равенство суммы углов в прямолинейном треугольнике двум прямым, побудили достопочтенного заслуженного профессора нашего университета предпринять изумительный труд - построить целую науку, геометрию, на новом предложении: сумма углов в прямолинейном треугольнике меньше двух прямых – труд . который рано или поздно найдет своих ценителей”. За исключением этого выступления неизвестны другие официальные положительные отзывы о Лобачевском, как о творце новой геометрии. На “Аппендикс” Я. Бояи и вовсе не имелось откликов. Гаусс же, как уже говорилось, избегал публикации своих открытий.
Ситуация изменилась только в 60-х годах XIX века. Несмотря на враждебное отношение отдельных влиятельных математиков старших поколений, к изучению и разработке неевклидовой геометрии приступает все большее число выдающихся молодых ученых. Некоторую роль в этом сыграло посмертное издание писем Гаусса. В Европе идеи неевклидовой геометрии воспринимаются с энтузиазмом, появляются переводы трудов Лобачевского. Меняется отношение к новой геометрии и в России. В 1868 г. профессор Московского высшего технического училища А. В. летников (1837-1888) поместил в III тому “Математического сборника” русский перевод “Геометрических исследований” Лобачевского с предисловием, в котором геометрические труды Лобачевского характеризуются как “весьма замечательные, но мало известные”, а профессор Э. П. Янишевский опубликовал в Казани “Историческую записку о жизни и деятельности Н. И. Лобачевского”. И, наконец, в том же 1868 году выходит статья Э. Бельтрами(1835 - 1900) об интерпретациях геометрии Лобачевского “опыт интерпретации неевклидовой геометрии”, в которой он отправлялся от работ Миндинга. В этой работе Бельтрами вычислил линейный элемент (квадрат дифференциала дуги) плоскости Лобачевского в координатах u, v
,
равных расстояниям точки от двух взаимно перпендикулярных прямых, деленным на r
(в настоящее время эти координаты называют бельтрамиевыми), и нашел, что в этой системе координат линейный элемент имеет вид
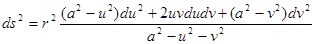 . .
Вычисляя далее гауссову кривизну поверхности с таким линейным элементом, Бельтрами обнаружил, что гауссова кривизна плоскости Лобачевского во всех ее точках равна одному и тому же числу 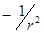 , то есть что плоскость Лобачевского можно рассматривать как поверхность постоянной отрицательной кривизны. , то есть что плоскость Лобачевского можно рассматривать как поверхность постоянной отрицательной кривизны.
Так как всякую поверхность с точки зрения ее внутренней геометрии можно рассматривать как интерпретацию любой поверхности, наложимой на нее, а необходимым и достаточным условием наложимости поверхностей является равенство гауссовых кривизн в соответственных точках поверхностей, Бельтрами сделал вывод, что плоскость Лобачевского может быть интерпретирована любой поверхностью постоянной отрицательной кривизны.
Впоследствии (1900) Гильберт доказал, что всякая поверхность постоянной отрицательной кривизны в евклидовом пространстве изометрична только части или нескольким частям плоскости Лобачевского, но никогда не изометрична плоскости Лобачевского целиком.
С другой стороны, рассматривая точки евклидовой плоскости с координатами, численно равными “бельтрамиевым координатам” u, v
плоскости Лобачевского, Бельтрами получает вторую интерпретацию. Так как координаты u, v
связаны условием
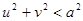 , (3) , (3)
при этой интерпретации вся плоскость Лобачевского изображается внутренностью круга, ограниченного окружностью
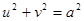 . (4) . (4)
Бальтрами показал, что прямые линии плоскости Лобачевского при этом изображаются хордами этого круга, а расстояние токи Р с координатами (u,v
) до начала координат 0 равно
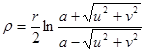 . (5) . (5)
Хотя Бельтрами не дал формулы для расстояния между двумя произвольными точками и не выяснил, как в его интерпретации изображаются движения плоскости Лобачевского, эта интерпретация Бельтрами явилась первым, правда, неполным, доказательством непротиворечивости плоскости Лобачевского.
Впоследствии появились интерпретации Кэли и Клейна
Лобачевский указывал но связь геометрии с физикой, и хотя его измерения углов с треугольника с громадными астрономическими размерами показали еще справедливость евклидовой геометрии, на самом деле, как оказалось позже, поправки, полученные в рамках теории, основанной именно на неевклидовой геометрии, оказались заметными даже внутри планетной системы, объяснив знаменитую аномалию движения Меркурия, обнаруженную в XIX столетии Леверье.
Неевклидова геометрия сыграла огромную роль во всей современной математике, и фактически в теории геометризованной гравитации марселя Гросмана-Гильберта-Эйнштейна(1913-1915). Довольно неожиданно, еще раньше была установлена вязь кинематики Лоренца-Пуанкаре с геометрией Лобачевского. В 1909 году Зоммерфельд показал, что закон сложения скоростей данной кинематики связан с геометрией сферы мнимого радиуса (подобное соотношение уже отмечали Лобачевский и Бояйи). В 1910 году Варичак указал на аналогию данного закона сложения скоростей и сложения отрезков на плоскости Лобачевского.
Предположение Лобачевского, что реальные геометрические отношения зависят от физической структуры материи, нашло подтверждение не только в космических масштабах. Современная теория квант все с большей настоятельностью выдвигает необходимость применения геометрии, отличной от евклидовой, к проблемам микромира.
Список литературы:
1. Математика XIX века, “Наука”, М., 1981
2. Юшкевич А.П., История математики в России, “Наука”, М., 1968
3. Ефимов Н.В., Высшая геометрия, “Наука”, М.,1971.
4. Неевклидовы пространства и новые проблемы физики, “Белка”, М., 1993
5. Клайн М., Математика. Утрата определенности, “Мир”, М., 1984
|