ИСПОЛЬЗОВАНИЕ ТАБЛИЧНОГО СИМПЛЕКС-МЕТОДА ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ДЛЯ
ОПТИМИЗАЦИИ ЭКОНОМИЧЕСКИХ ЗАДАЧ
ВВЕДЕНИЕ
Цель данного курсового проекта - составить план производства требуемых изделий, обеспечивающий максимальную прибыль от их реализации, свести данную задачу к задаче линейного программирования, решить её симплекс - методом и составить программу для решения задачи этим методом на ЭВМ.
1.
КРАТКИЙ ОБЗОР АЛГОРИТМОВ РЕШЕНИЯ ЗАДАЧ ДАННОГО ТИПА
1.1 Математическое программирование
Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи математического программирования формулируются следующим образом : найти экстремум некоторой функции многих переменных f ( x1
, x2
, ... , xn
) при ограничениях gi
( x1
, x2
, ... , xn
) * bi
, где gi
- функция, описывающая ограничения, * - один из следующих знаков £ , = , ³ , а bi
- действительное число, i = 1, ... , m. f называется функцией цели ( целевая функция ).
Линейное программирование - это раздел математического программирования, в котором рассматриваются методы решения экстремальных задач с линейным функционалом и линейными ограничениями, которым должны удовлетворять искомые переменные.
Задачу линейного программирования можно сформулировать так . Найти max
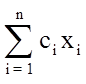
при условии : a11
x1
+ a12
x2
+ . . . + a1n
xn
£ b1
;
a21
x1
+ a22
x2
+ . . . + a2n
xn
£ b2
;
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
am1
x1
+ am2
x2
+ . . . + amn
xn
£ bm
;
x1
³ 0, x2
³ 0, . . .
, xn
³ 0 .
Эти ограничения называются условиями неотрицательности. Если все ограничения заданы в виде строгих равенств, то данная форма называется канонической.
В матричной форме задачу линейного программирования записывают следующим образом. Найти max cT
x
при условии
A x £ b ;
x ³ 0 ,
где А - матрица ограничений размером ( m´n), b(m
´
1)
- вектор-столбец свободных членов, x(n
´
1)
- вектор переменных, сТ
= [c1
, c2
, ... , cn
] - вектор-строка коэффициентов целевой функции.
Решение х0
называется оптимальным, если для него выполняется условие сТ
х0
³ сТ
х, для всех х Î R(x).
Реклама

Поскольку min f(x) эквивалентен max [ - f(x) ] , то задачу линейного программирования всегда можно свести к эквивалентной задаче максимизации.
Для решения задач данного типа применяются методы:
1) графический;
2) табличный ( прямой, простой ) симплекс - метод;
3) метод искусственного базиса;
4) модифицированный симплекс - метод;
5) двойственный симплекс - метод.
1.2 Табличный симплекс - метод
Для его применения необходимо, чтобы знаки в ограничениях были вида “ меньше либо равно ”, а компоненты вектора b - положительны.
Алгоритм решения сводится к следующему :
Приведение системы ограничений к каноническому виду путём введения дополнительных переменных для приведения неравенств к равенствам.
Если в исходной системе ограничений присутствовали знаки “ равно ”или “ больше либо равно ”, то в указанные ограничения добавляются
искусственные переменные, которые так же вводятся и в целевую функцию со знаками, определяемыми типом оптимума.
Формируется симплекс-таблица.
Рассчитываются симплекс-разности.
Принимается решение об окончании либо продолжении счёта.
При необходимости выполняются итерации.
На каждой итерации определяется вектор, вводимый в базис, и вектор, выводимый из базиса. Таблица пересчитывается по методу Жордана-Гаусса или каким-нибудь другим способом.
1.3 Метод искусственного базиса
Данный метод решения применяется при наличии в ограничении знаков “ равно ”, “ больше либо равно ”, “ меньше либо равно ” и является модификацией табличного метода. Решение системы производится путём ввода искусственных переменных со знаком, зависящим от типа оптимума, т.е. для исключения из базиса этих переменных последние вводятся в целевую функцию с большими отрицательными коэффициентами m , а в задачи минимизации - с положительными m . Таким образом из исходной получается новая m - задача.
Если в оптимальном решении m - задачи нет искусственных переменных, это решение есть оптимальное решение исходной задачи. Если же в оптимальном решении m - задачи хоть одна из искусственных переменных будет отлична от нуля, то система ограничений исходной задачи несовместна и исходная задача неразрешима.
1.4 Модифицированный симплекс - метод
В основу данной разновидности симплекс-метода положены такие особенности линейной алгебры , которые позволяют в ходе решения задачи работать с частью матрицы ограничений. Иногда метод называют методом обратной матрицы.
В процессе работы алгоритма происходит спонтанное обращение матрицы ограничений по частям, соответствующим текущим базисным векторам. Указанная способность делает весьма привлекательной машинную реализацию вычислений вследствие экономии памяти под промежуточные переменные и значительного сокращения времени счёта. Хорош для ситуаций, когда число переменных n значительно превышает число ограничений m.
Реклама

В целом, метод отражает традиционные черты общего подхода к решению задач линейного программирования, включающего в себя канонизацию условий задачи, расчёт симплекс-разностей, проверку условий оптимальности, принятие решений о коррекции базиса и исключение Жордана-Гаусса.
Особенности заключаются в наличии двух таблиц - основной и вспомагательной, порядке их заполнения и некоторой специфичности расчётных формул.
2. СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ
Для производства двух видов изделий А и В используется три типа технологического оборудования. На производство единицы изделия А идёт времени, часов : оборудованием 1-го типа - а1
, оборудованием 2-го типа - а2
, оборудованием 3-го типа - а3
.На производство единицы изделия В идёт времени, часов : оборудованием 1-го типа - b1
, оборудованием 2-го типа - b2
,,
оборудованием 3-го типа - b3
.
На изготовление всех изделий администрацияпредприятия может предоставить оборудование 1-го типа не более, чем на t1
,оборудование 2-го типа не более, чем на t2
, оборудование 3-го типа не более, чем на t3
часов.
Прибыль от реализации единицы готового изделия А составляет a рублей, а изделия В - b рублей.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу простым симплекс-методом. Дать геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами.
а1
= 1 b1
= 5 t1
= 10 a = 2
а2
= 3 b2
= 2 t2
= 12 b = 3
а3
= 2 b3
= 4 t3
= 10
3. РАЗРАБОТКА И ОПИСАНИЕ АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ
3.1 Построение математической модели задачи
| На произв-во изделия А, часов |
На произв-во изделия B, часов |
Предпр-е предоставит, часов |
| Оборуд-е 1го
типа |
1 |
5 |
10 |
| Оборуд-е 2го
типа |
3 |
2 |
12 |
| Оборуд-е 3го
типа |
2 |
4 |
10 |
| Прибыль от реализации, за ед. изд-я |
2 |
3 |
Построение математической модели осуществляется в три этапа :
1. Определение переменных, для которых будет составляться математическая модель.
Так как требуется определить план производства изделий А и В, то переменными модели будут:
x1
- объём производства изделия А, в единицах;
x2
- объём производства изделия В, в единицах.
2. Формирование целевой функции.
Так как прибыль от реализации единицы готовых изделий А и В известна, то общий доход от их реализации составляет 2x1
+ 3x2
( рублей ). Обозначив общий доход через F, можно дать следующую математическую формулировку целевой функции : определить допустимые значения переменных x1
и x2
, максимизирующих целевую функцию F = 2x1
+ 3x2
.
3. Формирование системы ограничений.
При определении плана производства продукции должны быть учтены ограничения на время, которое администрация предприятия сможет предоставить на изготовления всех изделий. Это приводит к следующим трём ограничениям :
x1
+ 5x2
£10;3x1
+ 2x2
£ 12 ; 2x1
+ 4x2
£ 10 .
Так как объёмы производства продукции не могут принимать отрицательные значения, то появляются ограничения неотрицательности :
x1
³ 0 ; x2
³ 0 .
Таким образом, математическая модель задачи представлена в виде : определить план x1
, x2
, обеспечивающий максимальное значение функции :
max F = max ( 2x1
+ 3x2
)
при наличии ограничений :
x1
+ 5x2
£10;
3x1
+ 2x2
£ 12 ;
2x1
+ 4x2
£ 10 .
x1
³ 0 ; x2
³ 0 .
3.2 Решение задачи вручную
Табличный метод ещё называется метод последовательного улучшения оценки. Решение задачи осуществляется поэтапно.
1. Приведение задачи к форме :
x1
+ 5x2
£10;
3x1
+ 2x2
£ 12 ;
2x1
+ 4x2
£ 10 .
x1
³ 0 ; x2
³ 0 .
2. Канонизируем систему ограничений :
x1
+ 5x2
+ x3
=10;
3x1
+ 2x2
+ x4
= 12 ;
2x1
+ 4x2
+ x5
= 10 .
x1
³ 0 ; x2
³ 0 .
A1
A2
A3
A4
A5
A0
3. Заполняется исходная симплекс-таблица и рассчитываются симплекс-разности по формулам :
d0
= 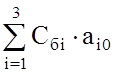 - текущее значение целевой функции - текущее значение целевой функции
di
= 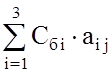 - расчёт симплекс-разностей, где j = 1..6 . - расчёт симплекс-разностей, где j = 1..6 .
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A3
|
0 |
10 |
1 |
5 |
1 |
0 |
0 |
| A4
|
0 |
12 |
3 |
2 |
0 |
1 |
0 |
| A5
|
0 |
10 |
2 |
4 |
0 |
0 |
1 |
| d
|
0 |
-2 |
-3 |
0 |
0 |
0 |
Так как при решении задачи на max не все симплекс-разности положительные, то оптимальное решение можно улучшить.
4. Определяем направляющий столбец j*
. Для задачи на max он определяется минимальной отрицательной симплекс-разностью. В данном случае это вектор А2
5. Вектор i*
, который нужно вывести из базиса, определяется по отношению :
min 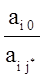 при аi j
> 0 при аi j
> 0
В данном случае сначала это А3
.
5. Заполняется новая симплекс-таблица по исключеню Жордана - Гаусса :
а). направляющую строку i*
делим на направляющий элемент :
a i j
= a i j
/ a i j
, где j = 1..6
б). преобразование всей оставшейся части матрицы :
a ij
= aij
- a i j
× aij
, где i ¹ i*
, j ¹ j*
В результате преобразований получаем новую симплекс-таблицу :
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A2
|
3 |
2 |
1/5 |
1 |
1/5 |
0 |
0 |
| A4
|
0 |
8 |
13/5 |
0 |
-2/5 |
1 |
0 |
| A5
|
0 |
2 |
6/5 |
0 |
-4/5 |
0 |
1 |
| d
|
6 |
-7/5 |
0 |
3/5 |
0 |
0 |
Повторяя пункты 3 - 5, получим следующие таблицы :
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A2
|
3 |
5/3 |
0 |
1 |
1/3 |
0 |
-1/6 |
| A4
|
0 |
11/3 |
0 |
0 |
4/3 |
1 |
-13/6 |
| A1
|
2 |
5/3 |
1 |
0 |
-2/3 |
0 |
5/6 |
| d
|
8 1/3 |
0 |
0 |
-1/3 |
0 |
7/6 |
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A2
|
3 |
3/4 |
0 |
1 |
0 |
-1/4 |
3/8 |
| A3
|
0 |
11/4 |
0 |
0 |
1 |
3/4 |
-13/8 |
| A1
|
2 |
7/2 |
1 |
0 |
0 |
1/2 |
-1/4 |
| d
|
9 1/4 |
0 |
0 |
0 |
1/4 |
5/8 |
Так как все симплекс-разности положительны, то оптимальное решение найдено :
X = ( 7/2 , 3/4 , 11/4 , 0 , 0 ) ( единиц )
max F = 9 1/4 ( рублей )
4. АНАЛИЗ МОДЕЛИ НА ЧУВСТВИТЕЛЬНОСТЬ
4.1 Построение двойственной задачи и её численное решение
Проведение анализа на чувствительность связано с теорией двойственности, поэтому в курсовой работе необходимо построить двойственную задачу и найти её численное решение.
Для рассматриваемой модели двойственная задача имеет вид :
min T( y ) = min ( 10y1
+ 12y2
+ 10y3
) при условиях
y1
+ 3y2
+ 2y3
³ 2 А1
5y1
+ 2y2
+ 4y3
³ 3 А2
y1
³ 0 , y2
³0 , y3
³ 0. А3
, А4
, А5
Оптимальное решение двойственной задачи получается при решении прямой задачи из последней симплекс-таблицы. В результате получаем оптимальное решение двойственной задачи :
Yопт
= ( 0, 1/4, 5/8, 0, 0 ), для которого Т(yопт
) = 9 1/4.
Оптимальное значение целевой функции в двойственной задачи совпадает с оптимумом целевой функции прямой задачи, в чём не трудно убедиться.
4.2 Определение статуса ресурсов
Ресурсы относятся к дефицитным, если оптимальный план предусматривает их полное использование, при частичном использовании ресурсов, они считаются не дефицитными. Статус ресурсов для любой модели линейного программирования можно установить непосредственно из оптимальной симплекс-таблицы исходной по значению дополнительных переменных. Положительное значение дополнительной переменной указывает на неполное использование соответствующего ресурса, т.е. на его недефицитность, нулевое значение дополнительной переменной указывает на дефицитность ресурса.
Для данного примера дополнительные переменные х4
и х5
равны нулю, следовательно, оборудование второго и третьего типов являются “дефицитными”, а первого типа - “недефицитным” ( х3
= 2,75 ). Такой же вывод можно сделать из решения двойственной задачи.
4.3 Определение значимости ресурсов
Значимость ресурса характеризуется величиной улучшения оптимального значения целевой функции F, приходящейся на единицу прироста данного ресурса. Значимость ресурсов всегда можно определить по значению двойственных переменных в оптимальном решении двойственной задачи.
В данном случае Yопт
= ( 0, 1/4, 5/8, 0, 0 ). Таким образом, из двух “дефицитных” ресурсов оборудование второго типа имеет большую значимость и увеличении интервала работы на этом оборудовании более выгодно с точки зрения влияния на значение целевой функции.
4.4 Определение допустимого интервала изменения запаса ресурсов
Изменение отведённого администрацией предприятия времени ( т.е. правых частей ограничений ) может привести к недопустимости текущего решения. Поэтому важно определить диапазон изменений компонент вектора ограничений, в котором допустимость решений не нарушается.
Оборудование второго типа, которое используется для изготовления изделий, является “дефицитным и имеет большую значимость. Определим диапазон допустимых изменений интервала работы на этом оборудовании. Оптимальная симплекс-таблица задачи имеет вид :
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A2
|
3 |
3/4 |
0 |
1 |
0 |
-1/4 |
3/8 |
| A3
|
0 |
11/4 |
0 |
0 |
1 |
3/4 |
-13/8 |
| A1
|
2 |
7/2 |
1 |
0 |
0 |
1/2 |
-1/4 |
| d
|
9 1/4 |
0 |
0 |
0 |
1/4 |
5/8 |
Так как начальными базисными переменными являлись x1
, x2
, x3
в оптимальной симплексной таблице в соответствующих столбцах расположена матрица А-1
Изменим время работы на оборудование второго типа на величину D2
, тогда время работы будет 12 + D2
.
Найдём базисное решение, соответствующее изменённому времени работы на оборудовании второго типа :
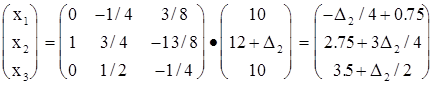
0.75 - D2
/ 4 ³ 0 , D2
= 3;
2.75 + 3D2
/ 4 ³ 0 , D2
= -3.66;
3.5 + D2
/ 2 ³ 0 , D2
= -7.
Отсюда видно, что -3.66 £D2
£ 3 , т.е. 8.34 £ b2
£ 15 .
Таким образом первоначальный интервал работы на оборудовании второго типа может быть увеличен до 15 часов или уменьшен до 8.34 часа без нарушения допустимого решения. Уменьшение времени влечёт за собой уменьшение единиц вырабатываемой продукции, поэтому является не целесообразным.
4.5 Исследование зависимости оптимального решения от изменений запасов ресурсов
Изменение свободного члена ограничения исходной задачи на величину D2
вызывает изменение целевой функции на DF = Di
× y j
.Если приращение времени работы берется из интервала допустимых изменений, значений двойственных оценок остаются неизменными. Таким образом, изменение целевой функции будет линейно зависеть от изменения времени работы.
В данном примере DF = Di
× 12 = 12 ×Di
. Ищется зависимость значений целевой функции от изменения времени работы на оборудовании второго типа. Для этого изменяется время работы начиная от 0 часов с шагом h = 0.5 до 3 часов. Результаты измерений приведены в таблице 1.
Таблица 1
| D2
, часов |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
| b2
, часов |
12 |
12.5 |
13 |
13.5 |
14 |
14.5 |
15 |
| DF, руб. |
0 |
6.25 |
13 |
20.25 |
28 |
36.25 |
45 |
| F, руб. |
9.25 |
- |
- |
- |
- |
- |
Т.к. зависимость F( b2
) - линейная, то достаточно подсчитать значение функции в двух крайних точках интервала.
Cледовательно, с увеличением времени работы на оборудовании второго типа на 2 часа увеличивается и объём изделий на общей стоимостью 28 рублей.
5. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Графический метод применим только для двух и менее переменных х, что подходит к данному заданию. Линии, соответствующие ограничения, строятся на осях Ох. Заштрихованная область - область допустимых стратегий.
x1
+ 5x2
£10;
3x1
+ 2x2
£ 12 ;
2x1
+ 4x2
£ 10 .
x1
³ 0 ; x2
³ 0 .
1). x1
+ 5x2
£10;
x1
= 0, x2
= 2;
x1
= 10, x2
= 0.
2). 3x1
+ 2x2
£ 12 ;
x1
= 0, x2
= 6;
x1
= 4, x2
= 0.
3). 2x1
+ 4x2
£ 10 ;
x1
= 0, x2
= 2.5;
x1
= 5, x2
= 0.
4). Найдём экстремум функции :
F = 2x1
+ 3x2
,

6. ВЫВОДЫ И РЕКОМЕНДАЦИИ ПО ПРАКТИЧЕСКОМУ ИСПОЛЬЗОВАНИЮ
Составление математической модели и решение систем линейных неравенств часто имеет место в реальной жизни. Примеры таких задач :
Пример 1.
Рассматривается работа промышленного предприятия под углом зрения его рентабельности, причём приводится ряд мер с целью повышения этой рентабельности. Показатель эффективности - прибыль ( или средняя прибыль ), приносимая предприятием за хозяйственный год.
Пример 2.
Группа истребителей поднимается в воздух для перехвата одиночного самолёта противника. Цель операции - сбить самолёт. Показатель эффективности - вероятность поражения цели.
Пример 3.
Ремонтная мастерская занимается обслуживанием машин; её рентабельность определяется количеством машин, обслуженных в течение дня. Показатель эффективности - среднее число машин, обслуженных за день.
Пример 4.
Группа радиолокационных станций в определённом районе ведёт наблюдение за воздушным пространством. Задача группы - обнаружить любой самолёт, если он появится в районе. Показатель эффективности - вероятность обнаружения любого самолёта, появившегося в районе.
Пример 5.
Предпринемается ряд мер по повышения надёжности электронной цифровой вычислительной техники ( ЭЦВТ ). Цель операции - уменьшить частоту появления неисправностей ( “сбоев” ) ЭЦВТ, или, что равносильно, увеличить средний промежуток времени между сдоями ( “наработку на отказ” ). Показатель эффективности - среднее время безотказной работы ЭЦВТ.
Пример 6.
Проводится борьба за экономию средств при производстве определённого вида товара. Показатель эффективности - количество сыкономленных средств.
С помощью анализа модели на чувствительность определить параметр, от которого результат зависит больше и решить, каким способом возможно увеличение эффективности и на сколько, а так же многое другое.
В данной части пояснительной записки к курсовой работе представлена и описана программа, реализующая решение систем линейных неравенств табличным методом.
1. НАЗНАЧЕНИЕ ПРОГРАММЫ
Программа предусмотрена для решения систем линейных неравенств табличным методом, а так же для попытки оптимизации различных экономических, социальных и т. д. проблем.
Метод, описанный в программе, может применяться на государственных и частных предприятиях для улучшения эффективности производства.
2. УСЛОВИЯ ПРИМЕНЕНИЯ
1.1 Ограничения и область применения
Из программных средств требуется операционная система MS DOS версии 5.0, программная Среда NORTON COMMANDER, язык программирования Borland Pascal 7.0 . Кроме того НГМД должен содержать файлы в директории KURSOVIK:
1. Файл входных данных - KURS97.DAT
2. Программный файл - KURS97.EXE
1.2 Требования к техническим средствам
IBM PC или IBM PC - совместимый компьютер с дисководом 3.25” ёмкостью 1.2 Мб.
3. ВХОДНЫЕ И ВЫХОДНЫЕ ДАННЫЕ
Входные и выходные данные заносятся в файлы KURS97.DAT и KURS97.RES соответственно. Входные данные записываются в определённом порядке. Выходные данные записываются в виде симплекс-таблиц.
4. ИНСТРУКЦИЯ ПОЛЬЗОВАТЕЛЮ
Входные данные вносятся в файл KURS 97.DAT в следующей очерёдности :
сначача вводятся коэффициенты при неизвестных в целевой функции, затем вводятся элементы вектора ограничений, а потом - элементы матрицы ограничений по столбцам.
Результаты вычислений вы найдёте в файле KURS 97.REZ.
5. ТЕКСТ ИСХОДНОГО МОДУЛЯ
Полный текст программы KURS97.PAS выглядит следующим образом :
. program Kurs97;
uses crt;
const
n = 2;
m = 3;
Epsilon = 0.000001;
var
VectorA : array [1..m, 0..m+n] of real;
TargetVector : array [1..m+n] of real;
SimplexVector : array [0..m+n] of real;
DigitOfBasisVector : array [1..m] of real;
BasisVector : array [1..m] of integer;
IndexOfEnterVector : integer;
IndexOfOutputString : integer;
MinimumBuffer : real;
key : char;
FileOfOutput : text;
{ Описание процедур }
procedure ReadDates; { считывание данных из файла }
var
DateFile : text;
procedure ReadDatesTargetVector; { считывание данных целевого вектора }
var i : integer;
begin
for i:=1 to n do Readln(DateFile, TargetVector[i]);
end;
procedure ReadDatesVectorA; { считывание вектора А и заполнение единицами диагонали}
var i,j : integer;
begin
for j:=0 to n do
for i:=1 to m do
Readln(DateFile, VectorA[i, j]);
i:=1;
for j:=n+1 to n+m do
begin
VectorA[i, j]:=1;
inc(i)
end;
end;
procedure ReadDatesBasisVector;
var i : integer;
begin
for i:=1 to m do BasisVector[i]:=n+i;
end;
begin
Assign(DateFile, 'kurs97.dat');
Reset(DateFile);
ReadDatesTargetVector;
ReadDatesVectorA;
ReadDatesBasisVector;
Close(DateFile);
end;
procedure CountSimplexVector; { расчет симплек-вектора }
var
i,j : integer;
Summa : real;
Simplex : real;
begin
SimplexVector[0]:=0;
for i:=1 to m do
SimplexVector[0]:=SimplexVector[0] + DigitOfBasisVector[i]*VectorA[i, 0];
for j:=1 to m+n do
begin
Summa:=0;
for i:=1 to m do Summa:=Summa + DigitOfBasisVector[i]*VectorA[i, j];
SimplexVector[j]:=Summa - TargetVector[j];
if abs(SimplexVector[j]) <= Epsilon then SimplexVector[j]:=0;
end;
end;
function GetEnterVector : integer; { поиск вводимого вектора }
var
i : integer;
Min : real;
begin
GetEnterVector:=1;
Min:=SimplexVector[1];
for i:=2 to m+n do
if Min > SimplexVector[i]
then
begin
GetEnterVector:=i;
Min:=SimplexVector[i];
end;
end;
function GetOutputString : integer; { поиск выводимой строки }
var
i : integer;
Temp : real;
begin
GetOutputString:=1;
if VectorA[1, IndexOfEnterVector] > 0 then MinimumBuffer:=VectorA[1, 0] / VectorA[1, IndexOfEnterVector];
for i:=2 to m do
begin
Temp:=VectorA[i, 0] / VectorA[i, IndexOfEnterVector];
if Temp > 0 then
if MinimumBuffer >= Temp then
begin
MinimumBuffer:=Temp;
GetOutputString:=i;
end;
end;
end;
procedure ReCountOutputString; { пересчет коэффициентов выводимой строки }
var
i,j : integer;
Buffer : real;
procedure ReCountDigitOfBasisVector;
begin
DigitOfBasisVector[IndexOfOutputString]:=TargetVector[IndexOfEnterVector];
end;
procedure ReCountBasisVector;
begin
BasisVector[IndexOfOutputString]:=IndexOfEnterVector;
end;
begin
ReCountDigitOfBasisVector;
ReCountBasisVector;
Buffer:=VectorA[IndexOfOutputString, IndexOfEnterVector];
for i:=0 to m+n do
begin
VectorA[IndexOfOutputString, i]:=VectorA[IndexOfOutputString, i] / Buffer;
end;
end;
procedure ReCountVectorA;
var i,j : integer;
begin
for j:=0 to m+n do
begin
for i:=1 to m do
begin
if i <> IndexOfOutputString then
if j <> IndexOfEnterVector
then VectorA[i, j]:=VectorA[i, j] - VectorA[i ,IndexOfEnterVector]*VectorA[IndexOfOutputString,j];
end;
end;
for i:=1 to m do
if i <> IndexOfOutputString then VectorA[i, IndexOfEnterVector]:=0;
end;
function AllIsPositiv : boolean;
var i : integer;
begin
AllIsPositiv:=True;
for i:=1 to m+n do
if SimplexVector[i] < 0 then AllIsPositiv:=False;
end;
function ToStr(const D : real) : string;
var S : string;
begin
str(D:6:2, S);
ToStr:=' ' + S + ' ';
end;
procedure WriteMatrixs;
procedure WriteTargetMatrix;
var i : integer;
begin
writeln(' +-----------------------------------------------------+');
write (' ¦ Target ¦');
for i:=1 to n+m do write(ToStr(TargetVector[i]),'¦'); writeln;
end;
procedure WriteMatrixA;
var i,j : integer;
begin
writeln(' +-----------------+--------+--------+--------+--------+--------+--------¦');
writeln(' ¦ Basis ¦ D.Basis¦ A 0 ¦ A 1 ¦ A 2 ¦ A 3 ¦ A 4 ¦ A 5 ¦');
writeln(' +--------+--------+--------+--------+--------+--------+--------+--------¦');
for i:=1 to m do
begin
write(' ¦ A ',BasisVector[i],' ¦',ToStr(DigitOfBasisVector[i]),'¦');
for j:=0 to m+n do write(ToStr(VectorA[i, j]),'¦'); writeln;
if i = m then writeln(' +--------+--------+--------+--------+--------+--------+--------+--------¦')
else writeln(' +--------+--------+--------+--------+--------+--------+--------+--------¦');
end;
end;
procedure WriteMatrixSimplex;
var i : integer;
begin
write(' ¦ Simplex¦');
for i:=0 to m+n do write(ToStr(SimplexVector[i]),'¦'); writeln;
writeln(' +--------------------------------------------------------------+');
end;
begin
clrscr;
WriteTargetMatrix;
WriteMatrixA;
WriteMatrixSimplex;
end;
procedure WriteMatrixsInFile;
procedure WriteTargetMatrix;
var i : integer;
begin
writeln(FileOfOutput, ' +-----------------------------------------------------+');
write (FileOfOutput, ' ¦ Target ¦');
for i:=1 to n+m do write(FileOfOutput, ToStr(TargetVector[i]),'¦'); writeln(FileOfOutput);
end;
procedure WriteMatrixA;
var i,j : integer;
begin
writeln(FileOfOutput, ' +-----------------+--------+--------+--------+--------+--------+--------¦');
writeln(FileOfOutput, ' ¦ Basis ¦ D.Basis¦ A 0 ¦ A 1 ¦ A 2 ¦ A 3 ¦ A 4 ¦ A 5 ¦');
writeln(FileOfOutput, ' +--------+--------+--------+--------+--------+--------+--------+--------¦');
for i:=1 to m do
begin
write(FileOfOutput, ' ¦ A ',BasisVector[i],' ¦',ToStr(DigitOfBasisVector[i]),'¦');
for j:=0 to m+n do write(FileOfOutput, ToStr(VectorA[i, j]),'¦'); writeln(FileOfOutput);
if i = m then writeln(FileOfOutput, ' +--------+--------+--------+--------+--------+--------+--------+--------¦')
else writeln(FileOfOutput, ' +--------+--------+--------+--------+--------+--------+--------+--------¦');
end;
end;
procedure WriteMatrixSimplex;
var i : integer;
begin
write(FileOfOutput, ' ¦ Simplex¦');
for i:=0 to m+n do write(FileOfOutput, ToStr(SimplexVector[i]),'¦'); writeln(FileOfOutput);
writeln(FileOfOutput, ' +--------------------------------------------------------------+');
end;
begin
clrscr;
WriteTargetMatrix;
WriteMatrixA;
WriteMatrixSimplex;
end;
{ Головная программа }
BEGIN
ClrScr;
ReadDates;
Assign(FileOfOutput, 'kurs97.res');
Rewrite(FileOfOutput);
CountSimplexVector;
WriteMatrixs;
while not AllIsPositiv do
begin
IndexOfEnterVector:=GetEnterVector;
IndexOfOutputString:=GetOutputString;
ReCountOutputString;
ReCountVectorA;
CountSimplexVector;
WriteMatrixsInFile;
WriteMatrixs;
if key=#0 then key:=readkey; key:=#0;
end;
Close(FileOfOutput);
END.
6. ОПИСАНИЕ ЛОГИКИ СТРУКТУРНОЙ СХЕМЫ
В программе реализованны следующие процедуры :
1. Процедура ReadDates - считывает данные из файла.
2. Процедура ReadDatesTargetVector - считывает коэффициенты при неизвестных в целевой функции из файла.
3. Процедура ReadDatesVector - считывание их входного файла матрицы А и заполнение диагональной матрицы.
4. Процедура CountSimplexVector - рассчёт симплекс-разностей.
5. Процедура GetEnterVector - поиск вводимого в базис столбца.
6. Процедура GetOutputString - поиск выводимой из базиса строки.
7. Процедура ReCountOutputString- пересчёе выводимой строки.
8. Процедура ReCountVectorA - пересчёт остальной матрицы ограничений.
9. Процедуры WriteMatrixA, WriteTargetMatrix, WriteMatrixSimplex - печать результирующих таблиц на экран и в файл.
|