Оптимизация отбора оптимальных признаков на основе применения методов моделирования эволюции для задачи распознавания текста
В.В. Хашковский, А.Н.Толкачёв
1. Введение
За последние почти 40 лет, прошедшие после появления первых работ, посвященных проблеме распознавания образов, были достигнуты значительные успехи. Научно-технический прогресс привел к появлению новых как узкоспециализированных методов, так и методов, предназначенных для решения широкого круга задач. Методы распознавания образов применяются для идентификации различных визуальных и слуховых образов, а также для выработки оптимальных решений в управлении различными технологическими процессами.
Круг задач, которые могут решаться с помощью распознающих систем, очень широк. Сюда относятся не только задачи распознавания зрительных и слуховых образов, но и задачи распознавания сложных процессов и явлений, возникающих, например, при выборе целесообразных действий руководителем предприятия или выборе оптимального управления технологическими, экономическими или транспортными операциями.
2. Распознавание образов
В целом задача распознавания образов состоит из 2-х частей: обучения и распознавания. Обучение осуществляется путём показа отдельных объектов или явлений, в результате чего распознающая система должна приобрести способность реагировать одинаковыми реакциями на изображения одинаковых образов и различными на изображения различных образов. Распознавание характеризует действия уже обученной системы. Автоматизация этих процедур и составляет проблему обучения распознаванию образов. В тех случаях, когда человек придумывает и навязывает машине правило классификации, проблема распознавания решается лишь частично, так как основную и главную часть проблемы человек берёт на себя.
Кроме того, характерное свойство образа состоит в том, что объекты, входящие в образ, могут претерпевать существенные изменения и вместе с тем оставаться объектами одного и того же образа. Однако, обладая этим свойством, образы в некотором смысле неопределённы, расплывчаты. Часто трудно определить к какому образу принадлежит объект. Примером может служить превращение головастика в лягушку. Так как не все образы имеют четкие границы, то человек, а тем более машина, не всегда может гарантировать безошибочное распознавание. Тем не менее были определены основные подходы к решению задачи распознавания, и значительное число разработанных методов было создано в рамках этих подходов. Рассмотрим кратко эти подходы.
Реклама

В своей работе Селфридж (1959) предложил осуществлять распознавание образов вычислением взвешенной суммы ряда «рекомендованных» классификаций, каждая из которых основана на разных характеристиках распознаваемого объекта (признаках). Хотя индивидуальные рекомендации могут носить почти случайный характер, система в целом может быть достаточно точной. Можно считать, что каждый объект имеет простейшее описание, представляемое вектором, элементы которого служат аргументами для ряда функций, и значения этих функций в свою очередь служат аргументами для некоторой решающей функции, которая определяет окончательную классификацию.
Другой подход к проблеме распознавания образов заключается в аналогии с биологическими процессами. Поскольку распознавание образов должно быть функцией нейронов, можно искать ключ к биологическому распознаванию образов в свойствах самого нейрона. Мак-Каллок и Питтс (1943) доказали, что любую вычислимую функцию можно реализовать с помощью должным образом организованной сети идеальных нейронов - пороговых элементов, логические свойства которых с достаточным основанием можно приписать реальному нейрону. Проблема состоит в том, можно ли найти какой-то разумный принцип реорганизации сети, позволяющий случайно объединенной вначале группе идеальных нейронов самоорганизоваться в «вычислительное устройство», способное решать произвольную задачу распознавания образов. К настоящему времени разработано достаточно большое число архитектур искусственных нейронных сетей (ИНС), но рассмотрение их выходит за рамки данной статьи.
Нейрологическая теория обучения, выдвинутая канадским психологом Хеббом (1948), хотя и была вначале рассчитана на использование в области психологии, оказала большое влияние на искусственный интеллект. Ее модификация применялась при определении принципов системы распознавания образов, получившей название персептрон (Розенблатт 1958, 1962).
3. Постановка задачи
В настоящее время существует большое число методов, позволяющих с меньшей или большей точностью решать задачу распознавания текста. Создано много систем, реализующих те или иные методы, так называемые OCR-системы. Кроме того, что эти системы разнятся по качеству распознавания, существуют серьезные ограничения на пределы применимости тех или иных методов. Так, например, совершенно очевидно, насколько различные требования будут предъявляться к настольной системе распознавания текста и к системе автоматического определения индекса на почтовом конверте.
Реклама

Несколько слов следует сказать о различиях в текстах, подлежащих распознаванию. Они могут быть печатными и рукописными. Разница весьма существенна - при распознавании рукописного текста требуется решить дополнительно задачу разделения изображений, сложность которой не меньше, чем сложность задачи непосредственно распознавания. Абстрагируясь от частных проблем, связанных с выделением изображения, нормализацией его по размерам и положению на растре, имеет смысл ввести в рассмотрение задачу распознавания нормализованных растровых изображений. Примером такой задачи может служить задача распознавания почтового индекса.
Однако, вследствие того, что вопросы нормализации могут быть успешно решены для печатного текста, составные элементы которого (далее - изолированные изображения) могут быть выделены без применения сложных специальных алгоритмов, задачу распознавания почтового индекса можно считать частным случаем задачи распознавания печатного текста.
В [1], [2], [3] предложен метод распознавания изолированных изображений, главными характеристиками которого являются:
довольно длительное обучение.
малое время распознавания.
Для данного метода полагается, что распознаванию подлежат изображения X=xn
...x1
, где компоненты xÎ{0,1}. В обучающую выборку входит по N0
изображений каждого образа. Функция принадлежности f(X) равна +1 или -1 в зависимости от принадлежности изображения к образу с номером j=1 или к образу с номером j=2. Обучение сводится к вычислению весов q разложения f(X) в ряд по системе признаков j(L,X). При этом на основе случайного поиска отбирается и фиксируется в памяти M признаков.
Критерий оптимальности p-го признака
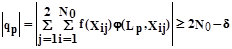
Формула
1
где d - малая величина, 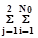 означает сложение по всем изображениям каждого из двух образов. Результат обучения - М пар Lp
sign(qp
) или Lp
, qp
. означает сложение по всем изображениям каждого из двух образов. Результат обучения - М пар Lp
sign(qp
) или Lp
, qp
.
Распознавание сводится к восстановлению знака f(X) по формуле
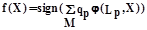
Формула 2
где 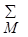 означает сложение по всем М оптимальным признакам. означает сложение по всем М оптимальным признакам.
Проведенные эксперименты показали, что для достижения достаточно хороших результатов распознавания, необходимо использовать относительно жесткие условия (критерии) при обучении. При этом длительность обучения может быть неприемлемо велика (в экспериментах - до 10 часов).
В данной работе предлагается способ ускорить обучение, что позволит в значительной мере усилить критерии обучения и, при этом, оставить время обучения в разумных пределах.
Описание предложенной модификации начнем с того, что рассмотрим кратко метод отбора оптимальных признаков, предложенный в [1], в части, требующей модификации.
4. Метод отбора оптимальных признаков
Многоальтернативная задача с S образами может быть сведена к S элементарным дихотомиям, каждая из которых позволяет отделить изображения какого-либо образа от остальных. В каждой дихотомии отыскивается определённое число оптимальных признаков, так что длительность обучения, по крайней мере, в S раз превышает длительность обучения в одной дихотомии. Фактически длительность обучения оказывается ещё большей, так как обучающая выборка содержит SN0
изображений.
Так как обработка многокомпонентных изображений X=xn
...x1
требует определённых временных затрат, тем больших, чем больше n, то общее время обучения может оказаться неприемлемо большим.
Один из способов ускорения обучения связан с преобразованием исходных изображений в промежуточные изображения Y=ym
...y1
, где m<<n. Рассмотрим этот способ. Введем m функций h(X), разделяющих, каждая по-своему, все изображения на две приблизительно равночисленные группы, для одной из которых hp
(X)=1, а для другой hp
(X)=-1. Для hp
(X) можно найти оптимальный признак j(Lp
,X), где критерий оптимальности р-го признака:
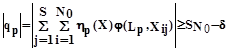
Формула
3
Однако, субъективность группирования обуславливает неприемлемо длительный перебор при поиске оптимальных признаков. Отказываясь от заданности h(X), можно установить деление на группы в процессе поиска j(L,X). Такая возможность существует, так как j(L,X) и hp
(X) однозначно связаны между собой, поскольку равенство |qp
|=SN0
выполняется лишь тогда, когда знаки j(Lp
,X) и hp
(X) либо одинаковы и qp
=SN0
, либо противоположны и qp
=(-SN0
). Это позволяет при поиске j(Lp
,X) заменить критерий (Формула 3) эквивалентным
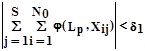
Формула 4
Введём двоичную переменную yp
такую, что yp
=0, если j(Lp
,X)=-1, и yp
=1, если j(Lp
,X)=1. Совокупность m таких переменных может рассматриваться как искомое промежуточное изображение.
Недостатком критерия является то, что он может пропускать в число оптимальных признаки, сумма которых внутри образа близка к 0, то есть признаки, которые на половине изображений образа равны +1, а на другой половине изображений равны -1. В связи с малой информативностью таких признаков критерий целесообразно дополнить, расщепив его
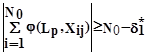
Формула 5
j=1,2,..,S.
где d*
1
- достаточно малая величина. Критерий определяет условие совпадения признака для большинства изображений каждого образа.
Тип признаков зависит от характера изображений конкретной задачи. В частности для рукописных и печатных цифро-буквенных символов оптимальным является тип полосовых признаков, обеспечивающий максимальную по сравнению с другими обобщающую способность.
Итак, первый этап обучения сводится к отысканию m оптимальных признаков j(L,X) первого уровня и фиксации m параметров L. Это позволяет на первом этапе распознавания преобразовать любое исходное изображение в некоторое промежуточное изображение с малым числом компонентов. Последующие процедуры выполняются с этими малокомпонентными изображениями.
Как следует из описания, в данном методе качество распознавания можно повышать путем ужесточения критериев на первом этапе, однако при этом значительно увеличивается время обучения. Важно понимать, что именно первый этап обучения существенно влияет на время обучения системы. Это происходит потому, что второй этап обучения (см. [1],[2],[3]) реализуется за счет перебора конечного числа точечных признаков, а именно 2m
. Число всех этих признаков зависит, конечно, от числа признаков первого этапа m, и все-таки оно является конечным и относительно небольшим.
В противоположность признакам второго этапа обучения, которые выявляются из небольшого конечного числа точечных признаков, признаки первого этапа обучения (полосовые признаки) генерируются случайным образом, и процесс этот, при достаточно жестких критериях, может стать «бесконечным». Здесь следует уточнить, что на самом деле общее число полосовых признаков ограничено, но это число зависит от размера растра и для сколько-нибудь практических задач настолько велико, что при существующих вычислительных мощностях практически недостижимо. Например, для растра 32*32, общее число полосовых признаков составит 17976,93134861Е+304.
Экспериментально установлено, что при увеличении обучающей выборки частота оптимальных признаков быстро уменьшается. Таким образом, определенная модификация процедуры, осуществляющей генерацию полосовых признаков, проведенная так, чтобы частота оптимальных признаков первого этапа обучения увеличилась, является, по крайней мере, желательной.
Учитывая особенности решений, сгенерированных при помощи методов моделирования эволюции, имеет смысл использовать генетические алгоритмы (ГА) для поиска полосовых признаков, используемых на первом этапе обучения.
5. Генетическая модификация МООП
В работе [4] описаны модели наследственности и эволюции из области популяционной генетики. Эволюция осуществляется в результате взаимодействия трех основных факторов: изменчивости, наследственности и естественного отбора.
Генетический алгоритм (ГА) - это поисковый алгоритм, основанный на моделировании механизмов естественной эволюции. На каждом шаге генетического алгоритма создается новое множество решений, в котором используются части предыдущих решений и добавляются новые части. Таким образом генетические алгоритмы используют историческую информацию.
Основные отличия ГА состоят в следующем:
ГА осуществляют поиск из множества (популяции) точек, а не из единственной точки;
ГА используют целевую функцию для оценки информации, а не ее различные приращения.
Рассмотрим механизм простого ГА (ПГА): сначала ГА случайно генерирует популяцию последовательностей (стрингов); далее он копирует последовательности и переставляет их части; затем ГА применяет некоторые операторы к начальной популяции и генерирует новые популяции.
В ПГА используется 3 оператора: репродукция, кроссовер, мутация. Поясним кратко действие некоторых используемых генетических операторов.
Оператор Репродукции (ОР): механизм репродукции включает копирование стргингов. Репродукция - процесс, в котором стринги воспроизводятся согласно их функции фитности. Стринги с большим значением функции фитности имеют большую вероятность попадания в следующую генерацию. Один из способов алгоритмической реализации ОР – моделирование колеса рулетки, в котором каждый стринг имеет сектор, величина которого пропорциональна значению функции фитности стринга.
Оператор Кроссовера (ОК): оператор кроссовера может выполниться в 2 шага. На первом шаге элементы множества стрингов случайно разбиваются на пары. Затем из каждой пары стрингов формируется новая пара по правилу: случайно выбирается целочисленная позиция вдоль стринга между 1 и длиной стринга L - точка скрещивания. Новая пара стрингов создается вследствие обмена частями исходных стрингов, относительно точки скрещивания. Например, X и Y представляют собой два стринга (родители). Если теперь случайным или заранее заданным способом выбрать точку скрещивания, то смешивая части исходных векторов можно получить два новых потомка:X' и Y'.
X: x1
x2
x3
x4
x5
|x6
x7
x8
Y: y8
y7
y6
y5
y4
|y3
y2
y1
X': x1
x2
x3
x4
x5
|y3
y2
y1
Y': y8
y7
y6
y5
y4
|x6
x7
x8
Возможно проводить операцию скрещивания не относительно одной точки (одноточечный кроссовер), а относительно нескольких точек (многоточечный кроссовер). В этом случае обеспечивается большее отличие потомков от предков.
Оператор Мутации (ОМ): соответствует случайному нарушению последовательности битов в стринге; например, применяя ёоператор мутации к X', можно получить X''1
:x1
x2
x3
x4
x5
y2
y3
y1
или X''2
:x1
x3
x2
x4
x5
y3
y2
y1
и т.д. Обычно выбирают одну мутацию на 1000 бит. Считается, что мутация - вторичный механизм в ГА.
Для оптимизации поиска оптимальных признаков использование ГА может быть описано следующим образом.
Сначала определяется соответствие между хромосомой и полосовым признаком. В данном случае полосовой признак (растровое изображение) "вытягивается" в вектор (стринг). Далее случайным образом генерируется некоторое множество возможных полосовых признаков - начальная популяция P0
=X0
1
, X0
2
, … X0
n
. Затем для каждой хромосомы вычисляется функция фитности, которая в данном случае представляет собой комплексную оценку, вычисляемую с учетом критериев отбора оптимальных признаков первого рода.
Далее к популяции применяется оператор репродукции (ОР), который формирует новую популяцию, оставляя в ней хромосомы с вероятностью, пропорциональной значению функции фитности. На следующем шаге, используя случайный выбор, генерируются пары для применения к ним оператора кроссовера. Здесь возможно также использование оператора кроссовера для каждой пары с вероятностью pc
, пропорциональной сумме значений функций фитности обеих хромосом. Это позволит воспроизвести некоторые из хромосом в следующем поколении и с большей вероятностью сохранить наиболее перспективные из них. Более эффективным является использование многоточечного скрещивания, так как это обеспечит большее разнообразие стрингов, что в данном случае весьма важно.
Так как при таком методе генерации решений существует возможность попадания в область локально-оптимальных решений, что для данной задачи будет характеризоваться тем, что для большого числа поколений не будет выполняться условие попарной совместной оптимальности стрингов (признаков), целесообразно использовать оператор мутации с некоторой вероятностью pm
.
Список литературы
Ефимов Ю.Н. Распознавание изображений с использованием оптимальных признаков АВТ.-1992.-№2.-С. 69-75.
1531115 СССР. Устройство для распознавания образов/ Ефимов Ю.Н. -заявлено 08.10.87// Открытия. Изобретения. Пром. образцы. Товар. знаки.-1989.-№47.- С.162.
1799359 СССР. Устройство для распознавания образов/ Ефимов Ю.Н. -заявлено 12.12.89// Открытия. Изобретения. Пром. образцы. Товар. знаки.-1992.-№4.- С.195.
Holland. I. Adaptation in Natural and Artifical Systems. University of Michigan Press, Ann Arbor, 1975.
Курейчик В. М. Применение генетических методов для компоновки схем СБИС. сб. Интеллектуальные САПР №4, 1994.
Хант Э. Искусственный интеллект, «Мир», М. 1978.
Rosenblatt F. The perceptron: A probalistic model for information storage and organization in the brain, Psychol. Rev., 65, 386-408, 1958.
Rosenblatt F. Principles of neurodynamics, Baltimore, 1962, (Русскийперевод: РозенблаттФ., Принципынейродинамики, «Мир», М., 1966).
Selfridge O. Pandemonium. A paradigm for learning, всб. «Proceedings of the Symposium on the Mechanization of Tought Processes» подред. Blake D., Utteley A., London, 1959.
McCulloch W., Pitts W. A logical calculus of the ideas imminent in nervous activiti, Bull. Math. Biophys., 5, 115-137., (Русский перевод в сб. «Автоматы» под ред. Маккарти Дж. и Шеннона К., ИЛ. М., 1956).
Hebb D. The organization of behavior, New York, 1948.
|