Введение
В современном мире машинная графика находит самое широкое применение в различных областях науки и техники, промышленности, в экономике, управлении, обучении. Выделим важнейшие области применения машинной графики:
Автоматизация проектно-конструкторских работ (САПР). Это традиционная область применения, с которой начиналось использование машинной графики.
Автоматизация научных исследований (АСНИ).
Графические информационные позволяют получать высококачественные тополого-геодезические, географические карта, карты для бурения, погодные карты и т.п.
Автоматизация процессов обучения.
Издательская деятельность, реклама, компьютерные игры, мультипликация.
В зависимости от возможности изменения получаемого изображения машинная графика подразделяется на пассивную и активную. Под пассивной машинной графикой подразумевается способ получения изображения на каком-либо носителе без возможности его динамического изменения. Интерактивная машинная графика позволяет динамически управлять содержанием изображения, его формой, размерами и цветом с помощью интерактивных устройств взаимодействия ( клавиатуры, мыши, джойстика и т.п. ). Интерактивная машинная графика стала стандартной формой связи человека и компьютера.
Объектом исследования в нашей работе будут являться методы генерации отрезков.
Цель нашей работы – рассмотреть методы генерации отрезков, выделить их основные характеристики, сделать вывод об их эффективности, быстродействии.
Для достижения поставленной цели определены следующие задачи:
1. На основе анализа литературы рассмотреть алгоритмы генерации отрезков, выделить их достоинства и недостатки.
2. Разработать приложение, реализующее три метода генерации отрезков и создающее все условия для работы с данными алгоритмами
3. Продемонстрировать различные алгоритмы генерации отрезков.
4. Сравнить быстродействие используемых алгоритмов.
5. Сделать вывод об эффективности различных алгоритмов генерации отрезков.
Методы исследования: теоретический, экспериментальный.
В данной программе реализованно три алгоритма вычерчивания отрезков: Цифровой дифференциальный анализатор (ЦДА), алгоритм Брезенхема и процедуру LineTo.
Реклама

1. Теоретическая часть
1.1. Компьютерная графика
Различают три вида компьютерной графики: растровая графика, векторная графика и фрактальная графика. Они отличаются принципами формирования изображения при отображении на экране монитора или при печати на бумаге.
Растровую графику применяют при разработке электронных (мультимедийных) и полиграфических изданий. Иллюстрации, выполненные средствами растровой графики, редко создают вручную с помощью компьютерных программ. Для этой цели сканируют иллюстрации, подготовленные художником на бумаге, или фотографии. В последнее время для ввода растровых изображений в компьютер нашли широкое применение цифровые фото- и видеокамеры. В Интернете пока применяются только растровые иллюстрации.
Программные средства для работы с векторной графикой, наоборот, предназначены для создания иллюстраций и в меньшей степени для их обработки. Такие средства широко используют в рекламных агентствах, дизайнерских бюро, редакциях и издательствах. Оформительские работы, основанные на применении шрифтов и простейших геометрических элементов, решаются средствами векторной графики проще. Имеются примеры высокохудожественных произведений, созданных средствами векторной графики, но они скорее исключение, чем правило.
Программные средства для работы с фрактальной графикой предназначены для автоматической генерации изображений путем математических расчетов. Создание фрактальной художественной композиции состоит не в рисовании или оформлении, & в программировании. Фрактальную графику чаще используют в развлекательных программах.
1.2 Растровая графика
В растровой графике основным элементом является точка. При экранном изображение эта точка называется пикселем.
Основная проблема и недостаток при использовании растровых изображений - это большие объемы данных. Для работ с большеразмерными иллюстрациями типа журнальной полосы требуются компьютеры с большими размерами оперативной памяти (128 Мбайт и более). Такие компьютеры, естественно, должны при этом иметь и высокопроизводительные процессоры.
Вторым недостатком растровых изображений является невозможность их увеличения для рассмотрения деталей. Так как изображение состоит из точек, то увеличение изображения приводит только к тому, что эти точки становятся крупнее. Никаких дополнительных деталей при увеличении растрового изображения рассмотреть не удается. Само увеличение точек растра визуально искажает иллюстрацию и делает ее грубой. Этот эффект называется пикселизацией.
Реклама

Любое изображение, в том числе и трехмерное, состоит из графических примитивов, поэтому необходимо знать специальные методы генерации изображения, вычерчивание прямых и кривых линий, закраски многоугольников, создающей впечатление сплошных объектов. Рассмотрим некоторые из этих методов.
Алгоритмы вычерчивания отрезков. Экран дисплея можно рассматривать как матрицу дискретных элементов (пикселей), каждый из которых может быть подсвечен. В связи с этим нельзя непосредственно провести отрезок из одной точки в другую. Процесс определения пикселей, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр. Для горизонтальных, вертикальных и наклоненных под углом 45° отрезков выбор растровых элементов очевиден. При любой другой ориентации выбрать нужные пиксели труднее. Существует несколько алгоритмов выполняющих эту задачу, например, цифровой дифференциальный анализатор и алгоритм Брезенхема.
Алгоритм Брезенхема для генерации окружностей. В растр нужно разлагать не только линейные, но и другие, более сложные функции. Разложению конических сечений, т.е. окружностей, эллипсов, парабол, гипербол, посвящено значительное число работ. Наибольшее внимание уделено окружности. Один из наиболее эффективных и простых для понимания алгоритмов генерации окружности принадлежит Брезенхему.
Вначале необходимо сгенерировать только одну восьмую часть окружности. Остальные ее части могут быть получены последовательными отражениями. Если сгенерирован первый октант (от 0° до 45° против часовой стрелки), то второй октант можно получить зеркальным отражением относительно прямой у = х, что дает в совокупности первый квадрант. Первый квадрант отражается относительно прямой х = 0 для получения соответствующей части окружности во втором квадранте. Верхняя полуокружность отражается относительно прямой у = О для завершения построения.
Растровая развертка сплошных областей. Возможность представления сплошных областей в растровом графическом устройстве является его уникальной характеристикой. Генерация сплошных областей из простых описаний ребер или вершин называется растровой разверткой сплошных областей, заполнением многоугольников или заполнением контуров. Для этого можно использовать несколько методов, которые обычно делятся на две широкие категории: растровая развертка и затравочное заполнение.
В методах растровой развертки пытаются определить в порядке сканирования строк, лежит ли точка внутри многоугольника или контура. Эти алгоритмы обычно идут от "верха" многоугольника или контура к "низу".
В методах затравочного заполнения предполагается, что известна некоторая точка (затравка) внутри замкнутого контура. В алгоритмах ищут точки, соседние с затравочной и расположенные внутри контура. Если соседняя точка расположена не внутри, значит, обнаружена граница контура. Если же точка оказалась внутри контура, то она становится новой затравочной точкой и поиск продолжается рекурсивно.
Растровая развертка многоугольников. Можно разработать эффективный метод растровой развертки многоугольников, если воспользоваться тем фактом, что соседние пиксели, вероятно, имеют одинаковые характеристики (кроме пикселов граничных ребер). Это свойство называется пространственной когерентностью.
Алгоритм с упорядоченным списком ребер. Используя эти методы, можно разработать эффективные алгоритмы растровой развертки сплошных областей, называемые алгоритмами с упорядоченным списком ребер. Эффективность этих алгоритмов зависит от эффективности сортировки.
Алгоритм заполнения по ребрам. Алгоритм, использующий список ребер и флаг, является двухшаговым. Первый шаг состоит в обрисовке контура, в результате чего на каждой сканирующей строке образуются пары ограничивающих пикселов. Второй шаг состоит в заполнении пикселов, расположенных между ограничивающими.
Алгоритмы заполнения с затравкой. В рассмотренных алгоритмах заполнение происходит в порядке сканирования. Иной подход используется в алгоритмах заполнения с затравкой. В них предполагается, что известен хотя бы один пиксель из внутренней области многоугольника. Алгоритм пытается найти и закрасить все другие пиксели, принадлежащие внутренней области. Области могут быть либо внутренние, либо гранично-определенные. Если область относится к внутренне-определенным, то все пиксели, принадлежащие внутренней части, имеют один и тот же цвет или интенсивность, а все пиксели, внешние по отношению к области, имеют другой цвет. Если область относится к гранично-определенным, то все пиксели на границе области имеют выделенное значение или цвет. Алгоритмы, заполняющие внутренне-определенные области, называются внутренне-за-полняющими, а алгоритмы для гранично-определенных областей - гранично-заполняющими.
1.3 Векторная графика
Как в растровой графике основным элементом изображения является точка, так в векторной графике основным элементом изображения является линия, при этом не важно, прямая это линия или кривая.
В растровой графике тоже существуют линии, но там они рассматриваются как комбинации точек. Для каждой точки линии в растровой графике отводится одна или несколько ячеек памяти (чем больше цветов могут иметь точки, тем больше ячеек им выделяется). Соответственно, чем длиннее растровая линия, тем больше памяти она занимает. В векторной графике объем памяти, занимаемый линией, не зависит от размеров линии, поскольку линия представляется в виде формулы, а точнее говоря, в виде нескольких параметров. Чтобы ни делали с этой линией, меняются только ее параметры, хранящиеся в ячейках памяти. Количество же ячеек остается неизменным для любой линии.
Линия - это элементарный объект векторной графики. Все, что есть в векторной иллюстрации, состоит из линий. Простейшие объекты объединяются в более сложные, например, объект четырехугольник можно рассматривать как четыре связанные линии, а объект куб еще более сложен: его можно рассматривать либо как двенадцать связанных линий, либо как шесть связанных четырехугольников. Из-за такого подхода векторную графику часто называют объектно-ориентированной графикой.
Объекты векторной графики хранятся в памяти в виде набора параметров, но надо помнить о том, что на экран все изображения все равно выводятся в виде точек. Перед выводом на экран каждого объекта программа производит вычисления координат экранных точек в изобра жении объекта, поэтому векторную графику иногда называют вычисляемой графикой. Аналогичные вычисления производятся и при выводе объектов на принтер.
Как и все объекты, линии имеют свойства. К этим свойствам относятся: форма линии, ее толщина, цвет, характер линии (сплошная, пунктирная и т.п.). Замкнутые линии имеют свойство заполнения. Внутренняя область замкнутого контура может быть заполнена цветом, текстурой, картой. Простейшая линия, если она не замкнута, имеет две вершины, которые называются узлами. Узлы тоже имеют свойства, от которых зависит, как выглядит вершина линии и как две линии сопрягаются между собой.
1.4 Алгоритмы вычерчивания отрезков
Поскольку экран растрового дисплея с электронно-лучевой трубкой (ЭЛТ) можно рассматривать как матрицу дискретных элементов (пикселов), каждый из которых может быть подсвечен, нельзя непосредственно провести отрезок из одной точки в другую. Процесс определения пикселов, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр. В сочетании с процессом построчной визуализации изображения он известен как преобразование растровой развертки. Для горизонтальных, вертикальных и наклоненных под углом 45° отрезков выбор растровых элементов очевиден. При любой другой ориентации выбрать нужные пикселы труднее, что показано на рис. 1.1.
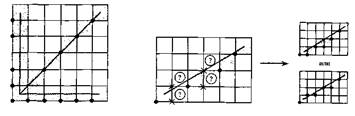
Рис. 1.1 Разложение в растр отрезков прямых
Прежде чем приступать к обсуждению конкретных алгоритмов рисования отрезков, полезно рассмотреть общие требования к таким алгоритмам и определить желаемые характеристики изображения. Очевидно, что отрезки должны выглядеть прямыми, начинаться и заканчиваться в заданных точках. Яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона. Наконец, рисовать нужно быстро. Как это часто бывает, не все из перечисленных критериев могут быть полностью удовлетворены. Сама природа растрового дисплея исключает генерацию абсолютно прямых линий (кроме ряда специальных случаев), равно как и точное совпадение начала и конца отрезка с заданными точками. Тем не менее при достаточно высоком разрешении дисплея можно получить приемлемое изображение.
Постоянная вдоль всего отрезка яркость достигается лишь при проведении горизонтальных, вертикальных и наклоненных под углом 45 ° прямых. Для всех других ориентации разложение в растр приведет к неравномерной яркости, как это показано на рис. 2.1. Даже для частных случаев яркость зависит от наклона: заметим, например, что расстояние между центрами соседних пикселов для отрезка под углом 45° больше, чем для вертикальных и горизонтальных прямых. Поэтому вертикальные и горизонтальные отрезки будут выглядеть ярче, чем наклонные. Обеспечение одинаковой яркости вдоль отрезков разных длин и ориентации требует извлечения квадратного корня, а это замедлит вычисления. Обычным компромиссом является нахождение приближенной длины отрезка, сведение вычислений к минимуму, предпочтительное использование целой арифметики, а также реализация алгоритмов на аппаратном или микропрограммном уровне.
2 Алгоритмы генерации отрезков
2.1 Цифровой Дифференциальный анализатор
Один из методов разложения отрезка в растр состоит в решении дифференциального уравнения, описывающего этот процесс. Для прямой линии имеем
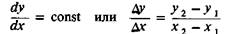
Решение представляется в виде
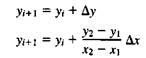
где x1, y1 и x2, y2 - концы разлагаемого отрезка и yi - начальное значение для очередного шага вдоль отрезка. Фактически уравнение [1] представляет собой рекурентное соотношение для последовательных значений y вдоль нужного отрезка. Этот метод, используемый для разложения в растр отрезков, называется цифровым дифференциальным анализатором (ЦДА). Впростом ЦДА либо Dx, либо Dy (большее из приращений) выбирается в качестве единицы растра. Ниже приводится простой алгоритм, работающий во всех квадрантах:
Процедура разложения в растр отрезка по методу цифрового дифференциального анализатора (ЦДА)
предполагается, что концы отрезка (x1, y1) и (x2, y2) не совпадают
Integer - функция преобразования вещественного числа в целое.
Sign - функция, возвращающая -1, 0, 1 для отрицательного, нулевого и положительного аргумента соответственно
аппроксимируем длину отрезка
if abs(x2 - x1) >= abs(y2 - y1) then
Длина = abs(x2 - x1) else
Длина = abs(y2 - y1) end
полагаем большее из приращений x или y равными единице растра
x = (x2 - x1) // Длина
y = (y2 - y1) // Длина
округляем величины, а не отбрасываем дробную часть
использование знаковой функции делает алгоритм пригодным для всех квадрантов
x = x1 + 0.5 * Sign(x)
y = y1 + 0.5 * Sign(y)
начало основного цикла
i =1
while (i <= Длина)
вывод точки PutPixel (Integer(x), Integer(y))
x = x + x
y = y + y
i = i + 1
end
2.2 Алгоритм Брезенхема
В 1965 году Брезенхеймом был предложен простой целочисленный алгоритм для растрового построения отрезка. Алгоритм выбирает оптимальные растровые координаты для представления отрезка. В процессе работы одна из координат — либо x, либо у (в зависимости от углового коэффициента) — изменяется на единицу. Изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние мы назовем ошибкой.
Алгоритм построен так, что требуется проверять лишь знак этой ошибки. На рис. 1.2 это иллюстрируется для отрезка в первом октанте, т. е. для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0, 0) больше чем 1/2, то его пересечение с прямой х = 1 будет расположено ближе к прямой у = 1, чем к прямой у = 0. Следовательно, точка растра (1, 1) лучше аппроксимирует ход отрезка, чем точка (1, 0). Если угловой коэффициент меньше 1/2, то верно обратное. Для углового коэффициента,
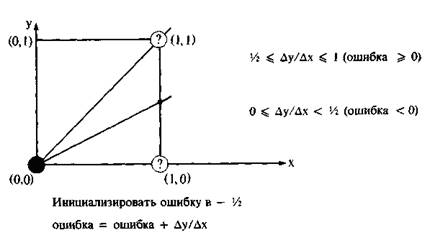
Рис. 1.2 Основная идея алгоритма Брезенхема
равного 1/2, нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1, 1).
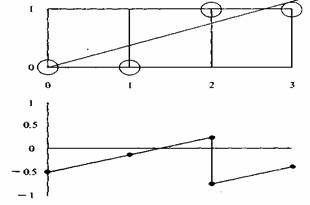
Рис. 1.3 График ошибки в алгоритме Брезенхема
Не все отрезки проходят через точки растра. Подобная ситуация иллюстрируется рис. 1.3, где отрезок с тангенсом угла наклона 3/8 сначала проходит через точку растра (0, 0) и последовательно пересекает три пиксела. Также иллюстрируется вычисление ошибки при представлении отрезка дискретными пикселами. Так как желательно проверять только знак ошибки, то она первоначально устанавливается равной —1/2. Таким образом, если угловой коэффициент отрезка больше или равен 1/2, то величина ошибки в следующей точке растра с координатами (1,0) может быть вычислена как
е = е + m
где m — угловой коэффициент. В нашем случае при начальном значении ошибки —1/2
е = -1/2+ 3/8 = -1/8
Так как е отрицательно, отрезок пройдет ниже середины пиксела. Следовательно, пиксел на том же самом горизонтальном уровне лучше аппроксимирует положение отрезка, поэтому у не увеличивается. Аналогично вычисляем ошибку
е = -1/8 + 3/8 = 1/4
в следующей точке растра (2, 0). Теперь е положительно, а значит, отрезок пройдет выше средней точки. Растровый элемент (2, 1) со следующей по величине координатой у лучше аппроксимирует положение отрезка. Следовательно, у увеличивается на единицу. Прежде чем рассматривать следующий пиксел, необходимо откорректировать ошибку вычитанием из нее единицы. Имеем
е = 1/4- 1 = -3/4
Заметим, что пересечение вертикальной прямой х = 2 с заданным отрезком лежит на 1/4 ниже прямой y = 1. Если же перенести отрезок 1/2 вниз, мы получим как раз величину -3/4. Продолжение вычислений для следующего пиксела дает
e = - 3/4 + 3/8 = - 3/8
Так как e отрицательно, то .у не увеличивается. Из всего сказанного следует, что ошибка — это интервал, отсекаемый по оси у рассматриваемым отрезком в каждом растровом элементе (относительно —1/2).
3. Описание программы
3.1. Описание интерфейса
Реализация каждого метода генерации отрезков проводилась в среде объектно-ориентированного программирования Delphi 7. Поставлена задача запрограммировать алгоритмы генерации отрезков, создать форму для ввода данных и вывода результата.
Для каждого из трех алгоритмов создается окно приложения (рис. 1.4).
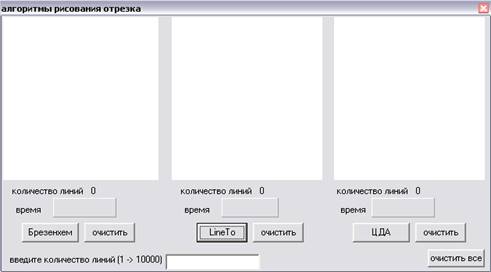
Рис. 1.4. Внешний вид окна приложения
В итоге создано приложение Windows.
На форме расположены:
Три поля, на которых будет отображаться результат построения отрезков для каждого метода в отдельности.
Поле «Ввод количества линий» служит для ввода количества линий, которые будут сгенерированы генератором случайных чисел.
Три поля «время», на которых отображается время построения отрезков для каждого метода в отдельности.
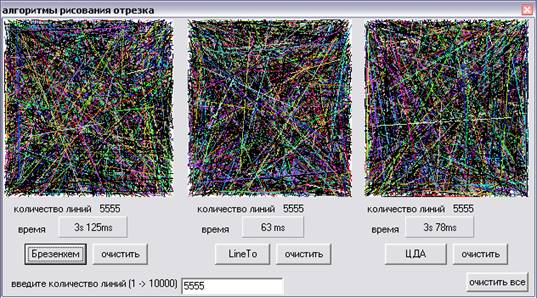
Рис.3.2 Результат работы приложения
3.2. Описание логической структуры
В проект добавлены компоненты Form1 – главная форма. На главной форме размещаются компоненты: Image – окно для вывода линий, Panel – панель для вывода времени, затраченного на генерацию отрезков, Edit1 – окошечко для ввода количества линий, которые будут сгенерированы генератором случайных чисел и Button – кнопка для подтверждения ввода количества линий / для очистки компонента Image и сброса всех настроек. Label – показывает число построенных линий
Заключение
Заканчивая наш обзор методов генерации отрезков, попытаемся сравнить их эффективность.
Метод Брезенхема определенно наихудший из всех сравниваемых, этот алгоритм обладает очень плохими временными характеристиками. Он имеет только учебно-исторический интерес и не может быть рекомендован для практического использования.
Алогритм Цифрового Дифференциального Анализатора в среднем (в зависимости от количества введенных линий) лучше, чем метод Брезенхема. По сравнению с методом Брезенхема метод ЦДА в большинстве случаев может оказаться более быстрым.
Процедура LineTo оказалась самой быстрой и результативной из всех трех алгоритмов
В данной работе рассмотрены некоторые простые и улучшенные методы генерации отрезков: Брезенхема, Цифрового Дифференциального Анализатора и стандартной процедуры LineTo. Мы оценили сложность этих алгоритмов генерации. Алгоритмы этих методов представлены в виде программ. Так же была проанализирована скорость, эффективность использования того или иного вида генерации отрезков.
Целью данной курсовой работы было исследование и сравнение трех наиболее эффективных алгоритмов генерации отрезков: Брезенхема, Цифрового Дифференциального Анализатора и стандартной процедуры LineTo. Поставленная цель была достигнута.
Список литературы
П.В.Вельтмандер "Машинная графика" Издательский дом «Вильямс», 2000.
информация с сайта http://alglib.sources.ru
информация с сайта http://joinbiz.ru
информация с сайта http://kladovka.net.ru
информация с сайта http://Mini-Soft.ru
Приложение
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs,Math, StdCtrls, ExtCtrls, Menus, ToolWin, ComCtrls, ExtDlgs,
ImgList;
type
TPointDrawer = procedure(X, Y: Integer) of object;
TForm1 = class(TForm)
Button1: TButton;
Button2: TButton;
Button3: TButton;
Image1: TImage;
Image2: TImage;
Edit1: TEdit;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Button4: TButton;
Button7: TButton;
Image3: TImage;
Button8: TButton;
Button9: TButton;
Label6: TLabel;
Label7: TLabel;
Panel1: TPanel;
Panel2: TPanel;
Panel3: TPanel;
Label8: TLabel;
Label9: TLabel;
Label10: TLabel;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Button7Click(Sender: TObject);
procedure Button8Click(Sender: TObject);
procedure Button9Click(Sender: TObject);
private
s:string;
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
time,tm1,tm2:integer;
implementation
//функция вычисления модуля числа
function AbsInt(Value: Integer): Integer;
begin
if Value >= 0 then
Result := Value
else
Result := - Value;
end;
//Цифровой Дифференциальный анализатор
procedure DDA(x1,y1,x2,y2:integer);
var dx,dy,sx,sy,d,d1,d2,x,y,i:integer;
T:tColor;
begin
randomize;
t:=random($7FFFFFFF);
dx:=abs(x2-x1);
dy:=abs(y2-y1);
if x2>=x1 then sx:=1 else sx:=-1;
if y2>=y1 then sy:=1 else sy:=-1;
if dy<=dx then
begin
d:=2*dy -dx;
d1:=2*dy;
d2:=2*(dy-dx);
Form1.Image3.Canvas.Pixels[x1,y1]:=t;
x:=x1+sx;
y:=y1;
for i:=1 to dx do
begin
if d>0 then
begin
d:=d+d2;
y:=y+sy;
end else d:=d+d1;
Form1.Image3.Canvas.Pixels[x,y]:=t;
x:=x+sx;
end;
end else
begin
d:=2*dx-dy;
d1:=2*dx;
d2:=2*(dx-dy);
Form1.Image3.Canvas.Pixels[x1,y1]:=t;
x:=x1;
y:=y1+sy;
for i:=1 to dy do
begin
if d>0 then
begin
d:=d+d2;
x:=x+sx;
end else d:=d+d1;
Form1.Image3.Canvas.Pixels[x,y]:=t;
y:=y+sy;
end;
end;
end;
//описание метода Брезенхема
procedure Bresenham(x1:Integer;y1:Integer;x2:Integer;y2:Integer);
var
x,y,dx,dy,sx,sy,z,e,i: Integer;
Ch : Boolean;
T:tColor;
begin
randomize;
t:=random($7FFFFFFF);
x:=x1;
y:=y1;
dx:=AbsInt(x2-x1); //модуль числа dx
dy:=AbsInt(y2-y1); //модуль числа dy
sx:=Sign(x2-x1);
sy:=Sign(y2-y1);
if (dx=0) and (dy=0) then
begin
form1.image1.Canvas.Pixels[x1,y1]:=t; //вывод точки
Exit;
end;
if dy>dx then
begin
z:=dx; dx:=dy; dy:=z; ch:=True;
end
else ch:=False;
e:=2*dy-dx;
i:=1;
repeat
form1.image1.Canvas.Pixels[x,y]:=t; //вывод точки в цикле
while e>=0 do
begin
if ch then x:=x+sx
else y:=y+sy;
e:=e-2*dx;
end;
if ch then y:=y+sy
else x:=x+sx;
e:=e+2*dy;
i:=i+1;
until i>dx;
end;
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
var k: integer;
begin
time:=GetTickCount;
label4.Caption:=inttostr(strtoint(label4.Caption)+strtoint(edit1.Text));
for k:=1 to strtoint(Edit1.text) do
Bresenham (random(image1.ClientWidth), random(image1.clientHeight), random (image1.ClientWidth), random(image1.ClientHeight));
time:=GetTickCount-time;
if time>1000 then
begin
tm1:=time mod 1000;
tm2:=time div 1000;
Form1.Panel1.Caption:=IntToStr(tm2)+'s '+IntToStr(tm1)+'ms';
end
else
Form1.Panel1.Caption:=IntToStr(time)+' ms';
end;
procedure TForm1.Button2Click(Sender: TObject);
var m:integer;
begin
time:=GetTickCount;
label5.Caption:=inttostr(strtoint(label5.Caption)+strtoint(edit1.Text));
for m:=1 to strtoint(Edit1.text) do
begin
image2.Canvas.Pen.Color:=random($7FFFFFFF);
image2.Canvas.LineTo(random(image2.ClientWidth),random(image2.ClientHeight));
image2.Canvas.MoveTo(random(image2.ClientWidth),random(image2.ClientHeight));
end;
time:=GetTickCount-time;
if time>1000 then
begin
tm1:=time mod 1000;
tm2:=time div 1000;
Form1.Panel2.Caption:=IntToStr(tm2)+'s '+IntToStr(tm1)+'ms';
end
else
Form1.Panel2.Caption:=IntToStr(time)+' ms';
end;
procedure TForm1.Button8Click(Sender: TObject);
var l:integer;
begin
time:=GetTickCount;
label7.Caption:=inttostr(strtoint(label7.Caption)+strtoint(edit1.Text));
for l:=1 to strtoint(Edit1.text) do DDA
(random(image3.ClientWidth),random(image3.ClientHeight),random(image3.ClientWidth),random(image3.ClientHeight));
time:=GetTickCount-time;
if time>1000 then
begin
tm1:=time mod 1000;
tm2:=time div 1000;
Form1.Panel3.Caption:=IntToStr(tm2)+'s '+IntToStr(tm1)+'ms';
end
else
Form1.Panel3.Caption:=IntToStr(time)+' ms';
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
randomize;
edit1.Text:=inttostr(random(500));
end;
procedure TForm1.Button4Click(Sender: TObject);
begin
form1.image1.Canvas.FillRect(Rect(0,0,ClientWidth,ClientHeight));
form1.Label4.Caption:=inttostr(0);
form1.Panel1.Caption:='';
end;
procedure TForm1.Button7Click(Sender: TObject);
begin
form1.image2.Canvas.FillRect(Rect(0,0,ClientWidth,ClientHeight));
form1.Label5.Caption:=inttostr(0);
form1.Panel2.Caption:='';
end;
procedure TForm1.Button9Click(Sender: TObject);
begin
form1.image3.Canvas.FillRect(Rect(0,0,ClientWidth,ClientHeight));
form1.Label7.Caption:=inttostr(0);
form1.Panel3.Caption:='';
end;
procedure TForm1.Button3Click(Sender: TObject);
begin
Form1.Button7.Click;
Form1.Button4.Click;
Form1.Button9.Click;
end;
end.
|