.
Т.С. Кармакова
,
доцент кафедры алгебры ХГПУ
В различных вопросах теории чисел, математического анализа, теории рекурсивных функций и в других вопросах математики используются понятия целой и дробной частей действительного числа.
В программу школ и классов с углубленным изучением математики включены вопросы, связанные с этими понятиями, но на их изложение в учебнике алгебры для 9 класса [1] отведено всего 34 строки. Рассмотрим более подробно эту тему.
Определение 1
Целой частью действительного числа х называется наибольшее целое число, не превосходящее х.
Целая часть числа обозначается символом [х ] и читается так: “целая часть х” или: “целая часть от х ”. Иногда целая часть числа обозначается Е(х) и читается так: “антье х ” или “ антье от х ”. Второе название происходит от французского слова entiere – целый.
Пример.
Вычислить [x], если х принимает значения:
1,5; 3; -1.3; -4.
Решение
Из определения [x] следует:
[1,5] = 1, т.к. 1 Z, 1 Z, 1  1,5 1,5
[ 3 ] = 3, т.к. 3 Z, 3 Z, 3  3 3
[-1,3]=-2, т.к. –2 Z, -2 Z, -2  -1,3 -1,3
[-4] =-4, т.к. -4 Z, -4 Z, -4 -4. -4.
Свойства целой части действительного числа.
1°. [ x ] = x , если х Z Z
2°. [ x ] x [ x ] + 1 x [ x ] + 1
3°. [ x + m ] = [ x ] + m , где m Z Z
Рассмотрим примеры использования этого понятия в различных задачах.
Пример 1
Решить уравнения:
1.1[ x ] = 3
[ x + 1,3 ] = - 5
[ x + 1 ] + [ x – 2] – [x + 3 ] = 5
1.4 [ x ] - 7 [ x ] + 10 = 0 - 7 [ x ] + 10 = 0
Решение
1.1 [ x ] = 3. По свойству 2° данное уравнение равносильно неравенству 3  х 4 х 4
Ответ : [ 3 ; 4 )
[ x + 1,3 ] = - 5. По свойству 2° :
- 5  х + 1,3 - 4 х + 1,3 - 4  - 6,3 - 6,3  х - 5,3 х - 5,3
Ответ : [ -6,3 ; -5,3 )
[ x + 1 ] + [ x – 2 ] – [ x + 3 ] = 5. По свойству 3°:
[ x ] + 1 + [ x ] – 2 – [ x ] – 3 = 5 
 [ x ] = 9 [ x ] = 9  9 9  x 10 (по 2° ) x 10 (по 2° )
Ответ : [ 9 ; 10 )
1.4 [ x ] - 7 [ x ] + 10 = 0 Пусть [ x ] = t , тогда t - 7 [ x ] + 10 = 0 Пусть [ x ] = t , тогда t - 7 t + 10 = 0 - 7 t + 10 = 0   , т.е. , т.е.
  
Ответ : [ 2 ; 3 )  [ 5 ; 6) [ 5 ; 6)
Пример 2.
Решить неравенства:
2.1 [ x ]  2 2
[ x ] > 2
[ x ]  2 2
[ x ] < 2
[ x ] - 8 [ x ] + 15 - 8 [ x ] + 15  0 0

Решение
2.1 Согласно определению [ x ] и 1°, этому неравенству удовлетворяют х
Ответ : [ 2 ;  ). ).
2.2 Решение этого неравенства: х . .
Ответ : [ 3 ;  ). ).
2.3 x < 3
2.4 x < 2
2.5 Пусть [ x ] = t , тогда данное неравенство равносильно системе  
Реклама

  3 3
Ответ : [ 3; 6 ).
2.6 Пусть [ x ] = t , тогда получим . 
Ответ : (- . .
Пример 4.
Постройте график функции y = [ x ]
Решение
1). ООФ: х  R R
2). МЗФ: y  Z Z

3). Т.к. при х О [ m ; m + 1), где m О Z , [ x ] = m, то и y = m, т.е. график представляет совокупность бесконечного множества горизонтальных отрезков, из которых исключены их правые концы. Например, х О [ -1 ; 0 ) Ю [ x ] = -1 Ю y = - 1 ; x О [ 0; 1) Ю [ x ] = 0 Ю y = 0.
Примечание.
1. Имеем пример функции, которая задается разными аналитическими выражениями на разных участках.
2. Кружочками отмечены точки, не принадлежащие графику.
Определение 2.
Дробной частью действительного числа х называется разность х – [ x ]. Дробная часть числа х обозначается символом { x }.
Пример.
Вычислить { x }, если х принимает значение : 2,37 ; -4  ; 3,14 . . .; 5 . ; 3,14 . . .; 5 .
Решение
{ 2,37 } = 0,37 , т.к. { 2,37 } = 2,37- [ 2,37 ] = 2,37 – 2 = 0,37.
 , т.к. , т.к. 
{ 3,14…} = 0,14… , т.к.  { 3,14…} = 3,14…-[ 3,14…] = 3,14…-3= 0,14… { 3,14…} = 3,14…-[ 3,14…] = 3,14…-3= 0,14…
{ 5 } = 0 , т.к. { 5 } = 5 – [ 5 ] = 5 – 5 = 0.
Свойства дробной части действительного числа.
1°. { x } = x – [ x ]
2°. 0  { x } < 1 { x } < 1
3°. { x + m } = { x }, где m О Z
4°. { x } = x , если х О [ 0 ; 1)
5° Если { x } = а , a О [ 0 ; 1), то х =а +m, где m О Z
6°. { x } = 0 , если х О Z.
Рассмотрим примеры применения понятия { x } в различных упражнениях.
Пример 1.
Решить уравнения:
1.1 { x } = 0,1
1.2 { x } = -0,7
{ x } = 2,5
{ x + 3 } = 3,2
{ x } - -  { x } + { x } + 
Решение
По 5° решением будет множество
х = 0,1 + m , m О Z
1.2 По 2° уравнение не имеет корней, х ОЖ
1.3 По 2° уравнение не имеет корней, х ОЖ
По 3° уравнение равносильно уравнению
{ x }+ 3 = 3,2 Ю { x } = 0,2 Ю x = 0,2 + m , m О Z
1.5 Уравнение равносильно совокупности двух уравнений
 Ответ: х Ответ: х = = 
х = = 
Пример 2.
Решить неравенства:
2.1 { x } 0,4 0,4
2.2 { x }  0 0
{ x + 4 } < 4,7

{ x } -0,7 { x } + 0,2 > 0 -0,7 { x } + 0,2 > 0
Решение
2.1 По 5° : 0,4 + m  x < 1 + m, где m О Z x < 1 + m, где m О Z
2.2 По 1° : х О R
По 3° : {x } + 4 < 4,7 Ю { x }< 0,7.
По 5° : m < x < 0,7 + m , m О Z
2.4 Так как { x }  0, то { x } - 1 > 0, следовательно, получим 2 { x } + 1 < 0, то { x } - 1 > 0, следовательно, получим 2 { x } + 1 <  Ю Ю Ю { x } < 1 Ю x О R Ю { x } < 1 Ю x О R
2.5 Решим соответствующее квадратное уравнение:
{ x } - 0,7 { x } + 0,2 = 0 Ю - 0,7 { x } + 0,2 = 0 Ю Данное неравенство равносильно совокупности двух неравенств: Данное неравенство равносильно совокупности двух неравенств: 
Ответ : ( 0,5 + m ; 1 + m )  ( k ; 0,2 + k ), ( k ; 0,2 + k ),
m О Z , k О Z
Пример 3.
Построить график функции y = { x }
Построение.
1). ООФ : x О R
2). МЗФ : y О [ 0 ; 1 )
3). Функция y = { x } периодическая и ее период
T = m , m О Z, т.к. если х О R, то (x+m) О R
Реклама

и (x-m) О R, где m О Z и по 3° { x + m } =
{ x – m } = { x }.
Наименьший положительный период равен 1, т.к. если m > 0, то m = 1, 2, 3, . . . и наименьшее положительное значение m = 1.
4). Так как y = { x } – периодическая функция с периодом 1, то достаточно построить ее график на каком-нибудь промежутке, длиной 1, например, на промежутке [ 0 ; 1 ), тогда на промежутках, получаемых сдвигами выбранного на m, m О Z, график будет таким же.
а). Пусть х О [ 0 ; 1 ), тогда { x } = x и y = x . Получим , что на промежутке [ 0 ; 1 ) график данной функции представляет отрезок биссектрисы первого координатного угла, из которого исключен правый конец.

б). Воспользовавшись периодичностью, получаем бесконечное множество отрезков, образующих с осью Ох угол в 45° , из которых исключен правый конец.
Примечание.
Кружочками отмечены точки, не принадлежащие графику.
Пример 4.
Решить уравнение 17 [ x ] = 95 {x }
Решение
Т.к. { x } О [ 0 ; 1 ), то 95 { x }О [ 0 ; 95), а, следовательно, и 17 [ x ]О [ 0 ; 95 ). Из соотношения
17 [ x ]О [ 0 ; 95 ) следует [ x ]О , т.е. [ x ] может равняться 0 , 1 , 2 , 3 , 4 , и 5. , т.е. [ x ] может равняться 0 , 1 , 2 , 3 , 4 , и 5.
Из данного уравнения следует, что { x } =  , т.е. с учетом полученного множества значений для , т.е. с учетом полученного множества значений для
[ x ] делаем вывод : { x }, соответственно, может равняться 0 ; 
Т. к. требуется найти х, а х = [ x ] + { x }, то получаем, что х может равняться
0 ; 
Ответ : 
Примечание.
Аналогичное уравнение предлагалось в 1 туре краевой математической олимпиады для десятиклассников в 1996 году.
Пример 5.
Построить график функции y = [ { x } ].
Решение
 ООФ : х О R, т.к. { x }О [ 0 ; 1 ) , а целая часть чисел из промежутка [ 0 ; 1) равна нулю, то данная функция равносильна y = 0 ООФ : х О R, т.к. { x }О [ 0 ; 1 ) , а целая часть чисел из промежутка [ 0 ; 1) равна нулю, то данная функция равносильна y = 0
y
 0 x 0 x
Пример 6.
Постройте на координатной плоскости множество точек, удовлетворяющих уравнению { x } =
Решение
Т. к. данное уравнение равносильно уравнению х =  , m О Z по 5°, то на координатной плоскости следует построить множество вертикальных прямых х = , m О Z по 5°, то на координатной плоскости следует построить множество вертикальных прямых х = + m, m О Z + m, m О Z
       y y
   
     0 0   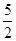 x x
Список литературы
Алгебра для 9 класса: Учеб. пособие для учащихся школ и классов с углубл. изучением математики /Н. Я. Виленкин и др., по ред. Н. Я. Виленкина.- М. Просвещение, 1995 г.
В. Н. Березин, И. Л. Никольская, Л. Ю. Березина Сборник задач для факультативных и внеклассных занятий по математике - М. 1985
А. П. Карп Даю уроки математики - М., 1982 г.
Журнал “Квант”, 1976, № 5
Журнал “Математика в школе”: 1973 №1, №3; 1981 №1; 1982 №2; 1983 №1; 1984 №1; 1985 №3.
|