В. М. Казиев
1. О некоторых принципах анализа и моделирования экосистем
Многие задачи информатизации и экологизации тесно связаны и базируются на фундаментальных принципах системного анализа, управления, экологии, методах математики и информатики. При моделировании экосистем, на наш взгляд, необходим учет важных принципов [1]:
экологию человека (прикладную) следует понимать как науку, занимающуюся изучением поведения человека по отношению к окружающей среде и выработке рациональных (экологически обоснованных) норм поведения в окружающей среде, а прогресс этой науки невозможен без методов информатики, имитационного моделирования и прогнозирования;
привлекательные для исследователя хорошо формализованные и структурированные модели экосистем часто можно строить лишь при достаточно общих, хотя и теоретически важных гипотезах, огрублении, а модели должны учитывать основные процессы в экосистеме, следовательно, в первом приближении можно ограничиться простыми для изучения и использования моделями, гипотезами - для отработки эффективных технологий моделирования;
необходимо исходить из общедоступной входной информации, использовать методы информатики, математики её получения при недостатке информации, так как зачастую невозможно или дорого провести соответствующий экомониторинг;
необходимо использовать как классические представления или описания математических моделей, так и неклассические модели, позволяющие, например, учитывать пространственную структуру экосистемы - клеточные автоматы и фракталы, структуру и иерархию подсистем экосистемы - графы и структуры данных, опыт и интуицию - эвристические и экспертные процедуры и др., а также различные операции моделирования;
обучение и адаптация простых моделей должны сочетаться с использованием качественного алгоритмического (а также - программного) обеспечения, гибких технологий использования их, например, имитационных технологий;
интерфейсно - ориентированное обеспечение этих моделей должно быть дружественно и привычно для пользователя - непрофессионала (например, - эколога);
декомпозиция, агрегирование экосистем (моделей) должны происходить по функциональным критериям, например, по управлению траекторией экосистемы, управление экосистемой же должно быть конечной целью моделирования, причем по своему характеру оно отличается от управления техническими системами, например, - тем, что необходимо при моделировании динамически переупорядочивать связи в системе;
Реклама

необходимо учитывать системную, структурную активность и сложность экосистемы - динамическую, вычислительную и структурную как и внутрисистемную способность экосистемы к саморегулированию, к противостоянию, возмущениям среды, ибо в процессе эволюции экосистемы она претерпевает - в соответствии с принципами синергетики, изменения, которые позволяют экосистеме максимизировать контакт с внешней окружающей средой в целях поиска эффективных обратных связей (см. [2]);
модель, особенно, компьютерная, должна быть пригодной для развития экологической, математической, компьютерной, информационной, технологической культуры пользователей;
модель должна поддерживать весь жизненный цикл модели - от содержательной постановки задачи до проектных решений;
математическое моделирование, если учитывать длительность экологических процессов, становится мощным, а часто и единственным, средством установления связей в экосистеме, определения, описания, изучения инвариантов, изоморфизмов экосистем; изучение их должно быть увязано с анализом сопутствующих проблем экоэнергоинформатики.
2. Процедура интегральной оценки воздействия загрязнителей
Рассмотрим n основных загрязнителей экосистемы, выделяемых экспертным путем, например. Концентрацию загрязнителя номер i обозначим через х(i), i=1,2,...,n, а оценку загрязнения среды - через y. Будем, для простоты, различать только 3 случая:
1) слабо выраженное загрязнение - 0 y(1) 1/3 ;
2) средне выраженное загрязнение - 1/3 y(2) 2/3 ;
3) сильно выраженное загрязнение - 2/3 y 1.
Под у понимается некоторая интегральная характеристика, оценка суммарного воздействия загрязнителей, например, она может быть ассоциирована с вероятностью загрязнения; оценки y(1), y(2) и y(3) могут быть выражениями оптимистической, реалистической и пессимистической оценок загрязнения среды.
Имитационная процедура моделирования состоит в следующем. Проводятся однофакторные эксперименты по нахождению ряда теоретико-экспериментальных зависимостей вида y(i)=f(x(i))=f(i), i=1, 2,..., n, где y(i) - оценка вклада i-го загрязнителя в общее загрязнение среды. Затем, используя эти зависимости в качестве базисных функций, в результате нелинейного регрессионного анализа по базисной системе {f(i)} строятся зависимости вида y(j)=F(y(1),y(2),...,y(n)), j=1,2,3. При этом учитывается эффект суммирования влияния отдельных загрязнителей. Определяются оценки среднего ожидаемого загрязнения и его дисперсии для данной экологической системы: M=(y(1)+4y(2)+y(3))/6, =(y(3)-y(1))/6.
Реклама

Приведенная процедура моделирования, при всей её простоте, технологична и, что наиболее важно, - позволяет оценивать загрязнение экосистемы, причем с априорными оценками математического ожидания и дисперсии, что актуально при экологическом прогнозировании, когда необходима априорная и достоверная информация о загрязнении, о базовых индексах состояния окружающей среды [3]. Эта процедура - хорошая иллюстрация принципов, изложенных в пункте 1. Покажем это на примере.
Рассмотрим экосистему, в которой загрязняющими факторами являются 11 загрязнителей: сероводород, аммиак, двуокись углерода, двуокись азота, серная кислота, ацетон, двуокись серы, стирол, фтористый водород, окись углерода и этилацетат. Выбор загрязнителей обусловлен как принципом 2, так и экосредой, для которой были найдены общедоступные экспериментальные данные, т.е. принципом 3. По вышеприведенной имитационной процедуре моделирования для слабо загрязняемых участков системы, например, вдали от источника загрязнения, получена зависимость по оценке влияния концентрации этих загрязнителей на человека:
y(1)=exp(-1.79+2.89x(1)+1732.87x(2)+11002.40x(3)+93.67x(4)+1980.42x(5)+
+1.58x(6)+26.16x(7)+34.66x(8)+42.01x(9)+3.47x(10)+0.05x(11)).
Для тестового примера (случай слабого загрязнения): х(1)=х(2)=х(3)=0, х(4)=х(5)=х(6)=х(7)=0.0001, х(8)=х(9)=0.001, х(10)=х(11)=0.01 (мг/л) получаем оценку загрязненности этого модельного участка среды y(1)=0.228.
При этом, используя аналогичные оценки для случаев средне и сильно загрязнённых участков, получим y(2)=0.556 и y(3)=0.979, что вполне согласуется с вышеприведенными оценками для 3 случаев загрязнения. Из этих оценок легко найти оценку математического ожидания загрязнения среды и его дисперсии: М=0.572, =0.016 . Отметим, что если все х(i)=0 (i=1-11), то, например, y(1)=0.1. Это может быть отражением как меры адекватности модели, так и отражением факта наличия в среде остаточного загрязнения (до и после выброса загрязнителей).
Из приведенного примера видно, что модель может быть полезна для планирования экологических мероприятий.
Компьютерная модель реализована автором (рис. 1а, б).
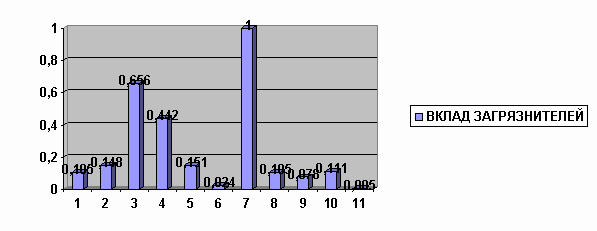 Рис. 1а. Гистограмма влияния загрязнителей на человека Рис. 1а. Гистограмма влияния загрязнителей на человека
Рис. 1б. Гистограмма влияния загрязнителей на животное
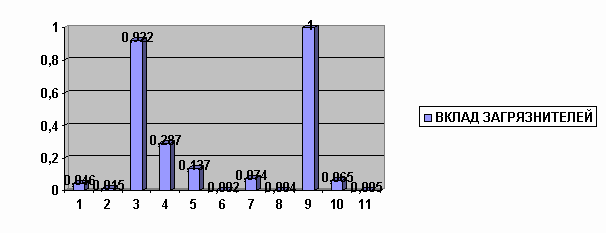
3. Процедура качественной оценки экологических воздействий и её использование при разработке экспертной системы
В ряде экологических проблем часто достаточно качественно оценить экологические воздействия, особенно, более существенные и определить причинно-следственные связи между воздействиями (человека, например) и вектором состояния экосистемы x, x=(x(1), x(2), ... , x(n)), где х(i) - фактор экологического состояния, i=1,2,...,n. Такого рода модели не позволяют нам оценить всю сложную и динамическую цепь взаимовлияний экологических параметров среды, но являются когнитивным инструментарием на начальных стадиях исследования экосистемы, например, на этапе формализации и структурирования системы.
Предлагается следующая процедура моделирования. Выбирается, например, экспертным путем вектор состояния экосистемы x=(x(1),x(2),...,x(n)) , - рассматриваемая область (или экониша), а также граничные векторы состояния среды a=(a(1),a(2),...,a(n)), b=(b(1), b(2),...,b(n)), где a(i)=min{x(i)}, b(i)=max{x(i)} . Составляется матрица V из элементов v(i,j), где v(i,j) - степень влияния x(i) на x(j), i=1,2,...,n. При этом можно использовать, например, модели корелляционного анализа, графовые или же динамические [4]. Далее выбираем начальное состояние х(0) и проводим имитационные расчеты по заданной временной сетке. Управление моделью (траекторией эволюции системы) можно осуществлять изменениями параметров x(i), a(i), b(i), v(i,j) или моделей взаимодействия, выбираемых из некоторого банка моделей [4], а также динамическим переупорядочиванием связей в экосистеме (модели). Наконец, оцениваем эффективность j-ой траектории (имитационного варианта номер s, приводящего к решению номер r, 1 r R): E(r) = c(s)g(s, r; x), c(s)=1, 1 r N, где суммирование ведётся от 1 до R, c(s) - экспертная оценка значимости цели номер s, g(s, r; x) - функционал эффективности траектории s приводящей к цели r. Определяем вероятность p(z, k) предпочтения траектории номер z другой траектории с номером k и функция правдоподобия этого предпочтения W:
d(z, k) N-d(z, k)
p(z, k)= p(k)/(p(k)+p(z)), W= p(z, k) (1-p(z, k)) ,
z<k
где N- число траекторий, p(z) и p(k) - вероятности предпочтений для траекторий номер z, k, соответственно, d(z, k) - экспертная (сравнительная) оценка траекторий z и k (его можно взять, в частности, равным сумме оценок или баллов, при которых траектория z предпочиталась траектории k).
Заметим, что более сложная и формализованная модель получается, если:
1) использовать гипотезу - воздействия или отклики воздействий образуют марковскую цепь {Х(j,h(j))}, j=1,2,...,J с матрицей переходных вероятностей h(j) из элементов h(j; z, k);
2) повторять имитационные расчеты с различными вероятностями p(z) и p(k), уточняемыми каждый раз, например, следующим образом (q(z) - экспертная оценка траектории z, например, сумма баллов, в которой отмечалась траектория номер z ): p(z):=q(z)/(N (1/(p(z)+p(j)))). Суммирование ведётся по всем z=1, 2,…, J, z k.
Данная процедура и её модификации позволяют построить экспертные системы прикладной экологии. Одна из таких систем построена автором и Тебуевым М. c использованием аппарата нечетких множеств и нечеткой логики [5]. Не вдаваясь в принципы разработки, укажем одну её предметную область.
Пусть для определения экологических факторов деятельности человека выбраны n воздействий человека на среду и набор из m индикаторов состояния, наиболее важные (по мнению ряда экспертов). В качестве тестового примера будем использовать, в соответствии с вышеприведенным принципом 3, данные работы [6]. Воздействие, соответствующее каждому действию и каждому фактору описывается через амплитуду и важность. Амплитуда - это мера общего уровня, масштаба воздействия, а важность - мера значимости данного действия в конкретном случае. Это позволяет отделить фактические данные об амплитудах от субъективных оценок важности. Амплитуда оценивается от -10 до 10. Амплитуда положительна (отрицательна), если влияние воздействия полезно (вредно). Важность измеряется в баллах от 0 до 9: 0 - максимально отрицательное воздействие, 1 - значительно отрицательное, 2 - выраженное отрицательное, 3 - некоторое отрицательное, 4 - слабое отрицательное, 5 - слабое положительное, 6 - некоторое положительное, 7 - выраженное положительное, 8 - значительное положительное, 9 - максимально положительное.
Приведем сценарий диалога с экспертной системой.
Экспертная система (04.06.1996 - Вторник, 11: 23: 37)
Входные данные:
1. Контроль над эррозией: 0.6
2. Сооружения для отдыха: 0.1
3. Ирригация: 0.9
4. Сжигание отходов: 1.0
5. Строительство мостов и дорог: 0.6
6. Искусственные каналы: 0.5
7. Плотины: 0.3
8. Туннели и подземные сооружения: 0.9
9. Взрывные и буровые работы: 0.45667
10. Открытая разработка: 0.567
11. Вырубка лесов: 0.345
12. Коммерческая охота и рыбная ловля: 0.234
13. Растениеводство: 0.678
14. Разведение и выпас скота: 0.648
15. Химическая промышленность: 0.2456
16. Лесопосадки: 0.54846
17. Удобрения: 0.6
18. Разведение и регулирование диких животных: IGNORE
19. Автомобильное движение: 0.6
20. Трубопроводы: 0.0
21. Хранилища отходов: 0.0
22. Использование ядохимикатов: 0.2
23. Течи и разливы: 0.0
Выходные данные (принятие решения):
1. Состояние почвы: 0.55177 (слабое положительное)
2. Состояние поверхностных вод: 0.52969 (слабое положительное)
3. Качественный состав вод: 0.62299 (некоторое положительное)
4. Качественный состав воздуха: 0.61298 (некоторое положительное)
5. Температура воздуха: 0.48449 ( слабое отрицательное)
6. Эррозия: 0.59051 (слабое положительное)
7. Деревья и кустарники: 0.54160 (слабое положительное)
8. Травы: 0.59051 (слабое положительное)
9. Сельхозкультуры: 0.51698 (слабое положительное)
10. Микрофлора: 0.48702 (слабое отрицательное)
11. Животные суши: 0.59804 (слабое положительное)
12. Рыбы и моллюски: 0.51525 (слабое положительное)
13. Насекомые: 0.56000 (слабое положительное)
14. Заболачивание территории: 0.50000 (слабое положительное)
15. Курорты на суше: 0.52729 (слабое положительное)
16. Парки и заповедники: 0.54668 (слабое положительное)
17. Здоровье и безопасность: 0.62870 (некоторое положительное)
18. Занятость людей: 0.51196 (слабое положительное)
19. Плотность населения: 0.55539 (слабое положительное)
20. Соленость воды: 0.48750 (слабое отрицательное)
21. Солончаки: 0.57000 (слабое положительное)
22. Заросли: 0.62935 (некоторое положительное)
23. Оползни: 0.70588 (выраженное положительное)
Список литературы
Казиев В.М. Математические и компьютерные модели экологических систем. Тезисы докладов региональной научной конференции “Современные проблемы экологии”, часть 2, Краснодар-Анапа, 1996, с.87.
Большаков В.Н., Криницин С.В., Кряжимский Ф.М., Мартинес Рика Х.П. Проблемы восприятия современным обществом основных понятий экологической науки. “Экология”, N 3, 1996, с. 165-170.
Пых Ю.А., Малкина-Пых И.Г. Об оценке состояния окружающей среды. Подходы к проблеме. “Экология”, N 5, 1996, с.323-329.
Казиев В.М. Некоторые оптимизационные задачи управления экосистемами. Доклады А(Ч)М АН, N 1, 1994, с. 19-21.
Прикладные нечеткие системы. Под редакцией Т.Тэрано, К.Асаи, М.Сугэно. М., Мир, 1993.
Экологические системы. Адаптивная оценка и управление. Под ред. К.С.Холинга. Мир, 1981.
|