Б. К. Лебедев
Введение
Ввиду грандиозной сложности трассировка СБИС разбивается на два этапа: глобальная и детальная. При глобальной трассировке решается две задачи: разбиение коммутационного поля на области и распределение соединений по областям. Детальная трассировка заключается в проектировании топологии соединений внутри областей. Традиционно коммутационное поле разбивается на два типа областей: канал и коммутационный блок (switchbox).
В классической постановке коммутационный блок - это прямоугольная область на всех четырех сторонах которой размещены в фиксированных позициях терминалы (выводы). Терминалы помечены цифрами - номерами подключенных к ним цепей. Задача состоит в том чтобы сделать терминалы каждой цепи электрически связными так, чтобы цепи и переходные отверстия, реализующие связи, вписывались в область трассировки и удовлетворяли конструктивным ограничениям.
Обычно проблема решается с дополнительно наложенными ограничениями, одним из которых является число слоев. В работе рассматривается двухслойная трассировка.
Задача трассировки в ограниченной прямоугольной области является NP-полной. Поэтому несмотря на обилие разработок, проблема построения эффективного трассировщика является актуальной.
Большинство алгоритмов трассировки в коммутационном блоке основываются на эвристиках, реализующих в той или иной степени идею последовательной трассировки [1,2,3,4]. В процессе прокладки на каждом шаге используются правила направленные на минимизацию воздействия прокладываемой цепи на непроложенные. Однако в полной мере проэкстраполировать все ситуации не представляется возможным. Это приводит к необходимости дополнительной трассировки. Основу этих алгоритмов составляют два принципа: локальная деформация, разрыв части соединений и перетрассировка их различными методами [2]. Но к сожалению и здесь возникает проблема очередности перетрассируемых соединений. В связи с этим интерес представляют комбинаторные алгоритмы, оперирующие со всеми соединениями. Среди математических методов обеспечивающих комбинаторный подход к решаемой задаче в последнее время наибольшее распространение получили методы моделирования отжига и эволюционного программирования. Особый интерес представляют генетические алгоритмы, основанные на механизмах природной селекции и генетики [5,6].
Реклама

В работе предложены новые генетические процедуры для решения задачи трассировки в коммутационном блоке, учитывающие знания о проблемной области. Разработаны новые структуры и принципы кодирования хромосом, модифицированные генетические операторы, и структура генетического поиска. Проведены экспериментальные исследования.
1. Формулировка задачи, основные термины и обозначения
Дадим формальное описание задачи трассировки коммутационного блока (ЗТКБ). Даны: верхний ряд контактов К1={к1i
} и нижний ряд контактов К2={к2i
}, пронумерованные слева направо, левый ряд контактов К3={к3i
} и правый ряд контактов К4={к4i
}, пронумерованные сверху вниз, и расположенные на сторонах прямоугольника. К ним соответственно подходят множества цепей N1={n1i
}, N2={n2i
}, N3={n3i
}, N4={n4i
}, N=N1 ÈN2 ÈN3 ÈN4 - общее множество цепей. На область трассировки (ОТ) наложена сетка (рис.1). Терминалы (контакты) совпадают с линиями сетки. Соединения подходят к контактам и распространяются в области трассировки только по линиям сетки.
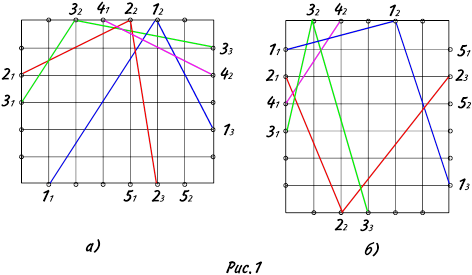
На рис.1в ОТ2 представляет собой развернутое на 90° ОТ1 на рис.1а. Каждая цепь представляется в виде связного набора вертикальных и горизонтальных фрагментов. Не допускаются наложения друг на друга вертикальных и горизонтальных фрагментов, принадлежащих различным цепям, не допускается их пересечение в совместном эскизе топологии. Каждая цепь разбивается на двухтерминальные соединения (ДС). В простейшем случае разбиение на ДС осуществляется при последовательном просмотре столбцов сетки слева направо, начиная с крайнего слева столбца. На рис.1 цепь 1 подходит к терминалам (11
,12
,13
), цепь 2 к (21
,22
,23
), цепь 3 к (31
,32
,33
), цепь 4 к (41
,42
), цепь 5 к (51
,52
). На рис.1 цепь 1 разбивается на ДС11=(11
,12
) и ДС12=(11
,13
), цепь 2 на ДС21=(21
,22
) и ДС22=(22
,23
), цепь 3 на ДС31=(31
,32
) и ДС32=(32
,33
).
Каждое ДС реализуется в виде связного набора горизонтальных и вертикальных фрагментов, связывающие соответствующие два терминала. В общем случае разбиение цепи на ДС осуществляется следующим образом. На множестве терминалов, связываемых одной цепью, алгоритмом Прима строится минимальное связывающее дерево. Каждое ребро этого дерева определяет ДС.
Реклама

Обозначим через S={si
|i=1,2,...,n} множество всех ДС. Пусть в области трассировки реализовано с соблюдениями всех ограничений множество ДС S1, S1ÌS, и пусть S2 множество ДС, которые не могут быть реализованы без нарушений в ОТ, заполненной S1, S2ÌS, S1ÈS2=S. Обозначим через d - мощность S2, т.е. d=½S2½.
В качестве оценки качества трассировки будет использоваться критерий:
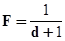
Цель оптимизации - максимизация F совпадает с минимизацией d, где d число нереализованных ДС.
В случае полной реализации цепей, т.е. при d=0 (или F=1), оценкой качества служит критерий:
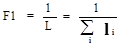
где li
суммарная длина реализованной (протрассированной) цепи ni
и L - суммарная длина всех цепей.
2. Генетический алгоритм трассировки в коммутационном блоке
Особенностью генетического алгоритма, моделирующего процесс естественной эволюции, является то, что оперирование производится с кодами решений. Каждому решению соответствует одна или несколько хромосом. Хромосомы состоят из генов. Гены могут иметь различные значения. Генетические алгоритмы работают с популяцией решений. Решения получаются на основе декодирования хромосом. Разработка генетического алгоритма включает этапы разработки структуры хромосом и принципов их кодирования и декодирования, генетических операторов, методики формирования исходной популяции и ее селекции, общей структуры генетического поиска.
2.1. Структура хромосом, их кодирование и декодирование
Построим множество 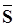 горизонтальных участков горизонтальных участков 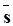 i
Î i
Î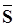 , являющихся проекциями всех двухтерминальных соединений , являющихся проекциями всех двухтерминальных соединений 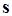 i
Î i
Î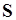 , т.е. каждому , т.е. каждому 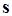 i
соответствует i
соответствует 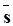 i
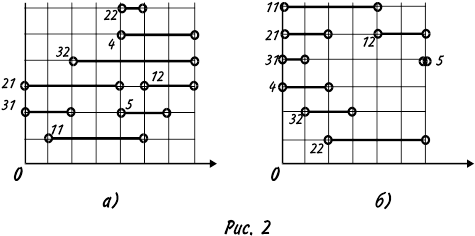
. На рис.2а и 2б приведены множества i
. На рис.2а и 2б приведены множества 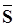 для ОТ1 и ОТ2. для ОТ1 и ОТ2.
Обозначим через O(li
) и O(ri
) координаты по горизонтали левого и правого конца участка 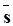 i
. i
.
Разобьем множество 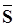 , на подмножества , на подмножества 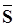 k
, в соответствии со следующими правилами: k
, в соответствии со следующими правилами:
1. 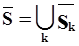 , " (ij) [ , " (ij) [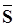 i
Ç i
Ç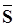 j
=0] j
=0]
2. В пределах каждого 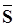 k
все участки накладываются друг на друга, т.е k
все участки накладываются друг на друга, т.е
" (ij ½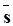 i
Î i
Î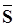 k
& k
& 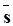 j
Î j
Î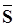 k
) [(O(lj
) £ O(li
) £ O(rj
))Ú((O(lj
) £ O(ri
) £ O(rj
))]. k
) [(O(lj
) £ O(li
) £ O(rj
))Ú((O(lj
) £ O(ri
) £ O(rj
))].
Подмножество 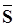 k
пронумерованы и сформированы так, что все левые концы участков k
пронумерованы и сформированы так, что все левые концы участков 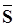 k
расположены левее левых концов участков k
расположены левее левых концов участков 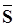 k
+1
, т.е. "(ij ½ k
+1
, т.е. "(ij ½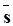 i
Î i
Î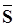 k
& k
& 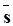 j
Î j
Î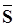 k+1
) [(O(li
) < O(lj
) )]. k+1
) [(O(li
) < O(lj
) )].
Линейный алгоритм разбиения 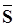 представлен в работе [7]. Разбиению представлен в работе [7]. Разбиению 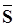 соответствует разбиение S. соответствует разбиение S.
Для участков, представленных на рис.2а, разбиение S имеет вид:
S1
={21,31,11} ,S2
={32,4,12,22,5};
Для участков, представленных на рис.2б, разбиение S имеет вид:
S1
={11,21,4,31}, S2
={22,32}, S3
={12,5}.
Для ОТ1, представленной на рисунке 1а, m=5, для ОТ2, представленной на рис.1б, m=6, где m - число горизонтальных линий на ОТ.
Формируем на основе каждого Sk
вектор Vk
путем добавления в Sk
нулевых элементов, так, чтобы мощность Vk
была равна m, и фиксируем взаимное расположение элементов.
Для ОТ1: V1
=<31,0,11,21,0>; V2
=<32,4,12,22,5>.
Для ОТ2: V1
=<11,21,4,31,0,0>; V2
=<22,32,0,0,0,0>; V3
=<12,5,0,0,0,0>.
Полученный после дополнения набор векторов V={Vi
} будем называть решением задачи трассировки коммутационного блока.
Представим решение в виде хромосомы. Хромосома Hm
является упорядоченной совокупностью генов 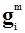 . Ген . Ген 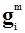 является одним из вариантов вектора Vi
, т.е. значением является одним из вариантов вектора Vi
, т.е. значением 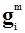 является некоторый вектор является некоторый вектор 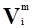 . Гены . Гены 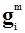 и и 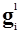 хромосом Hm
и Hl
гомологичны, они одинаковы по составу элементов, соответствуют одному и тому же подмножеству Si
двухтерминальных соединений, но отличаются порядком расположения элементов. хромосом Hm
и Hl
гомологичны, они одинаковы по составу элементов, соответствуют одному и тому же подмножеству Si
двухтерминальных соединений, но отличаются порядком расположения элементов.
Декодирование хромосомы осуществляется с помощью процедуры декодирования, использующей идеи алгоритма «левого конца» при канальной трассировке. Как и при канальной трассировке будем называть горизонтальные линии опорной сетки ОТ магистралями, пронумерованными сверху вниз.
Процедура декодирования заключается в последовательном заполнении магистралей, начиная с первой, фрагментами двухтерминальных соединений.
Порядок в котором ДС выбирают для заполнения магистралей задается соответствующей хромосомой и фактически определяется порядком расположения элементов в генах.
Заполнение магистралей двухтерминальными соединениями базируется на трех основных процедурах: укладки, трансформации, резервации.
В процессе укладки ДС в заполняемую магистраль оно может быть уложено либо полностью, либо частично, либо не укладываться вообще.
При полной укладке в заполняемую магистраль полностью помещаются все горизонтальные составляющие ДС и осуществляется подвод к ним всех вертикальных составляющих. Для этого необходимо, чтобы были свободны с одной стороны соответствующий участок горизонтальной магистрали, а с другой стороны вертикальные столбцы, по которым осуществляется прокладка вертикальных составляющих.
Вертикальный столбец считается занятым (зарезервированным) для любой цепи ni
не равной nf
если в нем расположен выше заполняемой магистрали терминал, помеченный цепью nf
и еще не связанный. Если терминал, расположенный выше n-ой магистрали, связывается по вертикали с горизонтальным участком, расположенным на n-ой магистрали, то столбец начиная с магистрали n+1, считается свободным. Изначально все столбцы, подходящие к помеченным цепями терминалам, расположенным на верхней стороне ОТ, считаются занятыми (зарезервированными). Например на рис.3а полностью размещены ДС1, ДС2 ДС3. На рис.3б частично размещены ДС1,ДС2,ДС4. При частичной укладке вводится точка разрыва ДС. Частично уложенное ДС связывает точку разрыва с одним из терминалов исходного ДС.
Точка разрыва вводится таким образом, чтобы у горизонтальной составляющей была максимально возможная длина.
После частичного размещения ДС проводится его трансформация, заключающаяся в том, что терминал, связанный с частично размещенным ДС переносится в точку разрыва. В дальнейшем ДС рассматривается как ДС, связывающее еще не связный терминал с терминалом в точке разрыва.

Возможно введение двух точек разрыва ДС. При этом два фрагмента ДС, связывающие каждый точку разрыва с терминалом исходного ДС, будут уложены, а третий фрагмент, связывающий две точки разрыва, будет укладываться в последующих магистралях. Таким образом исходное ДС трансформируется в ДС, связывающее две точки разрыва. Отметим, что ДС может в процессе укладки подвергаться нескольким последовательным трансформациям. На рис.3б в дальнейшем ДС1, ДС2, ДС4 будут рассматриваться, как ДС связывающие пары несвязных терминалов, помеченных соответственно (11
,1¢2
), (21
,2¢2
),(4¢1
,4¢2
).
Каждый раз после перехода к новой магистрали реализуется процедура резервации цель которой исключение возможности блокировки терминалов, лежащих по краям магистрали. Если терминалы левой и правой сторон коммутационного блока, лежащие на выбранной магистрали помечены цепями, то от них по магистрали проводятся горизонтальные фрагменты. От левого терминала вправо, от правого терминала влево. Фрагмент распространяется до ближайшего свободного столбца.
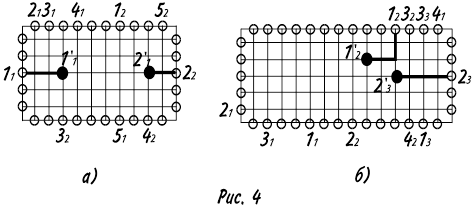
На рис.4а проведены горизонтальные фрагменты от терминалов 11
до 1¢1
и от 21
до 2¢2
. В дальнейшем ДС1 и ДС2 трансформируются, т.е. они будут инцидентны терминалам 1¢1
и 2¢2
соответственно. Перед резервацией анализируется состояние столбцов и если необходимо и существует возможность формируется ближайший к терминалу свободный столбец.
Если есть несколько столбцов, занятых терминалами одной цепи и эти терминалы уже связаны, то их можно объединить в один терминал, что приводит к освобождению столбцов. Например на рис.4в при резервации терминала 23
два столбца заняты терминалами 1¢2
и 12
. 1¢2
входит в ДС(1¢1
, 1¢2
), 12
входит в ДС (12
, 13
), но они связаны и их можно объединить в один терминал1¢2
, при этом ДС(12
,13
) трансформируется в ДС (1¢2
, 13
). Это приводит к освобождению столбца в который можно поместить терминал 2¢3
, связанный горизонтальным фрагментом с резервируемым терминалом 23
.
Представим хромосому Hk
виде матрицы Vk
, где каждый столбец соответствует гену. Магистрали заполняются последовательно, начиная с первой. Заполнение магистралей осуществляется следующим образом. Вначале осуществляется резервация терминалов левой и правой сторон ОТ, лежащих на магистрали. Затем последовательно по строкам, начиная с первой в пределах строки слева направо просматриваются элементы матрицы Vk
. Для каждого выбранного элемента матрицы (ДС) определяется возможность его размещения в формируемой магистрали. Если возможно, то ДС полностью или частично помещается в формируемую магистраль. Если ДС полностью помещается, то оно удаляется из матрицы Vk
. Если ДС помещается частично, то трансформируется и остается в матрице. По окончании просмотра матрицы Vk
осуществляется сжатие всех столбцов, из которых удалялись ДС, снизу вверх. После этого осуществляется переход к заполнению следующей магистрали. Процесс декодирования и заполнения магистралей показан на рис.5 и 6 для ОТ представленных соответственно на рис.1а и 1б. Отметим, что это фактически одна и та же задача трассировки.
Рассмотрим сначала процесс укладки в ОТ1, показанный на рис.1а. На рис.5а показаны два этапа заполнения первой магистрали: резервация и укладка. Вначале осуществляется резервация терминала 33
, лежащего на 1-й магистрали. Для этого от терминала 33
проводится горизонтальный фрагмент до ближайшего свободного столбца. Терминал 33
резервируется терминалом 3¢3
, а ДС32=(32
,33
) трансформируется в ДС32¢=(32
,3¢3
). Затем проводится укладка ДС в первую магистраль. Просматривается матрица Vk
и первым выбирается ДС31=(31
,32
). ДС31 укладывается частично, при этом трансформируясь в ДС31¢=(31
,3¢2
). Следующим из Vk
выбирается ДС32¢, которое полностью помещается в первую магистраль и удаляется из Vk
. Процесс заполнения завершается и Vk
сжимается. На рис.5б заполняется вторая магистраль. Вначале резервируются терминалы 21
и 42
, ДС21=(21
,22
) и ДС4=(41
,42
) трансформируются в ДС21¢=(2¢1
,22
) и ДС4¢=(41
,4¢2
).
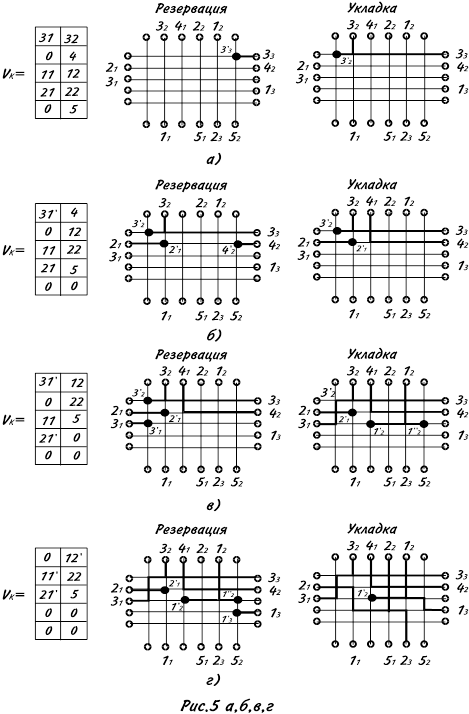
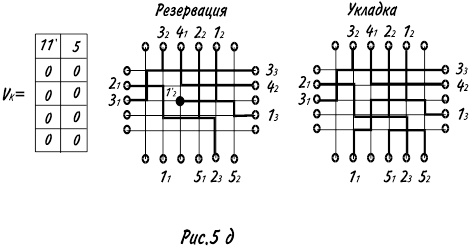
Затем просматривается матрица Vk
. ДС31¢ не помещается, ДС4¢ помещается полностью и удаляется из Vk
, которое потом сжимается. На рис.5в,г,д, показан процесс укладки 3, 4, и 5-й магистралей.
При заполнении 3-й магистрали (рис.5в) в результате трансформации образуются ДС31¢¢=(3¢1
,3¢2
), ДС11¢=(11
,1¢2
), ДС12¢=(1¢¢2
,1¢3
). Полностью помещается ДС31¢, частично ДС12 и ДС11.
При заполнении 4-й магистрали (рис.5г) при трансформации образуется ДС12¢¢=(1¢¢2
,1¢3
). Полностью помещаются ДС12¢, ДС22, ДС21¢.
При заполнении 5-й магистрали (рис.5д) полностью помещаются ДС11¢, ДС5.
Рассмотрим процесс заполнения ОТ2, представленной на рисунке 1б.
На рис.6а заполняется первая магистраль. Вначале резервируется терминал 51
лежащий на 1-й магистрали. ДС5=(51
,52
) трансформируется в ДС5¢=(5¢1
,52
). Затем при просмотре Vk
выбирается ДС11 которое частично укладывается в 1-ю магистраль и трансформируется в ДС11¢=(11
,1¢2
).
При заполнении 2-й магистрали (рис.6б) вначале резервируется терминал 11
при этом ДС11¢ трансформируется в ДС11¢¢=(1¢1
,1¢2
). Для резервации терминала 23
формируется свободный столбец. Для этого терминалы 1¢2
Î ДС11¢¢ и 12
Î ДС12, поскольку они уже связаны, объединяются в терминал 1¢2
, а столбец, занятый терминалом 12
, освобождается. ДС12=(12
,13
)трансформируется в ДС12¢=(1¢2
,13
). После этого терминал 23
резервируется терминалом 2¢3
, а ДС22=(22
,23
) трансформируется в ДС22¢=(22
,2¢3
). При просмотре Vk
полностью во 2-ю магистраль помещается только ДС11¢¢, которое удаляется из Vk
.
При заполнении 3-й магистрали (рис.6в) резервируются терминалы 21
и 52
.Трансформируются: ДС21=(21
,22
) в ДС21¢=(2¢1
,22
), ДС5¢=(5¢1
,52
) в ДС5¢¢=(5¢1
,5¢2
). Полностью помещается только ДС5¢¢, которое удаляется из Vk
.
При заполнении 4-й магистрали (рис.6г) резервируется терминал 41
. ДС4=(41
,42
) трансформируется в ДС4¢=(4¢1
,42
). При просмотре Vk
частично
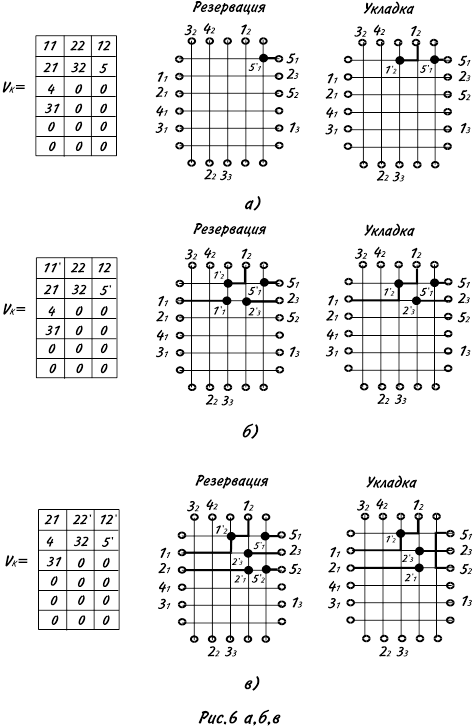
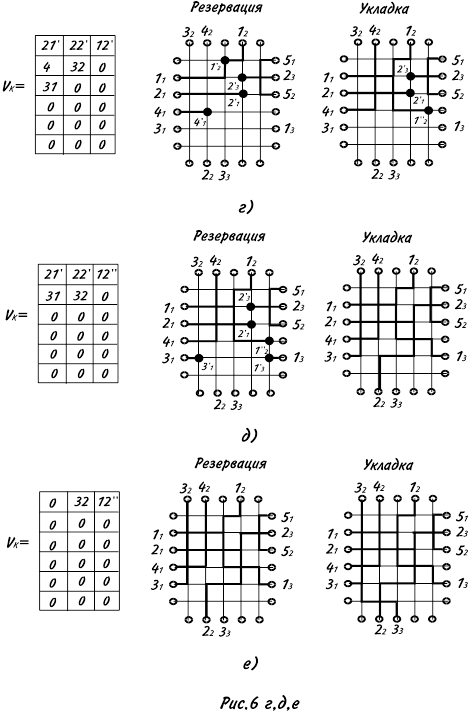
помещается ДС12¢ и полностью ДС4¢. ДС12¢ трансформируется в ДС12¢¢=(1¢¢2
,13
), а ДС4¢ удаляется из Vk
.
При заполнении 5-й магистрали (рис.6д) резервируются терминалы 31
.и 13
. ДС31=(31
,32
) трансформируется в ДС31¢=(3¢1
,32
), а ДС12¢¢=(1¢¢2
,13
) в ДС12¢¢¢=(1¢¢2
,1¢3
). При просмотре Vk
полностью помещаются ДС21¢, ДС22¢, ДС31¢, ДС12¢¢, которые удаляются из Vk
.
При заполнении 6-й магистрали (рис.6е) полностью помещается ДС32.
При заданных способах кодирования ОТ1 и ОТ2, при декодировании хромосом Hk
, соответствующих ОТ1 и ОТ2 и представляемых в виде вышеприведенных матриц Vk
, конечные результаты совпали, хотя это и не является обязательным.
Матрица Vk
просматривается при заполнении каждой магистрали. Размер матрицы Vk
пропорционален числу as
содержащихся в ней ДС.
as
=ak
-an
, где ak
- число терминалов, расположенных на границах ОТ, и an
- число цепей. Отсюда оценка трудоемкости процедуры декодирования пропорциональна O(m*as
).
Генетические операторы
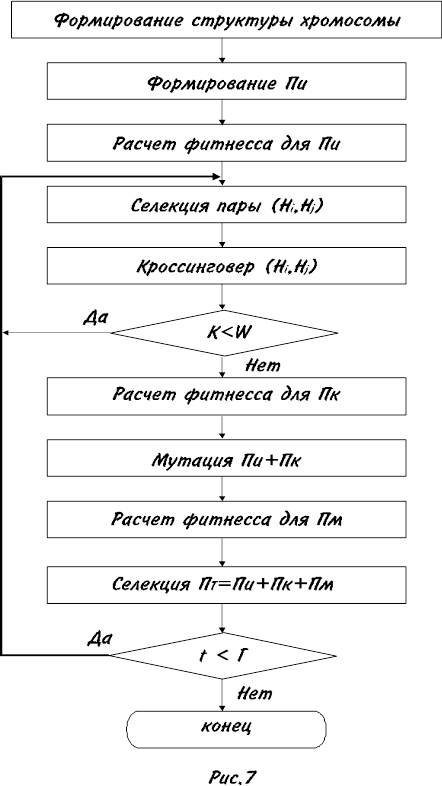
Общая структура генетического поиска представлена на рис.7.
Предварительно осуществляется формирование структуры хромосомы. Эта процедура включает разбиение каждой цепи на ДСj
, разбиение множества ДС на подмножества, определение числа и размера генов в составе хромосомы: определение состава каждого гена (т.е. определение ДС, входящих в каждый ген). Далее, случайным образом генерируется исходная популяция Пи хромосом размером М. Суть случайного формирования в том, что для каждого гена каждой хромосомы случайным образом устанавливается порядок расположения в нем элементов (ДС). Для каждой хромосомы рассчитывается фитнесс. Расчет фитнесса осуществляется на основе декодирования хромосомы, т.е. фактически решения задачи трассировки.
Целью генетического поиска является нахождение такой хромосомы и с таким расположением элементов в генах, которые обеспечивают при декодировании оптимальное значение фитнесса.
Основными генетическими операторами являются кроссинговер и мутация. В нашем случае операция кроссинговер реализуется путем вероятностного выбора родительской пары хромосом и формирования на ее основе потомков путем взаимооднозначного обмена гомологичными генами. В общем случае хромосомы могут обмениваться группами гомологичных генов. Оператор кроссинговера для выбранной пары выполняется следующим образом.
Задается вероятность кроссинговера Pk
. Затем последовательно просматриваются пары гомологичных генов (генов, расположенных в одном и том же локусе хромосом), которые с заданной вероятностью Pk
меняются местами. При выборе пары хромосом для кроссинговера используется ²принцип рулетки², при котором вероятность P(Hi
) Выбора хромосомы Hi
определяется как:
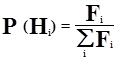 , ,
где Fi
- фитнесс хромосомы Hi
.
Число пар хромосом W является управляющим параметром процедуры генетического поиска.
В результате выполнения операции кроссинговера формируется дополнительная популяция Пк, которая объединяется с Пи и в дальнейшем подвергается мутации. Для каждой хромосомы популяции Пк рассчитывается фитнесс. Операция мутации заключается в выборе гена, который подвергается мутации и мутации этого гена. Мутация гена заключается в случайном выборе пары элементов, входящих в состав гена, и обмене местами их расположения в гене.
Реализация операции мутации осуществляется следующим образом. Задается вероятность мутации PM
, последовательно просматриваются все хромосомы из популяции Пи+Пк, а в хромосоме все гены, и с заданной вероятностью PM
ген мутирует. Мутация заключается в случайном выборе в гене пары элементов, которые затем обмениваются местами. Выполнение оператора мутации приводит к формированию дополнительной популяции Пм, для каждой хромосомы которой рассчитывается фитнесс.
Заключительной операцией в пределах одного поколения является селекция расширенной популяции Пт=Пи+Пк+Пм. В результате селекции на основе ²принципа рулетки² отбирается новая популяция Пи лучших решений, которая является исходной для следующей генерации. Число генераций (поколений) Т, размер популяции М и параметры Рк и Рм являются управляющими параметрами, влияющими на эффективность процесса генетического поиска.
3. Экспериментальные исследования
Алгоритм был реализован на языке С++ для ПЭВМ типа IBMPC.
Первой целью экспериментальных исследований - было нахождение наилучшего сочетания значений управляющих параметров таких, как PМ
, PК
, М и Т, где М - объем популяции.
Исследования проводились следующим образом. Для каждого примера сначала фиксировалось значение РМ
и изменялись параметры PК
и М. Затем фиксировалось значение PК
и изменялись PМ
и М. Для каждого набора значений PМ
, PК
, и М проводилась серия из 10 экспериментов в результате которой определялось среднее, максимальное и минимальное значение Т, при котором не наблюдалось улучшения лучшего решения. Было установлено, что при значении PК
=0,4 и PМ
=0,1, М=50 и Т=130 обеспечивается нахождение оптимального решения.
Исследования трудоемкости алгоритма показали, что при фиксированных значениях PМ
, PК
, М и Т она имеет линейную зависимость и пропорциональна O(N), где N - число связываемых контактов.
Заключение
В статье был представлен генетический алгоритм трассировки в коммутационном блоке. При разработке структуры и методов кодирования и декодирования хромосом, генетических операторов использовались специфические знания о проблеме. Исследования показали достаточно высокую эффективность разработки генетических процедур.
Источником усовершенствования может стать правильная настройка параметров управления. Другая возможность состоит в том, чтобы при частичной укладке вводить более двух точек разрыва, что приведет к трансформации укладываемого ДС в несколько ДС.
Понятие верхней и нижней сторон ОТ относительно, поскольку ОТ можно развернуть на 180° и верхняя сторона станет нижней, а нижняя верхней. В связи с этим возможно использовать прием, заключающийся в чередовании порядка заполнения магистралей: первая сверху, первая снизу, вторая сверху, вторая снизу и т.д. При заполнении n-ой сверху магистрали последовательно просматриваются строки матрицы Vk
, начиная с первой, а при заполнении n-й снизу магистрали строки матрицы Vk
просматриваются в обратном порядке, начиная с последней.
Средством повышения сходимости генетического алгоритма может стать представление решения в виде двух хромосом H1
k
и H2
k
. При этом ОТ представляется, как и было показано выше, в виде двух ОТ1 и ОТ2 одновременно. Структура H1
k
соответствует ОТ1, а структура H2
k
соответствует ОТ2. Заполнение магистралей производится последовательно и попеременно то в ОТ1, то в ОТ2. При трансформации некоторого ДС в ОТ1 осуществляется соответствующая трансформация в ОТ2, и наоборот.
Представление одного решения в виде двух хромосом, дает возможность использовать генетический оператор комбинирования набором хромосом в одном решении. При этом пара родительских решений дает четыре потомка.
Отметим, что предложенный подход полностью применим для «безсеточной» трассировки соединений разной ширины. Для этого на основе конструктивных параметров (ширина цепи, расстояние между цепями и окнами, размеры переходных контактов) рассчитываются допустимые расстояния между фрагментами. В этом случае задача трассировки сводится не к распределению фрагментов по магистралям, а к упаковке фрагментов. Модернизированная процедура декодирования будет последовательно размещать ДС «прижимая» их на допустимую величину к ранее размещенным. В качестве базиса выбирается верхняя сторона ОТ. Результатом работы будут физические координаты размещенных фрагментов.
Путем модификации процедур укладки, трансформации и резервации можно использовать выше приведенную методику для трассировки с числом слоев больше двух.
Список литературы
W.K.Luk. A greedy switch box router INTEGRATION, the VLCI Journal, 3: pp. 129-149, 1985.
H.Shin and A.Sangiovanni Vincentelli. Mighty: a rip-up and reroute detailed router. Proceedings of IEEE International conference on Computer-Aided Design, pages 2-5, November 1986.
J.P.Cohoon and P.L.Heek. Beaver: A computational geometry based tool for switch box routing. IEEE Transactions on Computer-Aided Design, 7:684-697,June,1988.
M.Marek-Sadowska. Switch box routing: a retrospective. INTEGRATION, the VLCI Journal, 13, pp. 36-65 1992.
Y.L. Lyn, Y.C. Hsu, and Tsai. Silk: A simulated evolution router. IEEE Transactions on Computer-Aided Design, 8:1108-1114,October,1989.
T.Cho, S. Pyo, and J. Heath. Parallex: A parallel approach to switch box routing. IEEE Transactions on CAD of Integrated Circuits and Systems, 13:684-693, June 1994.
Лебедев Б.К. Канальная трассировка на основе генетических процедур. Интеллектуальные САПР. Таганрог: ТРТУ, 1997, N3(6) с. 53-60.
|