Курсовая работа
на тему:
"Решение транспортных задач
методом потенциалов"
Содержание.
1. Линейная транспортная задача
2. Составление опорного плана
3. Метод потенциалов
3. Список использованной литературы
1. Транспортная задача.
Транспортная задача ставится следующим образом: имеется m
пунктов отправления,
в которых сосредоточены запасы каких-то однородных грузов. Имеется n пунктов назначения подавшие заявки соответственно на груза. Известны стоимости р
i
j
перевозки единицы груза от каждого пункта отправления до каждого пункта назначения. Все числа р
i
j
,
образующие прямоугольную таблицу заданы. Требуется составить такой план перевозок (откуда, куда и сколько единиц поставить), чтобы все заявки были выполнены, а общая стоимость всех перевозок была минимальна.
Далее, предполагается, что
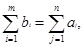 1 1
где bi
есть количество продукции, находящееся на складе i
, и aj
– потребность потребителя j
.
Замечание.
Если 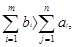 то количество продукции, равное то количество продукции, равное 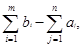 остается на складах. В этом случае мы введем "фиктивного" потребителя n
+1 с потребностью остается на складах. В этом случае мы введем "фиктивного" потребителя n
+1 с потребностью 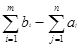 и положим транспортные расходы pi
,
n
+1
равными 0 для всех i
. и положим транспортные расходы pi
,
n
+1
равными 0 для всех i
.
Если 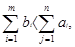 то потребность не может быть покрыта. В этом случае начальные условия должны быть изменены таким образом, чтобы потребность в продукции могла быть обеспечена. то потребность не может быть покрыта. В этом случае начальные условия должны быть изменены таким образом, чтобы потребность в продукции могла быть обеспечена.
Обозначим через xij
количество продукции, поставляемое со склада i
потребителю j
. В предложении (1) нам нужно решить следующую задачу (математическая модель транспортной задачи):
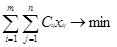
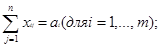 2 2
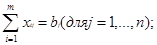
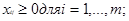
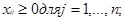
Транспортную задачу мы можем характеризовать транспортной таблицей
и таблицей издержек
:
| а1
|
…
|
а
n
|
b1
.
.
.
bm
|
.
|
| .
|
| .
|
| .
|
| .
|
| .
|
| p11
|
…
|
p1n
|
| .
|
.
|
| .
|
.
|
| .
|
.
|
| pm1
|
…
|
pmn
|
Допустимый план перевозок
будем представлять в виде транспортной таблицы:
| а1
|
…
|
а
n
|
b
.
.
.
bm
|
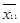

|
…
|
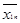
|
| .
|
.
|
| .
|
.
|
| .
|
.
|
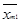
|
…
|

|
Cумма элементов строки i должна быть равна bi
, а сумма элементов столбца j должна быть равна aj
, и все  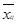 должны быть неотрицательными.
должны быть неотрицательными.
Пример 1.
| 5
|
6
|
3
|
5
|
9
|
| 6
|
4
|
7
|
3
|
5
|
| 2
|
5
|
3
|
1
|
8
|
Мы получаем следующую задачу:
х11
+х12
+х13
+х14
+х15
=15,
х21
+х22
+х23
+х24
+х55
=15,
х31
+х32
+х33
+х34
+х35
=20,
х11
+х21
+х31
=20,
х12
+х22
+х32
=5,
х13
+х23
+х33
=10,
х14
+х24
+х34
=10,
х15
+х25
+х35
=5;
х
ij
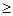 0 для
i
= 1,2,3;
j
= 1,2,3,4,5;
0 для
i
= 1,2,3;
j
= 1,2,3,4,5;
К
min
=
5х11
+6х12
+3х13
+5х14
+9х15
+6х21
+4х22
+7х23
+3х24
+5х25
+2х31
+5х32
+3х33
+х34
+8х35
;
Реклама

Такие задачи целесообразно решать при помощи особого варианта симплекс-метода – так называемого метода потенциалов
.
Все транспортные задачи имеют оптимальное решение
. Если все значение aj
и bi
в условиях транспортной задачи целочисленные, то переменныеxij
во всех базисных решениях (а так же и в любом оптимальном базисном решении) имеют целочисленные значения.
2. Составление опорного плана.
Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют различные способы, рассмотрим простейший, так называемый способ северо-западного угла. Пояснить его проще всего будет на конкретном примере:
Условия транспортной задачи заданы транспортной таблицей.
а
b
|
20
|
5
|
10
|
10
|
5
|
| 15
|
5
|
6
|
3
|
5
|
9
|
| 15
|
6
|
4
|
7
|
3
|
5
|
| 20
|
2
|
5
|
3
|
1
|
8
|
Будем заполнять таблицу перевозками постепенно начиная с левой верхней ячейки ("северо-западного угла" таблицы). Будем рассуждать при этом следующим образом. Пункт а1
подал заявку на 20 единиц груза. Удовлетворим эту заявку за счёт запаса 15, имеющегося в пункте b
1
, и запишем перевозку 15 в клетке (1,1). После этого дополним заявку за счет заявка пункта b
2
,
и запишем5 в клетке (1,2), теперь заявка удовлетворена, но в пункте b
2
осталось ещё 10 единиц груза. Удовлетворим за счёт них заявку пунктов а2
(5 единиц клетка 2,2) и а3
(5 единиц клетка 2,3). На складе b
3
есть запас в 20 единиц, за счет его мы удовлетворим оставшиеся заявки а3
(оставшиеся 5 единиц клетка 3,3), а3
(10 единиц клетка 3,4) и а5
(5 единиц клетка 3,5).
На этом распределение запасов закончено; каждый пункт назначения получил груз, согласно своей заявки. Это выражается в том, что сумма перевозок в каждой строке равна соответствующему запасу, а в столбце - заявке. Таким образом, нами сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является опорным решением транспортной задачи.
Составленный нами план перевозок, не является оптимальным по стоимости, так как при его построении мы совсем не учитывали стоимость перевозок С
ij
.
3. Метод потенциалов.
Пусть имеется транспортная таблица, соответствующая начальному решению, х
il
= 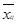 для базисного решения переменных, х
il
= 0
для свободных переменных(ячейки, соответствующие свободным переменным, остаются пустыми). Далее, нам требуется таблица расходов с заданными pij
.
для базисного решения переменных, х
il
= 0
для свободных переменных(ячейки, соответствующие свободным переменным, остаются пустыми). Далее, нам требуется таблица расходов с заданными pij
.
Реклама

Отыскание симплекс множителей.
Заполним таблицу расходов, оставив ячейки, соответствующие свободным переменным, пустыми. В крайний правый столбец внесем значения неизвестных u
1
,…,
um
, в нижнюю строку – значения неизвестных v
1
,…,
vn
,. Эти m
+
n
неизвестных для всех (
i
,
j
)
, соответствующих базисным переменным, должны удовлетворять линейной системе уравнений ui
+
vj
=
pij
.
| pll
|
plj
|
pln
|
ul
|
.
…
.
|
.
…
.
|
.
.
.
|
| pil
|
pij
|
pin
|
ui
|
.
…
.
|
.
…
.
|
.
.
.
|
| pml
|
pmj
|
pmn
|
um
|
| vl
|
…
|
vj
|
…
|
vn
|
Для всех базисных решений эта система имеет треугольный вид, ранг её матрицы равен n
+
m
– 1
. Следовательно, систему всегда можно решить следующим способом.
Полагают vn
= 0. Если значения k
неизвестных 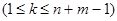 определены, то в системе всегда имеется уравнение, одно из неизвестных в котором уже найдено, а другое ещё нет. определены, то в системе всегда имеется уравнение, одно из неизвестных в котором уже найдено, а другое ещё нет.
Переменные ui
и vj
симплекс - множителями
. Иногда они называются также потенциалами
, а этот метод решения называют методом потенциалов
.
Пример 2.
| 5
|
u1
|
| 6
|
4
|
7
|
u2
|
| 3
|
1
|
8
|
u3
|
| v
1
|
v
2
|
v
3
|
v
4
|
v5
|
v
5
= 0 ®u
3
= 8, так как u
3
+ u
5
= p
35
= 8, ®v
4
= -7, так как u
3
+ v
4
= p
34
= 1, ®v
3
= -5, так как u
3
+ v
3
= 3, ®u
2
= 12 ®v
2
= -8, ®v
1
= -6 ®u
1
= 11.
Симплекс – множители нужны для того, чтобы найти свободную ячейку (
i
,
j
)
, которая при замене базиса переходит в базисную (это соответствует отысканию разрешающего столбца в симплекс – методе).
Для определения симплекс – множителей мы вносим на свободные места в таблице значения
p
¢
ij
=
pij
–
ui
–
vj
(коэффициенты целевой функции, пересчитанные для свободных переменных). Если все p
¢
ij
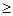 0,
то базисное решение оптимально. В противном случае мы выбираем произвольное p
¢
a
b
< 0, чаще всего наименьшее. Индексом a
b
помечено свободное переменное х
a
b
, которое должно войти в базис. Соответствующую ячейку транспортной таблицы мы отметим знаком +.
0,
то базисное решение оптимально. В противном случае мы выбираем произвольное p
¢
a
b
< 0, чаще всего наименьшее. Индексом a
b
помечено свободное переменное х
a
b
, которое должно войти в базис. Соответствующую ячейку транспортной таблицы мы отметим знаком +.
Пример 3.
| 5
|
6
|
3
|
5
|
9
|
| 6
|
4
|
7
|
3
|
5
|
| 2
|
5
|
3
|
1
|
8
|
pij
:
| 5
|
11
|
| 6
|
4
|
7
|
12
|
® |
| 3
|
1
|
8
|
8
|
| -6
|
-8
|
-5
|
-7
|
0
|
| 5
|
3
|
-3
|
1
|
-2
|
| ® |
6
|
4
|
7
|
-2
|
-7
|
| 0
|
5
|
3
|
1
|
8
|
Минимальный элемент –7 ® (a, b) = (2,5).
Кроме ячейки (a, b) транспортной таблицы, мы пометим значками – и + другие занятые числами ячейки таким образом, чтобы в каждой строке и в каждом столбце транспортной таблицы число знаков + было равно числу знаков -. Это всегда можно сделать единственным образом, причем в каждой строке и в каждом столбце будет содержаться максимум по одному знаку = и по одному знаку -.
Пример 4.
Знак + поставлен в ячейке (2,5). Соответственно в последнем столбце должен быть поставлен знак -, это можно сделать только в ячейке (3,5). Следовательно, знак + должен быть поставлен в последней строке. В ячейке с числом 10 этого сделать нельзя, так как тогда в соответствующем столбце не было бы знака -, и д.т.
Затем мы определяем минимум М из всех элементов, помеченных знаком -, и выбираем ячейку (g, d), где этот минимум достигается.
В нашем примере с М = 5 можно выбрать (g, d) = (2, 3); при этом (g, d) определяет базисное переменное, которое должно стать свободным, т.е. базисное переменное, соответствующее индексу разрешающей строки симплекс – метода.
| 20
|
5
|
10
|
10
|
5
|
| 15
|
15
|
| 15
|
5
|
5
|
5-
|
+
|
| 20
|
5+
|
10
|
5-
|
¯
¯
¯
¯
Копт
= 150
Переход к новой транспортной таблице (замена базиса) происходит следующим образом:
а). В ячейку (a, b) новой таблицызаписывается число М.
б). Ячейка (g, d) остается пустой.
в). В других ячейках помеченных знаками – или +, число М вычитается из стоящего в ячейке числа (-) или складывается с ним (+). Результат вносится в соответствующую ячейку новой таблицы.
г). Непомеченные числа переносятся в новую таблицу без изменений. Остальные ячейки новой таблицы остаются пустыми.
Пример 5.
Получается новая транспортная таблица, и повторяется ход предыдущих рассуждений. После конечного числа шагов критерий минимальности будет выполнен (если не учитывать теоретически возможного зацикливания в случае вырождения).
Пример 6. Ниже воспроизведен ход решения примера 1.
| 5
|
3
|
-3
|
1
|
-2
|
11
|
| 6
|
4
|
7
|
-2
|
-7
|
12
|
| 0
|
5
|
3
|
1
|
8
|
8
|
| -6
|
-8
|
-5
|
-7
|
0
|
| 5
|
3
|
4
|
8
|
5
|
4
|
| 6
|
4
|
7
|
5
|
5
|
5
|
| -7
|
-2
|
3
|
1
|
8
|
8
|
| -1
|
-1
|
2
|
0
|
0
|
| 5
|
3
|
-3
|
1
|
5
|
4
|
| 6
|
4
|
0
|
-2
|
5
|
5
|
| 2
|
5
|
3
|
1
|
7
|
1
|
| 1
|
-1
|
2
|
0
|
0
|
| 5
|
3
|
3
|
1
|
5
|
4
|
| 6
|
4
|
3
|
-2
|
5
|
5
|
| 2
|
5
|
3
|
1
|
7
|
1
|
| 1
|
-1
|
-1
|
0
|
0
|
| 5
|
1
|
3
|
1
|
3
|
6
|
| 2
|
4
|
5
|
3
|
5
|
5
|
| 2
|
3
|
3
|
1
|
5
|
3
|
| -1
|
-1
|
-3
|
-2
|
0
|
Первая транспортная таблица была получена в 1 главе (составление вспомогательной таблицы и второй транспортной таблицы описано выше). Затем по очередно находятся новая вспомогательная таблица и новая транспортная таблица до тех пор, пока (после четырех замен базисов) не будет достигнут минимум.
В вырожденном случае, как и в симплекс – методе, особый метод для предотвращения зацикливания применяется только тогда, когда после нескольких последовательных шагов М становится равным 0.
Если дана вырожденная транспортная таблица (её можно узнать по имеющемуся 0, то заменив am
на am
+
n
e
и все bj
на bj
+
e
, где e
>
0
подразумевается очень малым, исправим значения 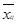 базисных переменныхтак, что бы для новых ai
и bj
получилось базисное решение. Это всегда можно сделать единственным способом (как и при отыскании симплекс – множителей).
базисных переменныхтак, что бы для новых ai
и bj
получилось базисное решение. Это всегда можно сделать единственным способом (как и при отыскании симплекс – множителей).
| 20 +
e
|
5 +
e
|
10 +
e
|
10 +
e
|
5 +
e
|
| 15
|
| 15
|
| 20 +
e
|
| 15 + 2
e
|
| 5 -
e
|
5 +
e
|
5 - 2
e
|
| 10 +
e
|
10 +
e
|
3
e
|
Если полученный таким образом элемент 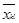 окажется отрицательным, то в этой же строке должен найтись положительный (ещё до изменения) элемент окажется отрицательным, то в этой же строке должен найтись положительный (ещё до изменения) элемент 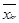 и в этом же столбце – положительный элемент и в этом же столбце – положительный элемент 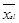 . Тогда ячейка (
s
,
r
)
свободна, отмечаем её знаком + и проводим замену базиса. Так можно избавиться от всех отрицательных значений*[1]
. . Тогда ячейка (
s
,
r
)
свободна, отмечаем её знаком + и проводим замену базиса. Так можно избавиться от всех отрицательных значений*[1]
.
Затем при помощи метода потенциалов расчеты продолжают дальше (вырождение уже никогда больше не встретится). Устремляя e® 0, приходим к оптимальному решению исходной задачи.
Список использованной литературы:
1. Еремин И.И., Астафьев Н.Н. Введение в теорию линейного и выпуклого программирования М.; Наука, 1976г.
2. Карманов В.Г. Математическое программирование. – М.; Наука, 1986г.
3. Моисеев Н.Н., Иванов Ю.П., Столярова Е.М. Методы оптимизации. – М.; Наука, 1978г.
4. Иванов Ю.П., Лотов А.В. Математические модели в экономике. – М.; Наука, 1979г.
5. Бронштейн И.Н., Семендяев К.А. Справочник по математике. – М.; Наука, 1986г.
[1]
Часто бывает достаточно везде заменить e на -e.
|