Содержание:
Общие сведения.............................................................. 2
Диамагнетики........................................................................................... 2
Парамагнетики......................................................................................... 2
Ферромагнетики....................................................................................... 3
Ферромагнетики............................................................... 6
Начальное намагничивание................................................................... 6
Циклическое перемагничивание........................................................... 7
Ферромагнитные материалы........................................... 9
Экспериментальное изучение свойств ферромагнетиков... 15
Лабораторная установка............................................... 21
Исследование ферромагнитных свойств электротехнической
стали........ 22
Исследование ферромагнитных свойств феррита.............................. 26
Лабораторная работа..................................................... 28
Приложение................................................................... 33
Схема установки /общий вид/............................................................. 33
Схема установки /электрическая/ .................................................... 34
Список используемой литературы................................ 35
Все вещества при рассмотрении их магнитных свойств принято называть магнетиками, т.е. они способны под действием магнитного поля приобретать магнитный момент (намагничиваться).
По своим магнитным свойствам магнетики подразделяются на три основные группы:
◊ диамагнетики;
◊ парамагнетики;
◊ ферромагнетики.
Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность J
.
Рассмотрим каждую группу в отдельности.
Диамагнетиками называются вещества, которые намагничиваются во внешнем магнитном поле в направлении, противоположном направлению вектора магнитной индукции поля.
К диамагнетикам относятся вещества, магнитные моменты атомов, молекул или ионов которых в отсутствие внешнего магнитного поля равны нулю. Диамагнетиками являются инертные газы, молекулярный водород и азот, цинк, медь, золото, висмут, парафин и многие другие органические и неорганические соединения.
Реклама

В случае отсутствия магнитного поля диамагнетик немагнитен, поскольку в данном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома равен нулю.
Т.к. диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойственен всем веществам.
Следует отметить, что магнитная проницаемость у диамагнетиков µ
<1. Вот, например, у золота µ
=0,999961, у меди µ
=0,9999897 и т.д.
Наряду с диамагнитными веществами существуют и парамагнитные вещества, – вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.
У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнетиков всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому парамагнитные вещества магнитными свойствами не обладают. При внесении парамагнетиков во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов).
Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его.
При ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается.
Вот некоторые парамагнитные вещества:
Алюминий µ
=1,000023;
Воздух µ
=1,00000038.
Особый класс магнетиков образуют вещества, способные обладать намагниченностью в отсутствии внешнего магнитного поля. По своему наиболее распространенному представлению (железу) их называют ферромагнетиками
.
Ферромагнетиками называются твердые вещества, обладающие при не слишком высоких температурах самопроизвольной (спонтанной) намагниченностью, которая сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, изменения температуры.
Ферромагнетики в отличие от слабомагнитных диа- и парамагнетиков являются сильномагнитными средами:
внутреннее магнитное поле в них может в сотни и тысячи раз превосходить внешнее поле.
Реклама

Большой вклад в экспериментальное изучение свойств ферромагнетиков внес А. Г. Столетов. В своей докторской диссертации он исследовал зависимость намагниченности мягкого железа от напряженности магнитного поля. Предложенный им способ заключался в измерении магнитного потокав ферромагнитных кольцах при помощи баллистического гальванометра.
Ферромагнитные материалы в большой или меньшей степени обладают магнитной анизотропией, т.е. свойством намагничиваться с различной степенью трудности в различных направлениях.
Магнитные свойства ферромагнитных материалов сохраняются до тех пор, пока их температура не достигнет значения, называемого точкой Кюри. При температурах выше точки Кюри ферромагнетик ведет себя во внешнем магнитном поле как парамагнитное вещество. Он не только теряет свои ферромагнитные свойства, но у него изменяется теплоемкость, электропроводимость и некоторые другие физические характеристики.
Точка Кюри для различных материалов различна:
◊ для железа +7700
С;
◊ для никеля +3650
С;
◊ для кобальта +11300
С.
При намагничивании ферромагнетиков происходит небольшое изменение их линейных размеров, т.е. увеличение или уменьшение их длины с одновременным уменьшением или увеличением поперечного сечения. Это явление называется магнитострикцией, оно зависит от строения кристаллической решетки ферромагнетика.
В чем же заключается природа ферромагнетизма?
 Согласно представлениям Вейсса (1865-1940), его описательной теории ферромагнетизма, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намагниченностью независимо от наличия внешнего намагничивающего поля. Однако это вносило некое противоречие, т.к. многие ферромагнитные материалы при температурах ниже точки Кюри не намагничены. Согласно представлениям Вейсса (1865-1940), его описательной теории ферромагнетизма, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намагниченностью независимо от наличия внешнего намагничивающего поля. Однако это вносило некое противоречие, т.к. многие ферромагнитные материалы при температурах ниже точки Кюри не намагничены.
Для устранения этого противоречия Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбивается на большое число малых микроскопических (порядка 10-3
– 10-2
см.) областей – доменов
, самопроизвольно намагниченных до насыщения.
При отсутствии внешнего магнитного поля магнитные моменты отдельных атомов ориентированы хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю, т.е. ферромагнетик не намагничен.
Внешнее магнитное поле ориентирует по полю магнитные моменты не отдельных атомов, как в парамагнетике, а целых областей спонтанной намагниченности. Поэтому с ростом H
намагниченность J
(рис. 1) и магнитная индукция B
уже в слабых полях растет довольно быстро.
Показанное на рис.1 намагничивание такого образца (ферромагнетик) в магнитном поле, напряженность H
которого медленно увеличивается, происходит за счет двух процессов: смещения границ доменов и вращения магнитных моментов доменов.
Процесс смешения границ доменов приводит к росту размеров тех доменов, которые самопроизвольно намагничены в направлениях, близких к направлению вектора H
.
Процесс вращения магнитных моментов доменов по направлению H
играет основную роль только в области, близкой к насыщению (т.е. при H
близких к Hs
).
Существование доменов в ферромагнетиках доказано экспериментально. Прямым экспериментальным методом их наблюдения является метод порошковых фигур
.
На тщательно отполированную поверхность ферромагнетика наносятся водная суспензия мелкого ферромагнитного порошка (магнетит). Частицы оседают преимущественно в местах максимальной неоднородности магнитного поля, т.е. на границах между доменами. Поэтому осевший порошок очерчивает границы доменов.
Дальнейшее развитие теории ферромагнетизма Френкелем и Гейзенбергом, а также ряд экспериментальных фактов позволили выяснить природу элементарных носителей ферромагнетизма.
В настоящий момент установлено, что магнитные свойства ферромагнетиков определяются спиновыми магнитными моментами электронов. Установлено также, что ферромагнитными свойства могут обладать только кристаллические вещества, в атомах которых имеются недостроенные внутренние электронные оболочки с некомпенсированными спинами. В подобных кристаллах могут возникать силы, которые вынуждают спиновые магнитные моменты электронов ориентироваться параллельно друг другу, что и приводит к возникновению областей спонтанного намагничивания. Эти силы, называемые обменными, имеют квантовую природу – они обусловлены волновыми свойствами электронов.
Итак, рассмотрим более детально процессы, происходящие с ферромагнетиком при воздействии на него внешнего магнитного поля.
 Под действием внешнего магнитного поля, созданного током в катушке, наложенной на стальной магнитопровод, происходит процесс ориентации доменов в магнитопроводе и смещение их границ. Это приводит к намагничиванию стального магнитопровода, причем намагниченность увеличивается с увеличением внешнего магнитного поля. Под действием внешнего магнитного поля, созданного током в катушке, наложенной на стальной магнитопровод, происходит процесс ориентации доменов в магнитопроводе и смещение их границ. Это приводит к намагничиванию стального магнитопровода, причем намагниченность увеличивается с увеличением внешнего магнитного поля.
Намагниченность М
ферромагнитного материала растет только до предельного значения, называемого намагниченностью насыщения М
s
. Зависимость намагниченности М
от напряженности поля М(
H
)
показана на рис. 2 штриховой линией. На том же рисунке показана линейная зависимость B
0
(
H
)=
m
0
М
. Складывая ординаты кривой m0
М(
H
)
и прямой М
0
(
H
)
, получаем ординаты новой кривой B(
H
)
– кривой первоначального намагничивания (рис 2). Кривую B(
H)
можно разделить на четыре участка:
1) почти линейный участок 0а
, соответствующий малым напряженностям поля, показывает, что магнитная индукция увеличивается относительно медленно и почти пропорционально напряженности поля;
2) почти линейный участок аб
, на котором магнитная индукция В
растет также почти пропорционально напряженности поля, но значительно быстрее, чем на начальном участке;
3) участок бв
– колено кривой намагничивания, который характеризует замедление роста индукции B
;
4) участок магнитного насыщения – участок, расположенный выше точки в
; здесь зависимость снова линейная, но рост индукции B
очень сильно замедлен по сравнению со вторым. Магнитная индукция, которая соответствует намагниченности насыщения, называется индукцией насыщения
B
s
.
Таким образом, зависимость магнитной индукции от напряженности поля у ферромагнитного материала достаточно сложная и не может быть выражена простой расчетной формулой. Поэтому при расчете магнитных цепей, содержащих ферромагнетики, применяют снятые экспериментально кривые намагничивания B(
H
)
магнитных материалов. Кривая намагничивания впервые была получена экспериментально в 1872 году профессором Московского университета А. Г. Столетовым.
Абсолютная магнитная проницаемость m
a
=
m
r
m0
ферромагнетика определяется для произвольной точки А
кривой намагничивания (рис. 3) через тангенс угла наклона секущей 0А
к оси абсцисс, т.е. Где m
B
, m
H
, m
m
- масштабы соответствующих величин.
 Кривая изменения магнитной проницаемости mr
для ферромагнитного материала дана на том же рис. 3. Как видно из графика, магнитная проницаемость с ростом напряженности поля изменяется в весьма широких границах, что затрудняет ее применение для расчетов. На кривой mr
(
H
)
отмечают два характерных значения магнитной проницаемости: Кривая изменения магнитной проницаемости mr
для ферромагнитного материала дана на том же рис. 3. Как видно из графика, магнитная проницаемость с ростом напряженности поля изменяется в весьма широких границах, что затрудняет ее применение для расчетов. На кривой mr
(
H
)
отмечают два характерных значения магнитной проницаемости:
1.
начальное (рис. 3)2.
максимальноеНачальная магнитная проницаемость характеризует возможность использования ферромагнетика в слабых магнитных полях. Максимальная магнитная проницаемость определяет верхнюю границу использования материала. Так, например, для листовой электротехнической стали mн
=
250¸1000, а mmax
=
500¸30000.
Рассмотрим процесс перемагничивания ферромагнетиков.
Допустим, что кольцевой магнитопровод из ферромагнитного материала не намагничен и тока в витках катушки нет, т.е. B=0 и
H
=0
(начало координат на рис. 4). При постепенном увеличении намагничивающего тока, т.е. МДС (магнито-движущая сила
), а следовательно, и напряженности поля от нуля до некоторого наибольшего значения  магнитная индукция увеличивается по кривой начального намагничивания (Оа
) и достигает соответствующего максимального значения B
a
. Если затем ток и напряженность поля уменьшаются, то и магнитная индукция уменьшается, при соответствующих значениях напряженности магнитная индукция несколько больше, чем при увеличении напряженности. Кривая изменения магнитной индукции (участок aб
на рис. 4) располагается выше кривой начального намагничивания. При нулевых значениях тока и напряженности поля магнитная индукция имеет некоторое значение B
r
, называемое остаточной индукцией
(отрезок Об
на рис. 4). магнитная индукция увеличивается по кривой начального намагничивания (Оа
) и достигает соответствующего максимального значения B
a
. Если затем ток и напряженность поля уменьшаются, то и магнитная индукция уменьшается, при соответствующих значениях напряженности магнитная индукция несколько больше, чем при увеличении напряженности. Кривая изменения магнитной индукции (участок aб
на рис. 4) располагается выше кривой начального намагничивания. При нулевых значениях тока и напряженности поля магнитная индукция имеет некоторое значение B
r
, называемое остаточной индукцией
(отрезок Об
на рис. 4).
Таким образом, магнитная индукция в ферромагнитном материале зависит не только от напряженности поля, но и от предшествующего состояния ферромагнетика. Это явление называется гистерезисом
. Оно обусловлено как бы внутренним трением, возникающим при изменении ориентации магнитных моментов доменов.
При изменении направления намагничивающего тока, а, следовательно, и направления напряженности поля и постепенном увеличении тока обратного направления напряженность поля достигает значения H
c
, называемого коэрцитивной силой
(отрезок Ов
), при котором магнитная индукция B=0
. При дальнейшем увеличении тока и напряженности поля магнитопровод намагничивается в противоположном направлении и при напряженности поля H
г
= -H
a
магнитная индукция достигнет значения B
г
= -B
a
. Затем при уменьшении тока и напряженности поля до нуля магнитная индукция B
д
становится равной -B
б
. Наконец, при следующем изменении направления тока и напряженности поля и увеличения ее до прежнего значения На
магнитная индукция увеличится также до прежнего значения B
a
. Рассмотренный цикл перемагничивания ферромагнетика по кривой абвгдеа
называется гистерезисным циклом
(петлей гистерезиса
).
Такая симметричная замкнутая петля гистерезиса (рис. 4) получается в действительности только после нескольких перемагничиваний с увеличением тока до значения I
a
. При первых циклах перемагничивания петля несимметричная и незамкнутая. Наибольшая замкнутая петля, которая может быть получена для данного ферромагнитного материала, называется предельной
(рис. 5). При напряженности поля H
> H
max
получается уже безгистерезисный участок кривой B(
H
)
.
 Если для данного ферромагнитного материала, выбирая различные наибольшие значения тока I
a
, получить несколько симметричных петель гистерезиса (рис. 5) и соединить вершины петель, то получим кривую, называемую основной кривой намагничивания
, близкую к кривой начального намагничивания. Если для данного ферромагнитного материала, выбирая различные наибольшие значения тока I
a
, получить несколько симметричных петель гистерезиса (рис. 5) и соединить вершины петель, то получим кривую, называемую основной кривой намагничивания
, близкую к кривой начального намагничивания.
Циклическое перемагничивание можно применить для размагничивания магнитопровода, т.е. для уменьшения остаточной индукции до нулевого значения. С этой целью магнитопровод подвергают воздействию изменяющегося по направлению и постепенно уменьшающегося магнитного поля.
Периодическое перемагничивание связано с затратой энергии, которая, превращаясь в тепло, вызывает нагрев магнитопровода. Площадь петли гистерезиса пропорциональна энергии, затраченной при одном цикле перемагничивания. Энергия, затраченная на процесс перемагничивания, называется потерями от гистерезиса. Мощность потерь на циклическое перемагничивание, выражаемая обычно в ваттах на килограмм, зависит от материала, максимальной магнитной индукции и числа циклов перемагничивания в секунду или, что тоже, частоты перемагничивания.
Ферромагнитные материалы делятся на две группы: магнитно-мягкие и магнитно-твердые.
а) Магнитно-мягкие
материалы (таблица №1) применяются в качестве магнитопроводов (сердечников) в устройствах и приборах, где магнитный поток постоянный (полюсные башмаки и сердечники измерительного механизма) или переменный (например, магнитопровод трансформатора). Они обладают низким значением коэрцитивной силы H
c
(ниже 400А/м), высокой магнитной проницаемостью и малыми потерями от гистерезиса. К этой группе материалов относятся: техническое железо и низкоуглеродистые стали, листовые электротехнические стали, железоникелевые сплавы с высокой проницаемостью (пермаллои) и оксидные ферромагнетики – ферриты и оксиферы.
Техническое железо с содержанием углерода до 0,04%, углеродистые стали и чугун широко применяются для магнитопроводов, работающих в условиях постоянных магнитных полей. Техническое железо обладает высокой индукцией насыщения (до 2,2 Тл), высокой магнитной проницаемостью и низкой коэрцитивной силой.
Электротехнические стали
– это сплавы железа с кремнием (1-4%). Путем изменения содержания кремния и применением различных технологических приемов получаются стали с широким диапазоном магнитных свойств. Кремний улучшает свойства технического железа: увеличиваются начальная и максимальная магнитные проницаемости, уменьшается коэрцитивная сила, уменьшаются потери энергии от гистерезиса, увеличивается удельное электрическое сопротивление, что важно для уменьшения так называемых вихревых токов, возникающих при циклически изменяющемся магнитном поле и нагревающих магнитопровод.
Стали, с низким содержанием кремния, имеют низкую магнитную проницаемость, большую индукцию насыщения и большие удельные потери, они применяются в установках и приборах цепей постоянного тока или переменного тока низкой частоты. Стали с высоким содержанием кремния применяются в тех случаях, когда нужно иметь высокую магнитную проницаемость в слабых и средних полях и малые потери от гистерезиса и вихревых токов, вследствие чего они могут применятся для магнитопроводов, работающих при повышенной частоте тока.
Рассмотрим некоторые виды магнито-мягких материалов, которые наиболее часто применяются в промышленности.
Пермаллои
– это сплавы различного процентного содержания железа и никеля, а некоторые из них, кроме того, молибдена, хрома, кремния, алюминия. Пермаллои имеют высокую магнитную проницаемость, в 10-15 раз большую, чем у листовой электротехнической стали. В этих сплавах индукция насыщения достигается при малых напряженностях поля (от десятых долей до нескольких сотен ампер на метр). Одни из них имеют низкую индукцию насыщения B
s
(около 0,6 –0,8 Тл), другие – относительно высокую (1,3 – 1,6 Тл). К первой группе относятся высоконикелевые пермаллои
, например содержащий 79% никеля и 3,8% молибдена, у которого mн
=22000; mmax
=120000; B
s
=0,75Тл. Ко второй группе относятся низконикелевые пермаллои
, например содержащие 45% никеля, у которого m
н
=2500; m
max
=23000; B
s
=1,5Тл.
У пермаллоевс прямоугольной петлей гистерезиса (рис. 6) степень прямоугольности петли характеризуется отношением остаточной индукции B
r
к максимальной индукции B
max
, под которой понимают индукцию при напряженности поля, в 5-10 раз превышающую коэрцитивную силу. Это отношение достигает 0,85-0,99. Коэрцитивная сила таких пермаллоев лежит в пределах от 1 до 30 А/м.
 Магнитные свойства пермаллоев в сильной степени зависят от технологии их изготовления. Магнитные свойства пермаллоев в сильной степени зависят от технологии их изготовления.
Ферритами
называют ферромагнитные материалы, получаемые из смеси окислов железа, цинка и других элементов. При изготовлении магнитопроводов смесь размалывают, прессуют и отжигают при температуре около 1200
0
С; таким образом, получают магнитопроводы нужной формы. Ферриты обладают очень большим удельным сопротивлением, вследствие чего потери из-за вихревых токов чрезвычайно, малы и их можно применять при высокой частоте.
Ферриты обладают значительной начальной магнитной проницаемостью, незначительной индукцией насыщения(0,18 – 0,32Тл) и малой коэрцитивной силой (8 – 80 А/м).
Магнитодиэлектрики
– это материалы, получаемые из смеси мелкозернистого ферромагнитного порошка с диэлектриком (поливинилхлорид, полиэтилен). Смесь формуют, прессуют и запекают; в результате мельчайшие частицы ферромагнетика оказываются разделенными электроизолирующей пленкой из немагнитного материала.
Ферриты
и магнитодиэлектрики
широко применяются в качестве сердечников в аппаратуре проводной и радиосвязи, в магнитных усилителя, вычислительных машинах и в других областях техники.
В настоящее время ведутся разработки новых видов магнито-мягких материалов. Одним из таких видов является ленточный магнитопровод
разработанный фирмой ГАММАМЕТ®
— гаммамет®
412А
.
Магнитопроводы ГАММАМЕТ®
412А изготавливаются из ленты толщиной 25 мкм с нанокристаллической структурой. Лента получается методом быстрой закалки из сплава на основе железа. Магнитопроводы после термической обработки в продольном магнитном поле имеют высокую прямоугольность петли магнитного гистерезиса (см. рис. 7) и низкие удельные магнитные потери.
Предельные значения температуры окружающей среды от -60 °С до +125°С. Полный срок службы магнитопроводов - 30 лет. Технические условия обеспечивают коэффициент прямоугольности B
r
/B
10
>0,85.
Магнитопроводы ГАММАМЕТ®
412А заменяют магнито-мягкие железоникелевые сплавы и ферриты с прямоугольной петлей магнитного гистерезиса.
Область применения:
магнитные усилители, импульсные трансформаторы, дроссели насыщения, магнитные ключи.

| Таблица №1
|
"Магнитные свойства некоторых магнито-мягких материалов".
|
В таблице приведены данные о магнитных свойствах некоторых магнито-мягких материалах. Такие материалы намагничиваются в относительно слабых магнитных полях и обладают высокими значениями начальной µн
и максимальной µmax
магнитных проницаемостей, малым значением коэрцитивной силы Hc
. Значения Bmax
- максимальной магнитной индукции – соответствует намагниченности насыщения ферромагнетиков.
| Ферромагнетик |
Вmax
Tл
|
µн
|
µmax
|
Нс
А/м
|
Свойства |
| Альсифер |
1,1 |
20000 |
117000 |
1,8 |
Отличается механической твердостью и хрупкостью. Обладает малой коэр-ой силой и высокими значениями магнитных проницаемостей.
Удельное эл. сопротивление 0,6 мкОм·м. Идет на изготовление магнитопро-д, корпусов приборов.
|
| Пермаллои высоко - никелевые |
0,70-0,75 |
14000-50000 |
60000-300000 |
0,8-4,8 |
Сплав, обладающий высокой магнитной проницаемостью и небольшой коэр-ой силой.
Применяется для изготовления сердечников слаботочных транс-ов звукового диапазона, дросселей и т.д.
|
| Электротехни-ческая сталь |
2 |
200-600 |
3000-8000 |
9,6-64,0 |
Сталь электротехническая (тран-ая) используется для изготовления сердечников транс-ов, дросселей, эл. машин и т.д. |
| Ферриты никель-цинковые и марганец-цинковые |
0,18-0,40 |
100-6000 |
3000-10000 |
8-120 |
| Железо(технически чистое, мин. кол-во примесей) |
2,16 |
250 |
7000 |
64 |
| Магнитопроводы ГАММАМЕТ®
412А
|
1,12
|
600 000
|
1,2
|
Область применения: магнитные усилители, импульсные трансформаторы, дроссели насыщения, магнитные ключи.
Температура Кюри 610 °C
Плотность:7400 кг/м3
Удельное электросопротивление:1,25•10-6
Ом•м
|
б) Магнитно-твердые
материалы (таблица №2) предназначены для изготовления постоянных магнитов самого различного назначения. Эти материалы характеризуются большой коэрцитивной силой и большой остаточной индукцией.
К магнитно-твердым материалам относятся: углеродистые, вольфрамовые, хромистые и кобальтовые стали; их коэрцитивная сила 5000-8000 А/м, остаточная индукция 0,8 – 1Тл. Они обладают ковкостью, поддаются прокатке, механической обработке и выпускаются промышленностью в виде полос или листов.
К магнитно-твердым материалам, обладающим лучшими магнитными свойствам, относятся сплавы: альни, альниси, альнико и др. Они характеризуются коэрцитивной силой H
c
=20 000¸60 000 А/м и остаточной индукцией B
r
=0,4¸0,7 Тл.
| Таблица №2
|
"Магнитные свойства некоторых магнито-твердых материалов".
|
В таблице приведены основные данные о магнитных свойствах некоторых магнито-твердых материалов. Эти материалы намагничиваются в сравнительно сильных магнитных полях и обладают большими значениями коэрцитивной силы Hc
, большой остаточной магнитной индукцией Br
, большими значениями плотности энергии магнитного поляω=
Br
ּH
c
и сравнительно малыми значениями магнитной проницаемости.
| Ферромагнетик |
Нс
,
А/м
|
Вr
,
Tл
|
ωmax
,
Дж/м3
|
Свойства |
| Альни-3 |
40000 |
0,5 |
7200 |
Сплавы обладают большими значениями коэрцитивной силы и остаточной индукцией. Плотность 6900 кг/м3
(альни) и 7100 кг/м3
(альнико). Применяются для изготовления литых постоянных магнитов. |
| Альнико-15 |
48000 |
0,75 |
12000 |
| Альнико-18 |
52000 |
0,90 |
19400 |
| Магнико |
40000 |
1,23 |
32250 |
Высококоэрцитивный сплав, плотностью 7000кг/м3
. Сплав используется для изготовления постоянных магнитов. Магниты из магнико при равномерной магнитной энергии в 4 раза легче магнитов из сплава альни. |
Экспериментальное изучение свойств ферромагнетиков.
Большой вклад в экспериментальное изучение свойств ферромагнетиков внес А. Г. Столетов. Предложенный им экспериментальный метод заключался в измерении магнитного потока Ф
m
в ферромагнитных кольцах при помощи баллистического гальванометра.
 Тороид, первичная обмотка которого состояла из N1
витков, имел сердечник из исследуемого материала (например, отожженного железа). Вторичная обмотка из N2
витков была замкнута на баллистический гальванометр G
(рис. А). Обмотка N1
включалась в цепь аккумуляторной батареи Б
. Напряжение, приложенное к этой обмотке, а, следовательно, и силу тока I1
в ней можно было изменять с помощью потенциометра R1
. Направление тока изменялось посредством коммутатора К
. Тороид, первичная обмотка которого состояла из N1
витков, имел сердечник из исследуемого материала (например, отожженного железа). Вторичная обмотка из N2
витков была замкнута на баллистический гальванометр G
(рис. А). Обмотка N1
включалась в цепь аккумуляторной батареи Б
. Напряжение, приложенное к этой обмотке, а, следовательно, и силу тока I1
в ней можно было изменять с помощью потенциометра R1
. Направление тока изменялось посредством коммутатора К
.

При изменении направления тока в обмотке N1
на противоположное, в цепи обмотке N2
возникал кратковременный индукционный ток и через баллистический гальванометр проходил электрический заряд q
, который равен отношению взятого с обратным знаком изменения потокосцепления вторичной обмотки к электрическому сопротивлению R
в цепи гальванометра:
Если сердечник тонкий, а площадь поперечного сечения равна S
, то магнитная индукция поля в сердечнике Напряженность магнитного поля в сердечнике вычисляется по следующей формуле

где L
ср
– средняя линия сердечника.
Зная B
и H
можно найти намагниченностьРассмотрим еще один способ экспериментального изучения свойств ферромагнетиков (на наш взгляд один из наиболее наглядных).
Данный метод аналогичен предыдущему, но отличие состоит в том, что в место гальванометра применяется электронный осциллограф. При помощи осциллографа Осц
(см. ниже схему) мы получаем наглядное подтверждение явления магнитного гистерезиса, наблюдая петлю на экране прибора.
Рассмотрим устройство экспериментальной установки.
Напряжение снимаемое с потенциометра R
р
пропорционально намагничивающему току I
, а следовательно, напряженности поля в экспериментальном образце
Эо
. Далее, сигнал, снимаемый с реостата R
р
, подается на вход (Х), т.е. на пластины горизонтального отклонения осциллографа. С входа интегрирующей цепочки (пунктирный прямоугольник на схеме) снимается напряжение U
c
, которое пропорционально скорости изменения магнитной индукции, т.е. подается на вход (Y) осциллографа, пластины вертикального отклонения.
Рассмотрим работу интегрирующей цепочки.
| Способ
I, расчета магнитной индукции.
|
Известно, что емкость конденсатора можно вычислить по следующей формуле
где dq
– заряд, значение которого можно определить зная ток I
Таким образом, напряжение на конденсаторе определяется по следующей формулой При достаточно больших величинах сопротивления R
 (по сравнению с сопротивлением остальной части цепи) напряжение на емкости U
c
значительно меньше напряжения на клеммах AD
(U
c
<< E
), поэтому (по сравнению с сопротивлением остальной части цепи) напряжение на емкости U
c
значительно меньше напряжения на клеммах AD
(U
c
<< E
), поэтому
Пренебрегая незначительным падением напряжения во вторичной обмотке экспериментального образца
Эо
, принимаем, что напряжение E
на клеммах AD
равно электродвижущей силе
(ЭДС
), индицируемой во вторичной обмотке, которая равна -d
Ф
/dt
.
Магнитный поток d
Ф
пропорционален изменению магнитной индукции d
В
в контуре площадью S
, т.е. d
Ф=
d
В·
S
.
Отсюда можно сделать вывод, что напряжение Е
на клеммах AD
равнот.е. пропорционально приращению магнитной индукции d
В
.
Подставляя значение напряжения Е
в формулу (*), и преобразовав ее получаемгде S
— площадь контура, который охватывает один виток обмотки, т.е. площадь поперечного сечения магнитопровода Эо
(экспериментального образца);
U
c
– значение напряжения снимаемое с конденсатора С
,которое определяется по показаниям осциллографа (вертикально отклоняющий сигнал).
Данная формула справедлива при условии, что мы рассматриваем один виток обмотки. Если у нас количество витков обмотки равно ω2
, то окончательно формула будет выглядеть следующем образомТаким образом, с выхода интегрирующей цепочки мы снимаем зависимость магнитной индукции В
от напряжения U
c
.
Теперь рассмотрим как зависит напряженность магнитного поля H
от напряжения снимаемого с реостата Rр
.
Для этого рассмотрим сигнал, поступающий на вход (Х) осциллографа. Ранее мы сказали, что напряжение, снимаемое с потенциометра R
р
, пропорционально напряженности поля в экспериментальном образце
Эо
. Покажем это.
Известно, что циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого контура равна результирующему макротоку, сквозь поверхность натянутую на этот контур:
В нашем случае значение макротока I
макр
о
определяется следующем образом:
с реостата Rр
мы снимаем напряжение U
R
р
, которое подается на горизонтально отклоняющие пластины осциллографа. Зная значение сопротивления на реостате R
р
и значение напряжения U
R
р
(которое фиксируется при помощи осциллографа) мы получаем, что значение I
макр
о
= U
R
р
/
R
р
.
Т.к. контур Эо
у нас постоянен, то окончательно формула примет видгде L
СрТр
– средняя магнитная линия магнитопровода.
| Способ
II, расчета магнитной индукции.
|
Рассмотренный ранее способ расчета магнитной индукции груб, т.к. в процессе расчета, формула (*), вносится некоторая не точность в вычисления (падение напряжения во вторичной обмотке). Существует более точный способ, который рассматривает переходные процессы в RC
— цепи (интегрирующей цепи).
Рассмотрим данный способ.
Для большей понятности построим схему RC–
цепи.
 Напряжение U
0
(входное напряжение или ЭДС вторичной обмотки) определяется как сумма (uR
+ uc
), при этом токи в резисторе и на конденсаторе равны I
R
=I
C
. Исходя из того, что емкость С
есть отношение заряда q
к падению напряжения на конденсаторе U
С
, а ток в цепи есть скорость изменения заряда, можно записать, что Напряжение U
0
(входное напряжение или ЭДС вторичной обмотки) определяется как сумма (uR
+ uc
), при этом токи в резисторе и на конденсаторе равны I
R
=I
C
. Исходя из того, что емкость С
есть отношение заряда q
к падению напряжения на конденсаторе U
С
, а ток в цепи есть скорость изменения заряда, можно записать, что
Таким образом, следует, что ток I
R
в резисторе можно вычислить по следующей формуле:Отсюда, входное напряжение U
0
равно
Полученному дифференциальному уравнению соответствует характеристическое уравнение следующего вида
где λ
— корень характеристического уравнения: λ=-1/
RC
.Общее решение будет в виде суммы двух составляющих:
uС
= u' + u"
где u'
— составляющая соответствующая установившемуся режиму;
u"
— составляющая, которой соответствует свободный процесс.
Т.к. u'
это установившийся режим при котором u'=U0
, таким образом, I'=0
.
Для того чтобы определить вторую составляющую u"
нам необходимо решить однородное дифференциальное уравнение, которому соответствует следующее выражение
Итак, мы пришли к решению общего вида
Найдем константу А
из начальных условий, т.е. при t=0
:
После преобразований, получаемгде RC
— постоянная времени, равная промежутку времени, по истечению которого напряжение в цени изменяется в е
раз, по сравнению со своим исходным напряжением U0
.
Зная, что eх
можно разложить в ряд Тейлора
который для нашего случая примет следующий видОграничимся двумя первыми членами разложения.
Подставляя полученное разложение в формулу (**) получаемТаким образом, конечный вид формулы будет следующий
Итак, из предыдущих рассуждений следует, что входное напряжение U0
равно скорости изменения магнитного потока Ф
через контур (вторичная обмотка экспериментального образца). В свою очередь магнитный поток Ф
есть произведение магнитной индукции В
на площадь контура S
. Иначе говоря, можно записать
илигде S
— площадь контура (поперечное сечение магнитопровода);
ω
— количество витков охватываемых контуром (в данном случае ω = ω2
).
Напряженность магнитного поля в данном способе рассчитывается аналогичным образомИсходя из полученных зависимостей, можно произвести исследование магнитных свойств ферромагнитных материалов, т.е. благодаря электронному осциллографу получаем на экране экспериментальную зависимость В
от Н
(петлю гистерезиса), по которой затем определяем напряженности (максимальную и коэрцитивную силу) и магнитные индукции (максимальную и остаточную) поля, а также можно определить магнитную проницаемость μ
данного материала.
В этой части курсовой работы опишем лабораторную установку, при помощи которой производят исследование ферромагнитного материала, а точнее двух типов ферромагнитных материалов (феррит и электротехническая сталь).
Схема установки приведена в приложении.
Установка работает в трех режимах (в зависимости от положения тумблера Тмб
):
◊0
– режим нейтрального положения, т.е. напряжение на исследуемые образцы не подано, цепь обесточена;
◊I
– в этом режиме производят измерение ферромагнитных свойств тороидального феррита М2000НМ типоразмера К20х12х6;
◊II
– в этом режиме производят исследование магнитопровода трансформатора ТВК-90-ПЦ-5.
  |
Необходимо помнить, что установка работает на переменном напряжении, и во избежании несчастных случаев нужно соблюдать технику безопасности.
Также не следует включать режим
I
при входном напряжении частотой 50 Гц, т.е. в "сеть" ибо это действие может привести к порче оборудования.
|
При исследовании явления магнитного гистерезиса производится расчеты напряженности магнитного поля и магнитной индукции по выше рассмотренным формулам.
В качестве исследуемого образца был взят трансформатор марки ТВК-90-ПЦ-5. Количество витков в первичной обмотке ω1
=173
, во вторичной ω2
=64
.
Питание схемы осуществляется от ЛАТра
(лабораторного автотрансформатора), выходное напряжение которого устанавливается равным 56 В
.
Перейдем к электрической схеме нашей установки, которая приведена в приложении, ниже фрагмент схемы для данного случая, т.е. при положении тумблера Тмб
в позиции II
: Для продолжения дальнейшей работы необходимо осуществить калибровку осциллографа, т.е. установить чувствительность на входах (Х) и (Y). Для этого падают сигнал постоянного напряжения определенной величины поочередно на вход (Х), а затем на вход (У). В результате чего по отклонению луча от первоначального положения устанавливают чувствительность осциллографа вольт/деление (в/дл
).
Итак, осциллограф Осц
находится во включенном положении и его выводы подключены согласно выше приведенной схеме. При это чувствительность по Х
составляет 4,8 В/дл
(в дальнейшем чувствительность по Х
не меняется), а по У
путем калибровки устанавливаем чувствительность равную 2,2 В/дл
.
 При замыкании тумблера Тмб
, подаем напряжение на первичную обмотку трансформатора. С реостата R
р
снимаем сигнал, который затем подается на вход Х
осциллографа. Известно, что ток в реостате R
р
пропорционален напряженности магнитного поля (формула ) в исследуемом объекте (трансформаторе), в свою очередь, зная сопротивление реостата и величину напряжения (которое измеряем при помощи осциллографа) можно определить ток, т.е. снимаем зависимость напряжения UR
р
от напряженности магнитного поля. При замыкании тумблера Тмб
, подаем напряжение на первичную обмотку трансформатора. С реостата R
р
снимаем сигнал, который затем подается на вход Х
осциллографа. Известно, что ток в реостате R
р
пропорционален напряженности магнитного поля (формула ) в исследуемом объекте (трансформаторе), в свою очередь, зная сопротивление реостата и величину напряжения (которое измеряем при помощи осциллографа) можно определить ток, т.е. снимаем зависимость напряжения UR
р
от напряженности магнитного поля.
 Затем, питание подается на вход интегрирующей цепочки (пунктирный прямоугольник на схеме). Далее преобразованный сигнал поступает на вход У
осциллографа. В результате чего получаем зависимость напряжения UС2
, которое снимается с выхода интегратора импульсов, от магнитной индукции (формула ). Затем, питание подается на вход интегрирующей цепочки (пунктирный прямоугольник на схеме). Далее преобразованный сигнал поступает на вход У
осциллографа. В результате чего получаем зависимость напряжения UС2
, которое снимается с выхода интегратора импульсов, от магнитной индукции (формула ).
На экране осциллографа получаем петлю гистерезиса, которая характеризует собой потери в магнитопроводе. Полученная зависимость графически представлена на рисунке ниже.
По форме петли определим значение максимальных магнитной индукции Bmax
и напряженности Hmax
магнитного поля, а также значения коэрцитивной силы Hс
и остаточной магнитной индукции Br
.
Т.к. магнитная индукция и напряженность магнитного поля пропорциональны соответствующем напряжениям, графическая зависимость которых приведена на рисунке (см. ниже), мы можем определить данные величины исходя из полученного графика.
Выше было рассмотрено, как магнитная индукция и напряженность зависят от напряжения, приведем лишь конечные формулы:где UC2
– значение напряжение подающиеся на У
осциллографа;
UR
р
– значение напряжение подающиеся на Х
осциллографа;
RР
– сопротивление реостата Rр
= 8 Ω
;
LСрТр2
– средняя магнитная линия в магнитопроводе трансформатора;
SСрТр2
– площадь поперечного сечения магнитопровода трансформатора;
ω1
и ω2
– соответственно число витков в первичной и вторичной обмотке (ω1
=173, ω2
=64
);
 R2
и С2
определяются по номинальным данным (см. приложение). R2
и С2
определяются по номинальным данным (см. приложение).
Для продолжения расчетов нам необходимо определить значения LСрТр2
и SТр2
.
LСрТр2
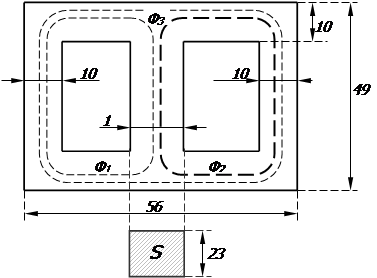
– средняя магнитная линия, которая определяется длиной линии по которой циркулирует магнитный поток Ф
.
В нашем случае магнитные потоки Ф1
=Ф2
, в силу симметричности магнитопровода, таким образом, LСрТр2
будет равна длине линии Ф2
(на рис. жирная линия).
После проделанных измерений, результаты которых приведены на рисунке, мы получаем, что LСрТр2
=1,14ּ10
-1
м
.
Площадь поперечного сечения магнитопровода определяется произведением ширины и толщины среднего участка магнитопровода, т.е. SСрТр2
= 3
,91·
10
-4
м2
.
При наблюдении явления гистерезиса на экрана осциллографа мы получили, что
◊ Bmax
соответствует значение равное 3,80 дл.
, т.е. напряжение при этом равно 8,36 В
;
◊ Hmax
соответствует 4,30 дл.
—
20,64 В
;
◊ В
r
равно 0,80 дл. — 1,76 В
;
◊ Hс
равно 0,40 дл.— 1,92 В
;
 Таким образом, подставляя эти данные в формулы (***), мы находим значения магнитной индукции и напряженности, которые равны Таким образом, подставляя эти данные в формулы (***), мы находим значения магнитной индукции и напряженности, которые равны
◊Bmax
=4,10 Тл;
◊Hmax
=3915,26 А/м;
◊В
r
=0,90 Тл;
◊Hс
=364,21 А/м;
Теперь определим максимальную магнитную проницаемость материала μ
max
. Известно, что магнитная проницаемость прямо пропорциональна напряженности, т.е.
B
=
μ
0
ּ
μ
ּ
H
где μ
0
— магнитная постоянная, μ
0
=4π
ּ
10 –7
[
Гн/м
]
Тогда искомая магнитная проницаемость материала Подставляя, полученные данные мы получаем следующее значение магнитной проницаемости, μ
max
=833 Гн/м
(электротехническая сталь).
Определим коэффициенты перевода напряжений, соответствующие определенным магнитным величинам
где Получаем следующие значения:
k
B
=
0,50 [Ω
ּ
Ф/м 2
] ;
k
H
=
189,69 [1
/(
Ω
ּ
м)
]
При помощи полученных коэффициентов мы можем определить магнитную проницаемость и напряженность магнитного поля в любой точке полученной кривой (петли гистерезиса), значения которых мы определяем при помощи осциллографа.
------>Пиши отсюда.
Изучение свойств ферромагнитных материалов
| Цель работы:
|
научится измерять электрические величины при помощи электронного осциллографа; получение экспериментальной зависимости магнитной индукции от напряженности магнитного поля. |
| Оборудование:
|
электронный осциллограф С1—93, лабораторная установка (технические данные которой приведены в приложении), лабораторный автотрансформатор (ЛАТр), генератор синусоидального сигнала ГЗ-103А, миллиметровая бумага, линейка, калькулятор, источник питания с выходным напряжением 0÷10 В. |
| Задание
I.
|
Подключение осциллографа.
Для начала произведем калибровку осциллографа.
Включите осциллограф. Оперируя ручками "яркость" и "контрастность" сфокусируйте луч таким образом, чтобы у Вас на экране появилась точка. Затем на соответствующие входы (вход (Х) и (Y)) подадим поочередно сигнал дискретной величины
(сигнал постоянного напряжения от выпрямительного блока). При этом точка, полученная ранее на экране, должна отклониться от своего первоначального положения.
Если Вы не наблюдаете точки на экране осциллографа, тогда Вам необходимо уменьшить, либо увеличить, чувствительность осциллографа. Для этого установите переключатель регулятора чувствительности для входа (Y) в требуемое положение.
Поворотом ручки регулятора напряжения на выпрямительном блоке добейтесь того, чтобы точка на экране осциллографа отклонилась на одну клетку (на экране осциллографа есть соответствующая сетка делений).
Зафиксируем положение точки и запишем соответствующие показания вольтметра на блоке питания. Полученное значение напряжения (вольт/деление
) и будет нашей чувствительностью на соответствующих входах.
При этом необходимо помнить, что чувствительность по (Х) не изменяется, а по (Y) для каждого случая соответствует определенное положение переключателя чувствительности осциллографа .
Согласно схеме (см. приложение, схема электрическая) подключите соответствующие выводы лабораторной установки к входам осциллографа.
|
 Задание
II. Задание
II.
|
Изучение ферромагнитных свойств феррита.
В качестве исследуемого образца используется феррита М2000НМ К20х12х6.
Произведите калибровку входа (Y) осциллографа. В начале установите регулятор чувствительности осциллографа в положение 0,02 в/дл
, а затем от калибруйте его, по приведенной выше методике.
Запишите значение чувствительности осциллографа по входам (Х) и (Y) в таблицу.
После калибровки осциллографа, установите тумблер в положение 0
, на лабораторной установке.
Подключите соответствующие выходы генератора частот к входу лабораторной установки, т.е. к входным клеммам. При этом на генераторе частот должны быть установлены следующие параметры:
◊Частота генератора синусоидального сигнала должна быть равной 20 кГц
;
◊Показание выходного напряжения равно 15 В
;
◊Нагрузочное сопротивление R
наг
= 50 Ω
;
Включите генератор частот и установите тумблер в положение I
, на лабораторной установке.
При этом на экране осциллографа Вы должны получить экспериментальную зависимость магнитной индукции от напряженности магнитного поля (петля гистерезиса).
Постарайтесь добиться, того чтобы полученная петля занимала большую часть экрана осциллографа и имела участки насыщения. Для этого поворотом ручки регулятора частот, на генераторе частот, добейтесь наиболее подходящего положения.
Зарисуйте полученную петлю и расставьте на ней соответствующие точки (Hmax
, Bmax
, Hc
, Br
).
Определите для этих точек значение напряжения, исходя из известной чувствительности осциллографа.
Запишите полученные данные в таблицу.
|
 Задание
III. Задание
III.
|
Изучение ферромагнитных свойств электротехнической стали.
В качестве исследуемого образца используется магнитопровод трансформатора
ТВК-90-ПЦ-5.
Произведите калибровку осциллографа по входу (Y), при этом регулятор чувствительности осциллограф должен быть установлен в положение 2,0 В/дл
.
Запишите значение чувствительности осциллографа по входам (Х) и (У) в таблицу, в раздел для данного случая.
Установите тумблер в положение 0
.
Подключите ЛАТр к входу установки, при этом установите регулятор напряжения на значение
U=56
В
.
Включите установку, переключите тумблер в положение II
.
|
Обратите внимание:
ни в коем случае не следует включать ЛАТр
при положении тумблера
в позиции
I
.
|
Проделайте те же самые измерения, что и для задания
II
.
Зарисуйте петлю для данного случая. И занесите соответствующие данные в ниже приведенную таблицу.
|
| Задание
IV.
|
Расчет магнитных величин.
Занесем полученные данные в таблицу.
|
| Феррит |
Электротехническая сталь
|
| Чувствительность по (Х), в/дл. |
| Чувствительность по (У), в/дл. |
| L
Cр
|
| S
|
| ω
1
|
| ω
2
|
| R
|
| C
|
| BUmax
, в/дл |
| HUmax
, в/дл |
Продолжение таблицы
-
-
>
|
| BUr
, в/дл |
| HUc
, в/дл |
| Bmax
|
| Hmax
|
| Br
|
| Hc
|
| μmax
|
Где B
и H
определяются по следующей формулеBU
— показание осциллографа по (Y), т.е. значение чувствительности по входу (Y) умножают на количество делений которым соответствует отклонение луча;
HU
— показание по (Х).
LC
р
— средняя магнитная линия, жирная пунктирная линия на рисунке ниже;
S
— площадь поперечного сечения.
R
р
— сопротивление реостата, R
р
=
8 Ω
.
LCр
и S
определяются по рисункам ниже:
Значение R
,С
и ω1
, ω2
определятся по данным приведенным в приложении.
μmax
— значение магнитной проницаемости, рассчитывается по следующей формуле:
где μ
0
— магнитная постоянная, μ
0
=4π
ּ
10 –7
[
Гн/м
]
.
Вопросы:
1.
Дайте определение ферромагнетика.
2.
В чем заключается явление магнитного гистерезиса.
3.
Объясните и покажите на полученных графиках характерные величины (Hmax
и Вmax
). Дайте их определение.
4.
Каков характер зависимости магнитной индукции и напряженности магнитного поля в цепях постоянного тока?
5.
Как повлияет на петлю магнитного гистерезиса изменение частоты питающего напряжения.
6.
Расскажите о магнито-твердых и магнито-мягких материалах. В чем заключается их отличие.
7.
Из каких материалов изготавливают постоянные магниты.
Литература.
1.
"Курс физики", А. А. Детлаф, Б. М. Яворский.
2.
"Теоретическая электротехника", В. С. Попов.
3.
"Курс физики", Т. И. Трофимова.
4.
"Физика", Д. Джанколи, том II.
5.
"Физический практикум", под редакцией проф. В. И. Вероновой.
| Обозначение |
Названиеэлемента, тип |
Тех. Характеристики |
| Тр2
|
Трансформатор ТВК-90-ПЦ-5 |
ω1
=173; ω2
=64 |
| R
р
|
Реостат |
R=8Ω;P=25W |
| C2
|
Конденсатор МБГЧ-1 |
С=2мкФ;Uраб
=250В |
| R2
|
Сопротивление МЛТ-2 |
R=6,2кΩ |
| Тр1
|
Феррит М2000НМ К20х12х6 |
ω1
=5; ω2
=5 |
| R1
|
Сопротивление МЛТ-2 |
R=1,3кΩ |
| C1
|
Конденсатор МБМ |
С=0,5мкФ; Uраб
=160В |
| Тмб
|
Тумблер трехпозиционный с нейтральным положением. |
II-0-I |
Схема установки /электрическая/ .
Список используемой литературы.
1.
А. А. Детлаф, Б. М. Яворский. "Курс общей физики". — М.: Высшая школа, 1989г.
2.
В. И. Иверонова и др. "Физический практикум". — М.: Физико-математическая литература, 1962г.
3.
В. С. Попов. "Теоретическая электротехника". — М.: Энергоатомиздат, 1990г.
4.
Т. И. Трофимова. "Курс физики". — М.: Высшая школа,1998г.
5.
Д. Джанколи. "Физика". Том II. — М.: Мир, 1989г.
6.
Г. Г. Рекус, В. Н. Чесноков. "Лабораторные работы по электротехнике и основам электроники". — М.: Высшая школа, 1989г.
|