Тема: "Расчет оптимального числа участков АЛ"
1. Цель работы
: практическое составление экономико-математической модели АЛ и на её основе определение оптимального числа участков АЛ.
2. Принадлежности
:
2.1. Чертёжные инструменты, карандаш.
2.2. Микрокалькулятор.
3. Общие положения
.
Лабораторно-практическая работа №9 проводится после изучения темы "Инженерные расчеты и оценка экономической эффективности машин-автоматов и их систем" с целью закрепления теоретического материала и приобретения практических навыков в составлении экономико-математических моделей и применение их при решении практических задач.
Выбор оптимального числа участков АЛ является классической экстремальной задачей.
Методически она решается на основе экономико-математической модели, разработанной в разделе 4. Годовой экономический эффект, выраженный через сравнительные технико-экономические показатели вариантов, формула (4.3):
Э=З1-З2
+DСсб
=0,35×К×(s-j)+Зп
×(j -1/e)+ m×j(1-d)+(g2
-g1
)M1
×
Qг×j ,
где З1
иЗ2
– приведенные затраты на производство единицы продукции производимой с помощью базовой (1) и новой (2) техники;
DCбр
– сокращение убытков от брака ;
К – капитальные вложения в производственные фонды;
М1
– стоимость материалов, необходимых для производства единицы изделия;
Qг
– годовой выпуск готовых изделий;
g1
и g2
– доля годных изделий, отвечающих требованиям качества, производимых с помощью базовой (1) и новой (2) техники, искомый вариант (2) по сравнению с базовым (1) имеет в j раз более высокую производительность (Q2
=Qг
×j), в s раз – стоимость (К2
=К×s); в e раз меньшее количество обслуживающих рабочих, в d раз меняются удельные эксплуатационные затраты, приходящиеся на единицу продукции; доля годных изделий повышается до g2
(g2
>g1
);
Зп
– зарплата основных и вспомогательных рабочих;
j - производительность анализируемого варианта по сравнению с базовым (как отношение объемов выпускаемой готовой продукции за одинаковый период времени);
s - увеличение стоимости (капитальных затрат);
e - сокращение количества обслуживающих рабочих (по фонду зарплаты);
d - изменение текущих затрат (на инструмент, электроэнергию, вспомогательные материалы), приходящихся на единицу выпускаемой продукции.
Упростим это выражение применительно к данному конкретному случаю.
Реклама

Так, при делении на участки ТП качество изделий не меняется, следовательно, g2
= g1
.
По аналогии, удельные затраты на инструмент, электроэнергию, вспомогательные материалы и др. можно принять постоянными, т.е. d=1.
Отсюда,
Э=0,35К(s-j)+Зп(j-1/e) (4.4)
Как было показано в лабораторно-практической работе №1, каждая система машин-автоматов может быть построена по различным структурным вариантам – от АЛ с жёсткой межагрегатной связью (одноучасковой) до АЛ с гибкой связью или поточной линии, где число участков –секций ny
равно числу последовательно соединенных по ТП машин-автоматов q (1£ny
£q).
Наиболее просты по конструкции линии с жесткой межагрегатной связью (ny
=1), которые целесообразно применять в качестве базовых. Любое структурное усложнение линии с делением её на участки и установкой межоперационных накопителей связано с повышением производительности линии (j<1), ее стоимость (s >1) и увеличением количества обслуживающих рабочих (e>1), т.е. данные показатели конфликтны друг с другом.
Задачу оптимизации решают следующим образом:
1. Сначала находят функциональные зависимости роста производительности j, увеличения s и изменения количества обслуживающих рабочих (по фонду зарплаты) e от варьируемого параметра – числа участков ny
, т.е. функции j = f1
(ny
); s = f2
(ny
); e = f3
(ny
).
2. Затем подставляя эти функциональные значения в общую экономико-математическую модель (4.4) и тем самым получают однопараметрическую функцию Э = f4
(ny
), которую можно решить путём нахождения экстремального значения ny
опт
, соответствующего максимальному экономическому эффекту Эmax
.
А
) Рост производительности линии при делении её на участки обуславливается сокращением простоев при неизменной длительности рабочего цикла. В многоучастковой линии (ny
>1) при отказе любого устройства останавливаются, как правило, только станки данного участка. В предельном случае (деление линии по методу равных потерь, полная их компенсация межучастковыми накопителями) простои каждого станка в линии сокращается во столько раз, сколько имеется участков.
Тогда коэффициент роста производительности,
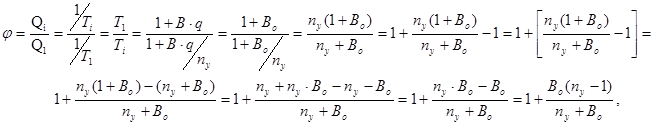 где В – внецикловые потери одного станка (простои, приходящиеся на единицу времени безотказной где В – внецикловые потери одного станка (простои, приходящиеся на единицу времени безотказной
работы);
q – число последовательно соединенных станков в линии;
Во
=В×q – суммарные внецикловые простои линии при жесткой межагрегатной связи.
Реклама

Строим график зависимости роста производительности труда j от числа участков ny
АЛ.
.
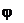   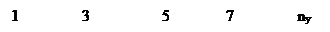 
Для упрощения строим график для Во
=1.
Тогда формула (4.5) примет вид:
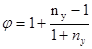
Присваиваем аргументу значения ny
=1, 2, 3, 5, 7, 9 100.
Тогда j будет принимать значения:
| ny
|
1 |
2 |
3 |
5 |
7 |
9 |
100 |
| j |
1 |
1,3 |
1,5 |
1,7 |
1,75 |
1,8 |
1,98 |
График на рис.4.1 показывает, что зависимость роста производительности j от числа участков имеет асимптотический характер, добавление каждого нового накопителя дает все меньший прирост производительности.
Б
) Анализ роста стоимости машин при делении её на участки.
Рост стоимости АЛ при делении её на участки приблизительно пропорционален числу участков. Если стоимость станков одной позиции в среднем К1
, то суммарная стоимость линии с жёсткой связью
К=К1
×q. При делении АЛ на участки (максимально можно встроить (ny
-1) накопителей) дополнительная стоимость будет равна:
К1
×a×(ny
-1),
где a - отношение средней стоимости накопителя к средней стоимости одного станка;
К1
×a - средняя стоимость накопителя.
Тогда формула показывает, что эта зависимость носит линейный характер. Построим график для значения 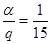 (построить самостоятельно). (построить самостоятельно).
В
) Рост количества обслуживающих рабочих при делении АЛ на участки.
Этот рост наблюдается при введении не только механизированных, но и автоматических накопителей, т.к. они имеют отказы в работе, требуют наладки и обслуживания.
В линиях с жесткой межагрегатной связью число наладчиков равно:
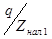 , ,
где Zнал.1
– норма обслуживания (число станков, обслуживаемых одним рабочим).
При делении линии на участки к наладчикам добавляется ещё 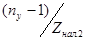 человек в смену, человек в смену,
где Zнал.2
– число накопителей, обслуживаемых по норме одним рабочим.
Тогда коэффициент сокращения затрат ручного труда (e<1):
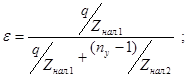
Удобнее пользоваться величиной 1/e (коэффициент роста фонда зарплаты):
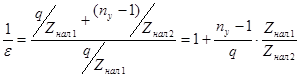 . .
Новый фонд зарплаты (З'п
) для линии, разделенной на участки:
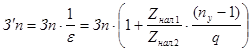 . .
Рост зарплаты обслуживающих рабочих (1/e) также пропорционален числу участков, на которые разделена линия. Построим график зависимости 1/e от ny
(для произвольных констант Зп
, Zнал.1,
Zнал.2
).
Как видим из графика 4.1 выигрыш в производительности j при делении на участки имеет убывающий характер, а проигрыш в стоимости (а следовательно и в ремонтных затратах) и в зарплате обслуживающих рабочих меняется пропорционально. Это показывает на конфликтность задачи и наличие экстремальных решений.
Подставляя значения  j, s и 1/e в формулу (4.4), получим: j, s и 1/e в формулу (4.4), получим:
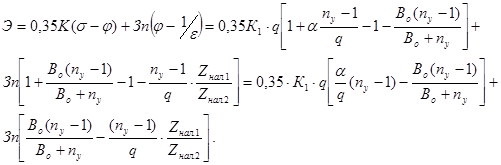
Составим график зависимости экономического эффекта Э от числа участков ny
. (рис.4.2);
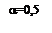
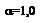

наибольший эффект деления на участки достигается при ny
=2¸3. При дальнейшем увеличении числа участков экономические показатели такой сложной системы могут оказаться ниже, чем у линии с жёсткой связью (при ny
>nmax
, Э=0). Математически оптимальное число участков можно получить, взяв производную 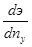 и приравняв её к нулю . Выполнив необходимые преобразования получим для автоматических накопителей, которые практически не требуют увеличения обслуживающего персонала (Zнал.2
=¥), но имеют значительную стоимость (которая иногда в 2- 3 раза превышает стоимость одного станка) формулу : и приравняв её к нулю . Выполнив необходимые преобразования получим для автоматических накопителей, которые практически не требуют увеличения обслуживающего персонала (Zнал.2
=¥), но имеют значительную стоимость (которая иногда в 2- 3 раза превышает стоимость одного станка) формулу :
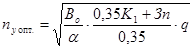 (4.5) (4.5)
Аналогично, если система делится на ряд независимых автоматических линий, между которыми располагаются механизированные накопители с ручным обслуживанием, стоимостью которых можно пренебречь (a=0),
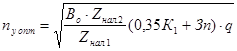 . .
Рассмотренные методы и полученные зависимости позволяют помимо конкретных расчетов производить инженерные обобщения, оценивать типовые структурные характеристики линий различных типов, решать задачи комплексной оптимизации при проектировании.
4
. Определение экономически оптимальных вариантов из числа множества технически возможных, т.е. комплексная оптимизация проектных решений.
Задачи решаются либо как граничные (Э=Э min
=0), либо как экстремальные (Э=Эmax
), при необходимости основное уравнение экономико-математической модели автомата или автоматических систем машин "реверсируют", т.е. значение Э=0 или Э=Эmax
ставят аргументом, а искомые характеристики – функцией.
Итак
, научной основой автоматизации производственных процессов является теория производительности машин и труда, которая не только позволяет решать практические задачи расчета и проектирования автоматического оборудования, но и проблемные вопросы анализа и оценки путей автоматизации, выбора наиболее перспективных её направлений.
Математическую основу теории производительности
составляют уравнения, связывающие показатели производительности машин и производительности труда с технологическими, конструктивными, структурными, стоимостными и другими показателями оборудования.
Тем самым методы теории производительности позволяют не только подсчитывать количественно производительность машин или экономическую эффективность их внедрения, но и анализировать различные возможные варианты автоматизированного оборудования и систем машин, выбрать такие параметры проектируемых машин, которые являются оптимальными и обеспечивают максимальную производительность или наибольший экономический эффект.
|