Е.А. Петрук, А.В. Лавренов, Омский государственный университет, кафедра химии нефти и аналитической химии,
1. Постановка задачи
Классическая модель [1] ("теория тарелок") была создана для объяснения процесса разделения веществ в хроматографической колонке. Так как эта модель рассчитана для весьма идеализированного случая линейной равновесной хроматографии [2], то после появления более общих и гораздо более сложных моделей (см.обзор [3]) теория тарелок применяется ограниченно, в основном для учебных целей. В частности, с ее помощью на качественном уровне объясняют форму хроматографического пика, демонстрируют влияние различных факторов на качество разделения двух веществ и т.п.[4]. При этом вопрос, можно ли с помощью модели [1] точно предсказывать времена удерживания и другие характеристики хроматографического разделения реальных смесей, не рассматривается [3].
Ранее в ОмГУ для учебных целей авторами этой статьи была разработана программа "Сhromat", позволяющая моделировать на ПЭВМ хроматографическое разделение смесей и демонстрировать (с применением эффекта мультипликации) постепенное разделение компонентов смеси по мере продвижения их по длине колонки [5]. Алгоритмы этой программы основаны на модели [1] в элюционном варианте хроматографического процесса. Цель настоящей работы - проверить, можно ли использовать алгоритмы типа [1] и основанные на них программы для прогнозирования реальных хроматограмм, насколько точно при этом предсказываются времена удерживания компонентов. При благоприятном результате проверки в дальнейшем можно было бы выявить граничные условия адекватного прогноза.
Для проверки были использованы реальные смеси различного состава (н-углеводороды, алкилбензолы, пестициды и др.), которые разделяли на колонках разного типа. Параллельно проводили компьютерные эксперименты по моделированию соответствующих хроматограмм и сопоставляли полученные результаты.
2. Методика эксперимента
По методу ГЖХ в изотермическом режиме получали реальные хроматограммы 4- и 5-компонентных смесей разного состава (табл.1) с концентрацией компонентов одного порядка. Условия хроматографирования также показаны в табл.1.
Таблица 1
Условия хроматографирования экспериментальных смесей
Реклама

| Смесь |
Хроматограф |
Детектор |
НЖФ |
|
П, % |
Ткол, K |
, см/мин |
| 1 |
н - алканы (С5 - С9) |
ЛХМ-8МД |
Катарометр |
Сквалан |
0.05 |
15 |
353 |
475.7 |
| 2 |
н - алканы (С5 - С9) |
Цвет-106 |
ПИД |
Апиезон L |
0.03 |
11 |
373 |
571.4 |
| 3 |
Пестициды |
Кристалл-2000 |
ДЭЗ |
SE-30 |
0.04 |
15 |
473 |
450.0 |
| 4 |
Алкилбензолы |
Цвет-106 |
ПИД |
Апиезон |
0.03 |
11 |
373 |
571.4 |
Примечание. П (степень пропитки) = mнжф/ mносителя·100 %.
Во всех случаях применялись насадочные колонки диаметром 0,3 см длиной 200 см (для смесей типа 1-100 см). Объем пробы - 0,002 см3. Условные обозначения в табл.1 традиционны для хроматографического анализа и поэтому приводятся без расшифровки. Пример реальной хроматограммы - на рис.1а.
Компьютерные эксперименты проводили на ПЭВМ IBM PC 386 и 586 в диалоговом режиме. Программа "СHROMAT" написана на языке Turbo Pascal, имеет стандартный пользовательский интерфейс, основанный на использовании функциональных меню и диалоговых окон. Исходными данными для расчета служат: число компонентов смеси (N = 1-5), длина хроматографической колонки в см (L = 1-5000), число теоретических тарелок колонки (ЧТТ = 1-100000), линейная скорость движения подвижной фазы (ПФ) в колонке (, см/мин), фазовое отношение в колонке (). Для каждого из компонентов пользователь вводит значение коэффициента распределения Кp (до 1000), относительное содержание компонента в смеси (%) и коэффициент чувствительности детектора к данному компоненту (Кчувств). В ходе каждого эксперимента вводилось значение ЧТТ, рассчитанное для соответствующей колонки по реальной хроматограмме при вводе отсутствующего в исследуемых смесях чистого вещества, принадлежащего к тому же гомологическому ряду. Справочные значения Кр использовали в случае н-алканов, для других смесей Кр заранее рассчитывали по временам удерживания.
Алгоритмы расчета по модели [1] предполагают следующие допущения:
а) значения Кр постоянны для каждого компонента и не зависят от концентрации (линейная равновесная хроматография при постоянной температуре);
б) для всех компонентов смеси ЧТТ принимается одинаковым;
в) расчет выполняется без учета взаимного вытеснения компонентов, то есть в однокомпонентном приближении.
Протокол компьютерного эксперимента содержит следующие результаты расчета: общее время хроматографирования смеси tобщ; характеристики пиков (абсолютное время удерживания, полуширину и относительную площадь), а также коэффициенты разрешения Кразр рядом стоящих пиков. Протокол и модельная хроматограмма смеси выводятся на экран, сохраняются на диске и могут быть выведены на печать. В протоколе также указываются все введенные пользователем данные. Пример рассчитанной компьютером хроматограммы - на рис.1б. Состав смеси и условия разделения на рис. 1а и 1б аналогичны.
Реклама

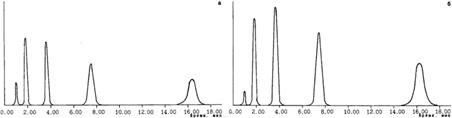
Рис. 1. Хроматограмма смеси н-алканов: а - реальная; б - модельная (смесь 1)
3. Результаты и их обсуждение
Для всех смесей вид реальных и рассчитанных хроматограмм совпадал. По каждой смеси рассчитывали t/t - относительную погрешность предсказания времен удерживания, которая для любого компонента по абсолютной величине не превышала 20 % и, судя по знакам, имела случайный характер. Одновременно оценивалась погрешность предсказания некоторых других характеристик (табл. 2). Средняя величина t/t по каждой смеси (в %) составляла для первой серии (н-алканы на сквалане) - 3.1, для второй (н-алканы на апиезоне) - 7.9, для третьей (пестициды на SE-30) - 11.6 и для четвертой (алкилбензолы на апиезоне) - 11.3. То есть, наблюдалось достаточно хорошее совпадение по временам удерживания, средняя погрешность предсказания во всех исследованных случаях не превышала 12 % отн.
Таблица 2
Сравнение реальных и расчетных параметров удерживания и разделения для алкилбензолов
| N |
Компонент |
Время удерживания, мин. |
Kразр |
| расч. |
эксп. |
|t/t· 100% |
расч. |
эксп. |
|Kразр/Kразр· 100% |
| 1 |
Толуол |
0.46 |
0.40 |
15.00 |
| 2 |
Этилбензол |
0.57 |
0.60 |
5.00 |
3.12 |
3.67 |
15.00 |
| 3 |
м-Ксилол |
0.60 |
0.68 |
12.00 |
0.78 |
0.79 |
1.00 |
| 4 |
о-Ксилол |
0.65 |
0.75 |
13.00 |
1.14 |
1.02 |
12.00 |
| Сред. - 11.30 |
Сред. - 9.30 |
Вероятно, расхождения между расчетом и экспериментом в первую очередь связаны с недостаточной точностью и надежностью использованных данных, а не с неадекватностью модели [1], поскольку состав смесей был выбран таким образом, чтобы выполнялись известные ограничения этой модели. В частности, компоненты каждой смеси имели близкие физические и химические свойства (например, рядом стоящие компоненты одного гомологического ряда), их концентрации были близки и малы по сравнению с концентрацией элюента, условия хроматографирования не менялись во времени. Основной проблемой в этом случае является правильный выбор вводимого для каждого компонента значения Кр, поскольку в справочной литературе эти значения в явном виде приводятся очень редко, даже для самых распространенных неподвижных фаз, а независимость приводимых данных по Кр от условий регистрации сомнительна.
Погрешность предсказания t/t на уровне 10-20 % позволяет достаточно хорошо предсказывать возможность разделения родственных компонентов в произвольных условиях, что наиболее важно для практики. Как видно из табл.2, коэффициенты разрешения рядом стоящих пиков также предсказываются с погрешностью порядка 10-20 %. Средняя величина Кразр/Кразр по каждой смеси (в %) составляет для первой - 16.4, для второй - 17.5, для третьей - 16.8 и для четвертой - 9.3. Это позволяет с достаточной для практики точностью подбирать в компьютерном эксперименте те параметры (природу НЖФ, длину колонки, линейную скорость газа-носителя и т.п.), которые обеспечат количественное разделение заданной пары компонентов. Реально возможность подобных расчетов лимитируется наличием банка данных по коэффициентам распределения или другим характеристикам веществ, по которым могут быть вычислены Кр.
Таким образом, модель хроматографического процесса, основанная на классической теории тарелок, в некоторых (простейших) случаях позволяет не только объяснить вид хроматограммы, но и с необходимой точностью предсказывать времена удерживания, коэффициенты разрешения пиков и другие количественные характеристики.
По мере перехода к большим количествам разделяемых компонентов или к смесям с неродственными компонентами точность прогноза хроматографических характеристик по модели [1] должна ухудшаться. Важно оценить границы применимости такого прогноза. Соответствующие данные будут приведены в следующем сообщении.
Авторы благодарят за ценные советы при создании программы и обсуждении результатов проф. В.И. Вершинина и доц. И.И. Медведовскую.
Список литературы
JamesA.T., MartinA.J.P., Biochem. J., 50, 1952, p. 679.
Жуховицкий А.А., Туркельтауб Н.М. Газовая хроматография. М.: Гостоптехиздат, 1962. 442 с.
Вигдергауз М.С. Расчеты в газовой хроматографии. М.: Химия, 1978. 248 с.
Гольберт К.А., Вигдергауз М.С. Введение в газовую хроматографию. М.: Химия, 1990. 352 с.
Петрук Е.А. Расчетные и моделирующие программы для преподавания аналитической химии в вузах: Дис. ... канд. хим. наук / ТПУ. Томск, 1997.- 156 с.
|