Люди привыкли, что геометрия имеет дело с нашим реальным пространством и что пространство описывается евклидовой геометрией. Многие профессиональные математики выделяли геометрию среди остальных разделов математики, считая её подобно механике экспериментальной наукой, но они же понимали, что, во-первых, возможны логически стройные геометрические построения ,за которыми не стоит физическая реальность, во-вторых, не столь бесспорно, что в астрономических масштабах в нашем мире царит геометрия Евклида. Новый этап в развитии неевклидовой геометрии наступил, когда появились первые её модели. Одну из самых интересных моделей придумал Анри Пуанкаре, занимаясь чисто аналитическими вопросами. Рассказу о модели Пуанкаре и посвящена эта заметка.
Рассмотрим круг. Пусть его населяют существа, которые твердо уверены, что их мир, то есть круг, неограничен. Этот круг устроен так, что когда они двигаются от центра круга к его границам, длина их шага = 1/(n2), где n - число шагов, которые они уже сделали. Тогда нетрудно видеть, что человечек никогда не дойдет до границ круга.
Докажем, что расстояние, пройденное человечком на любом шаге, меньше двух. Ясно, что длина шага= 1/(n2)<1/(n(n-1))= 1/n-1 – 1/n (*) Тогда расстояние R = 1/4 + 1/9 + ... + 1/n2 по неравенству (*) 1/4+ 1/9+...+1/n2 < 1-1/2 + 1/2-1/3 +.... 1/(n-1) -1/n Нетрудно видеть, что все слагаемые кроме 1 и 1/n сократятся. Тогда получим : 1+ 1/4 + 1/9+...+1/n2 < 2 – (1/n) Таким образом, никто из обитателей круга не сможет доказать, что их мир ограничен, и они верят, что справедлива аксиома Евклида: «Через точку вне прямой проходит единственная прямая, параллельная данной». Но в круге роль прямых для обитателей этого круга играют отрезки, соединяющие точки окружности. Но очевидно, что через любую точку вне отрезка можно провести сколько угодно отрезков, не пересекающих данный (см. рисунок).
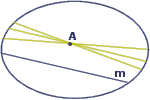
Аналогичный пример можно построить с шаром в пространстве. Но ничто не мешает нам поставить себя на место обитателей круга Пуанкаре. Тогда многие аксиомы Евклида становятся не столь интуитивно понятными. Стоит задуматься, нужно ли так бескомпромиссно доверять?
|