Муллакаев М.С., Габитов Э.В.
В настоящее время существуют макро- и микроскопические теории диффузии. Макроскопическая теория основана на формализме, связанном с термодинамикой необратимых процессов, и выражения для потоков получают как функции термодинамических сил и параметров. В микроскопической теории вычисляют потоки, опираясь на механизмы, которые основаны на представлении об атомных скачках.
Единого универсального механизма диффузионных перемещений для различных материалов и всевозможных условий нет. Эти механизмы зависят от вида химической связи, типа и компактности решетки, температуры, при которой происходит диффузия, природы диффундирующей примеси и других факторов. Для исследования механизма диффузии обычно принимают ту или иную модель, теоретически рассчитывают коэффициент диффузии D и предэкcпоненциальный множитель D0, а затем сравнивают их с экспериментально измеренными величинами.
Попытки распространить модели, используемые при описании диффузии в разбавленных сплавах, на концентрированные сталкиваются с трудностью выбора правильного приближения из-за увеличивающегося числа неизвестных параметров [1]. И поэтому во многих моделях применяют приближение с использованием малого числа энергий парного взаимодействия для стабильной и седловинной конфигурации, чтобы описать влияние локального окружения на высоту потенциального барьера [2-3].
Как следствие, подобные модели позволяют вычислить только энергии активации, а не сами коэффициенты диффузии. Предэкспоненциальные множители неизвестны и произвольно считаются постоянными. Не учитываются эффекты корреляции, хотя зависимость частоты скачков от локального состава окружения нарушает трансляционную симметрию решетки. Взаимодействие атомов в рамках указанных моделей описывают с помощью парных энергий, и энергия сплава представляет собой сумму таких энергий, что несправедливо в случае переходных металлов. Очевидно, для того, чтобы описать изменение характера взаимодействия атомов с изменением концентрации сплава, необходимо использовать расчеты на основе электронной теории.
Согласно [4], в твердых растворах вблизи вакансий существуют градиенты электрических полей, которые достигают заметной величины на расстоянии 4-5 атомных сфер от точечного дефекта. От величины таких градиентов зависит форма кривой изменения потенциальной энергии вдоль пути диффузии, а следовательно, и параметры диффузионного процесса.
Реклама

В работе [5] авторы приходят к выводу, что в неограниченных твердых растворах замещения переходных металлов, степень заполнения d-полосы, приводящая к изменению связи, коррелирует с изменением диффузионных характеристик. Однако авторы не учитывают возможность переноса заряда между сплавляемыми элементами, что также приводит к изменению характера сил связи в металлических сплавах.
Поэтому для достижения прогресса в микроскопической теории диффузии необходимо проведение ряда экспериментальных работ, где совместно рассматривались бы диффузионные параметры сплавов с особенностями их электронной структуры.
Оже-спектроскопия широко применяется для прямого исследования диффузионных процессов в тонких пленках. Если толщина слоев больше, чем диффузионная длина, то распределение атомов c (x, t) может быть описано функцией ошибок Гаусса [6]:
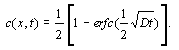 |
(1) |
Первым шагом процедуры является построение измеренных профилей в линейном виде. Для этого экспериментальные точки переносят в другую систему координат, осью абсцисс которой является расстояние от поверхности (или время травления), а осью ординат - концентрация элементов в атомных процентах в единицах функции erfc. Такое построение будет успешным при выполнении следующих условий:
а) скорость травления будет постоянна в данной области;
б) отсутствует диффузия по границам зерен;
в) коэффициент диффузии не зависит от концентрации элементов.
Если исходный переходный слой достаточно тонкий, можно определить коэффициент диффузии из линеаризованного профиля. Поскольку 50 % erfc.(0.5)=24 %, то:
где t - время диффузии.
Однако в реальных образцах такая ситуация практически не встречается. Исходные профили всегда имеют уширение, обусловленное влиянием ионной бомбардировки, влиянием границы раздела, шероховатостью поверхности и диффузией, предшествующей процессу измерения и т.д. В [7] показано, что в этом случае коэффициент диффузии можно определить, используя градиенты концентраций для исходного образца G0 и для отожженного Gt:
D=(4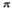 t)-1(Gt-2-Go-2), t)-1(Gt-2-Go-2), |
(3) |
где G0 и Gt находят из экстраполяции профилей в линейном виде, используя тот факт, что y=Gx+0.5. Значения x (при у=0 и у=1) составляют x0=-0.5/G и x1=0.5/G. Отсюда G=(x1-x0)-1. При этих x:
Реклама

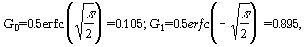 G=(x0.895-x0.105)-1. G=(x0.895-x0.105)-1. |
(4)
|
Таким образом, находя из рисунка значения расстояний, при которых концентрация становится 0.105 и 0.895, находим по [4] значения градиентов концентраций исходного и подвергнутого термообработке образцов. Далее из [3] вычисляем искомый коэффициент диффузии.
При взаимодействии никеля с переходными металлами, стоящими в начале соответствующих рядов, имеет место перенос заряда, приводящий к увеличению электронной плотности в 3d-зоне никеля. Поэтому в качестве легирующего элемента в никелевую матрицу вводился Та, с одной стороны, имеющий достаточно широкую область растворимости в никеле, а с другой - приводящий к значительному переносу заряда.
Как диффундирующие элементы были рассмотрены Co и Nb. Известно, что при взаимодействии Ni и Co сколько-нибудь заметного переноса заряда не происходит, в то же время в случае пары Ni-Nb, напротив, перенос заряда высок. Таким образом, в этих двух случаях мы имеем возможность определить влияние легирования, приводящего к заметному перераспределению электронной плотности, на диффузию элементов, природа химической связи которых с атомами металла-основы существенным образом отличается.
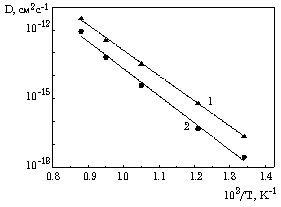
Рис. 1. Температурная зависимость коэффициентов диффузии (1 - Co в Ni; 2 - Co в Ni - 5 ат. % Ta).
Измерения коэффициентов диффузии проводились в диапазоне температур 500 9000 С. Для диффузии Co в чистый никель энергия активации составила 1.64 эВ, а предэкспоненциальный множитель - 1.75.10-15 см2.с-1 (рис. 1). Легирование Ta приводило к уменьшению коэффициента диффузии во всем исследуемом температурном диапазоне. При этом энергия активации процесса была равной 1.86 эВ, а предэкспоненциальный множитель составлял 8.9.10-16 см2.с-1. Некоторое увеличение энергии активации можно объяснить ростом энтальпии образования вакансий в твердом растворе. Кроме того, замедление диффузионных процессов может происходить и вследствие того, что в отличие от связи Co-Ni связь Co-Ta, которая будет образовываться в процессе миграции атомов Co в твердом растворе, имеет значительную ионную составляющую. Для диффузии Nb в Никель были получены следующие данные: энергия активации диффузии равнялась 3.08 эВ, а предэкспоненциальный множитель - 4.3.10-16 см2.с-1 (рис.2). 9000 С. Для диффузии Co в чистый никель энергия активации составила 1.64 эВ, а предэкспоненциальный множитель - 1.75.10-15 см2.с-1 (рис. 1). Легирование Ta приводило к уменьшению коэффициента диффузии во всем исследуемом температурном диапазоне. При этом энергия активации процесса была равной 1.86 эВ, а предэкспоненциальный множитель составлял 8.9.10-16 см2.с-1. Некоторое увеличение энергии активации можно объяснить ростом энтальпии образования вакансий в твердом растворе. Кроме того, замедление диффузионных процессов может происходить и вследствие того, что в отличие от связи Co-Ni связь Co-Ta, которая будет образовываться в процессе миграции атомов Co в твердом растворе, имеет значительную ионную составляющую. Для диффузии Nb в Никель были получены следующие данные: энергия активации диффузии равнялась 3.08 эВ, а предэкспоненциальный множитель - 4.3.10-16 см2.с-1 (рис.2).
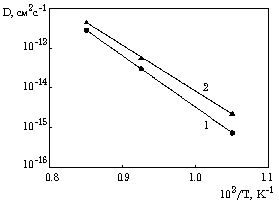
Рис. 2. Температурная зависимость коэффициентов диффузии (1 - Nb в Ni; 2 - Nb в Ni - 5 ат. % Ta).
Характер наблюдаемых изменений параметров процесса диффузии при легировании никеля Ta заметным образом отличался от описанного выше. В этом случае наблюдалось увеличение коэффициента диффузии Nb во всем температурном диапазоне при введении в сплав Ta. При этом энергия активации и предэкспоненциальный множитель составили соответственно 2.92 эВ и 1.6.10-15 см2.с-1. Такое поведение, по всей видимости, связано с тем, что перенос электронов с атомов Nb в твердом растворе Ni-Ta меньше, чем в чистом никеле.
Это предположение подтверждается данными спектроскопических исследований [8]; отношение интенсивностей оже-переходов I(MVV)/I(MNN) в никеле составляет 1.52, а в твердом растворе Ni - 8 ат. % Ta эта величина равна 1.64.
Приведенные экспериментальные данные свидетельствуют, что легирование Ni танталом, приводящее к росту электронной плотности в 3d-зоне никеля, различным образом влияет на диффузию переходных металлов. В твердом растворе Ni-Ta наблюдается замедление диффузии атомов Со, химическая связь которого с Та имеет значительную ионную составляющую. В то же время уменьшение переноса заряда с атомов Nb, находящихся в твердом растворе Ni-Ta, приводит к росту скорости диффузии атомов Nb по сравнению с диффузией этого элемента в чистый никель.
Список литературы
Bocquet J.l. // These. Univ. Paris-Sud. V. 22. P. 77-81.
Caplain A., Chambron W. Energies de formation et demigration des iacunes fer-nickel de structure G.F.C. par la method l`anisotropie magntique induite // Acta Metall. V. 9. P. 1001-1019.
Radelaar S. // Phys. Stat. Sol. V. 27. P. 63.
Hafizuddin S., Mohapatra N.C. A first-princip les theory of the strain-effect electric field gradient in cubic metalas duento point defects // J. Phys. F Met. Phys. 1986. № 1. P. 217-232.
Процессы взаимной диффузии в сплавах / Под ред. К.П.Гурова. М.: Наука, 1973. 358 с.
Hall P.M., Morabito J.M. A formalism for extracting diffusion coefficient from concentration profiles // Surf. Sci. 1976. V. 54. № 1. P. 79-90.
Stefanou N., Oswald A., Zeller R., Dedetisch P.H. Charge and magnetization perturbations around impurities in nickel // Phys. Rev. B. 1987. V. 35. № 13. P. 6911-6922.
Абрамов В.О., Белоконов А.Н., Гуссейнов А.С., Муллакаев М.С., Ширков А.В. Влияние особенностей электронной и зеренной структуры на характер упрочнения твердых растворов никеля, легированного переходными металлами // Краткие сообщения по физике ФИАН. 1991. № 4. C. 41-45.
|