Д.В. Калашников, В.И. Вершинин, Омский государственный университет, кафедра аналитической химии и химии нефти
Постановка задачи и выбор модели.
Моделирование комплексометрического титрования металлов позволяет в ходе вычислительного эксперимента провести априорную оптимизацию, что особенно важно при создании новых методик анализа. Известен ряд моделей и компьютерных программ на их основе [1-3], однако возможность титрования смесей металлов в подобных моделях обычно не предусматривалась(1) Именно этот случай имеет первостепенное значение для комплексометрии: методики, не требующие разделения определяемых металлов, как правило, менее трудоемки и дают более точные результаты [5]. Ранее мы использовали системы уравнений материального баланса для моделирования титрования одного металла произвольным лигандом в присутствии маскирующего вещества [6]. Данный подход позволяет обходиться без грубых упрощений (условных констант) и правильно моделировать кривые титрования, имеющие несколько скачков [7]. Целью настоящей работы было создание на этой же основе модели для комплексометрического анализа смесей металлов, в том числе в условиях маскирования.
В ходе данной работы необходимо было: построить модель, приближенную к реальным условиям комплексометрического анализа; разработать алгоритм расчетов; составить реализующую его программу для IBM-совместимых компьютеров и подтвердить правильность ее работы сопоставлением результатов расчета с литературными данными, относящимися к комплексонометрии.
По нашему мнению, необходимым и достаточным приближением можно считать следующую модель. Пусть при температуре 250С в водном растворе с нулевой ионной силой и произвольным значением рН присутствуют ионы нескольких (не более трех) металлов М1, М2, М3 и может присутствовать маскирующее вещество R, дающее с имеющимися металлами равновесную смесь комплексов. В ходе титрования раствор лиганда Y вводится отдельными небольшими порциями, причем после каждого прибавления достигается химическое равновесие. М1, М2 и М3 подвержены ступенчатому гидролизу, а R и Y ступенчато протонируются. Максимально возможное координационное число металлов - 6; дентатность лигандов может быть любой, основность их - не более 4. Наличие прочих компонентов раствора в модели не учитывается, т.е. требуется химическая инертность примесей. В системе не образуются смешанные, протонированные и полиядерные комплексы, не протекают окислительно-восстановительные реакции, не выпадают осадки. Начальные общие концентрации компонентов, рН раствора и константы равновесий известны. рН раствора и его температура в ходе титрования остаются постоянными. 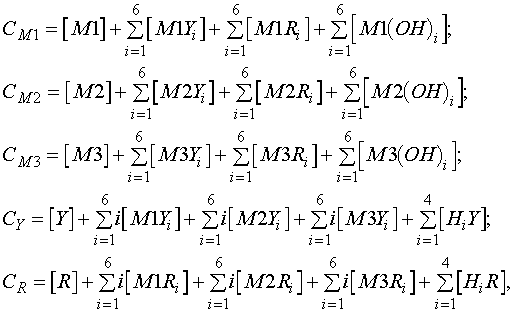
Реклама

В наиболее сложном случае (присутствуют 3 металла и 1 маскирующее вещество) условие материального баланса приводит к системе из пяти уравнений, а именно:
где СМ1, СМ2, СМ3, СY, СR - текущие общие концентрации M1, M2, M3, Y, R соответственно.
После подстановки констант и алгебраических преобразований получается пригодная для численного решения система из пяти нелинейных уравнений с пятью неизвестными, которыми являются равновесные концентрации [M1], [M2], [M3], [Y] и [R]. Аналогичная система для более простого случая приведена нами в [6].
Программная реализация модели. Решение системы уравнений осуществляется по квазиньютоновской схеме, предполагающей возможность дробления ньютоновского шага с целью недопущения выхода за пределы области локальной сходимости итерационного алгоритма [8]. Это позволяет обеспечить глобальную сходимость на множестве допустимых входных параметров и приемлемую скорость вычислений на современных ЭВМ. DVK Complexometry (ОмГУ, 1999) написана на языке Object Pascal и предназначена для работы в операционных системах Windows 95/98/NT. Пользовательский интерфейс организован в соответствии с основными принципами GUI. Кроме главного исполняемого файла дистрибутив содержит инсталлятор, деинсталлятор, справочный файл в формате MicroSoft Help Workshop, а также отдельные базы данных по протонированию, гидролизу и комплексообразованию, содержание которых в основном соответствует справочнику [9]. Время расчета самых сложных кривых титрования на машинах с процессором Pentium 200 не более 1 минуты.
Входными параметрами программы являются: рН, начальные общие концентрации металлов (С0М1, С0М2, С0М3), концентрация титранта (СТ) и его максимальный объем, добавляемый в ходе титрования (VT), начальный объем титруемого раствора (V0) и шаг ввода титранта. В случае учета маскирования необходимо задание начальной общей концентрации постороннего лиганда (С0R). В качестве компонентов моделируемой системы можно задавать вещества, имеющиеся во встроенной базе данных - в этом случае все необходимые константы равновесий подгружаются в программу автоматически. Для веществ, не включенных в базу данных, логарифмы констант учитываемых равновесий вводятся вручную.
Реклама

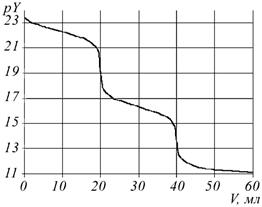
Рис. 1. Расчетная кривая комплексонометрического титрования
смеси Fe(III) и Co(II)
С0Fe = C0Co = 0,01 M; V0 = 20 мл; рН 4
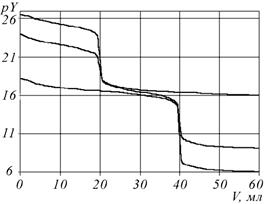
Рис. 2. Расчетные кривые комплексонометрического титрования
смеси In(III) и Cd(II) в разных условиях
С0In = C0Cd = 0,01 M; V0 = 20 мл; рН: a - 7; б - 5; в - 2
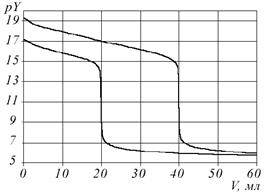
Рис. 3. Расчетные кривые комплексонометрического титрования
смеси Zn(II) и Pb(II) при использовании фенантролина в качестве
маскирующего реагента
С0Zn = C0Pb = 0,01 M; V0 = 20 мл; рН 7; CR: a - 0; б - 0,05 (моль/л)
Основной расчетной процедурой программы является построение интегральной и дифференциальных кривых титрования, т.е. функций вида рX = f(V), dpX/dV = f(V) и d2pX/dV2 = f(V), где V - добавленный объем титранта, а X - любой из компонентов моделируемой системы, а именно М1, М2, М3, Y или R. Предусмотрено исследование функции рY = f(V) на наличие точек перегиба и получение данных по всем скачкам титрования. Для любого значения V возможен расчет состава раствора, т.е. равновесных концентраций всех присутствующих в системе частиц; для каждого металла рассчитываются доли его нахождения в каждом из образующихся комплексов. Можно рассчитывать и сравнивать до пяти вариантов титрования, отличающихся по одному или нескольким входным параметрам; соответствующие кривые титрования строятся на одном графике. Результаты расчета и/или графики могут быть выведены на печать, а входные параметры любого из вариантов титрования сохранены на диске в отдельном файле. В качестве примера на рис.1 приведена расчетная дифференциальная кривая титрования смеси Fe(III) и Co(II) раствором ЭДТА. Отчетливо видны два скачка, причем положение точек перегиба соответствует теории.
Примеры использования программы. С помощью данной модели можно количественно прогнозировать влияние М2 на результат комплексометрического определения М1 в заданных условиях. Примером может быть определение Cu(II) в присутствии Ca(II) и Al(III) при рН 5 (титрант - ЭДТА). Расчет показывает, что определению меди не мешает кальций вплоть до стократного избытка, но мешает алюминий. Аналогичный расчет может быть проведен для подбора природы и концентрации вещества, селективно маскирующего М2. В вышеуказанных условиях таким веществом может служить фторид.
Не менее важно применение программы для оптимизации методик анализа смесей металлов. Известно, что комплексонометрический анализ смеси металлов без их предварительного разделения можно провести, варьируя рН раствора. Так, в нейтральной среде определяется сумма In(III) и Cd(II), а в сильнокислой - титруется только индий, содержание же кадмия определяется по разности [10]. Результаты компьютерного эксперимента согласуются с этими данными (рис. 2). Отметим, что при рН 5 на кривой титрования наблюдаются 2 скачка, что позволяет определять индий и кадмий порознь даже за одно титрование. Оптимальная кислотность раствора для раздельного определения других металлов в их смесях могут прогнозироваться аналогичным способом.
Раздельное определение концентраций Zn(II) и Pb(II) при их совместном присутствии не может быть выполнено аналогичным способом вследствие сходства констант устойчивости соответствующих комплексонатов. На основе компьютерного эксперимента можно предложить ряд селективных маскирующих реагентов (рис. 3). Этот принцип ранее был использован при анализе реальных объектов, содержащих цинк и свинец [11].
По нашему мнению, программа может использоваться не только для создания или оптимизации методик анализа любых реальных объектов, но и в учебном процессе при изучении студентами курса аналитической химии. Однако этот вопрос требует отдельного рассмотрения.
Список литературы
TripathiV.S. // Talanta. 1986. V.33. N 12. P. 1015-1020.
Hu N., Lin S. // J. Beijing Normal Univ. Nat. Sci. 1989. 3. P. 73-79; РЖХим. 1989. 7Г17.
Гармаш А.В., Барбалат Ю.А. Комплекс обучающих программ для ПЭВМ. М.: МГУ. 1991. 69 с.
Rozycki C. // Chem. Anal. 1988. V.33. 6. P. 977-986; РЖХим. 1990. 7Г10.
Шварценбах Г., Флашка Г. Комплексонометрическое титрование. М.: Химия, 1970. 286 с.
Калашников Д.В., Вершинин В.И., Петрук Е.А. // Вестник Омского университета. 1998. \No 3. C. 32-34.
Калашников Д.В., Вершинин В.И. // ЖАХ. 2000. Т. 55. N 1. (в печати).
Ортега Дж. Итерационные методы решения систем уравнений со многими неизвестными. М.: Мир, 1975. С. 178-211.
Лурье Ю.Ю. Справочник по аналитической химии. М.: Химия, 1989. 448 с.
Антонович В.П., Пресняк И.С., Шелехина Е.И., Ласовская О.Н. // ЖАХ. 1995. Т. 50. \No 3. C. 305-308.
Каролев А. // Год. Инст. цвет. мет. Пловдив, 1985. 23. C. 169-174; РЖХим. 1989. 2Г283.
|