Олег Лытнев
Усвоив базовые понятия финансовых расчетов, можно заметить, что все дальнейшие рассуждения строятся по довольно универсальному алгоритму. Определяется математическая природа понятия и основные ограничения, накладываемые на него при практическом использовании. Например, сложные проценты наращиваются в геометрической прогрессии. Они применяются по большей части в расчетах по долгосрочным финансовым операциям. Затем находится решение основных задач, связанных с данным понятием – начисление и дисконтирование по сложным процентным и учетным ставкам. После этого разрабатывается методика расчета остальных параметров уравнений, описывающих данное понятие, и решается проблема нахождения эквивалентных значений отдельных параметров. При этом основным методом решения задач является преобразование или приравнивание друг к другу множителей наращения (дисконтирования) различных показателей. Поняв эти закономерности, можно отказаться от заучивания всех возможных формул и попытаться применить данную методику для решения конкретных финансовых задач, держа при этом в памяти лишь полтора-два десятка основополагающих выражений (например, формулы расчета декурсивных и антисипативных процентов и т.п.).
Используем данный алгоритм для финансового анализа денежных потоков, в частности, для расчета отдельных параметров финансовых рент. Например, предприятию через три года предстоит погасить задолженность по облигационному займу в сумме 10 млн. рублей. Для этого оно формирует погасительный фонд путем ежемесячного размещения денежных средств на банковский депозит под 15% годовых сложных процентов с начислением 1 раз в год. Чему должна быть равна величина одного взноса на депозит, чтобы к концу третьего года в погасительном фонде вместе с начисленными процентами накопилось 10 млн. рублей?
Планируемые предприятием взносы представляют собой трехлетнюю p-срочную ренту, p = 12, m = 1, будущая стоимость которой должна быть равна 10 млн. рублей. Неизвестным является ее единственный параметр – член ренты R. В качестве базовой используем формулу (6) из табл. 3.3.3. Данное уравнение следует решить относительно R / 12 (так как планируются ежемесячные взносы) Обозначим r = R / 12. Преобразовав базовую формулу, получим
Реклама

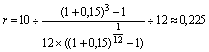
То есть, размер ежемесячного взноса должен составить примерно 225 тыс. рублей (более точная цифра 224,908).
Размер долга по займу (10 млн. рублей) был задан как условие предыдущего примера. На самом деле, часто данный параметр также является вычисляемой величиной, т.к. наряду с основной суммой займа должник обязан выплачивать проценты по нему. Предположим, что 10 млн. рублей – это основная задолженность по облигационному займу, кроме этого необходимо ежегодно выплачивать кредиторам 10% основной суммы в виде процентов. Чему будет равна сумма ежемесячного взноса в погасительный фонд с учетом процентных выплат по займу? Так как проценты должны выплачиваться ежегодно и их годовая сумма составит 1 млн. рублей (10 млн. рублей * 10%), нам опять следует рассчитать член ренты r (R / 12) по ренте сроком n = 1 год, p = 12, m =1, i = 15%. По базовой формуле (6) его величина составит:
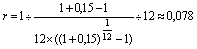
Ежемесячно в погасительный фонд будет необходимо вносить около 78 тыс. рублей (более точная цифра 78,0992) для ежегодной выплаты процентов в сумме 1 млн. рублей. Таким образом общая сумма ежемесячных взносов в погасительный фонд составит 303 тыс. рублей (225 + 78).
Условиями займа может быть предусмотрено присоединение суммы начисленных за год процентов к основному долгу и погашение в конце срока наращенной величины займа. То есть в конце срока эмитенту займа придется возвратить 13 млн. 310 тыс. рублей (10 * (1 + 0,1)3). Величину ежемесячного взноса в погасительный фонд найдем, используя все ту же базисную формулу (6):
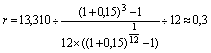
То есть ежемесячно необходимо вносить на банковский депозит около 300 тыс. рублей более точно – 299,35).
Аналогичный подход может быть применен к формированию амортизационного фонда. Известно, что амортизация основных фондов – важнейшая составная часть чистого денежного потока предприятия, остающаяся в его распоряжении. В каждом рубле получаемой предприятием выручки содержится доля амортизационных отчислений. Поэтому нет ничего противоестественного в том, чтобы предприятие, “расщепляя” поступающую выручку, перечисляло на банковский депозит сумму амортизации по каждому платежу от покупателя. В этом случае накопление амортизационного фонда происходило бы значительно быстрее за счет начисления процентов. Предположим, что по основным фондам первоначальной стоимостью 50 млн. рублей предприятие начисляет амортизацию по годовой ставке 12,5% (линейный метод). Срок службы оборудования 8 лет. Ежегодно начисляется 6,25 млн. рублей амортизационных отчислений. Но если предприятие располагает возможностью размещения денежных средств хотя бы под 10% годовых, то для накопления 50 млн. рублей в течение 8 лет ему понадобится ежегодно размещать на депозите лишь по 4, 37 млн. рублей: преобразовав формулу (2) из предыдущей главы, получим:
Реклама


Если же взносы на депозит производить ежемесячно (p = 12), то, снова применяя формулу (6), и деля полученный результат на 12, найдем:

Ежемесячный взнос на депозит должен составить около 350 тыс. рублей (более точно – 348,65). При этом ежемесячные амортизационные отчисления по линейному методу составят 520,8 тыс. рублей (6,25 / 12). Задачу можно сформулировать иначе: за сколько лет предприятие возместит первоначальную стоимость основных средств, размещая на депозите сумму амортизационных отчислений по линейному методу (520,8 тыс. рублей в месяц или 6,25 млн. рублей в год). Для решения этой задачи (нахождение срока ренты n) снова понадобится формула (6), но теперь она будет преобразована следующим образом:
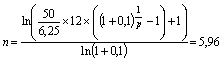
Полученное дробное число лет в соответствии с правилами выполнения финансовых расчетов должно быть округлено до ближайшего целого. Однако, при p > 1, округляется произведение np, в нашем случае оно составляет 71,52 (5,96 * 12). Округлив его до 71 и разделив на 12, получим n = 5,92 года. При любых способах округления, полученное значение на 2 года меньше, чем срок амортизации основных фондов по линейному методу. То есть предприятие таким способом может накопить сумму для замены изношеного оборудования на 2 года быстрее.
Необходимость выплачивать проценты кредитору на остаток банковской ссуды или коммерческого кредита ставит перед предприятиями задачу разработки оптимального плана погашения долга. Дело в том, что оставляя неизменной сумму основной задолженности в течение всего срока займа, предприятие будет вынуждено выплатить максимально возможную сумму процентов по этому займу. Если же оно периодически будет направлять часть средств на погашение основного долга, то сможет сэкономить на процентах, которые начисляются на остаток задолженности. Возможны различные стратегии амортизации займов. Например, предприятие может периодически уплачивать фиксированную сумму в погашение основной задолженности. Тогда в каждом новом периоде ему понадобится меньше денег на оплату процентов, то есть общие расходы по обслуживанию долга за период (срочная уплата) будут снижаться. Погашая ежегодно 2 млн. рублей из общей суммы 3-летнего займа 6 млн. рублей, выданного под 20 процента годовых, предприятие в 1-й год выплатит 1200 тыс. рублей процентов (6000 * 0,2). Срочная уплата за этот период составит 3200 тыс. рублей (2000 + 1200). За второй год проценты составят уже 800 тыс. рублей (4000 * 0,2), срочная уплата – 2800 тыс. рублей (2000 + 800) и т.д. Сумма выплачиваемых процентов будет снижаться в арифметической прогрессии с первым членом 1200 тыс. рублей (p*i) и разностью -400 тыс. рублей (-p * i / n), n означает число членов прогрессии, в данном примере оно равно 3. Сумма этой прогрессии будет равна 2400 тыс. рублей (3 * 1200 – 2 * 3 * 400 / 2), а это значительно меньше суммы процентов, которую пришлось бы уплатить предприятию в случае единовременного погашения основного долга в конце срока ссуды – 4368тыс. рублей (6000 * (1 + 0,2)3 - 6000).
Возможен другой вариант, когда величина срочной уплаты на протяжении всего срока займа остается неизменной, но постепенно меняется ее структура – уменьшается доля, идущая на погашение процентов и увеличивается доля, направляемая в уплату по основному долгу. В этом случае сначала необходимо определить размер срочной уплаты, которая рассчитывается как величина члена ренты, текущая стоимость которой равна первоначальной сумме долга при дисконтировании по процентной ставке, установленной по займу. Преобразовав формулу приведения аннуитета (4) из предыдущей главы, найдем значение R:
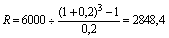
Для полного погашения задолженности по ссуде понадобится произвести 3 погасительных платежа по 2848 тыс. рублей каждый. Не вдаваясь в подробности расчета структуры срочной уплаты по каждому году, отметим, что в сумме предприятию придется заплатить по займу 8544 тыс. рублей, т.е. общая сумма процентов составит 2544 тыс. рублей (8544 – 6000), что заметно выше, чем по первому варианту.
Сопоставление различных вариантов погашения займа только по критерию общей величины выплаченных процентов, не вполне корректно – сравниваются различные денежные потоки, для которых кроме абсолютных сумм имеет значение, в каком конкретно периоде времени деньги были уплачены или получены. Рассмотрим подробнее, что из себя представляет каждый из этих потоков (табл. 2.4.1). Вследствие действия принципа временной ценности денег сложение членов этих потоков является бессмысленной операцией – платежи, производимые с интервалом 1 год, несопоставимы. Поэтому в стр. 5 табл. 2.4.1 рассчитана дисконтированная по ставке 20% величина каждого из потоков. Так как в последней графе этой таблицы представлен аннуитет, то его расчет произведен по формуле (4) из предыдущего параграфа. Два остальных потока состоят из неравных членов, их дисконтирование произведено по общей формуле (3). Как видно из результатов расчетов, наибольшую отрицательную величину (-6472,2) имеет приведенная сумма платежей по первому потоку, она даже превышает сумму полученного зацма. То есть, погашая долг на таких условиях, предприятие реально несет финансовые потери. Два последних варианта не ухудшают финансового положения предприятия.
Таблица 2.4.1
Сравнение вариантов выплаты займа
| Члены потока |
Варианты погашения займа, тыс. руб. |
| возврат основного долга в конце срока |
фиксированная выплата основного долга |
фиксированная срочная уплата |
| 1. Получение займа |
+6000 |
+6000 |
+6000 |
| 2. Платеж в конце 1 года |
-1200 |
-3200 |
-2848,4 |
| 3. Платеж в конце 2 года |
-1440 |
-2800 |
-2848,4 |
| 4. Платеж в конце 3 года |
-7728 |
-2400 |
-2848,4 |
| 5. Приведенная к моменту получения займа сумма выплат |
-6472,2 |
-6000 |
-6000 |
Сравнивая между собой приведенные величины денежных притоков и оттоков по финансовой операции, определяют важнейший финансовый показатель чистая приведенная стоимость (NPV – от английского net present value). Наиболее общая формула определения этого показателя:
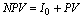 , (1) , (1)
где I0 – первоначальные инвестиции в проект (оттоки денег),
PV – приведенная стоимость будущих денежных потоков по проекту.
При использовании этой формулы все денежные притоки (доходы) обозначаются положительными цифрами, оттоки денежных средств (инвестиции, затраты) – отрицательными.
В нашем примере первоначально предприятие получало приток денежных средств (сумма займа 6 млн. рублей), а затем в течение 3 лет производило денежные расходы, т.е. оттоки средств. Поэтому к первоначальному моменту приводились не поступления, а затраты. Обычно при реализации инвестиционных проектов наблюдается обратная картина: сначала предприятие вкладывает средства, а затем получает периодические доходы от этих вложений. Поэтому, преобразуя (1) с учетом правил дисконтирования денежных потоков (формула (4) из предыдущей главы), получаем:
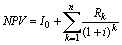 , (2) , (2)
где n – общий срок финансовой операции (проекта),
Rk – элемент дисконтируемого денежного потока (член ренты) в периоде k,
k – номер периода.
Под процентной ставкой i (в данном случае ее называют ставкой сравнения) понимается годовая сложная эффективная ставка декурсивных процентов. Срок операции n в общем случае измеряется в годах. Если же реальная операция не отвечает этим условиям, т.е. интервалы между платежами не равны году, то в качестве единицы измерения срока принимаются доли года, измеренные как правило в месяцах, деленных на 12. Например, инвестиции в сумме 500 тыс. рублей принесут в первый месяц 200 тыс. рублей дополнительного дохода, во второй 300 тыс. рублей и в третий – 700 тыс. рублей. Ставка сравнения равна 25%. Чистая приведенная стоимость данного проекта составит 1 млн. 147 тыс. руб.:

Довольно распространенной является ошибка, когда в подобных случаях пытаются рассчитать месячную процентную ставку делением годовой ставки на 12, а срок проекта измеряют в целых месяцах (вместо 1 / 12 года берут 1 месяц. вместо 2 / 12 – 2 и т.д.). В этом случае будет получен неправильный результат, т.к. возникнет эффект ежемесячного реинвестирования начисляемых сложных процентов. Чтобы получить эквивалентный результат, для нахождения месячной ставки необходимо предварительно пересчитать годовую эффективную ставку i в номинальную j при m = 12 по формуле j = m * ((1 + i)1/m – 1) (см. гл. 2.2) . В данном случае эквивалентной является номинальная годовая ставка 22,52% ставка, разделив которую на 12 можно получить значение для помесячного дисконтирования денежного потока.
Если денежный поток состоит из одинаковых и равномерно рапределенных выплат (то есть представляет собой аннуитет), можно упростить расчет NPV, воспользовавшись формулами дисконтирования аннуитетов из табл. 3.3.3 предыдущего параграфа. Например, если бы в рассматриваемом проекте было предусмотрено получение в течение трех месяцев по 400 тыс. рублей дохода ежемесячно (то есть R = 4800), то следовало рассчитать приведенную стоимость аннуитета сроком 3 / 12 года и числом выплат p = 3. Применив формулу (12) из предыдущего параграфа, получим

Кроме правильного вычисления чистой приведенной стоимости, необходимо понимать ее финансовый смысл. Положительное значение этого показателя указывает на финансовую целесообразность осуществления операции или реализации проекта. Отрицательная NPV свидетельствует об убыточности инвестирования капитала таким образом. В примере с проектом получено очень хорошее значение NPV, свидетельствующее о его инвестиционной привлекательности. Возвратившись к данным табл. 2.4.1, можно видеть, что два последних варианта погашения долга дают нулевую NPV, то есть в финансовом плане само по себе пользование заемными средствами не принесет предприятию ни вреда ни пользы. Если же оно изберет первый вариант (возврат основной суммы долга по окончании его срока), то получит отрицательную NPV –472,2 тыс. рублей, следовательно такой план погашения задолженности принесет ему финансовые потери.
О достоинствах и особенностях чистой приведенной стоимости будет очень подробно говориться в последующих главах. Остается только заметить, что значение ее для финансового менеджмента настолько высоко, что многократно окупает затраты труда по изучению и осмыслению всех вышеприведенных формул финансовых вычислений. Вторым столь же важным финансовым показателем является внутренняя норма доходности (IRR – от английского internal rate of return). Рассмотрим еще один инвестиционный проект. Внедрение новой технологии требует единовременных затрат в сумме 1,2 млн. рублей. Затем в течение 4 лет предприятие планирует получать дополнительный денежный поток от этих инвестиций в размере: 1-й год – 280 тыс. рублей, 2-й год – 750 тыс. рублей, 3-й год – 1 млн. рублей и 4-й год – 800 тыс. рублей. Рассчитаем NPV этого проекта при ставке сравнения 30% годовых:
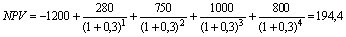
Реализация проекта может принести предприятию 194,4 тыс. рублей чистой приведенной стоимости при условии использования ставки сравнения 30%. А при какой процентной ставке проект будет иметь нулевую NPV, то есть, какой уровень доходности приравняет дисконтированную величину денежных притоков к сумме первоначальных инвестиций? Взглянув на формулу расчета NPV, можно сделать вывод, что увеличение ставки i снижает величину каждого члена потока и общую их сумму, следовательно, чем больше будет уровень ставки, приравнивающей NPV к нулю, тем более мощным будет сам положительный денежный поток. Иными словами, мы получаем характеристику финансовой эффективности проекта, которая как бы заложена внутри него самого. Поэтому данный параметр и получил название внутренняя норма доходности (иногда используется термин внутренняя норма рентабельности, внутренняя процентная ставка и др.). Итак IRR это такая годовая процентная ставка, которая приравнивает текущую стоимость денежных притоков по проекту к величине инвестиций, т.е. делает NPV проекта равным нулю.
Из определения IRR следует, что для ее расчета можно использовать формулу определения NPV (2), решив это уравнение относительно i. Однако данная задача не имеет прямого алгебраического решения, поэтому найти величину IRR можно или путем подбора значения или используя какой-либо итерационный способ (например, метод Ньютона-Рафсона). Широкое распространение вычислительной техники упростило решение подобных задач, поэтому в настоящем пособии не будет рассмотрен математический аппарат расчета IRR “вручную”. Наличие ПК с пакетом электронных таблиц практически снимает проблему. Подберем с помощью компьютера значение i, отвечающее заданным требованиям, оно составит около 37,9%. То есть данный инвестиционный проект обладает доходностью 37,9%. Сравнивая полученное значение с доходностью альтернативных проектов, можно выбрать наиболее эффективный из них.
|