Райнер Фелькер
С помощью теории игр предприятие получает возможность предусмотреть ходы своих партнеров и конкурентов
Сложный инструментарий следует использовать только при принятии принципиально важных стратегических решений
В последние годы значение теории игр существенно возросло во многих областях экономических и социальных наук. В экономике она применима не только для решения общехозяйственных задач, но и для анализа стратегических проблем предприятий, разработок организационных структур и систем стимулирования.
Уже в момент ее зарождения, которым считают публикацию в 1944 г. монографии Дж. Неймана и О. Моргенштерна “Теория игр и экономическое поведение”, многие предсказали революцию в экономических науках благодаря использованию нового подхода. Эти прогнозы нельзя было считать излишне смелыми, так как с самого начала данная теория претендовала на описание рационального поведения при принятии решений во взаимосвязанных ситуациях, что характерно для большинства актуальных проблем в экономических и социальных науках. Такие тематические области, как стратегическое поведение, конкуренция, кооперация, риск и неопределенность, являются ключевыми в теории игр и непосредственно связаны с управленческими задачами.
Первые работы по теории игр отличались упрощенностью предположений и высокой степенью формальной абстракции, что делало их малопригодными для практического использования. За последние 10 – 15 лет положение резко изменилось. Бурный прогресс в промышленной экономике показал плодотворность методов игр в прикладной сфере.
В последнее время эти методы проникли и в управленческую практику. Вполне вероятно, что теория игр наряду с теориями трансакционных издержек и “патрон – агент” будет восприниматься как наиболее экономически обоснованный элемент теории организации. Следует отметить, что уже в 80-х годах М. Портер ввел в обиход некоторые ключевые понятия теории, в частности такие, как “стратегический ход” и “игрок”. Правда, эксплицитный анализ, связанный с концепцией равновесия, в этом случае еще отсутствовал.
Основные положения теории игр
Чтобы описать игру, необходимо сначала выявить ее участников. Это условие легко выполнимо, когда речь идет об обычных играх типа шахмат, канасты и т.п. Иначе обстоит дело с “рыночными играми”. Здесь не всегда просто распознать всех игроков, т.е. действующих или потенциальных конкурентов. Практика показывает, что не обязательно идентифицировать всех игроков, надо обнаружить наиболее важных.
Реклама

Игры охватывают, как правило, несколько периодов, в течение которых игроки предпринимают последовательные или одновременные действия. Эти действия обозначаются термином “ход”. Действия могут быть связаны с ценами, объемами продаж, затратами на научные исследования и разработки и т.д. Периоды, в течение которых игроки делают свои ходы, называются этапами игры. Выбранные на каждом этапе ходы в конечном счете определяют “платежи” (выигрыш или убыток) каждого игрока, которые могут выражаться в материальных ценностях или деньгах (преимущественно дисконтированная прибыль).
Еще одним основным понятием данной теории является стратегия игрока. Под ней понимаются возможные действия, позволяющие игроку на каждом этапе игры выбирать из определенного количества альтернативных вариантов такой ход, который представляется ему “лучшим ответом” на действия других игроков. Относительно концепции стратегии следует заметить, что игрок определяет свои действия не только для этапов, которых фактически достигла конкретная игра, но и для всех ситуаций, включая и те, которые могут и не возникнуть в ходе данной игры.
Важна и форма предоставления игры. Обычно выделяют нормальную, или матричную, форму и развернутую, заданную в виде дерева. Эти формы для простой игры представлены на рис. 1а и 1б.
Чтобы установить первую связь со сферой управления, игру можно описать следующим образом. Два предприятия, производящие однородную продукцию, стоят перед выбором. В одном случае они могут закрепиться на рынке благодаря установлению высокой цены, которая обеспечит им среднюю картельную прибыль ПK. При вступлении в жесткую конкурентную борьбу оба получают прибыль ПW. Если один из конкурентов устанавливает высокую цену, а второй – низкую, то последний реализует монопольную прибыль ПM, другой же несет убытки ПG. Подобная ситуация может, например, возникнуть когда обе фирмы должны объявить свою цену, которая впоследствии не может быть пересмотрена.
При отсутствии жестких условий обоим предприятиям выгодно назначить низкую цену. Стратегия “низкой цены” является доминирующей для любой фирмы: вне зависимости от того, какую цену выбирает конкурирующая фирма, самой всегда предпочтительней устанавливать низкую цену. Но в таком случае перед фирмами возникает дилемма, так как прибыль ПK (которая для обоих игроков выше, чем прибыль ПW) не достигается.
Реклама

Стратегическая комбинация “низкие цены/низкие цены” с соответствующими платежами представляет собой равновесие Нэша, при котором ни одному из игроков невыгодно сепаратно отходить от выбранной стратегии. Подобная концепция равновесия является принципиальной при разрешении стратегических ситуаций, но при определенных обстоятельствах она все же требует усовершенствования.
Что касается указанной выше дилеммы, то ее разрешение зависит, в частности, от оригинальности ходов игроков. Если предприятие имеет возможность пересмотреть свои стратегические переменные (в данном случае цену), то может быть найдено кооперативное решение проблемы даже без жесткого договора между игроками. Интуиция подсказывает, что при многократных контактах игроков появляются возможности добиться приемлемой “компенсации”. Так, при известных обстоятельствах нецелесообразно стремиться к краткосрочным высоким прибылям путем ценового демпинга, если в дальнейшем может возникнуть “война цен”.
Как отмечалось, оба рисунка характеризуют одну и ту же игру. Предоставление игры в нормальной форме в обычном случае отражает “синхронность”. Однако это не означает “одновременность” событий, а указывает на то, что выбор стратегии игроком осуществляется в условиях неведения о выборе стратегии соперником. При развернутой форме такая ситуация выражается через овальное пространство (информационное поле). При отсутствии этого пространства игровая ситуация приобретает иной характер: сначала решение должен бы принимать один игрок, а другой мог бы делать это вслед за ним.
Применение теории игр для принятия стратегических управленческих решений
В качестве примеров здесь можно назвать решения по поводу проведения принципиальной ценовой политики, вступления на новые рынки, кооперации и создания совместных предприятий, определения лидеров и исполнителей в области инноваций, вертикальной интеграции и т.д. Положения данной теории в принципе можно использовать для всех видов решений, если на их принятие влияют другие действующие лица. Этими лицами, или игроками, необязательно должны быть рыночные конкуренты; в их роли могут выступать субпоставщики, ведущие клиенты, сотрудники организаций, а также коллеги по работе.
Инструментарий теории игр особенно целесообразно применять, когда между участниками процесса существуют важные зависимости в области платежей. Ситуация с возможными конкурентами приведена на рис. 2.

Квадранты 1 и 2 характеризуют ситуацию, когда реакция конкурентов не оказывает существенного влияния на платежи фирмы. Это происходит в тех случаях, когда у конкурента нет мотивации (поле 1) или возможности (поле 2) нанести “ответный удар”. Поэтому нет необходимости в детальном анализе стратегии мотивированных действий конкурентов.
Аналогичный вывод следует, хотя и по другой причине, и для ситуации, отражаемой квадрантом 3. Здесь реакция конкурентов могла бы изрядно воздействовать на фирму, но поскольку ее собственные действия не могут сильно повлиять на платежи конкурента, то и не следует опасаться его реакции. В качестве примера можно привести решения о вхождении в рыночную нишу: при определенных обстоятельствах у крупных конкурентов нет оснований реагировать на подобное решение небольшой фирмы.
Лишь ситуация, показанная в квадранте 4 (возможность ответных шагов рыночных партнеров), требует использования положений теории игр. Однако здесь отражены лишь необходимые, но недостаточные условия, чтобы оправдать применение базы теории игр для борьбы с конкурентами. Бывают ситуации, когда одна стратегия безусловно доминирует над всеми другими независимо от того, какие действия предпримет конкурент. Если взять, например, рынок лекарственных препаратов, то для фирмы часто бывает важно первой заявить новый товар на рынке: прибыль “первопроходца” оказывается столь значительной, что всем другим “игрокам” остается только быстрее активизировать инновационную деятельность.
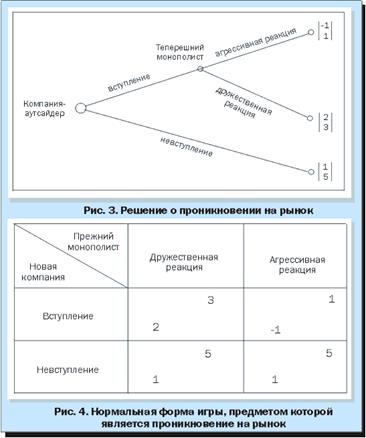
Тривиальным с позиций теории игр примером “доминирующей стратегии” является решение относительно проникновения на новый рынок. Возьмем предприятие, которое выступает в качестве монополиста на каком-либо рынке (например, IВМ на рынке персональных компьютеров в начале 80-х годов). Другое предприятие, действующее, к примеру, на рынке периферийного оборудования для ЭВМ, обдумывает вопрос о проникновении на рынок персональных компьютеров с переналадкой своего производства. Компания-аутсайдер может принять решение о вступлении или невступлении на рынок. Компания-монополист может отреагировать на появление нового конкурента агрессивно или дружественно. Оба предприятия вступают в двухэтапную игру, в которой первый ход делает компания-аутсайдер. Игровая ситуация с указанием платежей показана в виде дерева на рис.3.

Та же самая игровая ситуация может быть представлена и в нормальной форме (рис.4). Здесь обозначены два состояния – “вступление/дружественная реакция” и “невступление/ агрессивная реакция”. Очевидно, что второе равновесие несостоятельно. Из развернутой формы следует, что для уже закрепившейся на рынке компании нецелесообразно реагировать агрессивно на появление нового конкурента: при агрессивном поведении теперешний монополист получает 1(платеж), а при дружественном – 3. Компания-аутсайдер к тому же знает, что для монополиста не рационально начинать действия по ее вытеснению, и поэтому она принимает решение о вступлении на рынок. Грозившие потери в размере (-1) компания-аутсайдер не понесет.
Подобное рациональное равновесие характерно для “частично усовершенствованной” игры, которая заведомо исключает абсурдные ходы. Такие равновесные состояния на практике в принципе довольно просто найти. Равновесные конфигурации могут быть выявлены с помощью специального алгоритма из области исследования операций для любой конечной игры. Игрок, принимающий решение, поступает следующим образом: вначале делается выбор “лучшего” хода на последнем этапе игры, затем выбирается “лучший” ход на предшествующем этапе с учетом выбора на последнем этапе и так далее, до тех пор пока не будет достигнут начальный узел дерева игры.
Какую пользу могут извлечь компании из анализа на базе теории игр? Известен, например, случай столкновения интересов компаний IВМ и Telex. В связи с объявлением о подготовительных планах последней к вступлению на рынок состоялось “кризисное” совещание руководства IВМ, на котором были проанализированы мероприятия, направленные на то, чтобы заставить нового конкурента отказаться от намерения проникнуть на новый рынок.
Компании Telex, видимо, стало известно об этих мероприятиях. Анализ на базе теории игр показал, что угрозы IВМ из-за высоких затрат безосновательны.
Это свидетельствует, что компаниям полезно в эксплицитном виде обдумывать возможные реакции партнеров по игре. Изолированные хозяйственные расчеты, даже опирающиеся на теорию принятия решений, часто носят, как в изложенной ситуации, ограниченный характер. Так, компания-аутсайдер могла бы и выбрать ход “невступление”, если бы предварительный анализ убедил ее в том, что проникновение на рынок вызовет агрессивную реакцию монополиста. В этом случае в соответствии с критерием ожидаемой стоимости разумно выбрать ход “невступление” при вероятности агрессивного ответа 0,5.
Следующий пример связан с соперничеством компаний в области технологического лидерства. Исходной является ситуация, когда предприятие 1 ранее обладало технологическим превосходством, но в настоящее время располагает меньшими финансовыми ресурсами для научных исследований и разработок (НИР), чем его конкурент. Оба предприятия должны решить вопрос, попытаться ли с помощью крупных капиталовложений добиться доминирующего положения на мировом рынке в соответствующей технологической области. Если оба конкурента вложат в дело крупные средства, то перспективы на успех у предприятия 1 будут лучше, хотя оно и понесет большие финансовые расходы (как и предприятие 2). На рис. 5 эта ситуация представлена платежами с отрицательными значениями.
Для предприятия 1 лучше всего было бы, если бы предприятие 2 отказалось от конкуренции. Его выгода в таком случае составила бы 3 (платежа). С большой вероятностью предприятие 2 выиграло бы соперничество, когда предприятие 1 приняло бы урезанную программу инвестиций, а предприятие 2 – более широкую. Это положение отражено в правом верхнем квадранте матрицы.
Анализ ситуации показывает, что равновесие наступает при высоких затратах на НИР предприятия 2 и низких предприятия 1. При любом другом раскладе у одного из конкурентов появляется резон отклониться от стратегической комбинации: так, для предприятия 1 предпочтителен сокращенный бюджет, если предприятие 2 откажется от участия в соперничестве; в то же время предприятию 2 известно, что при низких затратах конкурента ему выгодно инвестировать в НИР.
Предприятие, имеющее технологическое преимущество, может прибегнуть к анализу ситуации на базе теории игр, чтобы в конечном счете добиться оптимального для себя результата. С помощью определенного сигнала оно должно показать, что готово осуществить крупные затраты на НИР. Если такой сигнал не поступил, то для предприятия 2 ясно, что предприятие 1 выбирает вариант низких затрат.
О достоверности сигнала должны свидетельствовать обязательства предприятия. В данном случае это может быть решение предприятия 1 о закупке новых лабораторий или найме на работу дополнительного научно-исследовательского персонала.
С точки зрения теории игр подобные обязательства равнозначны изменению хода игры: ситуация одновременного принятия решений сменяется ситуацией последовательных ходов. Предприятие 1 твердо демонстрирует намерение пойти на крупные затраты, предприятие 2 регистрирует этот шаг и у него нет больше резона участвовать в соперничестве. Новое равновесие вытекает из расклада “неучастие предприятия 2” и “высокие затраты на НИР предприятия 1”.
К числу известных областей применения методов теории игр следует отнести также ценовую стратегию, создание совместных предприятий, расчет времени разработки новой продукции.
Данная теория является базой подготовки рекомендаций для организационного строительства и проектирования систем стимулирования. Она полезна также для формирования и развития внутрифирменных культур.
Важный вклад в использование теории игр вносят экспериментальные работы. Многие теоретические выкладки отрабатываются в лабораторных условиях, а полученные результаты служат импульсом для практиков. Теоретически было выяснено, при каких условиях двум эгоистически настроенным партнерам целесообразно сотрудничать и добиваться лучших для себя результатов.
Эти знания можно использовать в практике предприятий, чтобы помочь двум фирмам достичь ситуации “выигрыш/выигрыш”. Сегодня консультанты с подготовкой в области игр быстро и однозначно выявляют возможности, которыми предприятия могут воспользоваться для заключения стабильных и долгосрочных договоров с клиентами, субпоставщиками, партнерами по разработкам и т.п.
Проблемы практического применения в управлении
Следует, однако, указать и на наличие определенных границ применения аналитического инструментария теории игр. В следующих случаях он может быть использован лишь при условии получения дополнительной информации.
Во-первых, это тот случай, когда у предприятий сложились разные представления об игре, в которой они участвуют, или когда они недостаточно информированы о возможностях друг друга. Например, может иметь место неясная информация о платежах конкурента (структуре издержек). Если неполнотой характеризуется не слишком сложная информация, то можно оперировать сопоставлением подобных случаев с учетом определенных различий.
Во-вторых, теорию игр трудно применять при множестве ситуаций равновесия. Эта проблема может возникнуть даже в ходе простых игр с одновременным выбором стратегических решений.
В-третьих, если ситуация принятия стратегических решений очень сложна, то игроки часто не могут выбрать лучшие для себя варианты. Легко представить более сложную ситуацию проникновения на рынок, чем та, которая рассмотрена выше. Например, на рынок в разные сроки могут вступить несколько предприятий или реакция уже действующих там предприятий может оказаться более сложной, нежели быть агрессивной или дружественной.

Экспериментально доказано, что при расширении игры до десяти и более этапов игроки уже не в состоянии пользоваться соответствующими алгоритмами и продолжать игру с равновесными стратегиями.
Отнюдь не бесспорно и принципиальное, лежащее в основе теории игр предположение о так называемом “общем знании”. Оно гласит: игра со всеми правилами известна игрокам и каждый из них знает, что все игроки осведомлены о том, что известно остальным партнерам по игре. И такое положение сохраняется до конца игры.
Но чтобы предприятие в конкретном случае приняло предпочтительное для себя решение, данное условие требуется не всегда. Для этого часто достаточны менее жесткие предпосылки, например “взаимное знание” или “рационализируемые стратегии”.
В заключение следует особо подчеркнуть, что теория игр является очень сложной областью знания. При обращении к ней надо соблюдать известную осторожность и четко знать границы применения. Слишком простые толкования, принимаемые фирмой самостоятельно или с помощью консультантов, таят в себе скрытую опасность. Анализ и консультации на основе теории игр из-за их сложности рекомендуются лишь для особо важных проблемных областей. Опыт фирм показывает, что использование соответствующего инструментария предпочтительно при принятии однократных, принципиально важных плановых стратегических решений, в том числе при подготовке крупных кооперационных договоров.
|