Кандидаты технических наук А.Ю. Бингелис, И.М. Данишявичюс, Литовский институт физической культуры
Зрелищность движений гребцов, пульсирующее движение и килевая качка академической лодки в такт с частотой гребков скрывают от наблюдателя некоторые немаловажные явления, присущие данному виду спорта. Изучение и использование этих явлений могут способствовать улучшению результатов в академической гребле. К этим вопросам относится выявление причин, обусловливающих выбор экономичного, эффективного или оптимального темпа гребли. В литературных источниках отсутствует тенденция выявления таких причин, рекомендации по выбору наилучшего темпа гребли основываются на интуиции, на практических случаях, статистических данных разных соревнований. Некоторые конкретные данные при таком подходе приведены в обзоре [3].
Цель нашей статьи - на основе законов физики теоретически показать зависимости эффективности (экономичности) работы экипажа от темпа гребли. Начнем с анализа вертикальных движений носа и кормы академической лодки в течение гребка. На рис. 1 показаны результаты исследований, которые проводил Венцель Джостэн [1]. Кривая 1 изображает вертикальное движение носа, а кривая 2 - кормы. С первого взгляда видны достаточно выраженные противофазные вертикальные движения носа и кормы. Оба движения указывают на принудительную килевую качку лодки. Однако по кривым 1 и 2 вычисленное вертикальное движение миделя (приблизительно центра массы) лодки (кривая 3) показывает наличие в общем вертикальном движении составляющей вертикальной качки с частотой большей, чем частота гребков. Данная частота является частотой свободной вертикальной качки лодки и не зависит от темпа гребли. На основе этого возникает идея - вычислить значение темпа гребли, при котором согласованные между собой процессы гребли и вертикальной качки дали бы наилучший результат.
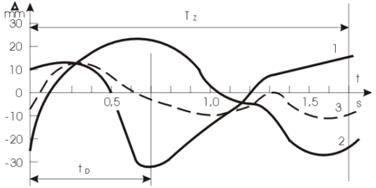
Рис. 1 Вертикальные движения отдельных точек (кривая 1 - носа, кривая 2 - кормы, кривая 3 - миделя) академической лодки в течение гребка
Вертикальную качку комплекса лодки (лодка + весла + экипаж) при гребле вызывает импульс силы, действующий на банку в окончательной стадии проводки. Этот импульс увеличивает осадку лодки. После окончания этого импульса происходит затухающая свободная качка лодки. При этом периодически меняются осадка и тем самым смачиваемая поверхность лодки. Совмещая момент максимальной силы проводки с моментом минимального сопротивления воды (при минимальной площади смачиваемой поверхности), можно получить наиболее экономичную или эффективную греблю.
Реклама

При установившемся темпе гребли процесс вертикальной качки комплекса лодки можно описать выражением изменения суммарного приращения осадки 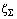 (t)от времени (t)от времени
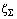 (t)= (t)=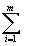 u[t-(i-1)Tz]· u[t-(i-1)Tz]·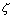 [t-(i-1)Tz], [t-(i-1)Tz],
где m - выбранное количество гребков (m >= 4);
Tz -период гребка u[t-(i-1)Tz] - единичная функция (u=0 при t<(i-1)Tz и u=1 при t >= (i-1)Tz; 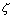 [t-(i-1)Tz]) - изменения приращения осадки под воздействием одиночного имульса силы, действующего на банку после момента времени t>(i-1)Tz. [t-(i-1)Tz]) - изменения приращения осадки под воздействием одиночного имульса силы, действующего на банку после момента времени t>(i-1)Tz.
Выражение изменения приращения осадки определяется в результате решения неоднородного дифференциального уравнения второго порядка, описывающего процесс вертикальной качки комплекса лодки [2] под воздействием одиночного импульса силы на банку.
Математическое описание этого импульса основано на кусочно-линейной аппроксимации кривых, полученных при тестировании гребцов на специальном гребном эргометре. Используемые в вычислениях значения угловой частоты качки -, коэффициента гашения - вертикальной качки, статической осадки Т в зависимости от нагрузки D (или массы D/g) комплекса лодки вычисляются по теоретическим чертежам лодок или определяются экспериментально для конкретных случаев.
На рис. 2 показан общий вид установившихся процессов вертикальной качки комплекса академической одиночки, вычисленных при помощи ЭВМ при разных темпах гребли: SF<SFopt (рис. 2,а), SF=SFopt (рис. 2,в), SF>SFopt (рис. 2, с). Исходными данными для расчета приняты вычисленные данные (Т, D/g, n, v) лодки [4, 5], изготовленной Рижским заводом спортивных судов, и результаты тестирования реального гребца (продолжительность tD и амплитуда импульса силы FD проводки, параметры формы, продолжительность tS и задержка tV импульса силы FS, действующей на банку). При вычислениях для упрощения допущено постоянство исходных данных во всем диапазоне темпа гребли. Форма импульса силы FD проводки, действующей на рукоятке весла, аппроксимирована положительным полупериодом синусоиды.
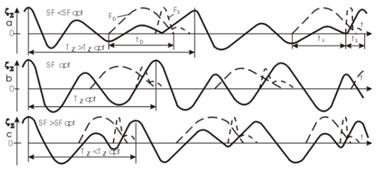
Рис 2. Общий вид установившихся процессов вертикальной качки комплекса академической одиночки при разных значениях темпа гребли
Для количественной оценки эффективности гребли вводится коэффициент эффективности ЕК. Его величина принимается равной 1 при оптимальном темпе гребле, обеспечивающем самое экономичное использование силы FD на рукоятке весла.
Реклама

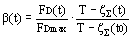 , ,
В основу расчета берется относительная величина где t0 - момент времени, при котором совпадают максимальная сила FDmax на рукоятке весла и минимальная осадка, 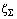 (t0) по составляющей вертикальной качки. (t0) по составляющей вертикальной качки.
ЕК при i-м гребке равен
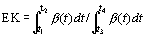 , ,
где t1 = (i-1)TZ - tV; t2 = t1+tD; t3 = t0-tD/2 = (i-1)TZopt-tV; t4 = t0 + tD/2 = t3 + tD.
Таким образом вычисленные зависимости ЕК от темпа гребли SF представлены на рис. 3, а для академической одиночки 1х и на рис. 3,в для академической двойки 2х(2-). Для вычисления графиков рис. 3,а использованы параметры по [4, 5] комплекса одиночки 1х: D/g = 106 кг; Т = 99 мм; n = 8,0 1/с; v = 0,8 1/с; результаты тестирования гребца: tD = 0,74 с; tV = 0,54 с, tS = 0,34 с; импульс силы FS = 77,8 Нс (кривая 1); 126 Нс (кривая 2); 156 Нс (кривая 3). Для вычисления графиков рис. 3,в использованы параметры по [5, 6] комплекса двойки 2х(2-): D/g = 207 кг; Т = 119 мм; - = 7,3 1/с; - = 1,41 1/с; результаты тестирования гребцов: tD = 0,74 с; tV = 0,54 с; tS = 0,34 с; импульс силы FS = 2х77,8 Нс (кривая 1); 2х126 Нс (кривая 2); 2=156 Нс (кривая 3). Результаты вычислений при разных массах комплексов лодок (т.е. разных экипажах по общей массе) дали возможность составить эмпирические выражения для расчета оптимального темпа в зависимости от массы комплекса: для одиночки 1х SFopt = 49,7-0,12 D/g, для двойки 2х(2-) SFopt = 43,4-0,05 D/g.
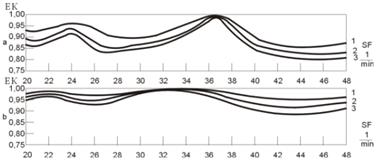
Рис. 3 Теоретическая зависимость коэффициента эффективности EK от темпа SF гребли для академической одиночки (а) и двойки 2х или 2- (б)
Анализ теоретических зависимостей ЕК = f(SF) позволяет делать следующие выводы:
1. Значение оптимального темпа практически линейно увеличивается с уменьшением нагрузки (массы) комплекса лодки.
2. Уменьшение усилий гребцов расширяет диапазон значений оптимального темпа. Усталый экипаж имеет больше возможностей менять темп.
3. Самый экономичный способ достигнуть хороших результатов в гребле - поддержать оптимальный темп; эффективность может быть достигнута увеличением усилий во время проводки.
4. Благодаря большему значению коэффициента гашения исследуемая двойка 2х(2-) оказывается менее чувствительной к отклонению от оптимального темпа гребли, чем одиночка 1х. Оптимальный темп гребли на двойке меньше, чем на одиночке.
5. Для академических лодок других классов расчеты аналогичны. При этом используются суммарные показатели экипажей и соответствующие характеристики лодок.
Результаты исследований и дополнительные сведения о некоторых академических лодках, выпускаемых Рижским заводом спортивных судов, расширят кругозор спортсменов и специалистов, занимающихся академической греблей.
Список литературы
1. Академическая гребля (часть 1).- Л. ЛНИИФК, 1989.
2. Дробленков В.Ф. и др. Справочник по теории корабля.- М.: Воениздат, 1984.
3. Зациорский В.М., Вершинскас Р.С. Биомеханика академической гребли.-Вильнюс, Респ. кабинет методики спорта, 1987.
4.Одиночка гоночная. Теоретический чертеж 7520.00.00ТЧ.
5. Судна спортивные гребные. Общие технические условия ОСТ 62-159-86.
6. Судно спортивное гребное из стеклопластика. Академическая двойка распашная без рулевого и двойка парная 7606.00.00ТЧ.
|