С. А. Ивахненко, О. А. Заневский, А. А. Будяк, И. С. Белоусов
Кристаллизацию алмаза в области термодинамической стабильности с применением металлов-растворителей следует классифицировать как процесс фазовых превращений углерода в расплавах металлов.
Основным методом выращивания монокристаллов алмаза на затравке является метод Стронга— Венторфа, разработанный в 1970—1971 гг. [1, 2]. Перепад температуры между источником углерода и затравкой обычно составляет от нескольких единиц до нескольких десятков градусов; величина градиентов температуры при этом изменяется от 2 до 20 град/мм [3, 4]. Перепад температуры между источником углерода и затравкой, величины осевых и радиальных градиентов температуры обычно подбираются экспериментально, что достаточно трудоемко и требует много времени. Основным материалом нагревателя является графит. Резистивные свойства различных марок графитов отличаются незначительно, поэтому возникают проблемы при задании конфигурации нагревательной системы реакционной ячейки, если требуется изменить величину осевого или радиального градиента температуры или их соотношения.
Расширить класс резистивных материалов позволяет использование композиционных материалов из мелкодисперсных смесей графита с оксидами магния, алюминия, циркония. Такие композиты можно изготавливать путем прессования и термической обработки при атмосферном давлении соответствующих смесей в соотношении, обеспечивающем необходимое значение удельного сопротивления материала. Для улучшения технологии изготовления и повышения прочности изделий из дисперсно-композиционных материалов применяют связующие вещества, например жидкое стекло, силикатный клей, каучук. Достаточно хорошие результаты удается получить при использовании в качестве электропроводной составляющей дисперсно-композиционных материалов нанопо-рошков, полученных термической обработкой интер-калированных графитов [5].
Применение дисперсно-композиционных материалов для формирования резистивной системы нагрева ячеек позволяет значительно упростить процесс задания распределения температуры в реакционном объеме. Особенно эффективно использование методов компьютерного моделирования потенциальных и тепловых полей. Эти методы подробно изложены ранее [6, 7]; они позволяют путем поэтапного моделирования изучить распределение температуры в ячейке и выполнить расчет полей концентраций углерода.
Реклама

Рассмотрим этот подход на примере используемой нами ростовой ячейки для аппарата высокого давления типа тороид (диаметр полости высокого давления составляет 40 мм).
Схема ячейки для выращивания монокристаллов алмаза на затравке представлена на рис. 1. Нагрев ячейки осуществляется электрическим током через токоподводы 7, 75, трубчатый нагреватель 8, конфигурационные и нагревательные диски 3—5, и 11—13. В стационарном режиме в реакционной ячейке устанавливается тепловое поле с перепадом температуры между источником углерода и кристаллом-затравкой 10— 40 °С. Рост алмаза осуществляется на кристалле-затравке путем диффузии углерода через слой металла-растворителя. Поскольку растворимость углерода прямо пропорциональна температуре, то скорость
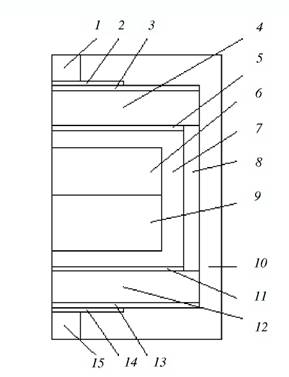
Рис. 1. Электрическая и тепловая схемы реакционной ячейки (1/2 часть осевого сечения):
1, 15 — токоподводы; 2, 14 — электрофокусы; 3, 5, 11, 13 — теплоразводящие диски; 4, 12 — верхний и нижний нагревательные диски; 7, 10 — электро- и теплоизоляционные втулки; 8 — трубчатый нагреватель; 6 — источник углерода; 9 — металл-растворитель
роста монокристалла алмаза зависит от величины вышеуказанного перепада температуры.
Эффективность схемы нагрева реакционной ячейки можно оценить по величине плотности диффузионного потока углерода, направленного на кристалл-затравку. Расчет стационарного теплового поля и поля концентрации углерода в реакционной ячейке заключается в решении при соответствующих граничных условиях дифференциального уравнения второго порядка (1) в частных производных:
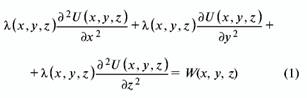
где Цх, у, z) — в зависимости от типа решаемой задачи коэффициент электропроводности, или теплопроводности, или диффузии; U (х, у, z) — потенциальная функция (электрическое напряжение, температура или концентрация углерода); W(x, у, z) — удельная мощность источников электрического тока, тепла или углерода.
Ввиду осевой симметрии ячейки при расчете электрического и теплового полей это уравнение удобно записать в цилиндрических координатах:
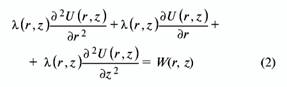
Представление решения уравнений электропроводности, теплопроводности или уравнения диффузии в виде ряда или интеграла практически невозможно ввиду сложности конфигурации ростовой ячейки и задания граничных условий, а также большого количества составляющих элементов. Для расчета теплового поля ростовой ячейки применялся метод конечных элементов в виде метода конечных разностей [7]. Если затравка будет помещена в центре подложки, то диффузионную задачу можно решать тоже как двумерную (осесимметричную); при расположении еще одной затравки на периферии подложки, диффузионную задачу уже нужно решать как трехмерную; в этом случае количество уравнений возрастает на порядок. Для решения системы уравнений нами был использован метод Гаусса—Зейделя [8].
Реклама

На начальном этапе расчета теплового поля ячейку роста кристаллов рассматривали с минимально необходимой степенью детализации, и определяли граничные условия для системы, а затем для этой области искали решение тепловой задачи с более высокой степенью детализации. Во всех вариантах расчета температуру на затравочном кристалле в начальный момент синтеза принимали постоянной и равной 1420 ± 20 °С. В каждом варианте расчета путем ряда приближений следовало подбирать напряжение электрического тока, обеспечивающее вышеуказанную температуру на затравке.
Расчет температурного поля в ячейке роста и распределения температуры в сплаве-растворителе позволил решить задачу диффузионного массопереноса углерода; при этом в качестве граничных условий брали значения растворимости углерода на нижней и верхней поверхностях металла-растворителя при температурах, определенных на предыдущем этапе решения задачи. Плотность диффузионного потока / можно рассчитать как:
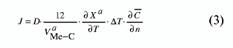
где D — коэффициент диффузии в расплаве; vMe-c ~~ мольный объем расплава, насыщенного углеродом, по отношению к алмазу; Ха — растворимость алмаза в расплаве металл-углерод; А Т — перепад температуры между источником углерода и затравкой;
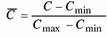
— безразмерная концентрация углерода; С — концентрация углерода; Cmin и Стах — минимальное и максимальное значение концентрации углерода, соответственно, п — нормаль к поверхности равной концентрации.
Проведенные расчеты показывают, что радиальные и осевые градиенты температуры в металле-растворителе можно существенно менять за счет общей скорости массопереноса углерода, варьируя конфигурацию системы нагрева.
На рис. 2 представлено распределение температуры в ростовой ячейке, обусловленное различными соотношениями длин и диаметров резистивных элементов. При температуре 1420 °С на затравке максимальная температура источника углерода составляет 1530 °С, а максимальная температура на затравочной плоскости равна 1482 °С. Варьируя размеры системы нагрева, массоперенос углерода можно изменить в направлении от центра к периферии подложки, на которой располагаются затравочные кристаллы; расчет указанным методом это хорошо демонстрирует (рис. 2, б, в).
Можно оценить зависимость величины диффузионного потока углерода от места размещения кристалла-затравки в центре подложки и на периферии. Расстояние между центральной и периферийной затравками составляло =2/3 радиуса подложки (5 мм для диаметра ростовой ячейки, равного 16 мм).
Для кристалла-затравки, расположенного в центре подложки, картина изолиний концентраций углерода показана на рис. 3. Из рисунка следует, что наибольшая плотность изолиний и максимальная плотность диффузионного потока составляет (1,1—1,4) • 10~3мг • мм~2 • с"1. На расстоянии -1/3 высоты уровня металла-растворителя эта плотность на два порядка ниже.
Для кристаллов-затравок, расположенных в центре подложки и на периферии, картина изолиний концентрации углерода показана на рис. 4. Максимальная плотность диффузионного потока должна быть в месте расположения центральной затравки. При соответст-
вующем подборе элементов резистивной цепи нагрева и их конфигурации можно обеспечить в этом случае максимальную плотность изолиний концентрации
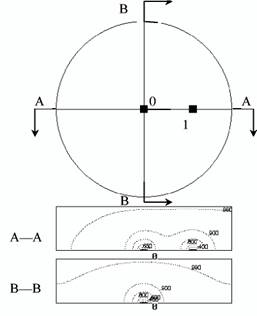
Рис. 4. Изолинии безразмерных концентраций в осевых сечениях ячейки с двумя затравками:
О — затравка в центре, 1 — затравка на периферии
углерода; величина значения диффузионного потока составляет не менее (1,1—1,4) • 10~3 мг • мм~2 • с"1.
Если затравка расположена на периферии (рис. 4), то она находится в менее благоприятных условиях для роста алмаза — наблюдается меньшая плотность изолиний углерода, значение плотности диффузионного потока составляет от 0,6-10~4 до 1,4-10~3 — мг<мм~2<с~1. На достаточном удалении от затравки плотность диффузионного потока также на два порядка ниже. Такая
схема массопереноса предпочтительна для выращивания крупных монокристаллов алмаза при размещении затравок на периферии подложки. Таким образом, для выращивания одного кристалла максимальной массы необходимо использование схемы с одной затравкой в центре; для выращивания нескольких монокристаллов целесообразно затравки располагать ближе к периферии.
Используя указанные выше методы расчета распределения температуры и концентрации углерода, возможно рассчитывать массоперенос углерода, его направление и плотность потока при выращивании монокристаллов алмаза на затравке методом температурного градиента. Для одной затравки, расположенной в центре подложки (рис. 2), можно обеспечить рост структурно совершенного монокристалла алмаза массой около 5 карат. Для трех затравок средняя масса выращенных кристаллов составляет 1,8 карата; для четырех затравок — от 1 до 1,4 карата.
Работа выполнена при содействии Государственного фонда фундаментальных исследований при Министерстве образования и науки Украины, проект № 10.01/037.
Список литературы
1. Чернов А.А., Гиваргизов Е.И., Багдасаров Х.С. и др. Современная кристаллография (в четырех томах). Том 3. Образование кристаллов. М.: Наука, 1980, 407 с.
2. Тимофеева В.А. Рост кристаллов из раствор-расплавов. М.: Наука, 1978, 268 с.
3. US Patent 4034066, 1973, МКИ С 01 В 31/06.
4. US Patent 4042673, 1973.
5. Lisakovskiy V.V., Ivakhnenko S.A., Serga M.A. e. a. In: Int. Conf. «Crystal Materials 2005» (ICCM 2005). May 30—June 2, 2005. Kharkov, Ukraine. Abstracts book, p. 16.
6. Ивахненко С.А. Дис. ... докт. техн. наук. Киев, 1998, 299 с.
7. Сверхтвердые материалы. Получение и применение (в 6 томах). Т. 1. Синтез алмаза и подобных материалов. Под общей ред. Н.В. Новикова. Киев: ИСМ им. В.Н. Бакуля, ИПЦ «АЛКОН» НАНУ, 2003, 320 с.
8. Decker D.L., Bassett W.A., Merill L. e. a. J. Phys. Chem. Ref. Data, 1972, v. 1, № 3, p. 773.
|