С О Д Е Р Ж А Н И Е Р А Б ОТ Ы :
Страница
§1. Введение. 1
§2. Задание на курсовую работу. 2
§3. Транспортная задача линейного программирования. 3
п.3.1. Математическая постановка задачи. 3
п.3.2. Математическая запись задачи. 3
п.3.3. Метод совмещённых планов. 4
§4. Расчёт по методу совмещённых планов. 6
п.4.1. Расчёт оптимального плана возврата порожняка. 7
п.4.2. Расчёт индексов для занятых клеток. 8
п.4.2.1. Расчёт суммарного холостого пробега. 8
п.4.2.2. Расчёт индексов. 8
п.4.2.3. Определение потенциальных клеток. 9
п.4.2.4. Оптимизация плана. 9
п.4.3. Составление матрицы совмещённых планов. 10
§ 5. Прикрепление образованных маршрутов к АТП. 12
§6. Технологический расчёт маршрутов. 14
§7. Выводы. 16
Литература. 17
§ 1
. ВВЕДЕНИЕ.
Маршрутизация перевозок – это прогрессивный, высокоэффективный способ организации транспортного процесса, позволяющий значительно сократить непроизводительные порожние пробеги подвижного состава, повысить качество обслуживания клиентуры и, в конечном счёте, сократить транспортные издержки самого автотранспортного предприятия.
Порожний пробег – это сумма холостых и нулевых пробегов. Величина порожних пробегов зависит от ряда факторов: от характера и направления грузопотоков; но главное влияние оказывает организация транспортного процесса и качество сменно-суточного планирования. Поэтому задачу ежедневного планирования можно сформулировать так: Сменно-суточное планирование перевозок грузов должно обеспечить выполнение заданного объёма перевозок с наименьшим порожним пробегом автомобилей.
Эта тема и будет являться основополагающей в данном курсовом проекте.
§ 2.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ.
В автотранспортное предприятие поступила заявка на перевозку грузов на завтрашний день.
Требуется составить оптимальный сменно-суточный план перевозки грузов (маршруты движения автомобилей и сменные задания водителям), обеспечивающих вывозку заданных объёмов при минимальном суммарном пробеге автомобилей.
Исходные данные для решения транспортной задачи приведены в таблицах N No
-1, 2, 3.
ТАБЛИЦА 1.
Заявка на перевозку грузов (в тоннах).
Пункт
отправления
|
А
1
|
А
1
|
А
1
|
А
2
|
А
3
|
А
4
|
А
4
|
А
5
|
А
5
|
А
6
|
А
6
|
Пункт
назначения
|
Б
1
|
Б
7
|
Б8
|
Б
2
|
Б
5
|
Б
3
|
Б
4
|
Б
1
|
Б
3
|
Б
5
|
Б
6
|
Объём
перевозок
|
189
|
81
|
81
|
81
|
81
|
36
|
54
|
108
|
54
|
54
|
54
|
ТАБЛИЦА 2.
Расстояния между пунктами отправления и назначения ( в км).
Реклама

| Пункт назначения |
Пункт
отправления
|
Б
1
|
Б
2
|
Б
3
|
Б
4
|
Б
5
|
Б
6
|
Б
7
|
Б
8
|
АТП
|
| А
1
|
5
|
1
|
7
|
8
|
4
|
2
|
14
|
15
|
3
|
| А
2
|
5
|
13
|
8
|
6
|
3
|
1
|
7
|
3
|
1
|
| А
3
|
12
|
4
|
14
|
13
|
11
|
4
|
12
|
10
|
12
|
| А
4
|
16
|
7
|
15
|
15
|
13
|
5
|
15
|
12
|
2
|
| А
5
|
9
|
1
|
13
|
6
|
1
|
1
|
4
|
1
|
10
|
| А
6
|
3
|
1
|
5
|
3
|
8
|
10
|
3
|
2
|
15
|
| АТП
|
8
|
17
|
16
|
11
|
4
|
6
|
9
|
9
|
--
|
ТАБЛИЦА 3.
Расчётные нормативы.
| Показатель |
Обозначение |
Значение |
| Грузоподъёмность |
q |
5 |
| Коэффициент использования грузоподъёмности |
g |
0,9 |
| Время в наряде * (в часах) |
Тн
|
12,5 |
| Среднетехническая скорость (в км/час) |
Vт
|
24 |
| Простой под погрузкой и выгрузкой на одну ездку с грузом (мин) |
tпв
|
85 |
* Примечание. Допустимое отклонение ± 35 минут.
** Примечание. Используется автомобиль ЗИЛ-130 грузоподъёмностью 5 тонн.
§
3. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
3.1. Математическая постановка задачи.
Рассмотрим и сформулируем в математической форме условие транспортной задачи. Потребителям Б1
,Б2
, ....,Бj
,...., Бn
требуется груз в количествах b1
, b2
,....., bj
,....., bn
(т) единиц, который имеется или производится у поставщиков A1
, A2
,......, Ai
,......, Am
в количествах a1
, a2
,......., ai
,......, am
(т) единиц соответственно. Обозначим через qij
объём перевозок из i-ого пункта отправления в j-ый пункт назначения. Объём перевозок известен для всех пунктов ( задана заявка на перевозки грузов, см. таблицу 1.). Расстояние между поставщиками и потребителями известно (см. таблицу 2.)и составляет lij
(км). В процессе выполнения перевозок в пунктах назначения Б1
,Б2
, ....,Бj
,...., Бn
после разгрузки автомобилей будет образовываться порожняк в количествах b`1
, b`2
,....., b`j
,....., b`n
который надо направить в пункты A1
, A2
,......, Ai
,......, Am
в количествах a`1
,a`2
,…a`j
,….a`m
.
С методической точки для решения задачи удобней пользоваться понятием “ездка”. Поэтому за единицу измерения будет приниматься ездка автомобиля с грузом и без него.
В задаче будет выполняться условие:
m
n
b`j
= bj
= Sqij
, где j=1,2,......,n и a`i
= ai
= Sqij
, где i=1,2,......,m ,
1
1
Дополнительным условием задачи является требование, чтобы за рабочую смену автомобиль направлялся не более, чем в четыре разных пункта отправления и в такое же количество пунктов назначения. Практически это означает, что при сменном задании с большим числом ездок необходимо составить кольцевой маршрут так, чтобы по нему можно было сделать несколько оборотов. Необходим план перевозок который обеспечит выполнение заданных объёмов с наименьшим холостым пробегом автомобиля.
3.2.
Математическая запись задачи.
Обозначим через Xij
количество порожняка (в автомобиле - ездках) предназначенного к отправке из пункта разгрузки Бj
в пункт погрузки Ai
, тогда суммарный холостой пробег автомобиля из всех пунктов с наличием порожняка во все пункты его подачи будет иметь вид:
n m
SSXij
*
lij
- min.{ 1 }
j=1 i=1
Условие полного удовлетворения спроса на порожняк каждого пункта отправления за счёт подачи его из разных пунктов с наличием порожняка выглядит так:
Реклама

n
SXij
= a`i
, где i= 1,2,...,m. { 2 }
j=1
Весь порожняк из каждого пункта назначения должен быть подан в пункт отправления под погрузку, т.е. :
m
SXij
=b`j
, где j= 1,2,...,n. { 3 }
i=1
Очевидно, что количество автомобилей не может быть отрицательным числом, т.е. Xij
> 0, при i= 1,2,...,m, j= 1,2,...,n. { 4 }
Таким образом, в математической форме транспортная задача формулируется так:
Определить значение переменных
Xij
минимизирующих линейную форму, выраженную
{1},
при ограничениях, указанных в
{2},{3},{4}.
Необходимо равенство общей потребности получателей и наличия груза у поставщиков или отправителей:
m n
Sb`j
= Sа`j
{ 5 }
i=1 j=1
Это равенство является необходимым и достаточным условием для совместимости уравнений {2},{3}.
Цель решения выражается уравнением {1}: найти минимальный суммарный холостой пробег автомобилей. Задачу, выраженную формулами {1—5} принято называть задачей минимизации холостых пробегов автомобилей.
3.3.
Метод совмещённых планов.
Для решения задачи разработан метод совмещённых планов. С его помощью она решается в три этапа.
На первом этапе решают задачу минимизации холостых пробегов автомобилей, в результате чего находят оптимальный план возврата порожняка под погрузку после разгрузки. Составление оптимального плана отражено в блок-схеме алгоритма метода потенциалов на рисунке 1.
На втором этапе из грузопотока ( линий перевозок ) заданных заявкой на перевозки и линий оптимального плана возврата порожняка, найденного на первом этапе, составляют схему кольцевых и маятниковых маршрутов движения автомобилей, в совокупности обеспечивающих минимум холостых пробегов автомобилей при выполнении заданных перевозок.
На третьем этапе найденные маршруты прикрепляют к АТП (автотранспортному предприятию), после чего разрабатывают сменно-суточные задания водителям по каждому маршруту.
Составление матрицы условий

 Составление допустимого исходного плана Составление допустимого исходного плана
   Подсчёт числа занятых клеток в матрице (N) и сравнение с (m+n-1) Подсчёт числа занятых клеток в матрице (N) и сравнение с (m+n-1)
N>m+n-1 N<m+n-1
Ликвидация лишних
занятых клеток
|
N=m+n-1 |
Создание недостающих
занятых клеток
|
 
 Расчёт индексов Расчёт индексов

  Проверка незанятых клеток на потенциальность Проверка незанятых клеток на потенциальность
 Построение цепочки возможных перемещений загрузок Построение цепочки возможных перемещений загрузок
Расчёт знаков “+” и “-“ по вершинам цепочки

Поиск наименьшей среди загрузок, отмеченных знаком “-“

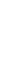 Изменение загрузки на вершинах цепочки Изменение загрузки на вершинах цепочки
 Решение закончено: оптимальный план составлен Решение закончено: оптимальный план составлен
Потенциальных клеток нет
Рис. 1. Блок-схема алгоритма метода потенциалов.
§
4. РАСЧЁТ
ПО
МЕТОДУ
СОВМЕЩЁННЫХ
ПЛАНОВ.
п.4.1.
Расчёт оптимального плана возврата порожняка.
Решение транспортной задачи начинается с разработки допустимого исходного плана, который разрабатывается в табличной форме. В матрицу условий (таблица 4) вводится дополнительный столбец и строка.
ТАБЛИЦА 4.
Матрица условий.
| Пункт назначения (образов. порожняка)
|
| Пункт назначения |
Вспом.
Индек.
|
Б1
|
Б2
|
Б3
|
Б4
|
Б5
|
Б6
|
Б7
|
Б8
|
Потребность в перевозках |
| Ui
/ Vi
|
| А1
|
5
|
1
|
7
|
8
|
4
|
2
|
14
|
15
|
| А2
|
5
|
13
|
8
|
6
|
3
|
1
|
7
|
3
|
| А3
|
12
|
4
|
14
|
13
|
11
|
4
|
12
|
10
|
| А4
|
16
|
7
|
15
|
15
|
13
|
5
|
15
|
12
|
| А5
|
9
|
1
|
13
|
6
|
1
|
1
|
4
|
1
|
| А6
|
3
|
1
|
5
|
3
|
8
|
10
|
3
|
2
|
| Наличие порожняка |
В строке записываются значения индексов Vj
, а в столбце – значения индексов Ui
.
Для дальнейших расчётов необходимо определить количество автомобиле-ездок, их находим по формуле :
Ze
= Q/ q*
g,
где Q – объём перевозок;
q – грузоподъёмность автомобиля (т);
g -- коэффициент использования грузоподъёмности.
Значения q и g возьмём из таблицы 3. Результаты вычисления занесём в таблицу 5.
ТАБЛИЦА 5.
Расчёт ездок от объёма перевозки грузов (в тоннах).
Пункт
отправления
|
А
1
|
А
1
|
А
1
|
А
2
|
А
3
|
А
4
|
А
4
|
А
5
|
А
5
|
А
6
|
А
6
|
Пункт
назначения
|
Б
1
|
Б
7
|
Б8
|
Б
2
|
Б
5
|
Б
3
|
Б
4
|
Б
1
|
Б
3
|
Б
5
|
Б
6
|
Объём
перевозок
|
189
|
81
|
81
|
81
|
81
|
36
|
54
|
108
|
54
|
54
|
54
|
| Количество автомобиле- ездок |
42
|
18
|
18
|
18
|
18
|
8
|
12
|
24
|
12
|
12
|
12
|
В правом верхнем углу клеток, представляющих собой реальные маршруты перевозок, указаны расстояния между соответствующими пунктами; условие Sbj
= Sаi
= 194 (ездки) выполняется.
ТАБЛИЦА 6.
Допустимый исходный план.
| Пункт назначения (образов. порожняка)
|
| Пункт назначения |
Вспом.
Индек.
|
Б1
|
Б2
|
Б3
|
Б4
|
Б5
|
Б6
|
Б7
|
Б8
|
Потребность в перевозках |
| Ui
\ Vi
|
| А1
|
425
|
1
|
7
|
8
|
4
|
2
|
1814
|
1815
|
78 |
| А2
|
5
|
1813
|
8
|
6
|
3
|
1
|
7
|
3
|
18 |
| А3
|
12
|
4
|
14
|
13
|
1811
|
4
|
12
|
10
|
18 |
| А4
|
16
|
7
|
815
|
1215
|
13
|
5
|
15
|
12
|
20 |
| А5
|
249
|
01
|
1213
|
6
|
01
|
1
|
4
|
1
|
36 |
| А6
|
3
|
1
|
5
|
3
|
128
|
1210
|
3
|
2
|
24 |
| Наличие порожняка |
66
|
18 |
20 |
12 |
30 |
12 |
18 |
18 |
194/194 |
План разрабатывается способом минимального элемента по строке. Разработка производится в следующем порядке: сначала, планируются перевозки с первого склада, записывая их в соответствующие клетки первой строки, при этом удовлетворяются запросы потребителя, находящегося ближе всего к этому складу.
Планируем перевозки ближайшим из неудовлетворённых ещё потребителей, записывая соответствующие загрузки в клетки с наименьшими расстояниями. При соблюдении условий, описанных выше, удовлетворяя спрос и предложения пунктов отправления и потребления, происходит заполнение необходимых клеток; остаток по столбцу или строке сносится в клетку остатков, который впоследствии заносится в свободные не вычеркнутые клетки. При этом необходимо соблюдать условие, что количество заполненных клеток должно соответствовать числу m + n -1, где m — число пунктов отправления или погрузки; n – число пунктов погрузки.
В таблице 6 количество занятых клеток равно числу m + n -1=13; а в таблице 6 количество занятых клеток не равно этому числу 13 . Поэтому необходимо создать недостающие клетки, поставив нулевые загрузки в клетки А5
-Б2
и А5
-Б5
.
Допустимый исходный план составлен, проверим его на оптимальность.
п.4.2.
Расчёт индексов для занятых клеток.
п.4.2.1.
Расчёт суммарного холостого пробега.
Рассчитываем суммарный холостой пробег для допустимого исходного плана (таблица 6) с помощью формулы:
n
m
SLx
= S S Xij *
lij
, { 6 }
j=1 i=1
где SLx
-- суммарный холостой пробег (км); Xij
– количество порожняка, подаваемого между i-ым пунктом назначения, ездки; lij
– расстояние от i-ого пункта отправления до j-ого пункта назначения (км).
п.4.2.2. Расчёт индексов.
Следующим пунктом вычислений находим индексы для загруженных клеток :
Ui
+ Vj
=lij
Xij
, { 7 }
Проверка допустимого плана на оптимальность заключается в соблюдении условий:
Ui
+ Vj
=lij
, для Xij
>0 { 8 } и Ui
+ Vj
=lij
, для Xij
=0 . { 9 }
Для определения индексов используются следующие правила:
а) индексы Ui
записываются во вспомогательный столбец ;
б) индексы Vj
записываются во вспомогательную строку;
в) индексы правой клетки вспомогательного столбца принимаются за нуль: U1
=0.
Тогда из уравнения {6} можно выразить Ui
и Vj
.
Далее, рассчитаем индексы для таблицы 7 допустимого исходного плана по этим правилам.
ТАБЛИЦА 7.
Допустимый исходный план ( предварительный вариант).
 V1
= A1
Б1
– U1
= 5-0= 5; V7
= A1
Б7
– U1
= 14-0=14; V8
= A1
Б8
– U1
= 15-0 =15 V1
= A1
Б1
– U1
= 5-0= 5; V7
= A1
Б7
– U1
= 14-0=14; V8
= A1
Б8
– U1
= 15-0 =15
……………………….. ………………………….. …………………………
U5
= A5
Б1
– V1
= 9-5= 4; V3
= A5
Б3
– U5
= 13-4= 9; U4
= A4
Б3
– V3
= 15-9 =6;
После расчёта индексов проверяем незанятые клетки на потенциальность.
п.4.2.3. Определение потенциальных клеток.
Незанятые клетки, для которых получилось, что Ui
+ Vj
>lij
– называются потенциальными. Проверяем незанятые клетки на потенциальность. Проверка сводится к сравнению расстояний каждой незанятой клетки с суммой соответствующих ей индексов.
А1
Б2
= u1
+ v2
= 0-3 = -3 < ( l1-2
=1)
;
 А1
Б3
= u1
+ v3
= 0+9 = 9 > ( l1-3
=7)
-- 2 ; А1
Б3
= u1
+ v3
= 0+9 = 9 > ( l1-3
=7)
-- 2 ;
 ....................................................................; ....................................................................;
А2
Б8
= u2
+ v8
= 16+15= 31> ( l2-8
=3)
-- 28 ;
.....................................................................;
 А6
Б8
= u6
+ v8
= 11+15= 26> ( l6-8
=2)
-- 24 . А6
Б8
= u6
+ v8
= 11+15= 26> ( l6-8
=2)
-- 24 .
По данным вычислений построим таблицу 7.
4.1.5. Оптимизация плана.
Проверка допустимого плана на оптимальность заключается в соблюдении условий: {8} и {9}. Если данные условия не соблюдаются для клеток Xij
=0, то значение потенциала отрицательно, что и определяет потенциальную клетку. Следует скорректировать допустимый план. Корректировка плана состоит в перемещении в потенциальную клетку с наименьшим по модулю потенциалом какую-нибудь загрузку. Перемещение производится при условии сохранения количества “+” и “-“ по строке и столбцу. Производя перемещение, следует повторить процесс определения потенциала до тех пор, пока условия {8} и {9} не будут соблюдены. Признаком оптимальности является отсутствие клеток, в которых сумма индексов будет больше расстояний.
Из наличия потенциальных клеток можно сделать вывод, что составленный план не является оптимальным. Выявленные клетки являются резервом улучшения плана, а превышение суммы индексов над расстоянием – потенциалом (в таблице 7 они размещены в нижнем правом углу клетки и выделены другим цветом). Улучшение неоптимального плана сводится к перемещению загрузки в потенциальную клетку матрицы.
Цепочку возможных перемещений определяют: для потенциальной клетки с наибольшим значением потенциала строят замкнутую цепочку из горизонтальных и вертикальных отрезков так, чтобы одна из её вершин находилась в данной клетке, а все остальные вершины в занятых клетках. Знаком “+” отмечают в цепочке её нечётные вершины, считая вершину в клетке с наибольшим потенциалом, а знаком “-“ – чётные вершины. Наименьшая загрузка в вершинах 18 ездок, уменьшая загрузку в вершинах со знаком “-“ и увеличивая её в вершинах со знаком “+” получают улучшенный план. Дальнейшие расчёты по его оптимизации производятся аналогично. Признаком оптимальности является отсутствие клеток, в которых сумма индексов будет больше расстояний.
В результате всех вычислений имеем конечный оптимальный план возврата порожняка в таблице 8.
ТАБЛИЦА 8.
Оптимальный план возврата порожняка.
| Пункт назначения (образов. порожняка)
|
| Пункт назначения |
Вспом.
Индек.
|
Б1
|
Б2
|
Б3
|
Б4
|
Б5
|
Б6
|
Б7
|
Б8
|
Потребность в перевозках |
| Ui
/ Vi
|
5 |
-1 |
7 |
6 |
3 |
-3 |
6 |
3 |
| А1
|
0 |
665
|
1
|
127
|
8
|
4
|
2
|
14
|
15
|
78 |
| А2
|
0 |
05
|
13
|
8
|
6
|
3
|
1
|
7
|
183
|
18 |
| А3
|
5 |
12
|
184
|
14
|
13
|
11
|
4
|
12
|
10
|
18 |
| А4
|
8 |
16
|
07
|
815
|
15
|
13
|
125
|
15
|
12
|
20 |
| А5
|
-2 |
9
|
1
|
13
|
6
|
301
|
1
|
64
|
01
|
36 |
| А6
|
-3 |
3
|
1
|
5
|
123
|
8
|
10
|
123
|
2
|
24 |
| Наличие порожняка |
66
|
18 |
20 |
12 |
30 |
12 |
18 |
18 |
194/194 |
После составления оптимального плана возврата порожняка произведём проверку клеток на потенциальность. Проверка сводится к сравнению расстояний каждой незанятой клетки с суммой соответствующих ей индексов.
А1
Б2
= u1
+ v2
= 0-1 = -1 < ( l1-2
=1)
; ……; А2
Б2
= u2
+ v2
= 0-1 = -1 < ( l2-2
=13)
;
А1
Б4
= u1
+ v4
= 0+6 = 6 < ( l1-4
=8)
; ……; А2
Б7
= u2
+ v7
= 0+6 = 6 < ( l2-7
=7)
;
.........................................................; ……; .…………………………………;
А3
Б8
= u3
+ v8
= 5+3 = 8 < ( l3-8
=10)
; …..; А4
Б8
= u4
+ v8
= 8+3 = 11 < ( l4-8
=12)
;
.........................................................; ….…; .…………………………………..;
А6
Б1
= u6
+ v1
= -3+5 = 2 ‡( l6-8
=2)
; ……; А6
Б8
= u6
+ v8
= -3+3 = 0 < ( l6-8
=2)
.
п.
4.3.
Составление матрицы совмещённых планов.
Матрица совмещённых планов составляется после окончания разработки оптимального плана возврата порожняка. В таблицу 9 подставляются груженые ездки из таблицы 5. С целью лучшей наглядности изображения данные выполняются разными цветами.
ТАБЛИЦА 9.
Матрица совмещенных планов.
| Пункт назначения |
Б1
|
Б2
|
Б3
|
Б4
|
Б5
|
Б6
|
Б7
|
Б8
|
| А1
|
66 425
|
1
|
12 7
|
8
|
4
|
2
|
18 14
|
18 15
|
| А2
|
0 5
|
1813
|
8
|
6
|
3
|
1
|
7
|
183
|
| А3
|
12
|
184
|
14
|
13
|
1811
|
4
|
12
|
10
|
| А4
|
16
|
07
|
8815
|
12 15
|
13
|
125
|
15
|
12
|
| А5
|
24 9
|
1
|
12 13
|
6
|
301
|
1
|
64
|
01
|
| А6
|
3
|
1
|
5
|
123
|
12 8
|
12 10
|
123
|
2
|
Вспомогательные и итоговые столбцы из матрицы удаляются, т.к. они не требуются для дальнейших расчётов.
Следующим этапом идёт расчёт маятниковых и кольцевых маршрутов. Маятниковые маршруты определяются в таблице 9 клетками с двойной загрузкой и рассчитываются по наименьшей загрузке. Таких клеток в матрице две: маршрут 1:
А1
-Б1
-А1
на 42 оборота и маршрут 2:
А4
-Б4
-А4
на 8 оборотов. После их образования происходит расчёт кольцевых маршрутов.
Кольцевой маршрут из двух звеньев ( две гружёные и две холостые ездки ) составляется путём образования прямоугольника из горизонтальных и вертикальных отрезков таким образом, что его чётные вершины должны лежать в клетках с порожними ездками, а нечётные вершины в клетках с гружёными клетками. Количество оборотов на маршруте определяется наименьшей из загрузок в клетке. В таблице 10 изображёны прямоугольники, обозначающие кольцевые маршруты.
ТАБЛИЦА 10.
Таблица образования двухзвенных кольцевых маршрутов.
| Пункт назначения |
Б1
|
Б2
|
Б3
|
Б4
|
Б5
|
Б6
|
Б7
|
Б8
|
 А1 А1
|
24 5
|
1
|
12 7
|
8
|
4
|
2
|
18 14
|
18 15
|
| А2
|
5
|
1813
|
8
|
6
|
3
|
1
|
7
|
183
|
| А3
|
12
|
184
|
14
|
13
|
1811
|
4
|
12
|
10
|
 А4 А4
|
16
|
7
|
15
|
12 15
|
13
|
12 5
|
15
|
12
|
| А5
|
24 9
|
1
|
12 13
|
6
|
30 1
|
1
|
6 4
|
1
|
| А6
|
3
|
1
|
5
|
12 3
|
12 8
|
12 10
|
12 3
|
2
|
Маршрут 3:
А1
-Б7
-А5
-Б1
-А1
на 6 оборотов (наименьшему значению загрузки) и маршрут 4:
А4
-Б6
-А6
-Б4
-А4
на 12 оборотов. Не шедшие на образование маршрута грузовые и порожние ездки исключаются.
Следующим этапом расчётов рассматриваются возможности образования многозвенных маршрутов.
ТАБЛИЦА 11.
Таблица образования трёхзвенного маршрута.
| Пункт назначения |
Б1
|
Б2
|
Б3
|
Б4
|
Б5
|
Б6
|
Б7
|
Б8
|
 А1 А1
|
18 5
|
1
|
12 7
|
8
|
4
|
2
|
1214
|
18 15
|
| А2
|
5
|
1813
|
8
|
6
|
3
|
1
|
7
|
183
|
| А3
|
12
|
18 4
|
14
|
13
|
1811
|
4
|
12
|
10
|
| А4
|
16
|
7
|
15
|
15
|
13
|
5
|
15
|
12
|
| А5
|
18 9
|
1
|
12 13
|
6
|
30 1
|
1
|
4
|
1
|
| А6
|
3
|
1
|
5
|
3
|
12 8
|
10
|
12 3
|
2
|
Маршрут 5:
А1
-Б7
-А6
-Б5
-А5
-Б3
-А1
на 12 оборотов.
ТАБЛИЦА 12.
Таблица образования четырёхзвенного маршрута.
| Пункт назначения |
Б1
|
Б2
|
Б3
|
Б4
|
Б5
|
Б6
|
Б7
|
Б8
|
| А1
|
18 5
|
1
|
7
|
8
|
4
|
2
|
14
|
18 15
|
| А2
|
5
|
1813
|
8
|
6
|
3
|
1
|
7
|
18 3
|
| А3
|
12
|
18 4
|
14
|
13
|
1811
|
4
|
12
|
10
|
| А4
|
16
|
7
|
15
|
15
|
13
|
5
|
15
|
12
|
 А5 А5
|
18 9
|
1
|
13
|
6
|
18 1
|
1
|
4
|
1
|
| А6
|
3
|
1
|
5
|
3
|
8
|
10
|
3
|
2
|
Маршрут 6:
А1
-Б8
-А2
-Б2
-А3
-Б5
-А5
-Б1
-А1
на 18 оборотов.
Когда все ездки в матрице совмещённых планов задействованы на различных маршрутах, тогда разработка маршрутов прекращается.
§ 5
. ПРИКРЕПЛЕНИЕ ОБРАЗОВАННЫХ МАРШРУТОВ К АТП.
После расчётов и образования всех типов маршрутов производится прикрепление полученных маршрутов к автотранспортному предприятию, при этом решаются две основные задачи:
¨ определяется пункт погрузки, с которого следует начинать работу по кольцевым маршрутам;
¨ выбирается автотранспортное предприятие, техника которого будет выполнять данные маршруты.
Рекомендуется выбирать первый пункт погрузки и АПТ на кольцевом маршруте так, чтобы получить наименьший нулевой пробег автомобиля. Критерием правильности выбора первого пункта назначения служит прирост порожнего пробега. Меньший прирост порожнего пробега соответствует наилучшему варианту выполнения маршрута.
Прирост порожнего пробега вычисляется по формуле:
Dlk ij
= lk i
+ ljk
- lji
, км , где { 10 }
l k i
– расстояние от k-ого АТП до i-ого пункта погрузки;
l jk
– расстояние от j-ого последнего пункта разгрузки до k-ого АТП;
lji
– расстояние от последнего j-ого пункта разгрузки до i-ого первого пункта погрузки.
Маятниковые маршруты выполняются любым АТП от места погрузки.
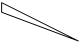
Маршрут 1.
АТП-А1
-Б1
-А1
-АТП на 42 оборота. Схема указана на рис 2.
5км
А1
А4 15 км
Б3
        Б1 2км Б1 2км
3км
АТП АТП
Рис.2. Схема маятникового Рис. 3. Схема маятникового марш-
маршрута 1. рута 2.
Маятниковый маршрут 2
АТП-А4
-Б3
-А4
-АТП на 8 оборотов. Схема изображена на рисунке 3.
Произведём расчёт прироста порожнего пробега кольцевых для маршрутов по формуле {10}.
Кольцевой маршрут
3
имеет четыре варианта привязки к АТП:
а) АТП-А1
-Б7
-А5
-Б1
-АТП для него Dlk ij
= 3 + 8 - 5 = 6 (км);
б) АТП-А1
-Б1
-А5
-Б7
-АТП для него
D
lk ij
= 3 + 9 - 14 = -2 (
км);
в) АТП-А5
-Б1
-А1
-Б7
-АТП для него Dlk ij
= 10 + 9 - 4 = 15 (км);
г) АТП-А5
-Б7
-А1
-Б1
-АТП для него Dlk ij
= 10 + 8 - 9 = 9 (км).
Следовательно, экономичным оказывается вариант б)
его и примем за окончательный.
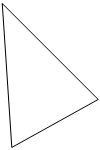
Б6
    А1 5 км
5км А1 5 км
5км
А4
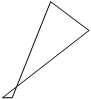  3км
Б1 2км 3км
Б1 2км
АТП 10км
АТП 9км 11км
  Б7
Б4 Б7
Б4
4км
А5 3км
А6
а) б)
Рисунок 4 . Схема двухзвенного кольцевого маршрута: а) маршрут 3; б) маршрут 4
.
Аналогично, для расчёта кольцевого двухзвенного маршрута 4
имеем экономичный вариант привязки АТП по маршруту движения АТП-А4
-Б6
-А6
-Б4
-А4
-АТП, с Dlk ij
= -2 км, схема которого указана на рисунке 4-б.
Для кольцевого трёхзвенного маршрута 5
имеем экономичный маршрут привязки АТП по маршруту движения АТП-А1
-Б3
-А5
-Б5
-А6
-Б7
-АТП сDlk ij
=-2 км, схема которого изображена на рисунке 5.
Для кольцевого четырёхзвенного маршрута 6
имеем экономичный маршрут привязки АТП по маршруту движения АТП-А1
-Б1
-А5
-Б5
-А3
-Б2
-А2
-Б8
- АТП сDlk ij
=-3км, схема которого изображена на рисунке 6.
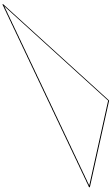   А2
3км
Б8 А2
3км
Б8
13км 9км
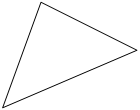     А1
7км
Б3
А1 5км
Б1 А1
7км
Б3
А1 5км
Б1
3км
АТП 3км
9км
 13км
Б2
АТП 9км 13км
Б2
АТП 9км
 Б7 Б7
4км
  А5
А5 А5
А5
 А6
8км
1км 1 км А6
8км
1км 1 км
 Б5
А3 11км
Б5 Б5
А3 11км
Б5
Рис.5. Схема трёхзвенного кольцевого Рис.6. Схема четырёхзвенного коль-
маршрута 5
. цевого маршрута 6.
§ 6.
ТЕХНОЛОГИЧЕСКИЙ РАСЧЁТ МАРШРУТОВ.
Рассчитаем один маятниковый и один кольцевой маршрут, а расчёты остальных маршрутов сведём в таблицу 13.
Маятниковый маршрут 1
АТП-А1
-Б1
-А1
-АТП.
а) Объём перевозок: Qm
= 189 тонн;
б) Время оборота на маршруте: to
= (2lге
/ Vт
) + tпв
= (2*
5 / 24) + 1,4 = 1,82 (ч);
в) Время на нулевые пробеги: tн
= ( lн1
+ lн2
- lx
)/Vт
= (3 + 8 - 5) / 24 = 0,25 (ч);
г) Время нахождения на маршруте: Тм
= Тн
- tн
= 750 - 15 = 735 (мин);
д) Число оборотов на маршруте: Zo
= Tм
/ to
= 735 / 109 = 6,74 » 6 (оборотов);
е) Пробег автомобиля с грузом: Lгр
= lге
*
Zo
= 5 *
6 = 30 (км);
ж)Пробег порожнего автомобиля: Lпор
= lге *
(Zo
- 1) + lн1
+ lн2
= =5*
5+3+8=38(км);
з) Общий пробег автомобиля за смену: Lo
= Lгр
+ Lпор
= 30+38 = 68 (км);
и) Коэффициент использования пробега за смену: b=Lгр
/Lo
= 30/68= 0,441;
к) Количество груза, перевозимого одним автомобилем: Qа
= q*
g*
Zo
= 5*
0,9*
6=
= 27(тонн);
л) Транспортная работа: Р = Qa *
lге
= 27 *
5 =135 (т*
км);
м) Число потребных автомобилей для перевозки всего груза: Ам
= Qм
/ Qa
=
= 189/ 27 = 7 (а/м).
н) Количество не довезенного груза: Qост
= Qм
- Qa *
Aм
= 189 - 27 *
7=189-189 = = 0 (тонн), т.е. весь груз будет вывезен.
Кольцевой маршрут 3
АТП-А1
-Б1
-А5
-Б7
-АТП на 6 оборотов.
а) Объём перевозок: Qм
= 81тонн;
б) Длина маршрута: lм
= l`
ге
+ l`
х
+ l``
ге
+ l``
х
= 14 + 4 + 9 + 5 = 32 (км);
в) Время оборота на маршруте: to
=(lм
/Vт
) + åtпв
= (32 / 24) + 2 *
1,42 = 4,17 (ч);
г) Время на нулевые пробеги: tн
=( l`
н
+ l``
н2
- lx
)/Vт
=(3+9-14)/24 = 0,08 » 0,1 (ч);
д) Время нахождения на маршруте: Тм
= Тн
- tн
= 750 - 6 = 744 = 12,4 (ч);
е) Число оборотов на маршруте: Zo
= Tм
/ to
= 12,4 / 4,17 = 2,98 » 3 (оборота);
ж) Фактическое время в наряде: Тн
= Zo *
to
+ tн
= 3*
4,17 + 0,1= 12,6 (ч);
з) Пробег автомобиля с грузом: Lгр
= (l`
ге
+ l``
ге
)*
Zo
= (5+4)*
3 = 27 (км);
и) Пробег порожнего автомобиля: Lпор
= ( l`
x
+ l``
x
)Zo
+ l`
н
+ l`
н
- l``
x
= =(9+14)*
3+5+4-14=63 (км);
к) Общий пробег автомобиля за смену: Lo
= Lгр
+ Lпор
= 27+ 63 = 90 (км);
л) Коэффициент использования пробега за смену: b= Lгр
/ Lo
= 27/90= 0,3;
м) Количество груза, перевозимого одним автомобилем: Qа
= q*
g*
Zo
*
Ze
= 5*
0,9*
3*
2= 27 (тонн);
н) Транспортная работа: Р = Qa *
(l`
ге
+ l``
ге
) = 27 *
(5 + 4) = 243 (т*
км);
o) Число потребных автомобилей для перевозки всего груза: Ам
= Qм
/ Qa
=
= 81/ 27= 3 (а/м).
п) Количество не довезенного груза: Qост
=Qм
-Qa*
Aм
=81- 27 *
3 = 0 (тонн), т.е. весь груз будет вывезен.
Аналогичным образом производится расчёт всех составленных маятниковых и кольцевых маршрутов.
ТАБЛИЦА 14.
Сводная таблица расчётов всех маршрутов.
| Н а и м |
е н о в |
а н и е |
м а р |
ш р у |
т о в. |
| Параметры |
Маршрут 1 |
Маршрут 2 |
Маршрут 3 |
Маршрут 4 |
Маршрут 5 |
Маршрут 6 |
| Qм
, т |
189 |
36 |
54 |
108 |
162 |
324 |
| lм
, км |
10 |
30 |
32 |
33 |
45 |
61 |
| to
, ч |
1,82 |
2,65 |
4,17 |
4,2 |
6,1 |
8,2 |
| tн
, ч |
0,25 |
0,125 |
0,1 |
0,1 |
0,1 |
0,33 |
| Тм
, ч |
12,15 |
12,33 |
12,4 |
12,4 |
12,4 |
12,17 |
| Zo
, ч |
6 |
4 |
3 |
3 |
2 |
1 |
| Тн ,
ч |
11,17 |
10,73 |
12,6 |
12,7 |
12,3 |
8,53 |
| Lгр
, км |
30 |
60 |
27 |
24 |
28 |
13 |
| Lпор
, км |
31 |
49 |
63 |
73 |
68 |
48 |
| Lo
, км |
61 |
139 |
90 |
97 |
96 |
61 |
| b , |
0,491 |
0,55 |
0,3 |
0,247 |
0,291 |
0,213 |
| Qa
, т |
27 |
18 |
27 |
27 |
27 |
18 |
| Р , т*
км |
135 |
270 |
243 |
648 |
756 |
864 |
| Ам
, шт. |
7 |
2 |
3 |
4 |
6 |
18 |
| Qост
, т |
0 |
0 |
0 |
0 |
0 |
0 |
После расчёта все составленные маршруты получают сменно-суточный план перевозок, обеспечивающий заданный объём перевозок с минимальным объёмом автомобилей.
§ 7.
ВЫВОДЫ.
В результате расчёта было представлено описание математической задачи и составлен план по методу потенциалов. Разработана матрица совмещённых планов и составлены маршруты перевозок груза. Обеспечен минимальный порожний пробег автомобиля. Произведён технологический расчёт, и сведён в таблицу, которая свидетельствует о том, что весь объём перевозок будет выполнен.
Литература:
1. Николин В.И. Автотранспортный процесс и оптимизация его элементов. М.: Транспорт, 1990
2. Боборыкин В.А. Математические методы решения транспортных задач. Л.: СЗПИ, 1986
3. Афанасьев Л.А., Островский И.В., Цукерберг С.М. Единая транспортная система и автомобильные перевозки. М.:Транспорт,1984
4. Геронимус Б.А. Экономико-математические методы в планировании на автомобильном транспорте. М.: Транспорт, 1982
|