СОДЕРЖАНИЕ
1. Задание.
2. Расчетно-пояснительная записка.
3. Аннотация.
4. Ведение.
5. Теория.
6. Алгоритмы.
7. Программы.
8. Инструкция пользователя.
9. Результаты экспериментов.
10.Заключение.
ЗАДАНИЕ
A.Выписать систему конечно-разностных уравнений.
B.Оценить вычислительные затраты, требуемые для выполнения аналитических решений с шестью десятичными цифрами в 100 и 1000 точках интервала. Определить и использовать разложение в ряд Тейлора для этих вычислений.
C.Оценить до проведения любых вычислений те вычислительные затраты, которые потребуются для решения конечно-разностных уравнений в 100 и 1000 точках при помощи:
1.
Исключения Гаусса,
2.Итерационного метода Якоби,
3.Итерационного метода Гаусса-Зейделя.
D.
Вычислить решения конечно-разностных уравнений при помощи каждого из трех методов из задания
C.
E.
Оценить применимость различных методов приближен-ного решения краевых задач для дифференциальных уравнений.
АННОТАЦИЯ
В данной работе по исследованию прямых и итерационных методов решения линейных систем
,
возникающих в краевых задачах для дифференциальных уравнений было составлено шесть программ непосредственно по алгоритмам Гаусса
,
Якоби
,
Гаусса-Зейделя
.
Каждый из методов был представлен в виде самостоятельной программы
,
которая имеет инструкцию для пользователя
.
Каждая программа работает по определенному управлению
,
причем программа Гаусса формирует матрицу сама
,
а в программах Якоби и Гаусса-Зейделя вводится только количество точек на интервал
,
исходя из чего формируется столбец неизвестных членов
.
Начальные значения неизвестных задаются автоматически
на основе результатов
,
полученных в ходе исследования были сделаны соответствующие выводы
.
ВВЕДЕНИЕ
Персональные компьютеры являются одним из самых мощных факторов развития человечества
.
Благодаря универсальности
,
высокому быстродействию
,
неутомимостью в работе
,
простоте в управлении
PC
нашли широкое применение в различных сферах деятельности человека
.
С развитием научно-технического прогресса все большая часть задач требует решения на ЭВМ
,
поэтому наш курсовой проект направили на развитие не только определенных навыков логического мышления
,
но и способность развивать и закреплять эти навыки
.
Реклама

ТЕОРИЯ
Дискретизация обыкновенных дифференциальных уравнений конечными разностями приводит к линейным уравнениям
;
если рассматривается краевая задача
,
то уравнения образуют совместную линейную систему
.
Прямым методом решения линейной системы
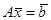 называется любой метод
,
который позволяет получить решение с помощью конечного числа элементарных арифметических операций
:
сложения
,
вычитания
,
деления и т
.
д
.
Этот метод основан на сведении матрицы
,
системы
A
к матрице простой структуры - диагональной (и тогда решение очевидно ) и треугольной - разработка эффективных методов решения таких систем
.
Например
,
если А является верхней треугольной матрицей
:
называется любой метод
,
который позволяет получить решение с помощью конечного числа элементарных арифметических операций
:
сложения
,
вычитания
,
деления и т
.
д
.
Этот метод основан на сведении матрицы
,
системы
A
к матрице простой структуры - диагональной (и тогда решение очевидно ) и треугольной - разработка эффективных методов решения таких систем
.
Например
,
если А является верхней треугольной матрицей
:
 ; ;
решение
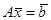 отыскивается с помощью последовательных обратных подстановок
.
Сначала из последнего уравнения вычисляется
отыскивается с помощью последовательных обратных подстановок
.
Сначала из последнего уравнения вычисляется
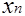 ,
затем полученные значения подставляются в предыдущие уравнения и вычисляется
,
затем полученные значения подставляются в предыдущие уравнения и вычисляется
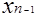 и т.д.
и т.д.
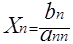 ;
;
 ;
;
или в общем виде
:
 ,
i=n, n-1, ..., 1.
,
i=n, n-1, ..., 1.
Стоимость такого решения составляет
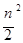 сложений умножений(а также и делении
,
которыми можно пренебречь).
сложений умножений(а также и делении
,
которыми можно пренебречь).
Сведение матриц А к одному из двух указанных выше видов осуществляется с помощью ее умножения на специально подобранную матрицу М
,
так что система
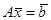 преобразуется в новую систему
преобразуется в новую систему
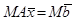 . .
Во многих случаях матрицу М подбирают таким образом
,
чтобы матрица МА стала верхней треугольной
.
Прямые методы решения СЛУ нельзя применять при очень больших, из-за нарастающих ошибок, округлениях, связанных с выполнением большого числа арифметических операций. Устранить эти трудности помогают итерационные методы. С их помощью можно получить, начиная с вектора
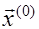 ,
бесконечную последовательность ,
бесконечную последовательность
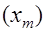 векторов, сходящихся к решению системы(
m
- номер итерации )
векторов, сходящихся к решению системы(
m
- номер итерации )
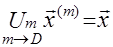 . .
Метод является сходящимся, если это состояние справедливо для произвольного начального вектора
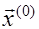 . .
Во всех методах, которые рассмотрены ниже, матрица А представляется в виде А=М-
N
( ниже показано, как это наполняется ) и последовательно решаются системы
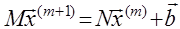 .
.
Формально решением системы является
:
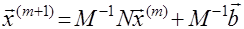
где -
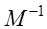 обратная матрица. Решение итерационным методом упрощается еще и потому, что на каждом шагу надо решать систему с одними и теми же матрицами. Очевидно, что матрица М должна быть легко обращаемой, а для получения желаемой точности надо выполнить определенное число итераций.
обратная матрица. Решение итерационным методом упрощается еще и потому, что на каждом шагу надо решать систему с одними и теми же матрицами. Очевидно, что матрица М должна быть легко обращаемой, а для получения желаемой точности надо выполнить определенное число итераций.
Реклама

Критерием окончания итерационного процесса является соблюдение соотношения
:
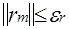 или
или
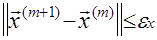 , ,
где
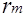 - вектор невязок уравнений
- вектор невязок уравнений
 ,
и ,
и
 и
и
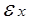 - допустимая погрешность СЛУ по неувязке или приращению вектора неизвестных на итерации.
- допустимая погрешность СЛУ по неувязке или приращению вектора неизвестных на итерации.
РАЗНОСТНЫЕ УРАВНЕНИЯ
Многие физические системы моделируются дифферинци-альными уравнениями, например :
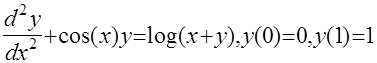
       которые не могут быть решены аналитически. Приближение этих уравнений конечными разностями основано на дискредитации интервала
[0,1]
как показано на рис.1 и замене производной. которые не могут быть решены аналитически. Приближение этих уравнений конечными разностями основано на дискредитации интервала
[0,1]
как показано на рис.1 и замене производной.
   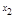 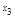 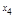 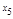 
простой разностью, например
:
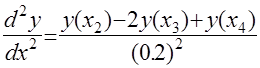
где, 0,2=1
/
5=
X4
-X3
.
Тогда аппроксимирующее разностное уравнение имеет вид:
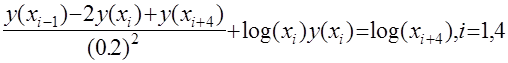
В каждой точке дискретизации справедливо одно такое уравнение, которое приводит к линейной системе для приближенных значений решения дифференциального уравнения.
Уравнения такого вида можно решить с помощью разложения в ряд Тейлора. В нашем случае уравнения решенные разложением в ряд Тейлора имеют вид;
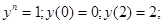
Найти
y’(0); y’’(0)=1; y’’’(0)=1;
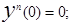
обозначим у
’
(0) как С.
Решение:
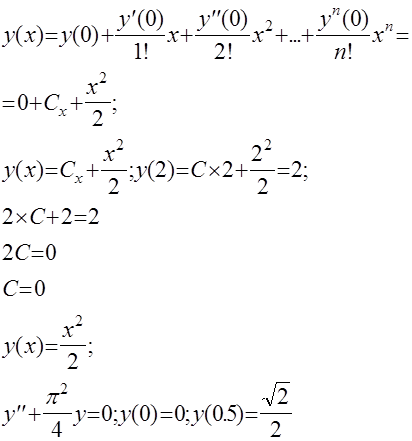
Решение:
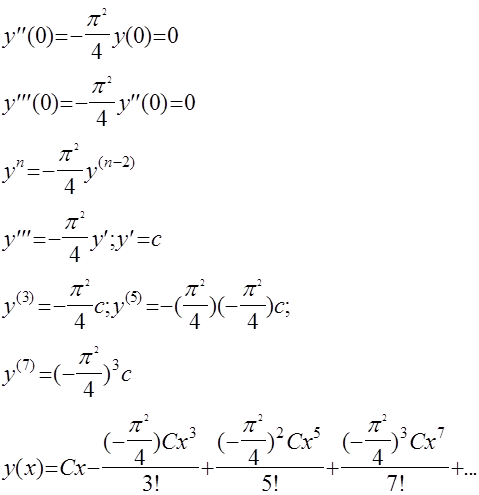
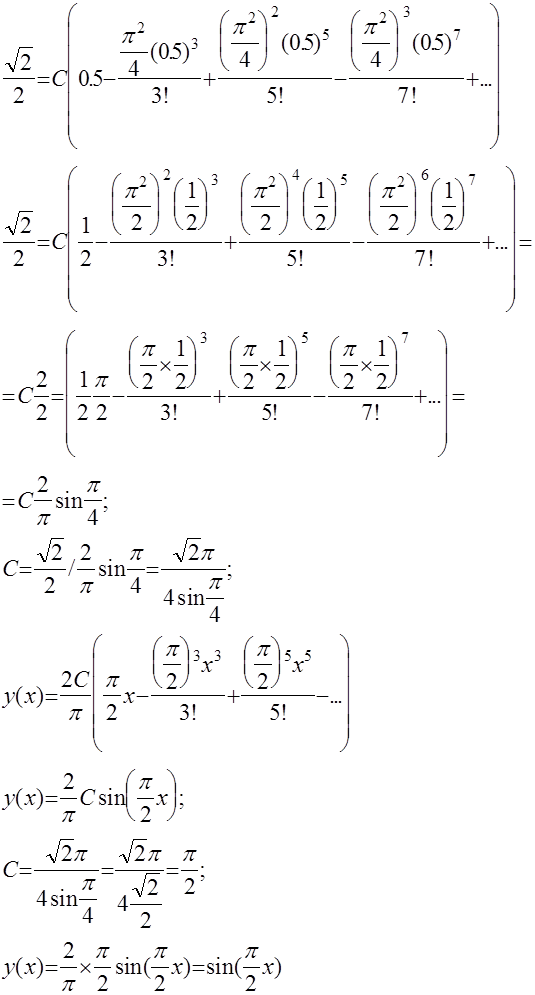
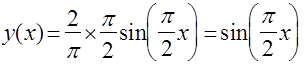
Система конечно-разностных уравнений
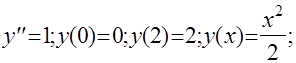
интервал
[0,2]
разделим на 10 точек
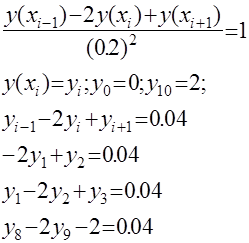
-2 1 0 0 0 0 0 0 0 0
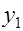 0.04 0.04
1 -2 1 0 0 0 0 0 0 0
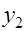 0.04 0.04
0 1 -2 1 0 0 0 0 0 0
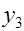 0.04 0.04
0 0 1 -2 1 0 0 0 0 0
 0.04 0.04
0 0 0 1 -2 1 0 0 0 0
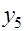 0.04 0.04
0 0 0 0 1 -2 1 0 0 0
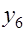 0.04 0.04
0 0 0 0 0 1 -2 1 0 0
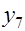 0.04 0.04
0 0 0 0 0 0 1 -2 1 0
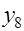 0.04 0.04
0 0 0 0 0 0 0 1 -2 1
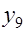 0.04 0.04
0 0 0 0 0 0 0 0 1 -2
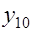 -2+0.04 -2+0.04
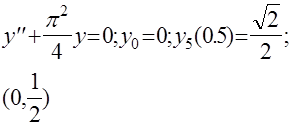
5 точек.
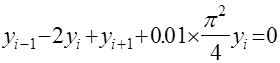
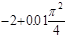 |
1
|
0
|
0
|
0
|
 |
0
|
| 1
|
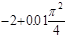 |
1
|
0
|
0
|
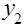 |
0
|
| 0
|
1
|
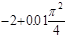 |
1
|
0
|
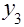 |
0
|
| 0
|
0
|
1
|
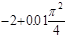 |
1
|
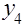 |
0
|
| 0
|
0
|
0
|
1
|
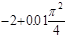 |
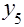 |
0
|
АЛГОРИТМ ГАУССА
Назначение: Решить
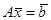 относительно Х.
относительно Х.
Входные параметры:
masheps
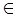 R, n R, n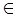 Z, Z,
Вектор правых частей
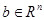 . .
Входно - выходные параметры
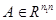 , ,
после разложения в А сохраняются ее верхние треугольные сомножители
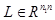 , ,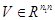 . .
Код возврата
retcode=0
при успешном решении и
retcode=1
при вырождении матрицы.
Выходные параметры:
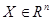 . .
Алгоритм
1.
retcode=0
2.
if n=1 then
2.1
if A[1,1]=0 then retcode=1
2.2
return
(*Гауссово исключение с частичным выбором ведущего элемента*)
3.
for k=1 to n do
(*найти ведущий элемент*)
3.1
Amax <= |A[k,k]|
3.2
Imax <= k
3.3
for i=k+1 to n do
3.3.1
if |[i,k]| > Amax then
3.3.1.1.
Amax <= |A[i,k]|
3.3.1.2.
Imax <= 1
(*
проверка на вырожденность*)
3.4.
if Amax < masheps
*n then
3.4.1.
retcode<=1
3.4.2.
return
3.5.
if Imax<> k then
3.5.1.
Amax <= A[Imax,k]
3.5.2.
A[Imax,k] <= A[k,k]
3.5.3.
A[Imax,k] <= Amax
3.7.
for i=k+1 to n do A[i,k] <= A[i,k]/Amax
(*перестановка и исключение по столбцам*)
3.8.
for j=k+1 to n do
3.8.1. Amax<=A[Imax,j]
3.8.2.
A[Imax,j]<=A[k,j]
3.8.3.
A[k,j]<=Amax
3.8.4.
if Amax<>0 then
for i=k+1 to n do
A[i,j]<=A[i,j]-A[i,k]*Amax
4.
if retcode=0 then (*
разложение успешно*)
(*решить СЛУ
Ly=b
и
Vx=y *)
5.
for i=2 to n do
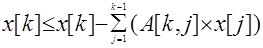
6.
for k=n downto 1 do
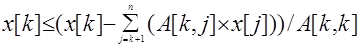
return
end.
АЛГОРИТМ ЯКОБИ
Входные параметры:
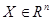 - вектор начальных значений Х, после окончания решения с заданной точностью. - вектор начальных значений Х, после окончания решения с заданной точностью.
Код возврата:
retcode=0
при успешном решении
u=1,
при не успешном решении превышение допустимого числа итераций.
Память: Требуется дополнительный массив
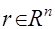 для хранения невязок. для хранения невязок.
Алгоритм
retcode=1
for Iter=1 to maxiter do (*
расчет вектора невязок*)
rmax=0
for i=1 to n do
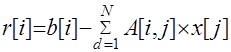
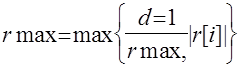
(*
проверка на окончание итерационного процесса*)
if rmax<eps then do retcode=0
return
(*
найти улучшенное решение*)
for i=1 to n do
x[i]=x[i]+r[i]/A[i,j]
АЛГОРИТМ ГАУССА-ЗЕЙДЕЛЯ
Входные параметры:
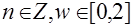
( релаксационный коэффициент )
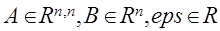 - точность решения, - точность решения,
maxiter-
максимальное число итераций.
Входно- выходные параметры:
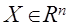 - вектор начальных значений
X,
после окончания; решение с заданной точностью. - вектор начальных значений
X,
после окончания; решение с заданной точностью.
Алгоритм
retcode=1
for iter=1 to maxiter do
rmax=0
(*
улучшить решение
*)
for i=1 to n do

(*
проверка на окончание итерационного процесса*)
if rmax<eps then
retcode=0
return
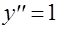
program GAUS1(input,output);
type
matrix=array[1..100,1..100] of real;
vektor=array[1..100] of real;
var
a:matrix;
x,b,y:vektor;
n:integer;
ret_code:integer;
procedure geradlini(var a:matrix;var b,y:vektor;var n:integer);
var
s:real;j,i:integer;
begin
for i:=1 to n do
begin
s:=0;
for j:=1 to (i-1) do
s:=s+a[i,j]*y[j];
y[i]:=b[i]-s;
end;
end;
procedure ruckgang(var a:matrix;var y,x:vektor;var n:integer);
var
s:real;i,j:integer;
begin
s:=0;
for i:=n downto 1 do
begin
s:=0;
for j:=(i+1) to n do
s:=s+a[i,j]*x[j];
x[i]:=(y[i]-s)/a[i,i];
end;
end;
procedure vvod(var a:matrix;var b:vektor;var n:integer);
var
i,j:integer;
q:real;
begin
writeln('Введите количество точек на интервал: ');
readln(n);
for i:=1 to n do
begin
for j:=1 to n do
a[i,j]:=0;
a[i,i]:=(-2);
end;
for i:=1 to (n-1) do
a[i,i+1]:=1;
for i:=2 to n do
a[i,i-1]:=1;
q:=sqr(2/n);
for i:=1 to n do
if i<>n then b[i]:=q else b[i]:=(q-2);
end;
procedure triangul(var a:matrix;var b:vektor;
var ret_code:integer;n:integer);
label 1;
var
eps,buf,max,c:real;
k,imax,i,j:integer;
begin
ret_code:=1;
eps:=1;
buf:=1+eps;
while buf>1.0 do
begin
eps:=eps/2;
buf:=1+eps;
end;
buf:=n*eps;
for k:=1 to (n-1) do
begin
max:=a[k,k];
imax:=k;
for i:=k to n do
if a[i,k]>max then
begin
max:=a[i,k];
imax:=i;
end;
if a[imax,k]>buf then
begin
for j:=1 to n do
begin
c:=a[imax,j];
a[imax,j]:=a[k,j];
a[k,j]:=c;
end;
c:=b[imax];
b[imax]:=b[k];
b[k]:=c;
for i:=(k+1) to n do
begin
a[i,k]:=a[i,k]/a[k,k];
for j:=(k+1) to n do
a[i,j]:=a[i,j]-a[i,k]*a[k,j];
end;
end
else
begin
ret_code:=0;
goto 1
end;
1: end;
end;
procedure vivod(var x:vektor;var n:integer);
var
i:integer;
begin
for i:=1 to n do
writeln('x',i:1,'=',x[i],' ');
end;
begin
vvod(a,b,n);
triangul(a,b,ret_code,n);
if ret_code=1 then
begin
geradlini(a,b,y,n);
ruckgang(a,y,x,n);
vivod(x,n);
end
else
writeln('Матрица вырожденна');
end.
program GAUS2(input,output);
type
matrix=array[1..100,1..100] of real;
vektor=array[1..100] of real;
var
a:matrix;
x,b,y:vektor;
n:integer;
ret_code:integer;
procedure geradlini(var a:matrix;var b,y:vektor;
var n:integer);
var
s:real;j,i:integer;
begin
for i:=1 to n do
begin
s:=0;
for j:=1 to (i-1) do
s:=s+a[i,j]*y[j];
y[i]:=b[i]-s;
end;
end;
procedure ruckgang(var a:matrix;var y,x:vektor;
var n:integer);
var
s:real;i,j:integer;
begin
s:=0;
for i:=n downto 1 do
begin
s:=0;
for j:=(i+1) to n do
s:=s+a[i,j]*x[j];
x[i]:=(y[i]-s)/a[i,i];
end;
end;
procedure vvod(var a:matrix;var b:vektor;
var n:integer);
var
i,j:integer;
q:real;
begin
writeln('Введите количество точек на интервал: ');
readln(n);
q:=(-2+sqr(0.5/n)*(sqr(4*arctan(1))/4));
for i:=1 to n do
begin
for j:=1 to n do
a[i,j]:=0;
a[i,i]:=(q);
end;
for i:=1 to (n-1) do
a[i,i+1]:=1;
for i:=2 to n do
a[i,i-1]:=1;
for i:=1 to n do
if i<>n then b[i]:=0 else b[i]:=(-sqr(2)/2);
end;
procedure triangul(var a:matrix;var b:vektor;var ret_code:integer;
n:integer);
label 1;
var
eps,buf,max,c:real;
k,imax,i,j:integer;
begin
ret_code:=1;
eps:=1;
buf:=1+eps;
while buf>1.0 do
begin
eps:=eps/2;
buf:=1+eps;
end;
buf:=n*eps;
for k:=1 to (n-1) do
begin
max:=a[k,k];
imax:=k;
for i:=k to n do
if a[i,k]>max then
begin
max:=a[i,k];
imax:=i;
end;
if a[imax,k]>buf then
begin
for j:=1 to n do
begin
c:=a[imax,j];
a[imax,j]:=a[k,j];
a[k,j]:=c;
end;
c:=b[imax];
b[imax]:=b[k];
b[k]:=c;
for i:=(k+1) to n do
begin
a[i,k]:=a[i,k]/a[k,k];
for j:=(k+1) to n do
a[i,j]:=a[i,j]-a[i,k]*a[k,j];
end;
end
else
begin
ret_code:=0;
goto 1
end;
1: end;
end;
procedure vivod(var x:vektor;var n:integer);
var i:integer;
begin
for i:=1 to n do
writeln('x',i:1,'=',x[i]);
end;
begin
vod(a,b,n);
triangul(a,b,ret_code,n);
if ret_code=1 then
begin
geradlini(a,b,y,n);
ruckgang(a,y,x,n);
vivod(x,n);
end
else
writeln('Матрица вырождена ');
end.
program jakobi1(input,output);
type
vektor=array[1..100] of real;
var
r,y:vektor;
z,ret_code,maxiter:integer;
eps:real;
procedure vvod(var z,maxiter:integer;var eps:real);
begin
writeln('Введите кол-во точек на интервал');
readln(z);
writeln('Введите точность');
readln(eps);
writeln('Введите кол-во итераций');
readln(maxiter);
end;
procedure ren(var r,y:vektor;var z,ret_kode,maxiter:integer;var eps:real);
label 1;
var
iter,i:integer;
rmax,q:real;
begin
q:=sqr(2/z);
for i:=1 to z do
y[i]:=1;
ret_code:=0;
for iter:=1 to maxiter do {c.1}
begin
rmax:=0;
for i:=1 to z do {c.2}
begin
if i=1 then
begin
r[i]:=q-(-2*y[1]+y[2]);
if rmax<abs(r[i]) then
rmax:=abs(r[i]);
end;
if i=z then
begin
r[z]:=(-2+q)-(y[z-1]-2*y[z]);
if rmax<abs(r[i]) then
rmax:=abs(r[i]);
end;
if(i<>1)and(i<>z) then
begin
r[i]:=q-(y[i-1]-2*y[i]+y[i+1]);
if rmax<abs(r[i]) then
rmax:=abs(r[i]);
end;
end;{c.2}
if rmax<=eps then
goto 1
else
for i:=1 to z do
y[i]:=y[i]+r[i]/(-2);
end; {c.1}
ret_code:=1;
1:
end;
procedure vivod(var y:vektor;var z:integer);
var
i:integer;
ch:char;
begin
for i:=1 to z do
writeln('y',i:1,y[i]);
end;
begin
vvod(z,maxiter,eps);
ren(r,y,z,ret_code,maxiter,eps);
if ret_code=0 then
vivod(y,z)
else
writeln('Превышено допустимое число итераций');
end.
program jakobi2(input,output);
type
vektor=array[1..100] of real;
var
r,y:vektor;
z,ret_code,maxiter:integer;
eps:real;
procedure vvod(var z,maxiter:integer;var eps:real);
begin
writeln('Введите кол-во точек на интервал');
readln(z);
writeln('Введите точность');
readln(eps);
writeln('Введите кол-во итераций');
readln(maxiter);
end;
procedure ren(var r,y:vektor;var z,ret_kode,maxiter:integer;var eps:real);
label 1;
var
iter,i:integer;
rmax,q:real;
begin
q:=sqr(2/z);
for i:=1 to z do
y[i]:=1;
ret_code:=0;
for iter:=1 to maxiter do
begin
rmax:=0;
for i:=1 to z do
begin
if i=1 then
begin
r[i]:=q-(-2*y[1]+y[2]);
if rmax<abs(r[i]) then
rmax:=abs(r[i]);
end;
if i=z then
begin
r[z]:=(-2+q)-(y[z-1]-2*y[z]);
if rmax<abs(r[i]) then
rmax:=abs(r[i]);
end;
if(i<>1)and(i<>z) then
begin
r[i]:=q-(y[i-1]-2*y[i]+y[i+1]);
if rmax<abs(r[i]) then rmax:=abs(r[i]);
end;
end;
if rmax<=eps then goto 1
else
for i:=1 to z do
y[i]:=y[i]+r[i]/q;
end;
ret_code:=1;
1:end;
procedure vivod(var y:vektor;var z:integer);
var
i:integer;
begin
for i:=1 to z do
writeln('y',i:1,y[i]);
end;
begin
vvod(z,maxiter,eps);
ren(r,y,z,ret_code,maxiter,eps);
if ret_code=0 then vivod(y,z)
else
write('Превышено допустимое число итераций');
end.
program zeidel1(input,output);
type
vector=array[1..1000] of real;
var
y:vector;
z,retcode,maxiter:integer;
eps:real;
procedure wod(var z,maxiter:integer;var eps:real);
begin
writeln;
writeln('введите количество точек на интервал ');
readln(z);
writeln('введите точность ');readln(eps);
writeln('введите количество итераций ');readln(maxiter);
writeln('коофицент релаксации W,принят равный 1');
end;
procedure reshen(var y:vector;var z,retcode,maxiter:integer;var eps:real);
label 1;
var
Iter,I:integer;R,Rmax,Q:real;
begin
Q:=sqr(2/z);
for i:=1 to z do y[i]:=1;
retcode:=1;
for Iter:=1 to maxiter do
begin
Rmax:=0;
for i:=1 to z do
begin
if i=1 then
begin
R:=Q-(-2*y[1]+y[2]);
if Rmax<Abs(R) then Rmax:=abs(R);
y[i]:=y[i]+R/(-2);
end;
if i=z then
begin
R:=(-2+Q)-(y[z-1]-2*y[z]);
if Rmax<ABS(R) then Rmax:=ABS(R);
y[i]:=y[i]+r/(-2);
end;
if (I<>1) and (i<>z) then
begin
r:=Q-(y[i-1]-2*y[i]+y[i+1]);
if Rmax<abs(r) then Rmax:=abs(r);
y[i]:=y[i]+R/-2;
end;
end;
if Rmax<=eps then
begin
retcode:=0;
goto 1;
end;
end;
1: end;
procedure vivod(var y:vector;var z:integer);
var
i:integer;
begin
for i:=1 to z do
write('y',i:2,'=',y[i]);
end;
begin
wod(z,maxiter,eps);
reshen(y,z,retcode,maxiter,eps);
if retcode=0 then vivod(y,z)
else
write('число итераций');
end.
program zeidel2(input,output);
type
vector=array[1..1000] of real;
var
y:vector;
z,retcode,maxiter:integer;
eps:real;
procedure wod(var z,maxiter:integer;var eps:real);
begin
writeln;
writeln('введите количество точек на интервал ');
readln(z);
writeln('введите точность ');readln(eps);
writeln('введите количество итераций ');readln(maxiter);
writeln('коофицент релаксации W,принят равный 1');
end;
procedure reshen(var y:vector;var z,retcode,maxiter:integer;var eps:real);
label 1;
var
Iter,I:integer;R,Rmax,Q:real;
begin
Q:=(-2+sqr(0.5/z)*sqr(4*arctan(1))/4);
for i:=1 to z do y[i]:=1;
retcode:=1;
for Iter:=1 to maxiter do
begin
Rmax:=0;
for i:=1 to z do
begin
if i=1 then
begin
r:=-(q*y[1]+y[z]);
if Rmax<Abs(R) then Rmax:=abs(R);
y[i]:=y[i]+R/q;
end;
if i=z then
begin
r:=-sqrt(z)/2-(y[z-1]+q*y[z]);
if Rmax<ABS(R) then Rmax:=R;
y[i]:=y[i]+r/q;
end;
if (I<>1) and (i<>z) then
begin
r:=-(y[i-1]+q*y[i]+y[i+1]);
if Rmax<abs(r) then Rmax:=r;
y[i]:=y[i]+R/q;
end;
end;
if Rmax<=eps then
begin
retcode:=0;
goto 1;
end;
end;
1: end;
procedure vivod(var y:vector;var z:integer);
var
i:integer;
begin
for i:=1 to z do
writeln (i:1,'=',y[i],);
end;
begin
wod(z,maxiter,eps);
reshen(y,z,retcode,maxiter,eps);
if retcode=0 then vivod(y,z)
else
write('число итераций');
end.
ИНСТРУКЦИЯ ДЛЯ ПОЛЬЗОВАТЕЛЯ
Программа
Jacobi1
предназначена для решения уравнений
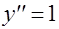 .
Jacobi2
для решения уравнений .
Jacobi2
для решения уравнений
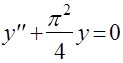 ,методом конечных разностей находят значение ,методом конечных разностей находят значение
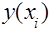 в точках интервала (0.2) максимальное количество точек на интервал 1000. Используется массив для хранения значений вектора невязок в точках интервала (0.2) максимальное количество точек на интервал 1000. Используется массив для хранения значений вектора невязок
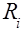 . В процедуре
reshen
находится вектор невязок
r [ i ]
. Для первого и последнего уравнения системы находят вектора невязок различными способами. Для остальных уравнений системы вектор невязок находится одинаково. Сама матрица не формируется , т.е. для нахождения вектора невязок ее не нужно, это видно из текста программы. . В процедуре
reshen
находится вектор невязок
r [ i ]
. Для первого и последнего уравнения системы находят вектора невязок различными способами. Для остальных уравнений системы вектор невязок находится одинаково. Сама матрица не формируется , т.е. для нахождения вектора невязок ее не нужно, это видно из текста программы.
Программы
Zeidel1
и
Zeidel2
, также решают уравнения
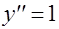 и и
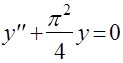 . Отличия от
Jacobi
состоит только в том, что отсутствует массив для вектора невязок. Программы
Gaus1
и
Gaus2
также решают эти уравнения, только методом Гаусса. В процедурах
vvod
задается количество точек на интервал(
max=100)
и формируются матрицы в зависимости от уравнения. Процедура
triangul
разлагает матрицу А на две треугольные. Процедура
geradlini
- прямой ход метода Гаусса. Процедура
ruckgang
- обратный ход. Процедура
vivod
- выводит значения . Отличия от
Jacobi
состоит только в том, что отсутствует массив для вектора невязок. Программы
Gaus1
и
Gaus2
также решают эти уравнения, только методом Гаусса. В процедурах
vvod
задается количество точек на интервал(
max=100)
и формируются матрицы в зависимости от уравнения. Процедура
triangul
разлагает матрицу А на две треугольные. Процедура
geradlini
- прямой ход метода Гаусса. Процедура
ruckgang
- обратный ход. Процедура
vivod
- выводит значения
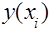 . .
Вычисление уравнений с помощью итерационного метода Якоби требует времени
t=0(maxiter Z)
, где
Z
- количество точек на интервал, а
maxiter
- количество итераций.
Вычисление уравнений с помощью метода Гаусса требует времени
t=0(
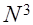 )
, где
N
- количество точек на интервал. )
, где
N
- количество точек на интервал.
Решение с помощью метода Гаусса требует больше времени чем решения другими двумя приведенными способами.
|