Кубанский государственный технологический университет
Кафедра автоматизации технологических процессов
Задание на контрольную работу
По дисциплине “Автоматизированное управление дискретными процессами” для студентов заочной формы обучения специальности 21.01 — “Автоматика и управление в технических системах” на тему: “Синтез управляющего автомата модели LEGO — “транспортная тележка” и моделирование её движения вдоль трассы”
Выдано:
Аспирантом каф. АПП 06.09.99 /Напылов Р.Н./
студенту гр. ____________ /____________/
Краснодар 1999
1 Исходные данные
1.1 Управляемый процесс — движение модели LEGO транспортной тележки вдоль заданной траектории в виде белой полосы. Ориентация тележки относительно трассы регулируется датчиками контраста.
1.2 Условная схема транспортной тележки приводится на рисунке 1.1. Тележка движется за счёт заднего привода, создающего постоянное тягловое усилие 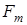 . Вращение переднего колеса тележки осуществляется с помощью реверсивного поворотного двигателя, отрабатывающего с постоянной угловой скоростью . Вращение переднего колеса тележки осуществляется с помощью реверсивного поворотного двигателя, отрабатывающего с постоянной угловой скоростью  , где , где 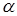 — угол поворота переднего колеса (рисунок 1.1) — угол поворота переднего колеса (рисунок 1.1)
1.3 Транспортная тележка, как объект управления имеет систему дискретных входных и выходных сигналов, структурно представленную на рисунке 1.2. Кодировка указанных сигналов следующая:
Таблица 1.1 – Кодировка управляющих сигналов
Разряд сигнала
X
|
Управляющее действие
|
| X0
|
1 – двигатель тележки включен
0 – двигатель тележки выключен
|
| X1
|
1 – поворотный двигатель отрабатывает влево
0 – двигатель влево не отрабатывает
|
| X2
|
1 – поворотный двигатель отрабатывает вправо
0 – двигатель вправо не отрабатывает
|
Таблица 1.2 – Кодировка выходных сигналов
Разряд сигнала
Y
|
Событие
|
| Y0
|
1 – левый датчик над светлой точкой трассы
0 – левый датчик над тёмной точкой трассы
|
| Y1
|
1 – правый датчик над светлой точкой трассы
0 – правый датчик над тёмной точкой трассы
|

Сигналы Y используются в качестве обратной связи управляющего автомата. По изменению этих сигналов возможно судить о текущем положении тележки относительно белой полосы трассы. Сигналы X вырабатываются управляющим автоматом в зависимости от поведения во времени сигналов Y так, что бы обеспечить совпадение траекторий движения тележки и трассы.
1.4 Решение о подачи питания на задний привод тележки и, расположенный на ней, управляющий автомат принимает внешний оператор. Поэтому, исходным состоянием тележки является активность двигателя привода. В этом случае задача управляющего автомата состоит только в обеспечении движения тележки вдоль трассы.
1.5 Допущения, делаемые при рассмотрении управляемой тележки в динамике:
1) тягловое усилие 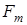 постоянное; постоянное;
2) приведённая сила трения 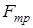 пропорциональна линейной скорости движения тележки; пропорциональна линейной скорости движения тележки;
3) сила трения 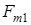 , подменяющая реакцию , подменяющая реакцию 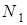 в момент, когда в момент, когда 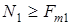 (переднее колесо проскальзывает), постоянна и пропорциональна массе тележки; (переднее колесо проскальзывает), постоянна и пропорциональна массе тележки;
4) сила трения 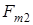 , подменяющая реакцию , подменяющая реакцию 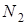 в момент, когда в момент, когда 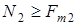 (тележку заносит), также постоянна и пропорциональна массе тележки; (тележку заносит), также постоянна и пропорциональна массе тележки;
5) масса тележки 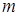 и её момент инерции и её момент инерции 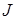 относительно центра масс связаны зависимостью: относительно центра масс связаны зависимостью: 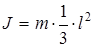 , как если бы вся масса тележки была сосредоточена в стержне , как если бы вся масса тележки была сосредоточена в стержне 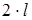 (рисунок 1.1). (рисунок 1.1).
2 Основное задание
2.1 Сформировать модель управляющего автомата в форме таблицы переходов и выходов автомата Милли, предварительно составив список его возможных состояний и перекодировав входной алфавит автомата во множество многозначной логики (Y - четырёхзначное);
2.2 Минимизировать, в случае возможности, таблицу переходов и выходов автомата Милли;
2.3 Составить алгебрологические выражения функции переходов и функции выходов минимизированного автомата, используя только двоичное представление входных и выходных сигналов;
2.4 Минимизировать полученные функции;
2.5 По минимизированным логическим функциям зарисовать цифровую схему управляющего автомата (стандарт условного графического изображения логических элементов — Российский).
3 Дополнительное задание
Вывести модель динамики транспортной тележки. Положение центра масс тележки в плоской системе координат задавать вектором положения 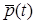 . Положение точки приложения силы тяги привода задавать вектором . Положение точки приложения силы тяги привода задавать вектором 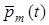 . .
Реклама

4 Список источников
4.1 Юдицкий С.А., Магергут В.Э. Логическое управление дискретными процессами. Модели, анализ, синтез. — М.: Машиностроение, 1987. — 176 c.
4.2 Кузнецов О.П., Адельсон-Вольский Г.М. Дискретная математика для инженеров. — М.: Энергоатомиздат, 1987. — 450 c.
4.3 Шварце Х., Хольцгрефе Г.-В. Использование компьютеров в регулировании и управлении: Пер. с нем.—М.: Энергоатомиздат, 1990. — 176 с.: ил.
4.4 Каган Б.М., Сташин В.В. Основы проектирования микропроцессорных устройств автоматики. — М.: Энергоатомиздат, 1987. — 304 c.
4.5 Мишель Ж., Лоржо К., Эспью Б., Программируемые контроллеры. — Пер. c французского А.П. Сизова — М.: Машиностроение, 1986.
4.6 Микропроцессоры: В 3-х кн. Кн. 2. Средства сопряжения. Контролирующее и информационно-управляющие системы: Учеб. Для втузов/В.Д. Вернер, Н.В. Воробьёв, А.В. Горячев и др.; Под ред. Л.Н. Преснухина. — М.: Высш. шк., 1986. — 383 c.: ил.
4.7 Фиртич В. Применение микропроцессоров в системах управления: Пер. с нем. — М.: Мир, 1984,—464 c., ил.
5 Решение основного задания
5.1 Выходной алфавит транспортной тележки является входным алфавитом управляющего автомата Y. Для возможности применения теории конечных автоматов перекодируем его во множество четырёх знаков в соответствии с таблицей 5.1.
Таблица
5.1 – Кодировка входного алфавита управляющего автомата
| Y0
|
Y1
|
Y |
0
0
1
1
|
0
1
0
1
|
0
1
2
3
|
5.2 При определении возможных состояний управляющего автомата будем руководствоваться правилом: — допустимо введение избыточных состояний, которые при последующей минимизации автомата исключаются; недопустим пропуск необходимого состояния, который уменьшает адаптированность автомата к внешним ситуациям.
Перечень возможных состояний автомата, отождествлённых с ситуационными событиями транспортной тележки, приводится ниже.
Таблица 5.2 – Перечень состояний управляющего автомата транспортной тележки
Код
состояния S |
Описание состояния |
0
1
2
3
|
Исходное состояние неуправляемого движения;
Поворот вправо (поворотный двигатель непрерывно отрабатывает вправо);
Поворот влево (поворотный двигатель непрерывно отрабатывает влево);
Конфликт поворотов.
|
5.3 Для возможности формирования математической модели управляющего автомата рассмотрим описательный алгоритм управления транспортной тележки по состояниям:
― В исходном состоянии тележка непрерывно движется под действием привода. Ни один из датчиков контраста не находится над белой полосой трассы. Поворотный двигатель остановлен;
― При возникновении белой полосы под левым датчиком контраста включается поворотный двигатель на отработку влево. Привод отключается и далее следует движение по инерции, что уменьшает вероятность заноса тележки;
― Как только левый датчик контраста “сходит” с белой полосы поворотный двигатель останавливается в текущем состоянии, а привод вновь запускается;
― При возникновении белой полосы под правым датчиком — поведение транспортной тележки аналогично;
― Возникновение белой полосы под правым и левым датчиком свидетельствует о том, что тележка движется перпендикулярно трассе. Это сбойная ситуация, при которой следует отключение привода и блокировка управляющего автомата. Нормальный ход работы автомата может быть восстановлен только “сбросом”.
5.4 Поскольку управляющий сигнал имеет три разряда, то для составления модели автомата Милли необходимо построить три таблицы переходов и выходов. Указанные таблицы, эквивалентные описательному алгоритму управления, приводятся ниже.
Таблица 5.3 – Таблицы переходов и выходов управляющего автомата
5.5 Как видно, состояния S0
, S1
, S2
явно эквивалентны, причём для каждого из выходов X. Представляется возможным эти эквивалентные состояния обозначить одним состоянием S0
– состояние управления тележкой. В этом случае, состояние блокировки S3
удобно переобозначить как S1
– состояние блокировки автомата. В результате получаем модель несократимого автомата Милли.
Таблица
5.4 – Таблицы переходов и выходов несократимого автомата
5.6 Учитывая, что код состояния полученной модели описывается одноразрядным сигналом S, а также учитывая кодировку входных сигналов Y (табл. 5.1), составим таблицу истинности комбинационной схемы автомата, непосредственно по таблице 5.4 и введя обозначения: S[j] — текущий сигнал состояния, S[j+1] — сигнал состояний на следующем такте автомата.
Судя по таблице 5.5, минимизации поддаётся только функция переходов 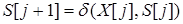 . Минимизируем её методом карт Карно (см. рис. 5.1). . Минимизируем её методом карт Карно (см. рис. 5.1).
Таблица
5.5 – Таблица истинности комбинационной схемы автомата
| S[j] |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
| Y0
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
| Y1
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
| S[j+1] |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
| X0
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| X1
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| X2
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
5.7 Теперь можно записать логические выражения для комбинационной схемы автомата.
Функция переходов:
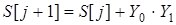 . (5.1) . (5.1)
Функции выходов в СДНФ по таблице истинности:
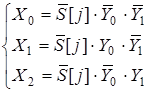 . (5.2) . (5.2)
Для удобства реализации комбинационной схемы представим рассматриваемые функции в базисе “ИЛИ-НЕ”:
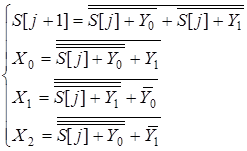 . (
5.3) . (
5.3)
5.8 На основе системы (5.3), окончательно получаем цифровую схему реализации управляющего автомата транспортной тележки, представленную на рисунке 5.2.
Особенностью полученной схемы является то, что она не содержит элементы памяти и задержки и, соответственно, не является тактируемой. Такой вариант реализации возможен для автоматов с двумя состояниями, одно из которых является абсолютно устойчивым. В нашем случае состояние блокировки есть абсолютно устойчивое состояние. Если комбинационная схема сформируем это состояние, то за счёт обратной связи по линии S запрещается реакция выходов X на изменение входных сигналов Y. Выход из этого устойчивого состояния возможен только принудительным обнулением линии S единичным уровнем на линии “Сброс”. Конфликтных “Состязаний” в рассматриваемом автомате не возникает.
Реклама


6 Решение дополнительного задания
6.1 Действующая на тележку в динамике система сил раскладывается на результирующую силу, приложенную к центру масс тележки 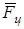 и вращающий момент и вращающий момент  , относительно того же центра масс. , относительно того же центра масс.
6.2 Как видно из рисунка
1.1 вращающий момент определяется только силой реакции опоры переднего колеса 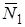 — —
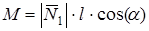 , (6.1) , (6.1)
где 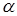 — угол поворота переднего колеса. — угол поворота переднего колеса.
Зная из рисунка, что
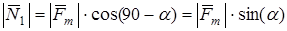 , (
6.2) , (
6.2)
получим:
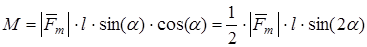 . (
6.3) . (
6.3)
Положительные значения вращающего момента соответствуют повороту тележки влево, отрицательные — вправо.
6.3 Результирующая сила, действующая на центр масс тележки, определяется векторной суммой всех сил на рисунке 1.1:
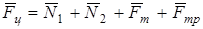 . (
6.4) . (
6.4)
Для нашего случая важно знать направление действия силы 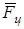 , которое зависит от направлений и величин составляющих рассматриваемой суммы. В свою очередь направления составляющих рассматриваются относительно положения габаритной определяющей, которое характеризуется единичным вектором: , которое зависит от направлений и величин составляющих рассматриваемой суммы. В свою очередь направления составляющих рассматриваются относительно положения габаритной определяющей, которое характеризуется единичным вектором:
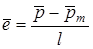 , (
6.5) , (
6.5)
где 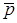 — вектор, задающий координаты центра масс тележки; — вектор, задающий координаты центра масс тележки;
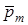 — вектор, задающий координаты точки приложения силы тяги — вектор, задающий координаты точки приложения силы тяги 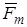 ; ;
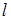 — габаритная определяющая транспортной тележки. — габаритная определяющая транспортной тележки.
6.4 Вектор 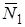 представляется в базисе вектора представляется в базисе вектора 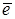 следующим образом: следующим образом:
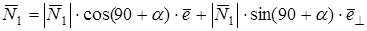 , (6.6) , (6.6)
где 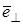 — единичный вектор, ортогональный вектору — единичный вектор, ортогональный вектору 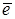 , ,
или
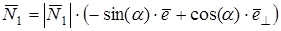 . (6.7) . (6.7)
Если 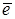 имеет координаты имеет координаты 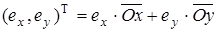 , то , то 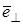 имеет координаты имеет координаты 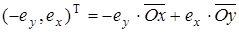 . Тогда вектор . Тогда вектор 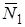 , выраженный в базисе Декартовой системы координат, имеет вид: , выраженный в базисе Декартовой системы координат, имеет вид:
 , (6.8) , (6.8)
где 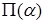 — матрица (оператор) поворота вектора — матрица (оператор) поворота вектора 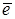 на угол на угол 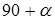 . .
Теперь, используя выражение (6.2), окончательно найдём, что
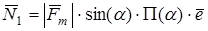 . (
6.9) . (
6.9)
6.5 Из рисунка 1.1 очевидным образом вытекают выражения для векторов силы тяги и приведённой силы трения, а именно:
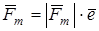 , (
6.10) , (
6.10)
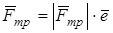 . (
6.11) . (
6.11)
6.6 Центростремительная реакция трассы 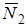 определяется произведением массы тележки и нормальной составляющей ускорения её центра масс, возникающей при закруглении траектории движения: определяется произведением массы тележки и нормальной составляющей ускорения её центра масс, возникающей при закруглении траектории движения:
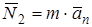 , (6.12) , (6.12)
где 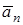 — центростремительное ускорение. — центростремительное ускорение.
Если траектория движения центра масс задаётся вектором 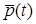 , то , то
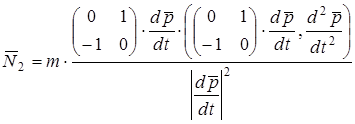 , (
6.13) , (
6.13)
где 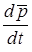 — вектор скорости центра масс; — вектор скорости центра масс;
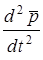 — вектор полного ускорения; — вектор полного ускорения;
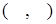 — оператор скалярного произведения векторов. — оператор скалярного произведения векторов.
Это физический факт. Вывод его опускаем.
6.7 Центр масс тележки смещается под действием результирующей силы 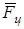 , при этом справедливо: , при этом справедливо:
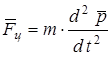 . (
6.14) . (
6.14)
6.8 Точка приложения силы тяги смещается под действием вращающего момента 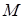 , за счёт которого ей придаётся угловое ускорение , за счёт которого ей придаётся угловое ускорение 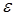 : :
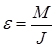 , (6.15) , (6.15)
где 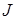 — момент инерции тележки относительно центра масс. — момент инерции тележки относительно центра масс.
Зная угловое ускорение можно найти тангенциальное 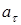 в скалярной форме: в скалярной форме:
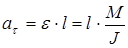 , ,
а затем и в векторной:
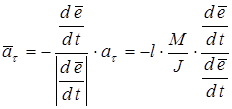 , (6.16) , (6.16)
где 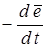 — векторная скорость изменения ориентации габаритной определяющей. — векторная скорость изменения ориентации габаритной определяющей.
С другой стороны, — вектор тангенциального ускорения может быть выражен через полное ускорение вектора 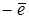 : :
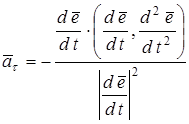 , (6.17) , (6.17)
где 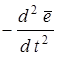 — вектор полного ускорения изменения ориентации габаритной определяющей; — вектор полного ускорения изменения ориентации габаритной определяющей;
В результате имеем связь:
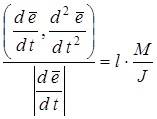 . (
6.18) . (
6.18)
6.9 Учитывая, что приведённая сила трения пропорциональна модулю скорости центра масс:
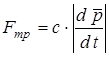 , (
6.19) , (
6.19)
где 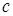 — коэффициент трения, — коэффициент трения,
на основании всех найденных зависимостей путём исключения неизвестных нетрудно получить систему дифференциальных уравнений, являющуюся моделью динамики транспортной тележки в векторной форме. Записать эту систему в одну строчку проблематично, поэтому ограничимся указанием того, что первое дифференциальное уравнение системы строится на основе выражений: (6.3), (6.4), (6.5), (6.9), (6.10), (6.11), (6.13), (6.14), (6.19), а второе на основе: (6.3), (6.5), (6.18). Решением первого уравнения является зависимость траектории центра масс тележки от времени, решением второго — ориентация во времени вектора 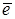 . .
Полученная система не имеет аналитического решения и поэтому должна решаться численно при любой зависимости от времени угла поворота 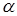 и четырёх начальных условиях типа: и четырёх начальных условиях типа:
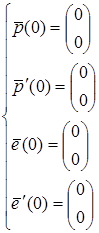 , (6.20) , (6.20)
которые показывают, что в нулевой момент времени центр масс тележки находится в начале координат, скорость тележки равна нулю (и поступательная и вращательная), тележка сориентирована вертикально по оси 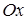 . .
Для более детального учёта свойств транспортной тележки в динамики выражения векторов реакций трассы должны быть заменены на выражения с условиями сравнений в соответствии с допущениями, сформулированными в задании контрольной работы.
|