| ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ЭММ и ПМ
КОНТРОЛЬНАЯ РАБОТА
Выполнил:
Проверил: Федосеев В.В.
г. Москва, 2001 г.
Задача 4.1
Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице (табл.1).
табл.1
| Тип сырья
|
Нормы расхода
|
Запасы
сырья
|
| А
|
Б
|
В
|
Г
|
| I
|
1
|
0
|
2
|
1
|
180
|
| II
|
0
|
1
|
3
|
2
|
210
|
| III
|
4
|
2
|
0
|
4
|
800
|
| Цена
изделия
|
9
|
6
|
4
|
7
|
|
При решении задачи на максимум общей себестоимости были получены следующие результаты:
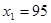 ; ; 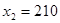 ; ; 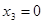 ; ; 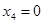 ; ;
Требуется:
1. Сформулировать прямую оптимизационную на максимум общей себестоимости, указать оптимальную производственную программу.
Пусть 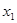 ; ;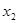 ; ;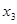 ; ;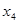 - объемы производства продукции каждого вида. - объемы производства продукции каждого вида.
Целевая функция: 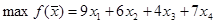
Функциональные ограничения:
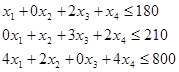
Прямые ограничения: 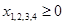
Оптимальная производственная программа заключается в выпуске 95 ед. первой продукции, 210 ед. второй продукции, 0 ед. третьей продукции и 0 ед. четвертой продукции.
Третий и четвертый вид продукции выпускать не выгодно, т.к. затраты превышают цену.
2. Сформулировать двойственную задачу и найти ее оптимальный план.
Пусть 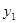 ; ;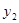 ; ;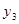 - двойственные оценки типов ресурсов соответственно. - двойственные оценки типов ресурсов соответственно.
Целевая функция: 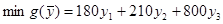
Функциональные ограничения:
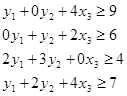
Прямые ограничения: 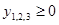
Найдем оптимальный план этой задачи, используя теорему двойственности:
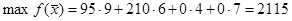
Прежде всего, проверим, является ли указанный в условии задачи план допустимым решением:
По ресурсу I: 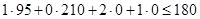
По ресурсу II: 
По ресурсу III: 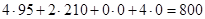
Следовательно, план оптимальный. Ресурс I остается в избытке, а ресурсы II и III расходуются полностью.
Воспользуемся соотношением второй теоремы двойственности:
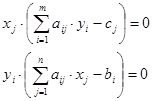
т.к. 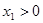 и и 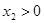 ,то ,то
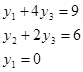 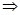 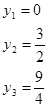
Вычислим значения целевой функции двойственной задачи:
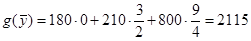 , ,
т.о. приведенный в условии план является оптимальным.
3. Проанализировать использование ресурсов в оптимальном плане.
Ресурс I является недефицитным (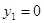 ). Ресурсы II и III являются дефицитными, причем ресурс III более дефицитный, чем ресурс II ( ). Ресурсы II и III являются дефицитными, причем ресурс III более дефицитный, чем ресурс II (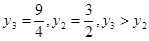 ). ).
Найдем норму заменяемости для дефицитных ресурсов:

Следовательно, ресурс III в 1,5 раза более эффективен, чем ресурс II с точки зрения влияния на максимум продукции.
4. Определить, как изменится общая стоимость продукции и план выпуска при увеличении запасов сырья II и III вида на 120 и 160 ед. соответственно и одновременном уменьшении запасов сырья I вида на 60 ед.
Реклама

Будем считать, что данные изменения объемов ресурсов находятся в пределах устойчивости оптимального решения (в пределах устойчивости двойственных оценок), тогда по третьей теореме двойственности имеем:
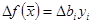
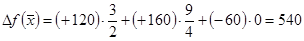
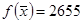
Запишем исходную и двойственную ЗЛП с измененными объемами ресурсов.
Исходная:
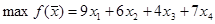
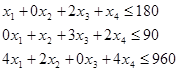
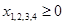
Двойственная:
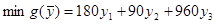
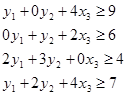
Воспользуемся соотношением второй теоремы двойственности:
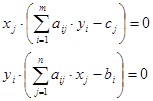 
Рассмотрим первые соотношения (их два):
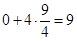
Следовательно, про 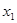 ничего сказать нельзя. ничего сказать нельзя.
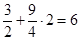
Следовательно, про 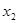 ничего сказать нельзя. ничего сказать нельзя.
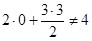 , , 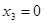 (затраты больше цены) (затраты больше цены)
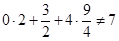 , , 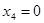 (затраты больше цены) (затраты больше цены)
Рассмотрим вторые соотношения:
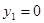 , ничего сказать нельзя , ничего сказать нельзя
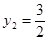 , второе ограничение обращается в равенство , второе ограничение обращается в равенство
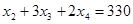
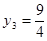 , третье ограничение обращается в равенство , третье ограничение обращается в равенство
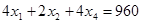
Запишем систему уравнений и решим ее:
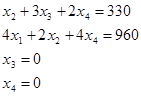 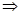 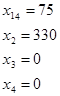
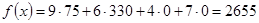
Это совпадает с выводом, сделанным ранее на основании теоремы об оценках.
5. Определить целесообразность включения в план изделия «Д» ценой 12 ед. на изготовление, которого расходуется по две единицы каждого вида сырья.
Это задание выполняется на основе третьего свойства двойственных оценок, т.е. оценки как определение эффективности.
Рассчитаем показатель эффективности для этой продукции:
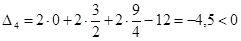
Следовательно, данную продукцию выпускать целесообразно (затраты меньше цены).
Задача 4.2
Решить транспортную задачу (табл.2). Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана.
табл.2
| Мощность
потребителя
|
25
|
10
|
20
|
30
|
15
|
|
|
Мощность поставщика
|
| 40
|
5
|
3
|
4
|
6
|
4
|
0
|
| 20
|
3
|
4
|
10
|
5
|
7
|
1
|
| 40
|
4
|
6
|
9
|
3
|
4
|
0
|
| 
|
4
|
2
|
4
|
3
|
4
|
|
Сформулируем ЭММ этой задачи:
Пусть 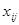 - объемы перевозок от - объемы перевозок от 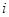 - того поставщика - того поставщика 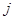 - тому потребителю. - тому потребителю.
Целевая функция:
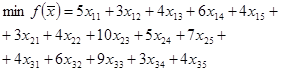
Проверим, выполняется ли условие баланса:
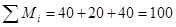
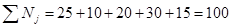
т.о. условие баланса выполнятся – транспортная задача закрытая.
Функциональные ограничения
по поставщикам:
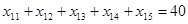
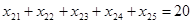
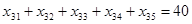
по потребителям:
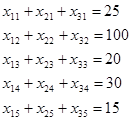
Оценим стоимость перевозки:
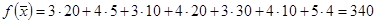
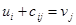 ; ; 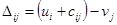
Ответ: оптимальный план перевозок представлен в табл.1. Стоимость перевозок по этому плану составляет 340 ден. ед. Оптимальный план является единственным.
Задача 5.
табл. 3
| |
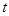
|
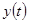
|
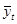
|
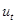
|
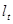
|
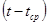
|
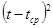
|
 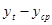
|
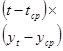
|
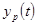
|
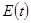
|
| 1
|
43
|
-
|
-
|
-
|
-4
|
16
|
-10,8
|
43,2
|
43,4
|
-0,4
|
| 2
|
47
|
46,7
|
1
|
0
|
-3
|
9
|
-6,8
|
20,4
|
46
|
1
|
| 3
|
50
|
48,3
|
1
|
0
|
-2
|
4
|
-3,8
|
7,6
|
48,6
|
1,4
|
| 4
|
48
|
50,7
|
0
|
0
|
-1
|
1
|
-5,8
|
5,8
|
51,2
|
-3,2
|
| 5
|
54
|
53
|
1
|
0
|
0
|
0
|
0,2
|
0
|
53,8
|
0,2
|
| 6
|
57
|
57,3
|
1
|
0
|
1
|
1
|
3,2
|
3,2
|
56,4
|
0,6
|
| 7
|
61
|
59
|
1
|
0
|
2
|
4
|
7,2
|
14,4
|
59
|
2
|
| 8
|
59
|
61,7
|
0
|
0
|
3
|
9
|
5,2
|
15,6
|
61,6
|
-2,6
|
| 9
|
65
|
-
|
1
|
0
|
4
|
16
|
11,2
|
44,8
|
64,2
|
0,8
|
| 
|
45
|
484
|
|
|
|
|
60
|
-0,2
|
155
|
|
|
1. m=3
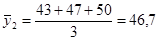 ; ; 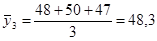 ; ; 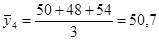
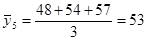 ; ; 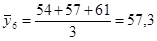 ; ; 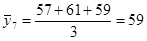
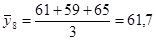
2. Для определения величины тренда воспользуемся методом Фостера-Стьюдента:
1 этап:
Формирование двух числовых последовательностей
Реклама

ì 1, если 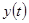 больше всех предыдущих значений больше всех предыдущих значений
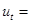 í í
î 0, если нет
ì 1, если 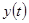 меньше всех предыдущих значений меньше всех предыдущих значений
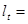 í í
î 0, если нет
2 этап:
Рассчитываются две величины:
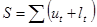 и и  , т.о. , т.о. 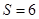 , а , а 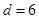
3 этап:
Затем рассчитываются два значения:
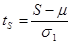 и и 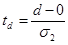 , при , при 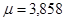 , , 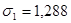 , , 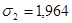
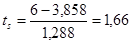 и и 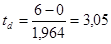
4 этап:
Сравним 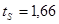 и и 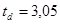 с табличными значениями критерия Стьюдента с табличными значениями критерия Стьюдента 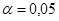 и и 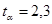 . .
т.к. 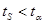 , а , а 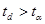 , то гипотеза об отсутствии тренда в среднем принимается, т.е. тренда в среднем нет, а гипотеза об отсутствии тренда в дисперсии отвергается, т.е. тренд есть. , то гипотеза об отсутствии тренда в среднем принимается, т.е. тренда в среднем нет, а гипотеза об отсутствии тренда в дисперсии отвергается, т.е. тренд есть.
3. Построить линейную модель 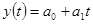 , параметры которой оценить МНК. , параметры которой оценить МНК.
Определим 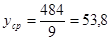 и и 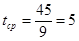
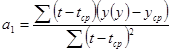 ; ; 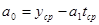
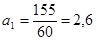 ; ; 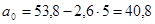
т.о. линейная модель имеет вид: 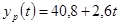
Последовательно подставляя в линейную модель вместо 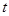 его значения от 1 до 9 получим расчетные значения уровня его значения от 1 до 9 получим расчетные значения уровня 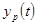 : :
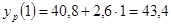 ; ; 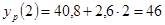
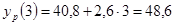 ; ; 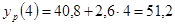
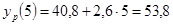 ; ; 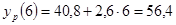
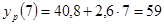 ; ; 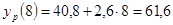
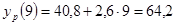
Вычислим отклонения расчетных значений от фактических:
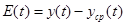 , ,
затем результаты запишем таблицу.
5. Оценить адекватность модели на основе исследования:
a) случайности остаточной компоненты по критерию пиков
| 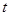
|
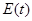
|
Поворотные
точки
|
| 1
|
-0,4
|
-
|
| 2
|
1
|
0
|
| 3
|
1,4
|
1
|
| 4
|
-3,2
|
0
|
| 5
|
0,2
|
0
|
| 6
|
0,6
|
0
|
| 7
|
2
|
1
|
| 8
|
-2,6
|
0
|
| 9
|
0,8
|
-
|
Общее число пиков p=2
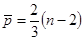 ; ; 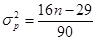 ; ; 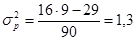
Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства 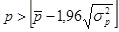 , т.о. имеем: , т.о. имеем:
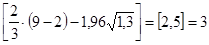 , ,
следовательно, свойство случайности не выполняется, трендовая модель является неадекватной.
б) независимости уровней ряда остатков по 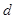 - критерию (в качестве критических используйте уровни - критерию (в качестве критических используйте уровни 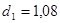 и и 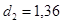 ) или по первому коэффициенту корреляции, критический уровень которого ) или по первому коэффициенту корреляции, критический уровень которого 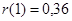 . .
Проверка независимости уровней остаточной последовательности осуществляется по формуле Дарбина-Уотсона:
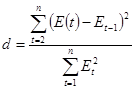 , имеем: , имеем: 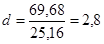
| |
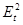
|
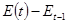
|
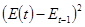
|
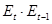
|
| 0,16
|
-
|
-
|
-
|
| 1
|
1,4
|
1,96
|
-0,4
|
| 1,96
|
0,4
|
0,16
|
1,4
|
| 10,24
|
-4,6
|
21,16
|
-4,48
|
| 0,04
|
3,4
|
11,56
|
-0,64
|
| 0,36
|
0,4
|
0,16
|
0,12
|
| 4
|
1,4
|
1,96
|
1,2
|
| 6,76
|
-4,6
|
21,16
|
-5,2
|
| 0,64
|
3,4
|
11,56
|
-2,08
|
| 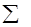
|
25,16
|
|
69,68
|
-10,08
|
т.к. 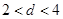 , то имеет место отрицательная связь, преобразуем значения , то имеет место отрицательная связь, преобразуем значения 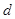 : :
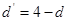 ; ; 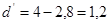 ; ; 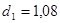 ; ; 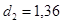
Сравним 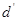 с с 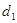 и и 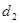 , Т.к. , Т.к. 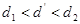 , то нет достаточных оснований сделать вывод об адекватности модели. , то нет достаточных оснований сделать вывод об адекватности модели.
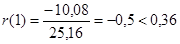
в) нормальности закона распределения остаточной последовательности по RS-критерию с критическими уровнями 2,7-3,7.
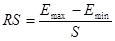 , где , где 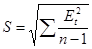 , т.о. имеем: , т.о. имеем:
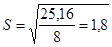 и и 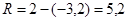
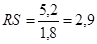
Расчетное значение RS-критерия равное 2,9 попадает внутрь [2,7-3,7], т.о. гипотеза о соответствии распределения остаточной компоненты нормальному закону распределения принимается.
г) Для оценки точности модели используйте среднее квадратическое отклонение и среднюю ошибку по модулю.
Т.к. модель неадекватна, то нет смысла говорить о ее точности.
6. Постройте точечный и интервальный прогнозы на два шага вперед.
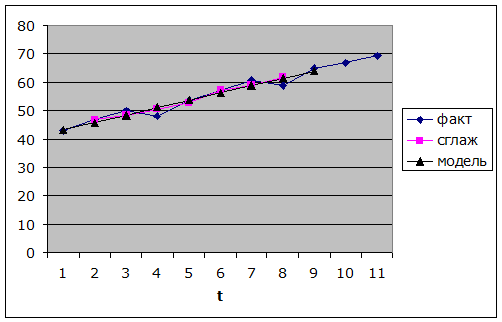
Точечный прогноз на K шагов вперед получается путем подстановки в модель 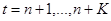 . При прогнозировании на два шага имеем: . При прогнозировании на два шага имеем:
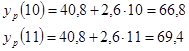
Доверительный интервал прогноза будет иметь следующие границы:
Верхняя: 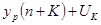
Нижняя: 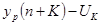
Величина 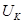 для линейной модели имеет вид: для линейной модели имеет вид:
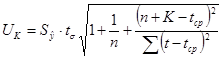 , где , где 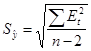 , т.о. имеем: , т.о. имеем:
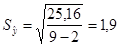
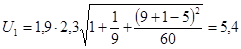 ; ; 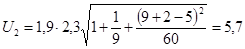
| 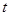
|
Шаг,
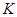
|
Прогноз,
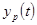
|
Нижняя
граница,
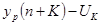
|
Верхняя
граница,
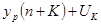
|
| 10
|
1
|
66,8
|
61,4
|
72,2
|
| 11
|
2
|
69,4
|
63,7
|
75,1
|
Тема 9.
Даны коэффициенты прямых поставок 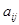 и конечный продукт и конечный продукт 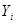 . Требуется: . Требуется:
1) Определить межотраслевые поставки продукции
2) Проверить продуктивность матрицы A
| Отрасли
|
Коэффициенты прямых поставок,
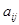
|
Конечный
продукт,
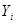
|
| 1
|
2
|
3
|
| 1
|
0,0
|
0,1
|
0,2
|
180
|
| 2
|
0,1
|
0,2
|
0,1
|
200
|
| 3
|
0,2
|
0,1
|
0,2
|
200
|
1) 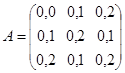 ; ; 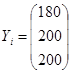
Найдем 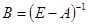 , где , где 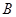 - матрица коэффициентов полных материальных затрат. - матрица коэффициентов полных материальных затрат.
2) 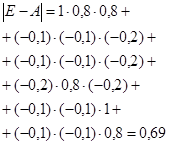
3) 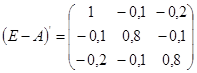
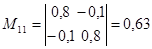 ; ; 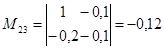
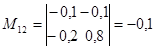 ; ; 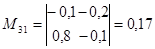
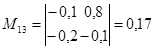 ; ; 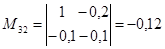
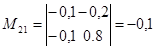 ; ; 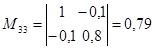
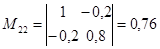
 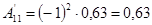 ; ; 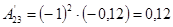
 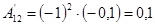 ; ; 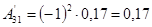
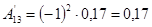 ; ; 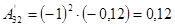
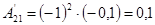 ; ; 
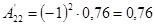 ; ;
т.о. 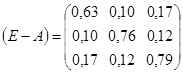
5) 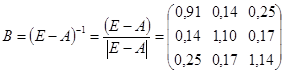
Диагональные элементы матрицы строго больше нуля.
Определим межотраслевые поставки:
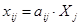 ; ; 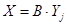
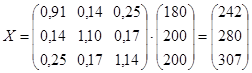
Находим матрицу межотраслевых поставок продукции:
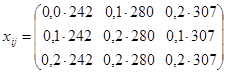 ; ; 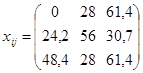
| |
1
|
2
|
3
|
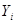
|
Валовой
продукт
|
| 1
|
0
|
28
|
61,4
|
180
|
242
|
| 2
|
24,2
|
56
|
30,7
|
200
|
280
|
| 3
|
48,4
|
28
|
61,4
|
200
|
307
|
| Условно
чистый продукт
|
266,2
|
336
|
337,7
|
580
|
|
| Шахматный
баланс
|
242
|
280
|
307
|
|
|
3) Матрица продуктивна, если норма матрицы (наибольшая сумма по столбцам)
Норма матрицы 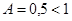 , т.о. матрица , т.о. матрица 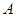 продуктивна. продуктивна.
|